State-Selective Differential Cross Sections for Single-Electron Capture in Slow He+–He Collisions
Abstract
1. Introduction
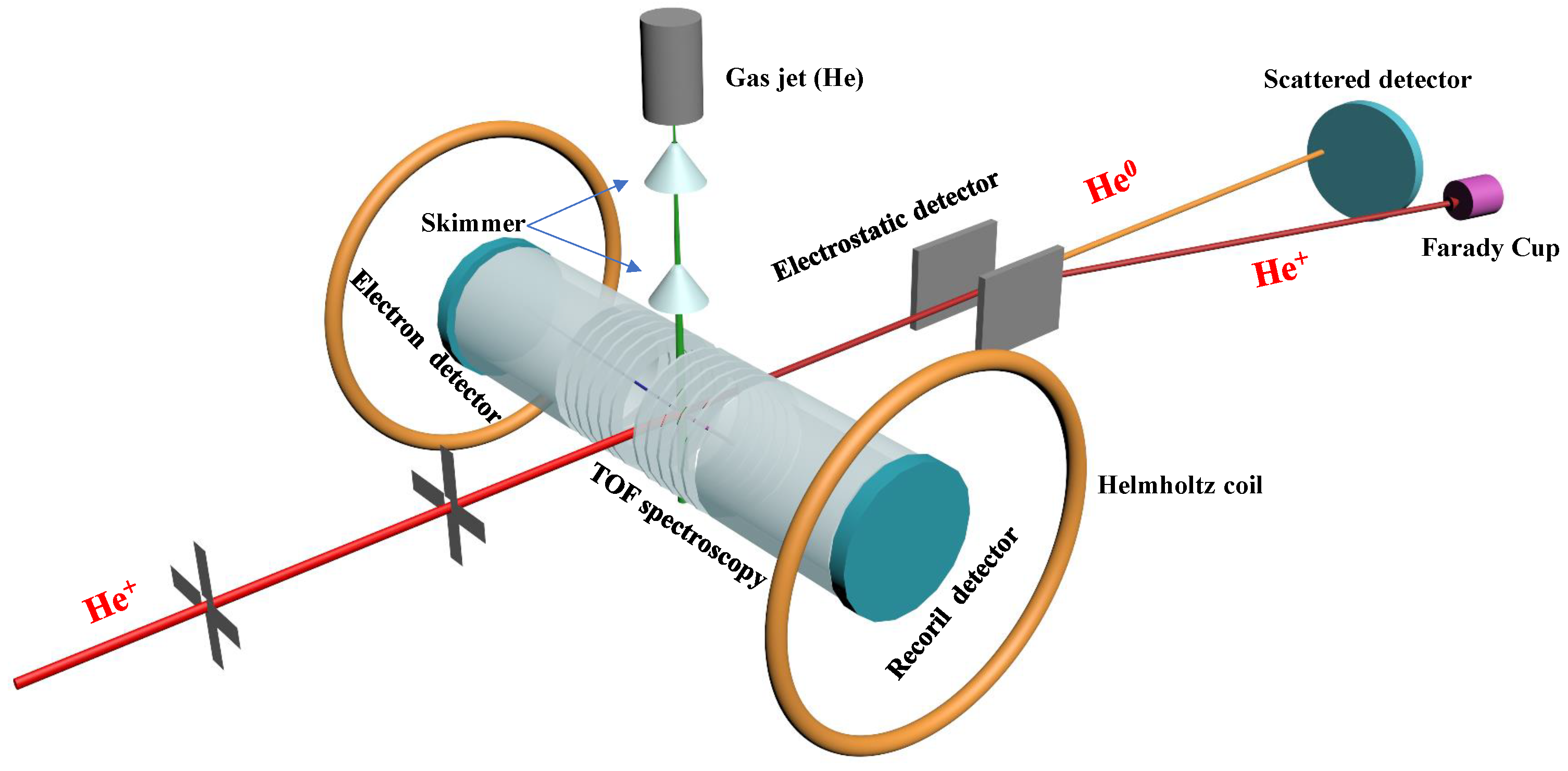
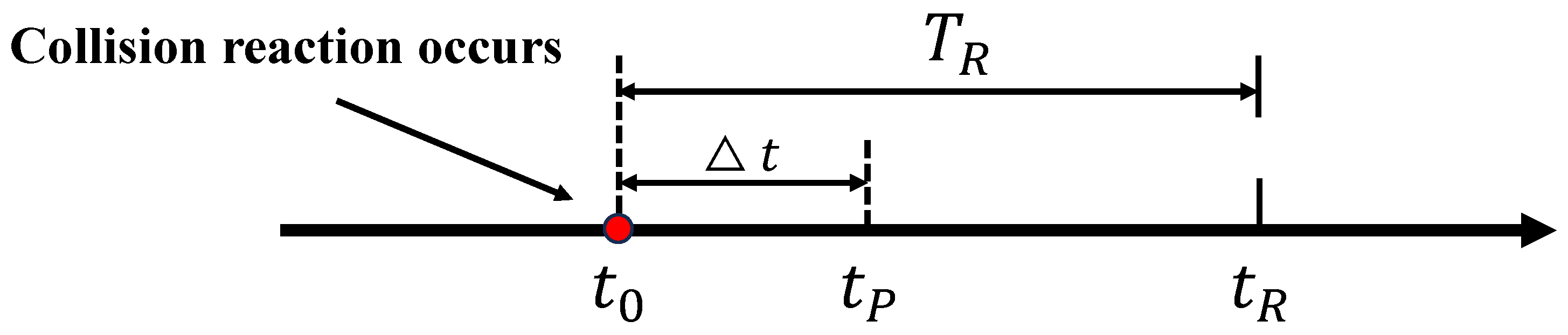
2. Experimental Setup
3. Results and Discussion
3.1. State-Selective Electron-Capture Process
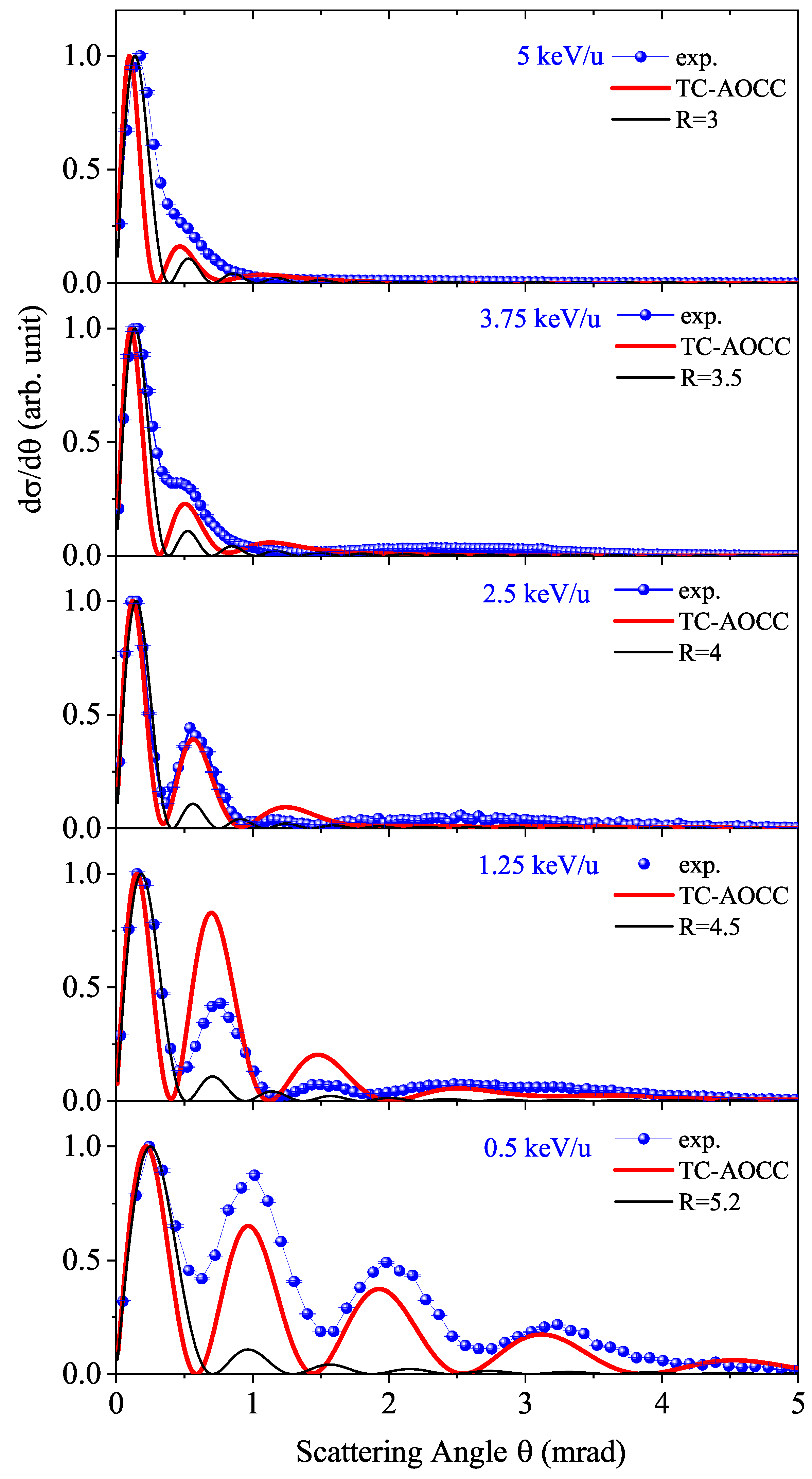
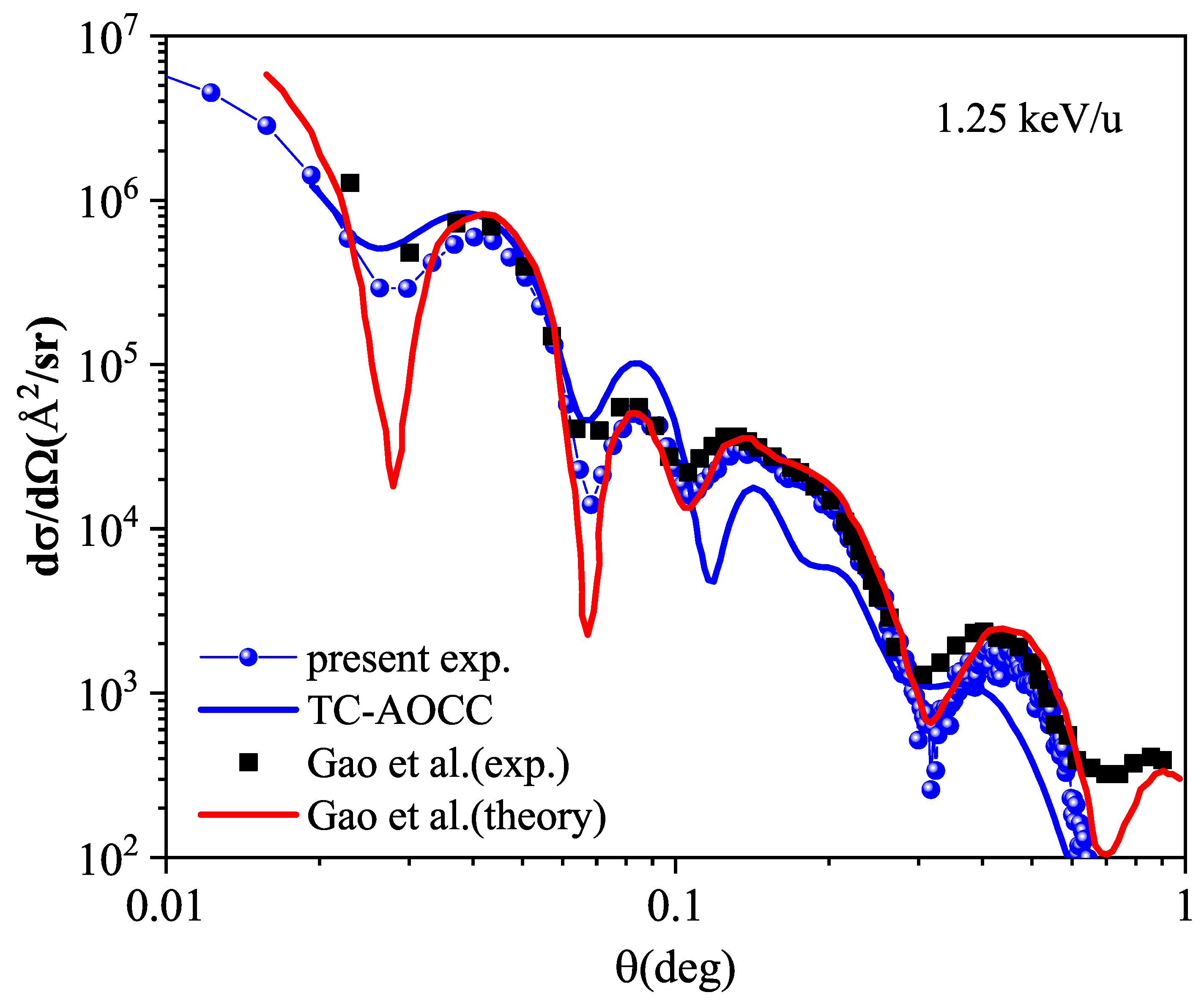
3.2. Angular Differential Cross Sections
4. Theoretical Method
4.1. Integrated Cross Sections
4.2. Differential Cross Sections
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lisse, C.M.; Dennerl, K.; Englhauser, J.; Harden, M.; Marshall, F.E.; Mumma, M.J.; Petre, R.; Pye, J.P.; Ricketts, M.J.; Schmitt, J.; et al. Discovery of X-ray and Extreme Ultraviolet Emission from Comet C/Hyakutake 1996 B2. Science 1996, 274, 205–209. [Google Scholar] [CrossRef]
- Cravens, T.E. Comet Hyakutake X-ray source: Charge transfer of solar wind heavy ions. Geophys. Res. Lett. 1997, 24, 105–108. [Google Scholar] [CrossRef]
- Cravens, T.E. X-ray Emission from Comets. Science 2002, 296, 1042–1045. [Google Scholar] [CrossRef] [PubMed]
- Krasnopolsky, V.A.; Mumma, M.J. Spectroscopy of Comet Hyakutake at 80–700 Å: First Detection of Solar Wind Charge Transfer Emissions. Astrophys. J. 2001, 549, 629. [Google Scholar] [CrossRef]
- Beiersdorfer, P.; Boyce, K.R.; Brown, G.V.; Chen, H.; Kahn, S.M.; Kelley, R.L.; May, M.; Olson, R.E.; Porter, F.S.; Stahle, C.K.; et al. Laboratory simulation of charge exchange-produced X-ray emission from comets. Science 2003, 300, 1558–1559. [Google Scholar] [CrossRef]
- Krasnopolsky, V.A.; Greenwood, J.B.; Stancil, P.C. X-ray and extreme ultraviolet emissions from comets. Space Sci. Rev. 2004, 113, 271–373. [Google Scholar] [CrossRef]
- Guo, D.L.; Ma, X.; Zhang, R.T.; Zhang, S.F.; Zhu, X.L.; Feng, W.T.; Gao, Y.; Hai, B.; Zhang, M.; Wang, H.B.; et al. State-selective electron capture in 30- and 100-keV He+ + He collisions. Phys. Rev. A 2017, 95, 012707. [Google Scholar] [CrossRef]
- Schöffler, M.S.; Titze, J.; Schmidt, L.P.H.; Jahnke, T.; Neumann, N.; Jagutzki, O.; Schmidt-Böcking, H.; Dörner, R.; Mančev, I. State-selective differential cross sections for single and double electron capture in He+,2+-He and p-He collisions. Phys. Rev. A 2009, 79, 064701. [Google Scholar] [CrossRef]
- Baxter, M.; Kirchner, T.; Engel, E. Time-dependent spin-density-functional-theory description of He+-He collisions. Phys. Rev. A 2017, 96, 032708. [Google Scholar] [CrossRef]
- Gao, J.W.; Wu, Y.; Wang, J.G.; Sisourat, N.; Dubois, A. State-selective electron transfer in He+ + He collisions at intermediate energies. Phys. Rev. A 2018, 97, 052709. [Google Scholar] [CrossRef]
- Mančev, I. Four-body continuum-distorted-wave model for charge exchange between hydrogenlike projectiles and atoms. Phys. Rev. A 2007, 75, 052716. [Google Scholar] [CrossRef]
- Isler, R.C. A Review of Charge-Exchange Spectroscopy and Applications to Fusion Plasmas. Phys. Scr. 1987, 35, 650. [Google Scholar] [CrossRef]
- Isler, R.C. An overview of charge-exchange spectroscopy as a plasma diagnostic. Plasma Phys. Control. Fusion 1994, 36, 171. [Google Scholar] [CrossRef]
- Sakabe, S.; Izawa, Y. Cross sections for resonant charge transfer between atoms and their positive ions: Collision velocity ≲ 1 a.u. At. Data Nucl. Data Tables 1991, 49, 257–314. [Google Scholar] [CrossRef]
- Atan, H.; Steckelmacher, W.; Lucas, M.W. Single electron loss and single electron capture for 0.6-2.2 MeV He+ colliding with rare gases. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2559. [Google Scholar] [CrossRef]
- Shevelko, V.P.; Kato, D.; Song, M.-Y.; Tawara, H.; Tolstikhina, I.Y.; Yoon, J.-S. One-electron capture and target-ionization in He+-neutral-atom collisions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2009, 267, 3395–3402. [Google Scholar] [CrossRef]
- Hegerberg, R.; Stefansson, T.; Elford, M.T. Measurement of the symmetric charge-exchange cross section in helium and argon in the impact energy range 1–10 keV. J. Phys. At. Mol. Phys. 1978, 11, 133. [Google Scholar] [CrossRef]
- DuBois, R.D. Multiple ionization in He+–rare-gas collisions. Phys. Rev. A 1989, 39, 4440–4450. [Google Scholar] [CrossRef]
- Ullrich, J.; Moshammer, R.; Dörner, R.; Jagutzki, O.; Mergel, V.; Schmidt-Böcking, H.; Spielberger, L. Recoil-ion momentum spectroscopy. J. Phys. At. Mol. Opt. Phys. 1997, 30, 2917. [Google Scholar] [CrossRef]
- Dörner, R.; Mergel, V.; Jagutzki, O.; Spielberger, L.; Ullrich, J.; Moshammer, R.; Schmidt-Böcking, H. Cold Target Recoil Ion Momentum Spectroscopy: A ‘momentum microscope’ to view atomic collision dynamics. Phys. Rep. 2000, 330, 95–192. [Google Scholar] [CrossRef]
- Sural, D.P.; Mukherjee, S.C.; Sil, N.C. Electron Capture and Excitation in He+-He Collisions. Phys. Rev. 1967, 164, 156–165. [Google Scholar] [CrossRef]
- Hildenbrand, R.; Grun, N.; Scheid, W. Coupled channel calculations with Cartesian Gaussian basis functions for H+He and He++He reactions. J. Phys. At. Mol. Opt. Phys. 1995, 28, 4781. [Google Scholar] [CrossRef]
- Zhao, G.P.; Liu, L.; Chang, Z.; Wang, J.G.; Janev, R.K. Total, state-selective and differential cross sections for single electron capture in He+–He collisions. J. Phys. At. Mol. Opt. Phys. 2018, 51, 085201. [Google Scholar] [CrossRef]
- Jana, D.; Purkait, K.; Haque, A.; Mondal, M.; Halder, S.; Purkait, M. State-selective differential and total cross sections for single-electron capture in He+-He collisions. Indian J. Phys. 2022, 96, 4071–4081. [Google Scholar] [CrossRef]
- Mergel, V.; Dörner, R.; Achler, M.; Khayyat, K.; Lencinas, S.; Euler, J.; Jagutzki, O.; Nüttgens, S.; Unverzagt, M.; Spielberger, L.; et al. Intra-atomic Electron-Electron Scattering in p-He Collisions (Thomas Process) Investigated by Cold Target Recoil Ion Momentum Spectroscopy. Phys. Rev. Lett. 1997, 79, 387–390. [Google Scholar] [CrossRef]
- Moshammer, R.; Ullrich, J.; Kollmus, H.; Schmitt, W.; Unverzagt, M.; Jagutzki, O.; Mergel, V.; Schmidt-Böcking, H.; Mann, R.; Wood, C.J.; et al. Double Ionization of Helium and Neon for Fast Heavy-Ion Impact: Correlated Motion of Electrons from Bound to Continuum States. Phys. Rev. Lett. 1996, 77, 1242–1245. [Google Scholar] [CrossRef]
- Zygelman, B.; Cooper, D.L.; Ford, M.J.; Dalgarno, A.; Gerratt, J.; Raimondi, M. Charge transfer of N4+ with atomic hydrogen. Phys. Rev. A 1992, 46, 3846–3854. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, R.T.; Zhang, S.F.; Zhu, X.L.; Feng, W.T.; Guo, D.L.; Li, B.; Liu, H.P.; Li, C.Y.; Wang, J.G.; et al. Electron emission from single-electron capture with simultaneous single-ionization reactions in 30-keV/u He2+-on-argon collisions. Phys. Rev. A 2011, 83, 052707. [Google Scholar] [CrossRef]
- Zhu, X.; Ma, X.; Li, J.; Schmidt, M.; Feng, W.; Peng, H.; Xu, J.; Zschornack, G.; Liu, H.; Zhang, T.; et al. A compact, flexible low energy experimental platform of highly charged ions for atomic physics experiments. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms 2019, 460, 224–229. [Google Scholar] [CrossRef]
- Lockwood, G.J.; Everhart, E. Resonant Electron Capture in Violent Proton-Hydrogen Atom Collisions. Phys. Rev. 1962, 125, 567–572. [Google Scholar] [CrossRef]
- van der Poel, M.; Nielsen, C.V.; Gearba, M.A.; Andersen, N. Fraunhofer Diffraction of Atomic Matter Waves: Electron Transfer Studies with a Laser Cooled Target. Phys. Rev. Lett. 2001, 87, 123201. [Google Scholar] [CrossRef]
- van der Poel, M.; Nielsen, C.V.; Rybaltover, M.; Nielsen, S.E.; Machholm, M.; Andersen, N. Atomic scattering in the diffraction limit: Electron transfer in keV Li+–Na(3s, 3p) collisions. J. Phys. At. Mol. Opt. Phys. 2002, 35, 4491. [Google Scholar] [CrossRef]
- Wang, Q.; Ma, X.; Zhu, X.L.; Zhang, S.F. Observation of atomic-size Fraunhofer-type diffraction for single electron capture in He2+ + He collision. J. Phys. At. Mol. Opt. Phys. 2011, 45, 025202. [Google Scholar] [CrossRef]
- Gao, R.S.; Johnson, L.K.; Schafer, D.A.; Newman, J.H.; Smith, K.A.; Stebbings, R.F. Absolute differential cross sections for small-angle He+-He elastic and charge-transfer scattering at keV energies. Phys. Rev. A 1988, 38, 2789–2793. [Google Scholar] [CrossRef] [PubMed]
- Horsdal, E.; Jensen, B.; Nielsen, K.O. Critical Angle in Electron Capture. Phys. Rev. Lett. 1986, 57, 1414–1416. [Google Scholar] [CrossRef]
- Knoop, S.; Olson, R.E.; Ott, H.; Hasan, V.G.; Morgenstern, R.; Hoekstra, R. Single ionization and electron capture in He2++Na collisions. J. Phys. At. Mol. Opt. Phys. 2005, 38, 1987. [Google Scholar] [CrossRef]
- Guo, D.L.; Ma, X.W.; Feng, W.T.; Zhang, S.F.; Zhu, X.L. Analysis of momentum and energy resolutions of the reaction microscope. Acta Phys. Sin. 2011, 60, 113401. [Google Scholar] [CrossRef]
- Fritsch, W.; Lin, C. The semiclassical close-coupling description of atomic collisions: Recent developments and results. Phys. Rep. 1991, 202, 1–97. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.G.; Janev, R.K. Dynamics of O8+ + H electron capture in Debye plasmas. Phys. Rev. A 2009, 79, 052702. [Google Scholar] [CrossRef]
- Kuang, J.; Lin, C.D. Convergent TCAO close-coupling calculations for electron transfer, excitation and ionization in intermediate keV collisions. J. Phys. At. Mol. Opt. Phys. 1997, 30, 101. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; NIST ASD Team. NIST Atomic Spectra Database; Version 5.12; NIST: Gaithersburg, MD, USA, 2024. Available online: https://www.nist.gov/pml/atomic-spectra-database (accessed on 18 August 2025).

| E (keV/u) | n = 1 | n ≥ 2 | ||
|---|---|---|---|---|
| Experiment | Theory | Experiment | Theory | |
| 0.5 | 100 | 99.27 | 0.73 | |
| 1.25 | 99.13 ± 0.66 | 98.62 | 0.87 ± 0.45 | 1.38 |
| 2.5 | 97.75 ± 0.51 | 97.71 | 2.25 ± 0.33 | 2.29 |
| 3.75 | 97.32 ± 0.68 | 96.87 | 2.68 ± 0.43 | 3.13 |
| 5 | 96.89 ± 0.42 | 96.19 | 3.11 ± 0.27 | 3.81 |
| State | Present | NIST |
|---|---|---|
| 1s2 | −0.90349 | −0.90395 |
| 1s2s | −0.15735 | −0.16797 |
| 1s2p | −0.12749 | −0.13087 |
| 1s3s | −0.06428 | −0.06686 |
| 1s3p | −0.05638 | −0.05736 |
| 1s3d | −0.05557 | −0.05565 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, S.; Lin, K.; Xing, D.; Liu, L.; Zhao, D.; Guo, D.; Gao, Y.; Zhang, S.; Wu, Y.; Dong, C.; et al. State-Selective Differential Cross Sections for Single-Electron Capture in Slow He+–He Collisions. Atoms 2025, 13, 74. https://doi.org/10.3390/atoms13090074
Cui S, Lin K, Xing D, Liu L, Zhao D, Guo D, Gao Y, Zhang S, Wu Y, Dong C, et al. State-Selective Differential Cross Sections for Single-Electron Capture in Slow He+–He Collisions. Atoms. 2025; 13(9):74. https://doi.org/10.3390/atoms13090074
Chicago/Turabian StyleCui, Shucheng, Kaizhao Lin, Dadi Xing, Ling Liu, Dongmei Zhao, Dalong Guo, Yong Gao, Shaofeng Zhang, Yong Wu, Chenzhong Dong, and et al. 2025. "State-Selective Differential Cross Sections for Single-Electron Capture in Slow He+–He Collisions" Atoms 13, no. 9: 74. https://doi.org/10.3390/atoms13090074
APA StyleCui, S., Lin, K., Xing, D., Liu, L., Zhao, D., Guo, D., Gao, Y., Zhang, S., Wu, Y., Dong, C., Zhu, X., & Ma, X. (2025). State-Selective Differential Cross Sections for Single-Electron Capture in Slow He+–He Collisions. Atoms, 13(9), 74. https://doi.org/10.3390/atoms13090074






