Thermal–Condensate Collisional Effects on Atomic Josephson Junction Dynamics
Abstract
1. Introduction
2. Methods
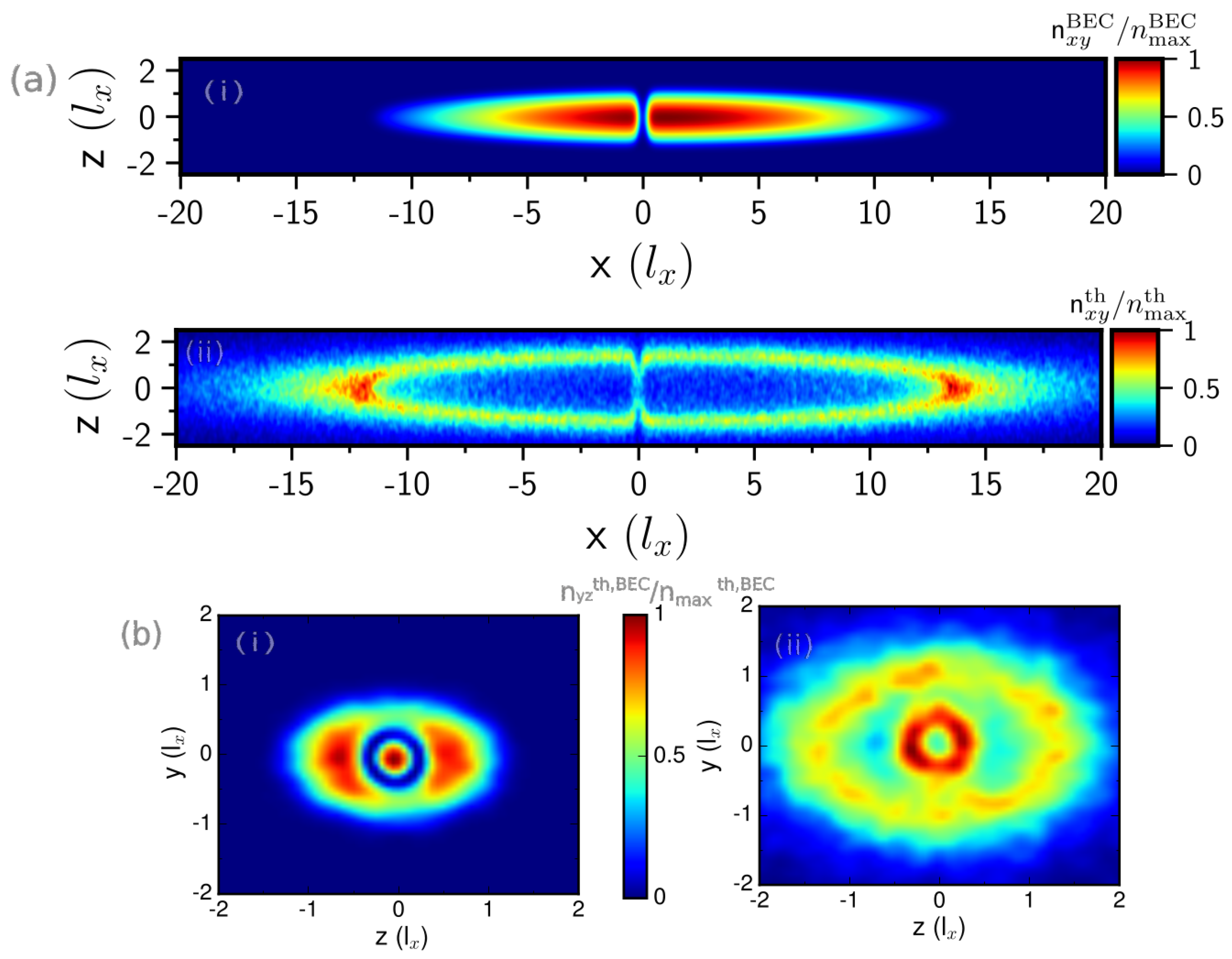
3. Results
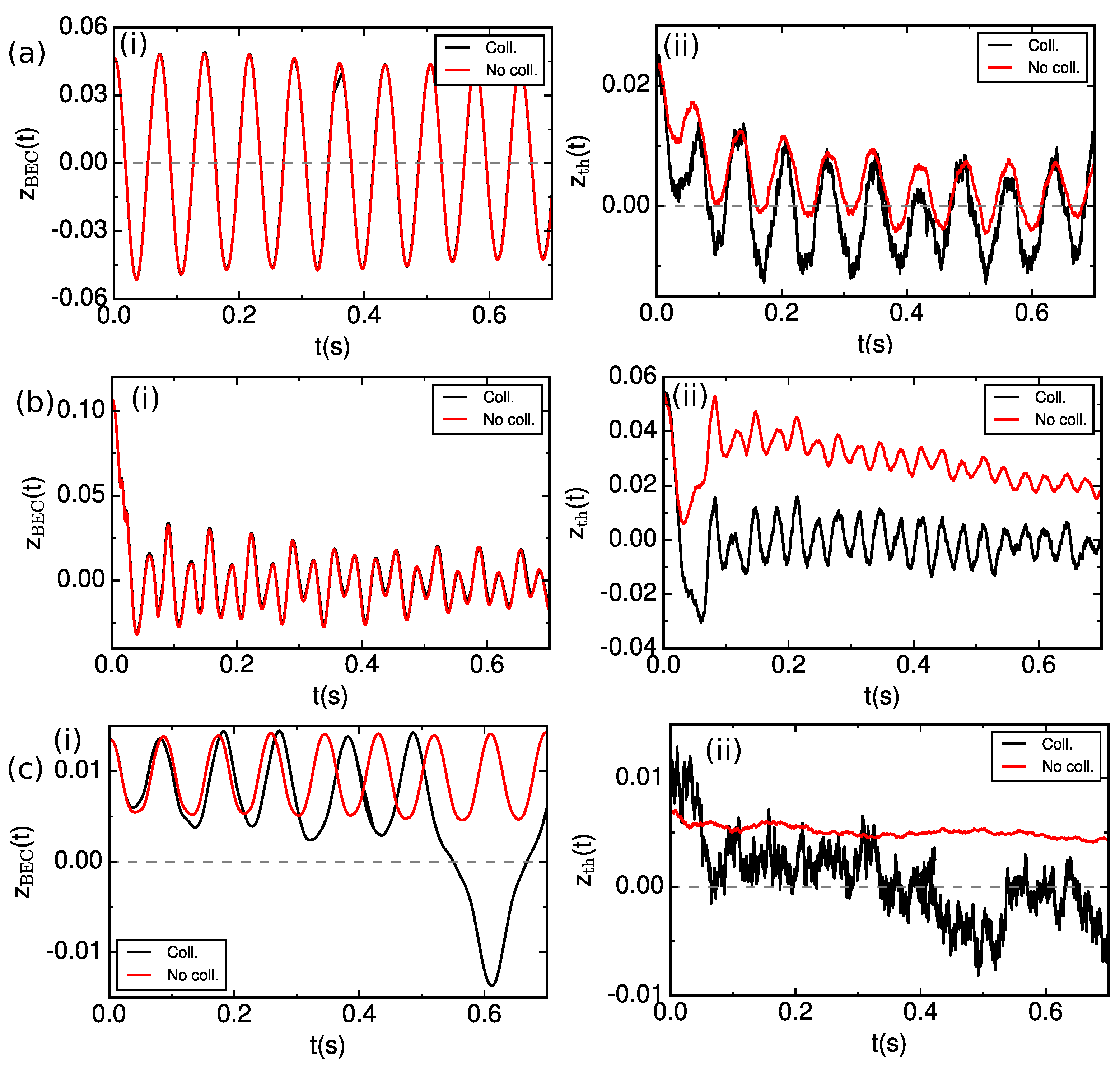
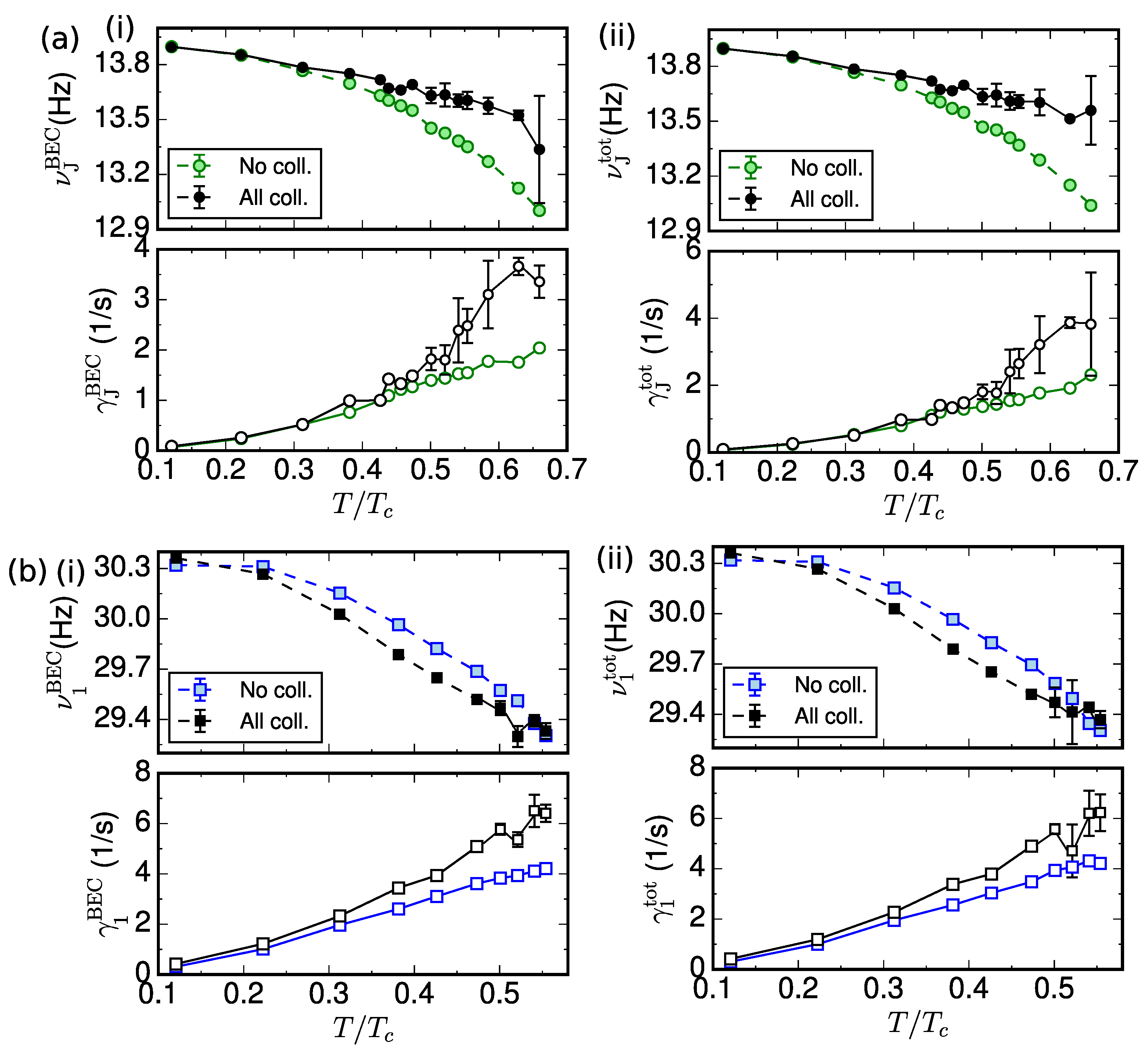
3.1. Effect of Collisions on the Frequency and Damping of Dominant Modes in the Josephson Plasma and Vortex-Induced Dissipative Regimes
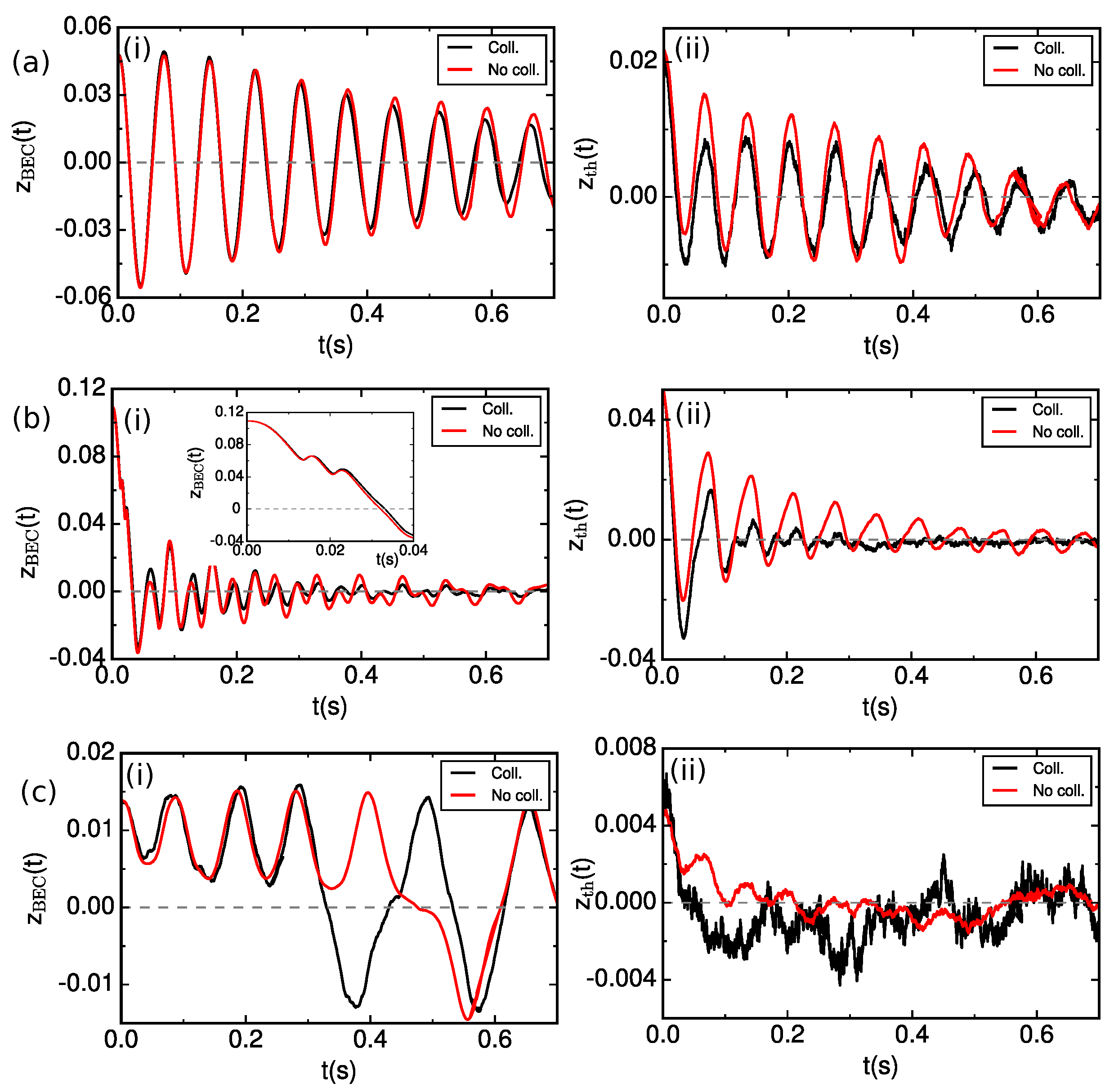
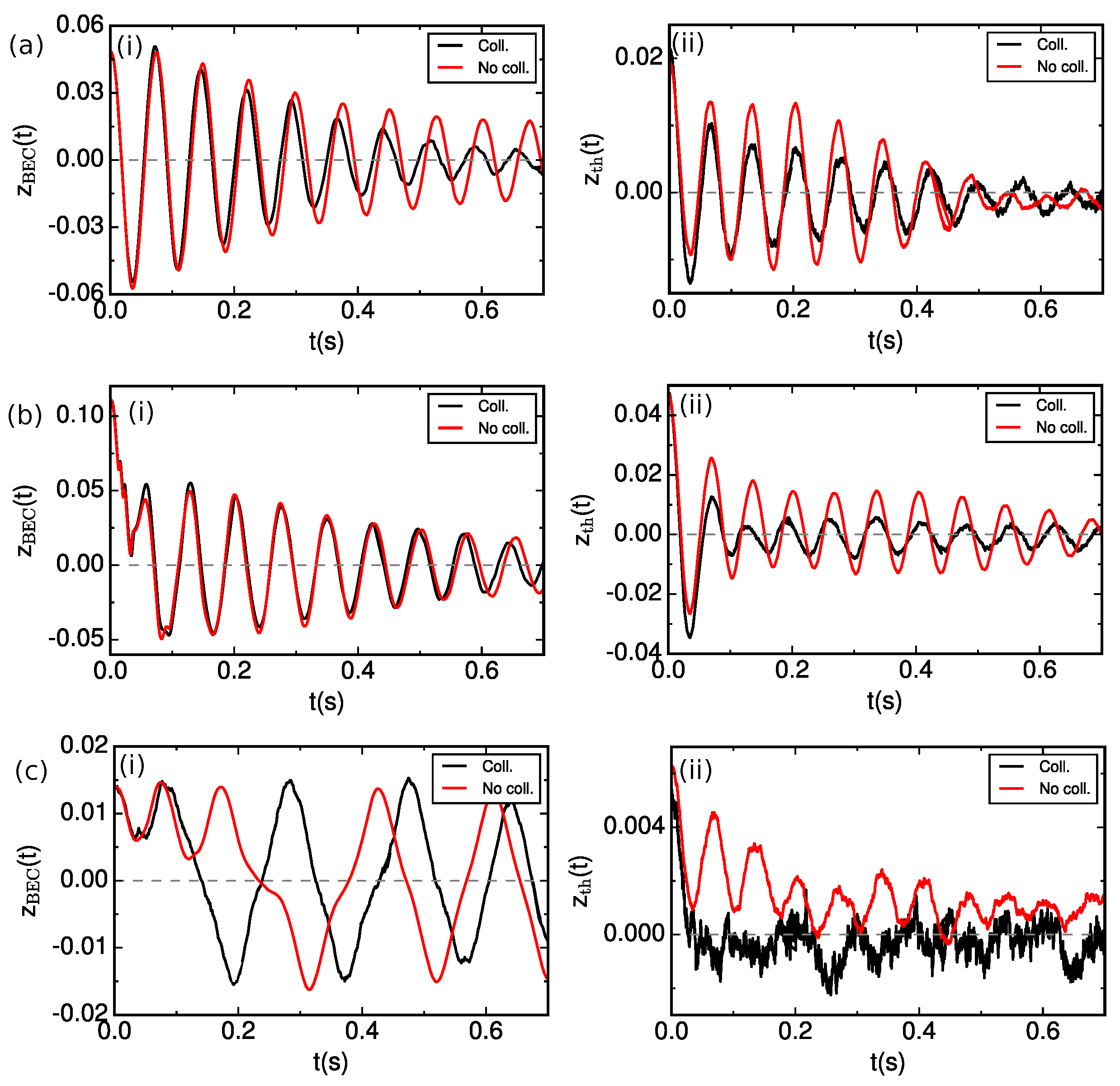
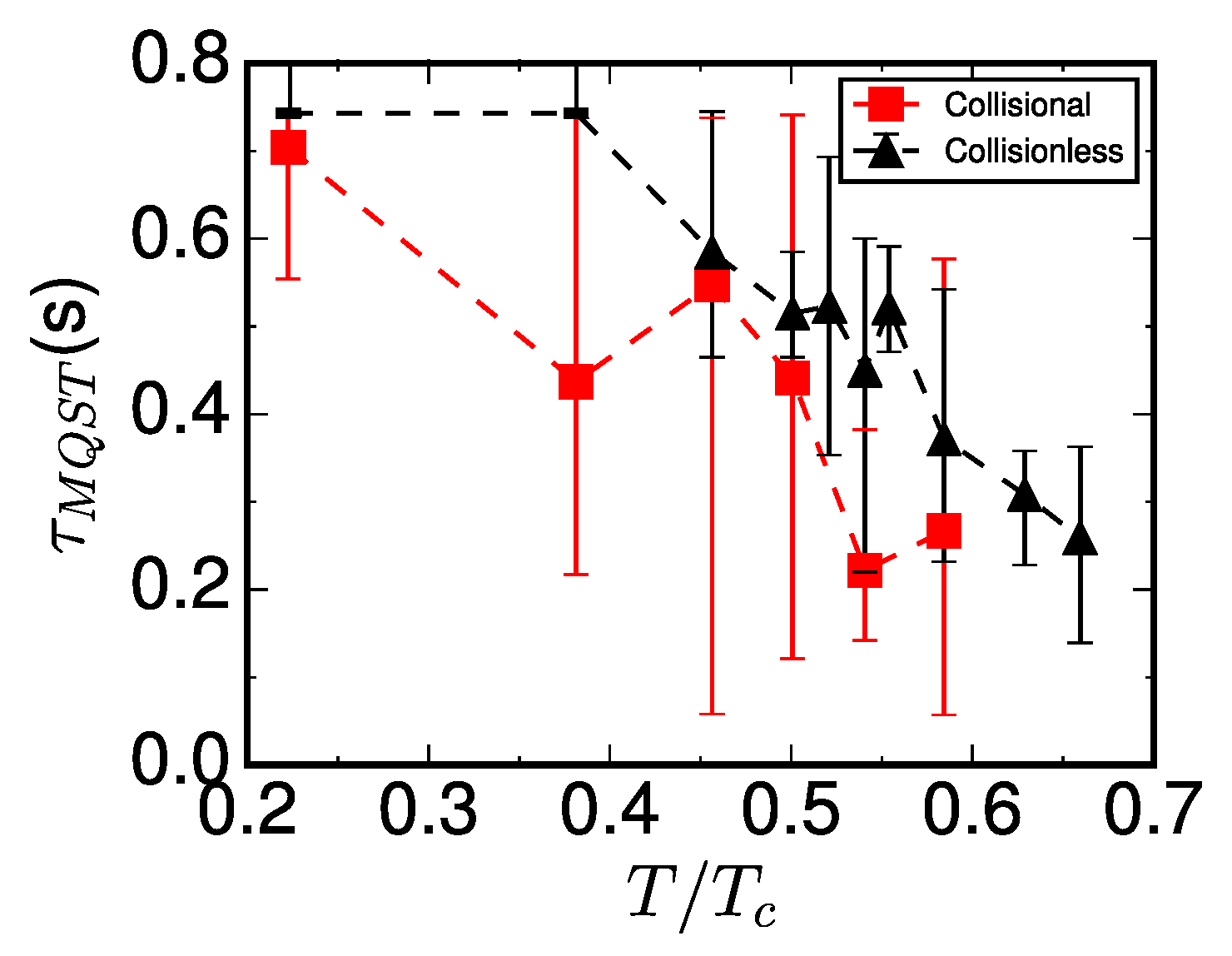
3.2. Role of Collisions on the Macroscopic Quantum Self-Trapping
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEC | Bose–Einstein condensate |
| GPE | Gross–Pitaevskii equation |
| ZNG | Zaremba–Nikuni–Griffin |
| JP | Josephson Plasma |
| VID | Vortex-Induced Dissipation |
| MQST | Macroscopic Quantum Self-Trapping |
References
- Avenel, O.; Varoquaux, E. Josephson effect and quantum phase slippage in superfluids. Phys. Rev. Lett. 1988, 60, 416–419. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.C.; Packard, R.E. Superfluid 3He Josephson weak links. Rev. Mod. Phys. 2002, 74, 741–773. [Google Scholar] [CrossRef]
- Sato, Y.; Hoskinson, E.; Packard, R. Josephson Effects in Superfluid Helium. In Fundamentals and Frontiers of the Josephson Effect; Tafuri, F., Ed.; Springer: Cham, Switzerland, 2019; Volume 286. [Google Scholar]
- Hoskinson, E.; Sato, Y.; Hahn, I.; Packard, R.E. Transition from phase slips to the Josephson effect in a superfluid 4He weak link. Nat. Phys. 2006, 2, 23–26. [Google Scholar] [CrossRef]
- Anderson, B.P.; Kasevich, M. Macroscopic quantum interference from atomic tunnel arrays. Science 1998, 282, 1686. [Google Scholar] [CrossRef]
- Cataliotti, F.S.; Burger, S.; Fort, C.; Maddaloni, P.; Minardi, F.; Trombettoni, A.; Smerzi, A.; Inguscio, M. Josephson Junction Arrays with Bose-Einstein Condensates. Science 2001, 293, 843–846. [Google Scholar] [CrossRef]
- Albiez, M.; Gati, R.; Fölling, J.; Hunsmann, S.; Cristiani, M.; Oberthaler, M.K. Direct Observation of Tunneling and Nonlinear Self-Trapping in a Single Bosonic Josephson Junction. Phys. Rev. Lett. 2005, 95, 010402. [Google Scholar] [CrossRef]
- Anker, T.; Albiez, M.; Gati, R.; Hunsmann, S.; Eiermann, B.; Trombettoni, A.; Oberthaler, M.K. Nonlinear Self-Trapping of Matter Waves in Periodic Potentials. Phys. Rev. Lett. 2005, 94, 020403. [Google Scholar] [CrossRef]
- Schumm, T.; Hofferberth, S.; Andersson, L.M.; Wildermuth, S.; Groth, S.; Bar-Joseph, I.; Schmiedmayer, J.; Krüger, P. Matter-wave interferometry in a double well on an atom chip. Nat. Phys. 2005, 1, 57–62. [Google Scholar] [CrossRef]
- Shin, Y.; Saba, M.; Pasquini, T.A.; Ketterle, W.; Pritchard, D.E.; Leanhardt, A.E. Atom Interferometry with Bose-Einstein Condensates in a Double-Well Potential. Phys. Rev. Lett. 2004, 92, 050405. [Google Scholar] [CrossRef]
- Levy, S.; Lahoud, E.; Shomroni, I.; Steinhauer, J. The a.c. and d.c. Josephson effects in a Bose–Einstein condensate. Nature 2007, 449, 579–583. [Google Scholar] [CrossRef]
- Spagnolli, G.; Semeghini, G.; Masi, L.; Ferioli, G.; Trenkwalder, A.; Coop, S.; Landini, M.; Pezzè, L.; Modugno, G.; Inguscio, M.; et al. Crossing Over from Attractive to Repulsive Interactions in a Tunneling Bosonic Josephson Junction. Phys. Rev. Lett. 2017, 118, 230403. [Google Scholar] [CrossRef]
- LeBlanc, L.J.; Bardon, A.B.; McKeever, J.; Extavour, M.H.T.; Jervis, D.; Thywissen, J.H.; Piazza, F.; Smerzi, A. Dynamics of a Tunable Superfluid Junction. Phys. Rev. Lett. 2011, 106, 025302. [Google Scholar] [CrossRef] [PubMed]
- Valtolina, G.; Burchianti, A.; Amico, A.; Neri, E.; Xhani, K.; Seman, J.A.; Trombettoni, A.; Smerzi, A.; Zaccanti, M.; Inguscio, M.; et al. Josephson effect in fermionic superfluids across the BEC-BCS crossover. Science 2015, 350, 1505–1508. [Google Scholar] [CrossRef] [PubMed]
- Burchianti, A.; Scazza, F.; Amico, A.; Valtolina, G.; Seman, J.A.; Fort, C.; Zaccanti, M.; Inguscio, M.; Roati, G. Connecting Dissipation and Phase Slips in a Josephson Junction between Fermionic Superfluids. Phys. Rev. Lett. 2018, 120, 025302. [Google Scholar] [CrossRef]
- Kwon, W.J.; Del Pace, G.; Panza, R.; Inguscio, M.; Zwerger, W.; Zaccanti, M.; Scazza, F.; Roati, G. Strongly correlated superfluid order parameters from dc Josephson supercurrents. Science 2020, 369, 84–88. [Google Scholar] [CrossRef]
- Luick, N.; Sobirey, L.; Bohlen, M.; Singh, V.P.; Mathey, L.; Lompe, T.; Moritz, H. An ideal Josephson junction in an ultracold two-dimensional Fermi gas. Science 2020, 369, 89–91. [Google Scholar] [CrossRef]
- Del Pace, G.; Kwon, W.J.; Zaccanti, M.; Roati, G.; Scazza, F. Tunneling Transport of Unitary Fermions across the Superfluid Transition. Phys. Rev. Lett. 2021, 126, 055301. [Google Scholar] [CrossRef]
- Josephson, B.D. Possible new effects in superconductive tunnelling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Anderson, P.W.; Rowell, J.M. Probable Observation of the Josephson Superconducting Tunneling Effect. Phys. Rev. Lett. 1963, 10, 230–232. [Google Scholar] [CrossRef]
- Barone, A.; Paterno, G. Physics and Applications of the Josephson Effect; John Wiley: New York, NY, USA, 1982. [Google Scholar]
- Milburn, G.J.; Corney, J.; Wright, E.M.; Walls, D.F. Quantum dynamics of an atomic Bose-Einstein condensate in a double-well potential. Phys. Rev. A 1997, 55, 4318–4324. [Google Scholar] [CrossRef]
- Smerzi, A.; Fantoni, S.; Giovanazzi, S.; Shenoy, S.R. Quantum Coherent Atomic Tunneling between Two Trapped Bose-Einstein Condensates. Phys. Rev. Lett. 1997, 79, 4950–4953. [Google Scholar] [CrossRef]
- Zapata, I.; Sols, F.; Leggett, A.J. Josephson effect between trapped Bose-Einstein condensates. Phys. Rev. A 1998, 57, R28–R31. [Google Scholar] [CrossRef]
- Raghavan, S.; Smerzi, A.; Fantoni, S.; Shenoy, S.R. Coherent oscillations between two weakly coupled Bose-Einstein condensates: Josephson effects, π oscillations, and macroscopic quantum self-trapping. Phys. Rev. A 1999, 59, 620–633. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Walls, D.F. Bose-Einstein condensate in a double-well potential as an open quantum system. Phys. Rev. A 1998, 58, R50–R53. [Google Scholar] [CrossRef]
- Meier, F.; Zwerger, W. Josephson tunneling between weakly interacting Bose-Einstein condensates. Phys. Rev. A 2001, 64, 033610. [Google Scholar] [CrossRef]
- Paraoanu, G.S.; Kohler, S.; Sols, F.; Leggett, A.J. The Josephson plasmon as a Bogoliubov quasiparticle. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 4689–4696. [Google Scholar] [CrossRef]
- Kohler, S.; Sols, F. Chemical potential standard for atomic Bose–Einstein condensates. New J. Phys. 2003, 5, 94. [Google Scholar] [CrossRef]
- Sakellari, E.; Leadbeater, M.; Kylstra, N.J.; Adams, C.S. Josephson spectroscopy of a dilute Bose-Einstein condensate in a double-well potential. Phys. Rev. A 2002, 66, 033612. [Google Scholar] [CrossRef]
- Sakellari, E.; Proukakis, N.P.; Leadbeater, M.; Adams, C.S. Josephson tunnelling of a phase-imprinted Bose–Einstein condensate in a time-dependent double-well potential. New J. Phys. 2004, 6, 42. [Google Scholar] [CrossRef]
- Zou, P.; Dalfovo, F. Josephson oscillations and self-trapping of superfluid fermions in a double-well potential. J. Low Temp. Phys. 2014, 177, 240. [Google Scholar] [CrossRef]
- Abad, M.; Guilleumas, M.; Mayol, R.; Piazza, F.; Jezek, D.M.; Smerzi, A. Phase slips and vortex dynamics in Josephson oscillations between Bose-Einstein condensates. EPL 2015, 109, 40005. [Google Scholar] [CrossRef]
- Bidasyuk, Y.M.; Weyrauch, M.; Momme, M.; Prikhodko, O.O. Finite-temperature dynamics of a bosonic Josephson junction. J. Phys. B 2018, 51, 205301. [Google Scholar] [CrossRef]
- Polo, J.; Ahufinger, V.; Hekking, F.W.J.; Minguzzi, A. Damping of Josephson Oscillations in Strongly Correlated One-Dimensional Atomic Gases. Phys. Rev. Lett. 2018, 121, 090404. [Google Scholar] [CrossRef] [PubMed]
- Polo, J.; Dubessy, R.; Pedri, P.; Perrin, H.; Minguzzi, A. Oscillations and Decay of Superfluid Currents in a One-Dimensional Bose Gas on a Ring. Phys. Rev. Lett. 2019, 123, 195301. [Google Scholar] [CrossRef]
- Xhani, K.; Neri, E.; Galantucci, L.; Scazza, F.; Burchianti, A.; Lee, K.L.; Barenghi, C.F.; Trombettoni, A.; Inguscio, M.; Zaccanti, M.; et al. Critical Transport and Vortex Dynamics in a Thin Atomic Josephson Junction. Phys. Rev. Lett. 2020, 124, 045301. [Google Scholar] [CrossRef]
- Xhani, K.; Galantucci, L.; Barenghi, C.F.; Roati, G.; Trombettoni, A.; Proukakis, N.P. Dynamical phase diagram of ultracold Josephson junctions. New J. Phys. 2020, 22, 123006. [Google Scholar] [CrossRef]
- Xhani, K.; Proukakis, N.P. Dissipation in a finite-temperature atomic Josephson junction. Phys. Rev. Res. 2022, 4, 033205. [Google Scholar] [CrossRef]
- Wlazłowski, G.; Xhani, K.; Tylutki, M.; Proukakis, N.P.; Magierski, P. Dissipation Mechanisms in Fermionic Josephson Junction. Phys. Rev. Lett. 2023, 130, 023003. [Google Scholar] [CrossRef]
- Furutani, K.; Tempere, J.; Salasnich, L. Quantum effective action for the bosonic Josephson junction. Phys. Rev. B 2022, 105, 134510. [Google Scholar] [CrossRef]
- Bardin, A.; Lorenzi, F.; Salasnich, L. Quantum fluctuations in atomic Josephson junctions: The role of dimensionality. New J. Phys. 2024, 26, 013021. [Google Scholar] [CrossRef]
- Ji, S.C.; Schweigler, T.; Tajik, M.; Cataldini, F.; Sabino, J.a.; Møller, F.S.; Erne, S.; Schmiedmayer, J. Floquet Engineering a Bosonic Josephson Junction. Phys. Rev. Lett. 2022, 129, 080402. [Google Scholar] [CrossRef]
- Pace, G.D.; Hernández-Rajkov, D.; Singh, V.P.; Grani, N.; Fernández, M.F.; Nesti, G.; Seman, J.A.; Inguscio, M.; Amico, L.; Roati, G. Shapiro steps in strongly-interacting Fermi gases. arXiv 2024, arXiv:2409.03448. [Google Scholar]
- Bernhart, E.; Röhrle, M.; Singh, V.P.; Mathey, L.; Amico, L.; Ott, H. Observation of Shapiro steps in an ultracold atomic Josephson junction. arXiv 2024, arXiv:2409.03340. [Google Scholar]
- Singh, V.P.; Luick, N.; Sobirey, L.; Mathey, L. Josephson junction dynamics in a two-dimensional ultracold Bose gas. Phys. Rev. Res. 2020, 2, 033298. [Google Scholar] [CrossRef]
- Zaccanti, M.; Zwerger, W. Critical Josephson current in BCS-BEC–crossover superfluids. Phys. Rev. A 2019, 100, 063601. [Google Scholar] [CrossRef]
- Piselli, V.; Pisani, L.; Strinati, G.C. Josephson current flowing through a nontrivial geometry: Role of pairing fluctuations across the BCS-BEC crossover. Phys. Rev. B 2023, 108, 214504. [Google Scholar] [CrossRef]
- Gauthier, G.; Szigeti, S.S.; Reeves, M.T.; Baker, M.; Bell, T.A.; Rubinsztein-Dunlop, H.; Davis, M.J.; Neely, T.W. An atomtronic oscillator circuit for quantum gases. arXiv 2019, arXiv:1903.04086. [Google Scholar]
- Pigneur, M.; Berrada, T.; Bonneau, M.; Schumm, T.; Demler, E.; Schmiedmayer, J. Relaxation to a Phase-Locked Equilibrium State in a One-Dimensional Bosonic Josephson Junction. Phys. Rev. Lett. 2018, 120, 173601. [Google Scholar] [CrossRef]
- Furutani, K.; Salasnich, L. Interaction-induced dissipative quantum phase transition in a head-to-tail atomic Josephson junction. Phys. Rev. B 2024, 110, L140503. [Google Scholar] [CrossRef]
- Saha, A.K.; Dubessy, R. Dynamical phase diagram of a one-dimensional Bose gas in a box with a tunable weak link: From Bose-Josephson oscillations to shock waves. Phys. Rev. A 2021, 104, 023316. [Google Scholar] [CrossRef]
- Momme, M.R.; Bidasyuk, Y.M.; Weyrauch, M. Collective excitations and tunneling dynamics in long bosonic Josephson junctions. Phys. Rev. A 2019, 100, 033601. [Google Scholar] [CrossRef]
- Labouvie, R.; Santra, B.; Heun, S.; Wimberger, S.; Ott, H. Negative Differential Conductivity in an Interacting Quantum Gas. Phys. Rev. Lett. 2015, 115, 050601. [Google Scholar] [CrossRef]
- Begg, S.E.; Davis, M.J.; Reeves, M.T. Nonequilibrium Transport in a Superfluid Josephson Junction Chain: Is There Negative Differential Conductivity? Phys. Rev. Lett. 2024, 132, 103402. [Google Scholar] [CrossRef] [PubMed]
- Saha, A.K.; Ray, D.S.; Deb, B. Phase diffusion and fluctuations in a dissipative Bose-Josephson junction. Phys. Rev. E 2023, 107, 034141. [Google Scholar] [CrossRef] [PubMed]
- Lagoudakis, K.G.; Pietka, B.; Wouters, M.; André, R.; Deveaud-Plédran, B. Coherent Oscillations in an Exciton-Polariton Josephson Junction. Phys. Rev. Lett. 2010, 105, 120403. [Google Scholar] [CrossRef]
- Adiyatullin, A.F.; Anderson, M.D.; Flayac, H.; Portella-Oberli, M.T.; Jabeen, F.; Ouellet-Plamondon, C.; Sallen, G.C.; Deveaud, B. Periodic squeezing in a polariton Josephson junction. Nat. Commun. 2017, 8, 1329. [Google Scholar] [CrossRef] [PubMed]
- D’Errico, C.; Abbate, S.S.; Modugno, G. Quantum transport in ultracold atoms. Philos. Trans. Royal Soc. A 2017, 375, 20160425. [Google Scholar]
- Wright, K.C.; Blakestad, R.B.; Lobb, C.J.; Phillips, W.D.; Campbell, G.K. Driving Phase Slips in a Superfluid Atom Circuit with a Rotating Weak Link. Phys. Rev. Lett. 2013, 110, 025302. [Google Scholar] [CrossRef]
- Griffin, A.; Nikuni, T.; Zaremba, E. Bose-Condensed Gases at Finite Temperatures; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Jackson, B.; Zaremba, E. Modeling Bose-Einstein condensed gases at finite temperatures with N-body simulations. Phys. Rev. A 2002, 66, 033606. [Google Scholar] [CrossRef]
- Proukakis, N.P.; Jackson, B. Finite-temperature models of Bose–Einstein condensation. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 203002. [Google Scholar] [CrossRef]
- Lee, K.L.; Proukakis, N.P. Non-equilibrium atomic condensates and mixtures: Collective modes, condensate growth and thermalisation. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 214003. [Google Scholar] [CrossRef]
- Lee, K.L.; Jørgensen, N.B.; Liu, I.K.; Wacker, L.; Arlt, J.J.; Proukakis, N.P. Phase separation and dynamics of two-component Bose-Einstein condensates. Phys. Rev. A 2016, 94, 013602. [Google Scholar] [CrossRef]
- Blakie, P.B.; Bradley, A.S.; Davis, M.J.; Ballagh, R.J.; Gardiner, C.W. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques. Adv. Phys. 2008, 57, 363–455. [Google Scholar] [CrossRef]
- Proukakis, N.; Gardiner, S.; Davis, M.; Szymańska, M. (Eds.) Quantum Gases: Finite Temperature and Non-Equilibrium Dynamics; Imperial College Press: London, UK, 2013. [Google Scholar]
- Rooney, S.J.; Allen, A.J.; Zülicke, U.; Proukakis, N.P.; Bradley, A.S. Reservoir interactions of a vortex in a trapped three-dimensional Bose-Einstein condensate. Phys. Rev. A 2016, 93, 063603. [Google Scholar] [CrossRef]
- Proukakis, N.P.; Rigopoulos, G.; Soto, A. Self-Consistent Stochastic Finite-Temperature Modelling: Ultracold Bose Gases with Local (s-wave) and Long-Range (Dipolar) Interactions. arXiv 2024, arXiv:2407.20178. [Google Scholar]
- Jackson, B.; Proukakis, N.P.; Barenghi, C.F.; Zaremba, E. Finite-temperature vortex dynamics in Bose-Einstein condensates. Phys. Rev. A 2009, 79, 053615. [Google Scholar] [CrossRef]
- Jackson, B.; Proukakis, N.P.; Barenghi, C.F. Dark-soliton dynamics in Bose-Einstein condensates at finite temperature. Phys. Rev. A 2007, 75, 051601. [Google Scholar] [CrossRef]
- Allen, A.J.; Zaremba, E.; Barenghi, C.F.; Proukakis, N.P. Observable vortex properties in finite-temperature Bose gases. Phys. Rev. A 2013, 87, 013630. [Google Scholar] [CrossRef]
- Allen, A.J.; Zuccher, S.; Caliari, M.; Proukakis, N.P.; Parker, N.G.; Barenghi, C.F. Vortex reconnections in atomic condensates at finite temperature. Phys. Rev. A 2014, 90, 013601. [Google Scholar] [CrossRef]
- Arahata, E.; Nikuni, T. Propagation of first and second sound in a highly elongated trapped Bose-condensed gas at finite temperatures. Phys. Rev. A 2013, 87, 033610. [Google Scholar] [CrossRef]
- Märkle, J.; Allen, A.J.; Federsel, P.; Jetter, B.; Günther, A.; Fortágh, J.; Proukakis, N.P.; Judd, T.E. Evaporative cooling of cold atoms at surfaces. Phys. Rev. A 2014, 90, 023614. [Google Scholar] [CrossRef]
- Jackson, B.; Zaremba, E. Quadrupole Collective Modes in Trapped Finite-Temperature Bose-Einstein Condensates. Phys. Rev. Lett. 2002, 88, 180402. [Google Scholar] [CrossRef]
- Jackson, B.; Zaremba, E. Finite-Temperature Simulations of the Scissors Mode in Bose-Einstein Condensed Gases. Phys. Rev. Lett. 2001, 87, 100404. [Google Scholar] [CrossRef]
- Straatsma, C.J.E.; Colussi, V.E.; Davis, M.J.; Lobser, D.S.; Holland, M.J.; Anderson, D.Z.; Lewandowski, H.J.; Cornell, E.A. Collapse and revival of the monopole mode of a degenerate Bose gas in an isotropic harmonic trap. Phys. Rev. A 2016, 94, 043640. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xhani, K.; Proukakis, N.P. Thermal–Condensate Collisional Effects on Atomic Josephson Junction Dynamics. Atoms 2025, 13, 68. https://doi.org/10.3390/atoms13080068
Xhani K, Proukakis NP. Thermal–Condensate Collisional Effects on Atomic Josephson Junction Dynamics. Atoms. 2025; 13(8):68. https://doi.org/10.3390/atoms13080068
Chicago/Turabian StyleXhani, Klejdja, and Nick P. Proukakis. 2025. "Thermal–Condensate Collisional Effects on Atomic Josephson Junction Dynamics" Atoms 13, no. 8: 68. https://doi.org/10.3390/atoms13080068
APA StyleXhani, K., & Proukakis, N. P. (2025). Thermal–Condensate Collisional Effects on Atomic Josephson Junction Dynamics. Atoms, 13(8), 68. https://doi.org/10.3390/atoms13080068





