Collision Kinematics for Fast Positron Impact Ionization of Argon

Abstract

Classical trajectory Monte Carlo calculations for 1 keV positron impact ionization of argon are presented. A combination of energy-weighted triple differential cross-sections is shown to provide good to excellent agreement compared with experimental data, depending on the ejected electron azimuthal angular acceptance range used to define in-plane scattering. For ejected electron energies less than 100 eV, information about the influence of pre- (the impact parameter) and post-(the direction of scattering) collision kinematics on the triple differential level is obtained. An overall picture of these kinematic properties is also presented for single differential cross-sections as a function of ejected electron energy and ejection angle.

1. Introduction

Since the advent of atomic physics a century ago, countless experimental and theoretical studies have been performed. In the earliest studies, the emphasis was on discovering the dominant processes and their overall probabilities. As more sophisticated studies became possible, detailed information on differential electron emission in ionizing collisions emerged. Differential studies provide much more insight into interactions, such as the amount of scattering and direction of electron emission, how much energy is transferred from the projectile to the target, et cetera. Reference [1] provides an excellent overview and detailed information about such studies. With the advent of differential electron emission studies, our theoretical understanding of the structure of atoms and molecules and interaction processes has increased immensely.

The next great advance took place in the 1970s when Ehrhardt and coworkers performed the first triply differential studies (see ref. [2] for example). Triply differential studies provide the most sensitive tests of theoretical collision models because the collisional kinematics are fully defined. Additional sensitivity can be achieved by comparing results for both positron and electron impact, where, for high-energy collisions, the only physical difference is a reversal in direction of various interparticle electric fields. The first triply differential studies for positron impact were performed in the late 1990s and early 2000s [3,4]. However, positron-based studies are extremely difficult to investigate experimentally because of the low beam intensities and hence, the extremely low signal rates, especially in triply differential measurements. This led to a study using recoil ion techniques [5]. In spite of the advantages of the recoil ion technique, no follow-up measurements have appeared.

On the theoretical side, numerous theoretical approaches have been used to model triply differential electron emission by positrons and electrons. These theoretical approaches for modeling collisional processes fall into two categories. The most common approaches are quantal approaches, such as distorted wave Born (DWBA) [6,7,8,9,10,11,12,13,14,15,16,17,18,19], continuum distorted wave (CDW) [20,21,22,23,24,25,26,27,28], or close coupling (CC) [29,30,31,32,33,34,35,36] type models. Other examples of various methods can be found in references [5,37,38,39,40] and references therein. In general, these methods show rather good agreement with experimental data for binary interactions, i.e., interactions consisting of a binary collision between the incoming projectile and a target electron with all the other target components acting as non-participating observers. However, often the description of recoil interactions, i.e., interactions where a target electron is ejected but is “turned around” by the combined electric fields of the other target components, is poor, in particular with regard to intensity. To improve agreement, various modifications of the models have been used.

The other approach is a classical method, e.g., the classical trajectory Monte Carlo method (CTMC), which is used here. In this approach, classical trajectories for the projectile and ejected electron are calculated where all two-body electric forces between the various components are included. By stepwise integrations as a function of time, energies, and angles are determined at a large distance from the target. This is conducted for a large number of randomly selected incoming trajectories, with quantal information being included by randomly selecting the initial target electron positions from a microcanonical distribution. Compared to the quantal methods, the CTMC method has several advantages. One is that post-collision interaction information is inherently present, rather than being included as a modification of a quantal output. Other advantages are that all, rather than just selected, scattering and emission angles and energies are determined, and that the output file contains event-by-event information. Thus, the output files can be sorted in various ways. Thus, correlated projectile-ejected electron behavior can be investigated as a function of specific parameters as opposed to quantal calculations, where only the overall sum of such events is available.

A downside of a classical approach is that tracking a large number of particles is computationally intensive. Therefore, a simplified model must be used for many-electron projectiles or targets. For example, in the present study of 3p ionization of argon by fast positrons, a two-body target model consisting of a single 3p electron and a central potential is used for the argon target. Thus, any pre- or post-collision effects introduced by other bound electrons are modified. However, our CTMC approach and two-body target model have already been shown to provide very good agreement on the absolute scale with experimentally measured singly and doubly differential cross-sections [41,42].

Recently, our CTMC method and model were used to investigate pre- and post-collision kinematics for fast positron and electron impact ionization of argon [43]. In that work, the focus was on how the impact parameter and direction of projectile scattering influence the fully differential ionization spectra, information that is totally unavailable in existing quantal methods. It was shown that, in addition to the “normal” direction of scattering from a repulsive atomic structure, as predicted by Born, there is a “reverse scattering” component and that the “normal” and “reverse” components are associated with different impact parameter regions. Of importance with respect to triply differential ionization studies (TDCS) is that the direction of scattering was shown to influence the relative intensity and shapes of the binary and recoil lobes.

Our previous study was also performed for 1 keV positron and electron impact using a wider range of energy transfers, e.g., 2–250 eV, but at a scattering angle of 10°. Thus, in our previous study, the momenta transfers were approximately 1 a.u. Here, we extend our investigation of positron impact to a smaller scattering angle of 3°, where the momentum transfer is approximately 1/3 a.u. A further incentive for this smaller angle is that experimental data are available for comparison [44].

2. The Classical Trajectory Monte Carlo Method

The classical trajectory Monte Carlo (CTMC) method is a well-established approach for describing atomic collisions and calculating cross-sections. In recent decades, CTMC calculations have been applied to atomic collisions involving three or more particles [45,46,47,48,49,50,51,52,53,54,55,56]. This approximation is particularly useful for atomic collisions where quantum mechanical approaches become complex or unfeasible, typically in cases requiring higher-order perturbations or involving multiple particles.

One advantage of the CTMC method is that it accurately accounts for many-body interactions during collisions at a classical level. The CTMC method is nonperturbative, as it numerically solves classical equations of motion [53,54,55,56]. In the present work, CTMC simulations were conducted using a three-body approximation, where the many-electron argon atom is simplified to a one-electron atom [55,56]. A detailed summary of the calculation procedure is available in [41]. Here, we provide a brief description of the model used. In our model, the three particles (target nucleus, target electron, and projectile) are characterized by their masses and charges. A central model potential developed by Green [57], which incorporates Z (the nuclear charge), N (the total number of electrons in the target), and r (the distance between the nucleus and the target electron Q), is expressed as:

$$V\left(r\right)=Q{\displaystyle \frac{\mathit{Z}-\left(\mathit{N}-\mathbf{1}\right)\left(1-{\mathit{\Omega }}^{-1}\left(\mathit{r}\right)\right)}{\mathit{r}}}=Q{\displaystyle \frac{\mathit{Z}\left(\mathit{r}\right)}{\mathit{r}}}, \mathrm{where} \Omega \left(r\right)={\displaystyle \frac{\eta }{\xi }}\left(e^{r\xi }-1\right)+1$$

(1)

The potential parameters ξ and η are such that they minimize the energy for a given atom or ion. Garvey et al. [58] obtained the following parameters for Ar: η = 3.50 and ξ = 0.957 (in atomic units, a.u.). We note that this type of potential has further advantages, because it has a correct asymptotic form for both small (Equation (2)) and large (Equation (3)) values of r.

$$\underset{r\to 0}{\lim }Z(r)=Z$$

(2)

$$\underset{r\to \infty }{\lim }Z(r)=Z-(N-1)$$

(3)

The Lagrange equation for the three particles can be written as:

$$L=L_K-L_V,$$

(4)

where

$$L_K={\displaystyle \frac{1}{2}}{m}_P{\dot{\overrightarrow{r}}}_P^2+{\displaystyle \frac{1}{2}}{m}_e{\dot{\overrightarrow{r}}}_e^2+{\displaystyle \frac{1}{2}}{m}_T{\dot{\overrightarrow{r}}}_T^2,$$

(5)

and

$$L_V={\displaystyle \frac{Z_P{Z}_e}{\left|{\overrightarrow{r}}_P-{\overrightarrow{r}}_e\right|}}+{\displaystyle \frac{Z_P{Z}_T(\left|{\overrightarrow{r}}_P-{\overrightarrow{r}}_T\right|)}{\left|{\overrightarrow{r}}_P-{\overrightarrow{r}}_T\right|}}+{\displaystyle \frac{Z_e{Z}_T(\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|)}{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}}.$$

(6)

$\overrightarrow{r}$, Z and m are the position vector, the charge, and the mass of the noted particle, i.e., P: projectile, T: target core, e: target electron, respectively. The equations of motion can be calculated as:

$${\displaystyle \frac{d}{dt}}{\displaystyle \frac{\partial L}{\partial {\dot{q}}_i}}={\displaystyle \frac{\partial L}{\partial q_i}}, (\mathrm{i}=\mathrm{P}, \mathrm{e}, \mathrm{T}).$$

(7)

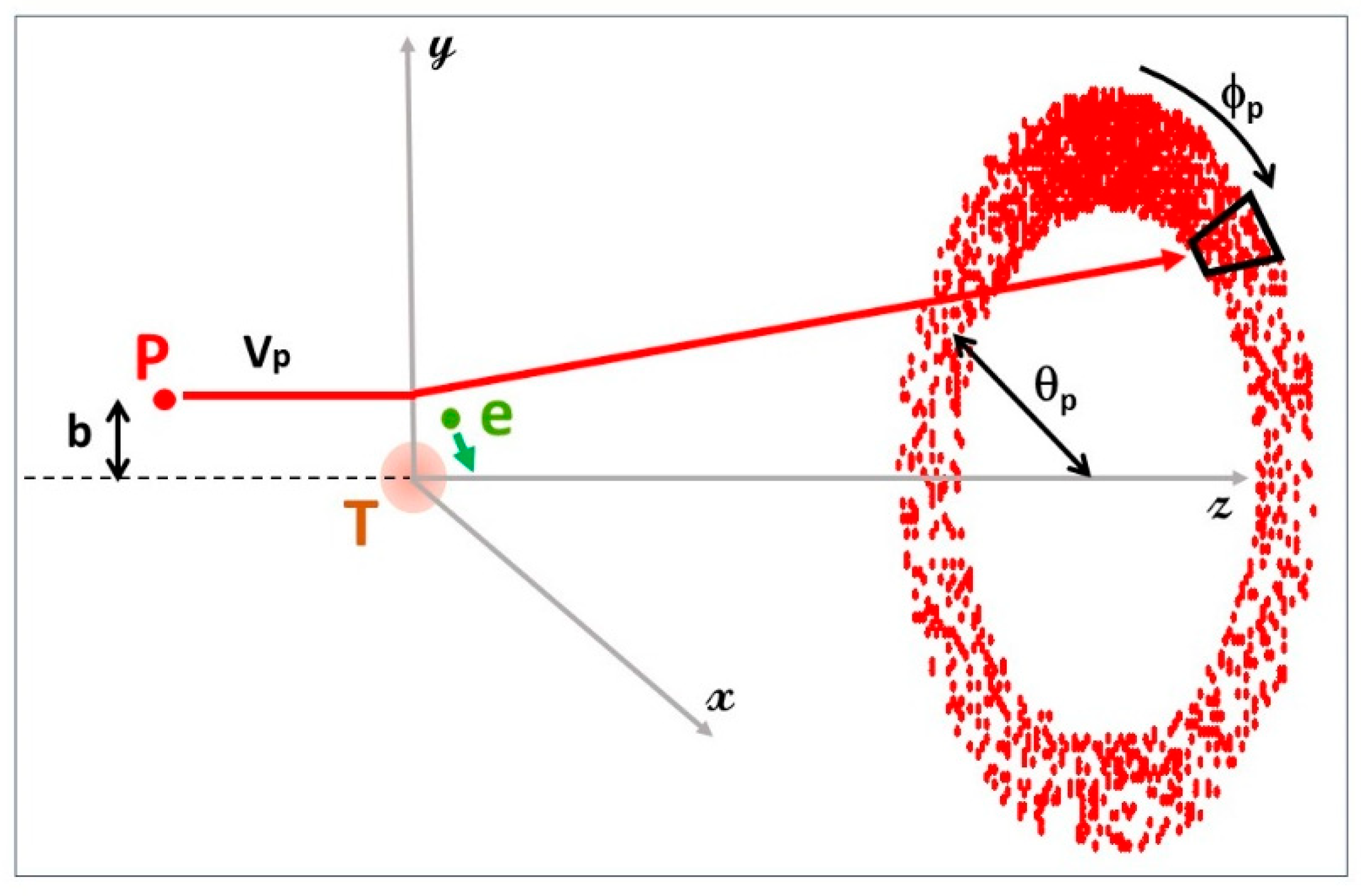
Collisions were modeled for a large number of trajectories (250,000,000) involving incoming positrons or electrons traveling in the y-z plane with a z-velocity V_p and impact parameters b ranging from 0 to 3 atomic units. The initial parameters for the projectile ion, defined with respect to the center of mass of the target system, included its position and a randomly selected impact parameter. The initial momentum was determined by the impact velocity, and the initial direction was chosen along the z-axis. The target electron was initially confined to the nucleus and subjected to a non-Coulombic potential described by Equation (1). The initial position of the 3p electron was randomly selected from the microcanonical distribution, following a method similar to that described by Reinhold and Falcon [59]. The target core was effectively positioned at the origin of the coordinate system (see Figure 1). For each set of input conditions, post-collision trajectories for the projectile and the ejected electron were determined. This was accomplished by incorporating all two-body interactions among the three particles in 12 coupled first-order Lagrangian equations of motion and integrating over time using the standard Runge–Kutta method. The integrations were stopped at a large distance from the target (100,000 atomic units for the present study), and the positions and velocities of the scattered projectile and ejected electron were recorded in the output file for each set of input conditions.

After solving the equations of motion for a large number of trajectories, the total, energy and angular single differential and the triple differential cross-sections were obtained using the following expressions:

$$\sigma ={\displaystyle \frac{2\pi b_{max}}{N_{tot}}}{\displaystyle \sum }_{i=1}^{N_t}{b}_i,$$

(8)

$${\displaystyle \frac{d\sigma }{dE}}={\displaystyle \frac{2\pi b_{max}}{N_{tot}\Delta E}}{\displaystyle \sum }_{i=1}^{N_t}{b}_i$$

(9)

$${\displaystyle \frac{d\sigma }{d\Omega }}={\displaystyle \frac{2\pi b_{max}}{N_{tot}\Delta \Omega }}{\displaystyle \sum }_{i=1}^{N_t}{b}_i$$

(10)

$${\displaystyle \frac{d^3\sigma }{d{\Omega }_{1}d{\Omega }_{2}dE}}={\displaystyle \frac{2\pi b_{max}}{N_{tot}\Delta {\Omega }_1\Delta {\Omega }_2\Delta E}}{\displaystyle \sum }_{i=1}^{N_t}{b}_i.$$

(11)

$${\displaystyle \frac{d^3\sigma }{d\Omega d{E}_{1}d{E}_2}}={\displaystyle \frac{2\pi b_{max}}{N_{tot}\Delta \Omega \Delta E_1\Delta E_2}}{\displaystyle \sum }_{i=1}^{N_t}{b}_i.$$

(12)

In Equations (8)–(12), ${\mathrm{N}}_{\mathrm{tot}}$ is the total number of trajectories calculated for impact parameters less than b_max, and $N_t$ is the number of trajectories that satisfy the criteria for ionization, and $b_i$ is the actual impact parameter for the trajectory corresponding to the ionization process under consideration in the energy interval $\Delta E$ and the emission angle interval $\Delta \Omega$ of the electron.

The statistical error for a given measurement has the form,

$$\Delta \sigma =\sigma \left({\displaystyle \frac{N_{tot}-N_t}{N_{tot}{N}_t}}\right) .$$

(13)

Using this method, cross-sections for direct comparison with experimental data were calculated. We note that this classical method contains information about the pre- and post-collision effects from all particles. In addition, impact parameter information is available, and various sorting techniques can be used in order to investigate correlations between the outgoing particle energies and directions.

3. Data Analysis

For data analysis, the velocity components were used to calculate the final energies and scattering angles for both particles for each 3p ionization event. The phi angles for both the scattered projectile (ϕ_p) and ejected electron (ϕ_e) were defined by arcsin (v_x/v) in the laboratory frame and arcsin (v_x/v_xy) in the xy frame. “Normal” and “reverse” projectile scattering (θ_p) and electron emission angles were defined by (v_y/|v_y|)arccos(v_z/v) which, in the x–y frame for positron impact, is equivalent to ϕ_p in the ranges of 360° to 90° or 90° to 360°. In Figure 1, the red circle shows a p_x-p_y plot (p_x and p_y being the momentum components of the scattered projectile) for an incoming projectile trajectory in the positive x-z frame. Events due to “normal” and “reverse” scattering are the upper and lower portions of the circle. Note that all events in the circle have the same scattering angle, θ_p while the xy plane phi angles range from 0 to 360°.

For “normal” scattering, i.e., for all events in the positive y direction, which is the direction shown by the outgoing projectile arrow, in-plane scattering, i.e., scattering within a narrow vertical band, dominates. However, for “reverse” scattering events, which are events in the lower half of the circle, in-plane and out-of-plane scattering have similar probabilities. The reader is reminded that Figure 1 illustrates a single incoming collision frame, whereas experimentally, the target atoms are subjected to a uniform incoming flux. This is equivalent to a continuous rotation of the coordinate system and trajectories shown in Figure 1 about the z-axis. Thus, in-plane scattering for a uniform beam is the sum of events within the black polygon as the polygon is rotated through a full circle. Associated binary and recoil events are those within a similar x–y plot for electron emission, where in-plane binary and recoil probabilities are those defined by |ϕ_p − ϕ_e| = 180° and 0°, ± (Δϕ_p + Δϕ_e) in both cases. To clarify, binary (recoil) events correspond to |ϕ_p − ϕ_e| = 180° (0°), i.e., when the scattered projectile and ejected electron exit in opposite or the same direction in the x–y plane.

To determine the in-plane triply differential probabilities, our CTMC output files were sorted for specific ranges of ejected electron energies and theta angles, with binary and recoil events defined by the |ϕ_p − ϕ_e| ranges described above. The addition of sorting criteria was with the direction and magnitude of projectile scattering. The TDCS probabilities for both “normal” and “reverse” scattering, which are presented here, were then determined by summing the impact parameters within these combined ranges.

4. Results and Discussion

In a recent paper [43], we used the procedure described above to investigate the pre- and post-collision kinematics for 3p ionization of argon by 1 keV positrons and electrons. Two new insights into collision kinematics were found in this study. One was concerned with post-collision kinematics, namely that in addition to the direction of scattering from a repulsive core (which we refer to as “normal” scattering), a portion of the incoming beam is scattered in the opposite direction (which we refer to as “reverse” scattering). The other was with pre-collision kinematics, where it was found that “normal” (“reverse”) scattering occurred when the impact parameter distribution was mostly inside (outside) the centroid of the 3p charge distribution. It was shown that the relative number of “reverse” scattering events increased from an insignificant amount to more than 50% for ejected electron energies between 0 and 100 eV. That study was performed for a scattering angle of 10° and a range of electron energies. Thus, the momentum transfer was ~1 a.u.

The present work investigates a smaller scattering angle, e.g., 2.9°, where experimental [44] and theoretical [39,40] data are available and the momentum transfer is approximately 1/3 atomic unit. In order to compare our CTMC predictions with the experimental data which consisted of a broad ejected energy distribution, we calculated TDCS probabilities for a number of energy bins between 0 and 100 eV, e.g., 0.1–1, 1–5, 5–10, and 10 eV bins between 10 and 100 eV. This was performed using the quoted experimental azimuthal angle acceptance ranges. Weighted contributions from each of these energy bins were determined using the experimental energy distribution. These were summed to generate the TDCS spectrum shown by the solid black curve in Figure 2. Note that this curve represents in-plane scattering where the difference in the azimuthal angles is less than the sum of the quoted values. For comparison with the experimental data, rather than using a normalization at some arbitrary angle, the binary area between 30 and 150 degrees was used. Although the experimental data are subject to scatter, the agreement in the binary region is good; in particular, the experimental and CTMC predicted centroids and widths agree quite well. In the recoil region, the experimental and CTMC shapes are very similar, but the experimental magnitudes are roughly a factor of two larger. We note that, in general, the data points and error bars of the classical results are obtained for values calculated for the contributing energies within energy bins centered on each data point.

Included in the figure are the DWBA2 predictions of Campeanu et al. [39], which are nearly the same as those of Purohit [40]. The DWBA2 calculations were performed using the quoted experimental mean and standard deviation energies of 26 ± 10 eV rather than a weighted energy distribution as is performed here. We note that our weighted CTMC values are dominated by ejection energies between 1 and 40 eV with the higher energy portion being responsible for the shift in the recoil distribution to larger angles. The DWBA2 normalization was again based on the binary peak area. Except for differences in the location of the recoil peak maximum, the CTMC and DWBA2 predictions are similar, and both predict a smaller recoil peak intensity than the experimental value. However, Campeanu and coworkers have recently obtained improved agreement with data at 200 eV by convoluting their DWBA2 calculations over a range of electron energies similar to those used experimentally [60].

To investigate the discrepancy between the experimental data and our CTMC predictions in the recoil region, several possible causes were tested. Because the binary–recoil ratio is known to change with ejection energy, one possibility is in the experimentally determined ejected electron energies. Experimentally, the ejected electron energies were determined using energy loss information. This was based on an energy calibration using beam energies of several hundred eV. Thus, any small error at several hundred eV becomes a large error at low ejection energies. Also, the large beam diameter and small angles used in the experimental study meant there was significant overlap between the main beam and small energy losses. To test if the experimental ejected electron energies were incorrect because of these factors, we determined weighted TDCS as the energy distribution centroid was shifted. No significant changes were found.

The other experimental parameter investigated was the azimuthal angle for ejected electrons. Experimentally, coincidences were measured between scattered projectiles and a band of electrons centered on the beam axis and ejected at various theta angles, for example, between a positive and negative x value in Figure 1. For θ = 90°, the geometric Δϕ angular range of this band was ±20° in the laboratory frame. This is the value used here in our CTMC calculations. However, the experimental ejection θ angles required corrections to account for the small electric field in the collision region and for the beam width. This increased the theta angular range from the geometric value. No such correction was made for the phi angular range. In our CTMC calculations, azimuthal angles in the x–y plane were used; these are larger than the laboratory azimuthal angles. To test the importance of Δϕ_e, we performed TDCS calculations where all Δϕ angles were included. The results are shown by the dashed curve in Figure 2. As seen, the agreement with the experiment is better in both the binary and recoil regions. This implies that the quoted experimental Δϕ_e value is too small and/or that a larger value is needed for theoretical comparisons, particularly if using azimuthal angles in the x–y plane. However, a definitive answer is not possible because of the scatter in the experimental data.

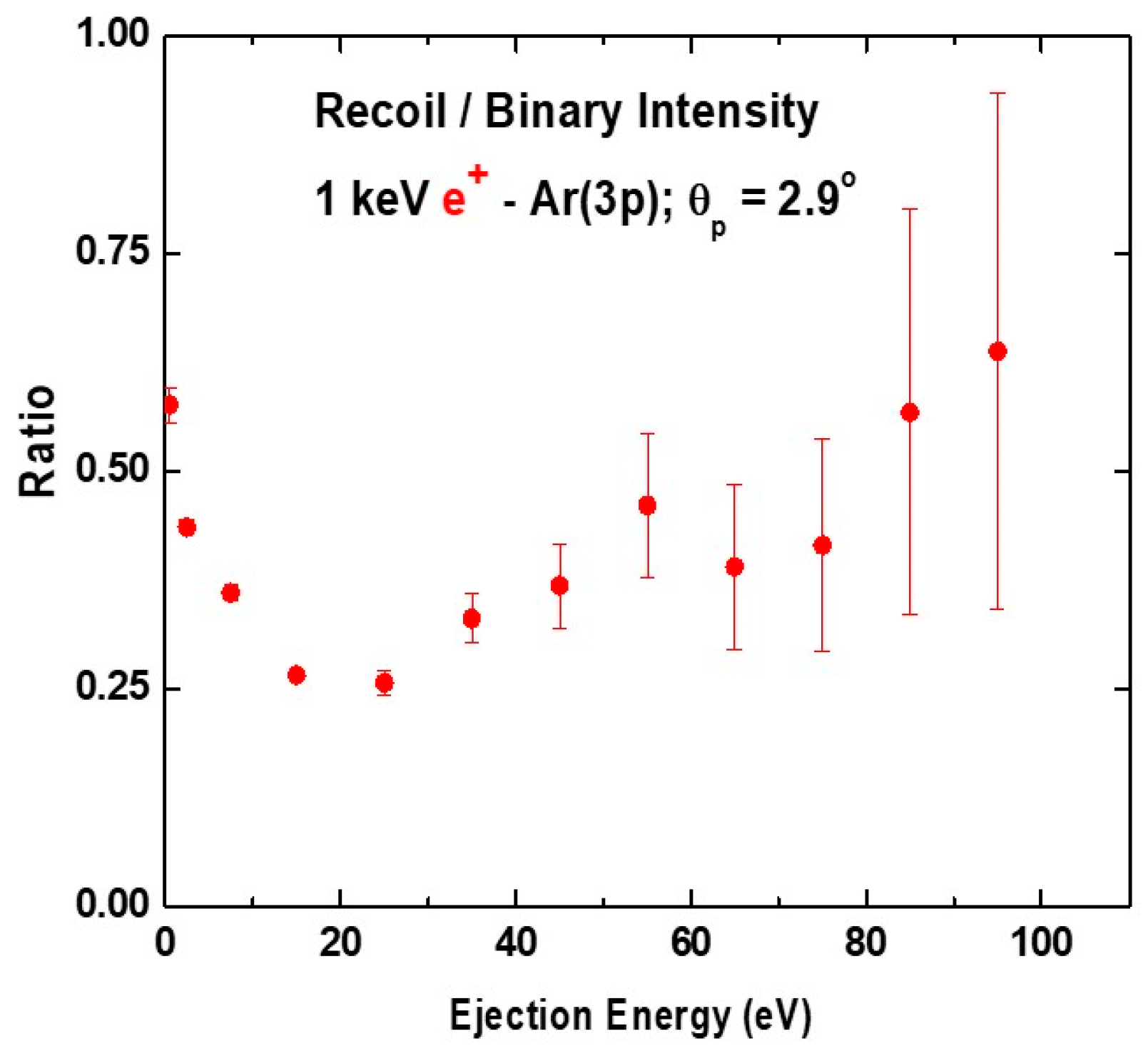
In Figure 3, our CTMC predictions for the recoil to binary intensity ratio are shown for ejection energies less than 100 eV. The relative importance of recoil interactions systematically decreases between 0 and 20 eV. This is followed by an increase as the ejection energy increases further. The step near 60 eV will be commented on below.

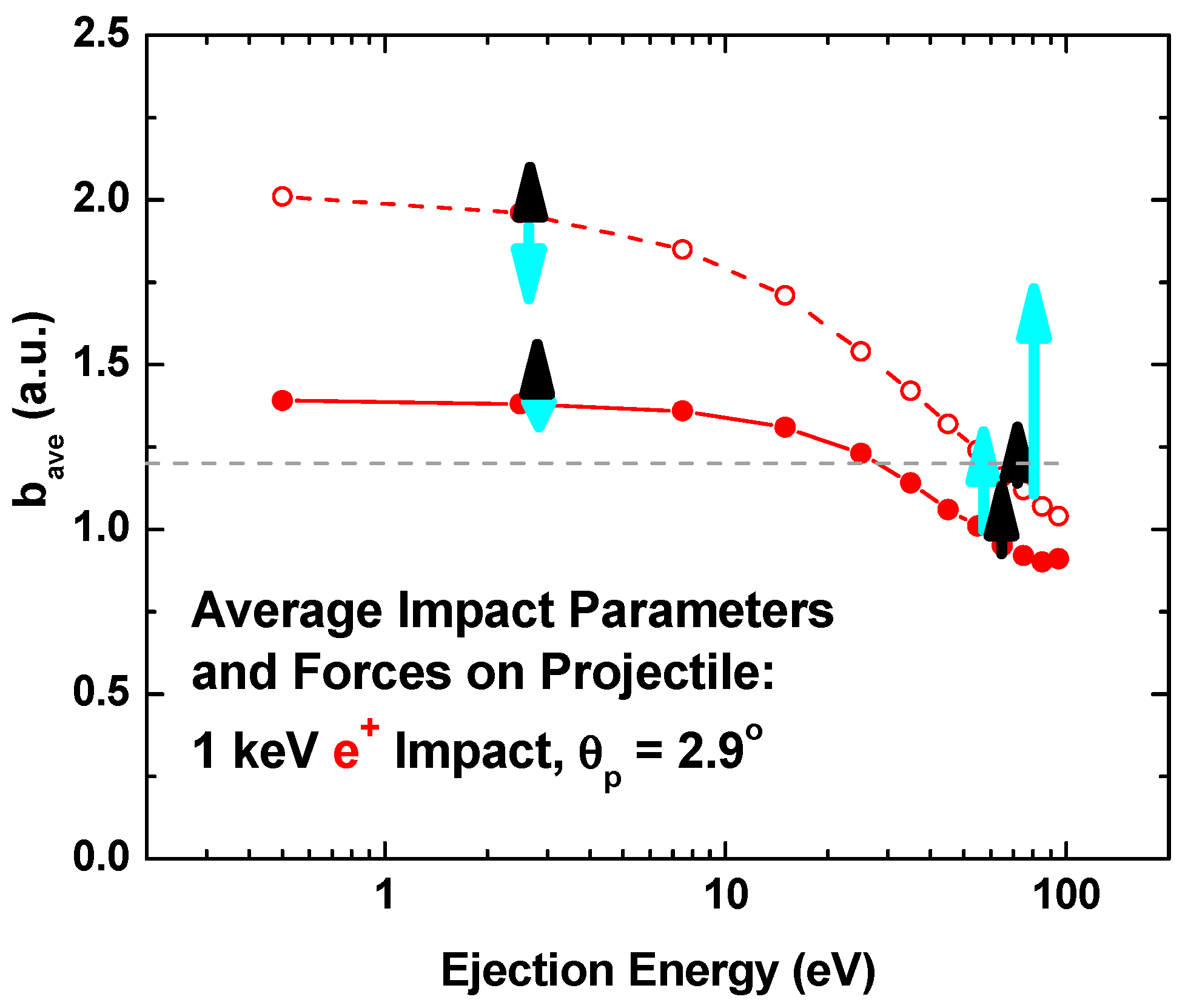
Having shown that our CTMC technique and two-body target model also work on the TDCS level, we now turn our attention to information about the pre- and post-collision kinematics. In the present study, the momentum transfer is between 0.31 and 0.46 a.u. In Figure 4, pre-collision information, namely the average impact parameters, is shown as functions of the ejected electron energy and the direction of scattering. Average impact parameters were obtained from the sum of all impact parameters contributing to a specific ejection energy divided by the number of events. Included are examples for the directions and relative magnitudes of the maximum forces on a 1 keV positron from the projectile core (black arrows) and a 3p electron at the centroid of the charge distribution (blue arrows). The solid curve and filled symbols are for “normal” scattering, i.e., away from the z-axis in Figure 1; the dashed curve and open symbols are for “reverse” scattering, i.e., toward the z-axis in Figure 1. Note that for low ejected electron energies, the combined forces on the projectile from this simplistic picture are consistent with the direction of scattering in both cases, while for high ejected electron energies, our simplistic picture is consistent for “normal” scattering but inconsistent for “reverse” scattering. Thus, an overall consistency between this force picture and predictions of the directions of scattering probably requires an improved picture where a spherical shell rather than a fixed point is used for the centroid of the 3p charge distribution. Another difference between this and our previous study is that here, i.e., for a scattering angle of ~3°, the impact parameters for “normal” scattering are larger than the centroid of the 3p charge distribution (the dashed line), rather than smaller as was found for a 10° scattering angle. With regard to the recoil/binary intensity energy dependence shown in Figure 3, it is interesting to note that the increase seen near 20 eV coincides with the impact parameter for “normal” scattering changing from larger to smaller than the centroid of the 3p charge distribution. Likewise, the step near 60 eV coincides with a similar change for the impact parameter for “reverse” scattering.

In Figure 5, our CTMC predictions for reverse scattering are shown as a function of the ejected electron energy (the filled red symbols). Again, the scattering angle is 2.9 ± 0.5 degrees, where the momentum transfer is approximately 1/3 a.u. For comparison, the black curve shows the fractions for a 10° scattering angle where the momentum transfer is ~1 a.u. There are similar systematic increases in energy transfer in both cases. These two sets of data imply a systematic decrease in the importance of “reverse” scattering for larger scattering angles.

Regarding post-collision kinematics, Figure 5 demonstrated that “reverse” scattering can be quite important on the fully differential level for ionization of argon by fast positrons. In Figure 6 and Figure 7, the relative importance is shown at the single-differential level. As a function of ejected electron energy, Figure 6 shows that the importance of “reverse” scattering increases from approximately 10% to roughly 1/3 around 200 eV, after which it systematically decreases. Included in the figure are average impact parameters, b_ave, for both “normal” and “reverse” scattering. For ejected electron energies less than a couple hundred eV, b_ave for “normal” scattering is roughly constant and significantly smaller than the centroid (magenta dashed line) of the 3p radial distribution (magenta curve on left vertical axis). For higher energy ejected electrons, b_ave systematically decreased. “Reverse” scattering is seen to occur for collisions outside the 3p radial centroid for ejected energies less than a couple of hundred eV, after which the collisions occur at smaller and smaller impact parameters. Note that the increase in the relative importance of “reverse” scattering is proportional to the decrease in the impact parameter for this process, and that the decrease at higher energies begins when the impact parameters for both “normal” and “reverse” scattering begin their decrease.

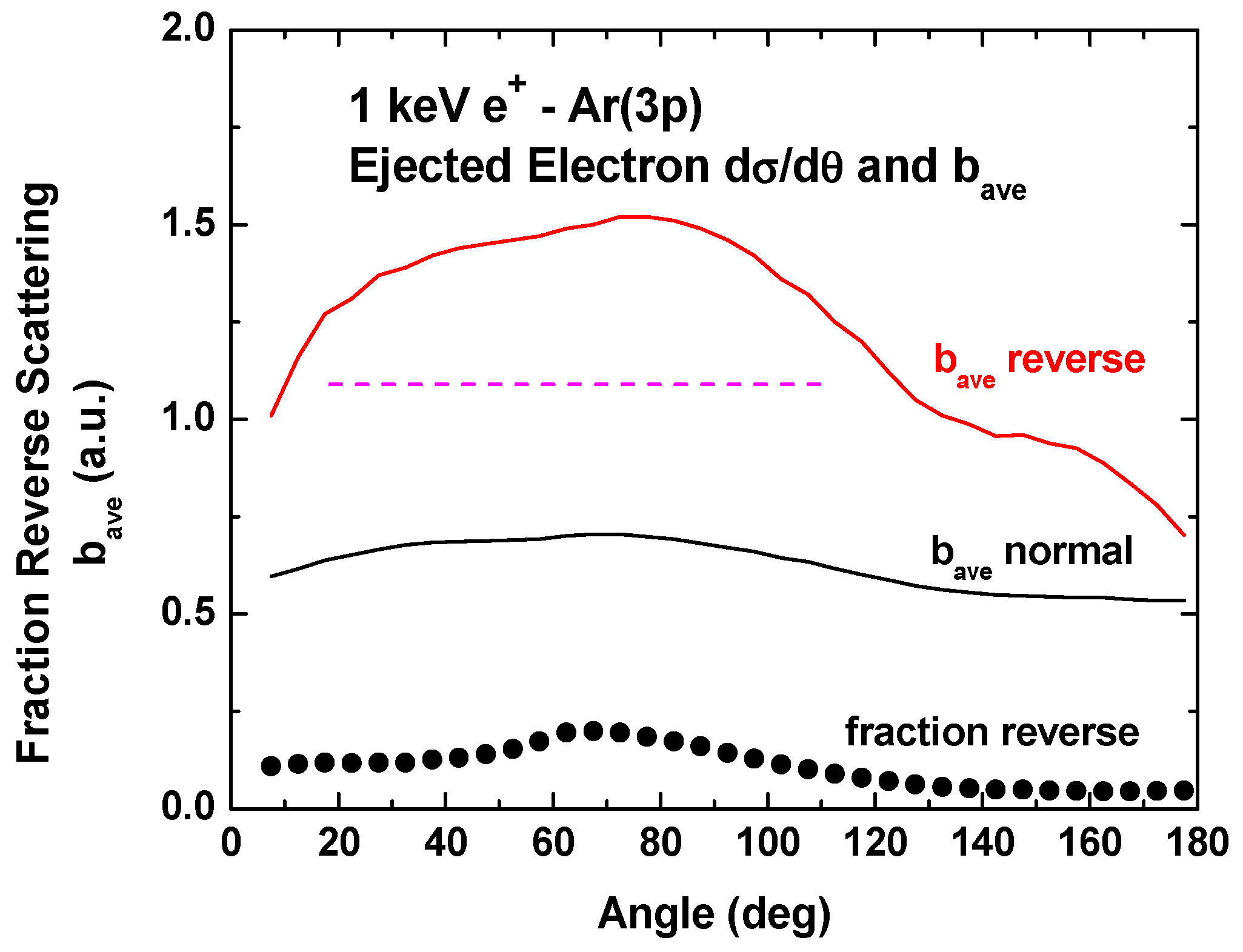
Figure 7 shows similar overall properties as a function of emission or scattering angle. On the single-differential level for electron emission by fast positrons, in the forward direction, the relative importance of “reverse” scattering increases from approximately 10% to a maximum of 20% at 70° and the collisions for “reverse” scattering occur in the outer region of the 3p charge distribution. In the backward direction, the importance is between 5 and 10%, and, for very backward angles, collisions for “reverse” scattering occur in the inner portion of the 3p charge distribution. Independent of emission angle, “normal” scattering occurs for collisions with the inner portion of the 3p charge distribution.

5. Summary

The CTMC method and a single electron-target core model were used to calculate differential cross-sections and to provide pre- and post-collision kinematic information for 1 keV positron ionization of argon. A comparison of experimental data with a weighted distribution of triply differential cross-sections calculated for a range of ejected electron energies was made. It was shown that for this high energy and small momentum transfer, very good agreement could be obtained by using an angular range for the ejected electron larger than the quoted value. Additionally, ejection energies between 1 and 40 eV were found to be dominant. Similar to what was found for a larger scattering angle, the recoil/binary intensity ratio was found to initially decrease with increasing ejected electron energy and then to systematically increase. Additionally, “reverse” projectile scattering was shown to systematically increase with ejected electron energy in a similar fashion to that found at a larger scattering angle. The onset for the increases in both cases occurs for energies where the impact parameters for “normal” and “reverse” scattering begin a systematic decrease. Singly differential cross-sections were used to show the relative importance of “reverse” scattering and average impact parameters for “normal” and “reverse” scattering as functions of the ejected electron energy and emission angle. “Reverse” scattering was found to be more important, approximately 10–20% of the overall cross-section, for forward electron emission, but unimportant for emission in the backward direction. As a function of emission energy, the relative importance increased from approximately 1/10 to 1/3 for energies up to a couple of hundred eV. For higher energies, a systematic decrease was found.

This work helps explain the binary and recoil structure in triply differential studies, specifically the relative importance of recoil interactions. The impact parameter, which provides important pre-collision kinematic information, is useful in improving various target models, while the scattering direction information, a post-collision kinematic, is important since the direction of scattering determines the direction of electron emission. This information is important since the partially screened target nucleus modifies the post-collision trajectories. Based on this and our previous study [43], a similar investigation for larger scattering angles is planned.