Triaxial Shapes in Even–Even Nuclei: A Theoretical Overview
Abstract
1. Introduction
2. Collective Model of Bohr and Mottelson
2.1. The Rigid Triaxial Rotor Model
2.2. The Algebraic Collective Model
2.3. Shape/Phase Transitions and Critical Point Symmetries
2.4. Special Solutions of the Bohr Hamiltonian
2.5. Modifications of the Bohr Hamiltonian
3. The Nuclear Shell Model
3.1. The SU(3) Symmetry
3.2. The Pseudo-SU(3) Symmetry
3.3. The Proxy-SU(3) Symmetry
3.4. Regions of High Triaxiality Predicted by the Proxy-SU(3) Symmetry
4. Algebraic Models Using Bosons
4.1. Interacting Boson Model-1
4.2. Interacting Boson Model-2
4.3. The Interacting Vector Boson Model
4.4. The Coherent State Model
5. Self-Consistent Mean-Field Methods
6. Empirical Signatures of Triaxiality
6.1. The Shape Parameter
6.2. Rigid Triaxiality vs. -Softness
7. Global Systematics of Triaxiality
8. Open Questions
9. Conclusions and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A. Theoretical Terms and Models
| Algebraic Collective Model (ACM) | Section 2.2 and Section 4.1 |
| deformation | Section 2.1 |
| BCS approximation | Section 5 |
| Coherent State Model (CSM) | Section 4.4 |
| collective model of Bohr and Mottelson | Section 2 |
| conformable fractional derivative | Section 2.5 |
| cranking | Section 3 |
| critical point symmetry (CPS) | Section 2.3 |
| cubic terms | Section 4.1 |
| deformation dependent mass (DDM) | Section 2.5 |
| deformed shell model | Section 3 |
| density functional theory (DFT) | Section 5 |
| E(5) CPS | Section 2.3 |
| E(5)- model | Section 6.2 |
| Elliott SU(3) model | Section 3.1 |
| energy-dependent potential | Section 2.5 |
| extended Thomas–Fermi plus Strutinsky integral method | Appendix C.3 |
| Finite-Range Droplet Model (FRDM) | Section 3 |
| Finite-Range Liquid-Drop Model (FRLDM) | Section 3 |
| fractional calculus | Section 2.5 |
| deformation | Section 2.1 |
| -unstable model of Wilets and Jean | Section 2.1 |
| Generalized Collective Model (GCM) | Section 2.2 |
| Generalized Triaxial Rotor Model (GTRM) | Section 2.1 |
| Gogny interaction | Section 5 |
| Hartree–Fock–Bogoliubov (HFB) method | Section 5 |
| Hartree–Fock (HF) method | Section 5 |
| highest-weight irreducible representation (hw irrep) | Section 3.3 |
| Interacting Boson Model-1 (IBM-1) | Section 4.1 |
| Interacting Boson Model-2 (IBM-2) | Section 4.2 |
| Interacting Vector Boson Model (IVBM) | Section 4.3 |
| irreducible representation (irrep) | Section 3.1 |
| mean field | Section 5 |
| minimal length (ML) | Section 2.5 |
| Monte Carlo Shell Model (MCSM) | Section 3 |
| next highest weight irreducible representation (nhw irrep) | Section 3.3 |
| Nilsson model | Section 3 |
| Nilsson–Strutinsky model | Section 5 |
| O(5) symmetry | Section 6.2 |
| O(6) symmetry | Section 4.1 |
| odd–even staggering | Section 6.2 |
| pairing interaction | Section 3 and Section 5 |
| Pauli principle | Section 3.3 |
| projected shell model (PSM) | Section 3 |
| prolate over oblate dominance | Section 3.3 |
| prolate-to-oblate transition | Section 3.3 |
| proxy-SU(3) symmetry | Section 3.3 |
| pseudo-SU(3) symmetry | Section 3.2 |
| quadrupole shape invariants | Section 4.1 and Section 6.1 |
| Quantum Monte Carlo Diagonalization (QMCD) method | Section 3 |
| quantum phase transition (QPT) | Section 2.3 |
| relativistic mean field (RMF) | Section 5 |
| Rigid Triaxial Rotor Model (RTRM) | Section 2.1 |
| Rotation-Vibration Model (RVM) | Section 2.1 |
| shape/phase transition (SPT) | Section 2.3 |
| Skyrme interaction | Section 5 |
| spherical shell model | Section 3 |
| Strutinsky’s method | Section 5 |
| SU(3) symmetry | Section 3.1 and Section 4.1 |
| SU(3)∗ symmetry | Section 4.2 |
| T(4) SPT | Section 2.3 |
| T(5) SPT | Section 2.3 |
| Triaxial Projected Shell Model (TPSM) | Section 3 |
| Triaxial Rotation Vibration Model (TRVM) | Section 2.1 |
| U(5) symmetry | Section 4.1 |
| U(6) symmetry | Section 4.1 |
| Vector Boson Model (VBM) | Section 4.3 |
| X(3) SPT | Section 2.3 |
| X(4) SPT | Section 2.3 |
| X(5) CPS | Section 2.3 |
| Y(5) SPT | Section 2.3 |
| Z(4) SPT | Section 2.3 |
| Z(5) SPT | Section 2.3 |
Appendix B. The Z=24–26 Region
Appendix B.1. The Cr (Z = 24) Isotopes
Appendix B.2. The Fe (Z = 26) Isotopes
Appendix C. The Z = 28–32 Region
Appendix C.1. The Ni (Z = 28) Isotopes
Appendix C.2. The Zn (Z = 30) Isotopes
Appendix C.3. The Ge (Z = 32) Isotopes
Appendix D. The Z = 34–48 Region
Appendix D.1. The Se (Z = 34) Isotopes
Appendix D.2. The Kr (Z = 36) Isotopes
Appendix D.3. The Sr (Z = 38) Isotopes
Appendix D.4. The Zr (Z = 40) Isotopes
Appendix D.5. The Mo (Z = 42) Isotopes
Appendix D.6. The Ru (Z = 44) Isotopes
Appendix D.7. The Pd (Z = 46) Isotopes
Appendix D.8. The Cd (Z = 48) Isotopes
Appendix E. The Z = 52–66 Region
Appendix E.1. The Te (Z = 52) Isotopes
Appendix E.2. The Xe (Z = 54) Isotopes
Appendix E.3. The Ba (Z = 56) Isotopes
Appendix E.4. The Ce (Z = 58) Isotopes
Appendix E.5. The Nd (Z = 60) Isotopes
Appendix E.6. The Sm (Z = 62) Isotopes
Appendix E.7. The Gd (Z = 64) Isotopes
Appendix E.8. The Dy (Z = 66) Isotopes
Appendix F. The Z = 68–72 Region
Appendix F.1. The Er (Z = 68) Isotopes
Appendix F.2. The Yb (Z = 70) Isotopes
Appendix F.3. The Hf (Z = 72) Isotopes
Appendix G. The Z=74–80 Region
Appendix G.1. The W (Z = 74) Isotopes
Appendix G.2. The Os (Z = 76) Isotopes
Appendix G.3. The Pt (Z = 78) Isotopes
Appendix G.4. The Hg (Z = 80) Isotopes
Appendix H. The Z = 88–98 Region
Appendix H.1. The Ra (Z = 88) Isotopes
Appendix H.2. The Th (Z = 90) Isotopes
Appendix H.3. The U (Z = 92) Isotopes
Appendix H.4. The Pu (Z = 94) Isotopes
Appendix H.5. The Cm (Z = 96) Isotopes
Appendix H.6. The Cf (Z = 98) Isotopes
References
- Lalazissis, G.A.; Raman, S.; Ring, P. Ground-state properties of even-even nuclei in the relativistic mean-field theory. At. Data Nucl. Data Tables 1999, 71, 1. [Google Scholar] [CrossRef]
- Raman, S.; Nestor, C.W., Jr.; Tikkanen, P. Transition probability from the ground to the first-excited 2+ state of even-even nuclides. At. Data Nucl. Data Tables 2001, 78, 1. [Google Scholar] [CrossRef]
- Pritychenko, B.; Birch, M.; Singh, B.; Horoi, M. Tables of E2 transition probabilities from the first 2+ states in even–even nuclei. At. Data Nucl. Data Tables 2016, 107, 1. [Google Scholar] [CrossRef]
- Delaroche, J.-P.; Girod, M.; Libert, J.; Goutte, H.; Hilaire, S.; Péru, S.; Pillet, N.; Bertsch, G.F. Structure of even-even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction. Phys. Rev. C 2010, 81, 014303. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Analytic predictions for nuclear shapes, prolate dominance, and the prolate-oblate shape transition in the proxy-SU(3) model. Phys. Rev. C 2017, 95, 064326. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Mertzimekis, T.J.; Minkov, N. The proxy-SU(3) symmetry in atomic nuclei. Symmetry 2023, 15, 169. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109-110, 1. [Google Scholar] [CrossRef]
- Spear, R.H. Reduced electric-octupole transition probabilities, B(E3:→), for even-even nuclides throughout the periodic table. At. Data Nucl. Data Tables 1989, 42, 55. [Google Scholar] [CrossRef]
- Kibédi, T.; Spear, R.A. Reduced electric-octupole transition probabilities, B(E3:→)—An update. At. Data Nucl. Data Tables 2002, 80, 35. [Google Scholar] [CrossRef]
- Butler, P.A.; Nazarewicz, W. Intrinsic reflection asymmetry in atomic nuclei. Rev. Mod. Phys. 1996, 68, 349. [Google Scholar] [CrossRef]
- Butler, P.A. Octupole collectivity in nuclei. J. Phys. G Nucl. Part. Phys. 2016, 43, 073002. [Google Scholar] [CrossRef]
- Martinou, A.; Minkov, N. Microscopic derivation of the octupole magic numbers from symmetry considerations. Phys. Scr. 2024, 99, 075311. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.J.; Bengtsson, R.; Sagawa, H.; Ichikawa, T. Global calculation of nuclear shape isomers. Phys. Rev. Lett. 2009, 103, 212501. [Google Scholar] [CrossRef] [PubMed]
- Möller, P.; Sierk, A.J.; Bengtsson, R.; Sagawa, H.; Ichikawa, T. Nuclear shape isomers. At. Data Nucl. Data Tables 2012, 98, 149. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Walker, P.M.; Kondev, F.G. Review of metastable states in heavy nuclei. Rep. Prog. Phys. 2016, 79, 076301. [Google Scholar] [CrossRef]
- Garg, S.; Maheshwari, B.; Singh, B.; Sun, Y.; Goel, A.; Jain, A.K. Atlas of nuclear isomers—Second edition. At. Data Nucl. Data Tables 2023, 150, 101546. [Google Scholar] [CrossRef]
- Walker, P.M.; Kondev, F.G. K isomers in atomic nuclei. Eur. Phys. J. Special Topics 2024, 233, 983. [Google Scholar] [CrossRef]
- Heyde, K.; Van Isacker, P.; Waroquier, M.; Wood, J.L.; Meyer, R.A. Coexistence in odd-mass nuclei. Phys. Rep. 1983, 102, 291. [Google Scholar] [CrossRef]
- Wood, J.L.; Heyde, K.; Nazarewicz, W.; Huyse, M.; Van Duppen, P. Coexistence in even-mass nuclei. Phys. Rep. 1992, 215, 101. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1467. [Google Scholar] [CrossRef]
- Garrett, P.E.; Zielińska, M.; Clément, E. An experimental view on shape coexistence in nuclei. Prog. Part. Nucl. Phys. 2022, 124, 103931. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Mertzimekis, T.J.; Minkov, N. Shape coexistence in even–even nuclei: A theoretical overview. Atoms 2023, 11, 117. [Google Scholar] [CrossRef]
- Leoni, S.; Fornal, B.; Bracco, A.; Tsunoda, Y.; Otsuka, T. Multifaceted character of shape coexistence phenomena in atomic nuclei. Prog. Part. Nucl. Phys. 2024, 139, 104119. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Metzimekis, T.J.; Karakatsanis, K.E.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. The islands of shape coexistence within the Elliott and the proxy-SU(3) Models. Eur. Phys. J. A 2021, 57, 84. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Peroulis, S.K.; Karakatsanis, K.E.; Mertzimekis, T.J.; Minkov, N. Islands of shape coexistence: Theoretical predictions and experimental evidence. Symmetry 2023, 15, 29. [Google Scholar] [CrossRef]
- Möller, P.; Bengtsson, R.; Carlsson, B.G.; Olivius, P.; Ichikawa, T. Global calculations of ground-state axial shape asymmetry of nuclei. Phys. Rev. Lett. 2006, 97, 162502. [Google Scholar] [CrossRef]
- Möller, P.; Bengtsson, R.; Carlsson, B.G.; Olivius, P.; Ichikawa, T.; Sagawa, H.; Iwamoto, A. Axial and reflection asymmetry of the nuclear ground state. At. Data Nucl. Data Tables 2008, 94, 758. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Petrellis, D.; Vasileiou, P.; Mertzimekis, T.J.; Minkov, N. Preponderance of triaxial shapes in atomic nuclei predicted by the proxy-SU(3) symmetry. J. Phys. G Nucl. Part. Phys. 2025, 52, 015102. [Google Scholar] [CrossRef]
- Otsuka, T.; Tsunoda, Y.; Abe, T.; Shimizu, N.; Van Duppen, P. Underlying structure of collective bands and self-organization in quantum systems. Phys. Rev. Lett. 2019, 123, 222502. [Google Scholar] [CrossRef]
- Tsunoda, Y.; Otsuka, T. Triaxial rigidity of 166Er and its Bohr-model realization. Phys. Rev. C 2021, 103, L021303. [Google Scholar] [CrossRef]
- Otsuka, T.; Tsunoda, Y.; Shimizu, N.; Utsuno, Y.; Abe, T.; Ueno, H. Prevailing triaxial shapes in atomic nuclei and a quantum theory of rotation of composite objects. arXiv 2023, arXiv:2303.11299. [Google Scholar]
- Rouoof, S.P.; Nazir, N.; Jehangir, S.; Bhat, G.H.; Sheikh, J.A.; Rather, N.; Frauendorf, S. Fingerprints of the triaxial deformation from energies and B(E2) transition probabilities of γ-bands in transitional and deformed nuclei. Eur. Phys. J. A 2024, 60, 40. [Google Scholar] [CrossRef]
- Bohr, A. The coupling of nuclear surface oscillations to the motion of individual nucleons. Dan. Mat. Fys. Medd. 1952, 26, 14. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Collective and individual-particle aspects of nuclear structure. Dan. Mat. Fys. Medd. 1953, 27, 16. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Nuclear Structure Vol. I: Single-Particle Motion; World Scientific: Singapore, 1998. [Google Scholar]
- Bohr, A.; Mottelson, B.R. Nuclear Structure Vol. II: Nuclear Deformations; World Scientific: Singapore, 1998. [Google Scholar]
- Wilets, L.; Jean, M. Surface oscillations in even-even nuclei. Phys. Rev. 1956, 102, 788. [Google Scholar] [CrossRef]
- Scharff-Goldhaber, G.; Weneser, J. System of even-even nuclei. Phys. Rev. 1955, 98, 212. [Google Scholar] [CrossRef]
- Rohoziński, S.G.; Srebrny, J.; Horbaczewska, K. Nuclei from the region 52 < Z, N < 80 as susceptible to the gamma-deformations. Z. Phys. 1974, 268, 401. [Google Scholar]
- Davydov, A.S.; Filippov, G.F. Rotational states in even atomic nuclei. Nucl. Phys. 1958, 8, 237. [Google Scholar] [CrossRef]
- Davydov, A.S.; Rostovsky, V.S. Relative transition probabilities between rotational levels of non-axial nuclei. Nucl. Phys. 1959, 12, 58. [Google Scholar] [CrossRef]
- Esser, L.; Neuneyer, U.; Casten, R.F.; von Brentano, P. Correlations of the deformation variables β and γ in even-even Hf, W, Os, Pt, and Hg nuclei. Phys. Rev. C 1997, 55, 206. [Google Scholar] [CrossRef]
- Davydov, A.S.; Chaban, A.A. Rotation-vibration interaction in non-axial even nuclei. Nucl. Phys. 1960, 20, 499. [Google Scholar] [CrossRef]
- Davydov, A.S. Collective excitations corresponding to quadrupole nuclear surface vibrations. Nucl. Phys. 1961, 24, 682. [Google Scholar] [CrossRef]
- Meyer-ter-Vehn, J. Collective model description of transitional odd-A nuclei: (I). The triaxial-rotor-plus-particle model. Nucl. Phys. A 1975, 249, 111. [Google Scholar] [CrossRef]
- Filippov, G.F.; Lisetskyi, A.F.; Draayer, J.P. Microscopic SUπ(3)⊗SUν(3) interpretation of a two triaxial rotor model. J. Math. Phys. 1998, 39, 1350. [Google Scholar] [CrossRef]
- Pan, F.; Draayer, J.P. Algebraic solutions for the asymmetric rotor. Ann. Phys. (N.Y.) 1999, 275, 224. [Google Scholar] [CrossRef]
- Jolos, R.V.; Gelberg, A.; von Brentano, P. Wave functions of the triaxial rotor model in the multiple ‘‘Q-excitation’’ scheme. Phys. Rev. C 1996, 53, 168. [Google Scholar] [CrossRef]
- Gheorghe, A.; Raduta, A.A.; Ceausescu, V. Semiclassical treatment of the cranked triaxial rotator. Nucl. Phys. 1998, 637, 201. [Google Scholar] [CrossRef]
- Raduta, A.A.; Budaca, R.; Raduta, C.M. Semiclassical description of a triaxial rigid rotor. Phys. Rev. C 2007, 76, 064309. [Google Scholar] [CrossRef]
- Meyer-ter-Vehn, J.; Stephens, F.S.; Diamond, R.M. Evidence for asymmetric shapes from high-spin odd-A spectra. Phys. Rev. Lett. 1974, 32, 1383. [Google Scholar] [CrossRef]
- Varshni, Y.P.; Bose, S. Some features of the Davydov-Filippov model. Nucl. Phys. A 1970, 144, 645. [Google Scholar] [CrossRef]
- Yan, J.; Vogel, O.; von Brentano, P.; Gelberg, A. Systematics of triaxial deformation in Xe, Ba, and Ce nuclei. Phys. Rev. C 1993, 48, 1046. [Google Scholar] [CrossRef]
- Bindra, A.; Mittal, H.M. The magnification of structural anomalies with Grodzins systematic in the framework of Asymmetric Rotor Model. Nucl. Phys. A 2018, 975, 48. [Google Scholar] [CrossRef]
- Rowe, D.J. Nuclear Collective Motion; Methuen: London, UK, 1970. [Google Scholar]
- Wood, J.L.; Oros-Peusquens, A.-M.; Zaballa, R.; Allmond, J.M.; Kulp, W.D. Triaxial rotor model for nuclei with independent inertia and electric quadrupole tensors. Phys. Rev. C 2004, 70, 024308. [Google Scholar] [CrossRef]
- Allmond, J.M.; Zaballa, R.; Oros-Peusquens, A.M.; Kulp, W.D.; Wood, J.L. Triaxial rotor model description of E2 properties in 186,188,190,192Os. Phys. Rev. C 2008, 78, 014302. [Google Scholar] [CrossRef]
- Allmond, J.M.; Wood, J.L.; Kulp, W.D. Triaxial rotor model description of quadrupole interference in collective nuclei: The P3 term. Phys. Rev. C 2009, 80, 021303(R). [Google Scholar] [CrossRef]
- Allmond, J.M.; Wood, J.L.; Kulp, W.D. Destructive interference of E2 matrix elements in a triaxial rotor model. Phys. Rev. C 2010, 81, 051305(R). [Google Scholar] [CrossRef]
- Allmond, J.M.; Wood, J.L. Empirical moments of inertia of axially asymmetric nuclei. Phys. Lett. B 2017, 767, 226. [Google Scholar] [CrossRef]
- Pittel, S.; Qin, Z.Z.; Lei, Y.; Bijker, R. Global correlations for low-lying collective 2+ states. Bulg. J. Phys. 2017, 44, 362. [Google Scholar]
- Sugawara, M. Empirical model with independent variable moments of inertia for triaxial nuclei applied to 76Ge and 192Os. Phys. Rev. C 2018, 97, 054320. [Google Scholar] [CrossRef]
- Sugawara, M. Attempt at describing triaxiality of 108,110,112Ru by the generalized triaxial rotor model with independent, variable moments of inertia. Phys. Rev. C 2019, 99, 054323. [Google Scholar] [CrossRef]
- Meyer, U.; Faessler, A.; Khadkikar, S.B. The triaxial rotation vibration model in the Xe-Ba region. Nucl. Phys. A 1997, 624, 391. [Google Scholar] [CrossRef]
- Meyer, U.; Raduta, A.A.; Faessler, A. Description of even-even triaxial nuclei within the coherent state and the triaxial rotation-vibration models. Nucl. Phys. A 1998, 641, 321. [Google Scholar] [CrossRef]
- Faessler, A.; Greiner, W. Die Rotations-Vibrations-Wechselwirkung in deformiertengg-Kernen. Z. Phys. 1962, 168, 425. [Google Scholar] [CrossRef]
- Faessler, A.; Greiner, W. Zur potentiellen Energie der γ-Schwingungen in deformiertengg-Kernen. Z. Phys. 1962, 105, 170. [Google Scholar] [CrossRef]
- Faessler, A.; Greiner, W. Vergleich der Davydov-Theorie mit dem Modell des achsialsymmetrischen Kreisels mit Rotation-Vibrations-Wechselwirkung für deformiertegg-Kerne. Z. Phys. 1964, 177, 190. [Google Scholar] [CrossRef]
- Faessler, A.; Greiner, W.; Sheline, R.K. Nuclear models and the Osmium isotopes. Phys. Rev. 1964, 135, B591. [Google Scholar] [CrossRef]
- Faessler, A.; Greiner, W.; Sheline, R.K. Rotation vibration interaction in deformed nuclei. Nucl. Phys. 1965, 70, 33. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Mullins, S.M.; Bark, R.A.; Gueorguieva, E.; Kau, J.; Komati, F.; Lawrie, J.J.; Maine, P.; Minkova, A.; Murray, S.H.T.; et al. Shape transitional nuclei: What can we learn from the yrare states? or hello the double vacuum; goodbye β-vibrations! AIP Conf. Proc. 2008, 1012, 19. [Google Scholar]
- Sharpey-Schafer, J.F.; Bark, R.A.; Bvumbi, S.P.; Lawrie, E.A.; Lawrie, J.J.; Madiba, T.E.; Majola, S.N.T.; Minkova, A.; Mullins, S.M.; Papka, P.; et al. A double vacuum, configuration dependent pairing and lack of β-vibrations in transitional nuclei: Band structure of N = 88 to N = 91 Nuclei. Nucl. Phys. A 2010, 834, 45c–49c. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Mullins, S.M.; Bark, R.A.; Kau, J.; Komati, F.; Lawrie, E.A.; Lawrie, J.J.; Madiba, T.E.; Maine, P.; Minkova, A.; et al. Congruent band structures in 154Gd: Configuration-dependent pairing, a double vacuum and lack of β-vibrations. Eur. Phys. J. A 2011, 47, 5. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Madiba, T.E.; Bvumbi, S.P.; Lawrie, E.A.; Lawrie, J.J.; Minkova, A.; Mullins, S.M.; Papka, P.; Roux, D.G.; Timár, J. Blocking of coupling to the excitation in 154Gd by the [505]11/2- neutron in 155Gd. Eur. Phys. J. A 2011, 47, 6. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F.; Bark, R.A.; Bvumbi, S.P.; Dinoko, T.R.S.; Majola, S.N.T. “Stiff” deformed nuclei, configuration dependent pairing and the β and γ degrees of freedom. Eur. Phys. J. A 2019, 55, 15. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F. A proton pairing isomer in 174Hf: Reinterpretation of data and support for the split prolate–oblate pairing approximation for deformed nuclei. Eur. Phys. J. A 2023, 59, 183. [Google Scholar] [CrossRef]
- Sharpey-Schafer, J.F. Decline and fall of nuclear β- and γ-vibrations. In Proceedings of the South African Institute of Physics (SAIP), Richards Bay, South Africa, 3–7 July 2023; SAIP: Pretoria, South Africa, 2023; p. 218. [Google Scholar]
- Hess, P.O.; Seiwert, M.; Maruhn, J.; Greiner, W. General collective model and its application to . Z. Phys. A 1980, 296, 147. [Google Scholar] [CrossRef]
- Hess, P.O.; Maruhn, J.; Greiner, W. The general collective model applied to the chains of Pt, Os and W isotopes. J. Phys. G Nucl. Phys. 1981, 7, 737. [Google Scholar] [CrossRef]
- Petkov, P.; Dewald, A.; Andrejtscheff, W. Low-lying collective states in 124–132Ba in the framework of the general collective model. Phys. Rev. C 1995, 51, 2511. [Google Scholar] [CrossRef]
- Gneuss, G.; Greiner, W. Collective potential energy surfaces and nuclear structure. Nucl. Phys. A 1971, 171, 449. [Google Scholar] [CrossRef]
- Próchniak, L.; Rohoziński, S.G. Quadrupole collective states within the Bohr collective Hamiltonian. J. Phys. G Nucl. Part. Phys. 2009, 36, 123101. [Google Scholar] [CrossRef]
- Rowe, D.J. A computationally tractable version of the collective model. Nucl. Phys. A 2004, 735, 372. [Google Scholar] [CrossRef]
- Rowe, D.J.; Turner, P.S. The algebraic collective model. Nucl. Phys. A 2005, 753, 94. [Google Scholar] [CrossRef]
- Rowe, D.J.; Welsh, T.A.; Caprio, M.A. Bohr model as an algebraic collective model. Phys. Rev. C 2009, 79, 054304. [Google Scholar] [CrossRef]
- Rowe, D.J.; Bahri, C. Rotation-vibrational spectra of diatomic molecules and nuclei with Davidson interactions. J. Phys. A Math. Gen. 1998, 31, 4947. [Google Scholar] [CrossRef]
- Davidson, P.M. Eigenfunctions for calculating electronic vibrational intensities. Proc. R. Soc. London Ser. A 1932, 135, 459. [Google Scholar]
- Szpikowski, S.; Góźdź, A. The orthonormal basis for symmetric irreducible representations of O(5)×SU(1, 1) and its application to the interacting boson model. Nucl. Phys. A 1980, 340, 76. [Google Scholar] [CrossRef]
- Rowe, D.J. An algebraic approach to problems with polynomial Hamiltonians on Euclidean spaces. J. Phys. A Math. Gen. 2005, 38, 10181. [Google Scholar] [CrossRef]
- De Baerdemacker, S.; Heyde, K.; Hellemans, V. Quadrupole collective variables in the natural Cartan–Weyl basis. J. Phys. A Math. Theor. 2007, 40, 2733. [Google Scholar] [CrossRef]
- De Baerdemacker, S.; Heyde, K.; Hellemans, V. Spectral properties of a tractable collective Hamiltonian. Phys. Rev. C 2009, 79, 034305. [Google Scholar] [CrossRef]
- Welsh, T.A.; Rowe, D.J. A computer code for calculations in the algebraic collective model of the atomic nucleus. Comput. Phys. Commun. 2016, 200, 220. [Google Scholar] [CrossRef]
- Caprio, M.A. Phonon and multi-phonon excitations in rotational nuclei by exact diagonalization of the Bohr Hamiltonian. Phys. Lett. B 2009, 672, 396. [Google Scholar] [CrossRef]
- Caprio, M.A. Exact diagonalization of the Bohr Hamiltonian for rotational nuclei: Dynamical γ softness and triaxiality. Phys. Rev. C 2011, 83, 064309. [Google Scholar] [CrossRef]
- Thiamova, G.; Abolghasem, M. Algebraic Collective Model and nuclear structure applications. Acta Phys. Polonica B 2014, 45, 1833. [Google Scholar] [CrossRef]
- Thiamova, G. Algebraic Collective Model description of 166Er. Int. J. At. Phys. Phys. 2015, 1, 001. [Google Scholar]
- Iachello, F. Dynamic Symmetries at the Critical Point. Phys. Rev. Lett. 2000, 85, 3580. [Google Scholar] [CrossRef]
- Iachello, F. Analytic description of critical point nuclei in a spherical-axially deformed shape phase transition. Phys. Rev. Lett. 2001, 87, 052502. [Google Scholar] [CrossRef]
- Casten, R.F. Shape phase transitions and critical-point phenomena in atomic nuclei. Nat. Phys. 2006, 2, 811. [Google Scholar] [CrossRef]
- Casten, R.F.; McCutchan, E.A. Quantum phase transitions and structural evolution in nuclei. J. Phys. G Nucl. Part. Phys. 2007, 34, R285. [Google Scholar] [CrossRef]
- Cejnar, P.; Jolie, J.; Casten, R.F. Quantum phase transitions in the shapes of atomic nuclei. Rev. Mod. Phys. 2010, 82, 2155. [Google Scholar] [CrossRef]
- Iachello, F. Quantum phase transitions in mesoscopic systems. Int. J. Mod. Phys. B 2006, 20, 2687. [Google Scholar] [CrossRef]
- Fortunato, L. Solutions of the Bohr Hamiltonian, a compendium. Eur. Phys. J. A 2005, 26 (Suppl. S1), 1. [Google Scholar] [CrossRef]
- Buganu, P.; Fortunato, L. Recent approaches to quadrupole collectivity: Models, solutions and applications based on the Bohr Hamiltonian. J. Phys. G Nucl. Part. Phys. 2016, 43, 093003. [Google Scholar] [CrossRef]
- Iachello, F. Phase transitions in angle variables. Phys. Rev. Lett. 2003, 91, 132502. [Google Scholar] [CrossRef]
- Jolie, J.; Linnemann, A. Prolate-oblate phase transition in the Hf-Hg mass region. Phys. Rev. C 2003, 68, 031301(R). [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A. Z(5): Critical point symmetry for the prolate to oblate nuclear shape phase transition. Phys. Lett. B 2004, 588, 172. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. γ-rigid solution of the Bohr Hamiltonian for γ=30° compared to the E(5) critical point symmetry. Phys. Lett. B 2005, 621, 102. [Google Scholar] [CrossRef]
- Caprio, M.A. Effects of β-γ coupling in transitional nuclei and the validity of the approximate separation of variables. Phys. Rev. C 2005, 72, 054323. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, F.; Luo, Y.-A.; Draayer, J.P. Critical point symmetry for the spherical to triaxially deformed shape phase transition. Phys. Lett. B 2015, 751, 423. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, F.; Liu, Y.-X.; Luo, Y.-A.; Draayer, J.P. γ-rigid solution of the Bohr Hamiltonian for the critical point description of the spherical to γ-rigidly deformed shape phase transition. Phys. Rev. C 2017, 96, 034323. [Google Scholar] [CrossRef]
- Budaca, R.; Budaca, A.I. Emergence of Euclidean dynamical symmetry as a consequence of shape phase mixing. Phys. Lett. B 2016, 759, 349. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Petrellis, D.; Terziev, P.A.; Yigitoglu, I. X(3): An exactly separable γ-rigid version of the X(5) critical point symmetry. Phys. Lett. B 2006, 632, 238. [Google Scholar] [CrossRef]
- Yigitoglu, I.; Bonatsos, D. Bohr Hamiltonian with Davidson potential for triaxial nuclei. Phys. Rev. C 2011, 83, 014303. [Google Scholar] [CrossRef]
- Naderi, L.; Hassanabadi, H. Bohr Hamiltonian with hyperbolic Pöschl-Teller potential for triaxial nuclei. Eur. Phys. J. Plus 2017, 132, 171. [Google Scholar] [CrossRef]
- Ajulo, K.R.; Oyewumi, K.J. Symmetry solutions at γ0=π/6 for nuclei transition between γ0=0 and γ0=π/3 via a variational procedure. Phys. Scr. 2022, 97, 075207. [Google Scholar] [CrossRef]
- Inci, I.; Boztosun, I.; Gonen, Y.E. Bohr Hamiltonian with a finite well for triaxial nuclei. J. Phys. G Nucl. Part. Phys. 2012, 39, 085112. [Google Scholar] [CrossRef]
- Fortunato, L. Soft triaxial rotovibrational motion in the vicinity of γ=π/6. Phys. Rev. C 2004, 70, 011302. [Google Scholar] [CrossRef]
- Fortunato, L.; De Baerdemacker, S.; Heyde, K. Solution of the Bohr Hamiltonian for soft triaxial nuclei. Phys. Rev. C 2006, 74, 014310. [Google Scholar] [CrossRef]
- Fortunato, L.; De Baerdemacker, S.; Heyde, K. Soft triaxial rotor in the vicinity of γ=π/6 and its extensions. Eur. Phys. J. A 2005, 25 (Suppl. S1), 439. [Google Scholar] [CrossRef]
- Lee, J.H. Solution of the Bohr Hamiltonian with the Davidson potential for a soft triaxial shape around γ=π/6 in nuclei. J. Kor. Phys. Soc. 2013, 63, 1907. [Google Scholar] [CrossRef]
- Inci, I. Exactly separable Bohr Hamiltonian with the Morse potential for triaxial nuclei. Int. J. Phys. E 2014, 23, 1450053. [Google Scholar] [CrossRef]
- Chabab, M.; Lahbas, A.; Oulne, M. Bohr Hamiltonian with Hulthén plus ring-shaped potential for triaxial nuclei. Eur. Phys. J. A 2015, 51, 131. [Google Scholar] [CrossRef]
- Neyazi, N.; Rajabi, A.A.; Hassanabadi, H. Exactly separable Bohr Hamiltonian with the Killingbeck potential for triaxial nuclei. Nucl. Phys. A 2016, 945, 80. [Google Scholar] [CrossRef]
- Raduta, A.A.; Buganu, P. Toward a new description of triaxial nuclei. Phys. Rev. C 2011, 83, 034313. [Google Scholar] [CrossRef]
- Buganu, P.; Raduta, A.A.; Faessler, A. New features of the triaxial nuclei described with a coherent state model. J. Phys. G Nucl. Part. Phys. 2012, 39, 025103. [Google Scholar] [CrossRef]
- Buganu, P.; Raduta, A.A. Can the coherent state model describe the triaxial nuclei? Rom. J. Phys. 2012, 57, 1103. [Google Scholar]
- Raduta, A.A.; Buganu, P. Towards a new solvable model for the even-even triaxial nuclei. J. Phys. Conf. Ser. 2013, 413, 012029. [Google Scholar] [CrossRef]
- Raduta, A.A.; Buganu, P. Application of the sextic oscillator potential together with Mathieu and spheroidal functions for triaxial and X(5) type nuclei. Eur. Phys. J. Web Conf. 2014, 66, 02086. [Google Scholar] [CrossRef]
- Alimohammadi, M.; Fortunato, L.; Vitturi, A. Is 198Hg a soft triaxial nucleus with γ=30°? Eur. Phys. J. Plus 2019, 134, 570. [Google Scholar] [CrossRef]
- Yigitoglu, I.; Gokbulut, M. Bohr Hamiltonian for γ=30° with Davidson potential. Eur. Phys. J. Plus 2018, 133, 129. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R. Analytical solution for the Davydov-Chaban Hamiltonian with a sextic potential for γ = 30°. Phys. Rev. C 2015, 91, 014306. [Google Scholar] [CrossRef]
- Buganu, P.; Budaca, R. Quadrupole shape phase transitions in the γ-rigid regime. Bulg. J. Phys. 2015, 42, 513. [Google Scholar]
- Buganu, P.; Budaca, R. Z(4)-Sextic: A γ-rigid solution of the Bohr Hamiltonian with sextic oscillator potential for β and γ = 30°. AIP Conf. Proc. 2015, 1681, 040014. [Google Scholar]
- Budaca, R.; Buganu, P.; Chabab, M.; Lahbas, A.; Oulne, M. Extended study on a quasi-exact solution of the Bohr Hamiltonian. Ann. Phys. 2016, 375, 65. [Google Scholar] [CrossRef]
- Ajulo, K.R.; Oyewumi, K.J.; Orosun, M.M.; Targema, T.V. Relative variation between γ coordinate and the potential of the Bohr Hamiltonian producing X(4) from Z(4). Phys. Scr. 2024, 99, 035306. [Google Scholar] [CrossRef]
- De Baerdemacker, S.; Fortunato, L.; Hellemans, V.; Heyde, K. Solution of the Bohr Hamiltonian for a periodic potential with minimum at γ=π/6. Nucl. Phys. A 2006, 769, 16. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin, Germany, 1980. [Google Scholar]
- Quesne, C.; Tkachuk, V.M. Deformed algebras, position-dependent effective masses and curved spaces: An exactly solvable Coulomb problem. J. Phys. A Math. Gen. 2004, 37, 4267. [Google Scholar] [CrossRef]
- Bagchi, B.; Banerjee, A.; Quesne, C.; Tkachuk, V.M. Deformed shape invariance and exactly solvable Hamiltonians with position-dependent effective mass. J. Phys. A Math. Gen. 2005, 38, 2929. [Google Scholar] [CrossRef]
- Quesne, C. Spectrum generating algebras for position-dependent mass oscillator Schrödinger equations. J. Phys. A Math. Theor. 2007, 40, 13107. [Google Scholar] [CrossRef]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry and quantum mechanics. Phys. Rep. 1995, 251, 267. [Google Scholar] [CrossRef]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry in Quantum Mechanics; World Scientific: Singapore, 2001. [Google Scholar]
- Bonatsos, D.; Georgoudis, P.; Lenis, D.; Minkov, N.; Quesne, C. Bohr Hamiltonian with deformation-dependent mass term. Phys. Lett. B 2010, 683, 264. [Google Scholar] [CrossRef]
- Bonatsos, D.; Georgoudis, P.E.; Lenis, D.; Minkov, N.; Quesne, C. Bohr Hamiltonian with a deformation-dependent mass term for the Davidson potential. Phys. Rev. C 2011, 83, 044321. [Google Scholar] [CrossRef]
- Bonatsos, D.; Georgoudis, P.E.; Minkov, N.; Petrellis, D.; Quesne, C. Bohr Hamiltonian with a deformation-dependent mass term for the Kratzer potential. Phys. Rev. C 2013, 88, 034316. [Google Scholar] [CrossRef]
- Ait El Korchi, S.; Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. Correlation between two quantum concepts within shape phase transitions in nuclei. Europhys. Lett. 2020, 132, 52001. [Google Scholar] [CrossRef]
- Buganu, P.; Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. Davydov–Chaban Hamiltonian with deformation-dependent mass term for γ = 30°. Nucl. Phys. A 2017, 970, 272. [Google Scholar] [CrossRef]
- Ait El Korchi, S.; Baid, S.; Buganu, P.; Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. A γ-rigid solution of the Bohr Hamiltonian with deformation-dependent mass term for Kratzer potential and γ = 30°. Bulg. J. Phys. 2021, 48, 514. [Google Scholar] [CrossRef]
- Ait El Korchi, S.; Baid, P.; Buganu, S.; Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. Davydov-Chaban Hamiltonian with deformation-dependent mass term for the Kratzer potential. Nucl. Phys. A 2022, 1017, 122354. [Google Scholar] [CrossRef]
- Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. On γ-rigid regime of the Bohr–Mottelson Hamiltonian in the presence of a minimal length. Phys. Lett. B 2016, 758, 212. [Google Scholar] [CrossRef]
- Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. Collective motion in prolate γ-rigid nuclei within minimal length concept via a quantum perturbation method. Ann. Phys. 2018, 392, 142. [Google Scholar] [CrossRef]
- Witten, E. Non-commutative geometry and string field theory. Nucl. Phys. B 1986, 268, 253. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. J. High Energy Phys. 1999, 9, 032. [Google Scholar] [CrossRef]
- Kempf, A. Uncertainty relation in quantum mechanics with quantum group symmetry. J. Math. Phys. 1994, 35, 4483. [Google Scholar] [CrossRef]
- Kempf, A. Non-pointlike particles in harmonic oscillators. J. Phys. A Math. Gen. 1997, 30, 2093. [Google Scholar] [CrossRef]
- Gross, D.J.; Mende, P.F. String theory beyond the Planck scale. Nucl. Phys. B 1988, 303, 407. [Google Scholar] [CrossRef]
- Mead, C.A. Possible connection between gravitation and fundamental length. Phys. Rev. 1964, 135, B849. [Google Scholar] [CrossRef]
- Ait El Korchi, S.; Chabab, M.; El Batoul, A.; Lahbas, A.; Oulne, M. Probing DDM and ML quantum concepts in shape phase transitions of γ-unstable nuclei. Nucl. Phys. A 2023, 1037, 122697. [Google Scholar] [CrossRef]
- Formánek, J.; Lombard, R.J.; Mareš, J. Wave equations with energy-dependent potentials. Czech. J. Phys. 2004, 54, 289. [Google Scholar] [CrossRef]
- Lombard, R.J.; Mareš, J.; Volpe, C. Description of heavy quark systems by means of energy dependent potentials. arXiv 2004, arXiv:hep-ph/0411067v1. [Google Scholar]
- Budaca, R. Spherical vibrator model with an energy increasing stiffness. Phys. Lett. B 2015, 751, 39. [Google Scholar] [CrossRef]
- Budaca, A.I.; Budaca, R. Energy-dependent collective excitations in Os and Pt isotopes. Phys. Scr. 2017, 92, 084001. [Google Scholar] [CrossRef]
- Budaca, A.I.; Budaca, R. Description of critical point nuclei within an energy-dependent geometric model. Eur. Phys. J. Plus 2019, 134, 145. [Google Scholar] [CrossRef]
- Budaca, R. Bohr Hamiltonian with an energy-dependent γ-unstable Coulomb-like potential. Eur. Phys. J. A 2016, 52, 314. [Google Scholar] [CrossRef]
- Budaca, A.I.; Budaca, R. Triaxiality and state-dependent shape properties of Xe isotopes. Phys. Rev. C 2020, 101, 064318. [Google Scholar] [CrossRef]
- Hammad, M.M. On the conformable fractional E(5) critical point symmetry. Nucl. Phys. A 2021, 1011, 122203. [Google Scholar] [CrossRef]
- Hammad, M.M. Conformable fractional Bohr Hamiltonian with Bonatsos and double-well sextic potentials. Phys. Scr. 2021, 96, 115304. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic: New York, NY, USA, 1999. [Google Scholar]
- Herrmann, R. Fractional Calculus; World Scientific: Singapore, 2011. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65. [Google Scholar] [CrossRef]
- Hammad, M.M.; Yaqut, A.S.H.; Abdel-Khalek, M.A.; Doma, S.B. Analytical study of conformable fractional Bohr Hamiltonian with Kratzer potential. Nucl. Phys. A 2021, 1015, 122307. [Google Scholar] [CrossRef]
- Hammad, M.M.; Yahia, M.M.; Bonatsos, D. Triaxial nuclei and analytical solutions of the conformable fractional Bohr Hamiltonian with some exponential-type potentials. Nucl. Phys. A 2023, 1030, 122576. [Google Scholar] [CrossRef]
- Ahmadou, K.; Atangana Likéné, A.; Ema’a, J.M.; Takembo, C.N.; Ele Abiama, P.; Ben-Bolie, G.H. Conformable fractional Bohr Hamiltonian with a four inverse power terms potential for triaxial nuclei. Int. J. Mod. Phys. E 2022, 31, 2250039. [Google Scholar] [CrossRef]
- Mayer, M.G.; Jensen, J.H.D. Elementary Theory of Nuclear Shell Structure; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Heyde, K.L.G. The Nuclear Shell Model; Springer: Berlin, Germany, 1990. [Google Scholar]
- Talmi, I. Simple Models of Complex Nuclei: The Shell Model and the Interacting Boson Model; Harwood: Chur, Switzerland, 1993. [Google Scholar]
- Haxel, O.; Jensen, J.H.D.; Suess, H.E. On the “magic numbers” in nuclear structure. Phys. Rev. 1949, 75, 1766. [Google Scholar] [CrossRef]
- Mayer, M.G. On closed shells in nuclei. II. Phys. Rev. 1949, 75, 1969. [Google Scholar] [CrossRef]
- Mayer, M.G. Nuclear configurations in the spin-orbit coupling model. II. Theoretical considerations. Phys. Rev. 1950, 78, 22. [Google Scholar] [CrossRef]
- Mayer, M.G. On closed shells in nuclei. Phys. Rev. 1948, 74, 235. [Google Scholar] [CrossRef]
- Wybourne, B.G. Classical Groups for Physicists; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Moshinsky, M.; Smirnov, Y.F. The Harmonic Oscillator in Modern Physics; Harwood: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Iachello, F. Lie Algebras and Applications; Springer: Berlin, Germany, 2006. [Google Scholar]
- Nilsson, S.G. Binding states of individual nucleons in strongly deformed nuclei. Dan. Mat. Fys. Medd. 1955, 29, 16. [Google Scholar]
- Nilsson, S.G.; Ragnarsson, I. Shapes and Shells in Nuclear Structure; Cambridge U. Press: Cambridge, UK, 1995. [Google Scholar]
- Rainwater, J. Nuclear energy level argument for a spheroidal nuclear model. Phys. Rev. 1950, 79, 432. [Google Scholar] [CrossRef]
- Möller, P.; Rayford Nix, J.R. Nuclear mass formula with a Yukawa-plus-exponential macroscopic model and a folded-Yukawa single-particle potential. Nucl. Phys. A 1981, 361, 117. [Google Scholar] [CrossRef]
- Möller, P.; Nix, J.R. Atomic masses and nuclear ground-state deformations calculated with a new macroscopic-microscopic model. At. Data Nucl. Data Tables 1981, 26, 165. [Google Scholar] [CrossRef]
- Möller, P.; Nix, J.R.; Myers, W.D.; Swiatecki, W.J. Nuclear ground-state masses and deformations. At. Data Nucl. Data Tables 1995, 59, 185. [Google Scholar] [CrossRef]
- Inglis, D.R. Particle derivation of nuclear rotation properties associated with a surface wave. Phys. Rev. 1954, 96, 10591065. [Google Scholar] [CrossRef]
- Inglis, D.R. Nuclear moments of inertia due to nucleon motion in a rotating well. Phys. Rev. 1956, 103, 1786–1795. [Google Scholar] [CrossRef]
- Shen, S.F.; Zheng, S.J.; Xu, F.R.; Wyss, R. Stability of triaxial shapes in ground and excited states of even-even nuclei in the A∼70 region. Phys. Rev. C 2011, 84, 044315. [Google Scholar] [CrossRef]
- Woods, R.D.; Saxon, D.S. Diffuse Surface Optical Model for Nucleon-Nuclei Scattering. Phys. Rev. 1954, 95, 577. [Google Scholar] [CrossRef]
- Caurier, E.; Martínez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Hara, K. Triaxial projected shell model approach. Phys. Rev. Lett. 1999, 82, 3968. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Bhat, G.H.; Dar, W.A.; Jehangir, S.; Ganai, P.A. Microscopic nuclear structure models and methods: Chiral symmetry, wobbling motion and γ-bands. Phys. Scr. 2016, 91, 063015. [Google Scholar] [CrossRef]
- Hara, K.; Sun, Y. Projected shell model and high-spin spectroscopy. Int. J. Mod. Phys. E 1995, 4, 637. [Google Scholar] [CrossRef]
- Bhat, G.H.; Dar, W.A.; Sheikh, J.A.; Sun, Y. Nature of γ deformation in Ge and Se nuclei and the triaxial projected shell model description. Phys. Rev. C 2014, 89, 014328. [Google Scholar] [CrossRef]
- Zhang, C.L.; Bhat, G.H.; Nazarewicz, W.; Sheikh, J.A.; Shi, Y. Theoretical study of triaxial shapes of neutron-rich Mo and Ru nuclei. Phys. Rev. C 2015, 92, 034307. [Google Scholar] [CrossRef]
- Nazir, N.; Jehangir, S.; Rouoof, S.P.; Bhat, G.H.; Sheikh, J.A.; Rather, N.; Frauendorf, S. Microscopic aspects of γ softness in atomic nuclei. Phys. Rev. C 2023, 107, L021303. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Bhat, G.H.; Palit, R.; Naik, Z.; Sun, Y. Multi-quasiparticle γ-band structure in neutron-deficient Ce and Nd isotopes. Nucl. Phys. A 2009, 824, 58. [Google Scholar] [CrossRef]
- Rajput, M.; Singh, S.; Verma, P.; Rani, V.; Bharti, A.; Bhat, G.H.; Sheikh, J.A. Triaxial projected shell model study of γ-bands in even even 104-122Cd nuclei. Nucl. Phys. A 2022, 1019, 122383. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Sun, Y.; Palit, R. Transition quadrupole moments in γ-soft nuclei and the triaxial projected shell model. Phys. Lett. B 2001, 507, 115. [Google Scholar] [CrossRef]
- Sun, Y.; Sheikh, J.A.; Long, G.-L. Nuclear magnetic dipole properties and the triaxial deformation. Phys. Lett. B 2002, 533, 253. [Google Scholar] [CrossRef]
- Sun, Y.; Hara, K.; Sheikh, J.A.; Hirsch, J.G.; Velázquez, V.; Guidry, M. Multiphonon γ-vibrational bands and the triaxial projected shell model. Phys. Rev. C 2000, 61, 064323. [Google Scholar] [CrossRef]
- Sheikh, J.A.; Bhat, G.H.; Sun, Y.; Vakil, G.B.; Palit, R. Triaxial projected shell model study of γ-vibrational bands in even-even Er isotopes. Phys. Rev. C 2008, 77, 034313. [Google Scholar] [CrossRef]
- Jehangir, S.; Bhat, G.H.; Sheikh, J.A.; Frauendorf, S.; Li, W.; Palit, R.; Rather, N. Triaxial projected shell model study of γ-bands in atomic nuclei. Eur. Phys. J. A 2021, 57, 308. [Google Scholar] [CrossRef]
- Honma, M.; Mizusaki, T.; Otsuka, T. Diagonalization of Hamiltonians for many-body systems by auxiliary field quantum Monte Carlo technique. Phys. Rev. Lett. 1995, 75, 1284. [Google Scholar] [CrossRef] [PubMed]
- Honma, M.; Mizusaki, T.; Otsuka, T. Nuclear shell model by the quantum Monte Carlo diagonalization method. Phys. Rev. Lett. 1996, 77, 3315. [Google Scholar] [CrossRef]
- Mizusaki, T.; Honma, M.; Otsuka, T. Quantum Monte Carlo diagonalization with angular momentum projection. Phys. Rev. C 1996, 53, 2786. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, T.; Michio Honma, M.; Mizusaki, T. Structure of the N = Z = 28 closed shell studied by Monte Carlo shell model calculation. Phys. Rev. Lett. 1998, 81, 1588. [Google Scholar] [CrossRef]
- Otsuka, T.; Honma, M.; Mizusaki, T.; Shimizu, N.; Utsuno, Y. Monte Carlo shell model for atomic nuclei. Prog. Part. Nucl. Phys. 2001, 47, 319. [Google Scholar] [CrossRef]
- Shimizu, N.; Abe, T.; Tsunoda, Y.; Utsuno, Y.; Yoshida, T.; Mizusaki, T.; Honma, M.; Otsuka, T. New-generation Monte Carlo shell model for the K computer era. Prog. Theor. Exp. Phys. 2012, 2012, 01A205. [Google Scholar] [CrossRef]
- Bonatsos, D.; Klein, A. Exact boson mappings for nuclear neutron (proton) shell-model algebras having SU(3) subalgebras. Ann. Phys. 1986, 169, 61. [Google Scholar] [CrossRef]
- Elliott, J.P. Collective motion in the nuclear shell model. I. Classification schemes for states of mixed configurations. Proc. R. Soc. A Ser. A 1958, 245, 128. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model II. The introduction of intrinsic wave-functions. Proc. R. Soc. A Ser. A 1958, 245, 562. [Google Scholar]
- Elliott, J.P.; Harvey, M. Collective motion in the nuclear shell model III. The calculation of spectra. Proc. R. Soc. A Ser. A 1963, 272, 557. [Google Scholar]
- Elliott, J.P.; Wilsdon, C.E. Collective motion in the nuclear shell model IV. Odd-mass nuclei in the sd shell. Proc. R. Soc. A Ser. A 1968, 302, 509. [Google Scholar]
- Harvey, M. The nuclear SU3 model. Adv. Nucl. Phys. 1968, 1, 67. [Google Scholar]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge U. Press: Cambridge, UK, 1987. [Google Scholar]
- Kota, V.K.B. SU(3) Symmetry in Atomic Nuclei; Springer Nature: Singapore, 2020. [Google Scholar]
- Castaños, O.; Draayer, J.P.; Leschber, Y. Shape variables and the shell model. Z. Phys. A 1988, 329, 33. [Google Scholar]
- Draayer, J.P.; Park, S.C.; Castaños, O. Shell-model interpretation of the collective-model potential-energy surface. Phys. Rev. Lett. 1989, 62, 20. [Google Scholar] [CrossRef] [PubMed]
- Arima, A.; Harvey, M.; Shimizu, K. Pseudo LS coupling and pseudo SU3 coupling schemes. Phys. Lett. B 1969, 30, 517. [Google Scholar] [CrossRef]
- Hecht, K.T.; Adler, A. Generalized seniority for favored J ≠ 0 pairs in mixed configurations. Nucl. Phys. A 1969, 137, 129. [Google Scholar] [CrossRef]
- Ratna Raju, R.D.; Draayer, J.P.; Hecht, K.T. Search for a coupling scheme in heavy deformed nuclei: The pseudo SU(3) model. Nucl. Phys. A 1973, 202, 433. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J.; Hecht, K.T. Strength of the Qπ · Qν interaction and the strong-coupled pseudo-SU(3) limit. Nucl. Phys. A 1982, 381, 1. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J. Shell-model description of the low-energy structure of strongly deformed nuclei. Phys. Rev. Lett. 1983, 51, 1422. [Google Scholar] [CrossRef]
- Draayer, J.P.; Weeks, K.J. Towards a shell model description of the low-energy structure of deformed nuclei I. Even-even systems. Ann. Phys. 1984, 156, 41. [Google Scholar] [CrossRef]
- Bahri, C.; Draayer, J.P.; Moszkowski, S.A. Pseudospin symmetry in nuclear physics. Phys. Rev. Lett. 1992, 68, 2133. [Google Scholar] [CrossRef]
- Ginocchio, J.N. Pseudospin as a Relativistic Symmetry. Phys. Rev. Lett. 1997, 78, 436. [Google Scholar] [CrossRef]
- Castaños, O.; Moshinsky, M.; Quesne, C. Transformation from U(3) to pseudo U(3) basis. In Group Theory and Special Symmetries in Nuclear Physics (AnnArbor, 1991); Draayer, J.P., Jänecke, J., Eds.; World Scientific: Singapore, 1992; p. 80. [Google Scholar]
- Castaños, O.; Moshinsky, M.; Quesne, C. Transformation to pseudo-SU(3) in heavy deformed nuclei. Phys. Lett. B 1992, 277, 238. [Google Scholar] [CrossRef]
- Castaños, O.; Velázquez, A.V.; Hess, P.O.; Hirsch, J.G. Transformation to pseudo-spin-symmetry of a deformed Nilsson hamiltonian. Phys. Lett. B 1994, 321, 303. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3) symmetry in heavy deformed nuclei. Phys. Rev. C 2017, 95, 064325. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Assimakis, I.E.; Peroulis, S.K.; Sarantopoulou, S.; Cseh, J. Proxy-SU(3) symmetry in the shell model basis. Eur. Phys. J. A 2020, 56, 239. [Google Scholar] [CrossRef]
- Lederer, C.M.; Shirley, V.S. (Eds.) Table of Isotopes, 7th ed.; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Martinou, A.; Bonatsos, D.; Karakatsanis, K.E.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.K.; Minkov, N. Why nuclear forces favor the highest weight irreducible representations of the fermionic SU(3) symmetry. Eur. Phys. J. A 2021, 57, 83. [Google Scholar] [CrossRef]
- Hamamoto, I.; Mottelson, B.R. Further examination of prolate-shape dominance in nuclear deformation. Phys. Rev. C 2009, 79, 034317. [Google Scholar] [CrossRef]
- Hamamoto, I.; Mottelson, B. Shape deformations in atomic nuclei. Scholarpedia 2012, 7, 10693. [Google Scholar]
- Bonatsos, D.; Karakatsanis, K.E.; Martinou, A.; Mertzimekis, T.J.; Minkov, N. Microscopic origin of shape coexistence in the N = 90, Z = 64 region. Phys. Lett. B 2022, 829, 137099. [Google Scholar] [CrossRef]
- Bonatsos, D.; Karakatsanis, K.E.; Martinou, A.; Mertzimekis, T.J.; Minkov, N. Islands of shape coexistence from single-particle spectra in covariant density functional theory. Phys. Rev. C 2022, 106, 044323. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.; Mertzimekis, T.; Minkov, N. Signatures for shape coexistence and shape/phase transitions in even-even nuclei. J. Phys. G Nucl. Part. Phys. 2023, 50, 075105. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.; Minkov, N. Parameter-free predictions for the collective deformation variables β and γ within the pseudo-SU(3) scheme. Eur. Phys. J. Spec. Top. 2020, 229, 2367. [Google Scholar] [CrossRef]
- Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Petrellis, D.; Vasileiou, P.; Mertzimekis, T.J.; Minkov, N. Robustness of the proxy-SU(3) symmetry in atomic nuclei and the role of the next-highest-weight irreducible representation. Symmetry 2024, 16, 1625. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Collective nuclear states as representations of a SU(6) group. Phys. Rev. Lett. 1975, 35, 1069. [Google Scholar] [CrossRef]
- Iachello, F.; Van Isacker, P. The Interacting Boson-Fermion Model; Cambridge U. Press: Cambridge, UK, 1991. [Google Scholar]
- Casten, R.F. (Ed.) Algebraic Approaches to Nuclear Structure: Interacting Boson and Fermion Models; Harwood: Chur, Switzerland, 1993. [Google Scholar]
- Frank, A.; Van Isacker, P. Symmetry Methods in Molecules and Nuclei; S y G Editores: Mexico City, Mexico, 2005. [Google Scholar]
- Arima, A.; Iachello, F. Interacting boson model of collective states I. The vibrational limit. Ann. Phys. 1976, 99, 253. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective nuclear states II. The rotational limit. Ann. Phys. 1978, 111, 201. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. Interacting boson model of collective nuclear states IV. The O(6) limit. Ann. Phys. 1979, 123, 468. [Google Scholar] [CrossRef]
- Casten, R.F. Nuclear Structure from a Simple Perspective; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Ginocchio, J.N.; Kirson, M.W. Relationship between the Bohr collective Hamiltonian and the Interacting-Boson Model. Phys. Rev. Lett. 1980, 44, 1744. [Google Scholar] [CrossRef]
- Dieperink, A.E.L.; Scholten, O.; Iachello, F. Classical limit of the Interacting-Boson Model. Phys. Rev. Lett. 1980, 44, 1747. [Google Scholar] [CrossRef]
- Ginocchio, J.N.; Kirson, M.W. An intrinsic state for the interacting boson model and its relationship to the Bohr-Mottelson model. Nucl. Phys. A 1980, 350, 31. [Google Scholar] [CrossRef]
- Van Isacker, P.; Chen, J.-Q. Classical limit of the interacting boson Hamiltonian. Phys. Rev. C 1981, 24, 684. [Google Scholar] [CrossRef]
- Heyde, K.; Van Isacker, P.; Waroquier, M.; Moreau, J. Triaxial shapes in the interacting boson model. Phys. Rev. C 1984, 29, 1420. [Google Scholar] [CrossRef]
- Meyer-ter-Vehn, J. On the relation between the O(6) limit of the Interacting Boson Model and triaxial nuclear models. In Interacting Bosons in Nuclear Physics; Iachello, F., Ed.; Plenum: New York, NY, USA, 1979; p. 157. [Google Scholar]
- Meyer-ter-Vehn, J. The O(6) limit of the interacting boson model and its relation to triaxial nuclear models. Phys. Lett. B 1979, 84, 10. [Google Scholar] [CrossRef]
- Cizewski, J.A.; Casten, R.F.; Smith, G.J.; Stelts, M.L.; Kane, W.R.; Börner, H.G.; Davidson, W.F. Evidence for a new symmetry in nuclei: The structure of 196Pt and the O(6) limit. Phys. Rev. Lett. 1978, 40, 167. [Google Scholar] [CrossRef]
- Casten, R.F.; Cizewski, J.A. The O(6) → rotor transition in the Pt Os nuclei. Nucl. Phys. A 1978, 309, 477. [Google Scholar] [CrossRef]
- Casten, R.F.; von Brentano, P. An extensive region of O(6)-like nuclei near A=130. Phys. Lett. B 1985, 152, 22. [Google Scholar] [CrossRef]
- Casten, R.F.; von Brentano, P.; Heyde, K.; Van Isacker, P.; Jolie, J. The interplay of γ-softness and triaxiality in O(6)-like nuclei. Nucl. Phys. A 1985, 439, 289. [Google Scholar] [CrossRef]
- Otsuka, T.; Sugita, M. Equivalence between γ instability and rigid triaxiality in finite boson systems. Phys. Rev. Lett. 1987, 59, 1541. [Google Scholar] [CrossRef] [PubMed]
- Sugita, M.; Otsuka, T.; Gelberg, A. Davydov-Filippov limit of the IBM. Nucl. Phys. A 1989, 493, 350. [Google Scholar] [CrossRef]
- Cohen, T.D. Nature of the equivalence between gamma instability and rigid triaxiality for finite boson number. Phys. Rev. C 1988, 38, 1038. [Google Scholar] [CrossRef]
- Gill, R.L.; Chou, W.-T.; Casten, R.F. Axial asymmetry in nearly symmetric deformed nuclei. Nucl. Phys. A 1992, 542, 32. [Google Scholar] [CrossRef]
- Sorgunlu, B.; Van Isacker, P. Triaxiality in the interacting boson model. Nucl. Phys. A 2008, 808, 27. [Google Scholar] [CrossRef]
- Elliott, J.P.; Evans, J.A.; Van Isacker, P. Definition of the shape parameter γ in the Interacting-Boson Model. Phys. Rev. Lett. 1986, 57, 1124. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K. Intrinsic quadrupole moments and shapes of nuclear ground states and excited states. Phys. Rev. Lett. 1972, 28, 249. [Google Scholar] [CrossRef]
- Cline, D. Nuclear shapes studied by Coulomb excitation. Annu. Rev. Nucl. Part. Sci. 1986, 36, 683. [Google Scholar] [CrossRef]
- Werner, V.; Meise, H.; Wiedenhöver, I.; Gade, A.; von Brentano, P. Collective bands in the triaxial nucleus 124Xe. Nucl. Phys. A 2001, 692, 451. [Google Scholar] [CrossRef]
- Werner, V.; Scholl, C.; von Brentano, P. Triaxiality and the determination of the cubic shape parameter K3 from five observables. Phys. Rev. C 2005, 71, 054314. [Google Scholar] [CrossRef]
- Poves, A.; Nowacki, F.; Alhassid, Y. Limits on assigning a shape to a nucleus. Phys. Rev. C 2020, 101, 054307. [Google Scholar] [CrossRef]
- Smirnov, Y.F.; Smirnova, N.A.; Van Isacker, P. SU(3) realization of the rigid asymmetric rotor within the interacting boson model. Phys. Rev. C 2000, 61, 041302(R). [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, F.; Dai, L.-R.; Draayer, J.P. Triaxial rotor in the SU(3) limit of the interacting boson model. Phys. Rev. C 2014, 90, 044310. [Google Scholar] [CrossRef]
- Zhang, Y.; He, Y.-W.; Karlsson, D.; Qi, C.; Pan, F.; Draayer, J.P. A theoretical interpretation of the anomalous reduced E2 transition probabilities along the yrast line of neutron-deficient nuclei. Phys. Lett. B 2022, 834, 137443. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.-N.; Pan, F.; Qi, C.; Draayer, J.P. Triaxial rotor modes in finite-N boson systems. Phys. Rev. C 2024, 110, 024303. [Google Scholar] [CrossRef]
- Pan, F.; Zhang, Y.; Wu, Y.; Dai, L.; Draayer, J.P. B(E2) anomaly along the yrast line in neutron-deficient A≈170 even-even nuclei induced by a triaxial rotor term. Phys. Rev. C 2024, 110, 054324. [Google Scholar] [CrossRef]
- Teng, W.; Wang, S.-N.; Zhang, Y.; Fortunato, L. Triaxial rotor in the O(6) limit of the interacting boson model. Phys. Scr. 2024, 99, 015305. [Google Scholar] [CrossRef]
- Castaños, O.; Frank, A.; Van Isacker, P. Effective triaxial deformations in the Interacting-Boson Model. Phys. Rev. Lett. 1984, 52, 263. [Google Scholar] [CrossRef]
- Casten, R.F.; Aprahamian, A.; Warner, D.D. Axial asymmetry and the determination of effective γ values in the interacting boson approximation. Phys. Rev. C 1984, 29, 356(R). [Google Scholar] [CrossRef]
- Dobeš, J. Interacting boson approximation and triaxial shapes. Phys. Lett. B 1985, 158, 97. [Google Scholar] [CrossRef]
- Caprio, M.A.; Rowe, D.J.; Welsh, T.A. Construction of SO(5)⊃SO(3) spherical harmonics and Clebsch–Gordan coefficients. Comput. Phys. Commun. 2009, 180, 1150. [Google Scholar] [CrossRef]
- Thiamova, G. The IBM description of triaxial nuclei. Eur. Phys. J. A 2010, 45, 81. [Google Scholar] [CrossRef]
- Thiamova, G.; Rowe, D.J.; Caprio, M.A. The relationship between the interacting boson model and the algebraic version of Bohr’s collective model in its triaxial limit. Nucl. Phys. A 2012, 895, 20. [Google Scholar] [CrossRef]
- Jolos, R.V. Phase transitions between axisymmetric and nonaxial nuclear shapes. Phys. At. Nucl. 2004, 67, 931. [Google Scholar] [CrossRef]
- Jolos, R.V. Triple point in the phase transition diagram of a cold nucleus. Phys. Part. Nucl. 2004, 35, 225. [Google Scholar]
- Fortunato, L.; Alonso, C.E.; Arias, J.M.; García-Ramos, J.E.; Vitturi, A. Phase diagram for a cubic-Q interacting boson model Hamiltonian: Signs of triaxiality. Phys. Rev. C 2011, 84, 014326. [Google Scholar] [CrossRef]
- Dieperink, A.E.L.; Bijker, R. On triaxial features in the neutron-proton IBA. Phys. Lett. B 1982, 116, 77. [Google Scholar] [CrossRef]
- Dieperink, A.E.L. Geometrical analysis of the interacting boson model. Prog. Part. Nucl. Phys. 1983, 9, 121. [Google Scholar] [CrossRef]
- Dieperink, A.E.L. The neutron-proton degree of freedom in the IBA model. Nucl. Phys. A 1984, 421, 189–204. [Google Scholar] [CrossRef]
- Iachello, F. Present status of the algebraic approach to nuclear and molecular physics. In Bosons in Nuclei; World Scientific: Singapore, 1984; p. 3. [Google Scholar]
- Dieperink, A.E.L.; Wenes, G. The Interacting Boson Model. Ann. Rev. Nucl. Part. Sci. 1985, 35, 77. [Google Scholar] [CrossRef]
- Walet, N.R.; Brussaard, P.J. A study of the SU(3)* limit of IBM-2. Nucl. Phys. A 1987, 474, 61. [Google Scholar] [CrossRef]
- Dieperink, A.E.L.; Talmi, I. Dynamic symmetries in the proton-neutron interacting boson model (IBA-2). Phys. Lett. B 1983, 131, 1. [Google Scholar] [CrossRef]
- Arias, J.M.; García-Ramos, J.E.; Dukelsky, J. Phase diagram of the proton-neutron Interacting Boson Model. Phys. Rev. Lett. 2004, 93, 212501. [Google Scholar] [CrossRef]
- Arias, J.M.; Dukelsky, J.; García-Ramos, J.E. Critical points in the Interacting Boson Model. AIP Conf. Proc. 2004, 726, 127. [Google Scholar]
- Caprio, M.A.; Iachello, F. Phase structure of the two-fluid proton-neutron system. Phys. Rev. Lett. 2004, 93, 242502. [Google Scholar] [CrossRef] [PubMed]
- Caprio, M.A. The transition between axial and triaxial structure in the IBM-2. AIP Conf. Proc. 2004, 726, 215. [Google Scholar]
- Sevrin, A.; Heyde, K.; Jolie, J. Triaxiality in the proton-neutron interacting boson model: Systematic study of perturbations in the SU*(3) limit. Phys. Rev. C 1987, 36, 2621. [Google Scholar] [CrossRef]
- Sevrin, A.; Heyde, K.; Jolie, J. Triaxiality in the proton-neutron interacting boson model: Perturbed O(6) symmetry with application to the mass A≃130 Xe, Ba nuclei. Phys. Rev. C 1987, 36, 2631. [Google Scholar] [CrossRef]
- Caprio, M.A.; Iachello, F. Phase structure of a two-fluid bosonic system. Ann. Phys. 2005, 318, 454. [Google Scholar] [CrossRef]
- Leviatan, A.; Kirson, M.W. Normal modes of the neutron-proton interacting-boson model of nuclei. Ann. Phys. 1990, 201, 13. [Google Scholar] [CrossRef]
- Ginocchio, J.N.; Leviatan, A. Neutron-proton collective motion. I. Nuclear shapes. Ann. Phys. 1992, 216, 152. [Google Scholar] [CrossRef]
- Duarte, J.L.M.; Borello-Lewin, T.; Maino, G.; Zuffi, L. Effective triaxial deformations of even-even Ru isotopes in the neutron-proton interacting boson model. Phys. Rev. C 1998, 57, 1539. [Google Scholar] [CrossRef]
- Wang, T.; He, B.-C.; Li, D.-K.; Zhou, C.-X. Prolate-oblate asymmetric shape phase transition in the interacting boson model with SU(3) higher-order interactions. Phys. Rev. C 2023, 107, 064322. [Google Scholar] [CrossRef]
- Wang, T.; He, B.-C.; Zhou, C.-X.; Li, D.-K.; Fortunato, L. Emerging γ-soft-like spectrum in 196Pt in the SU3-IBM (I). Chin. Phys. C 2024, 48, 094102. [Google Scholar] [CrossRef]
- Georgieva, A.; Raychev, P.; Roussev, R. Interacting two-vector-boson model of collective motions in nuclei. J. Phys. G Nucl. Phys. 1982, 8, 1377. [Google Scholar] [CrossRef]
- Georgieva, A.; Raychev, P.; Roussev, R. Rotational limit of the interacting two-vector boson model. J. Phys. G Nucl. Phys. 1983, 9, 521. [Google Scholar] [CrossRef]
- Georgieva, A.I.; Ganev, H.G.; Draayer, J.P.; Garistov, V.P. Description of mixed-mode dynamics within the symplectic extension of the Interacting Vector Boson Model. Phys. Part. Nucl. 2009, 40, 461. [Google Scholar] [CrossRef]
- Bargmann, V.; Moshinsky, M. Group theory of harmonic oscillators: (I). The collective modes. Nucl. Phys. 1960, 18, 697. [Google Scholar] [CrossRef]
- Bargmann, V.; Moshinsky, M. Group theory of harmonic oscillators (II). The integrals of Motion for the quadrupole-quadrupole interaction. Nucl. Phys. 1961, 23, 177. [Google Scholar] [CrossRef]
- Roussev, R.P.; Raychev, P.P.; Smirnov, Y.F. Generating function for the Interacting Vector Boson Model. I.Basis of Bargmann-Moshinsky. Bulg. J. Phys. 1990, 178, 273. [Google Scholar]
- Ganev, H.G. Triaxial shapes in the interacting vector boson model. Phys. Rev. C 2011, 84, 054318. [Google Scholar] [CrossRef]
- Minkov, N.; Drenska, S.B.; Raychev, P.P.; Roussev, R.P.; Bonatsos, D. Broken SU(3) symmetry in deformed even-even nuclei. Phys. Rev. C 1997, 55, 2345. [Google Scholar] [CrossRef]
- Minkov, N.; Drenska, S.B.; Raychev, P.P.; Roussev, R.P.; Bonatsos, D. Ground-γ band coupling in heavy deformed nuclei and SU(3) contraction limit. Phys. Rev. C 1999, 60, 034305. [Google Scholar] [CrossRef]
- Minkov, N.; Drenska, S.B.; Raychev, P.P.; Roussev, R.P.; Bonatsos, D. Ground-γ band mixing and odd-even staggering in heavy deformed nuclei. Phys. Rev. C 2000, 61, 064301. [Google Scholar] [CrossRef]
- Minkov, N.; Bonatsos, D. On a vector boson model realization of the proxy-SU(3) symmetry. EPJ Web Conf. 2024, 304, 04001. [Google Scholar] [CrossRef]
- Raduta, A.A.; Ceausescu, V.; Gheorghe, A.; Dreizler, R.M. Boson description of 190Pt and 192Pt. Phys. Lett. B 1981, 99, 444. [Google Scholar] [CrossRef]
- Raduta, A.A.; Ceausescu, V.; Gheorghe, A.; Dreizler, R.M. Phenomenological description of three interacting collective bands. Nucl. Phys. A 1982, 381, 253. [Google Scholar] [CrossRef]
- Raduta, A.A. Nuclear Structure with Coherent States; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Bender, M.; Heenen, P.-H.; Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar] [CrossRef]
- Greiner, W.; Maruhn, J.A. Nuclear Models; Springer: Berlin, Germany, 1996. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Gogny, D. Hartree-Fock Bogolyubov method with density-dependent interaction. In Proceedings of the International Conference on Nuclear Physics, Munich, Germany, 27 August–1 September 1973; de Boer, J., Mang, H.J., Eds.; North Holland: Amsterdam, The Netherlands, 1973; p. 48. [Google Scholar]
- Gogny, D. Perturbation theory with a soft core two nucleon interaction. In Proceedings of the International Conference on Nuclear Self-Consistent Fields, Trieste, Italy, 24–28 February 1975; Ripka, G., Porneuf, M., Eds.; North Holland: Amsterdam, The Netherlands, 1975; p. 149. [Google Scholar]
- Skyrme, T.H.R. CVII. The nuclear surface. Phil. Mag. 1956, 1, 1043. [Google Scholar] [CrossRef]
- Skyrme, T.H.R. The spin-orbit interaction in nuclei. Nucl. Phys. 1959, 9, 615. [Google Scholar] [CrossRef]
- Klüpfel, P.; Reinhard, P.-G.; Bürvenich, T.J.; Maruhn, J.A. Variations on a theme by Skyrme: A systematic study of adjustments of model parameters. Phys. Rev. C 2009, 79, 034310. [Google Scholar] [CrossRef]
- Erler, J.; Klüpfel, P.; Reinhard, P.-G. Self-consistent nuclear mean-field models: Example Skyrme–Hartree–Fock. J. Phys. G Nucl. Part. Phys. 2011, 38, 033101. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Baczyk, P.; Becker, P.; Bender, M.; Bennaceur, K.; Bonnard, J.; Gao, Y.; Idini, A.; Konieczka, M.; Kortelainen, M.; et al. Solution of universal nonrelativistic nuclear DFT equations in the Cartesian deformed harmonic-oscillator basis. (IX) HFODD (v3.06h): A new version of the program. J. Phys. G Nucl. Part. Phys. 2021, 48, 102001. [Google Scholar] [CrossRef]
- Chen, M.; Li, T.; Schuetrumpf, B.; Reinhard, P.-G.; Nazarewicz, W. Three-dimensional Skyrme Hartree-Fock-Bogoliubov solver in coordinate-space representation. Comput. Phys. Commun. 2022, 276, 108344. [Google Scholar] [CrossRef]
- Reinhard, P.-G. The relativistic mean-field description of nuclei and nuclear dynamics. Rep. Prog. Phys. 1989, 52, 439. [Google Scholar] [CrossRef]
- Ring, P. Relativistic Mean Field Theory in Finite Nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; König, J.; Ring, P. New parametrization for the Lagrangian density of relativistic mean field theory. Phys. Rev. C 1997, 55, 540. [Google Scholar] [CrossRef]
- Ring, P.; Gambhir, Y.K.; Lalazissis, G.A. Computer program for the relativistic mean field description of the ground state properties of even-even axially deformed nuclei. Comp. Phys. Commun. 1997, 105, 77. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Niksšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.V.; Lalazissis, G.A.; Ring, P. Relativistic Hartree–Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101. [Google Scholar] [CrossRef]
- Niksšić, T.; Vretenar, D.; Ring, P. Beyond the relativistic mean-field approximation: Configuration mixing of angular-momentum-projected wave functions. Phys. Rev. C 2006, 73, 034308. [Google Scholar] [CrossRef]
- Niksšić, T.; Vretenar, D.; Ring, P. Beyond the relativistic mean-field approximation. II. Configuration mixing of mean-field wave functions projected on angular momentum and particle number. Phys. Rev. C 2006, 74, 064309. [Google Scholar] [CrossRef]
- Niksšić, T.; Li, Z.P.; Vretenar, D.; Próchniak, L.; Meng, J.; Ring, P. Beyond the relativistic mean-field approximation. III. Collective Hamiltonian in five dimensions. Phys. Rev. C 2009, 79, 034303. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.Y.; Ring, P. A finite range pairing force for density functional theory in superfluid nuclei. Phys. Lett. B 2009, 676, 44. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.-Y.; Ring, P. Axially deformed relativistic Hartree Bogoliubov theory with a separable pairing force. Phys. Rev. C 2009, 80, 024313. [Google Scholar] [CrossRef]
- Maruhn, J.A.; Reinhard, P.-G.; Stevenson, P.D.; Umar, A.S. The TDHF code Sky3D. Comput. Phys. Commun. 2014, 185, 2195. [Google Scholar] [CrossRef]
- Reinhard, P.-G.; Schuetrumpf, B.; Maruhn, J.A. The axial Hartree-Fock + BCS code SkyAx. Comput. Phys. Commun. 2021, 258, 107603. [Google Scholar] [CrossRef]
- Niksšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comp. Phys. Commun. 2014, 185, 1808. [Google Scholar] [CrossRef]
- Dobaczewski, J. Current developments in nuclear density functional methods. J. Phys. Conf. Ser. 2011, 312, 092002. [Google Scholar] [CrossRef]
- Dobaczewski, J.; Bennaceur, K.; Raimondi, F. Effective theory for low-energy nuclear energy density functionals. J. Phys. G Nucl. Part. Phys. 2012, 39, 125103. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Drut, J.E.; Furnstahl, R.J.; Platter, L. Toward ab initio density functional theory for nuclei. Prog. Part. Nucl. Phys. 2010, 64, 120. [Google Scholar] [CrossRef]
- Åberg, S. Quadrupole operators in triaxial nuclei. Phys. Lett. B 1985, 157, 9. [Google Scholar] [CrossRef]
- Ragnarsson, I. Shell-energy ridges and valleys caused by special symmetries for triaxial nuclear shapes. Phys. Rev. Lett. 1989, 62, 2084. [Google Scholar] [CrossRef]
- Beuschel, T.; Blokhin, A.L.; Draayer, J.P. On the validity of the pseudo-spin concept for triaxially deformed nuclei. Nucl. Phys. A 1997, 619, 119. [Google Scholar] [CrossRef]
- Strutinsky, V.M. Shell effects in nuclear masses and deformation energies. Nucl. Phys. A 1967, 95, 420. [Google Scholar] [CrossRef]
- Ragnarsson, I.; Nilsson, S.G. Shell structure in nuclei. Phys. Rep. 1978, 45, 1. [Google Scholar] [CrossRef]
- Chasman, R.R.; Ahmad, I. Triaxiality and reflection asymmetry in the mass region A∼220. Phys. Lett. B 1986, 182, 261. [Google Scholar] [CrossRef]
- Luo, W.D.; Chen, Y.S. The triaxial motion in Mo isotopes. Nucl. Phys. 1993, 564, 413. [Google Scholar] [CrossRef]
- Juodagalvis, A.; Ragnarsson, I.; Åberg, S. Triaxiality in 48Cr. Phys. Lett. B 2000, 477, 66. [Google Scholar] [CrossRef]
- Nayak, S.S.; Mukherjee, G. Study of shape evolution of nuclei with 40 ≤ Z ≤ 48 and 50 < N < 60. Nucl. Phys. A 2022, 1023, 122449. [Google Scholar]
- Nomura, K.; Shimizu, N.; Otsuka, T. Mean-field derivation of the Interacting Boson Model Hamiltonian and exotic nuclei. Phys. Rev. Lett. 2008, 101, 142501. [Google Scholar] [CrossRef]
- Nomura, K.; Shimizu, N.; Otsuka, T. Formulating the interacting boson model by mean-field methods. Phys. Rev. C 2010, 81, 044307. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Shimizu, N.; Guo, L. Microscopic formulation of the interacting boson model for rotational nuclei. Phys. Rev. C 2011, 83, 041302. [Google Scholar] [CrossRef]
- Nomura, K.; Niksšić, T.; Otsuka, T.; Shimizu, N.; Vretenar, D. Quadrupole collective dynamics from energy density functionals: Collective Hamiltonian and the interacting boson model. Phys. Rev. C 2011, 84, 014302. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P.; Regan, P.H.; Stevenson, P.D.; Podolyák, Z. Spectroscopic calculations of the low-lying structure in exotic Os and W isotopes. Phys. Rev. C 2011, 83, 054303. [Google Scholar] [CrossRef]
- Nomura, K.; Otsuka, T.; Rodríguez-Guzmán, R.; Robledo, L.M.; Sarriguren, P. Collective structural evolution in neutron-rich Yb, Hf, W, Os, and Pt isotopes. Phys. Rev. C 2011, 84, 054316. [Google Scholar] [CrossRef]
- Nomura, K.; Shimizu, N.; Vretenar, D.; Niksšić, T.; Otsuka, T. Robust regularity in γ-soft nuclei and its microscopic realization. Phys. Rev. Lett. 2012, 108, 132501. [Google Scholar] [CrossRef] [PubMed]
- Nomura, K.; Vretenar, D.; Li, Z.P.; Xiang, J. Coupling of pairing and triaxial shape vibrations in collective states of γ-soft nuclei. Phys. Rev. C 2021, 103, 054322. [Google Scholar] [CrossRef]
- Nomura, K.; Vretenar, D.; Li, Z.P.; Xiang, J. Interplay between pairing and triaxial shape degrees of freedom in Os and Pt nuclei. Phys. Rev. C 2021, 104, 024323. [Google Scholar] [CrossRef]
- Vasileiou, P.; Bonatsos, D.; Mertzimekis, T.J. Mean-field-derived IBM-1 Hamiltonian with intrinsic triaxial deformation. Phys. Rev. C 2024, 110, 014313. [Google Scholar] [CrossRef]
- Vasileiou, P.; Bonatsos, D.; Mertzimekis, T.J. Triaxiality in Er isotopes in the framework of IBM-1. Phys. Scr. 2025, 100, 055306. [Google Scholar] [CrossRef]
- Bonche, P.; Flocard, H.; Heenen, P.H.; Krieger, S.J.; Weiss, M.S. Self-consistent study of triaxial deformations: Application to the isotopes of Kr, Sr, Zr and Mo. Nucl. Phys. A 1985, 443, 39. [Google Scholar] [CrossRef]
- Dutta, A.K.; Pearson, J.M.; Tondeur, F. Triaxial nuclei calculated with the extended Thomas-Fermi plus Strutinsky integral (ETFSI) method. Phys. Rev. C 2000, 61, 054303. [Google Scholar] [CrossRef]
- Flerackers, E.; Knuyt, G.; Bouten, M. Triaxial deformation in the 1p shell. Phys. Lett. B 1997, 76, 139. [Google Scholar] [CrossRef]
- Giraud, B.; Sauer, P.U. Restoration of rotational symmetry for triaxial Hartree-Fock solutions. Phys. Lett. B 1969, 30, 218. [Google Scholar] [CrossRef]
- Gupta, K.K.; Varshney, V.P.; Gupta, D.K. Experimental evidence in support of triaxial shape of 150,152,154Sm nuclei. Phys. Rev. C 1982, 26, 685. [Google Scholar] [CrossRef]
- Parikh, J.C. Consequences of a triaxial intrinsic state for 24Mg. Phys. Lett. B 1968, 26, 607. [Google Scholar] [CrossRef]
- Redon, N.; Meyer, J.; Meyer, M.; Quentin, P.; Weiss, M.S.; Bonche, P.; Flocard, H.; Heenen, P.-H. A self-consistent study of triaxial deformations in heavy nuclei. Phys. Lett. B 1986, 181, 223. [Google Scholar] [CrossRef]
- Sahu, R.; Satpathy, M.; Ansari, A.; Satpathy, L. Triaxial description of 188Os and 188Pt. Phys. Rev. C 1979, 19, 511. [Google Scholar] [CrossRef]
- van Dalen, E.N.E.; Müther, H. Triaxial deformation in nuclei with realistic NN interactions. Phys. Rev. C 2014, 90, 034312. [Google Scholar] [CrossRef]
- Girod, M.; Grammaticos, B. Quest for triaxial nuclei: Some Hartree-Bogoliubov predictions. Phys. Rev. Lett. 1978, 40, 361. [Google Scholar] [CrossRef]
- Hayashi, A.; Hara, K.; Ring, P. Existence of triaxial shapes in transitional nuclei. Phys. Rev. Lett. 1984, 53, 337. [Google Scholar] [CrossRef]
- Bonche, P.; Dobaczewski, J.; Flocard, H.; Heenen, P.-H. Generator coordinate method for triaxial quadrupole collective dynamics in strontium isotopes. Nucl. Phys. A 1991, 530, 149. [Google Scholar] [CrossRef]
- Oi, M.; Walker, P.M. Three-dimensional rotation of even–even triaxial nuclei. Phys. Lett. B 2003, 576, 75. [Google Scholar] [CrossRef]
- Hinohara, N.; Kanada-En’yo, Y. Triaxial quadrupole deformation dynamics in sd-shell nuclei around 26Mg. Phys. Rev. C 2011, 83, 014321. [Google Scholar] [CrossRef]
- Chen, F.-Q.; Egido, J.L. Triaxial shape fluctuations and quasiparticle excitations in heavy nuclei. Phys. Rev. C 2017, 95, 024307. [Google Scholar] [CrossRef]
- Schuck, P.; Urban, M. Macroscopic manifestations of rotating triaxial superfluid nuclei. Phys. Rev. C 2019, 100, 031301(R). [Google Scholar] [CrossRef]
- Girod, M.; Grammaticos, B. Triaxial Hartree-Fock-Bogolyubov calculations with D1 effective interaction. Phys. Rev. C 1983, 27, 2317. [Google Scholar] [CrossRef]
- Girod, M.; Delaroche, J.-P.; Görgen, A.; Obertelli, A. The role of triaxiality for the coexistence and evolution of shapes in light krypton isotopes. Phys. Lett. B 2009, 676, 39. [Google Scholar] [CrossRef]
- Robledo, L.M.; Rodríguez-Guzmán, R.; Sarriguren, P. Role of triaxiality in the ground-state shape of neutron-rich Yb, Hf, W, Os and Pt isotopes. J. Phys. G Nucl. Part. Phys. 2009, 36, 115104. [Google Scholar] [CrossRef]
- Rodríguez, T.R.; Egido, J.L. Triaxial angular momentum projection and configuration mixing calculations with the Gogny force. Phys. Rev. C 2010, 81, 064323. [Google Scholar] [CrossRef]
- Rodríguez-Guzmán, R.; Sarriguren, P.; Robledo, L.M.; García-Ramos, J.E. Mean field study of structural changes in Pt isotopes with the Gogny interaction. Phys. Rev. C 2010, 81, 024310. [Google Scholar] [CrossRef]
- Rodríguez-Guzmán, R.; Sarriguren, P.; Robledo, L.M.; Perez-Martin, S. Charge radii and structural evolution in Sr, Zr, and Mo isotopes. Phys. Lett. B 2010, 691, 202. [Google Scholar] [CrossRef]
- Tagami, S.; Shimizu, Y.R. Infinitesimal cranking for triaxial angular-momentum-projected configuration-mixing calculations and its application to the γ vibrational band. Phys. Rev. C 2016, 93, 024323. [Google Scholar] [CrossRef]
- Suzuki, Y.; Kimura, M. Triaxial deformation and the disappearance of the N=28 shell gap. Phys. Rev. C 2021, 104, 024327. [Google Scholar] [CrossRef]
- Heenen, P.-H.; Bonche, P.; Dobaczewski, J.; Flocard, H. Generator-coordinate method for triaxial quadrupole dynamics in Sr isotopes (II). Results for particle-number-projected states. Nucl. Phys. A 1993, 561, 367. [Google Scholar] [CrossRef]
- Shi, Y.; Dobaczewski, J.; Frauendorf, S.; Nazarewicz, W.; Pei, J.C.; Xu, F.R.; Nikolov, N. Self-consistent tilted-axis-cranking study of triaxial strongly deformed bands in 158Er at ultrahigh spin. Phys. Rev. Lett. 2012, 108, 092501. [Google Scholar] [CrossRef] [PubMed]
- Fracasso, S.; Suckling, E.B.; Stevenson, P.D. Unrestricted Skyrme-tensor time-dependent Hartree-Fock model and its application to the nuclear response from spherical to triaxial nuclei. Phys. Rev. C 2012, 86, 044303. [Google Scholar] [CrossRef]
- Benrabia, K.; Medjadi, D.E.; Imadalou, M.; Quentin, P. Triaxial quadrupole dynamics and the inner fission barrier of some heavy even-even nuclei. Phys. Rev. C 2017, 96, 034320. [Google Scholar] [CrossRef]
- Scamps, G.; Goriely, S.; Olsen, E.; Bender, M.; Ryssens, W. Skyrme-Hartree-Fock-Bogoliubov mass models on a 3D mesh: Effect of triaxial shape. Eur. Phys. J. A 2021, 57, 333. [Google Scholar] [CrossRef]
- Washiyama, K.; Yoshida, K. Triaxial-shape dynamics in the low-lying excited 0+ state: Role of the collective mass. Phys. Rev. C 2023, 108, 014323. [Google Scholar] [CrossRef]
- Koepf, W.; Ring, P. Has the nucleus 24Mg a triaxial shape? A relativistic investigation. Phys. Lett. B 1988, 212, 397. [Google Scholar] [CrossRef]
- Hirata, D.; Sumiyoshi, K.; Carlson, B.V.; Toki, H.; Tanihata, I. Triaxial deformation of unstable nuclei in the relativistic mean-field theory. Nucl. Phys. A 1996, 609, 131. [Google Scholar] [CrossRef]
- Abusara, H.; Ahmad, S.; Othman, S. Triaxiality softness and shape coexistence in Mo and Ru isotopes. Phys. Rev. C 2017, 95, 054302. [Google Scholar] [CrossRef]
- El Bassem, Y.; El Adri, M.; El Batoul, A.; Oulne, M. Shape evolution and shape coexistence in even-even Mo isotopic chain. Nucl. Phys. A 2024, 1043, 122831. [Google Scholar] [CrossRef]
- Yao, J.M.; Meng, J.; Ring, P.; Vretenar, D. Configuration mixing of angular-momentum-projected triaxial relativistic mean-field wave functions. Phys. Rev. C 2010, 81, 044311. [Google Scholar] [CrossRef]
- Nikšić, T.; Ring, P.; Vretenar, D.; Tian, Y.; Ma, Z.-Y. 3D relativistic Hartree-Bogoliubov model with a separable pairing interaction: Triaxial ground-state shapes. Phys. Rev. C 2010, 81, 054318. [Google Scholar] [CrossRef]
- Yao, J.M.; Mei, H.; Chen, H.; Meng, J.; Ring, P.; Vretenar, D. Configuration mixing of angular-momentum-projected triaxial relativistic mean-field wave functions. II. Microscopic analysis of low-lying states in magnesium isotopes. Phys. Rev. C 2011, 83, 014308. [Google Scholar] [CrossRef]
- Xiang, J.; Yao, J.M.; Fu, Y.; Wang, Z.H.; Li, Z.P.; Long, W.H. Novel triaxial structure in low-lying states of neutron-rich nuclei around A≈100. Phys. Rev. C 2016, 93, 054324. [Google Scholar] [CrossRef]
- Naz, T.; Bhat, G.H.; Jehangir, S.; Ahmad, S.; Sheikh, J.A. Microscopic description of structural evolution in Pd, Xe, Ba, Nd, Sm, Gd and Dy isotopes. Nucl. Phys. A 2018, 979, 1. [Google Scholar] [CrossRef]
- Yang, X.Q.; Wang, L.J.; Xiang, J.; Wu, X.Y.; Li, Z.P. Microscopic analysis of prolate-oblate shape phase transition and shape coexistence in the Er-Pt region. Phys. Rev. C 2021, 103, 054321. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Casten, R.F. Signatures of γ softness or triaxiality in low energy nuclear spectra. Phys. Lett. B 1991, 260, 265. [Google Scholar] [CrossRef]
- McCutchan, E.A.; Bonatsos, D.; Zamfir, N.V.; Casten, R.F. Staggering in γ-band energies and the transition between different structural symmetries in nuclei. Phys. Rev. C 2007, 76, 024306. [Google Scholar] [CrossRef]
- Bonatsos, D.; Lenis, D.; Minkov, N.; Raychev, P.P.; Terziev, P.A. Sequence of potentials interpolating between the U(5) and E(5) symmetries. Phys. Rev. C 2004, 69, 044316. [Google Scholar] [CrossRef]
- Bés, D.R. The γ-dependent part of the wave functions representing γ-unstable surface vibrations. Nucl. Phys. 1959, 10, 373. [Google Scholar] [CrossRef]
- Rakavy, G. The classification of states of surface vibrations. Nucl. Phys. 1957, 4, 289. [Google Scholar] [CrossRef]
- Liao, J.-Z. Staggering in low-spin nuclear spectra of γ-soft or triaxial nuclei. Phys. Rev. C 1995, 51, 141. [Google Scholar]
- Grosse, E.; Junghans, A.R. Broken axial symmetry as essential feature for a consistent modelling of various observables in heavy nuclei. Phys. Lett. B 2022, 833, 137328. [Google Scholar] [CrossRef]
- Casten, R.F.; Cakirli, R.B.; Bonatsos, D.; Blaum, K. Simple new signature of structure in deformed nuclei: Distinguishing the nature of axial asymmetry. Phys. Rev. C 2020, 102, 054310. [Google Scholar] [CrossRef]
- Bonatsos, D.; Assimakis, I.E.; Martinou, A.; Sarantopoulou, S.; Peroulis, S.K.; Minkov, N. Energy differences of ground state and γ1 bands as a hallmark of collective behavior. Nucl. Phys. A 2021, 1009, 122158. [Google Scholar] [CrossRef]
- Martinou, A.; Bonatsos, D.; Minkov, N.; Assimakis, I.E.; Sarantopoulou, S.; Peroulis, S. Highest weight SU(3) irreducible representations for nuclei with shape coexistence. arXiv 2018, arXiv:1810.11870. [Google Scholar]
- ENSDF Database. Available online: https://www.nndc.bnl.gov/ensdf (accessed on 1 March 2025).
- Sarantopoulou, S.; Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3) symmetry in heavy nuclei: Prolate dominance and prolate-oblate shape transition. Bulg. J. Phys. 2017, 44, 417. [Google Scholar]
- Bonatsos, D.; Martinou, A.; Sarantopoulou, S.; Assimakis, I.E.; Peroulis, S.; Minkov, N. Approximate SU(3) symmetries in heavy deformed nuclei. In Proceedings of the 5th Workshop of the Hellenic Institute of Nuclear Physics (HINPw5), Thessaloniki, Greece, 12–13 April 2019; Moustakidis, C., Ed.; p. 61. Available online: http://hinp.physics.uoi.gr (accessed on 24 May 2025).
- Martinou, A.; Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Parameter free predictions within the proxy-SU(3) model. Bulg. J. Phys. 2017, 44, 407. [Google Scholar]
- Martinou, A.; Peroulis, S.; Bonatsos, D.; Assimakis, I.E.; Sarantopoulou, S.; Minkov, N.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Parameter-independent predictions for nuclear shapes and B(E2) transition rates in the proxy-SU(3) model. arXiv 2017, arXiv:1712.04134. [Google Scholar] [CrossRef][Green Version]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Peroulis, S.K.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Proxy-SU(3): A symmetry for heavy nuclei. Bulg. J. Phys. 2017, 44, 385. [Google Scholar]
- Bonatsos, D.; Assimakis, I.E.; Minkov, N.; Martinou, A.; Sarantopoulou, S.; Cakirli, R.B.; Casten, R.F.; Blaum, K. Parameter-independent predictions for shape variables of heavy deformed nuclei in the proxy-SU(3) model. arXiv 2017, arXiv:1706.05832. [Google Scholar]
- Bonatsos, D.; Assimakis, I.E.; Martinou, A.; Peroulis, S.K.; Sarantopoulou, S.; Minkov, N. Proxy-SU(3) symmetry for heavy deformed nuclei: Nuclear spectra. Bulg. J. Phys. 2019, 46, 325. [Google Scholar]
- Peroulis, S.K. Electric Quadrupole Transitions in the Framework of Algebraic Collective Models. Master’s Thesis, National Technical U. of Athens, Athens, Greece, 2021. (In Greek). [Google Scholar]
- Vasileiou, P.; Bonatsos, D.; Mertzimekis, T.J. Investigating quadrupole bands in 180Hf and 182W. Acta Phys. Polon. B Proc. Suppl. 2025, 18, 2-A23. [Google Scholar]
- Vasileiou, P. Private communication. 2025. [Google Scholar]
- Kleemann, J.; Pietralla, N.; Friman-Gayer, U.; Isaak, J.; Papst, O.; Prifti, K.; Werner, V.; Ayangeakaa, A.D.; Beck, T.; Coló, G.; et al. Gamma decay of the 154Sm isovector giant dipole resonance: Smekal-Raman scattering as a novel probe of nuclear ground-state deformation. Phys. Rev. Lett. 2025, 134, 022503. [Google Scholar] [CrossRef]
- Lesher, S.R.; Aprahamian, A.; Trache, L.; Oros-Peusquens, O.; Deyliz, S.; Gollwitzer, A.; Hertenberger, R.; Valnion, B.D.; Graw, G. New 0+ states in 158Gd. Phys. Rev. C 2002, 66, 051305(R). [Google Scholar] [CrossRef]
- Aprahamian, A. What is the nature of Kπ=0+ bands in deformed nuclei? AIP Conf. Proc. 2002, 638, 77. [Google Scholar]
- Wirth, H.-F.; Graw, G.; Christen, S.; Cutoiu, D.; Eisermann, Y.; Günther, C.; Hertenberger, R.; Jolie, J.; Levon, A.I.; Möller, O.; et al. 0+ states in deformed actinide nuclei by the (p,t) reaction. Phys. Rev. C 2004, 69, 044310. [Google Scholar] [CrossRef]
- Bucurescu, D.; Graw, G.; Hertenberger, R.; Wirth, H.-F.; Lo Iudice, N.; Sushkov, A.V.; Shirikova, N.Y.; Sun, Y.; Faestermann, T.; Krücken, R.; et al. High-resolution study of 0+ and 2+ excitations in 168Er with the (p,t) reaction. Phys. Rev. C 2006, 73, 064309. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wood, V.; Casten, R.F.; Fitzpatrick, C.R.; Graw, G.; Bucurescu, D.; Jolie, J.; von Brentano, P.; Hertenberger, R.; Wirth, H.-F.; et al. Enhanced density of low-lying 0+ states: A corroboration of shape phase transitional behavior. Phys. Lett. B 2006, 638, 44. [Google Scholar] [CrossRef]
- Meyer, D.A.; Wood, V.; Casten, R.F.; Fitzpatrick, C.R.; Graw, G.; Bucurescu, D.; Jolie, J.; von Brentano, P.; Hertenberger, R.; Wirth, H.-F.; et al. Extensive investigation of 0+ states in rare earth region nuclei. Phys. Rev. C 2006, 74, 044309. [Google Scholar] [CrossRef]
- Lesher, S.R.; Orce, J.N.; Ammar, Z.; Hannant, C.D.; Merrick, M.; Warr, N.; Brown, T.B.; Boukharouba, N.; Fransen, C.; Scheck, M.; et al. Study of 0+ excitations in 158Gd with the (n,n’γ) reaction. Phys. Rev. C 2007, 76, 034318. [Google Scholar] [CrossRef]
- Aprahamian, A.; Lesher, S.R.; Stratman, A. First excited 0+ states in deformed nuclei. Bulg. J. Phys. 2017, 44, 372. [Google Scholar]
- Popa, G.; Hirsch, J.G.; Draayer, J.P. Shell model description of normal parity bands in even-even heavy deformed nuclei. Phys. Rev. C 2000, 62, 064313. [Google Scholar] [CrossRef]
- Zamfir, N.V.; Zhang, J.-Y.; Casten, R.F. Interpreting recent measurements of 0+ states in 158Gd. Phys. Rev. C 2002, 66, 057303. [Google Scholar] [CrossRef]
- Popa, G.; Georgieva, A.; Draayer, J.P. Systematics in the structure of low-lying, nonyrast bandhead configurations of strongly deformed nuclei. Phys. Rev. C 2004, 69, 064307. [Google Scholar] [CrossRef]
- Lo Iudice, N.; Sushkov, A.V.; Shirikova, N.Y. Microscopic structure of low-lying 0+ states in the deformed 158Gd. Phys. Rev. C 2004, 70, 064316. [Google Scholar] [CrossRef]
- Lo Iudice, N.; Sushkov, A.V.; Shirikova, N.Y. Microscopic structure of low-lying 0+ states in deformed nuclei. Phys. Rev. C 2005, 72, 034303. [Google Scholar] [CrossRef]
- Popa, G.; Aprahamian, A.; Georgieva, A.; Draayer, J.P. Systematics in the structure of low-lying, non-yrast band-head configurations of strongly deformed nuclei. Eur. Phys. J. A 2005, 25 (Suppl. S1), 451. [Google Scholar] [CrossRef]
- Gerçceklioğlu, M. Excited 0+ states in 156,158,160,162Gd. Ann. Phys. 2005, 14, 312. [Google Scholar] [CrossRef]
- Hirsch, J.G.; Popa, G.; Lesher, S.R.; Aprahamian, A.; Vargas, C.E.; Draayer, J.P. Low energy 0+ excitations in 158Gd. Rev. Mex. Fis. 2006, S52, 69. [Google Scholar]
- Gerçeklioğlu, M. Transfer strengths to the 0+ states excited by (p,t) reactions in 130,132,134Ba. Phys. Rev. C 2010, 82, 024306. [Google Scholar] [CrossRef]
- Gerçeklioğlu, M. The 0+ states excited by (p, t) reaction in 170Yb. Eur. Phys. J. A 2012, 48, 141. [Google Scholar] [CrossRef]
- Popa, G.; Georgieva, A. Description of heavy deformed nuclei within the pseudo-SU(3) shell model. J. Phys. G Conf. Ser. 2012, 403, 012009. [Google Scholar] [CrossRef]
- Garrett, P.E. Characterization of the β vibration and 02+ states in deformed nuclei. J. Phys. G Nucl. Part. Phys. 2001, 27, R1. [Google Scholar] [CrossRef]
- Jolos, R.V.; von Brentano, P. Bohr Hamiltonian with different mass coefficients for the ground- and γ bands from experimental data. Phys. Rev. C 2007, 76, 024309. [Google Scholar] [CrossRef]
- Jolos, R.V.; von Brentano, P. Bohr Hamiltonian for collective low-lying vibrational states of well deformed nuclei. Phys. Rev. C 2008, 77, 064317. [Google Scholar] [CrossRef]
- Jolos, R.V.; von Brentano, P. Bohr Hamiltonian, mass coefficients, and the structure of well deformed axially symmetric nuclei. Phys. Rev. C 2008, 78, 064309. [Google Scholar] [CrossRef]
- Jolos, R.V.; von Brentano, P. Mass tensor in the Bohr Hamiltonian from the nondiagonal energy weighted sum rules. Phys. Rev. C 2009, 79, 044310. [Google Scholar] [CrossRef]
- Ermamatov, M.J.; Fraser, P.R. Rotational-vibrational excited states of axially symmetric nuclei with different mass parameters. Phys. Rev. C 2011, 84, 044321. [Google Scholar] [CrossRef]
- Ermamatov, M.J.; Srivastava, P.C.; Fraser, P.R.; Stránský, P.; Morales, I.O. Coriolis contribution to excited states of deformed 163Dy and 173Yb nuclei with multiple mass parameters. Phys. Rev. C 2012, 85, 034307. [Google Scholar] [CrossRef]
- Egido, J.L.; Jungclaus, A. Predominance of triaxial shapes in transitional super-heavy nuclei: Ground-state deformation and shape coexistence along the Flerovium (Z = 114) chain of isotopes. Phys. Rev. Lett. 2020, 125, 192504. [Google Scholar] [CrossRef] [PubMed]
- Freer, M.; Horiuchi, H.; Kanada-En’yo, Y.; Lee, D.; Meissner, U.-G. Microscopic clustering in light nuclei. Rev. Mod. Phys. 2018, 90, 035004. [Google Scholar] [CrossRef]
- Frauendorf, S.; Meng, J. Tilted rotation of triaxial nuclei. Nucl. Phys. A 1997, 617, 131. [Google Scholar] [CrossRef]
- Petrache, C.M.; Bazzacco, D.; Lunardi, S.; Rossi Alvarez, C.; de Angelis, G.; De Poli, M.; Bucurescu, D.; Ur, C.A.; Semmes, P.B.; Wyss, R. Rotational bands in the doubly odd nucleus 134Pr. Nucl. Phys. A 1996, 597, 106. [Google Scholar] [CrossRef]
- Dimitrov, V.I.; Frauendorf, S.; Dönau, F. Chirality of nuclear rotation. Phys. Rev. Lett. 2000, 84, 5732. [Google Scholar] [CrossRef]
- Frauendorf, S. Spontaneous symmetry breaking in rotating nuclei. Rev. Mod. Phys. 2001, 73, 463. [Google Scholar] [CrossRef]
- Xiong, B.W.; Wang, Y.Y. Nuclear chiral doublet bands data tables. At. Data Nucl. Data Tables 2019, 125, 193. [Google Scholar] [CrossRef]
- Petrache, C.M.; Lv, B.F.; Astier, A.; Dupont, E.; Wang, Y.K.; Zhang, S.Q.; Zhao, P.W.; Ren, Z.X.; Meng, J.; Greenlees, P.T.; et al. Evidence of chiral bands in even-even nuclei. Phys. Rev. C 2018, 97, 041304(R). [Google Scholar] [CrossRef]
- Chen, Q.B.; Lv, B.F.; Petrache, C.M.; Meng, J. Multiple chiral doublets in four-j shells particle rotor model: Five possible chiral doublets in . Phys. Lett. B 2018, 782, 744. [Google Scholar] [CrossRef]
- Wang, Y.K.; Chen, F.Q.; Zhao, P.W.; Zhang, S.Q.; Meng, J. Multichiral facets in symmetry restored states: Five chiral doublet candidates in the even-even nucleus 136Nd. Phys. Rev. C 2019, 99, 054303. [Google Scholar] [CrossRef]
- Rocchini, M.; Hadyńska-Klȩk, K.; Nannini, A.; Goasduff, A.; Zielińska, M.; Testov, D.; Rodríguez, T.R.; Gargano, A.; Nowacki, F.; de Gregorio, G.; et al. Onset of triaxial deformation in 66Zn and properties of its first excited 0+ state studied by means of Coulomb excitation. Phys. Rev. C 2021, 103, 014311. [Google Scholar] [CrossRef]
- Hellgartner, S.; Mücher, D.; Wimmer, K.; Bildstein, V.; Egido, J.L.; Gernhäuser, R.; Krücken, R.; Nowak, A.K.; Zielińska, M.; Bauer, C.; et al. Axial and triaxial degrees of freedom in 72Zn. Phys. Lett. B 2023, 841, 137933. [Google Scholar] [CrossRef]
- Ayangeakaa, A.D.; Janssens, R.V.F.; Wu, C.Y.; Allmond, J.M.; Wood, J.L.; Zhu, S.; Albers, M.; Almaraz-Calderon, S.; Bucher, B.; Carpenter, M.P.; et al. Shape coexistence and the role of axial asymmetry in 72Ge. Phys. Lett. B 2016, 754, 254. [Google Scholar] [CrossRef]
- Sun, J.J.; Shi, Z.; Li, X.Q.; Hua, H.; Xu, C.; Chen, Q.B.; Zhang, S.Q.; Song, C.Y.; Meng, J.; Wu, X.G.; et al. Spectroscopy of 74Ge: From soft to rigid triaxiality. Phys. Lett. B 2014, 734, 308. [Google Scholar] [CrossRef]
- Toh, Y.; Chiara, C.J.; McCutchan, E.A.; Walters, W.B.; Janssens, R.V.F.; Carpenter, M.P.; Zhu, S.; Broda, R.; Fornal, B.; Kay, B.P.; et al. Evidence for rigid triaxial deformation at low energy in 76Ge. Phys. Rev. C 2013, 87, 041304(R). [Google Scholar] [CrossRef]
- Ayangeakaa, A.D.; Janssens, R.V.F.; Zhu, S.; Little, D.; Henderson, J.; Wu, C.Y.; Hartley, D.J.; Albers, M.; Auranen, K.; Bucher, B.; et al. Evidence for rigid triaxial deformation in 76Ge from a model-independent analysis. Phys. Rev. Lett. 2019, 123, 102501. [Google Scholar] [CrossRef]
- Srivastava, P.C.; Åberg, S.; Ragnarsson, I. Triaxial rotation-axis flip triggered by an isoscalar np pair. Phys. Rev. C 2017, 95, 011303(R). [Google Scholar] [CrossRef]
- Marchini, N.; Nannini, A.; Rocchini, M.; Rodríguez, T.R.; Ottanelli, M.; Gelli, N.; Perego, A.; Benzoni, G.; Blasi, N.; Bocchi, G.; et al. Emergence of triaxiality in 74Se from electric monopole transition strengths. Phys. Lett. B 2023, 844, 138067. [Google Scholar] [CrossRef]
- Henderson, J.; Wu, C.Y.; Ash, J.; Brown, B.A.; Bender, P.C.; Elder, R.; Elman, B.; Gade, A.; Grinder, M.; Iwasaki, H.; et al. Triaxiality in 76Se. Phys. Rev. C 2019, 99, 054313. [Google Scholar] [CrossRef]
- Xu, F.R.; Walker, P.M.; Wyss, R. Oblate stability of A≈110 nuclei near the r-process path. Phys. Rev. C 2002, 65, 021303(R). [Google Scholar] [CrossRef]
- Smith, A.G.; Durell, J.L.; Phillips, W.R.; Jones, M.A.; Leddy, M.; Urban, W.; Varley, B.J.; Ahmad, I.; Morss, L.R.; Bentaleb, M.; et al. Spin-dependent triaxial deformation in neutron-rich Mo isotopes. Phys. Rev. Lett. 1996, 77, 1711. [Google Scholar] [CrossRef] [PubMed]
- Urban, W.; Rza̧ca-Urban, T.; Wiśniewski, J.; Smith, A.G.; Simpson, G.S.; Ahmad, I. First observation of γ-soft and triaxial bands in Zr isotopes. Phys. Rev. C 2019, 100, 014319. [Google Scholar] [CrossRef]
- Snyder, J.B.; Reviol, W.; Sarantites, D.G.; Afanasjev, A.V.; Janssens, R.V.F.; Abusara, H.; Carpenter, M.P.; Chen, X.; Chiara, C.J.; Greene, J.P.; et al. High-spin transition quadrupole moments in neutron-rich Mo and Ru nuclei: Testing γ softness? Phys. Lett. B 2013, 723, 61. [Google Scholar] [CrossRef]
- Ralet, D.; Pietri, S.; Rodríguez, T.; Alaqeel, M.; Alexander, T.; Alkhomashi, N.; Ameil, F.; Arici, T.; Ataç, A.; Avigo, R.; et al. Lifetime measurement of neutron-rich even-even molybdenum isotopes. Phys. Rev. C 2017, 95, 034320. [Google Scholar] [CrossRef]
- Ha, J.; Sumikama, T.; Browne, F.; Hinohara, N.; Bruce, A.; Choi, S.; Nishizuka, I.; Nishimura, S.; Doornenbal, P.; Lorusso, G.; et al. Shape evolution of neutron-rich 106,108,110Mo isotopes in the triaxial degree of freedom. Phys. Rev. C 2020, 101, 044311. [Google Scholar] [CrossRef]
- Esmaylzadeh, A.; Blazhev, A.; Nomura, K.; Jolie, J.; Beckers, M.; Fransen, C.; Gerst, R.-B.; Harter, A.; Karayonchev, V.; Knafla, L.; et al. Investigation of γ softness: Lifetime measurements in 104,106Ru. Phys. Rev. C 2022, 106, 064323. [Google Scholar] [CrossRef]
- Lalkovski, S.; Minkov, M. Evolution of collectivity in a ground-γ-band mixing scheme for even–even transitional nuclei. J. Phys. G Nucl. Part. Phys. 2005, 31, 427. [Google Scholar] [CrossRef]
- Shannon, J.A.; Phillips, W.R.; Durell, J.L.; Varley, B.J.; Urban, W.; Pearson, C.J.; Ahmad, I.; Lister, C.J.; Morss, L.R.; Nash, K.L.; et al. The role of triaxiality in the ground states of even-even neutron-rich Ru isotopes. Phys. Lett. B 1994, 336, 136. [Google Scholar] [CrossRef]
- Doherty, D.T.; Allmond, J.M.; Janssens, R.V.F.; Korten, W.; Zhu, S.; Zielińska, M.; Radford, D.C.; Ayangeakaa, A.D.; Bucher, B.; Batchelder, J.C.; et al. Triaxiality near the 110Ru ground state from Coulomb excitation. Phys. Lett. B 2017, 766, 334. [Google Scholar] [CrossRef]
- Söderström, P.-A.; Lorusso, G.; Watanabe, H.; Nishimura, S.; Doornenbal, P.; Thiamova, G.; Browne, F.; Gey, G.; Jung, H.S.; Sumikama, T.; et al. Shape evolution in 116,118 Ru: Triaxiality and transition between the O(6) and U(5) dynamical symmetries. Phys. Rev. C 2013, 88, 024301. [Google Scholar] [CrossRef]
- Gray, T.J.; Allmond, J.M.; Janssens, R.V.F.; Korten, W.; Stuchbery, A.E.; Wood, J.L.; Ayangeakaa, A.D.; Bottoni, S.; Bucher, B.M.; Campbell, C.M.; et al. E2 rotational invariants of 01+ and 21+ states for 106Cd: The emergence of collective rotation. Phys. Lett. B 2022, 834, 137446. [Google Scholar] [CrossRef]
- Kern, B.D.; Mlekodaj, R.L.; Leander, G.A.; Kortelahti, M.O.; Zganjar, E.F.; Braga, R.A.; Fink, R.W.; Perez, C.P.; Nazarewicz, W.; Semmes, P.B. Transition through triaxial shapes of the light samarium isotopes and the beta decay of 136,138,140Eu. Phys. Rev. C 1987, 36, 1514. [Google Scholar] [CrossRef] [PubMed]
- Orce, J.N.; Bruce, A.M.; Emmanouilidis, A.; Byrne, A.P.; Dracoulis, G.D.; Kibédi, T.; Caamaño, M.; El-Masri, H.; Pearson, C.J.; Podolyák, Z.; et al. Shape-driving effects in the triaxial nucleus, 128Xe. Phys. Rev. C 2006, 74, 034318. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V. Evidence for a possible E(5) symmetry in 134Ba. Phys. Rev. Lett. 2000, 85, 3584. [Google Scholar] [CrossRef] [PubMed]
- Krücken, R.; Albanna, B.; Bialik, C.; Casten, R.F.; Cooper, J.R.; Dewald, A.; Zamfir, N.V.; Barton, C.J.; Beausang, C.W.; Caprio, M.A.; et al. B(E2) values in 150Nd and the critical point symmetry X(5). Phys. Rev. Lett. 2002, 88, 232501. [Google Scholar] [CrossRef] [PubMed]
- Petrache, C.M.; Ragnarsson, I.; Ma, H.-L.; Leguillon, R.; Zerrouki, T.; Bazzacco, D.; Lunardi, S. Multiple triaxial bands in 138Nd. Phys. Rev. C 2015, 91, 024302. [Google Scholar] [CrossRef]
- Casten, R.F.; Zamfir, N.V. Empirical realization of a critical point description in atomic nuclei. Phys. Rev. Lett. 2001, 87, 052503. [Google Scholar] [CrossRef]
- Dewald, A.; Möller, O.; Tonev, D.; Fitzler, A.; Saha, B.; Jessen, K.; Heinze, S.; Linnemann, A.; Jolie, J.; Zell, K.O.; et al. Shape changes and test of the critical-point symmetry X(5) in N = 90 nuclei. Eur. Phys. J. A 2004, 20, 173. [Google Scholar] [CrossRef]
- Tonev, D.; Dewald, A.; Klug, T.; Petkov, P.; Jolie, J.; Fitzler, A.; Möller, O.; Heinze, S.; von Brentano, P.; Casten, R.F. Transition probabilities in 154Gd: Evidence for X(5) critical point symmetry. Phys. Rev. C 2004, 69, 034334. [Google Scholar] [CrossRef]
- Paul, E.S.; Ahn, K.; Fossan, D.B.; Liang, Y.; Ma, R.; Xu, N. Rotational bands in 140Gd: Systematics of triaxial N=76 isotones. Phys. Rev. C 1989, 39, 153. [Google Scholar] [CrossRef]
- Caprio, M.A.; Zamfir, N.V.; Casten, R.F.; Barton, C.J.; Beausang, C.W.; Cooper, J.R.; Hecht, A.A.; Krücken, R.; Newman, H.; Novak, J.R.; et al. Low-spin structure of 156Dy through γ-ray spectroscopy. Phys. Rev. C 2002, 66, 054310. [Google Scholar] [CrossRef]
- Fahlander, C.; Thorslund, I.; Varnestig, B.; Bäcklin, A.; Svensson, L.E.; Disdier, D.; Kraus, L.; Linck, I.; Schulz, N.; Cline, D. Triaxiality in 166Er. Nucl. Phys. A 1992, 537, 183. [Google Scholar] [CrossRef]
- Wheldon, C.; Walker, P.M.; Regan, P.H.; Saitoh, T.; Hashimoto, N.; Sletten, G.; Xu, F.R. High-K structures and triaxiality in 186Os. Nucl. Phys. A 1999, 652, 103. [Google Scholar] [CrossRef]
- John, P.R.; Modamio, V.; Valiente-Dobón, J.J.; Mengoni, D.; Lunardi, S.; Rodríguez, T.R.; Bazzacco, D.; Gadea, A.; Wheldon, C.; Alexander, T.; et al. Shape evolution in the neutron-rich osmium isotopes: Prompt γ-ray spectroscopy of 196Os. Phys. Rev. C 2014, 90, 021301(R). [Google Scholar] [CrossRef]
- Dewald, A.; Möller, O.; Saha, B.; Jessen, K.; Fitzler, A.; Melon, B.; Pissulla, T.; Heinze, S.; Jolie, J.; Zell, K.O.; et al. Test of the critical point symmetry X(5) in the mass A = 180 region. J. Phys. G Nucl. Part. Phys. 2005, 31, S1427. [Google Scholar] [CrossRef]
- Bhat, G.H.; Sheikh, J.A.; Sun, Y.; Garg, U. Triaxial projected shell model study of the rapid changes in B(E2) for 180-190Pt isotopes. Phys. Rev. C 2012, 86, 047307. [Google Scholar] [CrossRef]


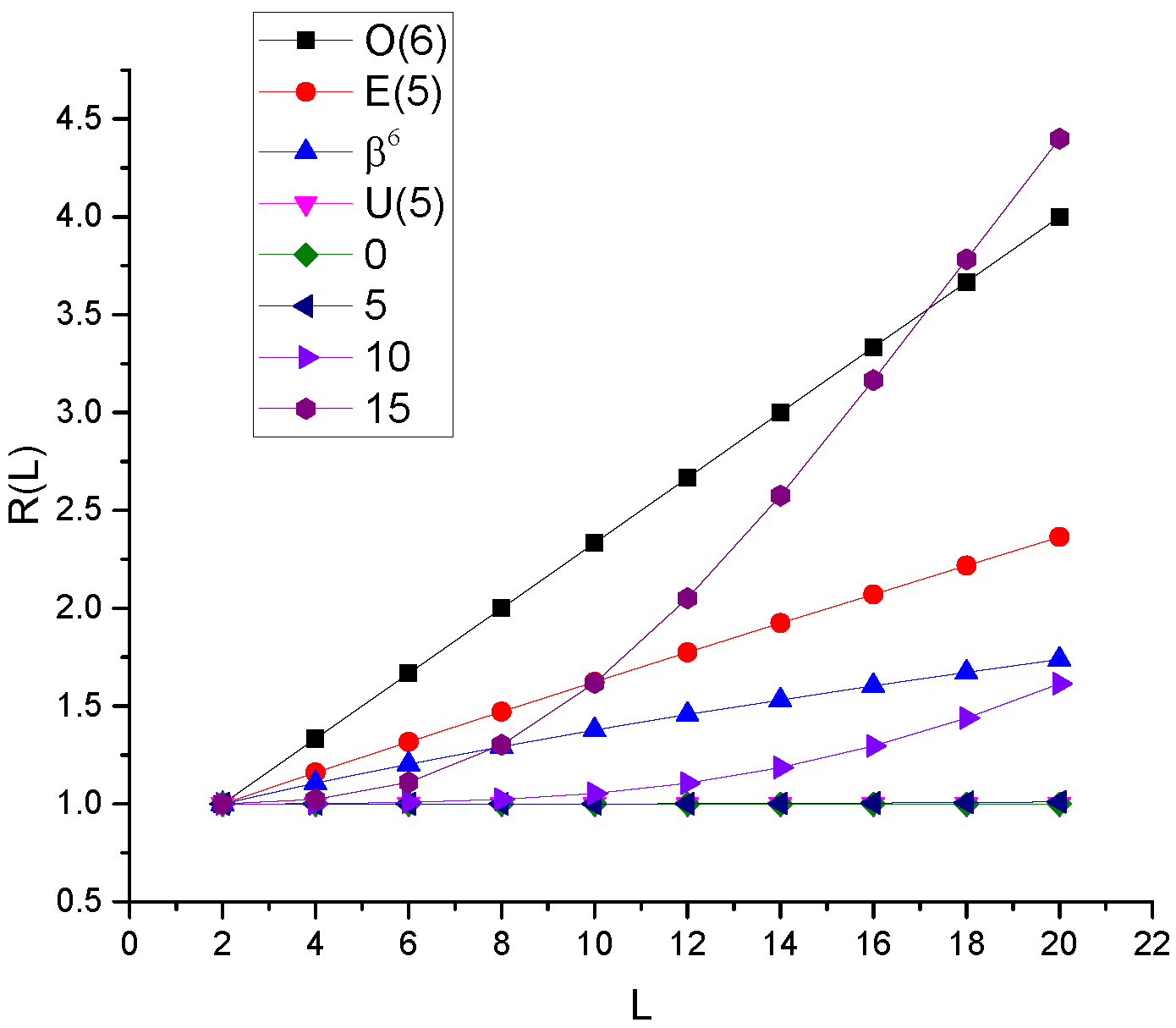
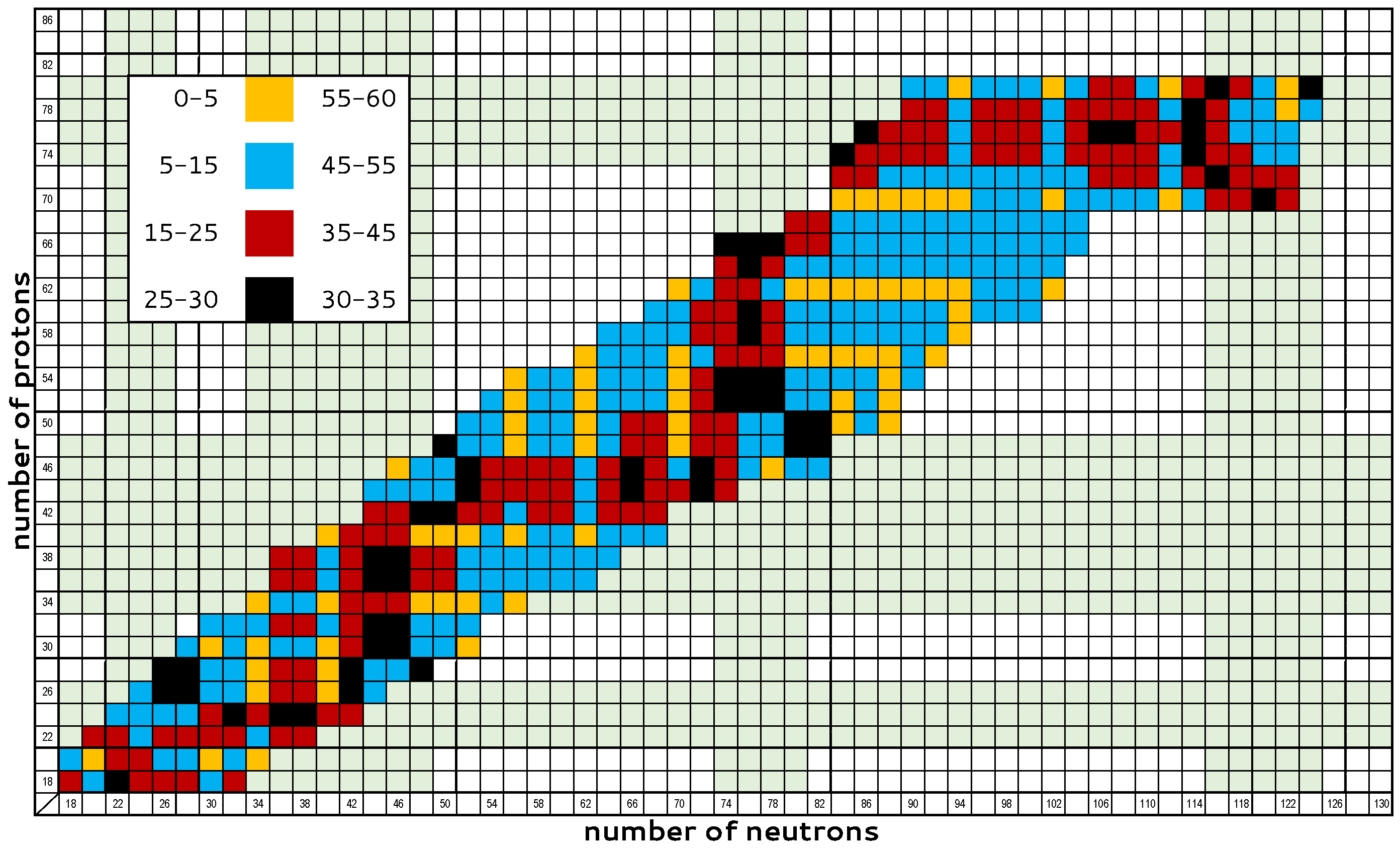
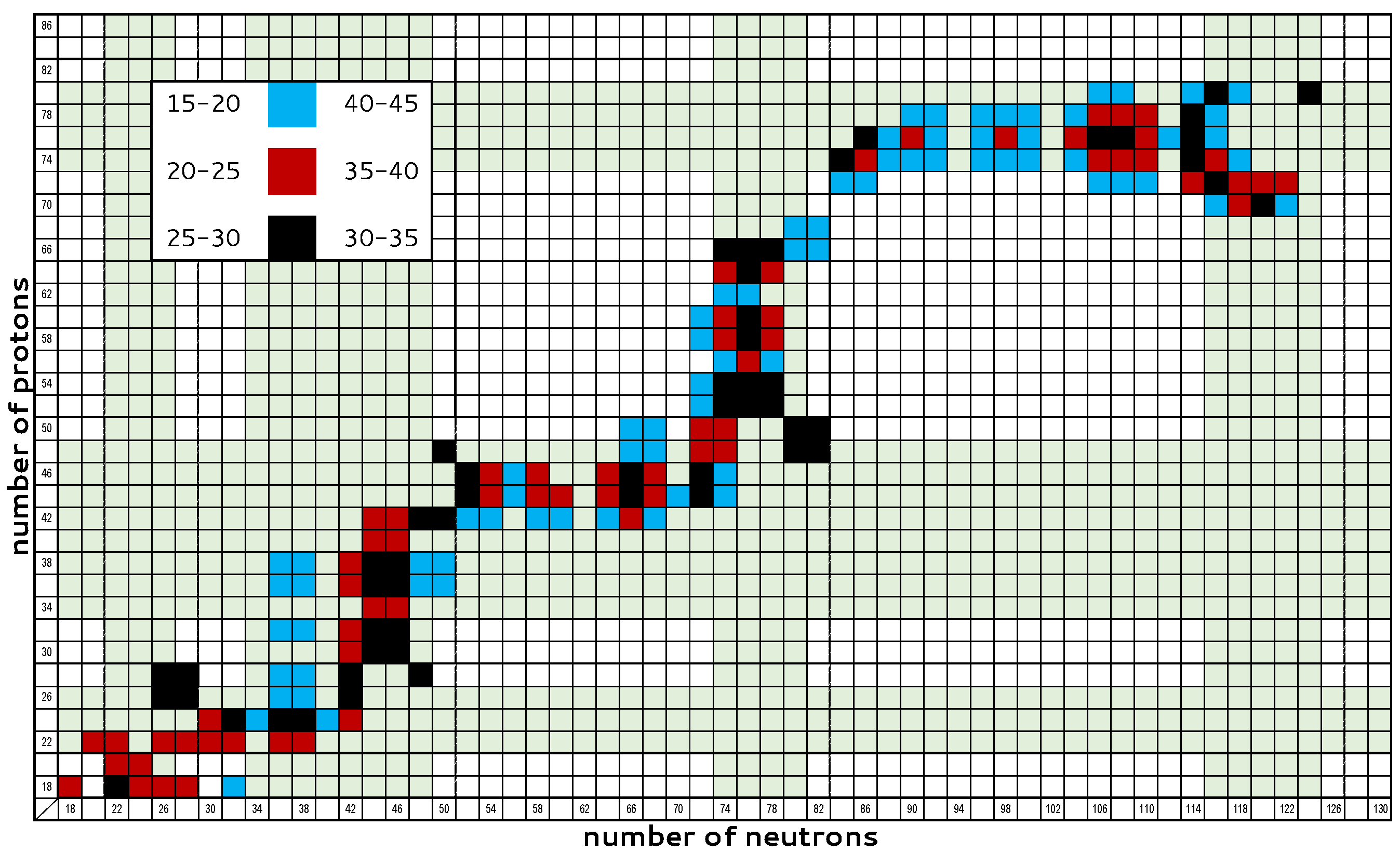

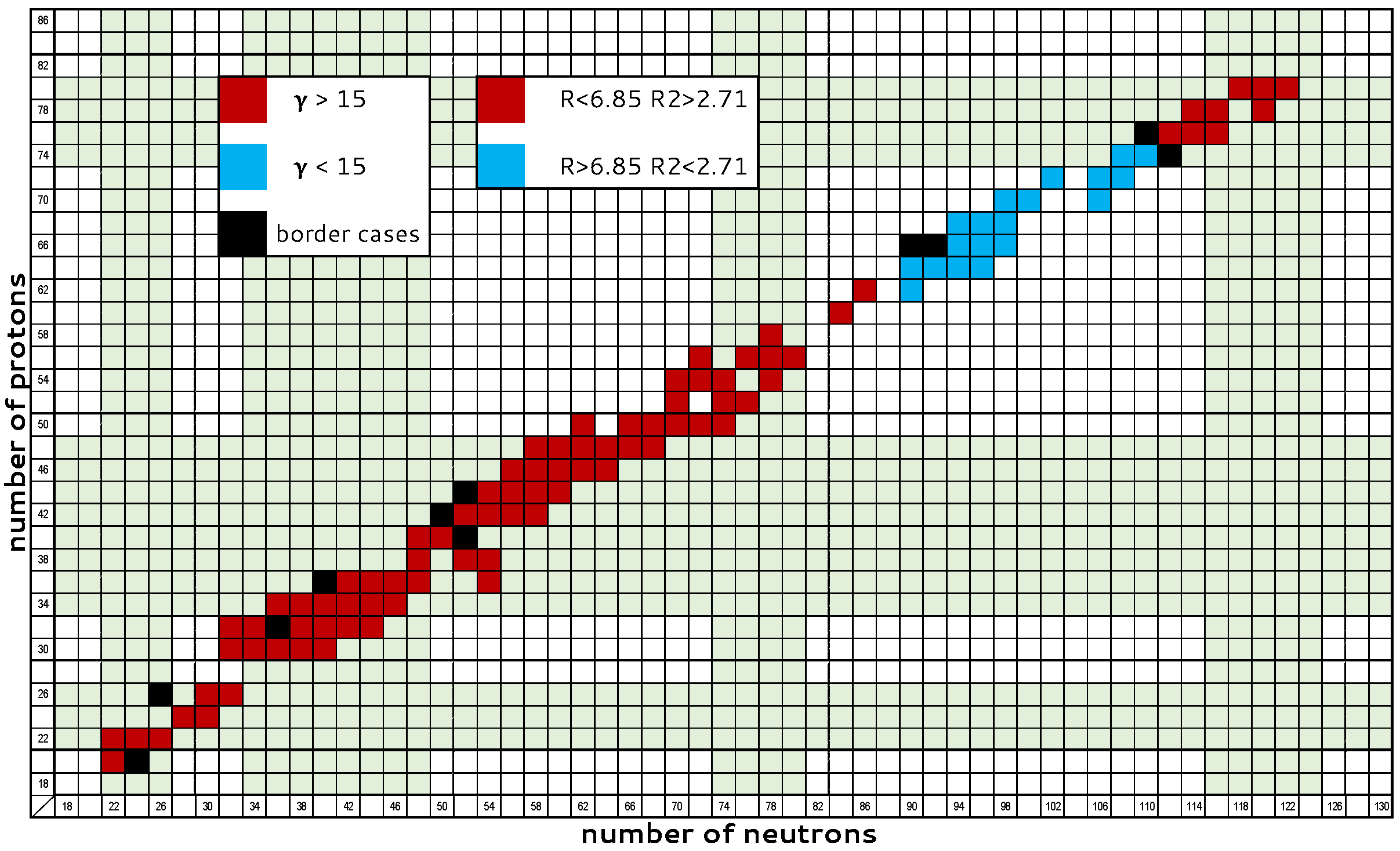
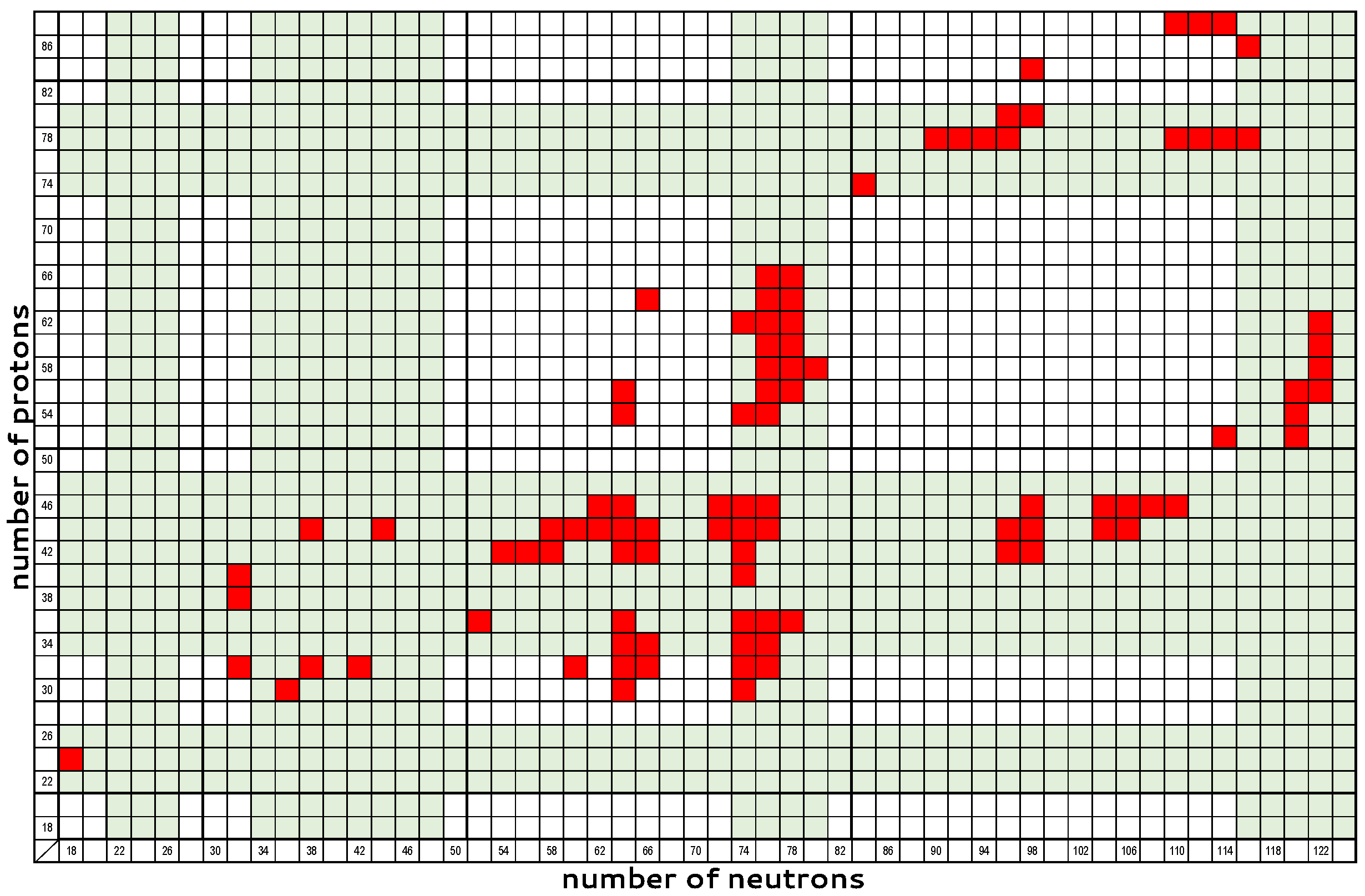
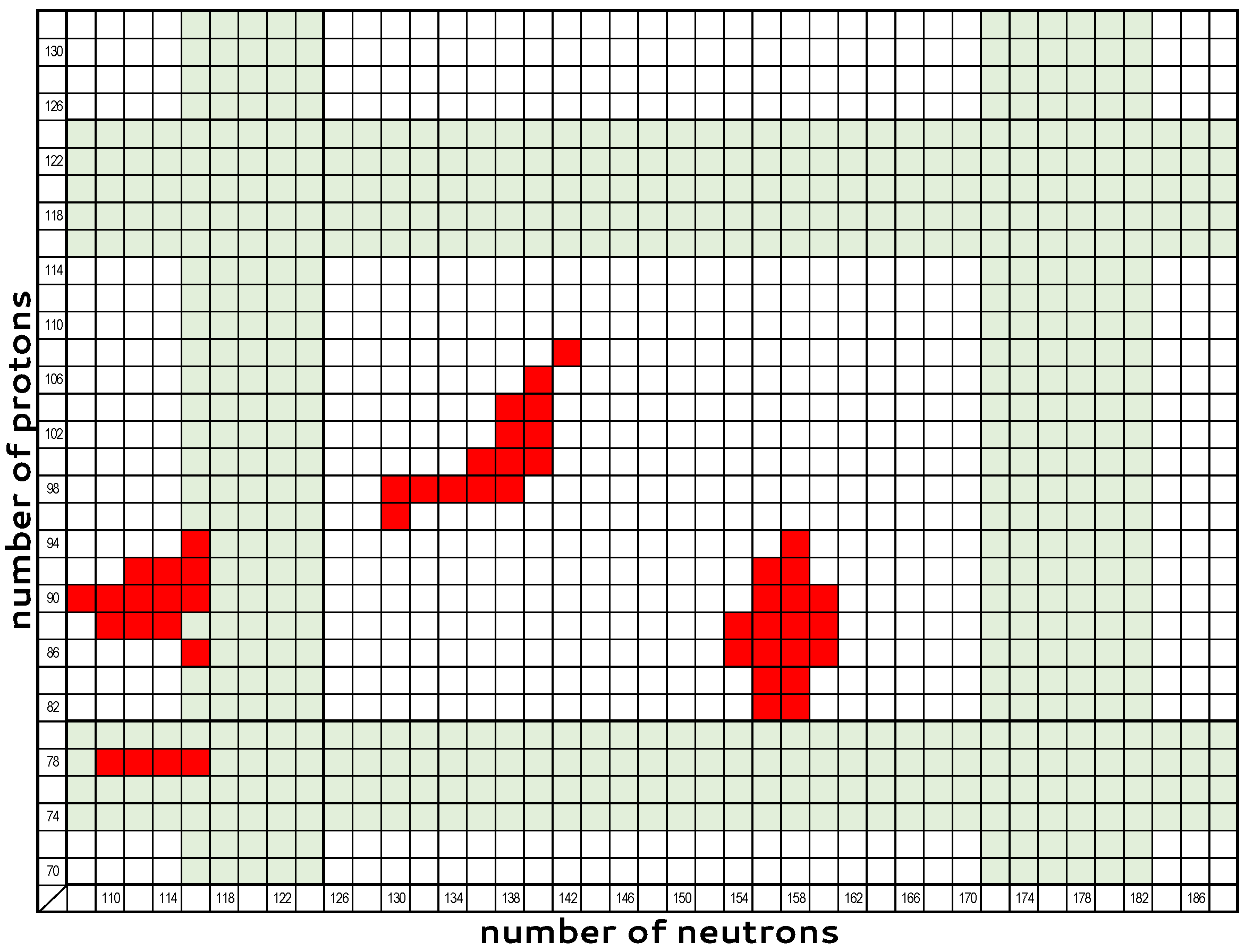
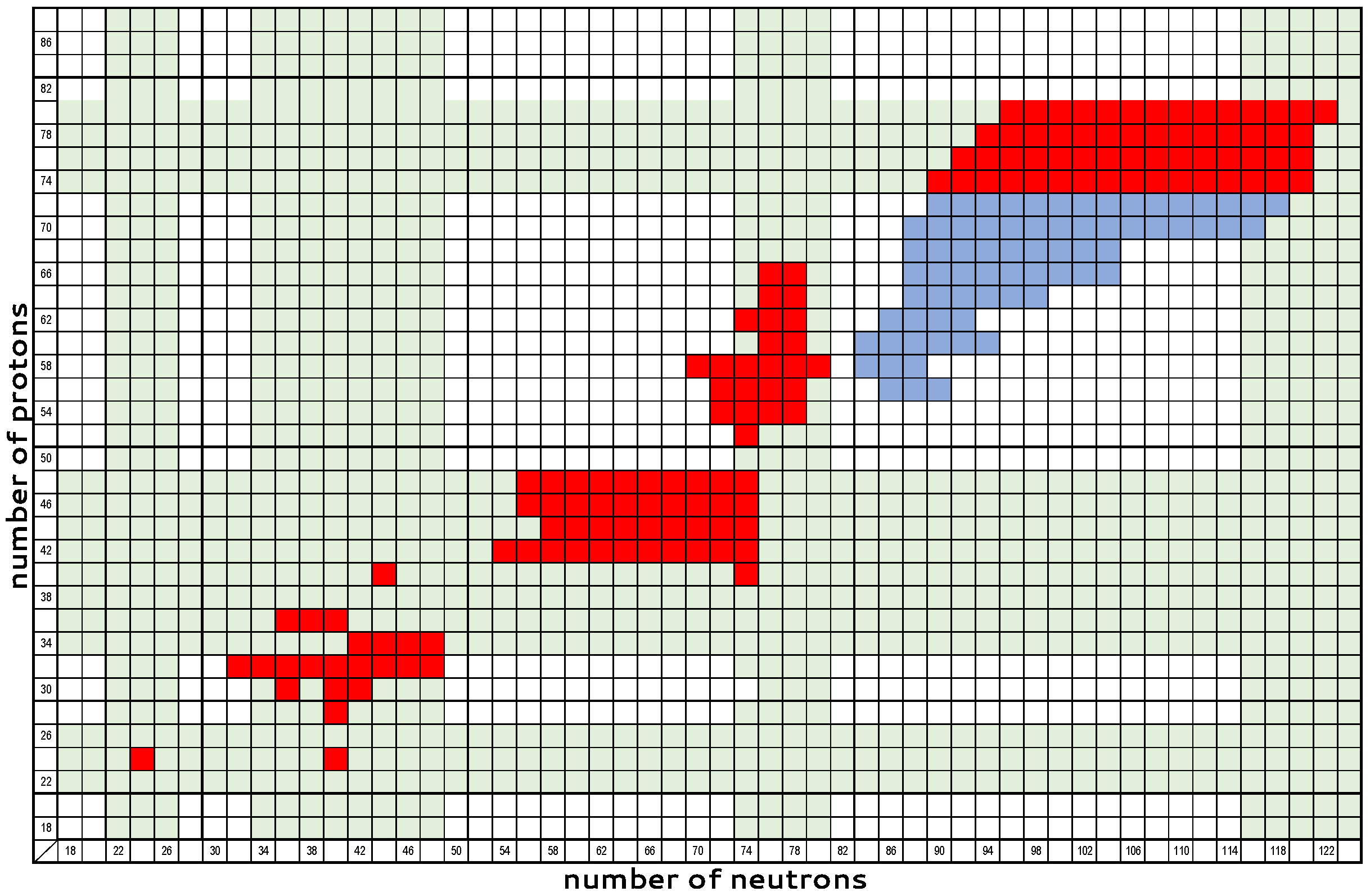
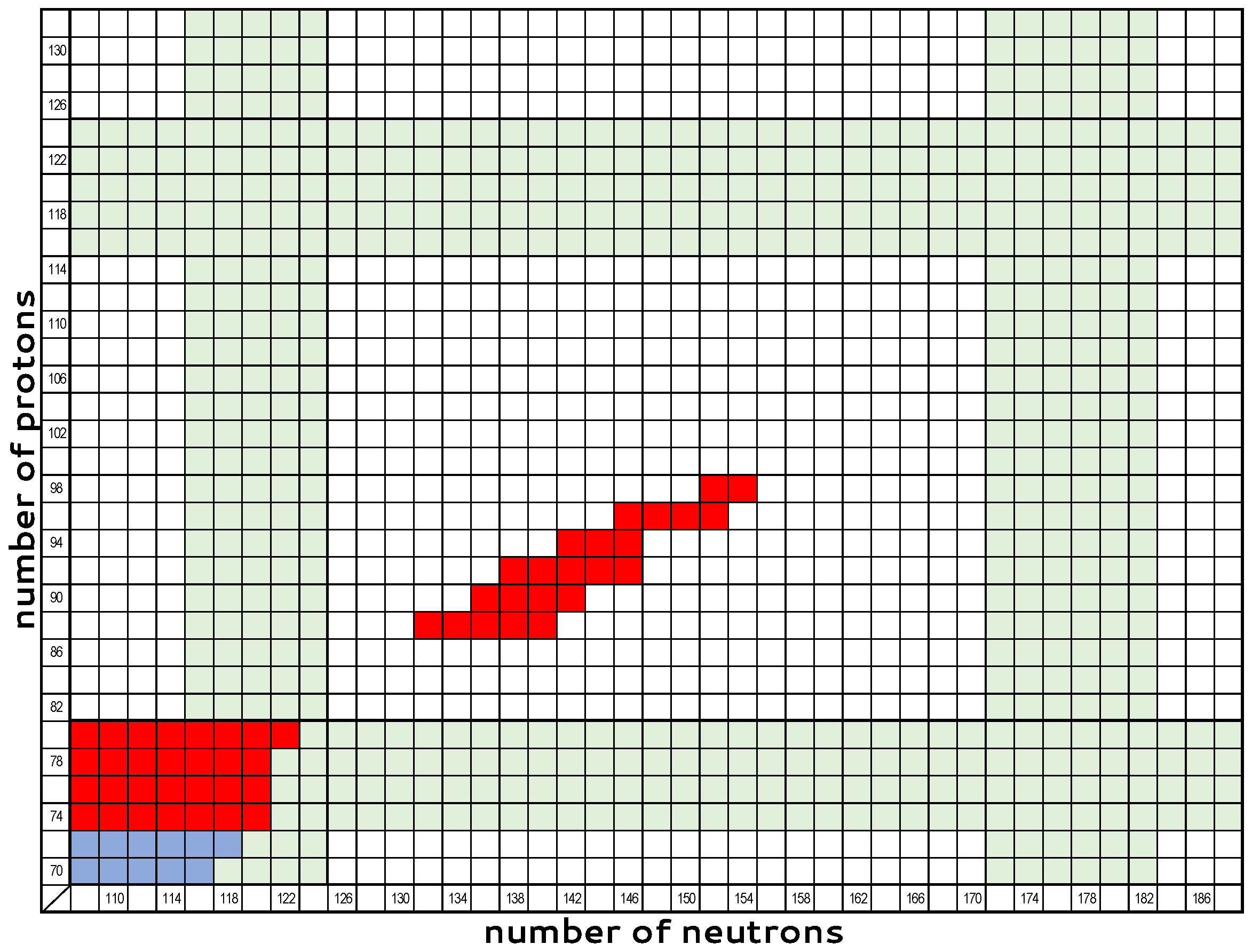



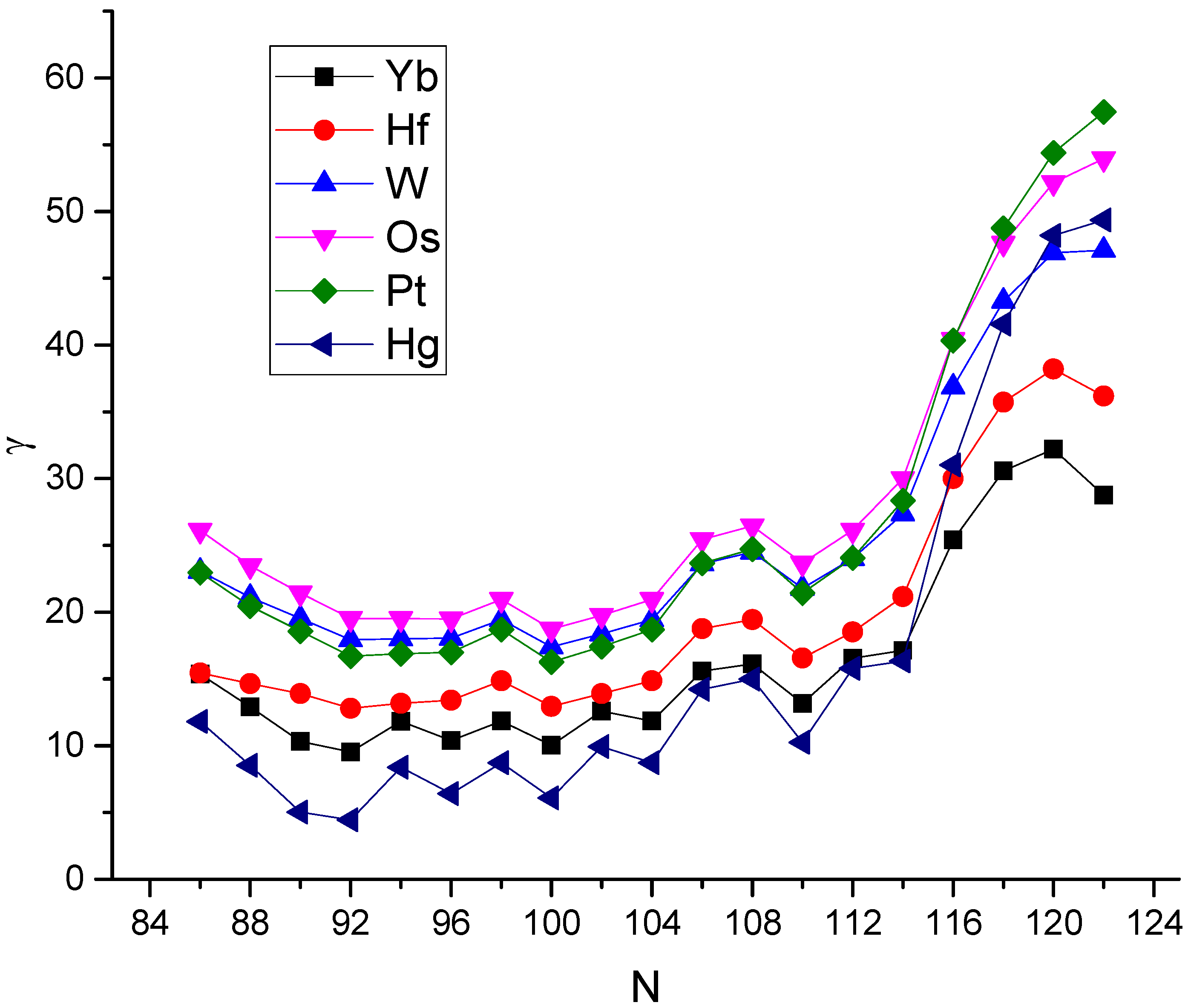
| Nucleus | R | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MeV | MeV | W.u. | W.u. | |||||||
| 0.053 | 0.781 | 14.68 | 2.9 | 5.5 | 1.90 | 3.271 | 10.4 | 10.4 | 6.8 | |
| 0.049 | 0.785 | 15.91 | 2.9 (4) | 7.2 (7) | 2.48 | 3.284 | 10.0 | 14.1 | 7.7 | |
| 0.043 | 0.927 | 21.31 | 2.9 (5) | 4.9 (8) | 1.69 | 3.296 | 8.7 | 8.1 | 7.3 | |
| 0.045 | 1.060 | 23.61 | 3.04 (18) | 5.3 (4) | 1.74 | 3.303 | 8.3 | 8.8 | 6.5 | |
| 0.043 | 1.032 | 24.15 | 2.3 (3) | 3.7 (4) | 1.61 | 3.321 | 8.2 | 6.9 | 10.4 |
| Nucleus | |||
|---|---|---|---|
| 26, 4 | 48, 6 | 74, 10 | |
| 26, 4 | 50, 8 | 76, 12 | |
| 30, 4 | 50, 8 | 80, 12 | |
| 30, 4 | 60, 0 | 90, 4 | |
| 34, 8 | 54, 12 | 88, 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonatsos, D.; Martinou, A.; Peroulis, S.K.; Petrellis, D.; Vasileiou, P.; Mertzimekis, T.J.; Minkov, N. Triaxial Shapes in Even–Even Nuclei: A Theoretical Overview. Atoms 2025, 13, 47. https://doi.org/10.3390/atoms13060047
Bonatsos D, Martinou A, Peroulis SK, Petrellis D, Vasileiou P, Mertzimekis TJ, Minkov N. Triaxial Shapes in Even–Even Nuclei: A Theoretical Overview. Atoms. 2025; 13(6):47. https://doi.org/10.3390/atoms13060047
Chicago/Turabian StyleBonatsos, Dennis, Andriana Martinou, Spyridon K. Peroulis, Dimitrios Petrellis, Polytimos Vasileiou, Theodoros J. Mertzimekis, and Nikolay Minkov. 2025. "Triaxial Shapes in Even–Even Nuclei: A Theoretical Overview" Atoms 13, no. 6: 47. https://doi.org/10.3390/atoms13060047
APA StyleBonatsos, D., Martinou, A., Peroulis, S. K., Petrellis, D., Vasileiou, P., Mertzimekis, T. J., & Minkov, N. (2025). Triaxial Shapes in Even–Even Nuclei: A Theoretical Overview. Atoms, 13(6), 47. https://doi.org/10.3390/atoms13060047








