Abstract
Various electron impact scattering cross sections of Sevoflurane are reported up to 5 keV. The elastic cross sections (differential and integral) are computed using the single-centre-expansion formalism within a molecular framework. The ground state target wavefunction is determined at the Hartree–Fock (HF) level. Post-HF corrections are incorporated to make a scattering realistic model. The total interacting potential is defined as the sum of static, correlation–polarization and exchange potentials. These potentials are numerically computed using their local forms. The long-range effects affecting the scattering due to the polar nature of the molecule are incorporated using the Born Top-up approach. The ionization cross sections are obtained from the semi-empirical binary-encounter-Bethe model. The total cross sections are estimated from the incoherent sum of Born-corrected elastic integral and ionization cross sections. The computed results show fairly good agreement with the experimental reported cross sections.
1. Introduction
Electron scattering studies from atoms and molecules are fundamental to understand the chemical and biological activity of a molecule [1], cometary and planetary atmospheres [2], semiconductor and plasma processing of materials [3,4,5,6], fusion plasma [7], combustion physics [8] and several other important fields [9,10]. These studies also facilitate making useful comparisons with an antiparticle positron due to the limited availability of positron scattering data. Additionally, the electron–target collision database and plasma simulation codes also rely on scattering cross sections of atoms and molecules [11,12,13,14]. The breakthroughs made in experimental set-ups and developments in theoretical formulations have greatly boosted scattering studies [9,15,16,17]. Commonly used detectors can measure differential cross sections (DCS) of a molecule over selective scattering range [18]. The resulting integral elastic or total cross sections obtained by integrating the DCS are, therefore, lower than the “true values” for polar targets, molecules having a large dipole polarizability, or both [18]. The correct cross sections are, therefore, obtained by including the contribution of missing angles by adopting a correction procedure [19]. Kadokura et al. used an electron beam of high-angular resolution to measure DCS at a scattering angle () [20]. Such measurements are necessary to test theoretical predictions in low angular regions, which have so far remained unexplored.
The developments on theoretical fronts have helped in modelling scattering phenomena for large multi-centric molecules of many-electron systems [16,17]. The non-perturbative methods compute scattering cross sections by solving the Schrdinger equation. The complexity of the molecule, the presence of open channels and their inter-coupling effects, and numerical issues limit the applicability of ab initio methods like the convergent close coupling [17], R-matrix [21], Schwinger multichannel [22] or complex Kohn [23] in the modelling of a given electron-molecule scattering process. Thus, the ab initio calculations remain intractable for many molecules. Simplified approaches are invariably required to model a given or total scattering process. The approach has provided reliable results for complex molecules [24]. The fundamental idea is to ignore the inter-process coupling and compute cross sections corresponding to a particular process. Cross sections obtained for open and closed channels are then summed to obtain total cross sections. This approach has also been effective in modelling positron scattering from molecules [25,26], which is undoubtedly more complex and intricate than electron-molecule scattering [27].
Sevoflurane is a complex molecule consisting of 15 atoms and 98 electrons. It is represented by the chemical formula . The molecule has a permanent electric dipole moment [28,29] and large polarizability [30]. These properties considerably influence the scattering process at low scattering angles and low energies. However, depending on the strength of these parameters, the range of impact on scattering may vary. Its large poly-centric nature and physico-chemical properties pose a serious challenge to model scattering phenomena. The problem is much more severe if the ab initio methods in close-coupling approximation [16,17] are used. The close-coupling calculations are expensive as well. These challenges make electron scattering from the Sevoflurane molecule an interesting case to investigate using alternative approaches.
Due to low solubility, Sevoflurane is widely used as an inhalation anaesthetic [31]. Being a volatile anaesthetic, its contribution to global warming has been investigated by Costa et al. [32]. Langbein et al. reported the role of volatile anaesthetics and their relevance to atmospheric chemistry [33].
The low-lying electronic states of this molecule were explored experimentally and theoretically by Lange et al. [34]. They measured photoabsorption spectra to calculate its photolysis lifetime in the Earth’s atmosphere. Ab initio studies using different quantum chemistry methods were performed to investigate the structure and charge distribution by Tang et al. [28].
Lozano et al. used a magnetically confined experimental system [35] to measure the total scattering cross sections (TCS) up to 300 eV. Their experimental results showed good agreement with the independent atom model (IAM)-based screened corrected additivity (SCAR) models, which included interference (I) effects (IAM-SCAR+I) and rotational (R) terms (IAM-SCAR+I+R) [36,37,38].
Vukalović et al. have reported elastic scattering results using a crossed electron beam set-up and the relative flow technique [39]. The absolute DCSs were measured in the 50–300 eV range for scattering angles 25–125° due to the limited angular dependence of their instrument. The experimental data were extrapolated to determine the integral and momentum transfer cross sections. The uncertainties in their results were in the range of 22 to 30%. These authors also performed theoretical calculations employing the IAM-SCAR+I model.
Through the present study, we have filled the void created due to the non-availability of data like DCS and integral cross sections in low energy regions and ionization cross sections. The low-energy region is particularly important due to the strong influence of long-ranged attractive potentials (dipole and polarizability) affecting the scattering process. The emergence of resonance structures [21] further adds complexity to the modelling of scattering phenomenon in this energy region. Furthermore, we demonstrate that simple approaches can provide valuable estimates of TCS over wide energy even with limited resources in cases where ab initio methods might fail.
The elastic scattering cross sections based on single-centre-expansion technique (SCE) [40,41,42,43] are reported using the local form of potentials. The relevant input parameters like density and potentials needed to perform scattering calculations are obtained at the molecular level only. This makes the present approach different from IAM calculations employing local potentials like one used by Vukalović et al. for this molecule and the spherical optical complex potential (SCOP) [44]. Jain and Baluja also used local potentials but obtained quantities such as charge density and potentials in molecular framework by considering only the spherical component [45]. The elastic cross sections were corrected using the Born Top-up formula [46]. It was carried out to include contributions of higher partial waves due to electron-molecule dipole potential.
As the incident energy increases, electronic excitation and ionization channels become accessible. The SCE model accounts only for elastic scattering. The ionization cross sections are obtained using the binary-encounter-Bethe (BEB) model [47]. The TCSs are computed using the elastic and ionization process data while ignoring the inter-channel coupling effects and channels like vibration and excitation. The excitation cross sections are significantly lower than elastic and ionization cross sections in the energy range opted for in this study. This justifies their omission in computing the TCS. The results show a good agreement with the experimentally reported TCS of Lozano et al. [35]. The discrepancies at lower energy levels are discussed and need to be addressed. One of the reasons attributed is the apparatus forward angle effects. The DCS also are in good accord with the experimental measurements of Vukalović et al. [39]. To check the consistency of SCE elastic cross sections, the reliance is made on the experimental TCS measurements of Lozano et al. [35]. The results compare well. The study provides reliable cross section dataset with minimal computational cost and hardware requirements.
2. Methodology
2.1. Single-Centre-Expansion Method
The method is elaborately explained in numerous publications. Some of them have been referred above; hence, only an outline is presented. The N-electron target in the SCE approach is expanded about the centre of mass (c.o.m.) using symmetry-adapted angular functions (SAAF) as
Here, p is the irreducible representation (IR) of a particular point group, represents its component, i is the orbital contributing to the density of bound electrons. refers to the radial coefficient of the wavefunction. h is the basis set for a given partial wave l associated with and distinguishes between different bases of the same IR corresponding to the same value of l. The orthonormal SAAF can further be expressed as a linear combination of spherical harmonics .
The polarization and exchange effects are included in scattering calculations via model potentials formulated by Perdew and Zunger [48] and Hara [49]. This is because the ground state of the target is determined at the HF level only, and the role of excited states is excluded in scattering. The excited states introduce correlation–polarization effects, and their inclusion in the description of the target wavefunction significantly alters the scattering parameters. This makes total interaction potential a sum of static, correlation–polarization and exchange potentials. The static potential () is constructed using the HF wavefunction. It represents an attractive electrostatic interaction between the projectile electron and the nuclear charge distribution of the target plus the local part of the repulsive interaction with the target electrons.
The correlation–polarization potential () gives the dynamic response of a target to the projectile electron. It consists of short- and long-range components of potential. The correlation potential () of Perdew and Zunger potential [48] is effective at short distances and is given by
where = −0.1423, = 1.0529, = 0.3334 and .
The long-ranged correlation potential is denoted by , and its form has been given by Sanna et al. [40].
where is the polarizability tensor, or = x, y, z for i, j = 1, 2, 3. Both the short- and long-range potentials match at value :
The indistinguishable nature of electrons (projectile and target) gives rise to exchange effects that are approximated by Hara type free-electron-gas-exchange potential [49]:
where ; , . is the undisturbed molecular charge density, is the ionization potential (in atomic units), and E is the kinetic energy of the projectile.
Potentials in their expanded form are expressed as
represents the type of potential, which can be static, correlation, polarization, exchange or total.
The solution of Schrdinger’s equation in the fixed nuclei approximation (FNA) provides scattering observables in the body-fixed frame (BF). This, in turn, provides the radial coefficients of the continuum electron wavefunction . The radial scattering equation for the continuum electron is represented as
Here, is the collision energy of the electron in atomic units. is the potential coupling element in local field approximation and is given by
The total interaction potential () is already clarified. r is the radial distance of the electron from the scattering centre, and is the unit vector in the direction of the projectile. The matrix elements like T, K or S [50] are obtained in Body-Fixed frame (BF) by solving a set of Volterra coupled equations [51]. The K-matrices are used to compute the DCS. The Born-corrected and converged elastic DCS between the initial and final rotor state and , respectively, in laboratory-frame after applying frame transformation are given by [52,53]
Here, is the Legendre polynomial, is the scattering angle, and is the scattering coefficient [54]. The quantities denoted with superscript B are evaluated within the Born approximation. is the maximum number of partial waves up to which the second term of Equation (9) is expanded. The rotationally summed DCS is obtained from the sum of DCS for each rotor state.
The integration of DCS given by Equation (10) over the scattering angle from 0–180° provides Born-corrected integral cross sections in lab-frame. The elastic cross sections can also be computed directly in BF from T-matrices.
These cross sections are corrected using the Born Top-up approach [46]. Thus, the Born-corrected cross sections are the sum of BF cross sections and the cross sections obtained using the Born Top-up approach:
where
The correction term under Born approximation is the difference in the cross sections computed under Born approximation () and the cross sections obtained for L partial waves within the Born formalism ().
2.2. Ionization Cross Section: The BEB Model
The non-relativistic BEB ionization cross sections [47] as a function of reduced energy are given by
here, , . . is the reduced energy. R is the Rydberg energy. is the Bohr radius. , and represent the orbital kinetic energy, binding energy and the occupancy number of the ith orbital.
3. Computational Details
The geometry of the Sevoflurane molecule was optimised at the HF level using the cc-pVTZ basis with the help of Gaussian software [55]. The ground state corresponds to the point group with A IR. The linear combinations of atomic constituents of the target (fluorine, hydrogen, carbon and oxygen) generate the symmetry-adapted basis functions. The bound state electron density and potentials as a function of r were expanded in terms of partial waves l using SCELiB code [56]. The maximum value of l, denoted as , was taken as 18 for the bound-state wavefunctions and 36 for the potentials. was equal to the IR of the molecule’s ground state, which is A. The numerical integration was carried out using a radial grid of step size 0.001 au. It resulted in the HF value of the dipole moment as 2.46 D. This value is slightly higher than the experimental value, which falls in the range 2.27 D–2.33 D [28,29]. This is not surprising as the HF calculations lack electron correlation effects. The target calculations were then performed in the correlated model using quantum-mechanical codes [57] by considering eight active electrons (out of 98) moving in nine active orbitals. This is represented as the (8,9) model. This multi-configuration SCF calculation resulted in a lower value of dipole moment of 2.408 D. This value is within 5–7% of the experimental value. Although one may choose any active space, the (8,9) representation gave the best value of the dipole moment. The value for the polarizability 60 au [30] was used to compute . The characteristics and parameters of the molecule are listed in Table 1 and compared with the corresponding experimental values. Lessari et al. have performed theoretical calculations at different levels like HF/DFT/MP-2 using different basis sets. The HF value of their dipole moment 2.49 D was obtained using a 6-311+G(2d,p) basis set and was higher than the DFT and MP-2 levels [29].

Table 1.
Target parameters at optimised geometry. The molecule rotation along the x, y and z axes, respectively.
The rotational eigenfunctions and energy values were computed using ASYMTOP code [58] for J up to 6. The inputs to the POLYDCS code [59] were the blm file corresponding to the point group. The was taken as 20 for incident energies up to 10 eV and 23 at higher energy values. This helped to obtain converged cross sections. The rotational energy for dipole transition was calculated using rotational constants.
The components of the dipole moment are required to correctly apply a Born correction to the molecules belonging to lower point groups [60]. Since the Born correction depends upon the square of the dipole moment [52], and the fact that the values of and are very small, the Born-correction was computed using the theoretical value of dipole moment 2.39 D corresponding to the dominant component .
4. Results and Discussion
Figure 1a exhibits Born−uncorrected and Born-corrected integral elastic cross sections (ECS). The Born-correction was applied to BF ECS through a Born Top-up procedure as mentioned above. The ECS obtained from the integration of Equation (9) using the POLYDCS code did not differ much. The Born-correction leads to enhanced cross sections at low energies. At 1 eV, the correction increases uncorrected cross sections by about 100% but is drastically reduced to 25% at 3 eV and less than 10% at 10 eV. At 50 eV, the difference between Born−uncorrected and Born-corrected ECS is minimal, indicating that the effect of long-ranged forces or dipole moment on scattering is minimal. This effect gradually diminishes at higher energies. The theoretically computed Born-corrected and Born−uncorrected SCE-ECS are in excellent agreement with the uncorrected forward angle experimental results of Vukalović et al. [39] from 50 eV onwards. At low energies, the ECS data are not available. In order to judge the correctness of the present results, the SCE results are compared with the forward angle uncorrected experimental TCS measurements of Lozano et al. [35] up to 13 eV. The estimated threshold of the first excited state is around 8 eV [29], and the ionization threshold from Koopman’s Theorem is 13.75 eV. Thus, it is expected that up to or below 13.75 eV, the major contribution would be from the elastic channel. Consequently, a good agreement between present ECS and experimental TCS is unsurprising. Below 4 eV, our results overestimate the experimental TCS data.
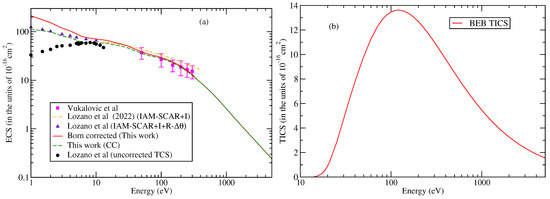
Figure 1.
“(Colour online)” (a) Elastic cross sections: Line curve, Born-corrected (This work); dashed curve; close coupling (CC) or Born−uncorrected (This work); dashed dotted curve, IAM-SCAR+I TCS of Lozano et al. [35]; Squares, Vukalović et al. [39]; circles, uncorrected TCS of Lozano et al. [35]; triangles, IAM-SCAR+I+R- results of Lozano et al. [35] (b) BEB ionization cross sections. The notations have also been explained in the text.
This shows that the impact angular resolution of the spectrometer is dominant up to 4 eV. We have also compared Born−uncorrected ECS with the IAM-based SCAR results of Lozano et al. [35]. These authors adopted two methods, namely (i) IAM-SCAR with interference term (I) and (ii) IAM-SCAR+I+R-. In the second method, the authors included rotational terms in the IAM-SCAR+I model but subtracted the missing angle contribution from TCS. This model is essentially the same as our Born−uncorrected model. The IAM-SCAR+I+R- results are slightly higher, whereas our Born−uncorrected are slightly lower than uncorrected experimental TCS of Lozano et al. [35]. The contribution of vibration and excitation channels is assumed to be less meaningful in the energy range, thus allowing a reasonable comparison between ECS and TCS.
In Figure 1b, the BEB ionization cross sections are plotted. The cross sections follow a well-established rule: they increase from the ionization threshold (13.75 eV), attain a maxima at around 120 eV, and fall according to ( E)/E. Again, no data are available to compare the computed results.
The incoherently summed Born−uncorrected elastic and BEB ionization cross sections are plotted from 10 eV in Figure 2a. These results are also compared with the experimental and IAM-SCAR+I+R- TCS of Lozano et al. [35]. While our results are a little underestimated, the SCAR+I+R- TCS of Lozano et al. [35] are overestimated with respect to experimental TCS. This difference is primarily due to the approach adopted and the basis sets employed in the calculations. Both sets show identical trends in cross sections with respect to energy. For convenience, the SCAR+I TCS of Lozano et al. [35] are displayed.
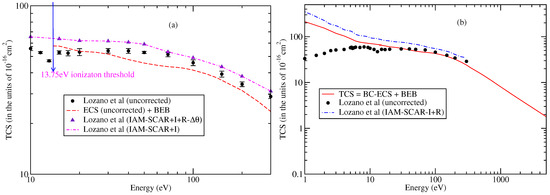
Figure 2.
“(Colour online)” TCS (a) Born−uncorrected from ionization threshold onwards. (b) Born−corrected from 1 eV onwards. Line curve, present results (sum of Born−corrected ECS and BEB), dashed curve, the sum of Born−uncorrected ECS and ionization cross sections (This work); dotted dashed curves, IAM-SCAR+I results of Lozano et al. [35]; dashed-dotted curves, IAM-SCAR+I+R results of Lozano et al. [35]; Circles, experimental uncorrected data of Lozano et al. [35]; triangles, (IAM-SCAR+I+R-).
In Figure 2b, TCS as a sum of Born-corrected elastic and BEB ionization cross sections are plotted from 1 eV onwards. The IAM-SCAR+I+R and uncorrected experimental results of Lozano et al. [35] are also shown. Below the ionization threshold, the TCS is approximated by Born−corrected ECS. Beyond the threshold, TCS is considered as the sum of Born−corrected elastic and BEB ionization cross sections. An excellent agreement is seen with the experimental results of Lozano et al. [35] above 4 eV. The calculations performed by Lozano et al. [35] using the IAM-SCAR+I+R model yield higher results, but the difference reduces above 40 eV.
Figure 3 and Figure 4 show DCS at different scattering energies. The Born−corrected DCSs are strongly peaked in forward direction due to the long-range nature of the electron-target dipole interactions. The Born−corrected DCSs, however, align with Born−uncorrected DCSs after at 1 eV and at 5 eV and at 20 eV. The DCS at 1, 2 and 5 eV are smooth but oscillatory at 15 eV and above. There are no data available at these energies for comparison.
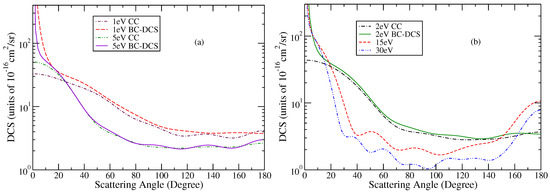
Figure 3.
“(Colour online)” Elastic DCS. (a) 1 eV and 5 eV. Dashed dotted curve, 1 eV Born−uncorrected or CC results; dashed curve, Born−corrected at 1 eV; double dotted dashed curve, CC results at 5 eV; dashed curve, Born−corrected at 5 eV. (b) 2 eV, 15 eV and 30 eV. dotted dashed curve, 2 eV CC results; line curve, Born−corrected at 2 eV; dashed curve, CC results at 15 eV; double dotted dashed curve, 30 eV.
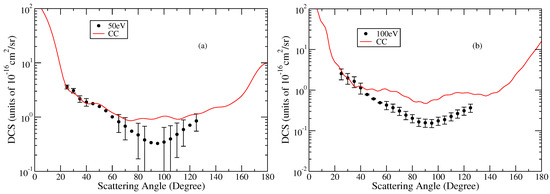
Figure 4.
“(Colour online)” Elastic DCS (a) 50 eV. (b) 100 eV. Line curve: This work, circles, Vukalović et al. [39]. The DCSs at 100 eV are Born−uncorrected. See text for details.
The results at 50 eV and 100 eV are compared with the experimental results of Vukalović et al. [39] in Figure 4a,b. The overall shape and trends of present results are similar to Vukalović et al. except that the SCE-DCSs are oscillatory and higher. The oscillatory behaviour has been observed in several molecules that employed POLYDCS code for scattering calculations [24,61]. This behaviour is due to the lack of complete convergence of higher partial waves accounting for the dipole potential term in the Born closure method. The higher DCS results may be due to the omission of inelastic channels, which may be strongly interacting with the elastic channels.
The study is based on two independent approaches to compute cross sections, which are then combined to estimate the total cross sections. The calculations were simplified by excluding the coupling between the two processes and neglecting the electronic excitation channel. This seems to be justified as electronic excitation cross sections are consistently smaller than elastic and ionization cross sections. The ionization cross sections increase until reaching a maximum and then decrease with the increase in energy. In contrast, the excitation cross sections rise sharply from the excitation threshold but then decrease rapidly with the increasing incident energy. This complimentary behaviour of two inelastic channels aids in estimating the total cross sections over a high energy range with optimal resources, aligning with the goal of our study. Furthermore, the exchange and correlation–polarization effects diminish with an increase in energy, leading to improved agreement with the experimental data at higher projectile energy. It is emphasised that the opening of electronic inelastic channels allows flux competition, thereby resulting in lowering the magnitude of the cross sections. A similar effect occurs while working with complex potentials where only elastic scattering is considered. The decrease in elastic DCS with an increasing number of open channels is particularly evident at higher impact energies due to greater multichannel coupling [62].
A significant deviation exists between experimental and theoretical results in the low energy range. Both the present and previous IAM-SCAR approaches fail to explain the reasons for this discrepancy. Insights obtained from ab initio methods would be valuable to understand the underlying reasons. However, due to resource limitations, we could not apply the R-matrix method [21,63] to solve the scattering problem. Till such calculations are performed, the present and existing results will serve as useful reference for future calculations.
5. Conclusions
The present study reports various electron impact cross sections for Sevoflurane from 1 to 5000 eV. The low-energy DCS and elastic cross sections are reported for the first time. To assess the reliability of the present data, comparisons were made with experimental TCS measurements, yielding encouraging results. The ionization results are also reported, although they are yet to be validated. A good agreement of the TCS between the experimental TCS and that obtained from the incoherent summation of ECS and ionization cross sections indicates the correct application of the methodology. It also indicates the reliable estimates of individual cross sections. In the local potential approach, only the ground state is considered, and quantities like density and potential are computed at the HF level only. Hence, only the elastic cross sections can be computed. A target wavefunction that is constructed using ground and excited states not only yields improved target properties like energy, moments but also gives a complete picture of the scattering process, i.e., it provides elastic and electronic excitation cross sections. It further helps in giving a description of different types of resonances (negative anion state) [21]. The HF calculations usually result in higher values of dipole moment and only the elastic cross sections. This is surely one of the limitations of the present model. As the energy of the projectile increases, the effects due to correlation–polarization and exchange decreases, and the scattering results obtained using model potentials tend to align with results computed using ab initio methods. The present approach is undoubtedly straightforward and resource-efficient due to the explicit neglect of inter channel coupling and channels like electronic excitations. Inter channel coupling refers to the mixing between the quantum states or channels involved in the scattering process. These channels are defined by quantum states of the target molecule (electronic, rotational, vibrational). Unarguably, the channel coupling and flux competition are important effects in scattering phenomenon. The absence of these effects and inelastic channels from model potential calculations is bound to introduce some uncertainties in cross sections when the scattering results are compared with sophisticated close-coupling results, where elastic and inelastic channels are coupled, or experimental values. The uncertainties arises due to neglect of inter channel coupling, and inelastic channels cannot be quantified. As an estimate, the results may be higher by about 10–15%. The work also highlights the challenges associated with the complex multi-centred molecules with a large number of electrons when dealing with ab initio methods. Overall, the approach offers an alternative path to explore scattering phenomena for any molecule. These results would be valuable, especially when ab initio calculations fail to provide scattering cross sections.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atoms13040029/s1, Supplementary Data sheet.
Author Contributions
Supervision, K.L.B. Calculations; writing; review and editing, S.K., A.K.A. and A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The optimised geometry of the molecule and the input BEB input parameters are attached in the Supplementary Data sheet.
Acknowledgments
The authors are grateful to Dr. J. Benda for useful insights to computation using the R-matrix method and Prof. Bratislav for providing numerical data of their work. The authors are also thankful to the University of Delhi for providing the necessary computational and other facilities to carry out the study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| SCE | Single-centre-expansion |
| BEB | binary-encounter-Bethe |
| ECS | Elastic cross sections |
| TCS | Total cross sections |
| TICS | Total ionization cross sections |
| DCS | Differential cross sections |
| IR | Irreducible representation |
| MO | Molecular orbitals |
| eV | electron volt |
| i.e. | that is |
References
- Sanche, L. Low energy electron-driven damage in biomolecules. Eur. Phys. J. D 2005, 35, 367–390. [Google Scholar] [CrossRef]
- Campbell, L.; Brunger, M.J. Modelling of plasma processes in cometary and planetary atmospheres. Plasma Sources Sci. Technol. 2013, 22, 013002. [Google Scholar] [CrossRef]
- Makabe, T.; Petrović, Z.L. Plasma Electronics: Applications in Microelectronic Device Fabrication, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Chu, P.K.; Lu, X. (Eds.) Low Temperature Plasma Technology: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Christophorou, L.G. (Ed.) Electron Molecule Interactions and Their Applications; Academic Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Christophorou, L.G.; Olthoff, J.K. Fundamental Electron Interactions with Plasma Processing Gases; Springer: Boston, MA, USA, 2004. [Google Scholar]
- Janev, R.K. Atomic and Molecular Processes in Fusion Edge Plasmas; Plenum Press: New York, NY, USA, 1995. [Google Scholar]
- Starikovskiy, A. Physics and chemistry of plasma-assisted combustion. Philos. Trans. R. Soc. A 2015, 373, 20150074. [Google Scholar] [CrossRef]
- Ptasinska, S.; Varella, M.T.d.N.; Khakoo, M.A.; Slaughter, D.S.; Denifl, S. Electron scattering processes: Fundamentals, challenges, advances, and opportunities. Eur. Phys. J. D 2022, 76, 179. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Możejko, P. Recent total cross section measurements in electron scattering from molecules. Eur. Phys. J. D 2020, 74, 90. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- Cooper, B.; Tudorovskaya, M.; Mohr, S.; O’Hare, A.; Hanicinec, M.; Dzarasova, A.; Gorfinkiel, J.D.; Benda, J.; Mašín, Z.; Al-Refaie, A.F.; et al. Quantemol Electron Collisions (QEC): An Enhanced Expert System for Performing Electron Molecule Collision Calculations Using the R-Matrix Method. Atoms 2019, 7, 97. [Google Scholar] [CrossRef]
- Mohr, S.; Tudorovskaya, M.; Hanicinec, M.; Tennyson, J. Targeted Cross-Section Calculations for Plasma Simulations. Atoms 2021, 9, 85. [Google Scholar] [CrossRef]
- Albert, D.; Antony, B.; Ba, Y.A.; Babikov, Y.L.; Bollard, P.; Boudon, V.; Delahaye, F.; Del Zanna, G.; Dimitrijević, M.S.; Drouin, B.J.; et al. A Decade with VAMDC: Results and Ambitions. Atoms 2020, 8, 76. [Google Scholar] [CrossRef]
- Bartschat, K.; Kushner, M.J. Electron collisions with atoms, ions, molecules, and surfaces: Fundamental science empowering advances in technology. Proc. Natl. Acad. Sci. USA 2016, 113, 7026–7034. [Google Scholar] [CrossRef]
- Bartschat, K.; Tennyson, J.; Zatsarinny, O. Quantum-Mechanical Calculations of Cross Sections for Electron Collisions with Atoms and Molecules. Plasma Process. Polym. 2017, 14, 1600093. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I. Electron- and positron-molecule scattering: Development of the molecular convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Sullivan, J.P.; Makochekanwa, C.; Jones, A.; Caradonna, P.; Slaughter, D.S.; Machacek, J.; McEachran, R.P.; Mueller, D.W.; Buckman, S.J. Forward angle scattering effects in the measurement of total cross sections for positron scattering. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 035201. [Google Scholar] [CrossRef]
- Brunger, M.J.; Buckman, S.J.; Ratnavelu, K. Positron scattering from molecules: An experimental cross section compilation for positron transport studies and benchmarking theory. J. Phys. Chem. Ref. Data 2017, 46, 023102. [Google Scholar] [CrossRef]
- Kadokura, R.; Loreti, A.; Kövér, Á.; Faure, A.; Tennyson, J.; Laricchia, G. Angle-Resolved Electron Scattering from H2O near 0°. Phys. Rev. Lett. 2019, 123, 033401. [Google Scholar] [CrossRef]
- Tennyson, J. Electron-molecule collision calculations using the R-matrix method. Phys. Rep. 2010, 491, 29–76. [Google Scholar] [CrossRef]
- da Costa, R.F.; Varella, M.T.d.N.; Bettega, M.H.F.; Lima, M.A.P. Recent advances in the application of the Schwinger multichannel method with pseudopotentials to electron-molecule collisions. Eur. Phys. D 2015, 69, 159. [Google Scholar] [CrossRef]
- Schneider, B.I.; Rescigno, T.N. Complex Kohn variational method: Application to low-energy electron-molecule collisions. Phys. Rev. A 1988, 37, 3749. [Google Scholar] [CrossRef]
- Luthra, M.; Garkoti, P.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. Electron impact cross-sections of tetraethyl silicate. Plasma Sources Sci. Technol. 2022, 31, 095013. [Google Scholar] [CrossRef]
- Kaur, S.; Arora, A.K.; Bharadvaja, A.; Baluja, K.L. Positron interactions with vinyl acetate from 0.1 eV to 5 keV. Phys. Scr. 2024, 99, 115411. [Google Scholar] [CrossRef]
- Prashant, A.; Luthra, M.; Goswami, K.; Bharadvaja, A.; Baluja, K.L. Positron Scattering from Pyrimidine. Atoms 2023, 11, 55. [Google Scholar] [CrossRef]
- Charlton, M.; Humberston, J.W. Positron Physics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Tang, P.; Zubrycki, I.; Xu, Y. Ab Initio Calculation of structures and properties of halogenated general anesthetics: Halothane and sevoflurane. J. Comput. Chem. 2001, 22, 436–444. [Google Scholar] [CrossRef]
- Lesarri, A.; Vega-Toribio, A.; Suenram, R.D.; Brugh, D.J.; Grabow, J.-U. The conformational landscape of the volatile anesthetic sevoflurane. Phys. Chem. Chem. Phys. 2010, 12, 9624–9631. [Google Scholar] [CrossRef]
- The Toxin and Toxin Target Database (T3DB). Available online: https://go.drugbank.com/drugs/DB01236 (accessed on 10 February 2025).
- Jones, R.M. Desflurane and sevoflurane: Inhalation anaesthetics for this decade? Br. J. Anaesth. 1990, 65, 527–536. [Google Scholar] [CrossRef] [PubMed]
- Gaya da Costa, M.; Kalmar, A.F.; Struys, M.M.R.F. Inhaled Anesthetics: Environmental Role, Occupational Risk, and Clinical Use. J. Clin. Med. 2021, 10, 1306. [Google Scholar] [CrossRef]
- Langbein, T.; Sonntag, H.; Trapp, D.; Hoffmann, A.; Malms, W.; Röth, E.P.; Mörs, V.; Zellner, R. Volatile anaesthetics and the atmosphere: Atmospheric lifetimes and atmospheric effects of halothane, enflurane, isoflurane, desflurane and sevoflurane. Br. J. Anaesth. 1999, 82, 66–73. [Google Scholar] [PubMed]
- Lange, E.; Ferreira da Silva, F.; Jones, N.C.; Hoffmann, S.V.; Duflot, D.; Limão-Vieira, P.M. The lowest-lying electronic states of isoflurane and sevoflurane in the 5.0–10.8 eV energy range investigated by experimental and theoretical methods. Chem. Phys. Lett. 2019, 716, 42–48. [Google Scholar] [CrossRef]
- Lozano, A.I.; Ferreira da Silva, F.; Blanco, F.; Limão-Vieira, P.M.; García, G. Total electron scattering cross section from sevoflurane by 1–300 eV energy electron impact. Chem. Phys. Lett. 2018, 706, 533–537. [Google Scholar] [CrossRef]
- Blanco, F.; Rosada, J.; Illana, A.; García, G. Comparison of two screening corrections to the additivity rule for the calculation of electron scattering from polyatomic molecules. Phys. Lett. A 2010, 374, 4420–4424. [Google Scholar] [CrossRef]
- Blanco, F.; Ellis-Gibbings, L.; García, G. Screening corrections for the interference contributions to the electron and positron scattering cross sections from polyatomic molecules. Chem. Phys. Lett. 2016, 645, 71–75. [Google Scholar] [CrossRef]
- Dubuis, A.T.; Verkhovtsev, A.; Ellis-Gibbings, L.; Krupa, K.; Blanco, F.; Jones, D.B.; Brunger, M.J.; García, G. Total cross section of furfural by electron impact: Experiment and theory. Chem. Phys. Lett. 2017, 147, 054301. [Google Scholar] [CrossRef]
- Vukalović, J.; Maljković, J.B.; Blanco, F.; García, G.; Predojević, B.; Marinković, B.P. Absolute Differential Cross-Sections for Elastic Electron Scattering from Sevoflurane Molecule in the Energy Range from 50–300 eV. Int. J. Mol. Sci. 2022, 23, 21. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Sanna, N. SCELIB: A parallel computational library of molecular properties in the single-center expansion approach. Comput. Phys. Commun. 2000, 128, 139–169. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Thompson, D.G.; Jain, A.K. Computational Methods for Electron Molecule Collisions; Huo, W.M., Gianturco, F.A., Eds.; Plenum: New York, NY, USA, 1995. [Google Scholar]
- Gianturco, F.A.; Lucchese, R.R.; Sanna, N.; Talamo, A. A.; Lucchese, R.R.; Sanna, N.; Talamo, A. A Generalized Single Center Approach for Treating Electron Scattering from Polyatomic Molecules. In Electron Collisions with Molecules, Clusters and Surfaces; Ehrhardt, H., Morgan, L.A., Eds.; Plenum: New York, NY, USA, 1994. [Google Scholar]
- Gianturco, F.A.; Lucchese, R.R.; Sanna, N.J. Calculation of low-energy elastic electron scattering by CF4. Chem. Phys. 1994, 100, 6464–6471. [Google Scholar] [CrossRef]
- Joshipura, K.N.; Mason, N. Atomic-Molecular Ionization by Electron Scattering: Theory and Applications; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Jain, A.K.; Baluja, K.L. Total (elastic plus inelastic) cross sections for electron scattering from diatomic and polyatomic molecules at 10–5000 eV: H2, Li2, HF, CH4, N2, CO, C2H2, HCN, O2, HCl, H2S, PH3, SiH4, and CO2. Phys. Rev. A 1992, 45, 202–218. [Google Scholar] [CrossRef]
- Kaur, S.; Baluja, K.L.; Tennyson, J. Electron-impact study of NeF using the R-matrix method. Phys. Rev. A 2008, 77, 032718. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Rudd, M.E. Binary-encounter-dipole model for electron-impact ionization. Phys. Rev. A 1994, 50, 3954. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Hara, S. The Scattering of Slow Electrons by Hydrogen Molecules. J. Phys. Soc. Jpn. 1967, 22, 710–718. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions: Application to Atomic, Molecular and Optical Processes; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Franz, J. Solution of coupled integral equations for quantum scattering in the presence of complex potentials. J. Math. Phys. 2015, 56, 012104. [Google Scholar] [CrossRef]
- Itikawa, Y. The Born closure approximation for the scattering amplitude of an electron-molecule collision. Theor. Chem. Acc. 2000, 105, 123–131. [Google Scholar] [CrossRef]
- Fabrikant, I.I. Long-range effects in electron scattering by polar molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 222005. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Jain, A. The theory of electron scattering from polyatomic molecules. Phys. Rep. 1986, 143, 347–425. [Google Scholar] [CrossRef]
- GAUSSIAN 03. Gaussian, Inc.: Wallingford, UK, 2003.
- Sanna, N.; Baccarelli, I.; Morelli, G. SCELib3.0: The new revision of SCELib, the parallel computational library of molecular properties in the Single Center Approach. Comput. Phys. Commun. 2009, 180, 2544–2549. [Google Scholar] [CrossRef]
- Psi4: An Open-Source Ab Initio Electronic Structure Package Psi4 1.3.2 Release. Available online: https://psicode.org/ (accessed on 13 December 2024).
- Jain, A.; Thompson, D.G. A program to generate the symmetry-adapted rotational eigenfunctions and energy levels for asymmetric top molecules. Comput. Phys. Commun. 1983, 30, 301–309. [Google Scholar] [CrossRef]
- Sanna, N.; Gianturco, F.A. Differential cross sections for electron/positron scattering from polyatomic molecules. Comput. Phys. Commun. 1998, 114, 142–167. [Google Scholar] [CrossRef]
- Franz, J.; Gianturco, F.A.; Baccarelli, I. Low-energy positron scattering from gas-phase uracil. Eur. Phys. J. D 2014, 68, 183. [Google Scholar] [CrossRef]
- Meltzer, T.; Tennyson, J.; Mašin, Z.; Zammit, M.C.; Scarlett, L.H.; Fursa, D.V.; Bray, I. Benchmark calculations of electron impact electronic excitation of the hydrogen molecule. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 145204. [Google Scholar] [CrossRef]
- Randi, P.A.S.; Moreira, G.M.; Bettega, M.H.F. Inelastic scattering by formamide: Elastic and electronically inelastic cross sections up to 179 energetically open states. Phys. Rev. A 2023, 107, 012806. [Google Scholar] [CrossRef]
- Mas̃in, Z.; Benda, J.; Harvey, A.G.; Al-Refaie, A.; Gorfinkiel, J.D.; Tennyson, J. UKRmol+: A suite for modelling electronic processes in molecules interacting with electrons, positrons and photons using the R-matrix method. Comp. Phys. Commun. 2020, 249, 107092. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).