Abstract
We present a theoretical investigation of the inelastic scattering of vortex electrons by many-electron atoms embedded in a solid-state environment. Special emphasis is placed on the probability of exciting a target atom and on the relative population of its magnetic substates as described by the set of alignment parameters. These parameters are directly related to the angular distribution of the subsequent radiative decay. To demonstrate the application of the developed theoretical approach, we present calculations for the excitation of a Mg atom and its subsequent radiative decay. Our results highlight the significance of the orbital angular momentum (OAM) projection as well as the relative position of the vortex electron with respect to the target atom.
1. Introduction
Inelastic electron–atom scattering plays a significant role in transmission electron microscopy (TEM). In particular, the investigation of plasmonic excitation, the probing of chirality in nanoparticles and molecules, and applying electron energy loss spectroscopy rely on this fundamental collision process. While highly focused Gaussian electron beams have traditionally been the primary tool in TEM, recent advancements have expanded the interest in this field to include vortex electron beams. These electrons, first generated in 2010 [1,2], possess unique properties: a non-zero orbital angular momentum (OAM) projection in their propagation direction, a winding phase front, and a “doughnut”-shaped probability density profile [3,4,5]. Beyond direct generation methods using holographic masks or spiral phase plates, vortex electrons can also be produced via atomic ionization by twisted light, intense laser pulses, and structured electric fields [6,7,8]. Besides interest in their fundamental physics and generation mechanisms, vortex electrons offer exciting opportunities for exploring electron scattering phenomena in the context of TEM and other fields.
Recent experiments have demonstrated various applications of vortex electron beams. Free-electron Landau states, previously observed only in condensed-matter systems, were observed for the first time in TEM [9]. Vortex electron beams have also been used in chiral energy-loss spectroscopy and magnetic dichroism, providing new insights into material properties, nanostructures, and biomolecules [2,10,11,12,13]. Focused free-electron vortices have been shown to reach sizes comparable to atomic orbitals, enabling atomic-scale magnetic mapping [14,15].
To date, most of the theoretical studies with vortex electrons focus on the elastic scattering by atoms, molecules, and solid states. In these works, the first Born approximation is usually employed to calculate total and differential cross sections [16,17,18,19,20,21,22]. Due to the distortion of an electron beam resulting from Coulomb interaction, the validity of the first Born approximation is questioned in Refs. [23,24,25], where distortion of an electron beam due to Coulomb interaction is discussed. Much less is known about inelastic processes involving vortex electrons. Two key channels are of particular interest: vortex electron impact ionization and excitation. The former is explored in Ref. [26] within the non-relativistic first Born approximation for hydrogen. The latter was first investigated by van Boxem et al. [27], also using the non-relativistic first Born approach. A more advanced treatment of the atomic excitation, which accounts for the interaction of the projectile electrons with a target, was performed by us recently within the framework of the non-relativistic distorted wave approximation [28]. However, all of these theoretical investigations [27,28] dealt with non-relativistic vortex electron scattering off a free hydrogen atom. In the present contribution, we extend the previous theoretical studies to a more realistic scenario of a many-electron atom embedded in a solid-state environment. For this purpose, we use the example of magnesium trapped in to demonstrate the applicability of our approach to consider atoms in different solid-state environments which can be approximated according to a suitable model potential. Previous works have mentioned that neutral atoms including Mg can be in stable equilibrium at the center of the shell [29,30,31]. Additionally, in the present work, we lay out the fully relativistic approach, which will allow for a better understanding of spin and magnetic interaction phenomena in the future.
A brief discussion of the relativistic theory of inelastic scattering of vortex electrons by many-electron atoms is presented in Section 2. In particular, we derive the scattering amplitude for the incident Bessel electrons, whose vortex line might be shifted from the position of the target atom. Based on this amplitude, we are able to evaluate both the excitation probability and the so-called alignment parameters of the excited atomic states. These parameters describe the relative population of the magnetic atomic sublevels and can be directly related to the angular distribution of the subsequent photon emission. Our interest in the radiative decay following inelastic electron scattering arises from its importance for the energy-dispersive X-ray spectroscopy technique (EDX) applied in TEM. The EDX method identifies the elemental composition of a sample by detecting characteristic X-rays emitted during electron bombardment [32]. Following the theory section, in Section 3 we present the calculation details. Here, we introduce an additional potential which accounts for the screening of an atom due to its embedding in a solid-state environment. Next, numerical results and their discussion are presented in Section 4 for the particular case of vortex electron scattering by a Mg atom. We consider the excitation and subsequent radiative decay and investigate how the properties of the scattering process can be affected by the solid-state screening of the target atom and by the orbital angular momentum projection of the incident beam. Finally, a conclusion is given in Section 5.
Atomic units are used throughout this article unless otherwise stated.
2. Theory
In this section, we briefly discuss the theory of inelastic scattering of vortex electrons by a target atom. By making use of the scattering amplitude, we derive both the probability of exciting an atom and the alignment parameters that describe the population of the different excited magnetic substates. These parameters will later be used to calculate the angular distribution of the subsequent radiative decay.
2.1. Scattering Amplitude
Before discussing the scattering of vortex electrons, we briefly reiterate that for the conventional non-vortex case, all of the properties of the scattering process can be traced back to the amplitude
In this amplitude, the initial and final atomic states are described by the quantum numbers , J and M, where J represents the total angular momentum and M is its projection on the quantization axis. The abbreviation encompasses all other quantum numbers required for a unique specification of the atomic states. The incident and scattered electrons are characterized by their asymptotical momenta and and their helicities and . The wave function for these electrons are generated within the framework of the distorted wave approximation which accounts for Coulomb distortion by the target atom (see Refs. [33,34,35,36] for further details). In Equation (1), the interaction between the projectile and bound atomic electrons is described by the potential , while is referred to as the distortion potential, which is discussed in Section 3. Finally, the antisymmetrization of the initial and final electronic states in Equation (1) has to be taken into account.
While the amplitude (1) is written for the conventional non-vortex electrons, it can be also used as a “building block” to describe the scattering of vortex electrons. In order to demonstrate this, we have to briefly discuss the construction of the distorted vortex electron wave function. In the present work, we deal with the so-called Bessel states [37]. These states are characterized by a fixed longitudinal momentum , the magnitude of the transverse momentum , and the total angular momentum projection in the propagation direction
Here, is the “standard” (non-votex) distorted wave and is the displacement of the vortex line from the target atom, located at the coordinate origin (see Figure 1). This displacement is usually referred to as the impact parameter and has been discussed in detail in our previous study [28]. By employing the wave function (2), one can easily find the scattering amplitude for the inelastic scattering of vortex electrons:
where is given by Equation (1). In this expression, we assumed that the vortex line is shifted from the z axis by the impact parameter b along the x axis (see Figure 1) and that the scattered electrons are in a non-vortex state.
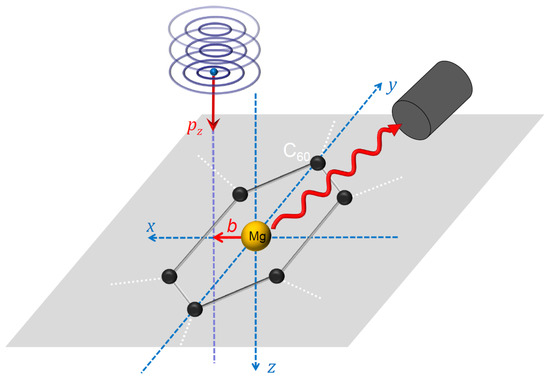
Figure 1.
The geometry of inelastic scattering of a vortex electron beam by a target Mg atom. The magnesium atom is confined within a fullerene molecule. The incident electron has a well-defined longitudinal momentum and projection of orbital angular momentum on the propagation axis. This axis is shifted from the coordinate origin (position of the target atom) by the vector . The photon detector is positioned at the polar angle and azimuthal angle .
2.2. Excitation Probabilities and Alignment Parameters
With the help of the scattering amplitude (3), we can derive all the properties of the scattering process. We start with the probability of exciting an atom to a particular magnetic substate . By assuming that the scattered electron is not observed and the atom is initially unpolarized, this probability is given by
where N is a prefactor whose explicit form is not relevant to the present study and is the so-called opening angle [20,22,38]. By making use of Equation (4), one can calculate the total excitation probability normalized to that for conventional non-vortex electrons
where is obtained from Equation (4) by setting and , thus recovering the non-vortex results. In what follows, we will refer to Equation (5) as the relative total excitation probability.
The population of the magnetic sublevels is usually described by a set of orientation (odd rank k) and alignment (even k) parameters
where is the Clebsch–Gordan coefficient [39]. For a particular atomic state with total angular momentum , the magnetic population is generally described by parameters with and projection .
Although the parameters cannot be directly observed, they determine the angular distribution and polarization of the emitted photons in the subsequent radiative decay. For example, the angular distribution of a decay is uniquely defined by the second rank alignment parameters . Among them, the zero projection parameter is of particular interest since it defines the relative population of the different magnetic substates
The parameter with characterizes the coherence between these substates—see Ref. [39] for further details.
2.3. Angular Distribution of Subsequent Decay
As mentioned above, orientation and alignment parameters define the angular and polarization properties of photons emitted in the radiative decay. For example, the angular distribution of photons emitted in a transition is given by
where are the spherical harmonics and is the intrinsic anisotropy parameter for photo emission. For the electric dipole transition and by assuming that a photodetector is not sensitive to the photon polarization, this parameter is [39].
3. Calculation Details
As seen from Equations (3)–(8), any analysis of the inelastic scattering as well as of the subsequent decay requires calculation of the distorted wave matrix elements (1). While the details of these calculations have been presented in a number of previous works [33,34,35,36], here we recall just a few important details. Specifically, regarding the interaction between the projectile and the bound electrons, both the Coulomb and Breit interactions are taken into account
where is the relative coordinate of two electrons and represents the vector of Dirac matrices of the ith electron. The potential only depends on the coordinates of the projectile electron and describes the distortion of its incident and scattered waves by an atomic potential [40]. Its composition is discussed in detail in Ref. [36].
By making use of Equations (1) and (9), one can generate the amplitude for the inelastic scattering of distorted electrons by a free target atom. In the present study, we aim to also investigate the electron scattering of atoms embedded in a solid-state environment. In order to estimate how this environment can affect the electron scattering, we consider an approximation in which the target atom is confined within a fullerene molecule. The cage potential has the form
and is added to the distortion potential . We use the parameters , and [41]. To achieve the most accurate results, it would be desirable to account for the correlations between the electrons of and those of the confined atom in first-principle (ab initio) calculations. However, due to the complexity of such calculations, these interactions are approximated using a model potential, which has been widely used in previous studies and demonstrated to be a reasonable approach [41]. Further details about this potential and the used parameters, as well as electron scattering by an atom confined within a fullerene molecule, can be found in Refs. [41,42,43].
4. Results
In order to illustrate the application of the theory developed above, we investigate the scattering of vortex electrons by a Mg target atom. In particular, we calculated the transition induced by Bessel electrons with a kinetic energy of 20 eV, an opening angle , a spin projection , and an OAM projection (red dashed line), (blue dash-dotted line), and (orange dotted line). Additionally, we display the prediction of the non-vortex electrons using the black solid line for reference. Finally, the left and right columns correspond to the electron scattering of a magnesium atom, either free or confined within a molecule, respectively. The choice of 20 eV as the kinetic energy was motivated by the low binding energy of Mg and C atoms. However, such low energies are rarely used in energy-dispersive X-ray spectroscopy (EDX) in TEM.
The upper panels of Figure 2 display the relative total excitation probability (5) as a function of the impact parameter b. As seen from this figure, is smaller than unity and exhibits characteristic oscillations that depend also on the OAM projection of the incident vortex electrons. This behavior reflects the oscillations of the electron probability density.
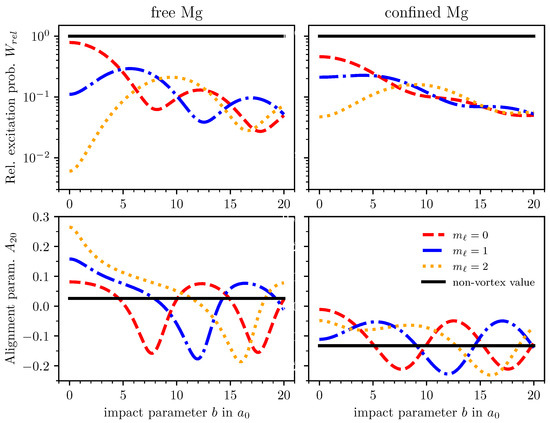
Figure 2.
(Upper row): Relative total excitation probability of the excitation of a Mg atom as a function of the impact parameter b. The incident vortex electron has a kinetic energy of 20 eV, an opening angle , and a spin projection . (Lower row): Alignment parameter of the excited atomic state, again as a function of b in units of Bohr radii . The columns correspond to the scattering of a free Mg atom and Mg confined within a fullerene molecule. The different curves represent the OAM projections (red dashed line), (blue dash-dotted line), and (orange dotted line), while the non-vortex values are displayed as black solid lines as references.
It is important to note that this expression is only an approximation. For , the Bessel wave function (2) can be considered approximately as the paraxial solution [44]. The total excitation probability corresponds to the probability density of the incident electron, as a lower electron density reduces the likelihood of excitation. The oscillatory behavior of the probability density (11) as a function of b is well illustrated for a free relativistic vortex electron in Figure 2a of Ref. [45]. As seen from Expression (11), both and are strongly suppressed for and , while they reach their maximum at this impact parameter for . Moreover, the period of oscillations as a function of b becomes larger with the increase in .
One can also mention that the oscillatory behavior of is significantly damped if a vortex electron is scattered not by free but by confined Mg (see the right upper panel of Figure 2). This can be understood by the fact that the presence of a confining potential acts like a shield, thus leading to more robustness of the Mg atom with respect to external perturbations. This effect can also be seen for the inelastic scattering of non-vortex electrons.
Having analyzed the total excitation probability, we now focus on the relative population of magnetic sublevels of as described by the parameter . This parameter is displayed in the lower row of Figure 2 as a function of b. As seen from these plots, exhibits oscillatory behavior similar to that observed for the relative total excitation probability. This can be attributed not only to the variation in the probability density profile but also to the orientation of the local linear momentum of the incoming vortex electron beam. By comparing the left and right bottom panels of Figure 2, we can also observe a remarkable effect of the confinement of the target Mg atom. In particular, while the alignment parameter is positive for a free atom and small impact parameters, for the confined atom and the entire b range. By inspecting Equation (7), we can conclude that excitation of the is enhanced compared to the other sublevels due to the screening of the target atom.
Apart from the alignment parameter , calculations were also performed for with , describing the coherence between the magnetic sublevels of the state. For the sake of simplicity, we will not present the results of these calculations here and turn to the discussion of the radiative decay (see Equation (8)). In Figure 3, we display this angular distribution for the confined Mg and as a function of the azimuthal angle , while the polar emission angle is fixed to . This particular polar angle corresponds to a typical setup of an energy-dispersive X-ray detector within a TEM. The calculations were performed for the incident Bessel electrons with kinetic energy 20 eV, opening angle and OAM projection . Moreover, the angular distribution in Figure 3 is displayed for the cases when the vortex line is displaced from the target atom by the impact parameter (red solid line), (blue dashed line), and (orange dotted line). For , the system exhibits perfect azimuthal symmetry, as the magnesium atom in its ground state is spherically symmetric, and the probability density of the electron vortex beam is also azimuthally symmetric. As a result, the subsequent decay is isotropic (see Figure 3). As seen from the figure, an increase in the impact parameter of the vortex electron results in an enhanced anisotropy in the angular distribution of the emitted photons. This behavior arises from the breaking of azimuthal symmetry of the system when the vortex line is shifted away from the coordinate origin that coincides with the position of the atomic nucleus. This broken symmetry leads to the predominant emission of photons in the plane, which is perpendicular to the shift vector (see Figure (Figure 1)).
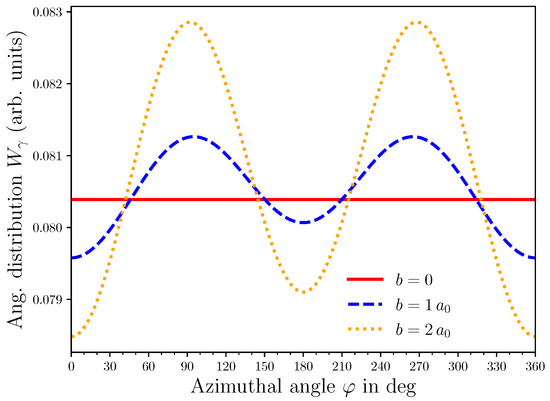
Figure 3.
Angular distribution of the radiative decay of the transition in confined Mg. The polar angle is fixed to and the dependence of the emitted photons is shown. The incident vortex electron has a kinetic energy of 20 eV, an opening angle , and a TAM projection . The curves belong to different impact parameters: (red solid line), (blue dashed line), and (orange dotted line).
While conventional transmission electron microscopes operate in the keV range, our study treats the inelastic vortex electron scattering at much lower energies. These findings highlight new aspects of excitation dynamics and radiative decay, which may inspire experiments with low-energy electron microscopes to further investigate and validate the theoretical predictions.
5. Conclusions
In this work, we investigated the excitation of a magnesium atom by means of vortex electron impact. Our theoretical analysis was performed within the framework of relativistic distorted wave approximation, considering a Mg atom in a solid-state environment. Detailed calculations have been performed for 20 eV electrons, carrying an OAM projection of , where the vortex beam’s axis may be displaced from the atom position by an impact parameter b. We found that both excitation probability and relative population of the excited magnetic sublevels, described by means of the alignment parameter , strongly depend on both b and .
The radiative decay, subsequent to the electron impact excitation, has also been explored. Here, special attention was paid to the transition. The angular distribution of this transition exhibits a remarkable b-dependence, showing enhanced anisotropy as b is increased. These results suggest that observation of the radiative decay following inelastic scattering of vortex electrons can be used for determining the position of a target atom with respect to the incident beam axis. Further refinement of the results can be achieved by employing vortex electron beams with different OAM projections. A more detailed discussion of these effects will be provided in an upcoming publication.
Author Contributions
Conceptualization, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; methodology, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; software, S.S., A.K.S., L.S., J.S. and A.S.; validation, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; formal analysis, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; investigation, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; resources, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; data curation, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; writing—original draft preparation, S.S. and A.S.; writing—review and editing, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S.; visualization, S.S.; supervision, L.S., D.P. and A.S.; project administration, A.S.; funding acquisition, S.S., A.K.S., L.S., J.S., D.P., C.B. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
J. Sommerfeldt acknowledges support from the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG) under the project 546193616.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Uchida, M.; Tonomura, A. Generation of electron beams carrying orbital angular momentum. Nature 2010, 464, 737–739. [Google Scholar] [CrossRef]
- Verbeeck, J.; Tian, H.; Schattschneider, P. Production and application of electron vortex beams. Nature 2010, 467, 301–304. [Google Scholar] [CrossRef] [PubMed]
- Bliokh, K.Y.; Ivanov, I.P.; Guzzinati, G.; Clark, L.; Van Boxem, R.; Béché, A.; Juchtmans, R.; Alonso, M.A.; Schattschneider, P.; Nori, F.; et al. Theory and applications of free-electron vortex states. Phys. Rep. 2017, 690, 1–70. [Google Scholar] [CrossRef]
- Lloyd, S.; Babiker, M.; Thirunavukkarasu, G.; Yuan, J. Electron vortices: Beams with orbital angular momentum. Rev. Mod. Phys. 2017, 89, 035004. [Google Scholar] [CrossRef]
- Larocque, H.; Kaminer, I.; Grillo, V.; Leuchs, G.; Padgett, M.J.; Boyd, R.W.; Segev, M.; Karimi, E. ‘Twisted’ electrons. Contemp. Phys. 2018, 59, 126–144. [Google Scholar] [CrossRef]
- Pavlov, I.; Chaikovskaia, A.; Karlovets, D. Generation of vortex electrons by atomic photoionization. Phys. Rev. A 2024, 110, L031101. [Google Scholar] [CrossRef]
- Bu, Z.; Ji, L.; Geng, X.; Liu, S.; Lei, S.; Shen, B.; Li, R.; Xu, Z. Generation of quantum vortex electrons with intense laser pulses. Adv. Sci. 2024, 11, 2404564. [Google Scholar] [CrossRef]
- Tavabi, A.H.; Larocque, H.; Lu, P.H.; Duchamp, M.; Grillo, V.; Karimi, E.; Dunin-Borkowski, R.E.; Pozzi, G. Generation of electron vortices using nonexact electric fields. Phys. Rev. Res. 2020, 2, 013185. [Google Scholar] [CrossRef]
- Schattschneider, P.; Schachinger, T.; Stöger-Pollach, M.; Löffler, S.; Steiger-Thirsfeld, A.; Bliokh, K.Y.; Nori, F. Imaging the dynamics of free-electron Landau states. Nat. Commun. 2014, 5, 4586. [Google Scholar] [CrossRef] [PubMed]
- Schattschneider, P.; Löffler, S.; Stöger-Pollach, M.; Verbeeck, J. Is magnetic chiral dichroism feasible with electron vortices? Ultramicroscopy 2014, 136, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Pohl, D.; Schneider, S.; Rusz, J.; Rellinghaus, B. Electron vortex beams prepared by a spiral aperture with the goal to measure EMCD on ferromagnetic films via STEM. Ultramicroscopy 2015, 150, 16–22. [Google Scholar] [CrossRef]
- Schachinger, T.; Löffler, S.; Steiger-Thirsfeld, A.; Stöger-Pollach, M.; Schneider, S.; Pohl, D.; Rellinghaus, B.; Schattschneider, P. EMCD with an electron vortex filter: Limitations and possibilities. Ultramicroscopy 2017, 179, 15–23. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Asenjo-Garcia, A.; García de Abajo, F. Dichroism in the interaction between vortex electron beams, plasmons, and molecules. Phys. Rev. Lett. 2014, 113, 066102. [Google Scholar] [CrossRef]
- Verbeeck, J.; Schattschneider, P.; Lazar, S.; Stöger-Pollach, M.; Löffler, S.; Steiger-Thirsfeld, A.; Van Tendeloo, G. Atomic scale electron vortices for nanoresearch. Appl. Phys. Lett. 2011, 99, 203109. [Google Scholar] [CrossRef]
- Rusz, J.; Idrobo, J.C.; Bhowmick, S. Achieving atomic resolution magnetic dichroism by controlling the phase symmetry of an electron probe. Phys. Rev. Lett. 2014, 113, 145501. [Google Scholar] [CrossRef]
- Van Boxem, R.; Partoens, B.; Verbeeck, J. Rutherford scattering of electron vortices. Phys. Rev. A 2014, 89, 032715. [Google Scholar] [CrossRef]
- Juchtmans, R.; Béché, A.; Abakumov, A.; Batuk, M.; Verbeeck, J. Using electron vortex beams to determine chirality of crystals in transmission electron microscopy. Phys. Rev. B 2015, 91, 094112. [Google Scholar] [CrossRef]
- Maiorova, A.; Fritzsche, S.; Müller, R.; Surzhykov, A. Elastic scattering of twisted electrons by diatomic molecules. Phys. Rev. A 2018, 98, 042701. [Google Scholar] [CrossRef]
- Serbo, V.; Ivanov, I.; Fritzsche, S.; Seipt, D.; Surzhykov, A. Scattering of twisted relativistic electrons by atoms. Phys. Rev. A 2015, 92, 012705. [Google Scholar] [CrossRef]
- Karlovets, D.V.; Kotkin, G.; Serbo, V.; Surzhykov, A. Scattering of twisted electron wave packets by atoms in the Born approximation. Phys. Rev. A 2017, 95, 032703. [Google Scholar] [CrossRef]
- Ivanov, I.; Seipt, D.; Surzhykov, A.; Fritzsche, S. Elastic scattering of vortex electrons provides direct access to the Coulomb phase. Phys. Rev. D 2016, 94, 076001. [Google Scholar] [CrossRef]
- Ivanov, V.; Chaikovskaia, A.; Karlovets, D. Studying highly relativistic vortex-electron beams by atomic scattering. Phys. Rev. A 2023, 108, 062803. [Google Scholar] [CrossRef]
- Kosheleva, V.; Zaytsev, V.; Surzhykov, A.; Shabaev, V.; Stöhlker, T. Elastic scattering of twisted electrons by an atomic target: Going beyond the Born approximation. Phys. Rev. A 2018, 98, 022706. [Google Scholar] [CrossRef]
- Ivanov, I.P. Promises and challenges of high-energy vortex states collisions. Prog. Part. Nucl. Phys. 2022, 127, 103987. [Google Scholar] [CrossRef]
- Harris, A.; Fritzsche, S. A distorted-wave approach to the elastic scattering of twisted electrons. arXiv 2024, arXiv:2411.14558. [Google Scholar]
- Harris, A.; Plumadore, A.; Smozhanyk, Z. Ionization of hydrogen by electron vortex beam. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 094001. [Google Scholar] [CrossRef]
- Van Boxem, R.; Partoens, B.; Verbeeck, J. Inelastic electron-vortex-beam scattering. Phys. Rev. A 2015, 91, 032703. [Google Scholar] [CrossRef]
- Strnat, S.; Sommerfeldt, J.; Sahoo, A.K.; Sharma, L.; Surzhykov, A. Inelastic scattering of vortex electrons beyond the Born approximation. arXiv 2024, arXiv:2412.08246. [Google Scholar]
- Dunlap, B.I.; Ballester, J.L.; Schmidt, P.P. Interactions between fullerene (C60) and endohedral alkali atoms. J. Phys. Chem. 1992, 96, 9781–9787. [Google Scholar] [CrossRef]
- Hasoğlu, M.F.; Zhou, H.L.; Manson, S.T. Correlation study of endohedrally confined alkaline-earth-metal atoms (A@C60). Phys. Rev. A 2016, 93, 022512. [Google Scholar] [CrossRef]
- Kilcoyne, A.; Aguilar, A.; Müller, A.; Schippers, S.; Cisneros, C.; Alna’Washi, G.; Aryal, N.; Baral, K.; Esteves, D.; Thomas, C.; et al. Confinement resonances in photoionization of Xe@ C 60+. Phys. Rev. Lett. 2010, 105, 213001. [Google Scholar] [CrossRef]
- Allen, L.J.; D’Alfonso, A.J.; Freitag, B.; Klenov, D.O. Chemical mapping at atomic resolution using energy-dispersive x-ray spectroscopy. MRS Bull. 2012, 37, 47–52. [Google Scholar] [CrossRef]
- Zuo, T.; McEachran, R.; Stauffer, A. Relativistic distorted-wave calculation of electron impact excitation of xenon. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 2853. [Google Scholar] [CrossRef]
- Chauhan, R.K.; Srivastava, R.; Stauffer, A. Electron impact excitation of the 41P1 state of calcium. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2385. [Google Scholar] [CrossRef]
- Sharma, L. Electron Induced Processes in Atomic Systems. Ph.D. Thesis, IIT Roorkee, Roorkee, India, 2008. [Google Scholar]
- Sharma, L.; Surzhykov, A.; Srivastava, R.; Fritzsche, S. Electron-impact excitation of singly charged metal ions. Phys. Rev. A 2011, 83, 062701. [Google Scholar] [CrossRef]
- Zaytsev, V.A.; Serbo, V.G.; Shabaev, V.M. Radiative recombination of twisted electrons with bare nuclei: Going beyond the Born approximation. Phys. Rev. A 2017, 95, 012702. [Google Scholar] [CrossRef]
- Karlovets, D.; Kotkin, G.; Serbo, V. Scattering of wave packets on atoms in the Born approximation. Phys. Rev. A 2015, 92, 052703. [Google Scholar] [CrossRef]
- Balashov, V.V.; Grum-Grzhimailo, A.N.; Kabachnik, N.M. Polarization and Correlation Phenomena in Atomic Collisions; Kluwer Academic: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Itikawa, Y. Distorted-wave methods in electron-impact excitation of atoms and ions. Phys. Rep. 1986, 143, 69–108. [Google Scholar] [CrossRef]
- Mahato, D.; Sharma, L.; Baral, S.; Saha, S.; Jose, J.; Srivastava, R. Study of electron impact elastic scattering from Kr@ C60 and Xe@ C60 using a fully relativistic approach. J. Phys. B At. Mol. Opt. Phys. 2022, 55, 165201. [Google Scholar] [CrossRef]
- Bharti, S.; Sharma, L.; Sahoo, B.; Malkar, P.; Srivastava, R. Application of relativistic coupled cluster theory to elastic scattering of electrons from confined Ca atoms. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 185003. [Google Scholar] [CrossRef]
- Dubey, K.A.; Jose, J. Effect of charge transfer on elastic scattering of electron from Ar@ C60: Dirac partial wave calculation. Eur. Phys. J. Plus 2021, 136, 713. [Google Scholar] [CrossRef]
- Knyazev, B.A.; Serbo, V. Beams of photons with nonzero projections of orbital angular momenta: New results. Physics-Uspekhi 2018, 61, 449. [Google Scholar] [CrossRef]
- Hayrapetyan, A.G.; Matula, O.; Aiello, A.; Surzhykov, A.; Fritzsche, S. Interaction of relativistic electron-vortex beams with few-cycle laser pulses. Phys. Rev. Lett. 2014, 112, 134801. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).