Calculations of Positron Scattering from Boron, BH, BF, BF2, and BF3
Abstract
1. Introduction
2. Method
2.1. Single-Center CCC Formalism
2.2. CCC-Scaled Complex Model Potential
2.3. Calculation Details
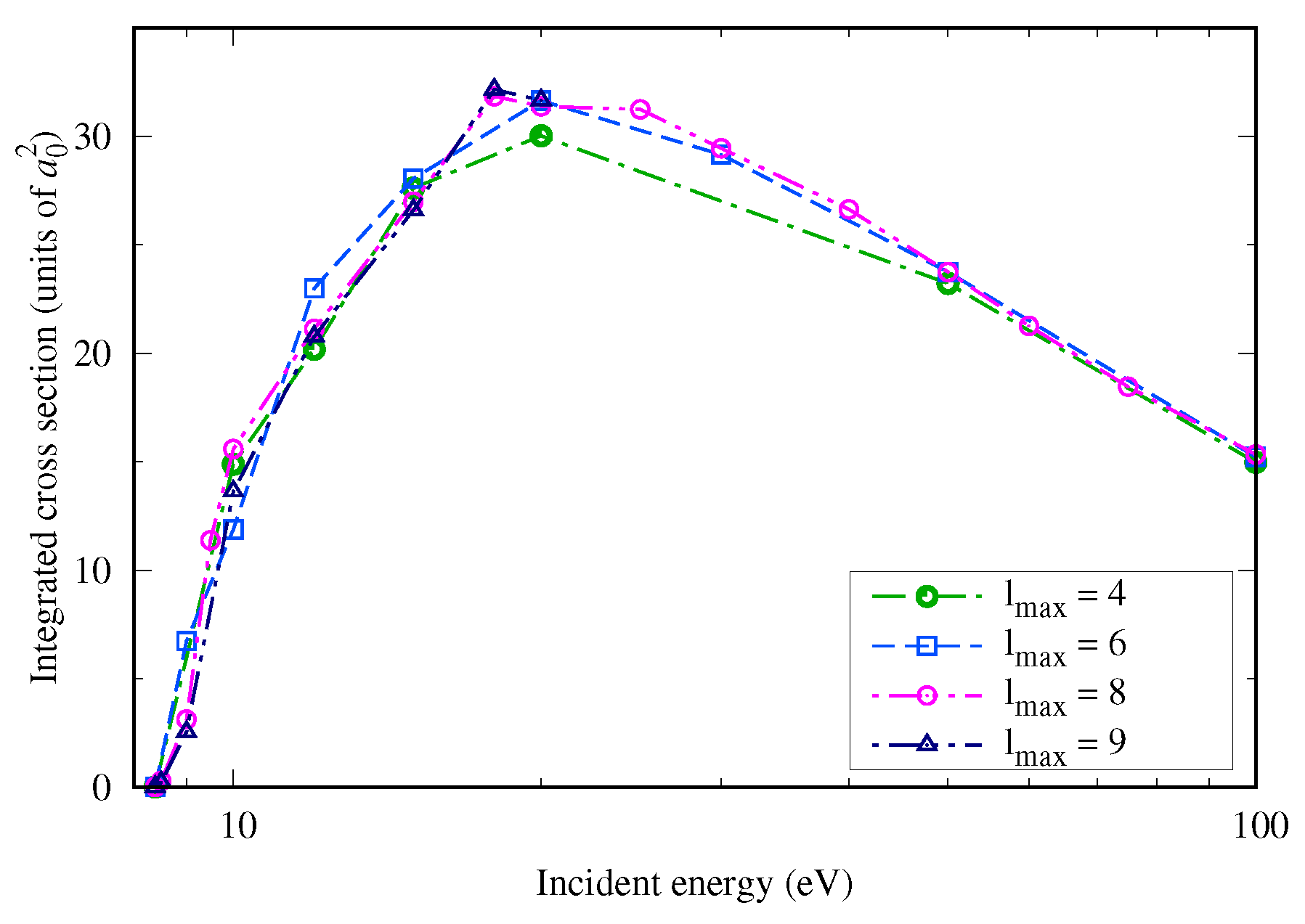
2.4. Convergence Study
2.5. CCC-SCAR
3. Results for Atomic Boron
3.1. Structure
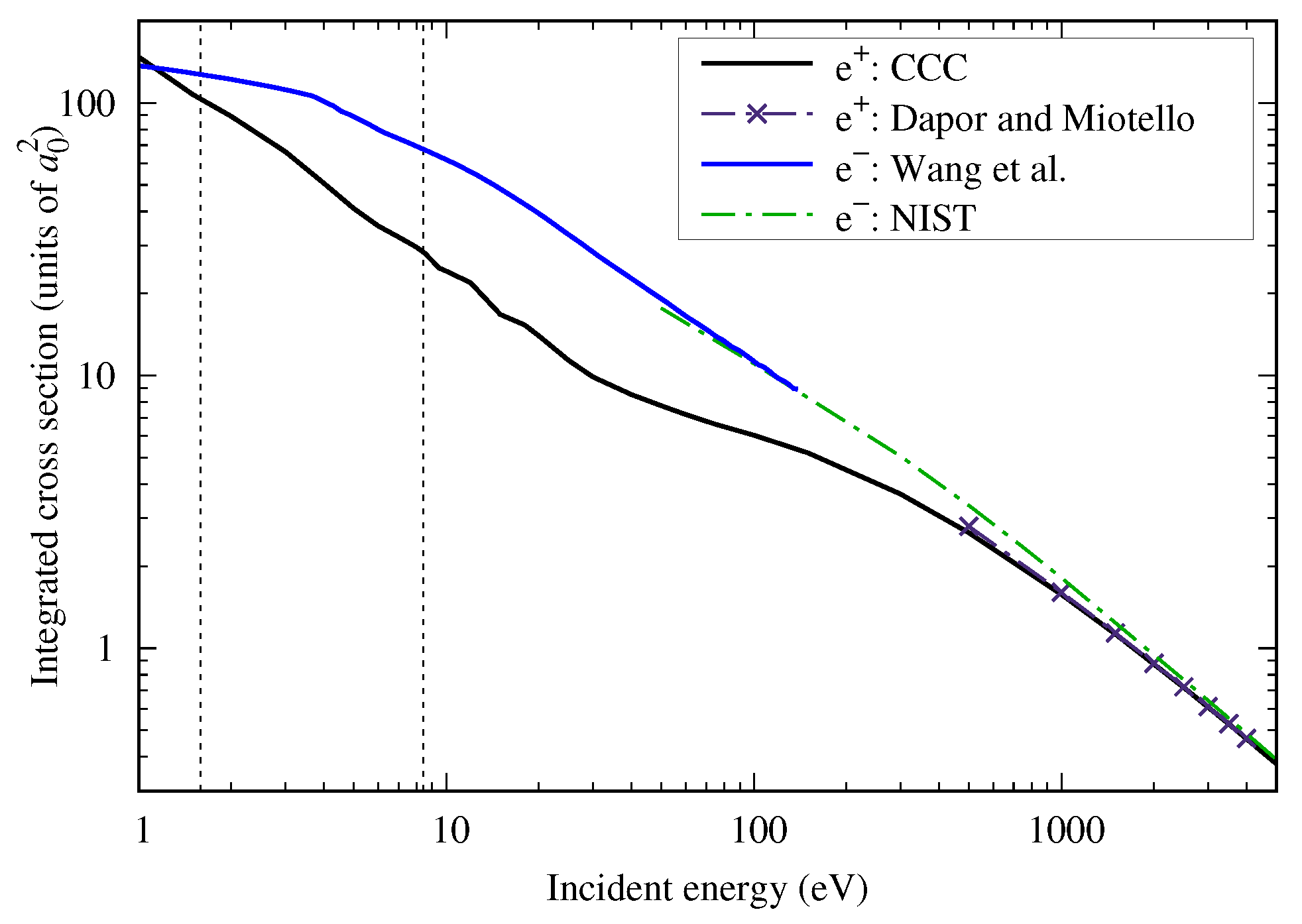
3.2. Total Cross Section
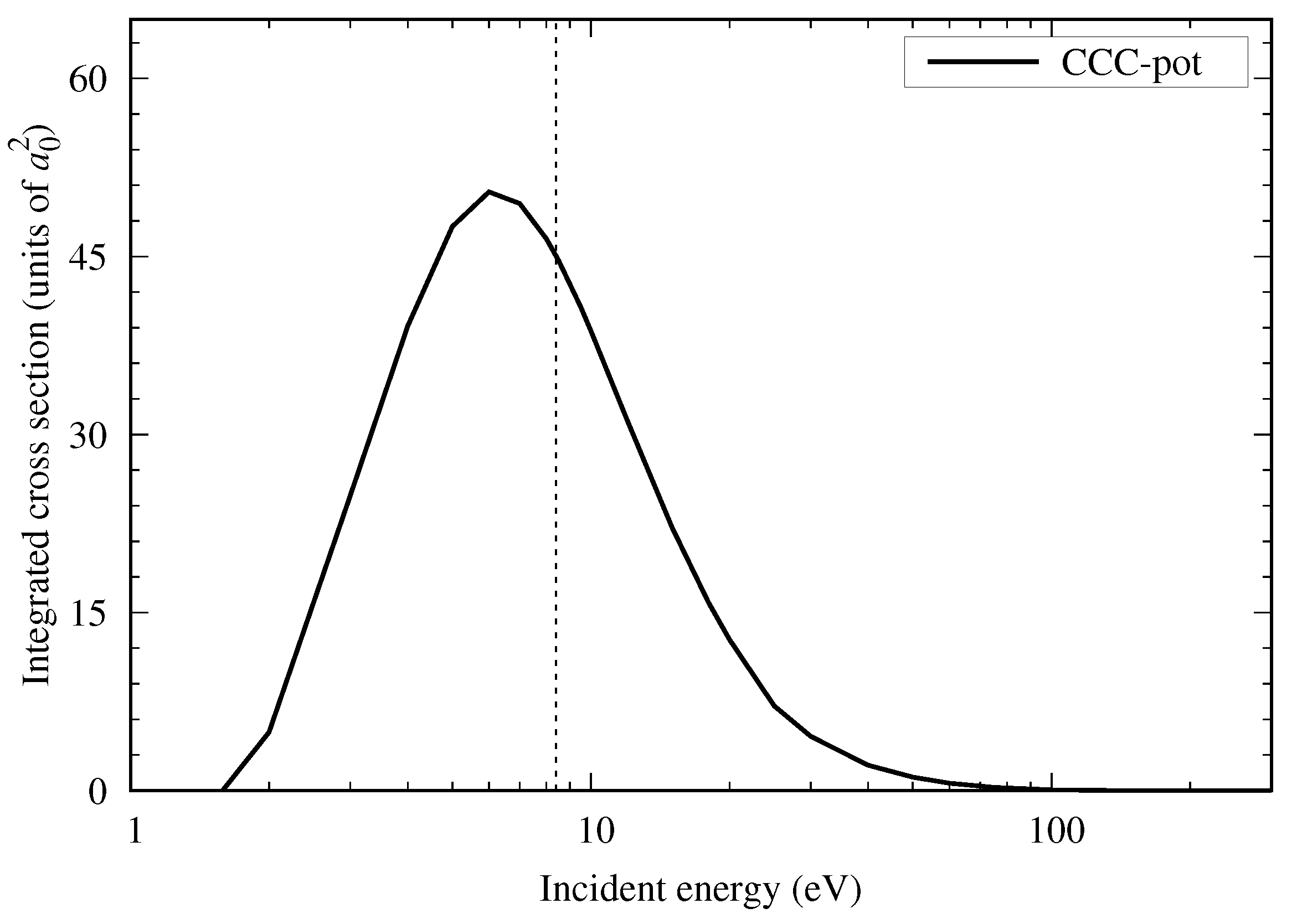
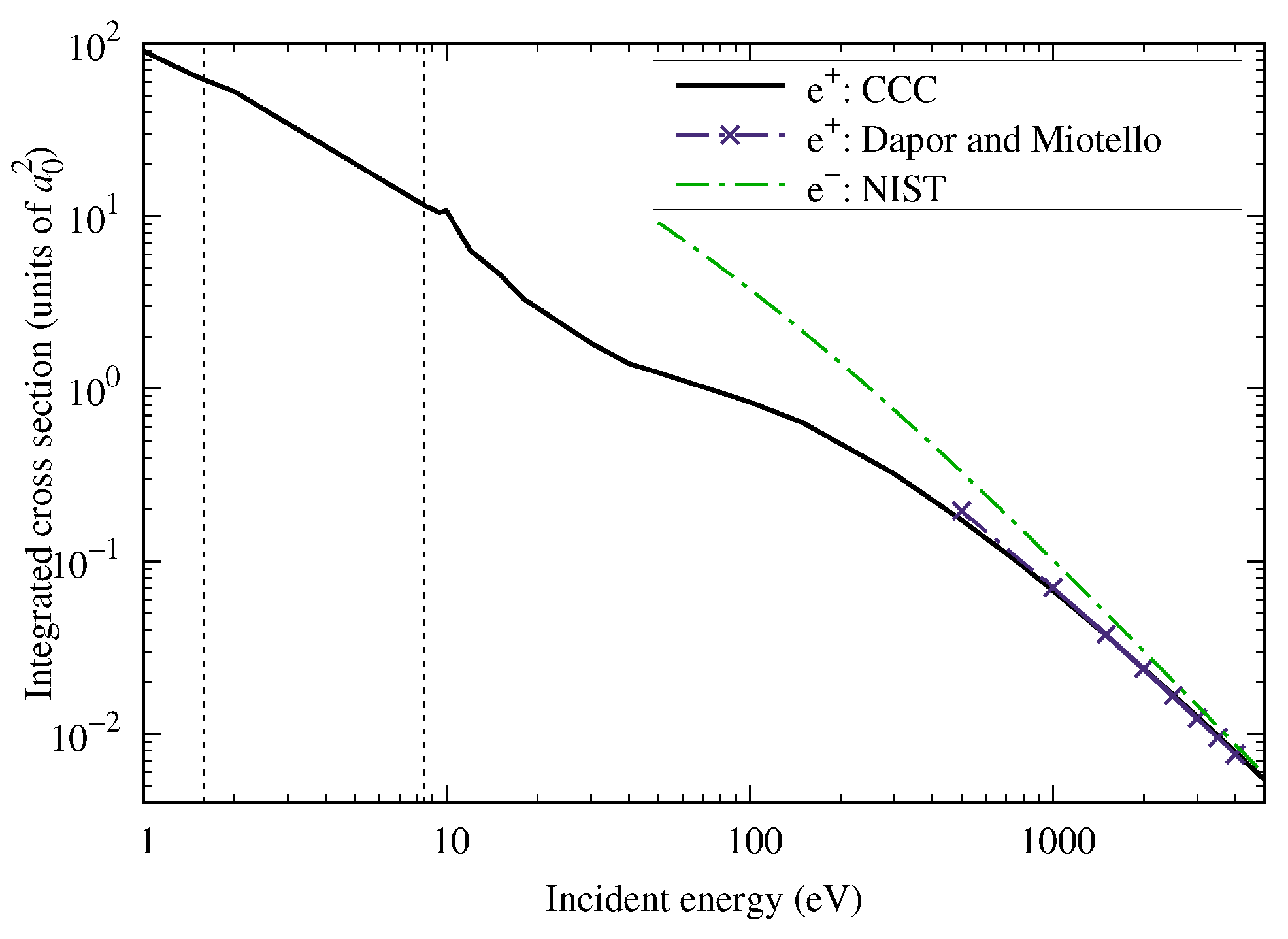
3.3. Positronium Formation and Ionization Cross Sections
3.4. Elastic Cross Section
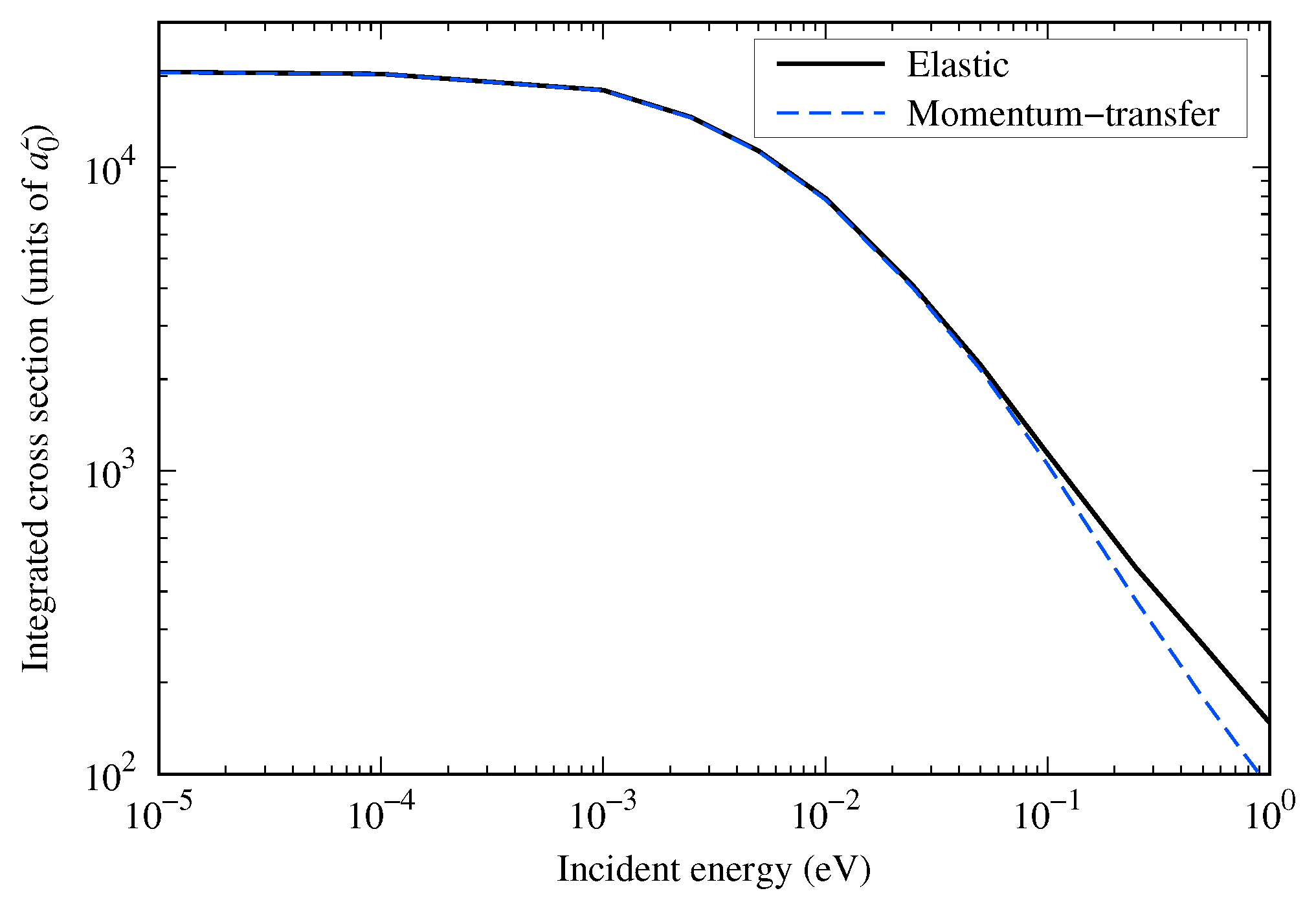
3.5. Momentum-Transfer Cross Section
3.6. Low Energy Scattering
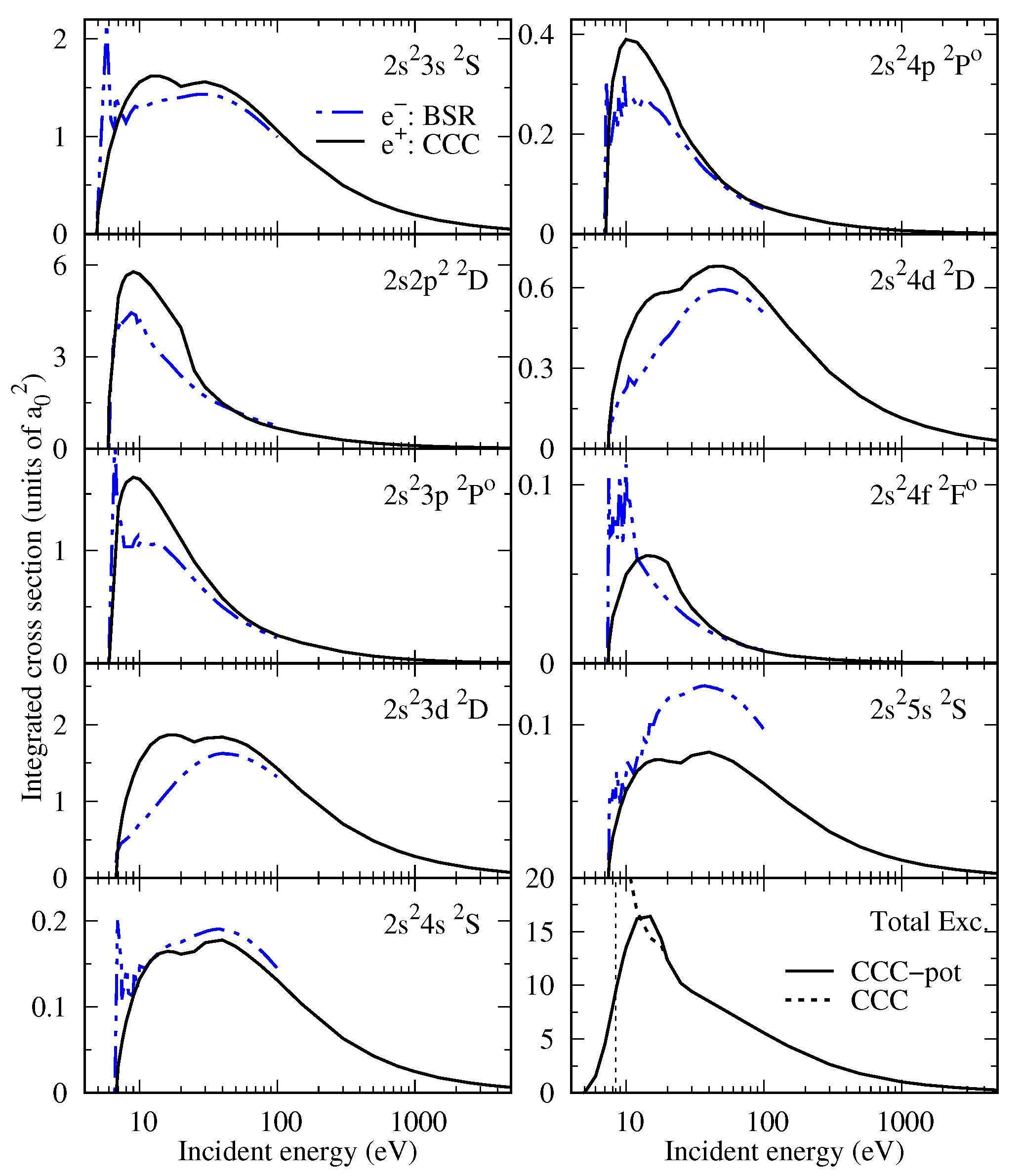
3.7. Excitation Cross Sections
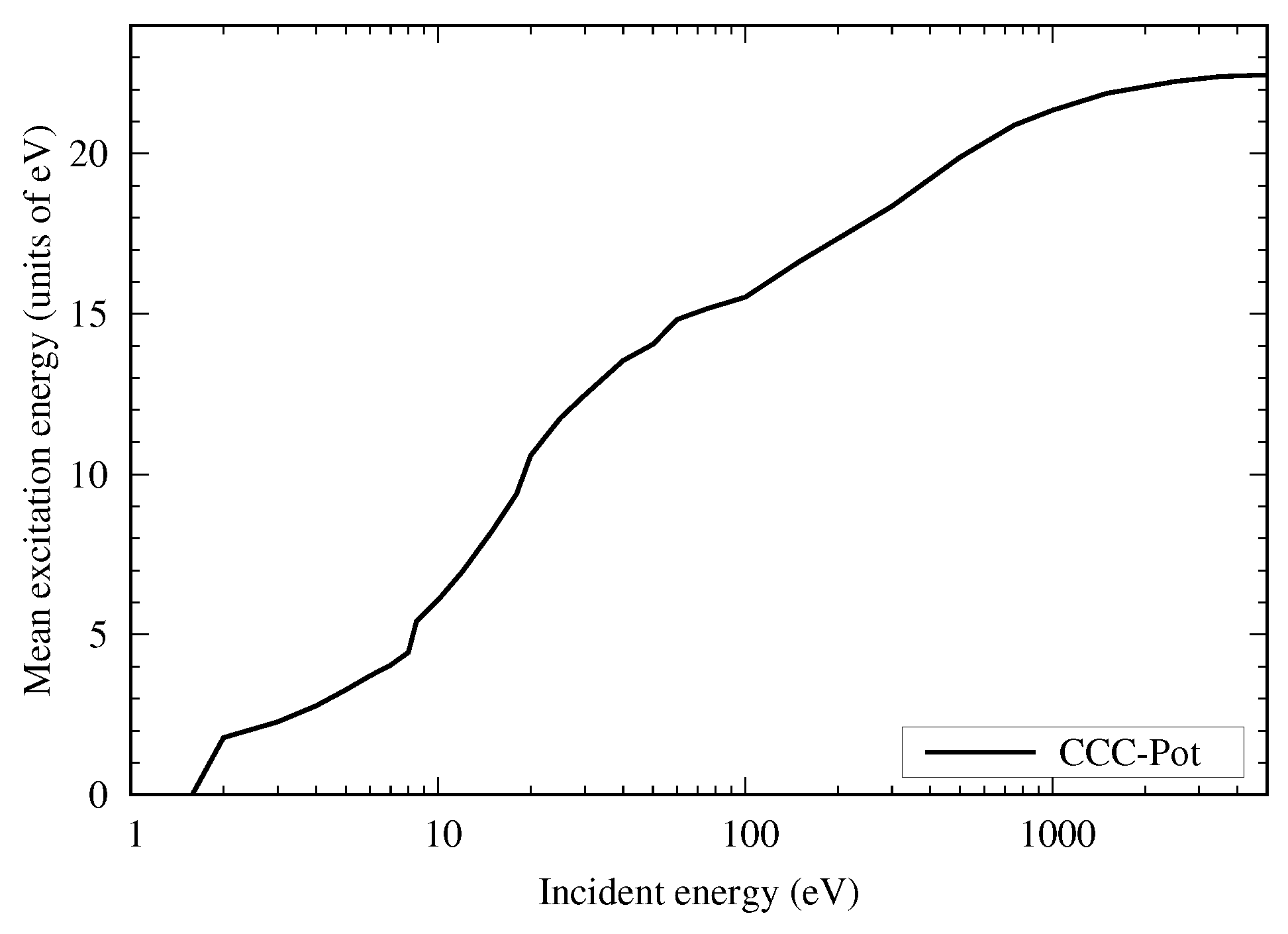
3.8. Stopping Power and Mean Excitation Energy
4. Results for Molecular Targets
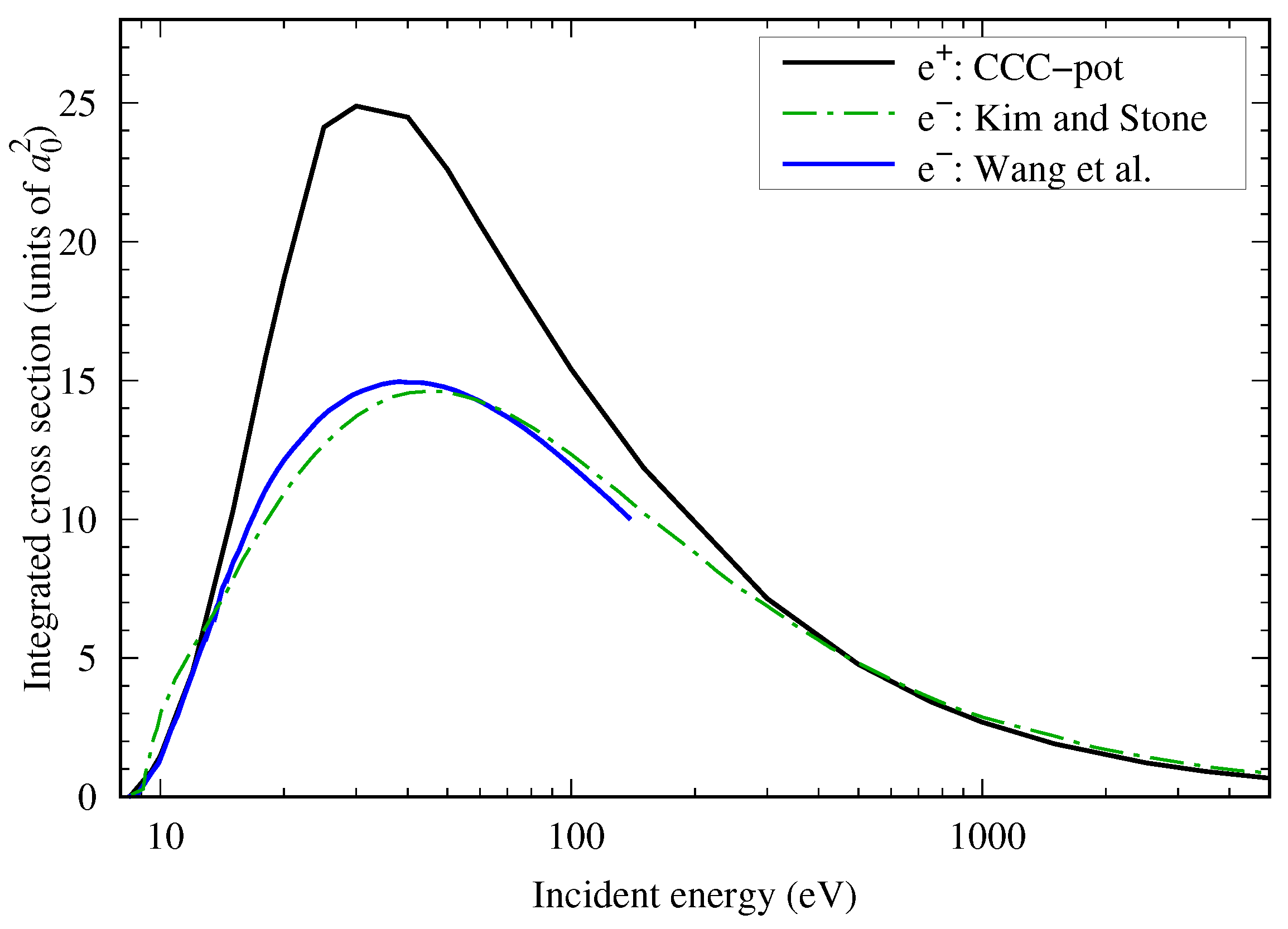
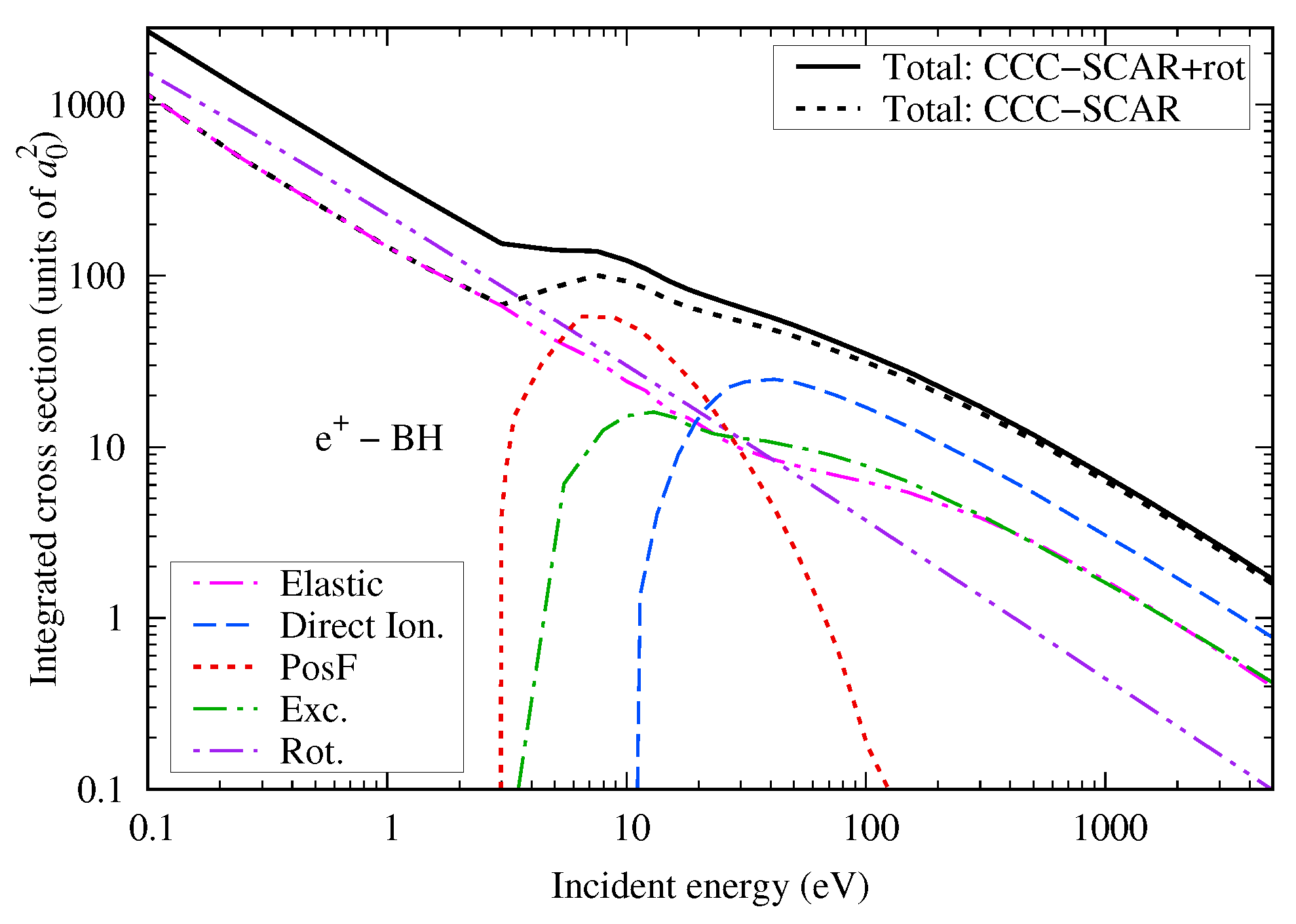
4.1. BH
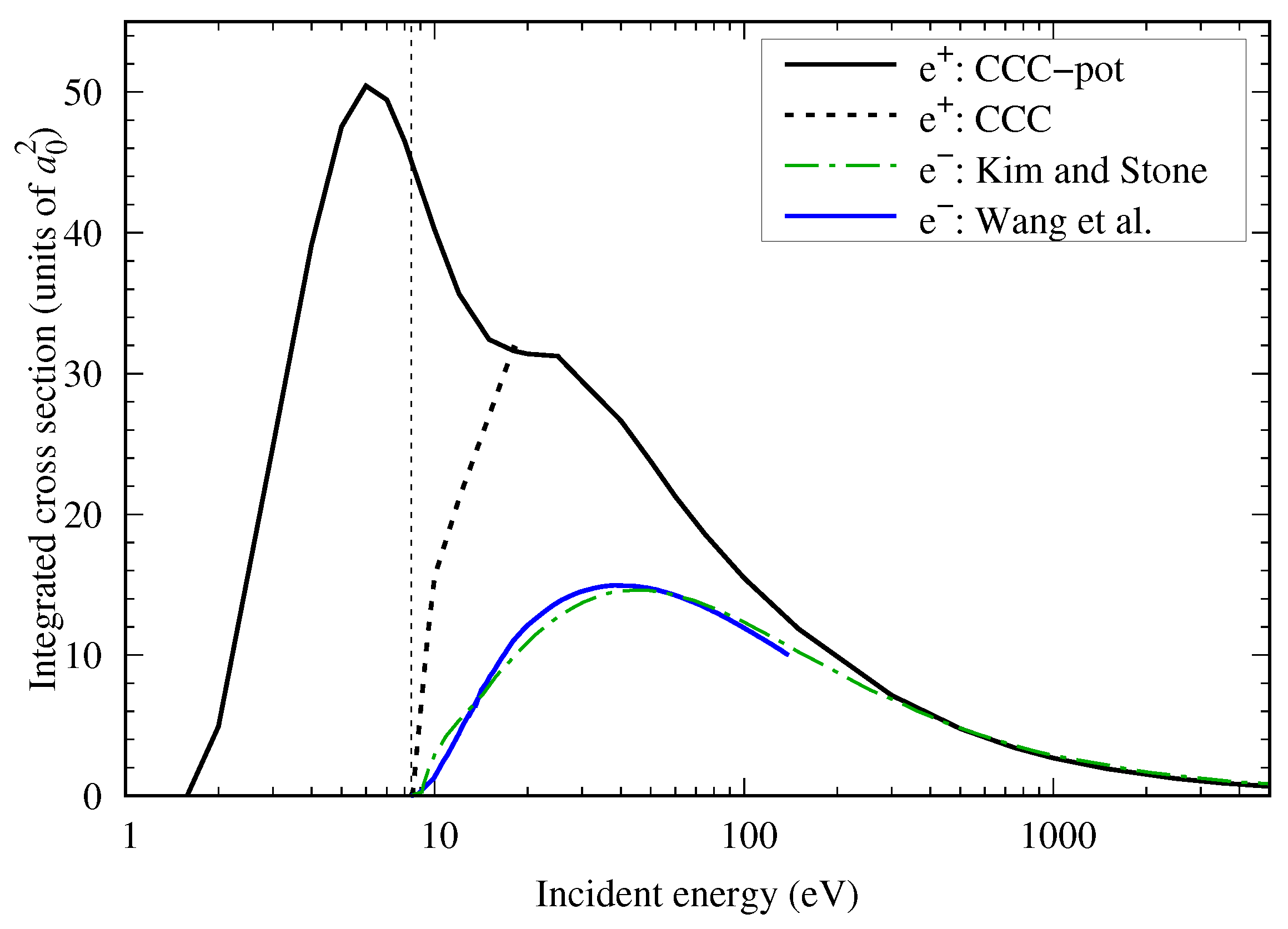
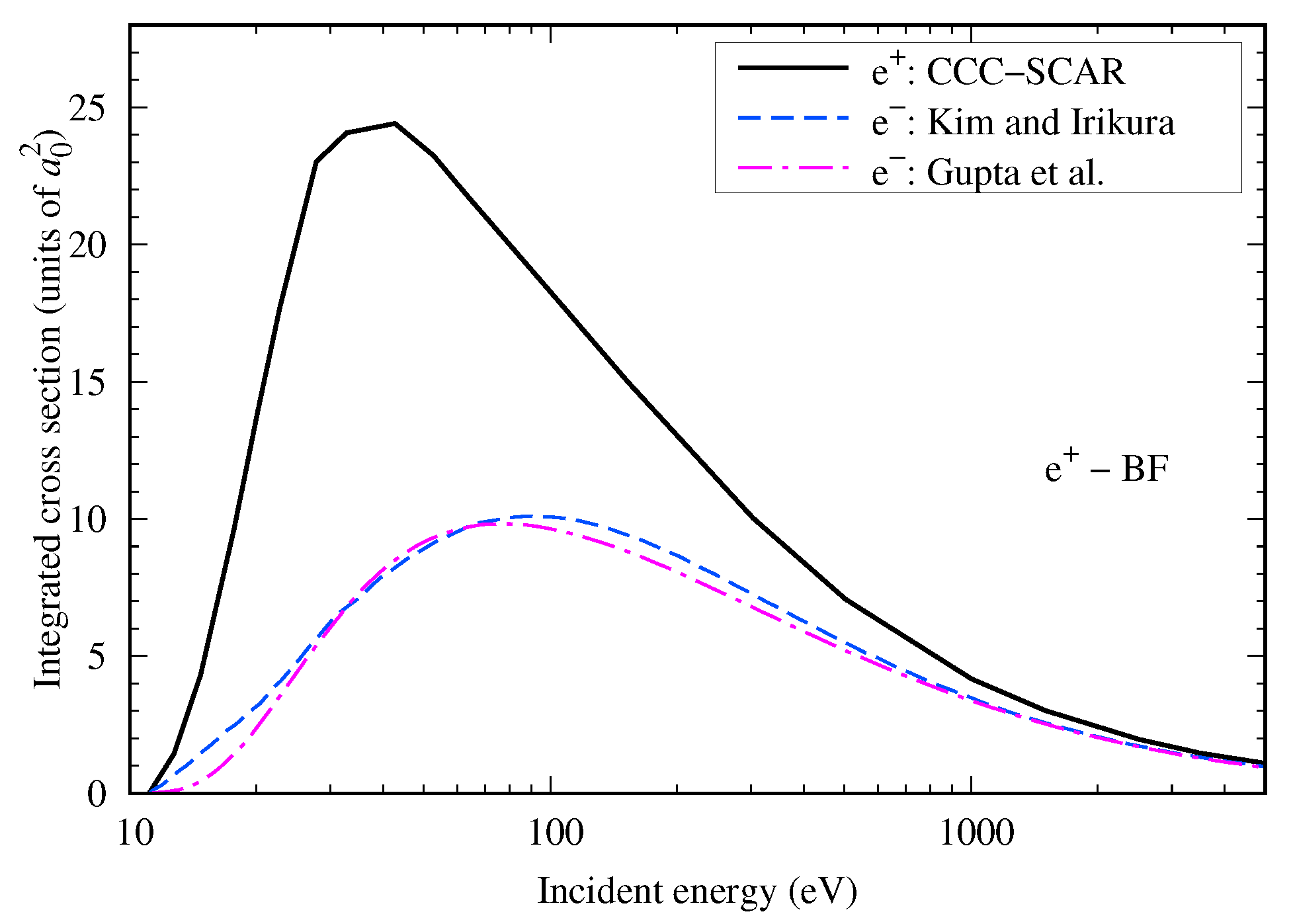
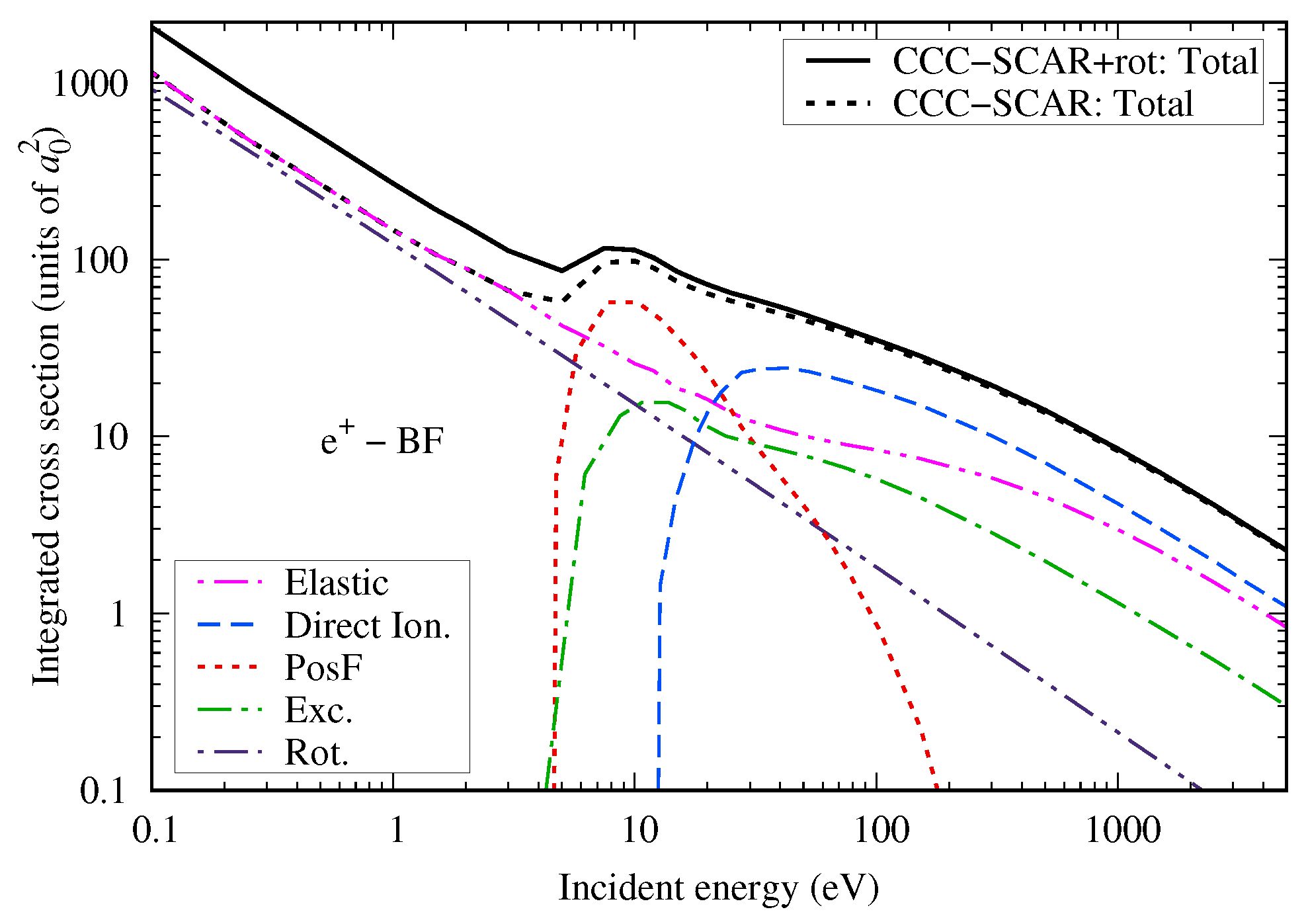
4.2. BF
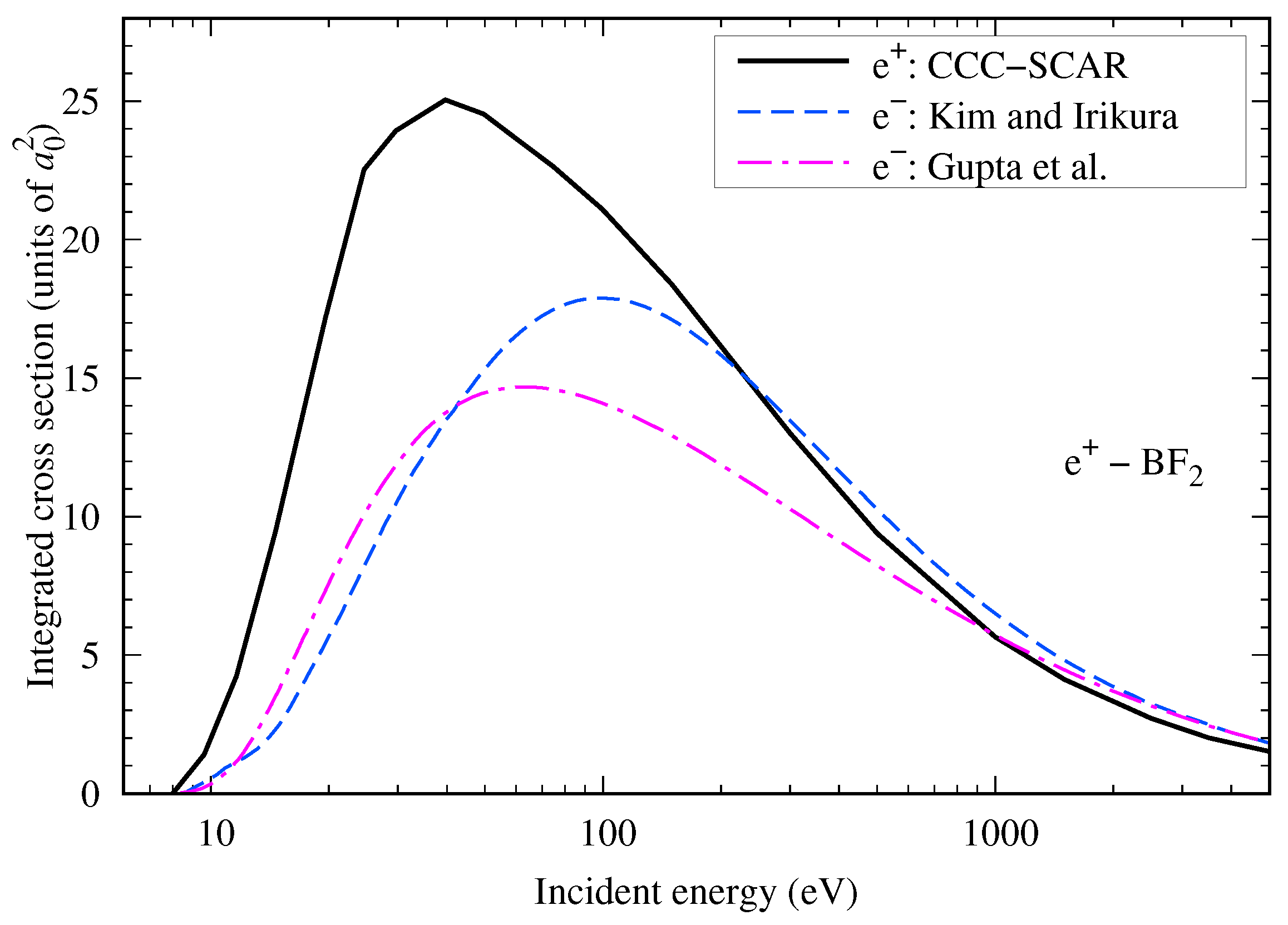
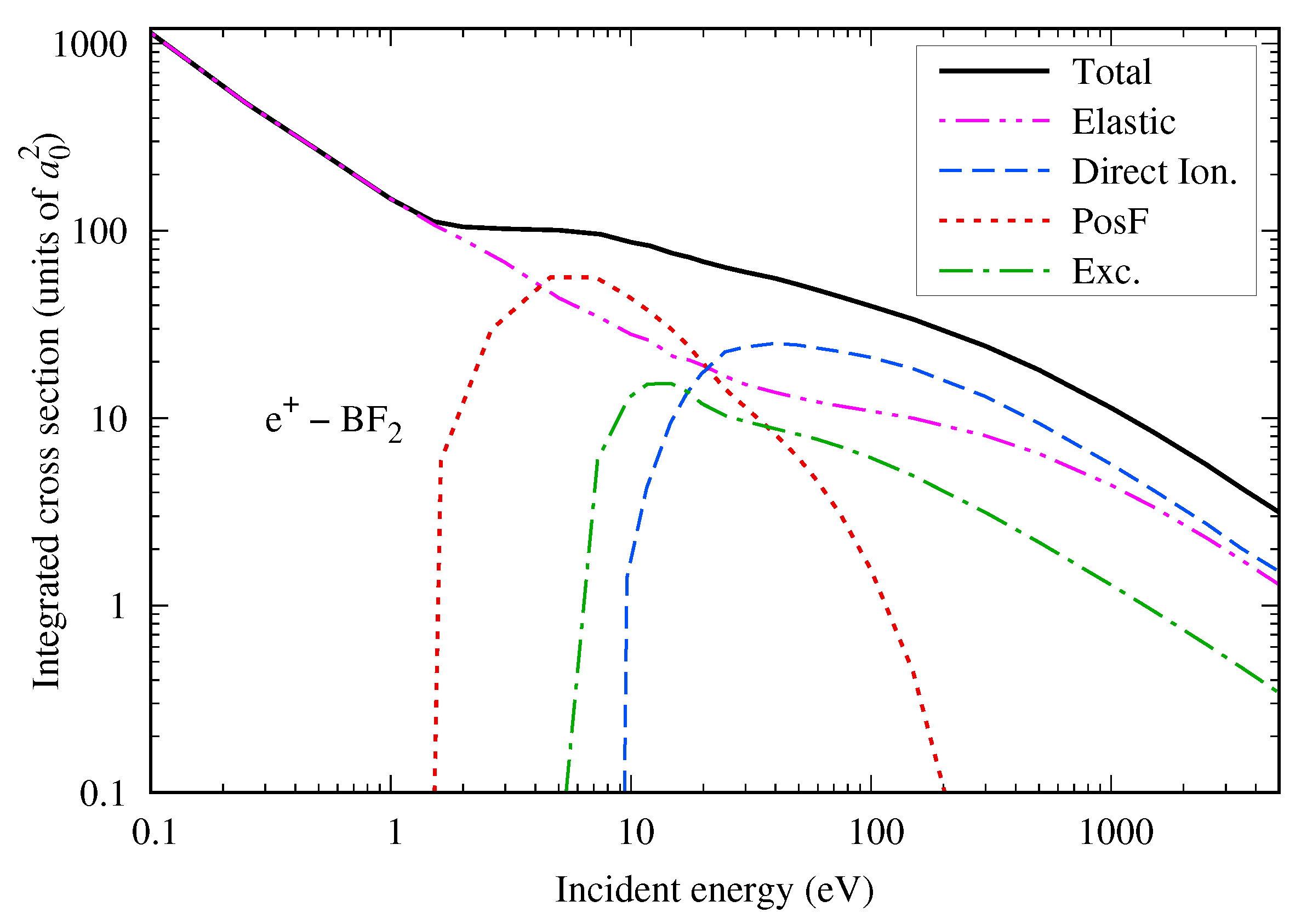
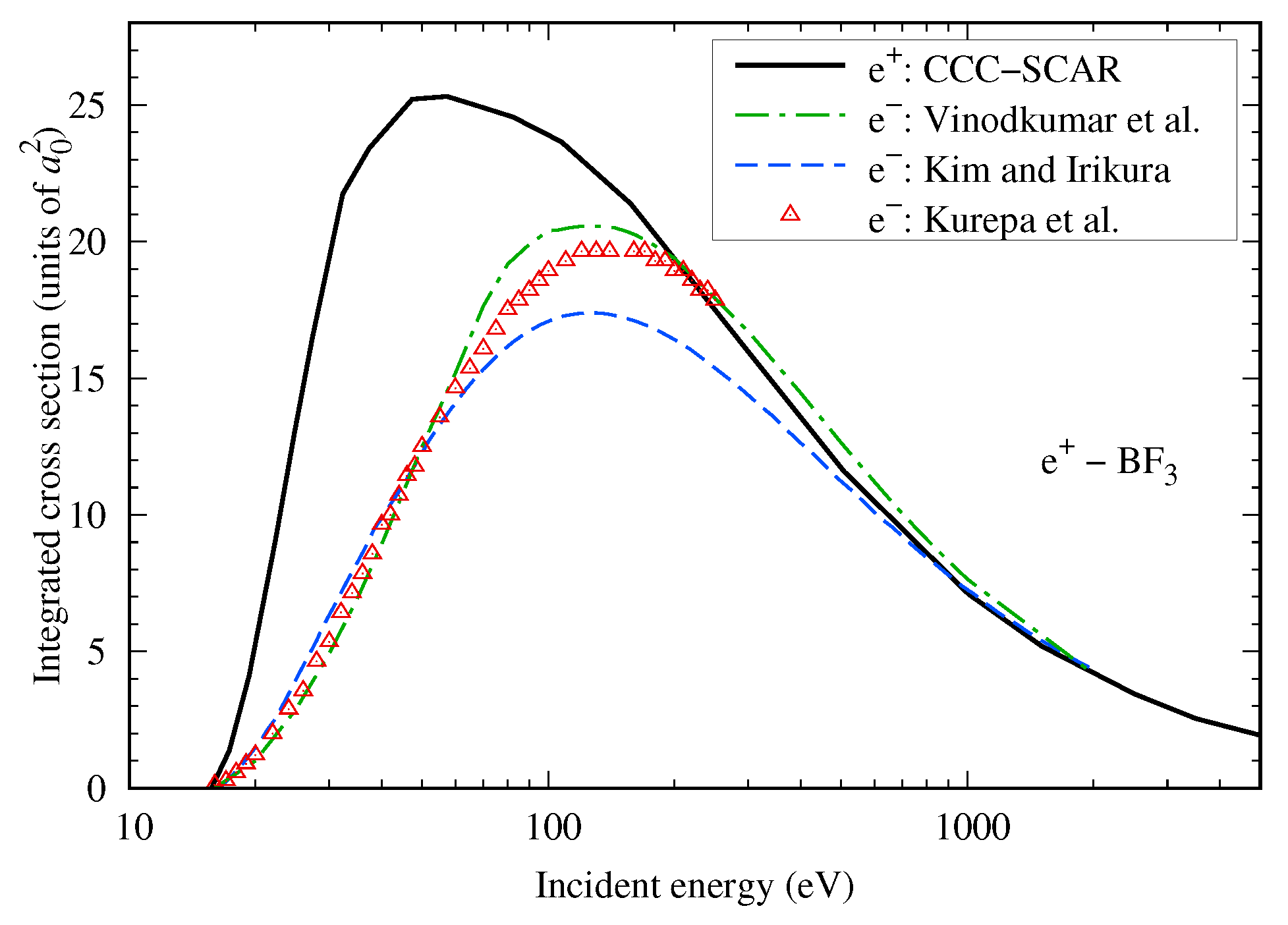
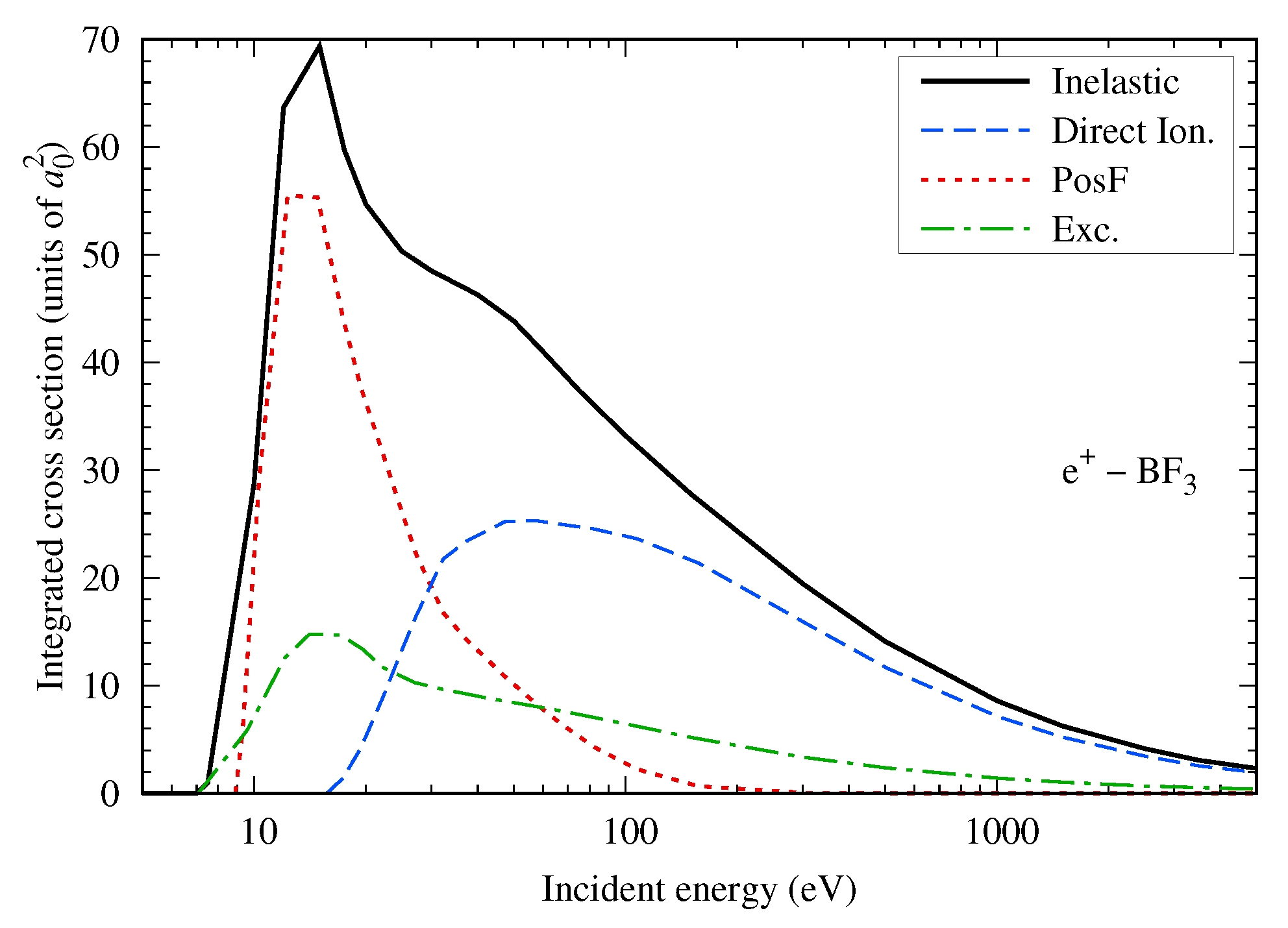
4.3.
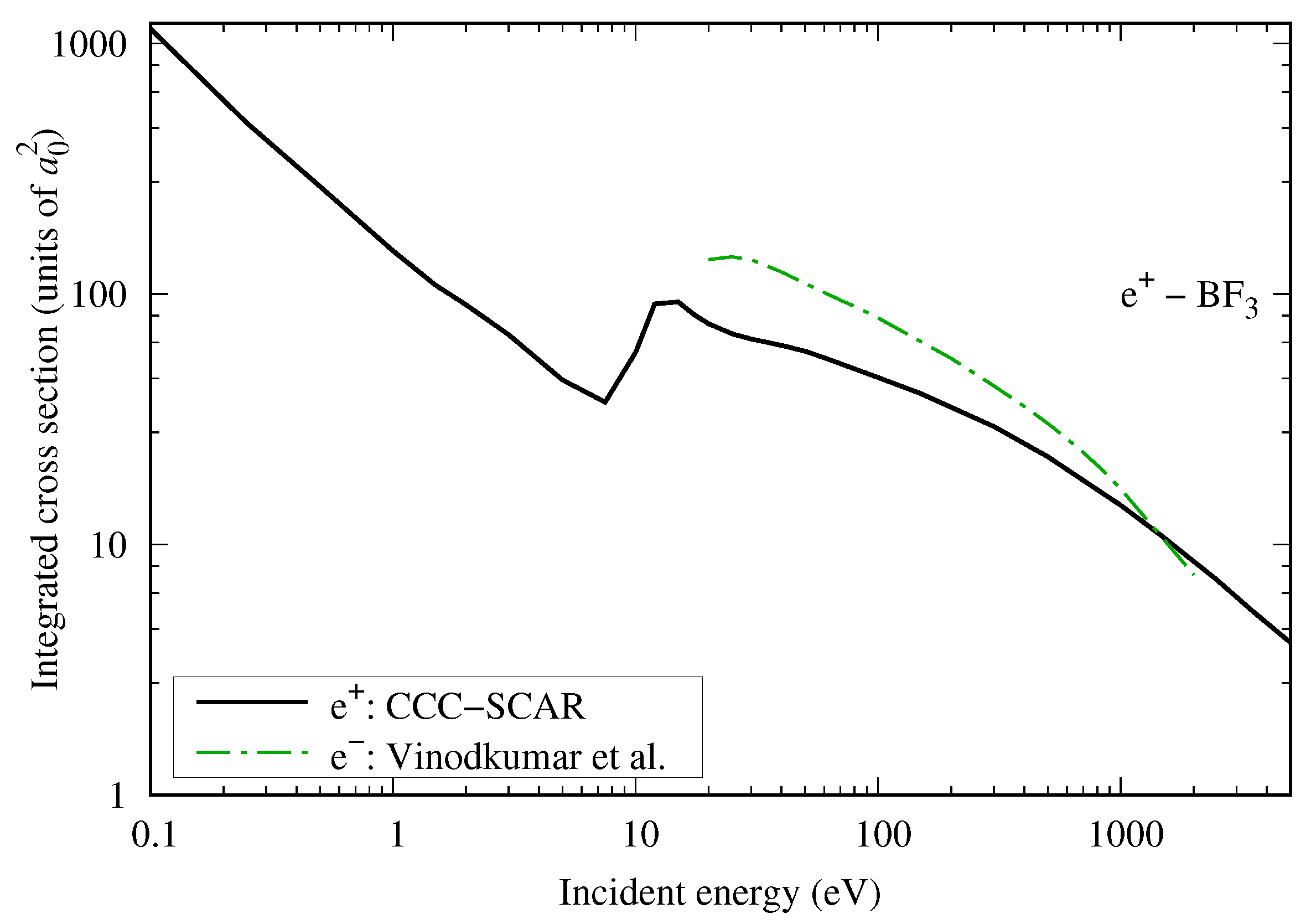
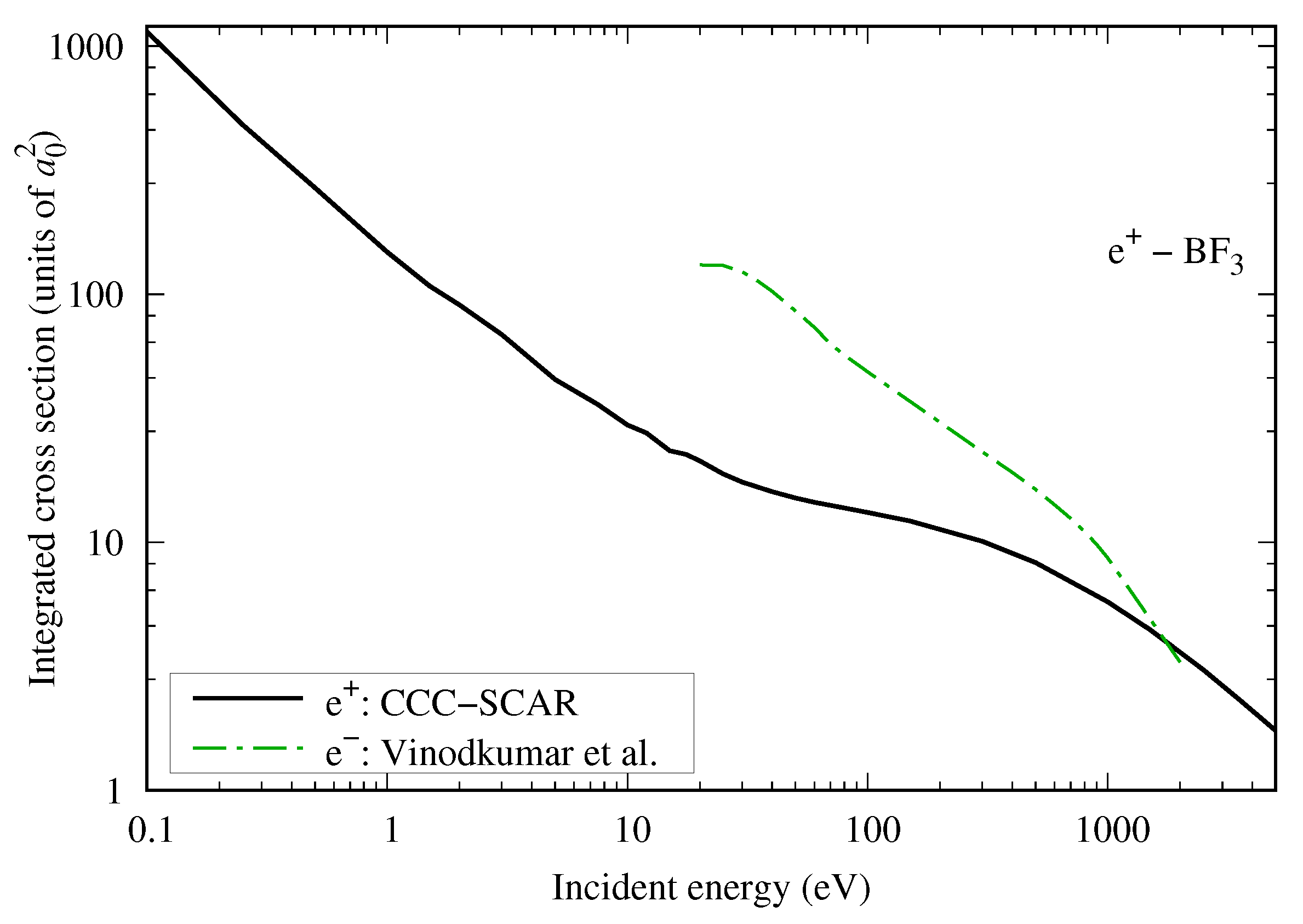
4.4.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gajjar, B.S.; Varshney, S.K.; Kumar, S.; Jindal, M.; Vaghasiya, P.; George, S.; Khan, Z.; Pandya, H.K.B. Boron Carbide as High-Energy Radiation Shielding Material for ITER. IEEE Trans. Plasma Sci. 2022, 50, 5078–5084. [Google Scholar] [CrossRef]
- Shoshin, A.; Burdakov, A.; Ivantsivskiy, M.; Klimenko, M.; Polosatkin, S.; Semenov, A. Properties of boron carbide ceramics made by various methods for use in ITER. Fusion Eng. Des. 2019, 146, 2007–2010. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Y.P.; Gu, X.M.; Li, C.F.; Wan, B.N.; Zhang, X.D.; Luo, J.R.; Gong, X.Z.; Xie, J.K.; Wan, Y.X.; et al. ICRF boronization-A new technique towards high efficiency wall coating for superconducting tokamak reactors. Nucl. Fusion 1999, 39, 973. [Google Scholar] [CrossRef]
- Magee, R.; Ogawa, K.; Tajima, T.; Allfrey, I.; Gota, H.; McCarroll, P.; Ohdachi, S.; Isobe, M.; Kamio, S.; Klumper, V.; et al. First measurements of p11B fusion in a magnetically confined plasma. Nat. Commun. 2023, 14, 955. [Google Scholar] [CrossRef] [PubMed]
- McKenzie, W.; Batani, D.; Mehlhorn, T.A.; Margarone, D.; Belloni, F.; Campbell, E.M.; Woodruff, S.; Kirchhoff, J.; Paterson, A.; Pikuz, S.; et al. HB11—Understanding hydrogen-boron fusion as a new clean energy source. J. Fusion Energy 2023, 42, 17. [Google Scholar] [CrossRef]
- Helander, P.; Ward, D.J. Positron Creation and Annihilation in Tokamak Plasmas with Runaway Electrons. Phys. Rev. Lett. 2003, 90, 135004. [Google Scholar] [CrossRef] [PubMed]
- Fülöp, T.; Papp, G. Runaway Positrons in Fusion Plasmas. Phys. Rev. Lett. 2012, 108, 225003. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Qin, H.; Fisch, N.J.; Teng, Q.; Wang, X. What is the fate of runaway positrons in tokamaks? Phys. Plasmas 2014, 21, 064503. [Google Scholar] [CrossRef]
- Dapor, M.; Miotello, A. Differential, total, and transport cross sections for elastic scattering of low energy positrons by neutral atoms (Z = 1–92, E = 500–4000 eV). At. Data Nucl. Data Tables 1998, 69, 1–100. [Google Scholar] [CrossRef]
- Wang, K.; Zatsarinny, O.; Bartschat, K. Electron-impact excitation and ionization of atomic boron at low and intermediate energies. Phys. Rev. A 2016, 93, 052715. [Google Scholar] [CrossRef]
- Kim, Y.K.; Stone, P.M. Ionization of boron, aluminum, gallium, and indium by electron impact. Phys. Rev. A 2001, 64, 052707. [Google Scholar] [CrossRef]
- Ballance, C.; Griffin, D.; Berrington, K.; Badnell, N. Electron-impact excitation of neutral boron using the R-matrix with the pseudostates method. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1131. [Google Scholar] [CrossRef]
- Marchalant, P.J.; Bartschat, K. R-matrix with pseudo-states calculation for electron-impact excitation and ionization of boron. J. Phys. B At. Mol. Opt. Phys. 1997, 30, 4373. [Google Scholar] [CrossRef]
- Joshi, F.M.; Joshipura, K.; Chaudhari, A.S. Electron impact ionization in plasma technologies; studies on atomic boron and BN molecule. In AIP Conference Proceedings; AIP Publishing: Bikaner, India, 2016; Volume 1728. [Google Scholar] [CrossRef]
- Nakazaki, S.; Berrington, K. Excitation cross sections of boron by electron impact. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 4263. [Google Scholar] [CrossRef]
- Berengut, J.; Loch, S.; Pindzola, M.; Ballance, C.; Griffin, D. Electron-impact ionization of the boron atom. Phys. Rev. A 2007, 76, 042704. [Google Scholar] [CrossRef]
- Braams, B.J.; Hill, C. Summary Report of a Consultancy Meeting in Preparation of a Coordinated Research Project on The Formation and Properties of Molecules in Edge Plasmas; Technical Report; International Atomic Energy Agency: Vienna, Austria, 2023. [Google Scholar]
- Kawate, T.; Murakami, I.; Goto, M. Calculation of electronic excitation cross sections and rate coefficients for boron monohydride (BH). Plasma Sources Sci. Technol. 2023, 32, 085006. [Google Scholar] [CrossRef]
- Stojanović, V.D.; Raspopović, Z.M.; Jovanović, J.; Radovanov, S.; Nikitović, Ž.D.; Petrović, Z.L. Cross sections and transport properties of positive ions in BF3 plasmas. Nucl. Instrum. Methods Phys. Res. B 2012, 279, 151–154. [Google Scholar] [CrossRef]
- Desai, S.S.; Rao, M.N. Effect of temperature on performance of Boron Trifluoride (BF3) gas-based neutron proportional counters. Radiat. Meas. 2021, 144, 106593. [Google Scholar] [CrossRef]
- Pastega, D.F.; da Costa, R.F.; Lima, M.A.; Bettega, M.H. Elastic scattering of low-energy electrons by BF3. Eur. Phys. J. D 2014, 68, 1–5. [Google Scholar] [CrossRef]
- Vinodkumar, M.; Korot, K.; Limbachiya, C.; Antony, B.K. Screening-corrected electron impact total and ionization cross sections for boron trifluoride (BF3) and boron trichloride (BCl3). J. Phys. B At. Mol. Opt. Phys. 2008, 41, 245202. [Google Scholar] [CrossRef]
- Karwasz, G.; Fedus, K. Some systematics in electron scattering cross sections. Fus. Sci. Tech. 2013, 63, 338–348. [Google Scholar] [CrossRef]
- Szmytkowski, C.; Piotrowicz, M.; Domaracka, A.; Kłosowski, Ł.; Ptasińska-Denga, E.; Kasperski, G. Electron collisions with trifluorides: BF3 and PF3 molecules. J. Chem. Phys. 2004, 121, 1790–1795. [Google Scholar] [CrossRef] [PubMed]
- Hoshino, M.; Limão-Vieira, P.; Suga, A.; Kato, H.; Ferreira da Silva, F.; Blanco, F.; García, G.; Tanaka, H. Crossed-beam experiment for the scattering of low-and intermediate-energy electrons from BF3: A comparative study with XF3 (X = C, N, and CH) molecules. J. Chem. Phys. 2015, 143, 024313. [Google Scholar] [CrossRef]
- Gupta, D.; Chakrabarti, K.; Yoon, J.S.; Song, M.Y. An R-matrix study of electron induced processes in BF3 plasma. Phys. Plasmas 2017, 24, 123511. [Google Scholar] [CrossRef]
- Gupta, D.; Choi, H.; Song, M.Y.; Singh, S.; Antony, B.; Chakrabarti, K.; Yoon, J.S.; Tennyson, J. Electron scattering studies of BF and BF2. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 225203. [Google Scholar] [CrossRef]
- Kim, Y.K.; Irikura, K.K. Electron-impact ionization cross sections for polyatomic molecules, radicals, and ions. In AIP Conference Proceedings; American Institute of Physics: Oxford, England, 2000; Volume 543, pp. 220–241. [Google Scholar] [CrossRef]
- Kurepa, M.; Pejcev, V.; Cadez, I. Total ionization and dissociative attachment cross-sections of boron trifluoride by electron impact. J. Phys. D Appl. Phys. 1976, 9, 481. [Google Scholar] [CrossRef]
- Harland, P.; Franklin, J. Partitioning of excess energy in dissociative resonance capture processes. J. Chem. Phys. 1974, 61, 1621–1636. [Google Scholar] [CrossRef]
- Zatsarinny, O. BSR: B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Fischer, C.F. The MCHF atomic-structure package. Comput. Phys. Commun. 1991, 64, 369–398. [Google Scholar] [CrossRef]
- Kadyrov, A.; Bray, I. Recent progress in the description of positron scattering from atoms using the convergent close-coupling theory. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 222002. [Google Scholar] [CrossRef]
- Utamuratov, R.; Fursa, D.V.; Mori, N.; Kadyrov, A.S.; Bray, I.; Zammit, M.C. Positron-impact electronic excitations and mass stopping power of H2. Phys. Rev. A 2019, 99, 042705. [Google Scholar] [CrossRef]
- Mori, N.A.; Utamuratov, R.; Scarlett, L.H.; Fursa, D.V.; Kadyrov, A.S.; Bray, I.; Zammit, M.C. Calculations of positron scattering on the hydrogen molecular ion. J. Phys. B At. Mol. Opt. Phys. 2019, 53, 015203. [Google Scholar] [CrossRef]
- Mori, N.A.; Scarlett, L.H.; Bray, I.; Fursa, D.V. Convergent close-coupling calculations of positron scattering from atomic carbon. Phys. Rev. A 2023, 107, 032817. [Google Scholar] [CrossRef]
- Blanco, F.; García, G. Screening corrections for calculation of electron scattering from polyatomic molecules. Phys. Lett. A 2003, 317, 458–462. [Google Scholar] [CrossRef]
- Kadyrov, A.S.; Bray, I. Two-center convergent close-coupling approach to positron-hydrogen collisions. Phys. Rev. A 2002, 66, 012710. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Bray, I. Convergent-close-coupling formalism for positron scattering from molecules. Phys. Rev. A 2013, 87, 020701. [Google Scholar] [CrossRef]
- Mori, N.A.; Scarlett, L.H.; Bray, I.; Fursa, D.V. Calculations of positron scattering from atomic oxygen. Eur. Phys. J. D 2023, 77, 182. [Google Scholar] [CrossRef]
- Mori, N.A.; Scarlett, L.H.; Bray, I.; Fursa, D.V. Convergent close-coupling calculations of positron scattering from neon and argon. Eur. Phys. J. D 2024, 78, 19. [Google Scholar] [CrossRef]
- Fursa, D.V.; Zammit, M.C.; Threlfall, R.L.; Savage, J.S.; Bray, I. Electron mass stopping power in H2. Phys. Rev. A 2017, 96, 022709. [Google Scholar] [CrossRef]
- Chiari, L.; Zecca, A.; Girardi, S.; Trainotti, E.; Garcia, G.; Blanco, F.; McEachran, R.P.; Brunger, M.J. Positron scattering from O2. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 215206. [Google Scholar] [CrossRef]
- Joshipura, K.; Antony, B.; Vinodkumar, M. Electron scattering and ionization of ozone, O2 and O4 molecules. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 4211. [Google Scholar] [CrossRef]
- Utamuratov, R.; Fursa, D.V.; Kadyrov, A.S.; Lugovskoy, A.V.; Savage, J.S.; Bray, I. Two-center convergent-close-coupling calculations of positron scattering on magnesium. Phys. Rev. A 2012, 86, 062702. [Google Scholar] [CrossRef]
- Mori, N.A.; Bray, I.; Fursa, D.V. Calculations of positron scattering from small molecules. Eur. Phys. J. D 2024, 78, 58. [Google Scholar] [CrossRef]
- Takayanagi, K. Rotational and Vibrational Excitation of Polar Molecules by Slow Electrons. J. Phys. Soc. Japan 1966, 21, 507. [Google Scholar] [CrossRef]
- Magoulas, I.; Kalemos, A.; Mavridis, A. An ab initio study of the electronic structure of BF and BF+. J. Chem. Phys. 2013, 138, 104312. [Google Scholar] [CrossRef] [PubMed]
- Koput, J. Ab Initio spectroscopic characterization of borane, BH, in its electronic state. J. Comput. Chem 2015, 36, 2219–2227. [Google Scholar] [CrossRef] [PubMed]
- Scarlett, L.H.; Rehill, U.S.; Zammit, M.C.; Mori, N.A.; Bray, I.; Fursa, D.V. Elastic scattering and rotational excitation of H2 by electron impact: Convergent close-coupling calculations. Phys. Rev. A 2023, 107, 062804. [Google Scholar] [CrossRef]
- Johnson, R.D., III. NIST Computational Chemistry Comparison and Benchmark Database. NIST Standard Reference Database Number 101. 2022. Available online: https://cccbdb.nist.gov/ (accessed on 1 May 2024).
- Huber, K.P. Molecular Spectra and Molecular Structure (Constants of Diatomic Molecules Volume 4); Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Huber, K.P.; Herzberg, G. Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Srivastava, R.; Farber, M. Thermodynamic properties of the B-Cl-F system from mass spectrometer investigations. Trans. Faraday Soc. 1971, 67, 2298–2302. [Google Scholar] [CrossRef]
- Atkinson, D.B.; Irikura, K.K.; Hudgens, J.W. Electronic Structure of the BF2 Radical Determined by ab Initio Calculations and Resonance-Enhanced Multiphoton Ionization Spectroscopy. J. Phys. Chem. A 1997, 101, 2045–2049. [Google Scholar] [CrossRef]
- Hughes, P.P.; Beasten, A.; McComb, J.C.; Coplan, M.A.; Al-Sheikhly, M.; Thompson, A.K.; Vest, R.E.; Sprague, M.K.; Irikura, K.K.; Clark, C.W. High-resolution, vacuum-ultraviolet absorption spectrum of boron trifluoride. J. Chem. Phys. 2014, 141, 194301. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.11); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023. Available online: https://physics.nist.gov/asd (accessed on 30 April 2024).
- Reinsch, E.A.; Meyer, W. Finite-perturbation calculation of static quadrupole and mixed dipole-octupole polarizabilities for the ground states of the first-row atoms. Phys. Rev. A 1978, 18, 1793. [Google Scholar] [CrossRef]
- Jablonski, A.; Salvat, F.; Powell, C.J.; Lee, A. NIST Electron Elastic-Scattering Cross-Section Database Version 4.0, NIST Standard Reference Database Number 64; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2016.
- Surko, C.M.; Gribakin, G.F.; Buckman, S.J. Low-energy positron interactions with atoms and molecules. J. Phys. B At. Mol. Opt. Phys. 2005, 38, R57–R126. [Google Scholar] [CrossRef]
- Berger, M.J.; Coursey, J.S.; Zucker, M.A.; Chang, J. NIST Standard Reference Database 124; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017. [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, N.A.; Umer, H.; Scarlett, L.H.; Bray, I.; Fursa, D.V. Calculations of Positron Scattering from Boron, BH, BF, BF2, and BF3. Atoms 2024, 12, 36. https://doi.org/10.3390/atoms12070036
Mori NA, Umer H, Scarlett LH, Bray I, Fursa DV. Calculations of Positron Scattering from Boron, BH, BF, BF2, and BF3. Atoms. 2024; 12(7):36. https://doi.org/10.3390/atoms12070036
Chicago/Turabian StyleMori, Nicolas A., Haadi Umer, Liam H. Scarlett, Igor Bray, and Dmitry V. Fursa. 2024. "Calculations of Positron Scattering from Boron, BH, BF, BF2, and BF3" Atoms 12, no. 7: 36. https://doi.org/10.3390/atoms12070036
APA StyleMori, N. A., Umer, H., Scarlett, L. H., Bray, I., & Fursa, D. V. (2024). Calculations of Positron Scattering from Boron, BH, BF, BF2, and BF3. Atoms, 12(7), 36. https://doi.org/10.3390/atoms12070036







