Efficient Time-Dependent Method for Strong-Field Ionization of Atoms with Smoothly Varying Radial Steps
Abstract
1. Introduction
2. Theoretical Approach
2.1. General Formalism Using a Uniform Radial Grid
2.2. Modification of the Formalism with a Non-Uniform Radial Grid
2.2.1. Finite Difference with Smoothly Varying Radial Steps
2.2.2. Modified Inner Product Rule with the Non-Uniform Grid
2.2.3. Calculation of Physical Observables
3. Results and Discussion
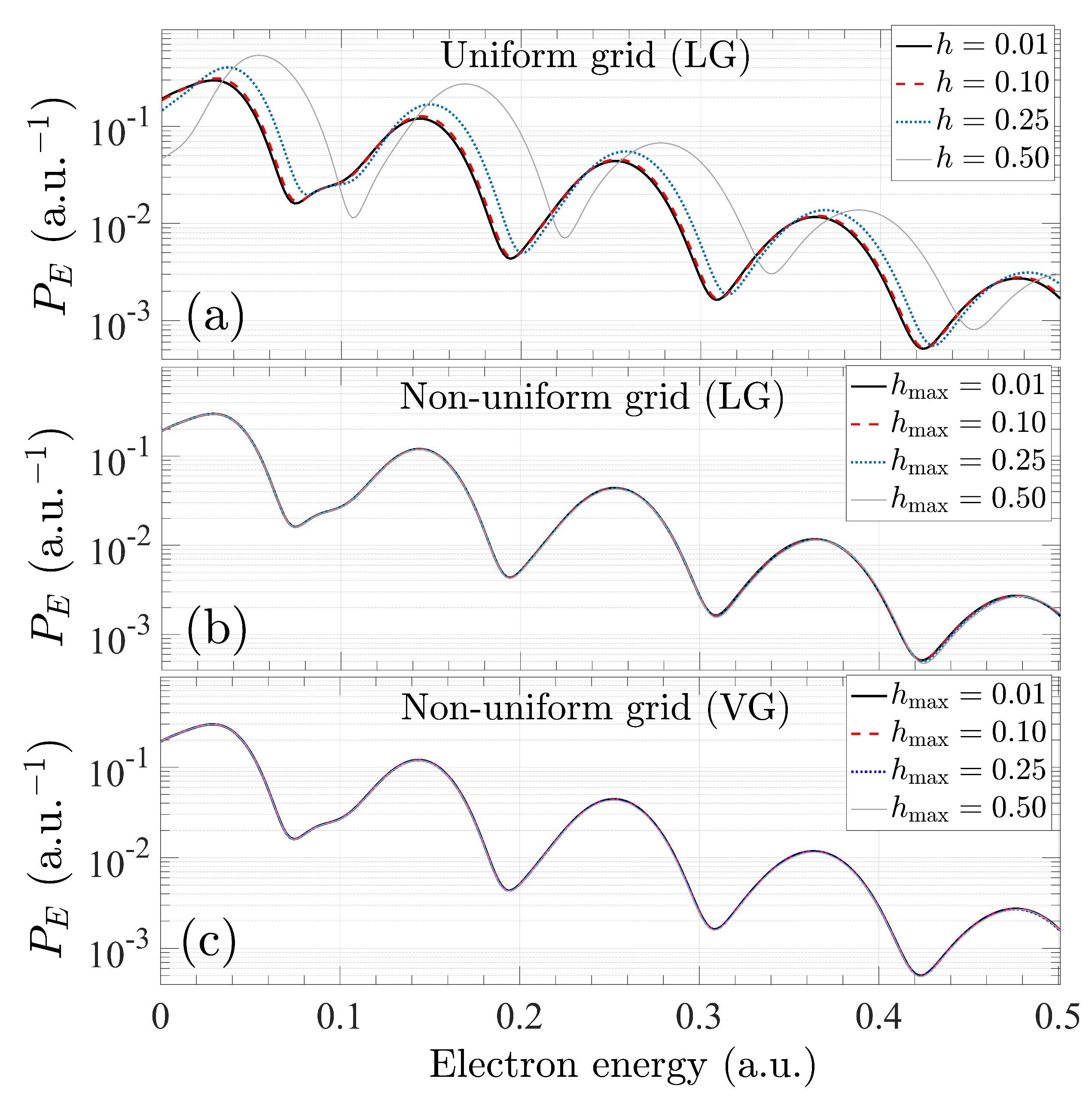
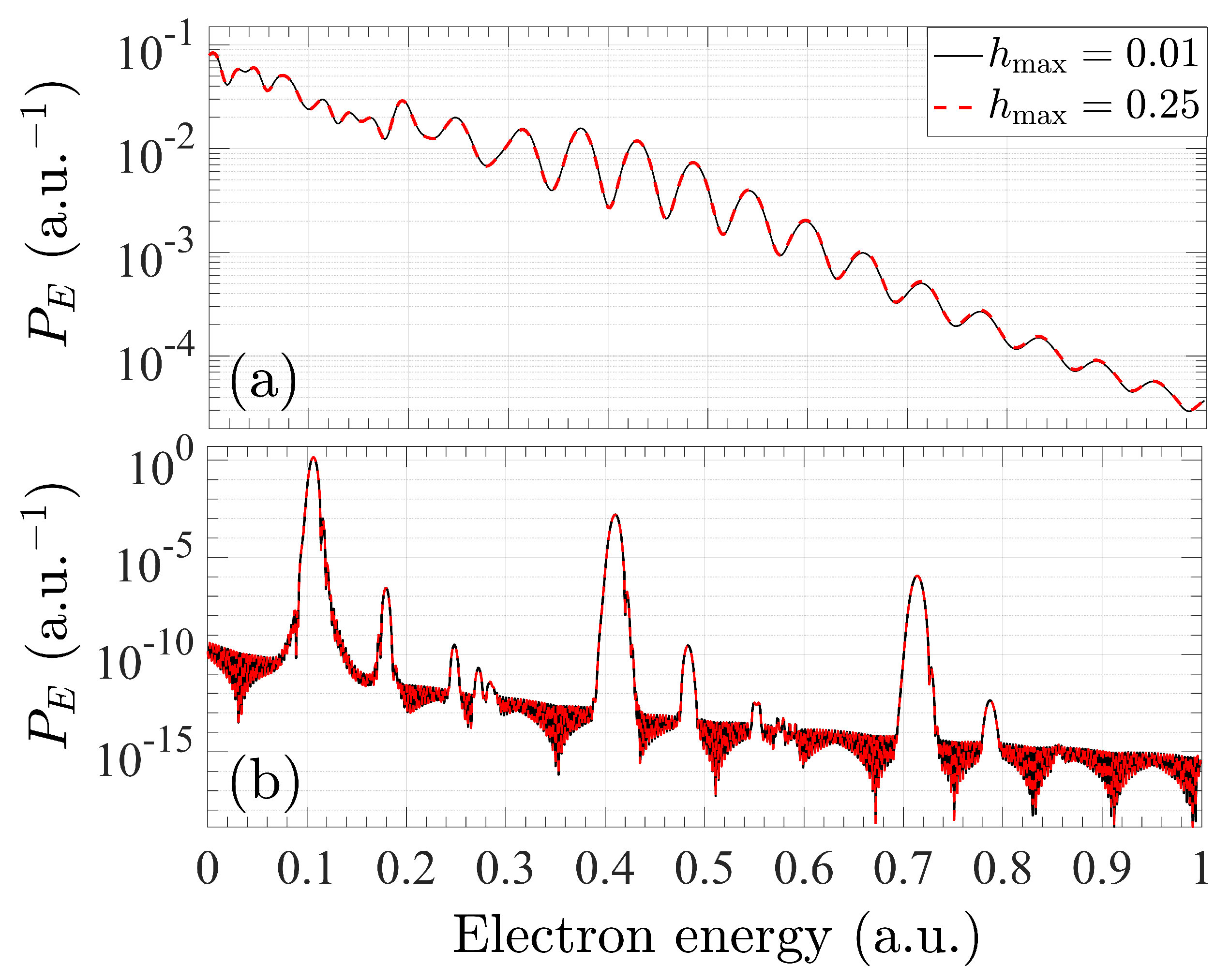
3.1. Benchmark Study on Strong-Field Ionization
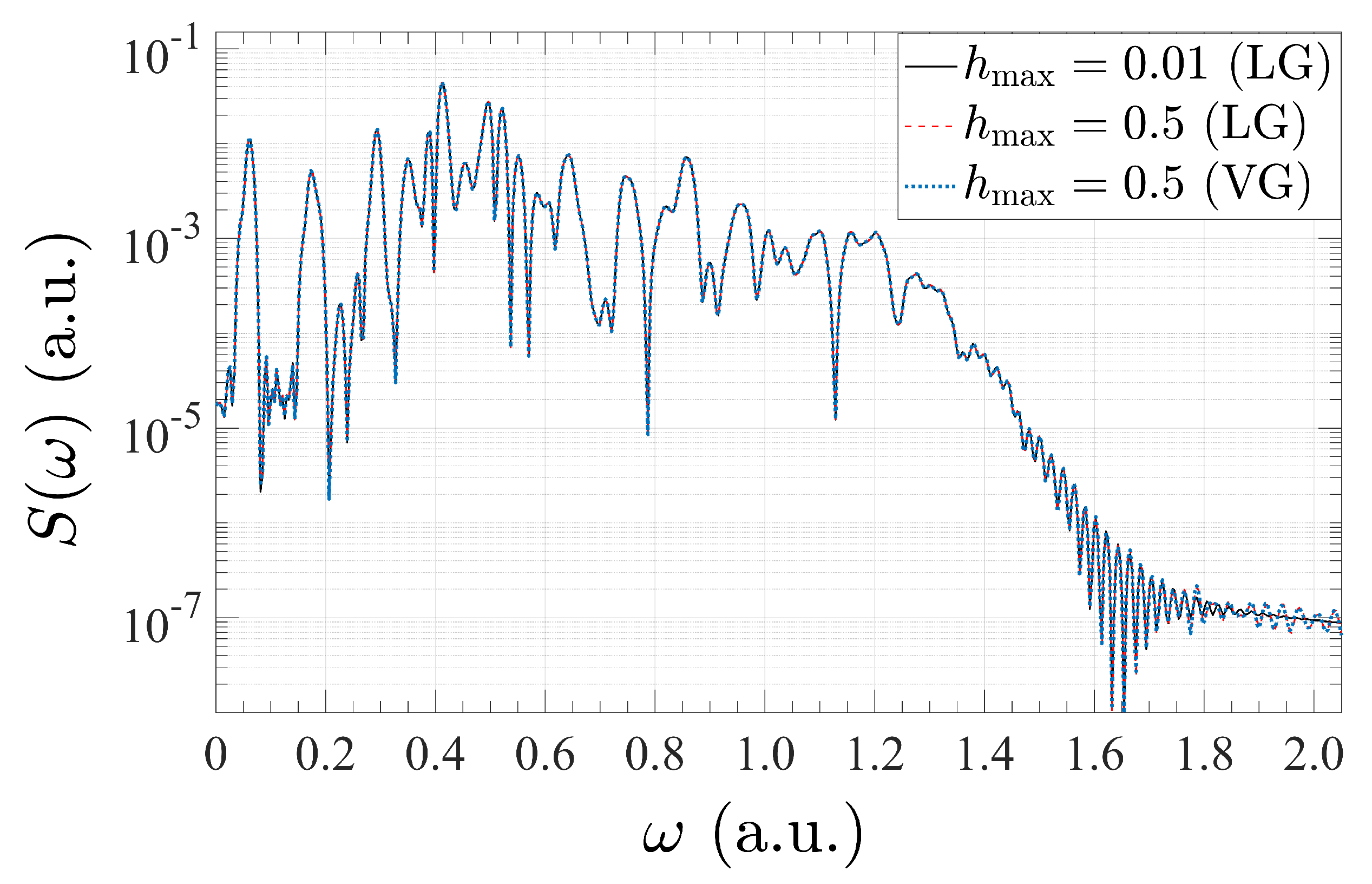
3.2. Application to High-Order Harmonic Generation
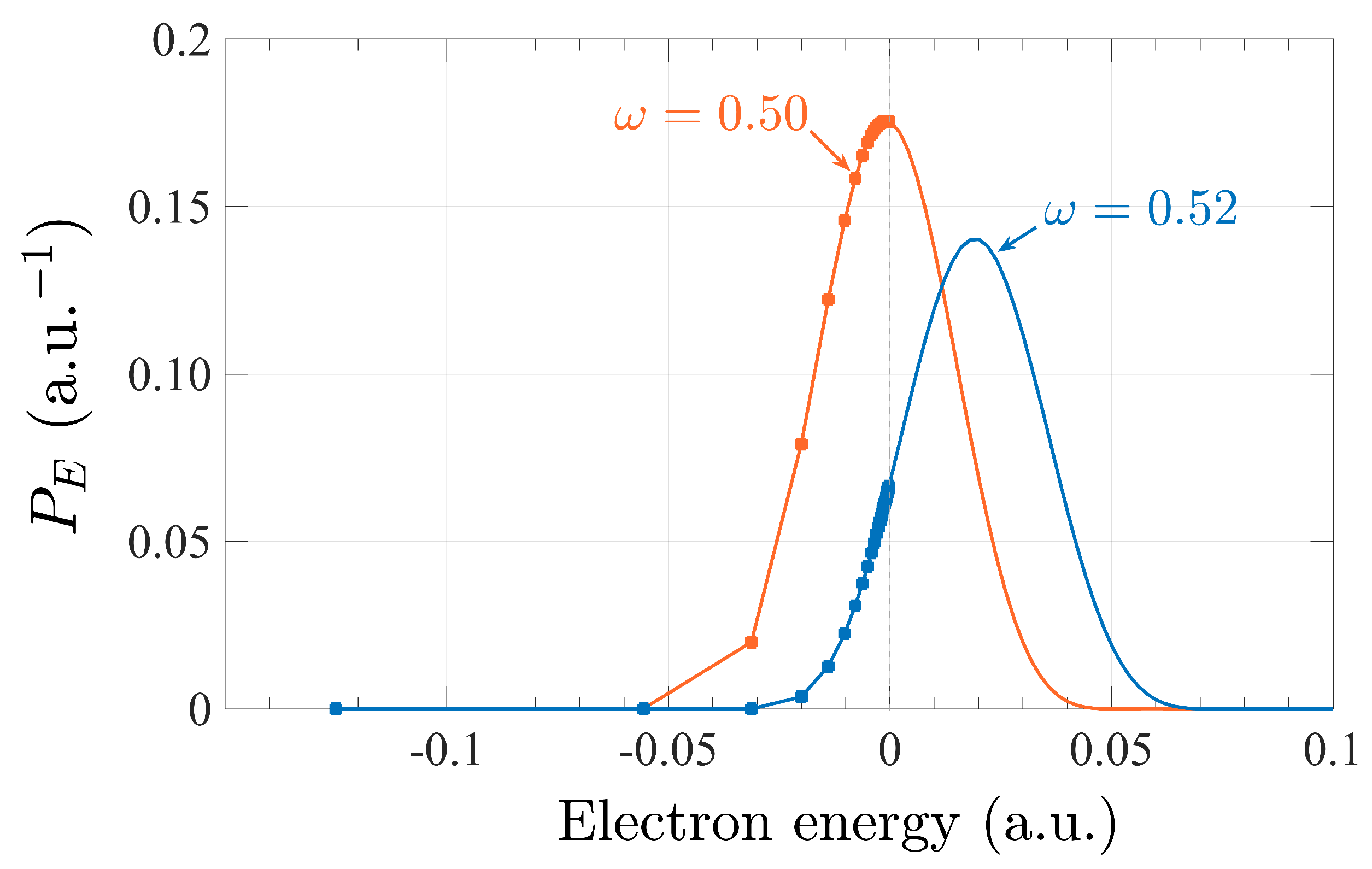
3.3. Application to the Study of Rydberg States
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Paulus, G.G.; Becker, W. High-order above-threshold ionization with few-cycle pulse: A meter of the absolute phase. Opt. Express 2003, 11, 1418–1429. [Google Scholar] [CrossRef]
- Scrinzi, A.; Elander, N.; Piraux, B. Stabilization of Rydberg atoms in superintense laser fields. Phys. Rev. A 1993, 48, R2527–R2530. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, M.V.; Fedorov, S.M. Stabilization and structure of wave packets in Rydberg atoms ionized by a strong light field. Opt. Express 1998, 3, 271–279. [Google Scholar] [CrossRef]
- Matula, O.; Hayrapetyan, A.G.; Serbo, V.G.; Surzhykov, A.; Fritzsche, S. Atomic ionization of hydrogen-like ions by twisted photons: Angular distribution of emitted electrons. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 205002. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
- Clarke, D.D.A.; Armstrong, G.S.J.; Brown, A.C.; van der Hart, H.W. R-matrix-with-time-dependence theory for ultrafast atomic processes in arbitrary light fields. Phys. Rev. A 2018, 98, 053442. [Google Scholar] [CrossRef]
- Randazzo, J.M.; Marante, C.; Chattopadhyay, S.; Schneider, B.I.; Olsen, J.; Argenti, L. ASTRA: Transition-density-matrix approach to molecular ionization. Phys. Rev. Res. 2023, 5, 043115. [Google Scholar] [CrossRef]
- Marante, C.; Klinker, M.; Corral, I.; González-Vázquez, J.; Argenti, L.; Martín, F. Hybrid-Basis Close-Coupling Interface to Quantum Chemistry Packages for the Treatment of Ionization Problems. J. Chem. Theory Comput. 2017, 13, 499–514. [Google Scholar] [CrossRef]
- Bachau, H.; Cormier, E.; Decleva, P.; Hansen, J.E.; Martín, F. Applications of B-splines in atomic and molecular physics. Rep. Prog. Phys. 2001, 64, 1815–1943. [Google Scholar] [CrossRef]
- Zatsarinny, O. B-spline atomic R-matrix codes. Comput. Phys. Commun. 2006, 174, 273–356. [Google Scholar] [CrossRef]
- Fischer, C.F. Towards B-Spline Atomic Structure Calculations. Atoms 2021, 9, 50. [Google Scholar] [CrossRef]
- Rescigno, T.N.; McCurdy, C.W. Numerical grid methods for quantum-mechanical scattering problems. Phys. Rev. A 2000, 62, 032706. [Google Scholar] [CrossRef]
- Yip, F.L.; McCurdy, C.W.; Rescigno, T.N. Hybrid Gaussian—Discrete-variable representation approach to molecular continuum processes: Application to photoionization of diatomic Li2+. Phys. Rev. A 2008, 78, 023405. [Google Scholar] [CrossRef]
- Scrinzi, A. Infinite-range exterior complex scaling as a perfect absorber in time-dependent problems. Phys. Rev. A 2010, 81, 053845. [Google Scholar] [CrossRef]
- Muhiddin, F.A.; Sulaiman, J. Performance analysis of fourth-order Crank-Nicolson scheme for solving diffusion equations. AIP Conf. Proc. 2018, 1974, 020099. [Google Scholar] [CrossRef]
- Tao, L.; Scrinzi, A. Photo-electron momentum spectra from minimal volumes: The time-dependent surface flux method. New J. Phys. 2012, 14, 013021. [Google Scholar] [CrossRef]
- Orimo, Y.; Sato, T.; Ishikawa, K.L. Application of the time-dependent surface flux method to the time-dependent multiconfiguration self-consistent-field method. Phys. Rev. A 2019, 100, 013419. [Google Scholar] [CrossRef]
- Morishita, T.; Chen, Z.; Watanabe, S.; Lin, C.D. Two-dimensional electron momentum spectra of argon ionized by short intense lasers: Comparison of theory with experiment. Phys. Rev. A 2007, 75, 023407. [Google Scholar] [CrossRef]
- Ilchen, M.; Douguet, N.; Mazza, T.; Rafipoor, A.J.; Callegari, C.; Finetti, P.; Plekan, O.; Prince, K.C.; Demidovich, A.; Grazioli, C.; et al. Circular Dichroism in Multiphoton Ionization of Resonantly Excited He+ Ions. Phys. Rev. Lett. 2017, 118, 013002. [Google Scholar] [CrossRef]
- De Silva, A.H.N.C.; Atri-Schuller, D.; Dubey, S.; Acharya, B.P.; Romans, K.L.; Foster, K.; Russ, O.; Compton, K.; Rischbieter, C.; Douguet, N.; et al. Using Circular Dichroism to Control Energy Transfer in Multiphoton Ionization. Phys. Rev. Lett. 2021, 126, 023201. [Google Scholar] [CrossRef] [PubMed]
- Tan, I.; Snider, G.L.; Chang, L.D.; Hu, E.L. A self-consistent solution of Schrödinger–Poisson equations using a nonuniform mesh. J. Appl. Phys. 1990, 68, 4071–4076. [Google Scholar] [CrossRef]
- Sundqvist, H.; Veronis, G. A simple finite-difference grid with non-constant intervals. Tellus 1970, 22, 26–31. [Google Scholar] [CrossRef]
- Diele, F.; Lopez, L.; Peluso, R. The Cayley transform in the numerical solution of unitary differential systems. Adv. Comput. Math. 1998, 8, 317. [Google Scholar] [CrossRef]
- Cormier, E.; Lambropoulos, P. Optimal gauge and gauge invariance in non-perturbative time-dependent calculation of above-threshold ionization. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 1667. [Google Scholar] [CrossRef]
- Han, Y.C.; Madsen, L.B. Comparison between length and velocity gauges in quantum simulations of high-order harmonic generation. Phys. Rev. A 2010, 81, 063430. [Google Scholar] [CrossRef]
- Keldysh, L.V. Ionization in the field of a strong electromagnetic wave. Sov. Phys. J. Exp. Theor. Phys. 1965, 20, 1307. [Google Scholar]
- Morales, F.; Bredtmann, T.; Patchkovskii, S. iSURF: A family of infinite-time surface flux methods. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 245001. [Google Scholar] [CrossRef]
- Tulsky, V.; Bauer, D. QPROP with faster calculation of photoelectron spectra. Comput. Phys. Commun. 2020, 251, 107098. [Google Scholar] [CrossRef]
- Joachain, C.J.; Kylstra, N.; Potvliege, R.M. Atoms in Intense Laser Fields; Cambridge University: New York, NY, USA, 2012. [Google Scholar]
- Christov, I.P.; Murnane, M.M.; Kapteyn, H.C. High-Harmonic Generation of Attosecond Pulses in the “Single-Cycle” Regime. Phys. Rev. Lett. 1997, 78, 1251–1254. [Google Scholar] [CrossRef]
- Finger, K.; Atri-Schuller, D.; Douguet, N.; Bartschat, K.; Hamilton, K.R. High-order harmonic generation in the water window from mid-IR laser sources. Phys. Rev. A 2022, 106, 063113. [Google Scholar] [CrossRef]
- Rothhardt, J.; Hädrich, S.; Klenke, A.; Demmler, S.; Hoffmann, A.; Gotschall, T.; Eidam, T.; Krebs, M.; Limpert, J.; Tünnermann, A. 53 W average power few-cycle fiber laser system generating soft x rays up to the water window. Opt. Lett. 2014, 39, 5224–5227. [Google Scholar] [CrossRef] [PubMed]
- Vos, R.J.; Gavrila, M. Effective stabilization of Rydberg states at current laser performances. Phys. Rev. Lett. 1992, 68, 170–173. [Google Scholar] [CrossRef] [PubMed]
- Reinhold, C.; Burgdörfer, J.; Frey, M.; Dunning, F. Creating and probing coherent atomic states. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 1997, 132, 316–325. [Google Scholar] [CrossRef][Green Version]
- Xia, Q.Z.; Ye, D.F.; Fu, L.B.; Han, X.Y.; Liu, J. Momentum distribution of near-zero-energy photoelectrons in the strong-field tunneling ionization in the long wavelength limit. Sci. Rep. 2015, 5, 11473. [Google Scholar] [CrossRef] [PubMed]
- Blaga, C.I.; Catoire, F.; Colosimo, P.; Paulus, G.G.; Muller, H.G.; Agostini, P.; DiMauro, L.F. Strong-field photoionization revisited. Nat. Phys. 2009, 5, 335–338. [Google Scholar] [CrossRef]
- Dutta, S.K.; Feldbaum, D.; Walz-Flannigan, A.; Guest, J.R.; Raithel, G. High-Angular-Momentum States in Cold Rydberg Gases. Phys. Rev. Lett. 2001, 86, 3993–3996. [Google Scholar] [CrossRef]
- Hölzl, C.; Götzelmann, A.; Pultinevicius, E.; Wirth, M.; Meinert, F. Long-Lived Circular Rydberg Qubits of Alkaline-Earth Atoms in Optical Tweezers. Phys. Rev. X 2024, 14, 021024. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313–2363. [Google Scholar] [CrossRef]
- Li, Q.; Tong, X.M.; Morishita, T.; Wei, H.; Lin, C.D. Fine structures in the intensity dependence of excitation and ionization probabilities of hydrogen atoms in intense 800-nm laser pulses. Phys. Rev. A 2014, 89, 023421. [Google Scholar] [CrossRef]
- Zimmermann, H.; Patchkovskii, S.; Ivanov, M.; Eichmann, U. Unified Time and Frequency Picture of Ultrafast Atomic Excitation in Strong Laser Fields. Phys. Rev. Lett. 2017, 118, 013003. [Google Scholar] [CrossRef] [PubMed]
- Fedorov, M.V.; Tehranchi, M.M.; Fedorov, S.M. Interference stabilization of Rydberg atoms: Numerical calculations and physical models. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 2907. [Google Scholar] [CrossRef]
- Freeman, R.R.; Bucksbaum, P.H.; Milchberg, H.; Darack, S.; Schumacher, D.; Geusic, M.E. Above-threshold ionization with subpicosecond laser pulses. Phys. Rev. Lett. 1987, 59, 1092–1095. [Google Scholar] [CrossRef] [PubMed]
- Grum-Grzhimailo, A.N.; Douguet, N.; Meyer, M.; Bartschat, K. Two-color XUV plus near-IR multiphoton near-threshold ionization of the helium ion by circularly polarized light in the vicinity of the 3p resonance. Phys. Rev. A 2019, 100, 033404. [Google Scholar] [CrossRef]

| 0.01 | 83,000 | 1.0 | |||
| 0.10 | 9490 | 6.3 | |||
| 0.25 | 4830 | 9.4 | |||
| 0.50 | 3290 | 12.2 |
| 0.01 | 84,100 | 1.0 | |||
| 0.10 | 9690 | 5.4 | |||
| 0.25 | 4910 | 7.5 | |||
| 0.50 | 3210 | 9.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Douguet, N.; Guchkov, M.; Bartschat, K.; Santos, S.F.d. Efficient Time-Dependent Method for Strong-Field Ionization of Atoms with Smoothly Varying Radial Steps. Atoms 2024, 12, 34. https://doi.org/10.3390/atoms12070034
Douguet N, Guchkov M, Bartschat K, Santos SFd. Efficient Time-Dependent Method for Strong-Field Ionization of Atoms with Smoothly Varying Radial Steps. Atoms. 2024; 12(7):34. https://doi.org/10.3390/atoms12070034
Chicago/Turabian StyleDouguet, Nicolas, Mikhail Guchkov, Klaus Bartschat, and Samantha Fonseca dos Santos. 2024. "Efficient Time-Dependent Method for Strong-Field Ionization of Atoms with Smoothly Varying Radial Steps" Atoms 12, no. 7: 34. https://doi.org/10.3390/atoms12070034
APA StyleDouguet, N., Guchkov, M., Bartschat, K., & Santos, S. F. d. (2024). Efficient Time-Dependent Method for Strong-Field Ionization of Atoms with Smoothly Varying Radial Steps. Atoms, 12(7), 34. https://doi.org/10.3390/atoms12070034








