Natural Orbitals and Targeted Non-Orthogonal Orbital Sets for Atomic Hyperfine Structure Multiconfiguration Calculations ^†

Abstract

Hyperfine structure constants have many applications, but are often hard to calculate accurately due to large and canceling contributions from different terms of the hyperfine interaction operator, and also from different closed and spherically symmetric core subshells that break up due to electron correlation effects. In multiconfiguration calculations, the wave functions are expanded in terms of configuration state functions (CSFs) built from sets of one-electron orbitals. The orbital sets are typically enlarged within the layer-by-layer approach. The calculations are energy-driven, and orbitals in each new layer of correlation orbitals are spatially localized in regions where the weighted total energy decreases the most, overlapping and breaking up different closed core subshells in an irregular pattern. As a result, hyperfine structure constants, computed as expectation values of the hyperfine operators, often show irregular or oscillating convergence patterns. Large orbital sets, and associated large CSF expansions, are needed to obtain converged values of the hyperfine structure constants. We analyze the situation for the states of the $\{2s^{2}2p^3,2s^{2}2p^{2}3p,2s^{2}2p^{2}4p\}$ odd and $\{2s^{2}2p^{2}3s,2s2p^4,2s^{2}2p^{2}4s,2s^{2}2p^{2}3d\}$ even configurations in N I, and show that the convergence with respect to the increasing sets of orbitals is radically improved by introducing separately optimized orbital sets targeted for describing the spin- and orbital-polarization effects of the $1s$ and $2s$ core subshells that are merged with, and orthogonalized against, the ordinary energy-optimized orbitals. In the layer-by-layer approach, the spectroscopic orbitals are kept frozen from the initial calculation and are not allowed to relax in response to the introduced layers of correlation orbitals. To compensate for this lack of variational freedom, the orbitals are transformed to natural orbitals prior to the final calculation based on single and double substitutions from an increased multireference set. The use of natural orbitals has an important impact on the states of the $2s^{2}2p^{2}3s$ configuration, bringing the corresponding hyperfine interaction constants in closer agreement with experiment. Relying on recent progress in methodology, the multiconfiguration calculations are based on configuration state function generators, cutting down the time for spin-angular integration by factors of up to 50, compared to ordinary calculations.

1. Introduction

In astrophysics, knowledge of hyperfine structures is needed for detailed line modeling and accurate abundance determinations [1,2]. The hyperfine interaction not only splits and broadens spectral lines, but also redistributes the radiation and may even open new decay channels that are useful for diagnosing electron densities in low-density astrophysical plasmas [3]. In nuclear physics, calculated hyperfine interaction constants, related to detailed electron–nucleus interactions [4], have been combined with high-precision measurements to extract nuclear information such as magnetic dipole, electric quadrupole [5,6,7], and magnetic octupole [8] moments.

Multiconfiguration methods, both non-relativistic multiconfiguration Hartree–Fock (MCHF) and relativistic multiconfiguration Dirac–Hartree–Fock (MCDHF), have been used for a long time to calculate hyperfine structure constants for a large number of states and elements of different complexities [5,6,9,10,11]. Common to these calculations is the fact that they often show slow and irregular convergence patterns, requiring large orbital sets and large CSF expansions for obtaining accurate and reliable values of the hyperfine interaction constants [12]. In this work, following the ideas of Verdebout et al. [13] and Li et al. [14], we analyze the situation for the states of the $\{2s^{2}2p^3,2s^{2}2p^{2}3p,2s^{2}2p^{2}4p\}$ odd and $\{2s^{2}2p^{2}3s,2s2p^4,2s^{2}2p^{2}4s,2s^{2}2p^{2}3d\}$ even-parity configurations in N I and show that the convergence with respect to the increasing sets of orbitals is substantially improved by introducing separately optimized orbital sets, targeted for describing the spin- and orbital-polarization effects on the $1s$ and $2s$ core subshells. These sets are merged with, and orthogonalized against, the ordinary energy-optimized orbitals. The selection of N I for the study is mainly motivated by the fact that the hyperfine interaction constant for the $2s^{2}2p^3{\hspace{0.25em}}^4{S}_{3/2}^o$ ground state is zero in the Hartree–Fock (HF) approximation and that the spin- and orbital-polarization effects on the $1s$ and $2s$ core subshells give large, but canceling, contributions, the balancing of which is crucial for the final constant; see [15] for a detailed account. Furthermore, experimental hyperfine interaction constants for states of the $2p^{2}3s{\hspace{0.25em}}^{4}P$ and $2p^{2}3p{\hspace{0.25em}}^4{P}^o,{\hspace{0.25em}}^4{D}^o$ terms are available for comparison. The constants were extracted from Doppler-free saturation spectra [16] and later reinterpreted by Carette et al. [17], who compared them with constants from large scale multiconfiguration Hartree–Fock calculations [18]. Finally, hyperfine interaction constants are needed to extract absolute frequencies connecting states of the $2p^{2}3s{\hspace{0.25em}}^{2}P$ and $2p^{2}3p{\hspace{0.25em}}^2{D}^o$ terms [19].

MCDHF calculations are usually performed with the layer-by-layer (LBL) approach [20], whereby the spectroscopic orbitals are kept frozen from a fully variational calculation of the targeted states, based on the most important reference configurations, and are not allowed to relax in response to the introduced layers of correlation orbitals. As shown by Schiffmann et al. [21], such variational restriction imposed on the spectroscopic orbitals may negatively affect the calculated hyperfine interaction constants, but can be compensated for by the use of natural orbitals (NOs). In analogy with the states in Na I studied by Schiffmann et al. [21], we expect that the effect is the largest for the hyperfine constants of the $2s^{2}2p^{2}3s$ states.

The paper is organized as follows: first, we describe the MCDHF and relativistic configuration interaction (RCI) methods, with a focus on the spin-angular integration and how it can be speeded up by the introduction of configuration state function generators (CSFGs) [22]. This is followed by a description of the hyperfine structure. After a section on the transformation to natural orbitals, we continue to discuss methods for generating CSF expansions and orbital bases to account for electron correlation effects that are important for the energies, ‘energy-driven’ calculations, and methods for generating CSF expansions and orbital bases to account for electron correlation effects, mainly spin and orbital polarization, that are important for the hyperfine structure constants. We present results from ordinary ‘energy-driven’ calculations of the hyperfine interaction constants of the targeted states, and study the convergence with respect to the increasing sets of orbitals. Additionally, we perform calculations in which separately optimized orbital sets, targeted to account for the spin- and orbital- polarization effects of the $1s$ and $2s$ subshells, are merged with, and orthogonalized against, the ordinary energy-optimized orbitals. To infer the effectiveness of the method with separately optimized orbital sets, the convergence trends for these calculations are compared with those based on the ‘energy-driven’ calculations. In a series of RCI calculations, we analyze the effect of NO and higher-order electron correlation effects on the hyperfine interaction constants and compare the results with experiments and other calculations. Finally, we summarize the results, analyze the implications, and consider perspectives of separately optimized orbital sets for calculations of hyperfine structure constants for other systems of relevance for astrophysics and nuclear physics.

2. Theory

2.1. The MCDHF and RCI Methods

In multiconfiguration methods, the wave function of an atomic state $\mathsf{\Gamma }J{M}_J$, with $\mathsf{\Gamma }$ being its identifying label, J the total angular momentum quantum number, and $M_J$ the total magnetic quantum number, is approximated by an atomic state function (ASF) $\mathsf{\Psi }$, which is a linear combination of configuration state functions (CSFs) $\mathsf{\Phi }$:

$$\mathsf{\Psi }\left(\mathsf{\Gamma }J{M}_J\right)=\sum _{i=1}^{N_{CSF}}{c}_{{\gamma }_i}\mathsf{\Phi }\left({\gamma }_{i}J{M}_J\right),$$

(1)

where ${\gamma }_i$ specifies the orbital occupancy and spin-angular coupling tree quantum numbers of each CSF, and $N_{CSF}$ stands for the number of CSFs. The CSFs are antisymmetrized and symmetry-adapted all-electron functions constructed from products of four-component relativistic one-electron orbitals:

$${\varphi }_{n\kappa m}=\frac{1}{r}\left(\begin{array}{c}{P}_{n\kappa }\left(r\right){\mathsf{\Omega }}_{\kappa m}(\theta ,\phi )\\ \mathrm{i}{Q}_{n\kappa }\left(r\right){\mathsf{\Omega }}_{-\kappa m}(\theta ,\phi )\end{array}\right),$$

(2)

where $P_{n\kappa }\left(r\right)$ and $Q_{n\kappa }\left(r\right)$ are the radial functions. The radial functions of the orbitals are a priori unknown and should be determined on a grid with the additional condition of orthogonality within each symmetry. The requirement that the energy computed from the multiconfiguration expansion should be stationary with respect to perturbations in the expansion coefficients leads to a matrix eigenvalue problem:

$$(\mathit{H}-E\mathit{I}){\mathit{c}}^T=\mathbf{0},$$

(3)

where $\mathit{c}=(c_1,c_2,\dots ,c_M)$ is the vector of expansion coefficients and $\mathit{H}$ is the Hamiltonian matrix with elements $H_{ij}=\langle \mathsf{\Phi }\left({\gamma }_{i}J\right)\parallel {\mathcal{H}}_{\mathrm{DC}}\parallel \mathsf{\Phi }\left({\gamma }_{j}J\right)\rangle$ of the Dirac–Coulomb (DC) Hamiltonian. The stationary condition with respect to variations in the radial functions, in turn, leads to a system of coupled integro-differential equations, subject to boundary conditions at the origin and in the infinity. Calculations where both the radial functions and the expansions are simultaneously determined are referred to as multiconfiguration Dirac–Hartree–Fock (MCDHF) calculations. Calculations for which the radial functions are frozen (i.e., determined in an earlier calculation), and only the expansion coefficients are determined, are referred to as relativistic configuration interaction (RCI) calculations [23,24,25].

The computation of matrix elements between two CSFs, as part of the construction of the Hamiltonian matrix or evaluation of expectation values, breaks down to spin-angular integration that gives spin-angular coefficients, which are then multiplied with radial one- or two-electron integrals and effective interaction strengths [23,24,26]. The spin-angular integration is, by the sheer number of matrix elements, a very time-consuming part of an RCI calculation. The integration is, however, independent of the principal quantum numbers of the orbitals, and arranging the CSFs in groups with the same spin-angular structure spanned by configuration state function generators (CSFGs), spin-angular integration has to be performed only for one or two pairs of CSFs in a group or between two groups, from which then spin-angular coefficients directly follow for all pairs in the group or between two groups. As a consequence, the CPU time for the spin-angular integration is substantially reduced compared with calculations where spin-angular integration is performed between all pairs of CSFs [22].

2.2. Hyperfine Structure

The hyperfine structure of an atomic energy level is caused by the interaction between the electrons and the electromagnetic multipole moments of the nucleus. The Hamiltonian for the interaction may be represented as a multipole expansion [27]:

$${\mathcal{H}}_{hfs}=\sum _{k\ge 1}{\mathbf{T}}^{\left(k\right)}·{\mathbf{M}}^{\left(k\right)},$$

(4)

where ${\mathbf{T}}^{\left(k\right)}$ and ${\mathbf{M}}^{\left(k\right)}$ are spherical tensor operators of rank k in the electronic and nuclear spaces, respectively [28]. The dominating k = 1 term represents the magnetic dipole interaction. For an N-electron atom, the electronic tensor operator is, in atomic units,

$${\mathbf{T}}^{\left(1\right)}=\sum _{i=1}^N{\mathbf{t}}^{\left(1\right)}\left(i\right)=\sum _{i=1}^N-\mathrm{i}\alpha r_i^{-2}\left({\mathit{\alpha }}_i·{\mathbf{l}}_i{\mathbf{C}}^{\left(1\right)}({\theta }_i,{\phi }_i)\right).$$

(5)

In the formula above, $\alpha$ is the fine-structure constant, $\mathit{\alpha }$ the Dirac matrix, and ${\mathbf{C}}^{\left(1\right)}$ the renormalized spherical harmonic, a spherical tensor operator of rank one. The splitting of atomic fine-structure levels due to the hyperfine interaction is often given in terms of the interaction constant A:

$$A_{\mathsf{\Gamma }J}=\frac{{\mu }_I}{I}\frac{1}{{\left[J(J+1)(2J+1)\right]}^{1/2}}\langle \mathsf{\Gamma }J\Vert {\mathbf{T}}^{\left(1\right)}\Vert \mathsf{\Gamma }J\rangle ,$$

(6)

where I is the nuclear spin and ${\mu }_I$ the nuclear magnetic dipole moment. Inserting the wave function expansions from Equation (1), the reduced matrix elements between the ASFs are given as sums over reduced matrix elements between CSFs weighted with the expansion coefficients. Performing the spin-angular integration, the latter matrix elements can be expressed in terms of spin-angular coefficients multiplied with radial hyperfine integrals. Just as for the Hamiltonian matrix elements, the need for spin-angular integration is reduced by the arrangement of CSFs into groups with the same spin-angular structure spanned by a generator. Nitrogen has two stable isotopes, ${\hspace{0.25em}}^{14}$N and ${\hspace{0.25em}}^{15}$N. The hyperfine constants in this work are computed for the most abundant isotope ${\hspace{0.25em}}^{14}$N, which has a nuclear spin $I=1$ and a nuclear magnetic dipole moment ${\mu }_I=+0.40376100\left(6\right)$ [29].

2.3. Transformation to Natural Orbitals

Since their introduction in 1955 by Löwdin [30], natural orbitals have been used in quantum chemistry to obtain more compact representations of correlated wave functions [31]. The electron density and natural orbitals of relativistic multiconfiguration expansions can be computed using the Rdensity program [32]. Introducing, for each relativistic symmetry $\kappa$, the density matrix ${\mathit{\rho }}^{\kappa }$ with elements

$${\rho }_{n{n}^{\prime }}^{\kappa }=\sum _{i,j}{c}_i{\nu }_{n{n}^{\prime }}^{ij}{c}_j,$$

(7)

where ${\nu }_{n{n}^{\prime }}^{ij}$ are angular coefficients, the computation of which are described in [32], the natural orbitals vector ${\tilde{\mathit{\varphi }}}^{\kappa }$ with elements ${\tilde{\varphi }}_{n\kappa }$ are obtained from the eigenvectors ${\mathit{U}}^{\kappa }$ of the density matrix

$${\left({\mathit{U}}^{\kappa }\right)}^{†}{\mathit{\rho }}^{\kappa }{\mathit{U}}^{\kappa }={\tilde{\mathit{\rho }}}^{\kappa }$$

(8)

such that

$${\tilde{\mathit{\varphi }}}^{\kappa }={\mathit{\varphi }}^{\kappa }{\mathit{U}}^{\kappa }.$$

(9)

Written explicitly, the radial parts of the natural orbitals are

$${\tilde{P}}_{n^{\prime }\kappa }\left(r\right)=\sum _n{u}_{n,n^{\prime }}^{\kappa }{P}_{n\kappa }\left(r\right)$$

(10)

$${\tilde{Q}}_{n^{\prime }\kappa }\left(r\right)=\sum _n{u}_{n,n^{\prime }}^{\kappa }{Q}_{n\kappa }\left(r\right).$$

(11)

As shown in [21], the modification of the spectroscopic orbitals due to the transformation has important effects on the computed hyperfine interactions that are hard to capture by just increasing the number of layers of correlation orbitals.

3. Selection of CSF Expansions and Generation of Orbital Sets

In multiconfiguration methods, the orbital sets are determined in MCDHF calculations. Guided by Z-dependent perturbation theory [23,33], MCDHF calculations are often based on CSF expansions obtained by single and double (SD) substitutions of orbitals in a number of important near-degenerate configurations, the multireference (MR) set, to increasing sets of correlation orbitals. Variational calculations are energy-driven, and correlation orbitals localize where the weighted energy decreases the most. An orbital set built up in this way may be inefficient in describing correlation effects for properties such as transition rates or hyperfine structures [14], which necessitates the generation of large correlation orbital sets in order to converge the properties in question to a desirable accuracy. To remedy this, one should start from a perturbative analysis of the CSFs that are important for the studied property to see how the orbital set should be constructed to ensure rapid convergence (cf., equation (30) in [13]). The hyperfine operator is a one-body operator, and CSFs obtained by S substitutions contribute to the lowest order. Out of these, the ones describing the spin and orbital polarization of the closed $1s$ and $2s$ subshells are the most important; see [14,15,34] for a detailed account. CSFs obtained by D substitutions have mainly indirect effects [35]. To the next order, there are CSFs obtained by S substitutions from energetically important configurations obtained by D substitutions. In accurate calculations, one also has to consider D substitutions from energetically important configurations obtained by D substitutions. These two classes are, respectively, formed by triple (T) and quadruple (Q) substitutions.

4. Calculations of Hyperfine Interaction Constants in Different Orbital Sets

Radial orbitals were obtained from MCDHF calculations performed using the Grasp2018 program package [20,36]. The RCI calculations based on configuration state function generators (CSFGs) [22] were performed with the Graspg program package [37]. The details of the calculations, which were performed separately for each parity, are described below.

4.1. Hyperfine Interaction Constants from Energy-Driven Calculations

Starting with the odd-parity states, we performed an extended optimal level (EOL) [38] Dirac–Hartree–Fock calculation of the 31 lowest states of the $\{2s^{2}2p^3,2s^{2}2p^{2}3p,2s^{2}2p^{2}4p\}$ configurations. The common $1s$ core shell of the MR configurations was not written out for simplicity. This calculation was followed by MCDHF calculations based on CSF expansions obtained by allowing single and double (SD) substitutions of orbitals in the MR configurations with orbitals in increasing orbital sets with the restriction that there should be at most one substitution from the $1s$ core shell (MR-SD VV + CV). Specified by the orbitals with the highest principal quantum numbers of each symmetry, and employing the non-relativistic notation, the orbital sets are listed in

Table 1. Orbital sets for odd-parity calculations. Sets specified by the orbitals with the highest principal quantum numbers of each symmetry in non-relativistic notation.

Label	Orbitals
set 1	$\{3s,5p,3d\}$
set 2	$\{4s,6p,4d,4f\}$
set 3	$\{5s,7p,5d,5f,5g\}$
set 4	$\{6s,8p,6d,6f,6g\}$
set 5	$\{7s,9p,7d,7f,7g\}$
set 6	$\{8s,10p,8d,8f,7g\}$
set 7	$\{9s,11p,9d,8f,7g\}$

.

The calculations were performed with the LBL approach, meaning that the orbitals from previous orbital sets were kept frozen, and only the outermost orbital of each symmetry of a new orbital set was optimized [20]. The restriction to $s,p,d,f,g$ symmetries can be motivated by the fact that hyperfine structure constants are less sensitive to orbitals with higher l, which are pushed away from the important region in the vicinity of the nucleus due to the centripetal force [39,40].

The calculations for the even-parity states were performed in a similar way. We started with an extended optimal level (EOL) Dirac–Hartree–Fock calculation of the 50 lowest states of the $\{2s^{2}2p^{2}3s,$ $2s2p^4,2s^{2}2p^{2}4s,2s^{2}2p^{2}3d\}$ configurations. This calculation was followed by MCDHF calculations based on CSF expansions obtained by allowing single and double (SD) substitutions of orbitals in the MR configurations with orbitals in increasing orbital sets, with the restriction that there should be at most one substitution from the $1s$ core shell (MR-SD VV + CV). Specified by the orbitals with the highest principal quantum numbers of each symmetry, the orbital sets are given in

Table 2. Orbital sets for even-parity calculations. Sets specified by the orbitals with the highest principal quantum numbers of each symmetry in non-relativistic notation.

Label	Orbitals
set 1	$\{5s,3p,4d\}$
set 2	$\{6s,4p,5d,4f\}$
set 3	$\{7s,5p,6d,5f,5g\}$
set 4	$\{8s,6p,7d,6f,6g\}$
set 5	$\{9s,7p,8d,7f,7g\}$
set 6	$\{10s,8p,9d,8f,7g\}$
set 7	$\{11s,9p,10d,8f,7g\}.$

.

As discussed below, oscillations in the hyperfine interaction constants are related to the varying spatial localization of the correlation orbitals. That conclusion is substantiated by the mean radii ${\langle r\rangle }_{n\kappa }={\int }_0^{\infty }r\left(P_{n\kappa }^2\left(r\right)+Q_{n\kappa }^2\left(r\right)\right)dr$ of the correlation orbitals, which are collected in

Table 3. Mean orbital radii $\langle r\rangle$ (in $a_0$ units), for the spectroscopic orbitals and for the outermost orbitals in each orbital set, and for the $1s$ and $2s$ polarization orbitals. See Section 4.2 for a description of the latter.

spectroscopic	odd states			even states
orbitals	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$
$n=1$	0.228	–	–	0.228	–	–
$n=2$	1.262	1.273	–	1.251	1.278	–
$n=3$	–	6.818	–	6.952	–	10.39
$n=4$	–	14.88	–	11.15	–	–
correlation orbital set	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$
set 1	1.769	2.373	1.427	2.061	1.912	1.452
set 2	0.994	1.024	1.040	0.955	0.950	1.053
set 3	1.711	1.403	1.330	1.359	1.406	1.387
set 4	3.501	2.706	3.868	2.368	3.442	1.777
set 5	0.969	0.970	0.986	0.931	0.823	3.636
set 6	4.223	6.623	0.927	7.193	1.158	0.708
set 7	0.711	0.715	3.705	0.783	6.121	0.733
$1s$ polarization orbitals	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$
	0.999	–	0.778	1.105	–	0.785
	3.842	–	0.818	0.804	–	0.816
$2s$ polarization orbitals	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$	$s_{1/2}$	$p_{3/2}$	$d_{5/2}$
	2.394	–	1.512	2.911	–	1.536
	4.421	–	4.287	3.230	–	1.182

. The first set of values reported in the Table 3 corresponds to the radii of the spectroscopic orbitals from the initial calculations. The second set refers to the radii of the outermost correlation orbitals within each orbital set. The data collected in Table 3 reveal that the localizations, as measured by the mean radii, of the important correlation orbitals of s symmetry are irregular and fluctuate in a region with the left boundary between ${\langle r\rangle }_{1s}$ and ${\langle r\rangle }_{2s}$ and the right boundary between ${\langle r\rangle }_{2p}$ and ${\langle r\rangle }_{3s,3p,3d}$.

The MCDHF calculations were followed by RCI calculations based on CSF expansion obtained by allowing SD substitutions of orbitals in an enlarged MR set consisting of additional near-degenerate configurations with orbitals in the correlations sets listed in Table 1 and Table 2. The enlarged MR sets for the odd- and even-parity states were

$$\{2s^{2}2p^3,2s^{2}2p^{2}3p,2s^{2}2p^{2}4p,2p^5,2p^{4}3p,2p^{4}4p,2s2p^{3}3s,2s2p^{3}3d,2s2p^{2}3p3d\}$$

(12)

and

$$\{2s^{2}2p^{2}3s,2s2p^4,2s^{2}2p^{2}4s,2s^{2}2p^{2}3d,2p^{4}3s,2p^{4}4s,2p^{4}3d,2s2p^{3}3p,2s2p^{2}3s3d,2s2p^{2}3s4d\}.$$

(13)

The RCI calculations included the Breit interaction and the leading QED corrections (vacuum polarization and self-energy). To speed up the calculations, the CSFs were arranged in groups, with the same spin-angular structure spanned by CSFGs, thus allowing the spin-angular coefficients for all pairs of CSFs in a group or between two groups to be inferred from one or two ’template’ pairs. Compared to the ordinary RCI calculations, for which spin-angular integration is performed between all pairs of CSFs, the use of CSFGs reduces the execution time for the largest calculations (based on orbital set 7) by a factor of 10.

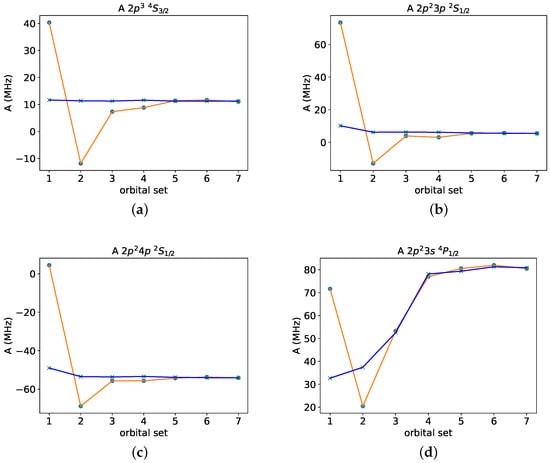
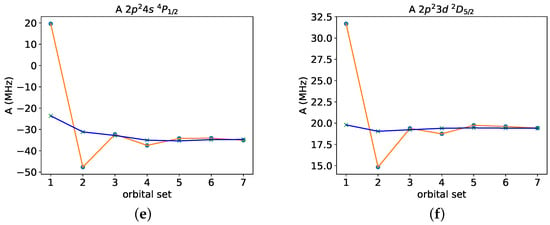
The calculated magnetic dipole hyperfine interaction constants are shown in

Table 4. Hyperfine interaction constants A (in MHz) for states of the $\{2s^{2}2p^3,2s^{2}2p^{2}3p,2s^{2}2p^{2}4p\}$ odd configurations in ${\hspace{0.25em}}^{14}$N from MR-SD RCI calculations as functions of the increasing set of correlation orbitals.

State	J P	Set 1	Set 2	Set 3	Set 4	Set 5	Set 6	Set 7	Exp.	MCHF ${\hspace{0.25em}}^{\mathit{d}}$
$2p^3{\hspace{0.25em}}^4{S}^o$	3/2 -	40.35	−11.84	7.331	8.838	11.40	11.65	11.04	10.4509 ${\hspace{0.25em}}^a$
$2p^3{\hspace{0.25em}}^2{D}^o$	5/2 -	117.2	112.7	114.5	116.1	115.9	115.9	115.9
$2p^3{\hspace{0.25em}}^2{D}^o$	3/2 -	59.29	72.17	67.10	67.41	66.13	66.19	66.17
$2p^3{\hspace{0.25em}}^2{P}^o$	1/2 -	294.3	332.2	320.5	324.0	321.8	321.1	321.8
$2p^3{\hspace{0.25em}}^2{P}^o$	3/2 -	73.36	58.09	63.10	64.12	64.46	64.65	64.43
$2p^{2}3p{\hspace{0.25em}}^2{S}^o$	1/2 -	73.47	−12.92	3.931	3.105	5.489	5.730	5.484
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	1/2 -	42.31	85.03	76.99	76.37	75.38	75.01	75.09	69.76(90) ${\hspace{0.25em}}^{b,c}$	74.15
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	3/2 -	37.96	28.93	30.69	31.02	31.16	31.38	31.26	30.3(15) ${\hspace{0.25em}}^c$	31.71
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	5/2 -	48.19	31.94	35.15	35.60	35.94	36.22	36.07	36.6(11) ${\hspace{0.25em}}^c$	36.76
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	7/2 -	68.28	50.09	53.88	54.23	54.72	54.96	54.84	55.2(11) ${\hspace{0.25em}}^c$	55.63
$2p^{2}3p{\hspace{0.25em}}^4{P}^o$	1/2 -	1.375	−72.31	−58.48	−56.97	−55.58	−54.54	−54.91	−50.78(17) ${\hspace{0.25em}}^c$	−52.25
$2p^{2}3p{\hspace{0.25em}}^4{P}^o$	3/2 -	70.89	39.73	45.91	46.35	47.14	47.41	47.29	46.2(15) ${\hspace{0.25em}}^c$	51.04
$2p^{2}3p{\hspace{0.25em}}^4{P}^o$	5/2 -	51.41	25.31	30.48	30.95	31.54	31.90	31.76	31.93(86) ${\hspace{0.25em}}^c$	33.16
$2p^{2}3p{\hspace{0.25em}}^4{S}^o$	3/2 -	43.68	23.31	9.971	11.23	12.69	13.18	13.07
$2p^{2}3p{\hspace{0.25em}}^2{D}^o$	3/2 -	58.23	51.77	72.10	72.85	72.41	71.63	71.62
$2p^{2}3p{\hspace{0.25em}}^2{D}^o$	5/2 -	82.04	66.07	69.31	69.26	69.69	69.89	69.80
$2p^{2}3p{\hspace{0.25em}}^2{P}^o$	1/2 -	122.7	151.1	145.5	145.9	145.4	146.2	146.3
$2p^{2}3p{\hspace{0.25em}}^2{P}^o$	3/2 -	74.44	47.74	53.10	53.20	53.82	53.97	53.85
$2p^{2}4p{\hspace{0.25em}}^2{S}^o$	1/2 -	72.28	−16.06	−0.08142	−1.692	0.2150	0.3925	−0.1555
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	1/2 -	31.76	74.09	66.03	65.53	64.49	64.11	64.24
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	3/2 -	28.99	20.20	21.64	21.36	21.47	21.56	21.45
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	5/2 -	39.05	22.71	25.59	25.26	25.56	25.68	25.53
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	7/2 -	67.53	49.21	52.90	52.80	53.31	53.45	53.34
$2p^{2}4p{\hspace{0.25em}}^4{P}^o$	1/2 -	4.462	−68.78	−55.68	−55.64	−54.24	−53.66	−54.07
$2p^{2}4p{\hspace{0.25em}}^4{P}^o$	3/2 -	73.67	42.53	48.15	46.96	47.72	47.34	47.20
$2p^{2}4p{\hspace{0.25em}}^4{P}^o$	5/2 -	57.41	31.38	36.42	36.50	37.14	37.35	37.22
$2p^{2}4p{\hspace{0.25em}}^2{D}^o$	3/2 -	55.21	72.13	69.78	68.92	68.67	67.47	67.55
$2p^{2}4p{\hspace{0.25em}}^2{D}^o$	5/2 -	83.69	68.58	72.20	72.37	72.90	73.00	72.92
$2p^{2}4p{\hspace{0.25em}}^4{S}^o$	3/2 -	45.89	1.977	11.55	13.77	15.04	16.13	15.90
$2p^{2}4p{\hspace{0.25em}}^2{P}^o$	1/2 -	138.5	171.0	168.5	171.0	171.1	171.8	172.1
$2p^{2}4p{\hspace{0.25em}}^2{P}^o$	3/2 -	77.82	53.14	58.39	57.88	58.51	57.91	57.78

^a Hirsch et al. [41], ^b Jennerich et al. [16], ^c Carette et al. [17] revisiting and reinterpreting the spectra of Jennerich et al. [16], ^d Jönsson et al. [18].

and

Table 5. Hyperfine interaction constants A (in MHz) for states of the $\{2s^{2}2p^{2}3s,2s2p^4,2s^{2}2p^{2}4s,2s^{2}2p^{2}3d\}$ even configurations in ${\hspace{0.25em}}^{14}$N from MR-SD RCI calculations as function of the increasing set of correlation orbitals.

State	J P	Set 1	Set 2	Set 3	Set 4	Set 5	Set 6	Set 7	Exp.	MCHF ${\hspace{0.25em}}^{\mathit{c}}$
$2p^{2}3s{\hspace{0.25em}}^{4}P$	1/2 +	71.65	20.48	53.27	76.00	80.54	81.98	80.51	112.3(13) ${\hspace{0.25em}}^{a,b}$	100.21
$2p^{2}3s{\hspace{0.25em}}^{4}P$	3/2 +	52.23	28.82	43.04	52.98	54.92	55.59	54.91	68.33(69) ${\hspace{0.25em}}^b$	62.46
$2p^{2}3s{\hspace{0.25em}}^{4}P$	5/2 +	116.9	99.51	110.9	118.8	120.2	120.7	120.2	129.52(84) ${\hspace{0.25em}}^b$	124.84
$2p^{2}3s{\hspace{0.25em}}^{2}P$	1/2 +	47.24	71.56	64.82	65.16	63.85	64.07	64.28
$2p^{2}3s{\hspace{0.25em}}^{2}P$	3/2 +	124.0	97.45	104.9	104.1	105.4	105.3	10.50
$2p^4{\hspace{0.25em}}^{4}P$	5/2 +	344.1	361.3	360.3	354.9	350.8	350.3	350.2
$2p^4{\hspace{0.25em}}^{4}P$	3/2 +	355.5	368.7	371.0	365.0	361.4	360.5	360.7
$2p^4{\hspace{0.25em}}^{4}P$	1/2 +	782.0	810.6	818.8	808.4	801.5	799.4	800.0
$2p^{2}3s{\hspace{0.25em}}^{2}D$	5/2 +	130.5	134.3	135.1	135.2	135.5	135.8	135.7
$2p^{2}3s{\hspace{0.25em}}^{2}D$	3/2 +	146.4	150.5	148.6	148.6	148.0	147.9	147.9
$2p^{2}4s{\hspace{0.25em}}^{4}P$	1/2 +	19.61	−47.67	−32.29	−37.49	−34.22	−34.08	−35.06
$2p^{2}4s{\hspace{0.25em}}^{4}P$	3/2 +	25.31	−4.749	2.476	0.4206	1.824	1.931	1.488
$2p^{2}4s{\hspace{0.25em}}^{4}P$	5/2 +	94.72	72.02	79.28	78.34	79.43	79.47	79.07
$2p^{2}4s{\hspace{0.25em}}^{2}P$	1/2 +	31.53	54.29	49.66	51.58	49.49	49.78	49.80
$2p^{2}4s{\hspace{0.25em}}^{2}P$	3/2 +	117.5	92.85	103.9	105.0	104.7	104.4	103.3
$2p^{2}3d{\hspace{0.25em}}^{2}P$	3/2 +	−1.712	−32.21	−30.62	−35.77	−31.49	−31.78	−31.90
$2p^{2}3d{\hspace{0.25em}}^{2}P$	1/2 +	−115.4	−93.35	−102.0	−102.5	−102.8	−102.6	−101.9
$2p^{2}3d{\hspace{0.25em}}^{4}F$	3/2 +	14.85	38.14	34.50	37.09	34.50	35.32	35.93
$2p^{2}3d{\hspace{0.25em}}^{4}F$	5/2 +	21.56	24.68	24.19	24.39	24.63	24.61	24.59
$2p^{2}3d{\hspace{0.25em}}^{4}F$	7/2 +	30.59	23.23	25.44	25.06	25.97	25.85	25.66
$2p^{2}3d{\hspace{0.25em}}^{2}F$	5/2 +	31.71	38.24	35.44	9.579	28.50	27.93	22.38
$2p^{2}3d{\hspace{0.25em}}^{4}P$	5/2 +	7.241	−24.46	−21.45	0.8877	−17.02	−16.59	−11.41
$2p^{2}3d{\hspace{0.25em}}^{4}P$	3/2 +	−5.061	−47.84	−43.43	−42.84	−41.73	−42.03	−42.24
$2p^{2}3d{\hspace{0.25em}}^{4}P$	1/2 +	−16.48	−88.26	−35.85	−6.957	−5.629	−6.556	−5.808
$2p^{2}3d{\hspace{0.25em}}^{2}F$	7/2 +	60.53	46.81	50.66	49.96	50.57	50.51	50.27
$2p^{2}3d{\hspace{0.25em}}^{4}D$	1/2 +	222.2	266.3	217.2	184.4	184.0	184.7	183.4
$2p^{2}3d{\hspace{0.25em}}^{4}D$	3/2 +	75.66	79.77	81.81	77.55	78.02	78.07	77.69
$2p^{2}3d{\hspace{0.25em}}^{4}D$	5/2 +	47.82	36.13	40.88	40.11	40.50	40.46	40.25
$2p^{2}3d{\hspace{0.25em}}^{4}D$	7/2 +	28.54	11.15	15.51	14.71	15.34	15.24	15.06
$2p^{2}3d{\hspace{0.25em}}^{2}D$	3/2 +	49.17	64.39	60.97	61.75	61.00	61.13	61.40
$2p^{2}3d{\hspace{0.25em}}^{2}D$	5/2 +	31.68	14.83	19.38	18.74	19.74	19.60	19.42

^a Jennerich et al. [16], ^b Carette et al. [17] revisiting and reinterpreting the spectra of Jennerich et al. [16], ^c Jönsson et al. [18].

as functions of the increasing orbital sets. They exhibit several different convergence patterns. The hyperfine interaction constants of some odd-parity states (e.g., $2p^3{\hspace{0.25em}}^4{S}_{3/2}^o$, $2p^{2}3p{\hspace{0.25em}}^2{S}_{1/2}^o$ and $2p^{2}4p{\hspace{0.25em}}^2{S}_{1/2}^o$) oscillate heavily as the orbital set is increased, and they are not converged even after seven layers of correlation orbitals. Other states, e.g., $2p^3{\hspace{0.25em}}^2{D}_{3/2,5/2}^o$ and $2p^3{\hspace{0.25em}}^2{P}_{1/2,3/2}^o$ are very stable and remain virtually unchanged as the orbital set is increased. In the case of even-parity states, the oscillations are not as pronounced, although there is a large change when going from orbital set 1 to orbital set 2. Worth noting are the large correlation effects for the $2p^{2}3s{\hspace{0.25em}}^4{P}_{1/2,3/2,5/2}$ states and the slow convergence with respect to the increasing orbital set.

In the same Table 4 and Table 5, the few experimental values available are also reported for comparison with the present calculations. For the odd parity, the experimental value of Hirsch et al. [41], obtained using a hydrogen maser technique, has an extraordinary accuracy, i.e., $A\left(2p^3{\hspace{0.25em}}^4{S}^o\right)=10.45092912\left(10\right)$ MHz. The corresponding error bars are not explicitly given in Table 4 for this specific level to save room in the table. For all other levels, the hyperfine constant values have been determined using saturation laser spectroscopy by Jennerich et al. [16]. As demonstrated by Carette et al. [17], the presence of crossover resonances is problematic and the original spectra of Jennerich et al. had to be revisited to reconcile theory with observation. As written in their work, while the strong hyperfine lines are relatively easy to identify, the weak components are usually not. Most of the weak hyperfine lines were reinterpreted as crossover signals, producing hyperfine constant values that completely differ from the original ones. The uncertainty in these saturation spectroscopy measurements in the near-infrared is much larger than the one mentioned above for the ground level [41].

4.2. Polarization Orbitals Merged with the Orbitals from Energy-Driven Calculations

To improve the convergence of the hyperfine interaction constants, the orbital basis should, based on the discussion in Section 3, include orbitals specially targeted for capturing the important spin- and orbital-polarization effects. In this work, following [14], we keep the spectroscopic orbitals from the first calculation of the odd-parity states frozen and optimize two s and two d orbitals on the weighted average of the targeted states based on CSF expansions formed by allowing single substitutions from the closed $1s$ subshell of the reference configurations. These orbitals and the corresponding CSFs capture most of the spin- and orbital-polarization effects of the $1s$ subshell. In the same way, we optimize two s and two d orbitals on the weighted average of the targeted states based on CSF expansions formed by allowing single substitutions from the closed $2s$ subshell of the reference configurations. These orbitals and the corresponding CSFs capture most of the spin- and orbital-polarization effects of the $2s$ subshell. Being separately optimized, the two sets of spin- and orbital-polarization orbitals are not orthogonal. Similar calculations of spin- and orbital-polarization orbitals were performed for the even states. The mean orbital radii of the spin- and orbital-polarization orbitals are reported at the bottom of Table 3.

Due to orthogonality restrictions, the separately optimized and optimally localized polarization orbitals cannot be directly added into the orbital sets from the previous energy-driven LBL calculations. To deal with the orthogonality issue, we use the rwfnrelabel program of Grasp2018 to relabel the orbitals in the $1s$ polarization set (i.e., to change their principal quantum numbers which, together with the orbital quantum numbers, serve as the orbital identifiers), so that they carry unique identifiers, and on the hierarchical orbital list they eventually appear after the orbitals from the energy-driven LBL calculation. In the same way, we use the rwfnrelabel program to relabel the orbitals in the $2s$ polarization set, so that they appear after the relabeled orbitals from the $1s$ polarization set. The relabeled polarization sets were added to, and orthogonalized against, the orbital sets from the energy-driven LBL calculation, forming final orthonormal orbital sets

$$\left\{\mathrm{set} i\right\}\cup \left\{1s \mathrm{polarization} \mathrm{set}\right\}\cup \left\{2s \mathrm{polarization} \mathrm{set}\right\}i=1,2,\dots ,7.$$

(14)

Then, RCI calculations were performed for the odd- and even-parity states, based on CSF expansions obtained by allowing SD substitutions from the orbitals in the enlarged MR set (Equations (12) and (13)) to the correlation orbital sets in Table 1 and Table 2 generated by the energy-driven LBL calculations. These expansions were augmented with CSFs obtained by allowing S substitutions from the closed $1s$ subshell of the configurations in the enlarged MR set to the correlation orbitals in the $1s$ polarization set, and with CSFs obtained by allowing S substitutions from the closed $2s$ subshell of the configurations in the enlarged MR set to the correlation orbitals in the $1s$ and $2s$ polarization sets. It should be noted that the computational overhead incurred by including polarization orbitals is completely negligible. This becomes evident by comparing the number of CSFs generated from the largest orbital set in the energy-driven LBL calculation with the number of CSFs generated in the same expansion, but augmented with the CSFs based on the polarization sets, and accounting for the spin and orbital polarization. This comparison is reported in

Table 6. Number of CSFs generated from the largest orbital set in the energy-driven LBL calculation, compared with the number of CSFs obtained in the same expansion, but augmented with the polarization sets (accounting for the spin and orbital polarization).

Expansion	Odd States	Even States
set 7	10,883,618	9,333,523
set 7 ∪ pol. sets	10,901,511	9,347,089

for the odd and even parities.

The hyperfine interaction constants from the RCI calculations with CSF expansions generated in the energy-driven LBL approach, and augmented with the CSFs based on the polarization sets, are shown in

Table 7. Hyperfine interaction constants A (in MHz) for states of the $\{2s^{2}2p^3,2s^{2}2p^{2}3p,2s^{2}2p^{2}4p\}$ odd configurations in ${\hspace{0.25em}}^{14}$N from MR-SD RCI calculations as functions of the increasing set of correlation orbitals. Separately optimized spin- and orbital-polarization orbitals for $1s$ and $2s$, respectively, have been merged with, and orthogonalized against, the ordinary energy-optimized orbitals. The TQ column holds results from calculations for which the MR set has been increased to capture part of the effects of the TQ substitutions. The NO column holds results from calculations that account for the effects of the TQ substitutions in the basis of natural orbitals.

State	J P	Set 1	Set 2	Set 3	Set 4	Set 5	Set 6	Set 7	TQ	TQ + NO	Exp.	MCHF ${\hspace{0.25em}}^{\mathit{d}}$
$2p^3{\hspace{0.25em}}^4{S}^o$	3/2 -	11.66	11.35	11.27	11.58	11.26	11.22	11.29	10.49	10.77	10.4509 ${\hspace{0.25em}}^a$	10.395
$2p^3{\hspace{0.25em}}^2{D}^o$	5/2 -	111.8	117.4	115.3	116.7	115.9	115.9	115.9	115.2	115.3
$2p^3{\hspace{0.25em}}^2{D}^o$	3/2 -	63.38	67.57	66.08	66.75	66.26	66.14	66.13	65.97	66.00
$2p^3{\hspace{0.25em}}^2{P}^o$	1/2 -	309.1	325.5	320.0	323.4	321.5	321.6	321.7	320.5	320.7
$2p^3{\hspace{0.25em}}^2{P}^o$	3/2 -	62.36	65.08	64.10	64.95	64.47	64.48	64.50	63.67	63.79
$2p^{2}3p{\hspace{0.25em}}^2{S}^o$	1/2 -	10.17	6.227	6.269	6.212	5.751	5.575	5.486	7.147	6.663
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	1/2 -	72.06	74.51	74.87	74.58	74.99	74.98	75.01	74.26	74.44	69.76(90) ${\hspace{0.25em}}^{b,c}$	74.15
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	3/2 -	31.51	31.21	31.35	31.28	31.28	31.29	31.25	31.60	31.57	30.3(15) ${\hspace{0.25em}}^c$	31.71
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	5/2 -	36.74	36.12	36.24	36.18	36.12	36.14	36.09	36.61	36.54	36.6(11) ${\hspace{0.25em}}^c$	36.76
$2p^{2}3p{\hspace{0.25em}}^4{D}^o$	7/2 -	55.27	54.74	54.92	54.95	54.71	54.91	54.87	55.39	55.28	55.2(11) ${\hspace{0.25em}}^c$	55.63
$2p^{2}3p{\hspace{0.25em}}^4{P}^o$	1/2 -	−50.54	−54.56	−54.65	−54.22	−54.70	−54.71	−54.80	−53.24	−53.60	−50.78(17) ${\hspace{0.25em}}^c$	−52.25
$2p^{2}3p{\hspace{0.25em}}^4{P}^o$	3/2 -	48.42	47.21	47.34	47.53	47.42	47.36	47.33	47.92	47.73	46.2(15) ${\hspace{0.25em}}^c$	51.04
$2p^{2}3p{\hspace{0.25em}}^4{P}^o$	5/2 -	32.63	31.60	31.74	31.95	31.86	31.83	31.80	32.38	32.22	31.93(86) ${\hspace{0.25em}}^c$	33.16
$2p^{2}3p{\hspace{0.25em}}^4{S}^o$	3/2 -	15.52	13.16	13.29	13.55	13.22	13.13	13.08	14.12	13.96
$2p^{2}3p{\hspace{0.25em}}^2{D}^o$	3/2 -	70.44	72.83	72.84	72.17	72.25	71.57	71.57	70.63	70.69
$2p^{2}3p{\hspace{0.25em}}^2{D}^o$	5/2 -	69.95	69.80	69.83	69.92	69.85	69.87	69.83	70.27	70.16
$2p^{2}3p{\hspace{0.25em}}^2{P}^o$	1/2 -	142.6	144.1	143.9	145.0	145.1	146.4	146.3	146.9	147.0
$2p^{2}3p{\hspace{0.25em}}^2{P}^o$	3/2 -	54.50	54.21	54.25	54.30	54.15	53.93	53.89	54.29	54.12
$2p^{2}4p{\hspace{0.25em}}^2{S}^o$	1/2 -	7.448	2.200	1.834	1.062	0.5278	0.02129	−0.1153	2.625	2.153
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	1/2 -	61.85	64.54	64.63	63.99	64.32	64.23	64.24	62.51	62.65
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	3/2 -	22.42	22.04	22.05	21.57	21.55	21.52	21.48	21.49	21.32
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	5/2 -	27.15	26.32	26.30	25.74	25.66	25.63	25.59	25.83	25.58
$2p^{2}4p{\hspace{0.25em}}^4{D}^o$	7/2 -	53.97	53.32	53.50	53.43	53.31	53.38	53.35	54.07	53.96
$2p^{2}4p{\hspace{0.25em}}^4{P}^o$	1/2 -	−48.99	−53.44	−53.62	−53.37	−53.83	−54.01	−54.11	−51.56	−51.84
$2p^{2}4p{\hspace{0.25em}}^4{P}^o$	3/2 -	49.34	47.89	47.98	47.76	47.70	47.18	47.18	47.83	47.73
$2p^{2}4p{\hspace{0.25em}}^4{P}^o$	5/2 -	37.96	36.79	36.95	37.34	37.27	37.20	37.16	38.41	38.42
$2p^{2}4p{\hspace{0.25em}}^2{D}^o$	3/2 -	66.12	69.31	69.68	68.40	68.59	67.48	67.54	65.52	65.65
$2p^{2}4p{\hspace{0.25em}}^2{D}^o$	5/2 -	71.69	72.37	72.91	72.95	73.01	72.94	72.93	73.27	73.18
$2p^{2}4p{\hspace{0.25em}}^4{S}^o$	3/2 -	17.73	15.21	15.37	16.04	15.70	16.00	15.89	18.17	18.01
$2p^{2}4p{\hspace{0.25em}}^2{P}^o$	1/2 -	159.2	166.2	168.3	170.4	170.9	172.0	172.1	171.1	171.2
$2p^{2}4p{\hspace{0.25em}}^2{P}^o$	3/2 -	58.17	59.13	59.44	58.78	58.71	57.80	57.79	57.95	57.84

^a Hirsch et al. [41], ^b Jennerich et al. [16], ^c Carette et al. [17] revisiting and reinterpreting the spectra of Jennerich et al. [16], ^d Jönsson et al. [18].

and

Table 8. Hyperfine interaction constants A (in MHz) for states of the $\{2s^{2}2p^{2}3s,2s2p^4,2s^{2}2p^{2}4s,2s^{2}2p^{2}3d\}$ even configurations in ${\hspace{0.25em}}^{14}$N from MR-SD RCI calculations as functions of the increasing set of correlation orbitals. Separately optimized spin- and orbital-polarization orbitals for $1s$ and $2s$, respectively, have been merged with, and orthogonalized against, the ordinary energy-optimized orbitals. The TQ column holds results from calculations for which the MR set has been increased to capture part of the effects of the TQ substitutions. The NO column holds results from calculations that account for the effects of the TQ substitutions in the basis of natural orbitals.

State	J P	Set 1	Set 2	Set 3	Set 4	Set 5	Set 6	Set 7	TQ	TQ + NO	Exp.	MCHF ${\hspace{0.25em}}^{\mathit{c}}$
$2p^{2}3s{\hspace{0.25em}}^{4}P$	1/2 +	32.66	37.44	52.53	78.15	79.37	81.29	80.87	94.71	97.87	112.3(13) ${\hspace{0.25em}}^{a,b}$	100.21
$2p^{2}3s{\hspace{0.25em}}^{4}P$	3/2 +	33.43	35.98	42.57	53.94	54.40	55.27	55.08	61.20	62.58	68.33(69) ${\hspace{0.25em}}^b$	62.46
$2p^{2}3s{\hspace{0.25em}}^{4}P$	5/2 +	102.7	105.7	110.6	119.6	119.8	120.5	120.2	125.2	126.3	129.52(84) ${\hspace{0.25em}}^b$	124.84
$2p^{2}3s{\hspace{0.25em}}^{2}P$	1/2 +	62.25	64.39	64.62	64.23	64.30	64.33	64.16	63.65	63.80
$2p^{2}3s{\hspace{0.25em}}^{2}P$	3/2 +	104.9	104.2	104.8	105.1	105.0	105.0	105.2	105.9	105.8
$2p^4{\hspace{0.25em}}^{4}P$	5/2 +	358.7	367.0	360.3	354.7	350.6	350.1	350.2	344.1	342.7
$2p^4{\hspace{0.25em}}^{4}P$	3/2 +	372.1	375.4	370.9	364.9	361.1	360.4	360.8	353.7	352.2
$2p^4{\hspace{0.25em}}^{4}P$	1/2 +	822.1	826.5	819.0	808.1	801.1	799.1	800.3	785.0	782.2
$2p^{2}3s{\hspace{0.25em}}^{2}D$	5/2 +	131.6	134.6	134.9	135.2	135.5	135.8	135.7	136.3	136.5
$2p^{2}3s{\hspace{0.25em}}^{2}D$	3/2 +	145.2	150.1	148.6	148.6	148.0	147.9	147.9	147.1	146.7
$2p^{2}4s{\hspace{0.25em}}^{4}P$	1/2 +	−23.62	−31.15	−32.82	−35.04	−35.37	−34.80	−34.70	−31.91	−31.76
$2p^{2}4s{\hspace{0.25em}}^{4}P$	3/2 +	4.536	2.300	2.091	1.540	1.315	1.600	1.656	2.896	3.023
$2p^{2}4s{\hspace{0.25em}}^{4}P$	5/2 +	78.43	78.30	79.10	79.27	78.99	79.20	79.07	80.39	80.45
$2p^{2}4s{\hspace{0.25em}}^{2}P$	1/2 +	44.66	47.70	49.49	50.73	49.91	50.01	49.69	48.06	47.51
$2p^{2}4s{\hspace{0.25em}}^{2}P$	3/2 +	97.52	99.82	103.6	106.1	104.3	104.1	103.4	103.8	102.4
$2p^{2}3d{\hspace{0.25em}}^{2}P$	3/2 +	−18.45	−25.77	−30.84	−34.71	−31.98	−32.09	−31.75	−30.13	−28.86
$2p^{2}3d{\hspace{0.25em}}^{2}P$	1/2 +	−98.12	−99.42	−101.9	−103.4	−102.4	−102.4	−102.0	−102.8	−102.1
$2p^{2}3d{\hspace{0.25em}}^{4}F$	3/2 +	28.17	32.78	34.66	36.22	35.40	35.57	35.81	35.41	35.43
$2p^{2}3d{\hspace{0.25em}}^{4}F$	5/2 +	23.08	23.91	24.17	24.29	24.67	24.63	24.59	24.63	24.68
$2p^{2}3d{\hspace{0.25em}}^{4}F$	7/2 +	24.87	25.12	25.34	25.35	25.83	25.76	25.71	26.20	26.28
$2p^{2}3d{\hspace{0.25em}}^{2}F$	5/2 +	36.01	36.50	35.47	9.842	28.58	27.95	22.38	19.45	20.54
$2p^{2}3d{\hspace{0.25em}}^{4}P$	5/2 +	−6.712	−19.03	−21.64	1.233	−17.38	−16.78	−11.41	−7.861	−8.905
$2p^{2}3d{\hspace{0.25em}}^{4}P$	3/2 +	−15.17	−42.66	−43.61	−41.87	−42.17	−42.31	−42.11	−40.81	−40.89
$2p^{2}3d{\hspace{0.25em}}^{4}P$	1/2 +	2.199	−81.80	−35.97	−4.722	−6.624	−7.182	−5.495	−0.8566	−1.526
$2p^{2}3d{\hspace{0.25em}}^{2}F$	7/2 +	50.74	50.38	50.57	50.49	50.32	50.35	50.34	50.97	50.96
$2p^{2}3d{\hspace{0.25em}}^{4}D$	1/2 +	189.6	266.1	217.3	182.9	184.6	185.1	183.2	179.7	180.4
$2p^{2}3d{\hspace{0.25em}}^{4}D$	3/2 +	62.48	83.24	81.77	77.84	77.88	77.98	77.73	77.72	77.81
$2p^{2}3d{\hspace{0.25em}}^{4}D$	5/2 +	35.54	40.21	40.77	40.67	40.23	40.30	40.25	40.89	40.88
$2p^{2}3d{\hspace{0.25em}}^{4}D$	7/2 +	16.49	15.39	15.36	15.37	15.03	15.05	15.15	15.73	15.70
$2p^{2}3d{\hspace{0.25em}}^{2}D$	3/2 +	59.89	60.98	61.16	61.20	61.26	61.29	61.31	60.75	60.70
$2p^{2}3d{\hspace{0.25em}}^{2}D$	5/2 +	19.79	19.04	19.22	19.39	19.44	19.41	19.41	20.18	20.13

^a Jennerich et al. [16], ^b Carette et al. [17] revisiting and reinterpreting the spectra of Jennerich et al. [16], ^c Jönsson et al. [18].

. When the spin- and orbital-polarization effects, based on separately optimized and optimally localized orbitals, are included, the convergence with respect to the increasing orbital set from the energy-driven LBL calculations becomes remarkably smooth.

The improvements in convergence of the hyperfine interaction constants for the $2p^3{\hspace{0.25em}}^4{S}_{3/2}^o,2p^{2}3p{\hspace{0.25em}}^2{S}_{1/2}^o,2p^{2}4p{\hspace{0.25em}}^2{S}_{1/2}^o$ odd states and the $2p^{2}3s{\hspace{0.25em}}^4{P}_{1/2},2p^{2}4s{\hspace{0.25em}}^4{P}_{1/2},2p^{2}3d{\hspace{0.25em}}^2{D}_{5/2}$ even states are graphically illustrated in Figure 1. For the calculations using polarization orbitals, only three or four layers (orbital sets up to 3 or 4) from the energy-driven calculations are needed to achieve converged hyperfine constants. The convergence pattern for the $2p^{2}3s{\hspace{0.25em}}^4{P}_{1/2}$ even state, however, differs from the other ones, and here, five or even six orbital layers from the energy-driven calculations are needed for convergence. As we will see later, this state is particularly sensitive to higher-order correlation effects as well as to the transformation to natural orbitals.

4.3. Higher-Order Correlation Effects and Transformation to Natural Orbitals

For accurate hyperfine interaction constants, higher-order electron correlation effects should be accounted for. This can be achieved by augmenting the CSFs from the previous RCI calculations with CSFs obtained by triple (T) and quadruple (Q) substitutions to increasing orbital sets. However, the orbital set cannot include more than a few layers, in order to keep the number of added CSFs at a manageable level. Alternatively, and this is the way we will follow, the CSFs from the previous RCI calculations can be augmented by CSFs obtained by SD substitutions from a larger MR set. For the odd-parity states, the enlarged MR set consisted of the 52 most energetically important configurations, with an accumulated squared weight of 99.5%. Allowing SD substitutions from these configurations to the $\{8s,6p,6d\}$ orbital set resulted in a final expansion of 18,565,748 CSFs. For the even-parity states, the enlarged MR set consisted of the 61 most energetically important configurations, again with an accumulated squared weight of 99.5%. Allowing SD substitutions from these configurations to the $\{8s,6p,6d\}$ orbital set resulted in an expansion of 16,431,197 CSFs. The hyperfine interaction constants from these calculations are collected in Table 7 and Table 8, in the columns with the TQ header. The influence of the higher-order correlation effects is rather small, with the exception of a few states. For the $2p^3{\hspace{0.25em}}^4{S}_{3/2}^o$ odd state, the hyperfine interaction constant is reduced by 7 %, bringing the value in better agreement with the experimental value. For the $2p^{2}3s{\hspace{0.25em}}^4{P}_{1/2,3/2}$ even states, the hyperfine interaction constants are increased by 17% and 11%, respectively. Incidentally, for the latter states the total correlation effects were largest. Similar observations of their sensitivity to higher-order correlation effects were made by Jönsson et al. [18], based on MCHF calculations.

In the LBL calculations, as discussed in Section 1, orbitals are kept frozen from a fully variational EOL calculation of the targeted states, based on the most important reference configurations, and are not allowed to relax in response to the introduced layers of correlation orbitals. More specifically, the $3s,4s,3p,4p,3d$ valence orbitals do not respond to the effects which result from the interaction with the $1s^{2}2s^{2}2p^2$ core (core–valence). The transformation to natural orbitals accounts for these effects, and in

Table 9. Mean orbital radii $\langle r\rangle$ (in $a_0$ units) for the spectroscopic orbitals after transformation to natural orbitals. The radii should be compared to those in Table 3.

Spectroscopic	Odd States			Even States
Orbitals	${\mathit{s}}_{\mathbf{1}/\mathbf{2}}$	${\mathit{p}}_{\mathbf{3}/\mathbf{2}}$	${\mathit{d}}_{\mathbf{5}/\mathbf{2}}$	${\mathit{s}}_{\mathbf{1}/\mathbf{2}}$	${\mathit{p}}_{\mathbf{3}/\mathbf{2}}$	${\mathit{d}}_{\mathbf{5}/\mathbf{2}}$
$n=1$	0.226	–	–	0.227	–	–
$n=2$	1.262	1.275	–	1.249	1.268	–
$n=3$	–	7.782	–	5.241	–	10.37
$n=4$	–	13.98	–	12.64	–	–

we provide orbital radii after the transformation.

For the odd states, the main effects are the expansion of the $3p$ orbital and the contraction of the $4p$ orbital. The effects on the hyperfine constants, as seen from Table 7, are small, the exception being the $2s^{2}2p^3{\hspace{0.25em}}^4{S}_{3/2}^o$ state, for which the constant increases by 2.6%. The hyperfine interaction constant for this state results mainly from large and canceling contributions from the spin polarization of the $1s$ and $2s$ closed subshells, and the effect of the orbital transformation is to change this balance slightly. For the even states, the main effects are the contraction of the $3s$ orbital and the expansion of the $4s$ orbital. The effects of the contraction can be seen for the $2s^{2}2p^{2}3s{\hspace{0.25em}}^4{P}_{1/2,3/2}$ states, for which the constants increase by 3.3% and 2.6%, respectively. The effects for the remaining states are small; see Table 8. The final values of the hyperfine interaction constants are in good agreement with both the extensive MCHF calculations of Jönsson et al. [18] and with the experimental values deduced by Carette et al. [17] from the spectral profiles published by Jennerich et al. [16], but revisiting their analysis on the basis of crossover signals. Using the presently available set of experimental data, some differences with respect to observation are, however, worth noting. The hyperfine interaction constants for the $2s^{2}2p^{2}3s{\hspace{0.25em}}^4{P}_{1/2,3/2}$ even states are strongly affected by electron correlation effects. Even using specifically targeted spin- and orbital-polarization orbitals, the values change by factors of 3 and 2, respectively, as the energy-driven orbital set is increased. These states are also sensitive to higher-order correlation effects and to transformation to natural orbitals. Both the results of the current calculations and of the MCHF calculations in Ref. [18] are 10% smaller than the respective experimental values.

5. Conclusions and Outlook

Correlation orbitals generated in the energy-driven LBL approach often yield oscillating convergence patterns for the calculated hyperfine interaction constants, which in turn requires large orbital sets in order to converge the constants. Separately optimized orbitals accounting for the most important correlation effects, i.e., spin and orbital polarization, orthogonalized against, and merged with, the orbitals from the energy-driven calculations lead to considerably improved convergence at a marginal increase in computational cost. In the LBL approach, the spectroscopic orbitals are determined in initial calculations including only configurations in the MR set. These orbitals are then kept frozen and are not allowed to relax in response to the core–valence correlation effects. This lack of variational freedom can, seemingly, be compensated for by the use of natural orbitals. We foresee that the use of separately optimized orbital sets, targeted for those correlation effects which are important in the calculation of a specific atomic property, but less important for the total energy, will be valuable in future studies of hyperfine interaction constants and also of transition rates. At present, separately optimized orbitals need to be orthogonalized against the orbitals from the energy-driven calculations, but with the use of the methods based on biorthonormal transformation, as proposed in [13,22], this can be circumvented. As far as the theory–observation comparison is concerned, the present study appeals for measurements of hyperfine structures involving more excited levels. For the levels arising from the $2p^{2}3p{\hspace{0.25em}}^4{D}^o$, $2p^{2}3p{\hspace{0.25em}}^4{P}^o$ and $2p^{2}3s{\hspace{0.25em}}^{4}P$ terms, the original spectra of Jennerich et al. [16] should be carefully reinvestigated, as suggested by Carette et al. [17], according to their new interpretation and assignments to refine the set of available experimental hyperfine constants and associated uncertainties. Perhaps a more definite approach would be to perform new high-resolution spectroscopy experiments that could avoid the confusion of real hyperfine components with undesirable crossover signals.