Enhancement of the NORAD-Atomic-Data Database in Plasma
Abstract
1. Introduction: NORAD-Atomic-Data
2. Atomic Processes and Parameters in NORAD-Atomic-Data
- (i)
- Energy levels
- (ii)
- Radiative atomic transition of excitation and de-excitation
- (iii)
- Photoionization (PI)
- (iv)
- Electron–ion recombination
- (v)
- Electron-impact excitation (EIE)
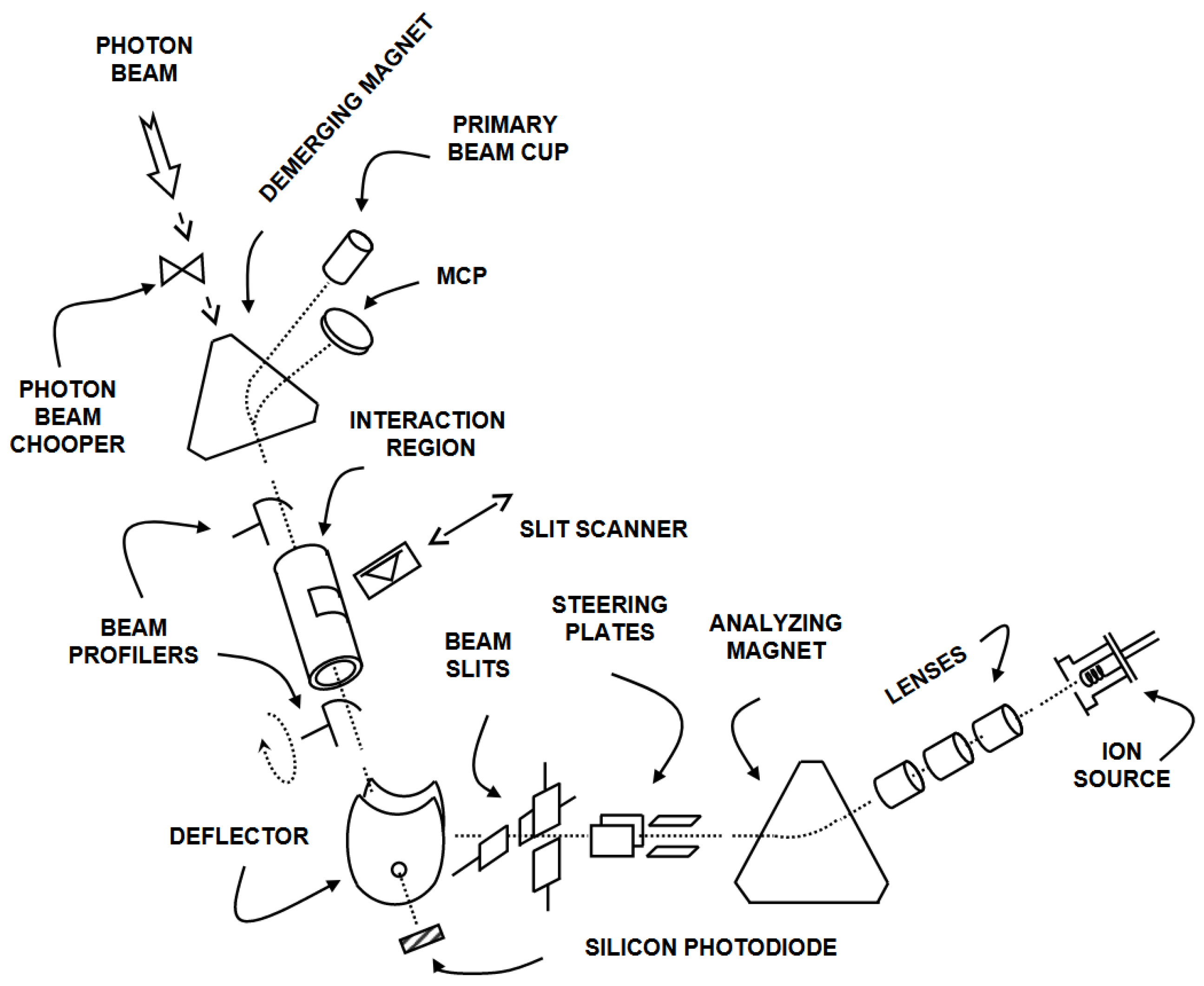
3. Merged Beam Technique at the Advanced Light Source at the Lawrence Berkeley National Laboratory
3.1. The Photon Beam
3.2. The Ion Beam
3.3. Past Reviews on Measured Photoionization of Ions
| Photoionization | Reference | ||
|---|---|---|---|
| Li II | ⟶ | Li III | S. W. J. Scully, et al., J. Phys. B: At. Mol. Opt. Phys., 39, 3957, 2006 [32] (https://iopscience.iop.org/article/10.1088/0953-4075/39/18/024, accessed on 13 December 2023) |
| B III | ⟶ | B IV | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 43, 135602, 2010 [40] (https://iopscience.iop.org/article/10.1088/0953-4075/43/13/135602/meta, accessed on 13 December 2023) |
| B II | ⟶ | B III | S. Schippers, et al., J. Phys. B: At. Mol. Opt. Phys., 36, 3371, 2003 [41] (https://iopscience.iop.org/article/10.1088/0953-4075/36/16/301/meta, accessed on 13 December 2023) |
| B II | ⟶ | B III | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 47, 135201, 2014 [42] (https://iopscience.iop.org/article/10.1088/0953-4075/47/13/135201/meta, accessed on 13 December 2023) |
| C IV | ⟶ | C V | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 42, 235602, 2009 [43] (https://iopscience.iop.org/article/10.1088/0953-4075/42/23/235602/meta, accessed on 13 December 2023) |
| C III | ⟶ | C IV | A. Müller, et al., Nucl. Instrum. Meth. B, 205, 301, 2003 [44] (https://www.sciencedirect.com/science/article/pii/S0168583X02019699, accessed on 13 December 2023) |
| C III | ⟶ | C IV | S. W. J. Scully, et al., J. Phys. B: At. Mol. Opt. Phys., 38, 1967, 2005 [45] (https://iopscience.iop.org/article/10.1088/0953-4075/38/12/011/meta, accessed on 13 December 2023) |
| C III | ⟶ | C IV | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 35, L137, 2002 [46] (https://dx.doi.org/10.1088/0953-4075/35/7/101, accessed on 13 December 2023) |
| C III, N IV, O V | ⟶ | C IV, N V, O VI | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 43, 225201, 2010 [28] (https://iopscience.iop.org/article/10.1088/0953-4075/43/22/225201/meta, accessed on 13 December 2023) |
| C II | ⟶ | C III | A. S. Schlachter, et al., J. Phys. B: At. Mol. Opt. Phys., 37, L103, 2004 [47] (https://dx.doi.org/10.1088/0953-4075/37/5/L03, accessed on 13 December 2023) |
| O II | ⟶ | O III | A. M. Covington, et al., Phys. Rev. Lett. 87, 243002, 2001 [29] (https://link.aps.org/doi/10.1103/PhysRevLett.87.243002, accessed on 13 December 2023) |
| O II | ⟶ | O III | A. Aguilar, et al., ApJS 146, 467, 2003 [48] (https://dx.doi.org/10.1086/368077, accessed on 13 December 2023) |
| Ne IV, F III | ⟶ | Ne V, F IV | A. Aguilar, et al., J. Phys. B: At. Mol. Opt. Phys., 38, 343, 2005 [49] (https://dx.doi.org/10.1088/0953-4075/38/4/003, accessed on 13 December 2023) |
| Ne III | ⟶ | Ne IV | S. N. Nahar, et al., Int. J. Mass Spectrom., 443, 61–69, 2019 [50] (https://www.sciencedirect.com/science/article/pii/S1387380618304056, accessed on 13 December 2023) |
| Ne II | ⟶ | Ne III | A. M. Covington, et al., Phys. Rev. A 66, 062710, 2002 [30] (https://link.aps.org/doi/10.1103/PhysRevA.66.062710, accessed on 13 December 2023) |
| Na− | ⟶ | Na+ | A. M. Covington, et al., J. Phys. B: At. Mol. Opt. Phys., 34, L735, 2001 [31] (https://dx.doi.org/10.1088/0953-4075/34/22/105, accessed on 13 December 2023) |
| Mg II, Al III | ⟶ | Mg III, Al IV | A. Aguilar, et al., Phys. Rev. A, 67, 012701, 2003 [51] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.67.012701, accessed on 13 December 2023) |
| Al II | ⟶ | Al III | C. E. Hudson, et al., J. Phys. B: At. Mol. Opt. Phys., 38, 2911, 2005 [52] (https://iopscience.iop.org/article/10.1088/0953-4075/38/16/005/meta, accessed on 13 December 2023) |
| CO+ | ⟶ | CO2+ | G. Hinojosa, et al., Phys. Rev. A, 66, 032718, 2002 [53] (https://link.aps.org/doi/10.1103/PhysRevA.66.032718, accessed on 13 December 2023) |
| CO+ | ⟶ | O+ | G. Hinojosa, et al., J. Phys. B: At. Mol. Opt. Phys., 38, 2701, 2005 [54] (https://dx.doi.org/10.1088/0953-4075/38/15/010, accessed on 13 December 2023) |
| P III, P IV | ⟶ | P IV, P V | L. Hernández, et al., J. Quant. Spectroc. Ra., 159, 80–86, 2015 [55] (https://www.sciencedirect.com/science/article/pii/S0022407315000953, accessed on 13 December 2023) |
| P II | ⟶ | P III | S. N. Nahar, et al., J. Quant. Spectroc. Ra., 187, 215–223, 2017 [56] (https://www.sciencedirect.com/science/article/pii/S002240731630365X?via%3Dihub, accessed on 13 December 2023) |
| Cl III | ⟶ | Cl IV | S. N. Nahar, et al., Atoms, 11, 28, 2023 [57] (https://www.mdpi.com/2218-2004/11/2/28, accessed on 13 December 2023) |
| Cl II | ⟶ | Cl III | E. M. Hernández, et al., J. Quant. Spectroc. Ra., 151, 217, 2015 [58] (https://www.sciencedirect.com/science/article/pii/S0022407314004191, accessed on 13 December 2023) |
| Ar VI | ⟶ | Ar VII | Jing Cheng Wang, et al., Phys. Rev. A, 75, 062712, 2007 [59] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.75.062712, accessed on 13 December 2023) |
| Ar II | ⟶ | Ar III | A. M. Covington, et al., Phys. Rev. A 84, 013413, 2011 [60] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.84.013413, accessed on 13 December 2023) |
| Ar II | ⟶ | Ar IV | A. Müller, et al., Phys. Rev. A, 103, L031101, 2021 [61] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.103.L031101, accessed on 13 December 2023) |
| K III | ⟶ | K IV | G. A. Alna’Washi, et al., Phys. Rev. A, 90, 023417, 2014 [62] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.90.023417, accessed on 13 December 2023) |
| Ca IV | ⟶ | Ca V | Ghassan A. Alna’washi, et al., Phys. Rev. A, 81, 053416, 2010 [63] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.81.053416, accessed on 13 December 2023) |
| Ca II | ⟶ | Ca III | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 50, 205001, 2017 [64] (https://iopscience.iop.org/article/10.1088/1361-6455/aa8ba8/pdf, accessed on 13 December 2023) |
| Sc III | ⟶ | Sc IV | S. Schippers, et al., Phys. Rev. Lett., 89, 193002, 2002 [65] (https://link.aps.org/doi/10.1103/PhysRevLett.89.193002, accessed on 13 December 2023) |
| Sc III | ⟶ | Sc IV | S. Schippers, et al., Phys. Rev. A, 67, 032702, 2003 [66] (https://link.aps.org/doi/10.1103/PhysRevA.67.032702, accessed on 13 December 2023) |
| Sc III | ⟶ | Sc IV | S. Schippers, et al., Nucl. Instrum. Meth. B, 205, 297, 2003 [67] (https://www.sciencedirect.com/science/article/pii/S0168583X02019651, accessed on 13 December 2023) |
| Ti IV | ⟶ | Ti V | S. Schippers, et al., J. Phys. B: At. Mol. Opt. Phys., 37, L209, 2004 [68] (https://dx.doi.org/10.1088/0953-4075/37/10/L02, accessed on 13 December 2023) |
| Fe IV, VI, VIII | ⟶ | Fe V, VII, IX | M. F. Gharaibeh, et al., Phys. Rev. A, 83, 043412, 2011 [69] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.83.043412, accessed on 13 December 2023) |
| Zn II | ⟶ | Zn III | G. Hinojosa, et al., Mon. Not. R. Astron. Soc., 470, 4048–4060, 2017 [70] (https://academic.oup.com/mnras/article/470/4/4048/3869632, accessed on 13 December 2023) |
| Se IV, Se VI | ⟶ | Se V, Se VII | D. A. Esteves, et al., J. Phys. B: At. Mol. Opt. Phys., 45, 115201, 2012 [71] (https://iopscience.iop.org/article/10.1088/0953-4075/45/11/115201/meta, accessed on 13 December 2023) |
| Se III | ⟶ | Se IV | D. A. Macaluso, et al., Phys. Rev. A, 92, 063424, 2015 [72] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.92.063424, accessed on 13 December 2023) |
| Se II | ⟶ | Se III | N. C. Sterling, et al., J. Phys. B: At. Mol. Opt. Phys., 44, 025701, 2011 [73] (https://iopscience.iop.org/article/10.1088/0953-4075/44/2/025701/meta, accessed on 13 December 2023) |
| Se II | ⟶ | Se III | D. A. Esteves, et al., Phys. Rev. A, 84, 013406, 2011 [23] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.84.013406, accessed on 13 December 2023) |
| Kr VI | ⟶ | Kr VII | M. Lu, et al., Phys. Rev. A. 74, 012703, 2006 [27] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.74.012703, accessed on 13 December 2023) |
| Kr IV | ⟶ | Kr V | M. Lu, et al., Phys. Rev. A, 74, 062701, 2006 [74] (https://link.aps.org/doi/10.1103/PhysRevA.74.062701, accessed on 13 December 2023) |
| Kr II | ⟶ | Kr III | G. Hinojosa, et al., Phys. Rev. A, 86, 063402, 2012 [75] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.86.063402, accessed on 13 December 2023) |
| Xe V–VII | ⟶ | Xe VI–VIII | A. Aguilar, et al., Phys. Rev. A, 73, 032717, 2006 [76] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.73.032717, accessed on 13 December 2023) |
| Xe IV | ⟶ | Xe V | E. D. Emmons, et al., Phys. Rev. A, 71, 042704, 2005 [77] (https://link.aps.org/doi/10.1103/PhysRevA.71.042704, accessed on 13 December 2023) |
| Xe VIII | ⟶ | Xe IX | A Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 47, 215202, 2014 [78] (https://iopscience.iop.org/article/10.1088/0953-4075/47/21/215202, accessed on 13 December 2023) |
| W VI | ⟶ | W VII | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 52, 195005, 2019 [79] (https://iopscience.iop.org/article/10.1088/1361-6455/ab39c8, accessed on 13 December 2023) |
| W V | ⟶ | W VI | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 50, 085007, 2017 [80] (https://iopscience.iop.org/article/10.1088/1361-6455/aa65df, accessed on 13 December 2023) |
| W III–IV | ⟶ | W IV–V | B. M. McLaughlin, et al., J. Phys. B: At. Mol. Opt. Phys., 49, 065201, 2016 [81] (https://iopscience.iop.org/article/10.1088/0953-4075/49/6/065201, accessed on 13 December 2023) |
| W II, IV, VI | ⟶ | W III, V, VII | A. Müller, et al., Phys. Scr., T144, 014052, 2011 [82] (https://iopscience.iop.org/article/10.1088/0031-8949/2011/T144/014052/meta, accessed on 13 December 2023) |
| W II | ⟶ | W III | A. Müller, et al., J. Phys. B: At. Mol. Opt. Phys., 48, 235203, 2015 [22] (https://iopscience.iop.org/article/10.1088/0953-4075/48/23/235203, accessed on 13 December 2023) |
| Ce III–Ce V | ⟶ | Ce IV–Ce VI | A. Müller, et al., Phys. Rev. Lett., 101, 133001, 2008 [83] (https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.101.133001, accessed on 13 December 2023) |
| Ce II–Ce X | ⟶ | Ce III–Ce XI | M. Habibi, et al., Phys. Rev. A, 80, 033407, 2009 [84] (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.80.033407, accessed on 13 December 2023) |
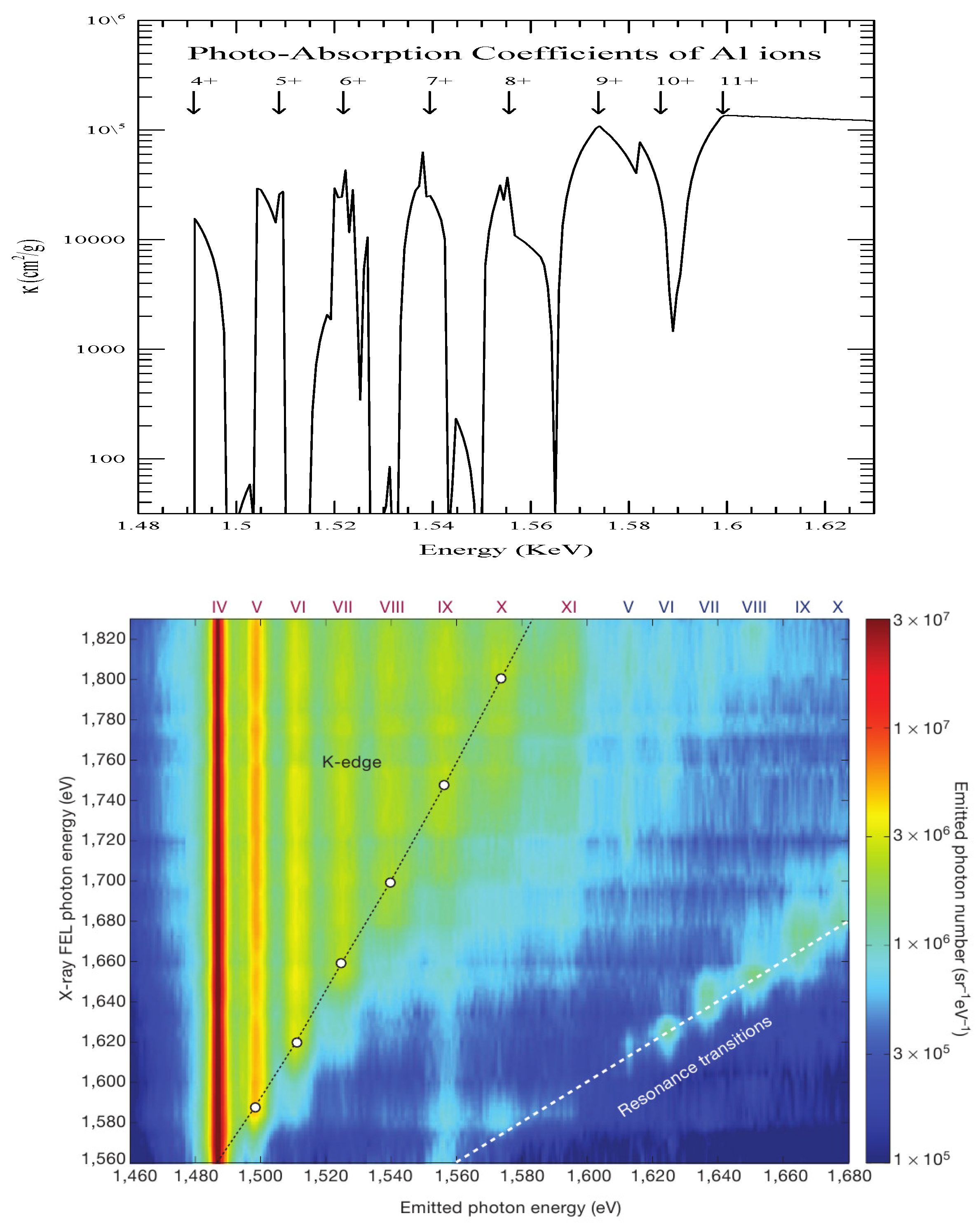
4. New Additions to NORAD-Atomic-Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms
| NORAD | Nahar OSU RADiative |
| LBNL | Lawrence Berkeley National Laboratory |
| ALS | Advanced Light Source |
| OP | Opacity Project |
| IP | Iron Project |
| SNN | Sultana N. Nahar |
| TOPbase | The Opacity Project Atomic Database |
| TIPbase | The Iron Project Atomic Database |
| SS | SUPERSTRUCTURE |
| BPRM | Relativistic Breit–Pauli R-matrix |
| NIST | National Institute of Standards and Technology |
| CC | Close Coupling Approximation |
| DR | Intermediate Recombination |
| AI | Autoionization |
| DES | Dielectronic Recombination |
| EIE | Electron-Impact Excitation |
| MBT | Merged Beam Technique |
| FWHM | Full Width Half Maximum |
| ECR | Electron Cyclotron Resonance |
| LCLS-XFEL | Linac Coherent-Light Source X-ray free-electron laser |
| JWST | James Webb Space Telescope |
| BESSY | Berlin Electron Storage Ring Society for Synchrotron Radiation (From German name) |
| PETRA | Positron-Electron Tandem Ring Accelerator |
References
- Nahar, S. Database NORAD-Atomic-Data for atomic processes in plasma. Atoms 2020, 8, 68. [Google Scholar] [CrossRef]
- Nahar, S.N. NaharOSURadiative(NORAD)-Atomic-Data. The Ohio State University. 2007. Available online: http://norad.astronomy.osu.edu/ (accessed on 7 August 2007).
- Seaton, M.J. Atomic data for opacity calculations. I. General description. J. Phys. B 1987, 20, 6363–6378. [Google Scholar] [CrossRef]
- The Opacity Project; The Opacity Project Team, Institute of Physics Publishing: London, UK, 1995; Volume 1.
- Hummer, D.G.; Berrington, K.A.; Eissner, W.; Pradhan, A.K.; Saraph, H.E.; Tully, J.A. Atomic data from the IRON Project. 1: Goals and methods. Astron. Astrophys. 1993, 279, 298–309. [Google Scholar]
- Cunto, W.; Mendoza, C.; Ochsenbein, F.; Zeippen, C.J. TOPbase at the CDS. Astron. Astrophys. 1993, 275, L5–L8. Available online: http://cdsweb.u-strasbg.fr/topbase/topbase.html (accessed on 27 September 1993).
- TIPbase. 2001. Available online: http://cdsweb.u-strasbg.fr/tipbase/home.html (accessed on 27 September 2020).
- Pradhan, A.K.; Nahar, S.N. Atomic Astrophysics and Spectroscopy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Berrington, K.A.; Burke, P.G.; Butler, K.; Seaton, M.J.; Storey, P.J.; Taylor, K.T.; Yan, Y. Atomic data for opacity calculations. II. Computational methods. J. Phys. B 1987, 20, 6379–6397. [Google Scholar] [CrossRef]
- Berrington, K.A.; Eissner, W.; Norrington, P.H. RMATRIX1: Belfast atomic R-matrix codes. Comput. Phys. Commun. 1995, 92, 290–420. [Google Scholar] [CrossRef]
- Nahar, S.N. Atomic Data from the Iron Project VII. Radiative dipole transition probabilities for Fe II. Astron. Astrophys. 1995, 293, 967–977. [Google Scholar]
- Nahar, S.N. Fine structure transitions in Fe XIV. New Astron. 2013, 21, 8–16. [Google Scholar] [CrossRef]
- Eissner, W.; Jones, M.; Nussbaumer, H. Techniques for the calculation of atomic structures and radiative data including relativistic corrections. Comput. Phys. Commun. 1974, 8, 270–306. [Google Scholar] [CrossRef]
- Nahar, S.N.; Eissner, W.; Chen, G.X.; Pradhan, A.K. Atomic data from the Iron Project-LIII. Relativistic allowed and forbidden transitionstic probabilities for Fe XVII. Astron. Astrophys. 2003, 408, 789–8016. [Google Scholar] [CrossRef]
- NIST. Available online: https://physics.nist.gov/PhysRefData/ASD/levels_form.html (accessed on 1 January 1996).
- Nahar, S.N.; Pradhan, A.K. Unified Treatment of Electron-Ion Recombination in the Close Coupling Approximation. Phys. Rev. A 1994, 49, 1816. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.L.; Nahar, S.N.; Pradhan, A.K. Close coupling R-matrix calculations for electron-ion recombination cross sections. J. Phys. B 1999, 32, 1459–1479. [Google Scholar] [CrossRef]
- Nahar, S.N.; Pradhan, A.K. Electron-ion recombination in the close coupling approximation. Phys. Rev. Lett. 1992, 68, 1488–1491. [Google Scholar] [CrossRef] [PubMed]
- Bell, R.H.; Seaton, M.J. Dielectronic recombination: I. General theory. J. Phys. B 1985, 18, 1589–1629. [Google Scholar] [CrossRef]
- Phaneuf, R.A.; Havener, C.C.; Dunn, G.H.; Müller, A. Merged-beams experiments in atomic and molecular physics. Rep. Prog. Phys. 1999, 62, 1143. [Google Scholar] [CrossRef]
- Margaritondo, G. Synchrotron light: A success story over six decades. Riv. Nuovo Cimento 2017, 40, 411–471. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Hellhund, J.; Holste, K.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Ballance, C.P.; McLaughlin, B.M. Single-photon single ionization of W+ ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 235203. [Google Scholar] [CrossRef]
- Esteves, D.A.; Bilodeau, R.C.; Sterling, N.C.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Red, E.C.; Aguilar, A. Absolute high-resolution Se+ photoionization cross-section measurements with Rydberg-series analysis. Phys. Rev. A 2011, 84, 013406. [Google Scholar] [CrossRef]
- Domke, M.; Schulz, K.; Remmers, G.; Kaindl, G.; Wintgen, D. High-resolution study of 1 P0 double-excitation states in helium. Phys. Rev. A 1996, 53, 1424–1438. [Google Scholar] [CrossRef]
- King, G.C.; Tronc, M.; Read, F.H.; Bradford, R.C. An investigation of the structure near the L2,3 edges of argon, the M4,5 edges of kryton and the N4,5 edges of xenon, using electron impact with high resolution. J. Phys. B At. Mol. Opt. 1977, 10, 2479–2495. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; Version 5.10, Online; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [CrossRef]
- Lu, M.; Gharaibeh, M.F.; Alna’washi, G.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Levenson, E.; Schlachter, A.S.; Müller, A.; Schippers, S.; Jacobi, J.; et al. Photoionization and electron-impact ionization of Kr5+. Phys. Rev. A 2006, 74, 012703. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Bräuning, H.; Schlachter, A.S.; Lu, M.; McLaughlin, B.M. State-resolved valence shell photoionization of Be-like ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 225201. [Google Scholar] [CrossRef][Green Version]
- Covington, A.M.; Aguilar, A.; Covington, I.R.; Gharaibeh, M.; Shirley, C.A.; Phaneuf, R.A.; Alvarez, I.; Cisneros, C.; Hinojosa, G.; Bozek, J.D.; et al. Photoionization of Metastable O+ Ions: Experiment and Theory. Phys. Rev. Lett. 2001, 87, 243002. [Google Scholar] [CrossRef] [PubMed]
- Covington, A.M.; Aguilar, A.; Covington, I.R.; Gharaibeh, M.F.; Hinojosa, G.; Shirley, C.A.; Phaneuf, R.A.; Álvarez, I.; Cisneros, C.; Dominguez-Lopez, I.; et al. Photoionization of Ne+ using synchrotron radiation. Phys. Rev. A 2002, 66, 062710. [Google Scholar] [CrossRef]
- Covington, A.M.; Aguilar, A.; Davis, V.T.; Alvarez, I.; Bryant, H.C.; Cisneros, C.; Halka, M.; Hanstorp, D.; Hinojosa, G.; Schlachter, A.S.; et al. Correlated processes in inner-shell photodetachment of the Na-ion. J. Phys. B At. Mol. Opt. Phys. 2001, 34, L735. [Google Scholar] [CrossRef]
- Scully, S.W.J.; Alvarez, I.; Cisneros, C.; Emmons, E.D.; Gharaibeh, M.F.; Leitner, D.; Lubell, M.S.; Müller, A.; Phaneuf, R.A.; Püttner, R.; et al. Doubly excited resonances in the photoionization spectrum of Li +: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3957. [Google Scholar] [CrossRef]
- Schmidt, V. Photoionization of atoms using synchrotron radiation. Rep. Prog. Phys. 1992, 55, 1483. [Google Scholar] [CrossRef]
- Sonntag, B.; Zimmermann, P. XUV spectroscopy of metal atoms. Rep. Prog. Phys. 1992, 55, 911. [Google Scholar] [CrossRef]
- West, J.B. Photoionization of atomic ions. J. Phys. B At. Mol. Opt. 2001, 34, R45. [Google Scholar] [CrossRef]
- Lyon, I.C.; Peart, B.; West, J.B.; Dolder, K. Measurements of absolute cross sections for the photoionisation of Ba+ ions. J. Phys. B At. Mol. Opt. 1986, 19, 4137. [Google Scholar] [CrossRef]
- Kjeldsen, H. Photoionization cross sections of atomic ions from merged-beam experiments. J. Phys. B At. Mol. Opt. 2006, 39, R325. [Google Scholar] [CrossRef]
- Martins, M.; Godehusen, K.; Richter, T.; Wernet, P.; Zimmermann, P. Open shells and multi-electron interactions: Core level photoionization of the 3d metal atoms. J. Phys. B At. Mol. Opt. 2006, 39, R79. [Google Scholar] [CrossRef]
- Schippers, S.; Müller, A. Photoionization of Astrophysically Relevant Atomic Ions at PIPE. Atoms 2020, 8, 45. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Cisneros, C.; Gharaibeh, M.F.; Schlachter, A.S.; McLaughlin, B.M. K-shell photoionization of ground-state Li-like boron ions [B2+]: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 135602. [Google Scholar] [CrossRef]
- Schippers, S.; Müller, A.; McLaughlin, B.M.; Aguilar, A.; Cisneros, C.; Emmons, E.D.; Gharaibeh, M.F.; Phaneuf, R.A. Photoionization studies of the B+ valence shell: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 3371. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Cisneros, C.; Gharaibeh, M.F.; Schlachter, A.S.; McLaughlin, B.M. K-shell photoionization of Be-like boron (B+) ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 135201. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Covington, A.M.; Álvarez, I.; Cisneros, C.; Emmons, E.D.; Gharaibeh, M.F.; et al. K-shell photoionization of ground-state Li-like carbon ions [C3+]: Experiment, theory and comparison with time-reversed photorecombination. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 235602. [Google Scholar] [CrossRef]
- Müller, A.; Phaneuf, R.A.; Aguilar, A.; Gharaibeh, M.F.; Schlachter, A.S.; Álvarez, I.; Cisneros, C.; Hinojosa, G.; McLaughlin, B.M. Photoionization of C2+ ions. Nucl. Instruments Methods Phys. Res. Sect. Beam Interact. Mater. Atoms. 2003, 205, 301–305. [Google Scholar] [CrossRef]
- Scully, S.W.J.; Aguilar, A.; Emmons, E.D.; Phaneuf, R.A.; Halka, M.; Leitner, D.; Levin, J.C.; Lubell, M.S.; Püttner, R.; Schlachter, A.S.; et al. K-shell photoionization of Be-like carbon ions: Experiment and theory for C2+. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 1967. [Google Scholar] [CrossRef]
- Müller, A.; Phaneuf, R.A.; Aguilar, A.; Gharaibeh, M.F.; Schlachter, A.S.; Alvarez, I.; Cisneros, C.; Hinojosa, G.; McLaughlin, B.M. Photoionization of C2+ ions: Time-reversed recombination of C3+ with electrons. J. Phys. B At. Mol. Opt. Phys. 2002, 35, L137. [Google Scholar] [CrossRef]
- Schlachter, A.S.; Sant’Anna, M.M.; Covington, A.M.; Aguilar, A.; Gharaibeh, M.F.; Emmons, E.D.; Scully, S.W.J.; Phaneuf, R.A.; Hinojosa, G.; Álvarez, I.; et al. Lifetime of a K-shell vacancy in atomic carbon created by 1s → 2p photoexcitation of C+. J. Phys. B At. Mol. Opt. Phys. 2004, 37, L103. [Google Scholar] [CrossRef]
- Aguilar, A.; Covington, A.M.; Hinojosa, G.; Phaneuf, R.A.; Álvarez, I.; Cisneros, C.; Bozek, J.D.; Dominguez, I.; Sant’Anna, M.M.; Schlachter, A.S.; et al. Absolute Photoionization Cross Section Measurements of O II Ions from 29.7 to 46.2 eV. ApJS 2003, 146, 467. [Google Scholar] [CrossRef]
- Aguilar, A.; Emmons, E.D.; Gharaibeh, M.F.; Covington, A.M.; Bozek, J.D.; Ackerman, G.; Canton, S.; Rude, B.; Schlachter, A.S.; Hinojosa, G.; et al. Photoionization of ions of the nitrogen isoelectronic sequence: Experiment and theory for F2+ and 3+. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 343. [Google Scholar] [CrossRef]
- Nahar, S.N.; Covington, A.M.; Kilcoyne, D.; Davis, V.T.; Thompson, J.F.; Hernández, E.M.; Antillón, A.; Juárez, A.M.; Morales-Mori, A.; Hinojosa, G. Single-photon photoionization of oxygen-like Ne III. Int. J. Mass Spectrom. 2019, 443, 61–69. [Google Scholar] [CrossRef]
- Aguilar, A.; West, J.B.; Phaneuf, R.A.; Brooks, R.L.; Folkmann, F.; Kjeldsen, H.; Bozek, J.D.; Schlachter, A.S.; Cisneros, C. Photoionization of isoelectronic ions: Mg+ and Al2+. Phys. Rev. A 2003, 67, 012701. [Google Scholar]
- Hudson, C.E.; West, J.B.; Bell, K.L.; Aguilar, A.; Phaneuf, R.A.; Folkmann, F.; Kjeldsen, H.; Bozek, J.; Schlachter, A.S.; Cisneros, C. A theoretical and experimental study of the photoionization of AlII. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2911. [Google Scholar]
- Hinojosa, G.; Covington, A.M.; Phaneuf, R.A.; Sant’Anna, M.M.; Hernez, R.; Covington, I.R.; Domínguez, I.; Bozek, J.D.; Schlachter, A.S.; Álvarez, I.; et al. Formation of long-lived CO2+ via photoionization of CO+. Phys. Rev. A 2002, 66, 032718. [Google Scholar] [CrossRef]
- Hinojosa, G.; Sant’Anna, M.M.; Covington, A.M.; Phaneuf, R.A.; Covington, I.R.; Domínguez, I.; Schlachter, A.S.; Alvarez, I.; Cisneros, C. Photofragmentation of ionic carbon monoxide. J. Phys. B At. Mol. Opt. Phys. 2005, 38, 2701. [Google Scholar] [CrossRef]
- Hernández, L.; Covington, A.M.; Hernández, E.M.; Antillón, A.; Morales-Mori, A.; Chartkunch, K.; Aguilar, A.; Hinojosa, G. Single photoionization of aluminum-like P2+ and magnesium-like P3+. J. Quant. Spectrosc. Radiat. Transf. 2015, 159, 80–86. [Google Scholar] [CrossRef]
- Nahar, S.N.; Hernández, E.M.; Hernández, L.; Antillon, A.; Morales-Mori, A.; González, O.; Covington, A.M.; Chartkunch, K.C.; Hanstorp, D.; Juárez, A.M.; et al. Photoionization of P+: Experiment and theory. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 215–223. [Google Scholar] [CrossRef]
- Nahar, S.N.; Hernández, E.M.; Kilcoyne, D.; Antillón, A.; Covington, A.M.; González-Magaña, O.; Hernández, L.; Davis, V.; Calabrese, D.; Morales-Mori, A.; et al. Experimental and Theoretical Study of Photoionization of Cl III. Atoms 2023, 11, 28. [Google Scholar] [CrossRef]
- Hernández, E.M.; Juárez, A.M.; Kilcoyne, A.L.D.; Aguilar, A.; Hernández, L.; Antillón, A.; Macaluso, D.; Morales-Mori, A.; González-Magaña, O.; Hanstorp, D.; et al. Absolute measurements of chlorine Cl+ cation single photoionization cross section. J. Quant. Spectrosc. Radiat. Transf. 2015, 151, 217–223. [Google Scholar] [CrossRef]
- Wang, J.C.; Lu, M.; Esteves, D.; Habibi, M.; Alna’washi, G.; Phaneuf, R.A.; Kilcoyne, A.L.D. Photoionization and electron-impact ionization of Ar5+. Phys. Rev. A 2007, 75, 062712. [Google Scholar]
- Covington, A.M.; Aguilar, A.; Covington, I.R.; Hinojosa, G.; Shirley, C.A.; Phaneuf, R.A.; Álvarez, I.; Cisneros, C.; Dominguez-Lopez, I.; Sant’Anna, M.M.; et al. Valence-shell photoionization of chlorinelike Ar+ ions. Phys. Rev. A 2011, 84, 013413. [Google Scholar] [CrossRef]
- Müller, A.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Holste, K.; Schippers, S.; Kheifets, A.S. Direct double ionization of the Ar+ M shell by a single photon. Phys. Rev. A 2021, 103, L031101. [Google Scholar] [CrossRef]
- Alna’Washi, G.A.; Lu, M.; Habibi, M.; Esteves-Macaluso, D.; Wang, J.C.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Cisneros, C.; McLaughlin, B.M. Valence-shell single photoionization of chlorine-like K2+ ions: Experiment and theory. Phys. Rev. A 2014, 90, 023417. [Google Scholar] [CrossRef]
- Alna’washi, G.A.; Lu, M.; Habibi, M.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Schlachter, A.S.; Cisneros, C.; McLaughlin, B.M. Valence-shell photoionization of the chlorinelike Ca3+ ion. Phys. Rev. A 2010, 81, 053416. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Covington, A.M.; Aguilar, A.; Hinojosa, G.; Bozek, J.; Sant’Anna, M.M.; Schlachter, A.S.; Cisneros, C.; et al. Photoionisation of Ca+ ions in the valence-energy region 20–56 eV: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 205001. [Google Scholar] [CrossRef]
- Schippers, S.; Müller, A.; Ricz, S.; Bannister, M.E.; Dunn, G.H.; Bozek, J.; Schlachter, A.S.; Hinojosa, G.; Cisneros, C.; Aguilar, A.; et al. Experimental Link of Photoionization of Sc2+ to Photorecombination of Sc3+: An Application of Detailed Balance in a Unique Atomic System. Phys. Rev. Lett. 2002, 89, 193002. [Google Scholar] [CrossRef] [PubMed]
- Schippers, S.; Müller, A.; Ricz, S.; Bannister, M.E.; Dunn, G.H.; Schlachter, A.S.; Hinojosa, G.; Cisneros, C.; Aguilar, A.; Covington, A.M.; et al. Photoionization of Sc2+ Ions by Synchrotron Radiation: Measurements and Absolute Cross Sections in the Photon Energy Range 23–68 eV. Phys. Rev. A 2003, 67, 032702. [Google Scholar] [CrossRef]
- Schippers, S.; Müller, A.; Ricz, S.; Bannister, M.E.; Dunn, G.H.; Bozek, J.; Schlachter, A.S.; Hinojosa, G.; Cisneros, C.; Aguilar, A.; et al. Photoionization of Sc2+: Experimental Link with Photorecombination of Sc3+ by Application of Detailed Balance. Nucl. Instrum. Methods B 2003, 205, 297–300. [Google Scholar] [CrossRef]
- Schippers, S.; Müller, A.; Phaneuf, R.A.; van Zoest, T.; Álvarez, I.; Cisneros, C.; Emmons, E.D.; Gharaibeh, M.F.; Hinojosa, G.; Schlachter, A.S.; et al. Threshold truncation of a ‘giant’ dipole resonance in photoionization of Ti3+. J. Phys. B At. Mol. Opt. Phys. 2004, 37, L209–L216. [Google Scholar] [CrossRef]
- Gharaibeh, M.F.; Aguilar, A.; Covington, A.M.; Emmons, E.D.; Scully, S.W.J.; Phaneuf, R.A.; Müller, A.; Bozek, J.D.; Kilcoyne, A.L.D.; Schlachter, A.S.; et al. Photoionization measurements for the iron isonuclear sequence Fe3+, Fe5+, and Fe7+. Phys. Rev. A 2011, 83, 043412. [Google Scholar] [CrossRef]
- Hinojosa, G.; Davis, V.T.; Covington, A.M.; Thompson, J.S.; Kilcoyne, A.L.D.; Antillón, A.; Hernández, E.M.; Calabrese, D.; Morales-Mori, A.; Juárez, A.M.; et al. Single photoionization of the Zn ii ion in the photon energy range 17.5–90.0 eV: Experiment and theory. Mon. Not. R. Astron. Soc. 2017, 470, 4048–4060. [Google Scholar] [CrossRef]
- Esteves, D.A.; Aguilar, A.; Bilodeau, R.C.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Red, E.C.; Sterling, N.C. Absolute single photoionization cross-section measurements of Se3+ and Se5+. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 115201. [Google Scholar] [CrossRef]
- Macaluso, D.A.; Aguilar, A.; Kilcoyne, A.L.D.; Red, E.C.; Bilodeau, R.C.; Phaneuf, R.A.; Sterling, N.C.; McLaughlin, B.M. Absolute single-photoionization cross sections of Se2+: Experiment and theory. Phys. Rev. A 2015, 92, 063424. [Google Scholar] [CrossRef]
- Sterling, N.C.; Esteves, D.A.; Bilodeau, R.C.; Kilcoyne, A.L.D.; Red, E.C.; Phaneuf, R.A.; Aguilar, A. Experimental photoionization cross-section measurements in the ground and metastable state threshold region of Se+. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 025701. [Google Scholar] [CrossRef]
- Lu, M.; Gharaibeh, M.F.; Alna’washi, G.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Levenson, E.; Schlachter, A.S.; Cisneros, C.; Hinojosa, G. Photoionization and electron-impact ionization of Kr3+. Phys. Rev. A 2006, 74, 012701. [Google Scholar]
- Hinojosa, G.; Covington, A.M.; Alna-Washi, G.A.; Lu, M.; Phaneuf, R.A.; Sant-Anna, M.M.; Cisneros, C.; Alvarez, I.; Aguilar, A.; Kilcoyne, A.L.D.; et al. Valence-shell single photoionization of Kr+ ions: Experiment and theory. Phys. Rev. A 2012, 86, 063402. [Google Scholar] [CrossRef]
- Aguilar, A.; Gillaspy, J.D.; Gribakin, G.F.; Phaneuf, R.A.; Gharaibeh, M.F.; Kozlov, M.G.; Bozek, J.D.; Kilcoyne, A.L.D. Absolute photoionization cross sections for Xe4+, Xe5+, and Xe6+ near 13.5 nm: Experiment and theory. Phys. Rev. A 2006, 73, 032717. [Google Scholar] [CrossRef]
- Emmons, E.D.; Aguilar, A.; Gharaibeh, M.F.; Scully, S.W.J.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Schlachter, A.S.; Álvarez, I.; Cisneros, C.; Hinojosa, G. Photoionization and electron-impact ionization of Xe3+. Phys. Rev. A 2005, 71, 042704. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Esteves-Macaluso, D.; Habibi, M.; Aguilar, A.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Ballance, C.P.; McLaughlin, B.M. Valence-shell photoionization of Ag-like Xe7+ ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 215202. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Hellhund, J.; Kilcoyne, A.L.D.; Phaneuf, R.A.; McLaughlin, B.M. Photoionization of tungsten ions: Experiment and theory for W5+. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 195005. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Hellhund, J.; Kilcoyne, A.L.D.; Phaneuf, R.A.; McLaughlin, B.M. Photoionization of tungsten ions: Experiment and theory for W4+. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 085007. [Google Scholar] [CrossRef]
- McLaughlin, B.M.; Ballance, C.P.; Schippers, S.; Hellhund, J.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Müller, A. Photoionization of tungsten ions: Experiment and theory for w2+ and w3+. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 065201. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Kilcoyne, A.L.D.; Esteves, D. Photoionization of tungsten ions with synchrotron radiation. Phys. Scr. 2011, 2011, 014052. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Habibi, M.; Esteves, D.; Wang, J.C.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Aguilar, A.; Dunsch, L. Significant redistribution of Ce 4d oscillator strength observed in photoionization of endohedral Ce@C+82 ions. Phys. Rev. Lett. 2008, 101, 133001. [Google Scholar] [CrossRef] [PubMed]
- Habibi, M.; Esteves, D.A.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Aguilar, A.; Cisneros, C. Photoionization cross sections for ions of the cerium isonuclear sequence. Phys. Rev. A 2009, 80, 033407. [Google Scholar] [CrossRef]
- Pradhan, A.K.; Nahar, S.N.; Montenegro, M.; Yu, Y.; Hang, H.L.; Sur, C.; Mrozik, M.; Pitzer, R. Resonant X-Ray Enhancement of the Auger Effect in High-Z atoms, molecules, and Nanoparticles: Biomedical Applications. J. Phys. Chem. A 2009, 113, 12356–12363. [Google Scholar] [CrossRef] [PubMed]
- Vinko, S.M.; Ciricosta, O.; Cho, B.I.; Engelhorn, K.; Chung, H.-K.; Brown, C.R.D.; Burian, T.; Chalupský, J.; Falcone, R.W.; Graves, C.; et al. Creation and diagnosis of a solid-density plasma with an X-ray free-electron laser. Nature 2012, 482, 59–62. [Google Scholar] [CrossRef] [PubMed]
- Nahar, S.N.; Pradhan, A.K. Kα resonance fluorescence in Al, Ti, Cu and potential applications for X-ray sources. J. Quant. Spectrosc. Radiat. Transf. 2015, 155, 32–48. [Google Scholar] [CrossRef]
- Nahar, S.N.; Shafique, B. Spectra of phosphorus ions for astrophysical modeling: PI–PXV. Can. J. Phys. 2024; in press. [Google Scholar] [CrossRef]
- Nahar, S.N. Theoretical spectra of lanthanides for kilonovae events: Ho I-III, Er I-IV, Tm I-V, Yb I-VI, Lu I-VII. Atoms, 2024; in press. [Google Scholar]
- Nahar, S.N.; Shafique, B. Collisional- and photo-excitations of Ca IV including strong 3.2 μm emission line. Eur. Phys. J. D 2023, 77, 45. [Google Scholar] [CrossRef]
- Ankita, S.; Tauheed, A. Revised and extended analysis of the third spectrum of silver: Ag III. J. Quant. Spectros. Rad. Transf. 2018, 217, 130–154. [Google Scholar] [CrossRef]
- Ankita, S.; Tauheed, A. Spectral analysis of triply ionized silver (Ag IV). J. Quant. Spectros. Rad. Transf. 2020, 254, 107193. [Google Scholar] [CrossRef]
- Tauheed, A.; Rashid, A. Energy structure and radiative parameter calculations in the Re-like Pt IV, Au V and Hg VI spectra and preliminary line identifications in Hg VI. J. Quant. Spectrosc. Radiat. Transf. 2021, 261, 107435. [Google Scholar] [CrossRef]
- Arya, N.K.; Tauheed, A. Energy levels, wavelengths and radiative rates for transitions in Hg-like Bismuth. J. Quant. Spectros. Rad. Transf. 2022, 292, 108353. [Google Scholar] [CrossRef]
- Rashid, A.; Tauheed, A. Revised analysis of doubly ionized mercury: Hg III-3. J. Quant. Spectrosc. Radiat. Transf. 2019, 233, 119–133. [Google Scholar] [CrossRef]
- Rashid, A.; Tauheed, A. Energy structure investigations in triply ionized mercury: Hg IV. J. Quant. Spectrosc. Radiat. Transf. 2021, 270, 107668. [Google Scholar] [CrossRef]
- Hoy, K.; Nahar, S.N.; Pradhan, A.K. Biosignature Line Ratios of [P II] in Exoplanetary andNebular Environments. Mon. Not. R. Astron. Soc. Lett. 2023, 521, L48–L52. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nahar, S.N.; Hinojosa-Aguirre, G. Enhancement of the NORAD-Atomic-Data Database in Plasma. Atoms 2024, 12, 22. https://doi.org/10.3390/atoms12040022
Nahar SN, Hinojosa-Aguirre G. Enhancement of the NORAD-Atomic-Data Database in Plasma. Atoms. 2024; 12(4):22. https://doi.org/10.3390/atoms12040022
Chicago/Turabian StyleNahar, Sultana N., and Guillermo Hinojosa-Aguirre. 2024. "Enhancement of the NORAD-Atomic-Data Database in Plasma" Atoms 12, no. 4: 22. https://doi.org/10.3390/atoms12040022
APA StyleNahar, S. N., & Hinojosa-Aguirre, G. (2024). Enhancement of the NORAD-Atomic-Data Database in Plasma. Atoms, 12(4), 22. https://doi.org/10.3390/atoms12040022







