Line Shape Code Comparison of the Effect of Periodic Fields on Hydrogen Lines
Abstract
1. Introduction
2. Models and Codes
3. Results
3.1. Overview of the Line Shapes Submitted
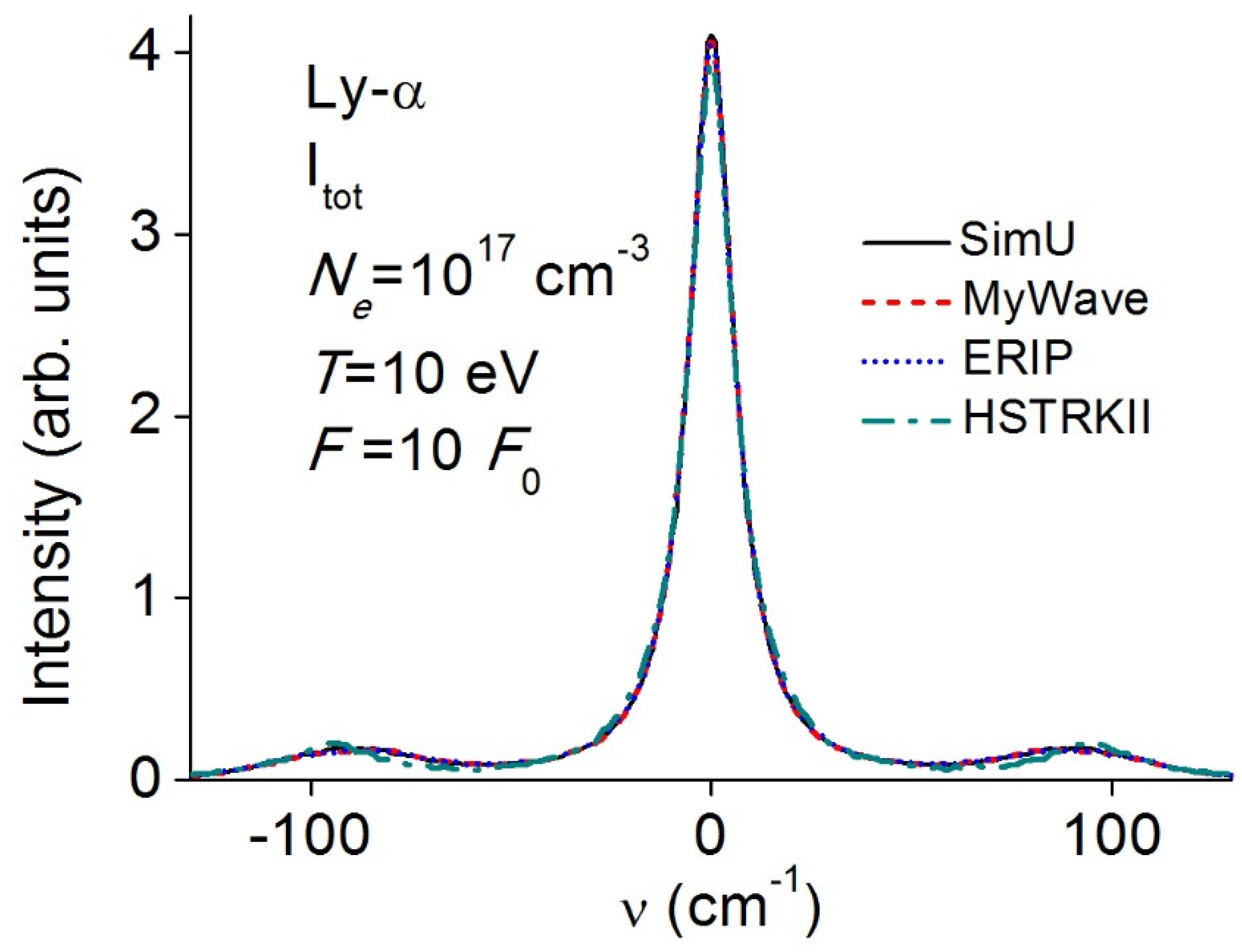
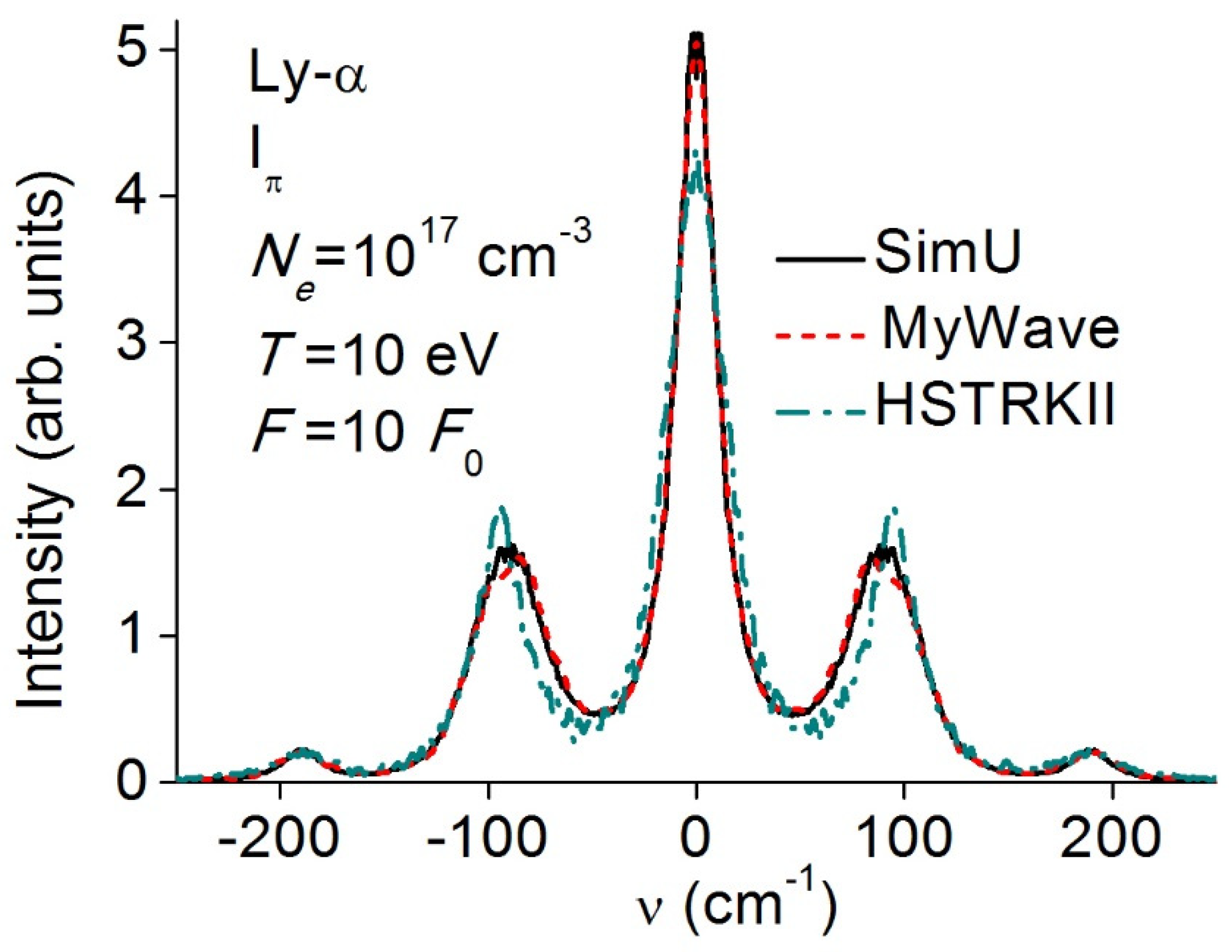
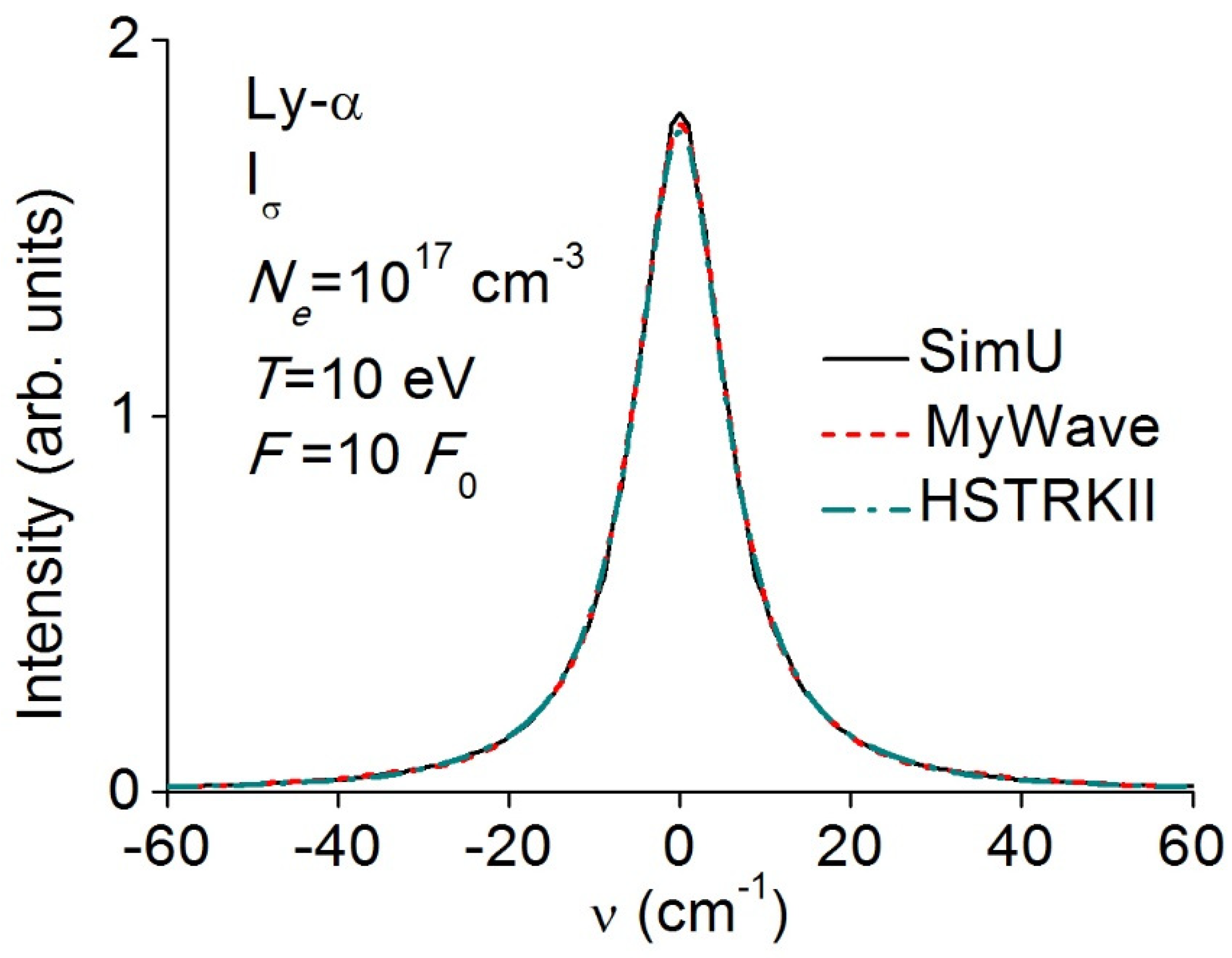
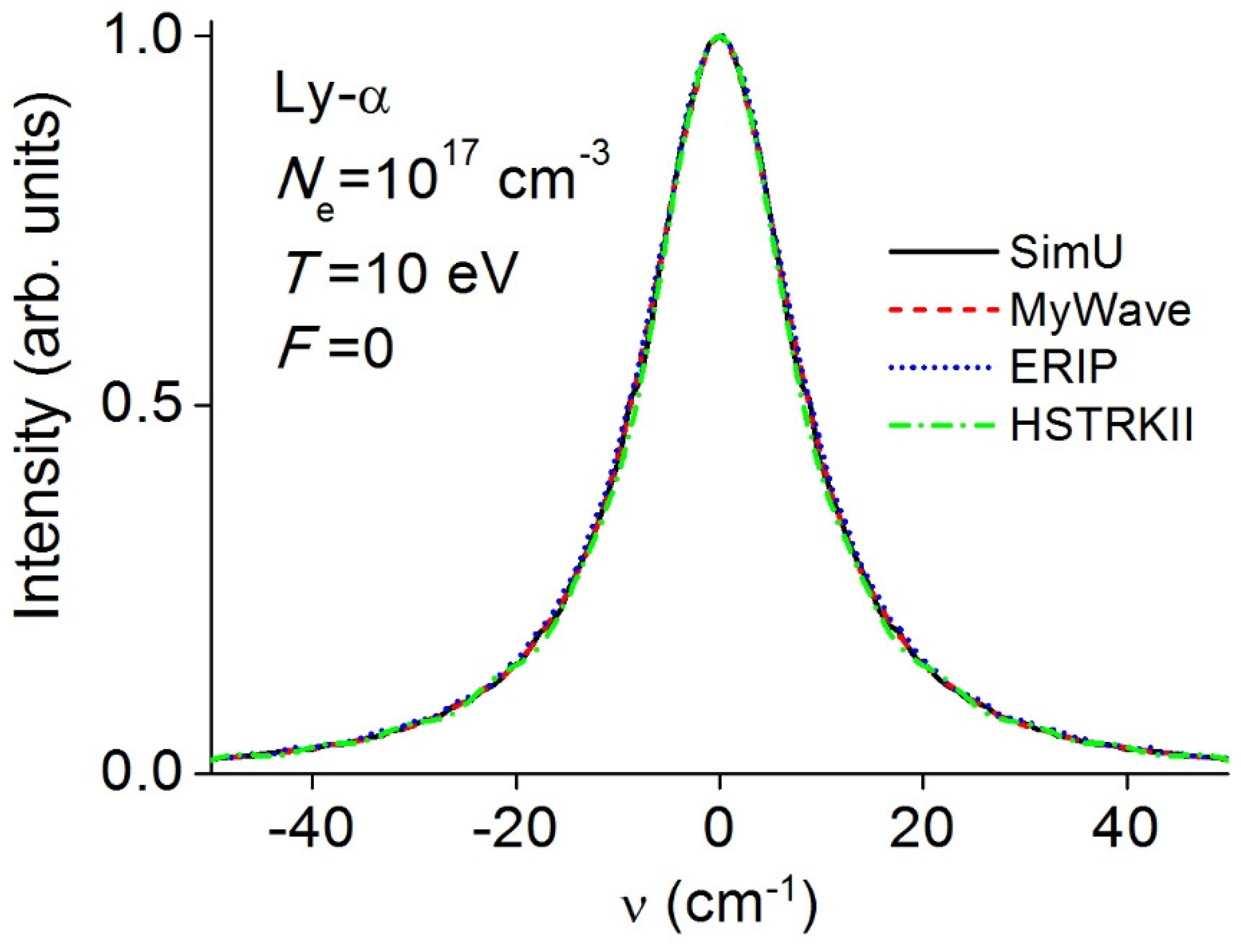
3.2. Lyman-α (Ly-α)
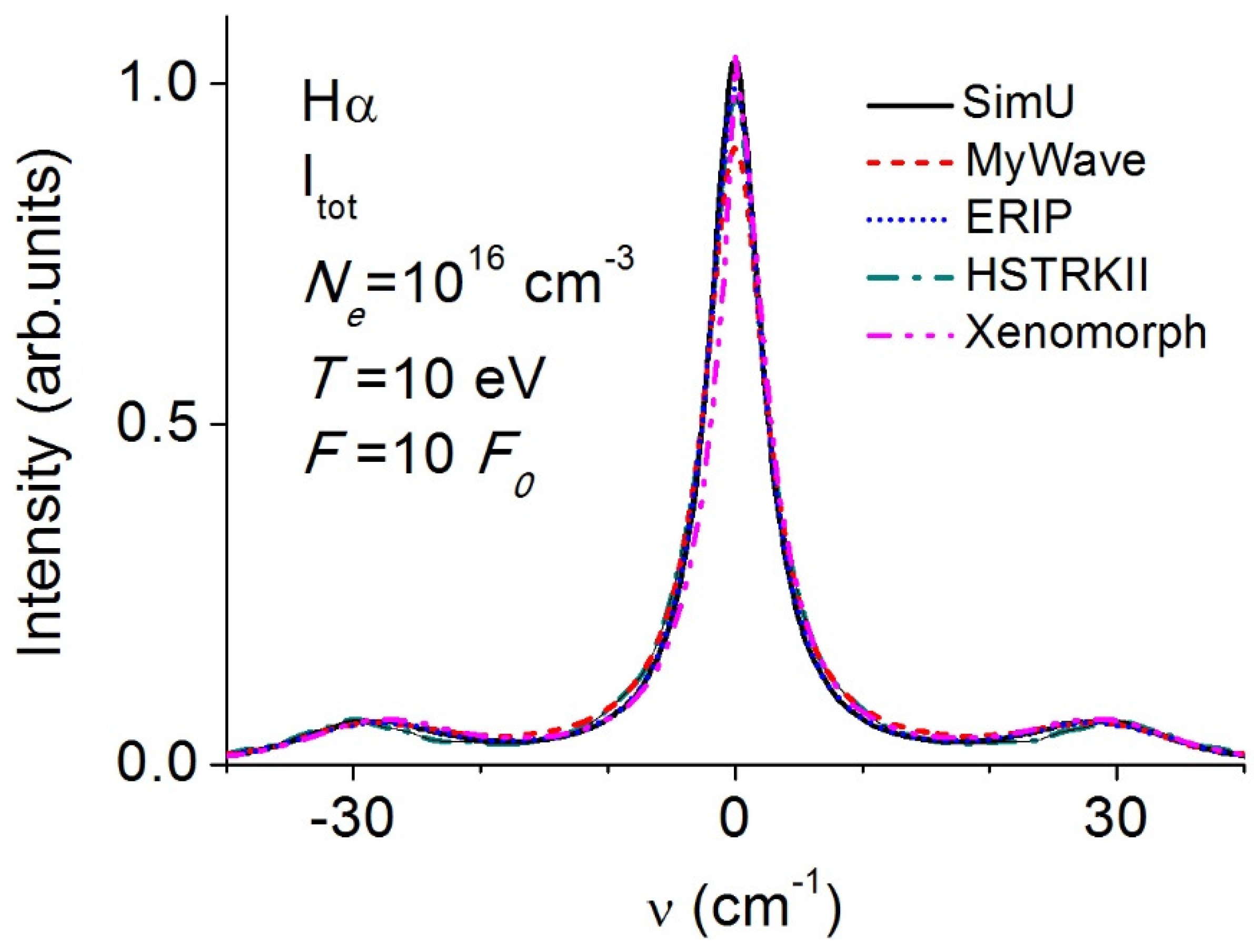
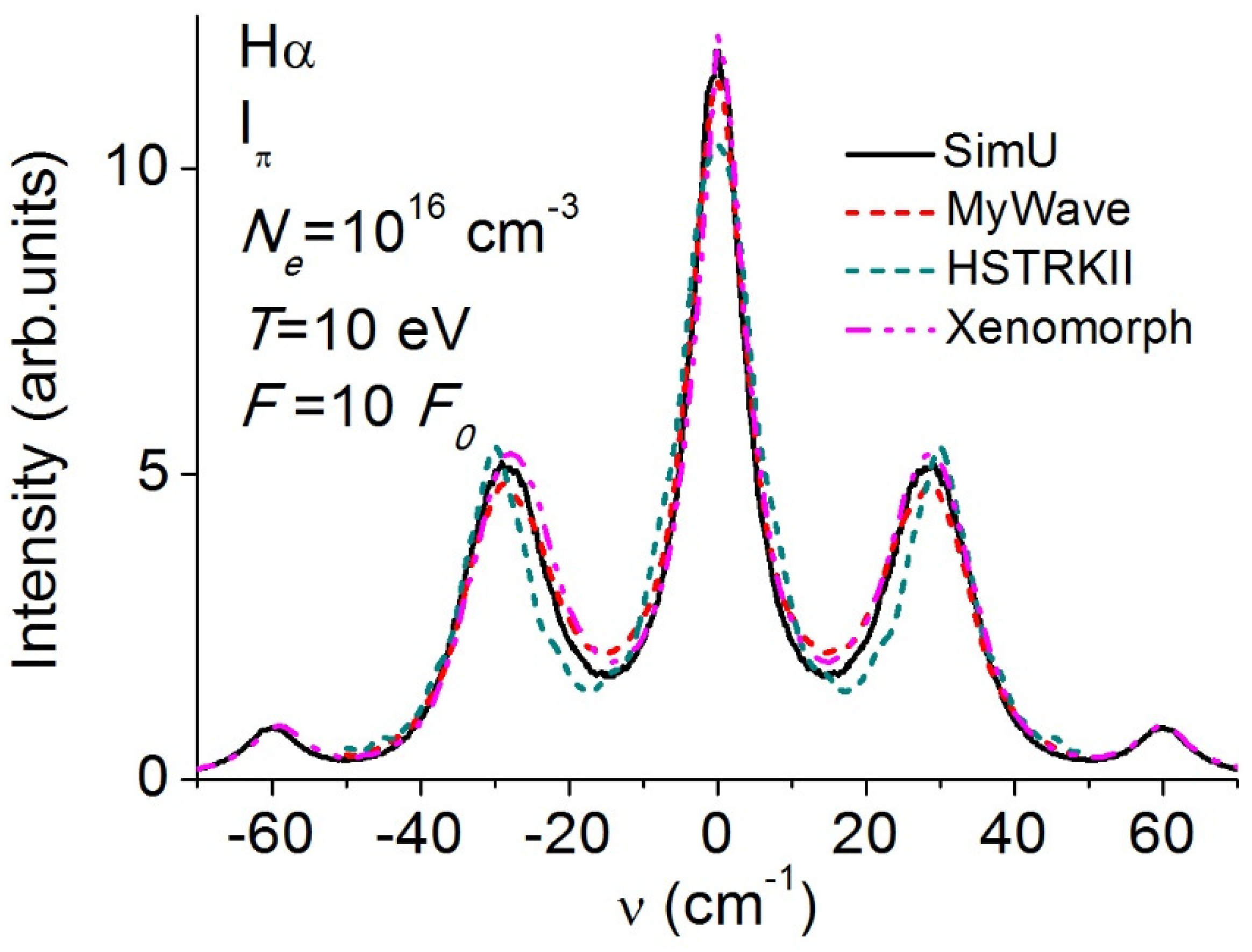
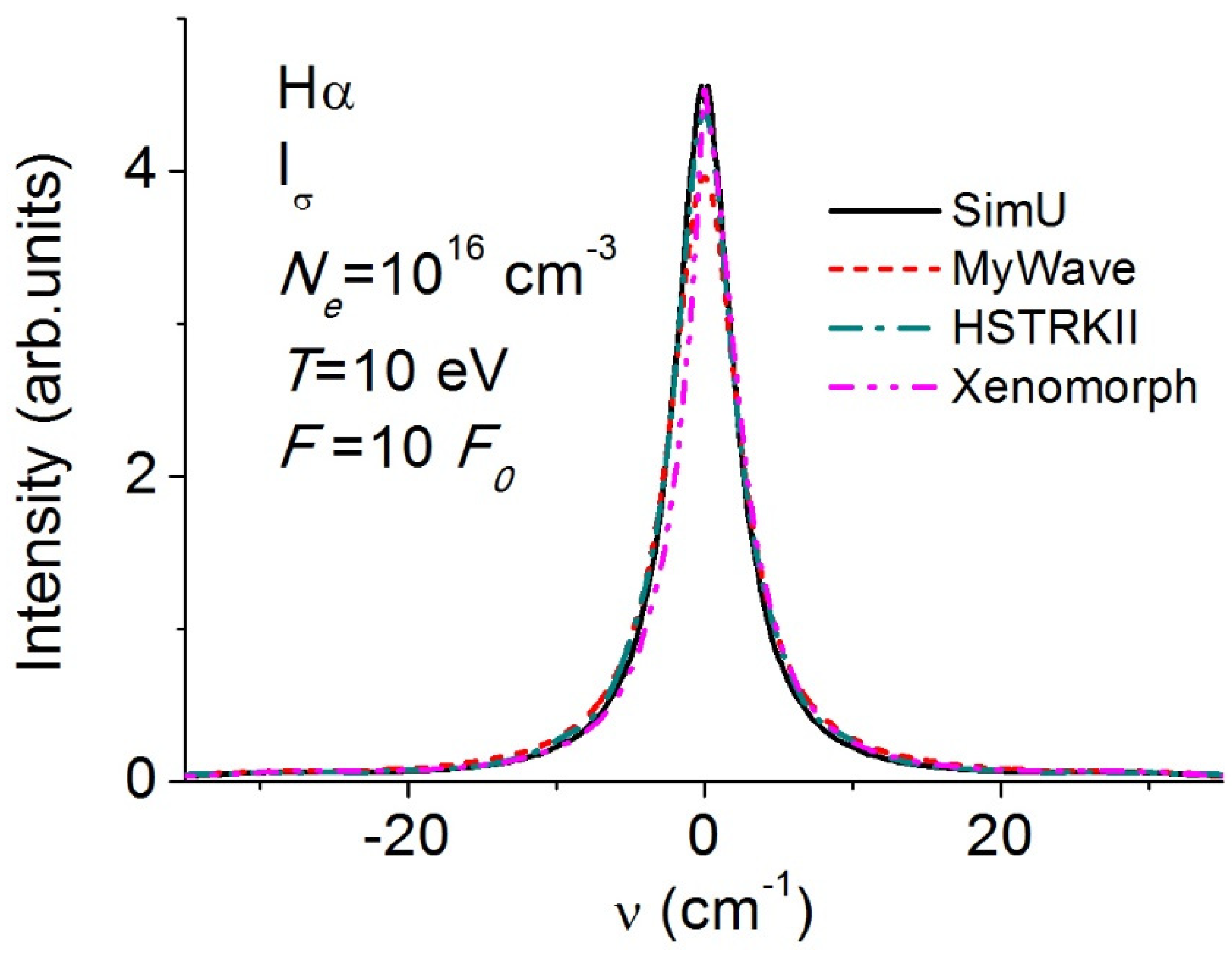
3.3. Balmer-α (Hα)
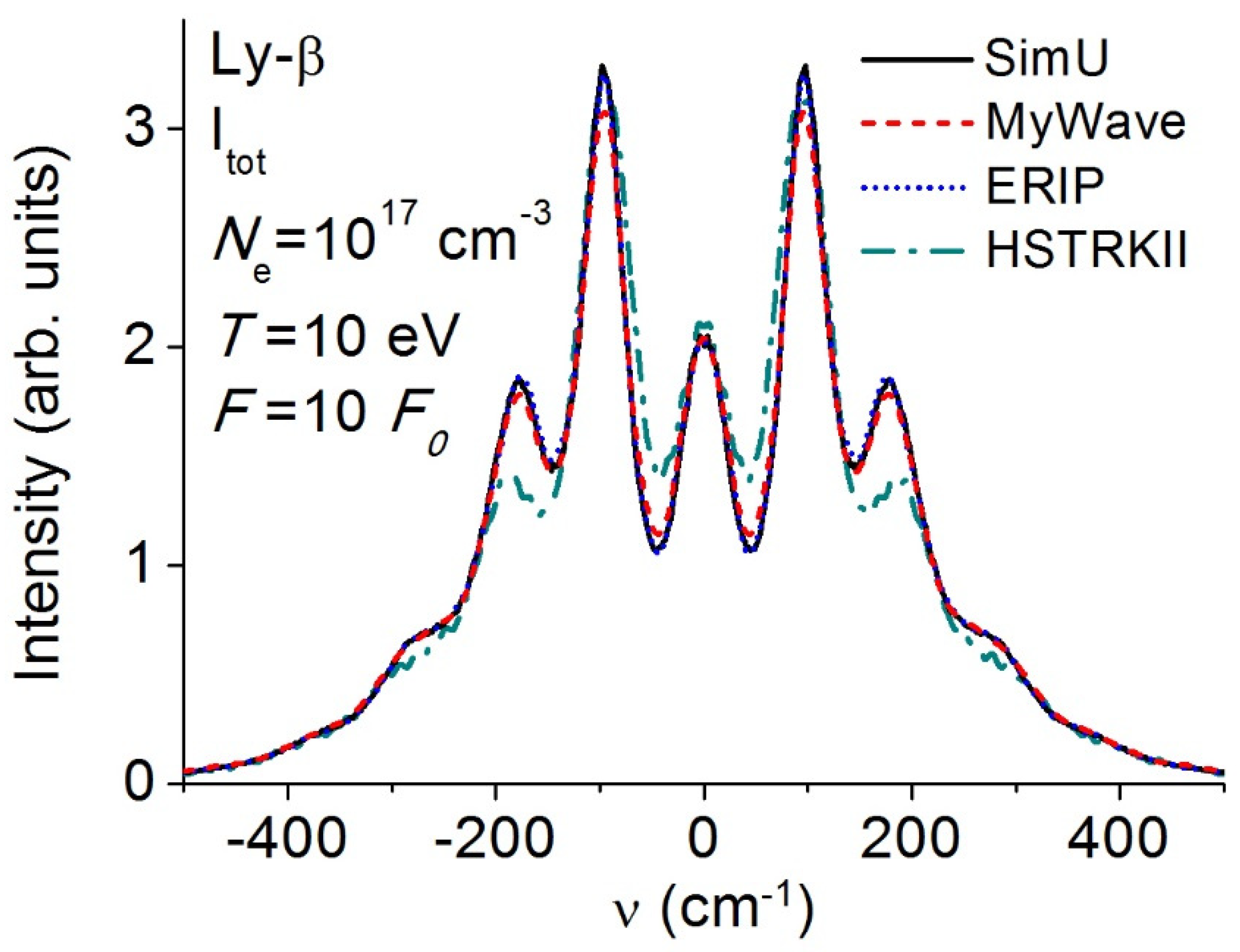
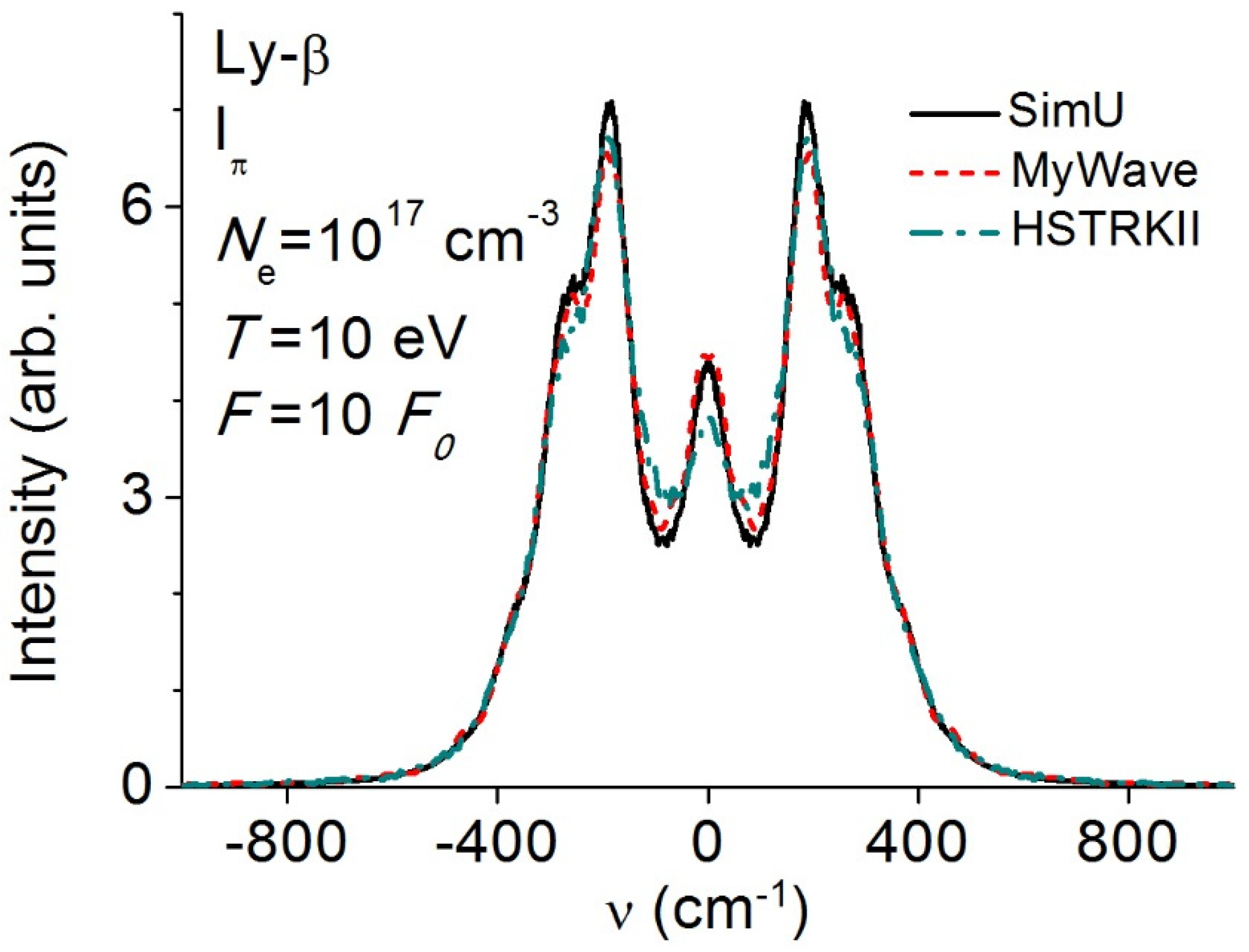
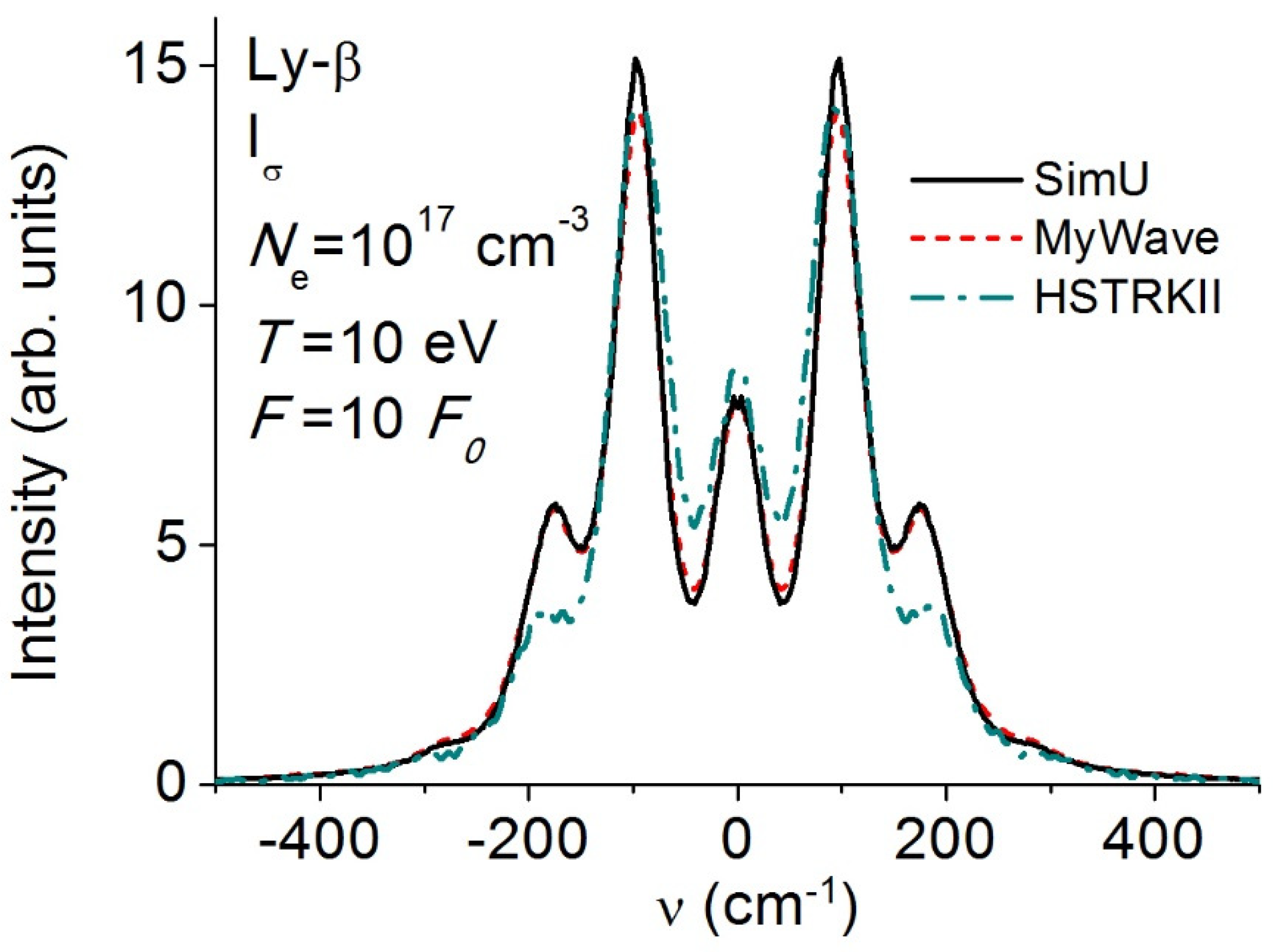
3.4. Lyman-β (Ly-β)
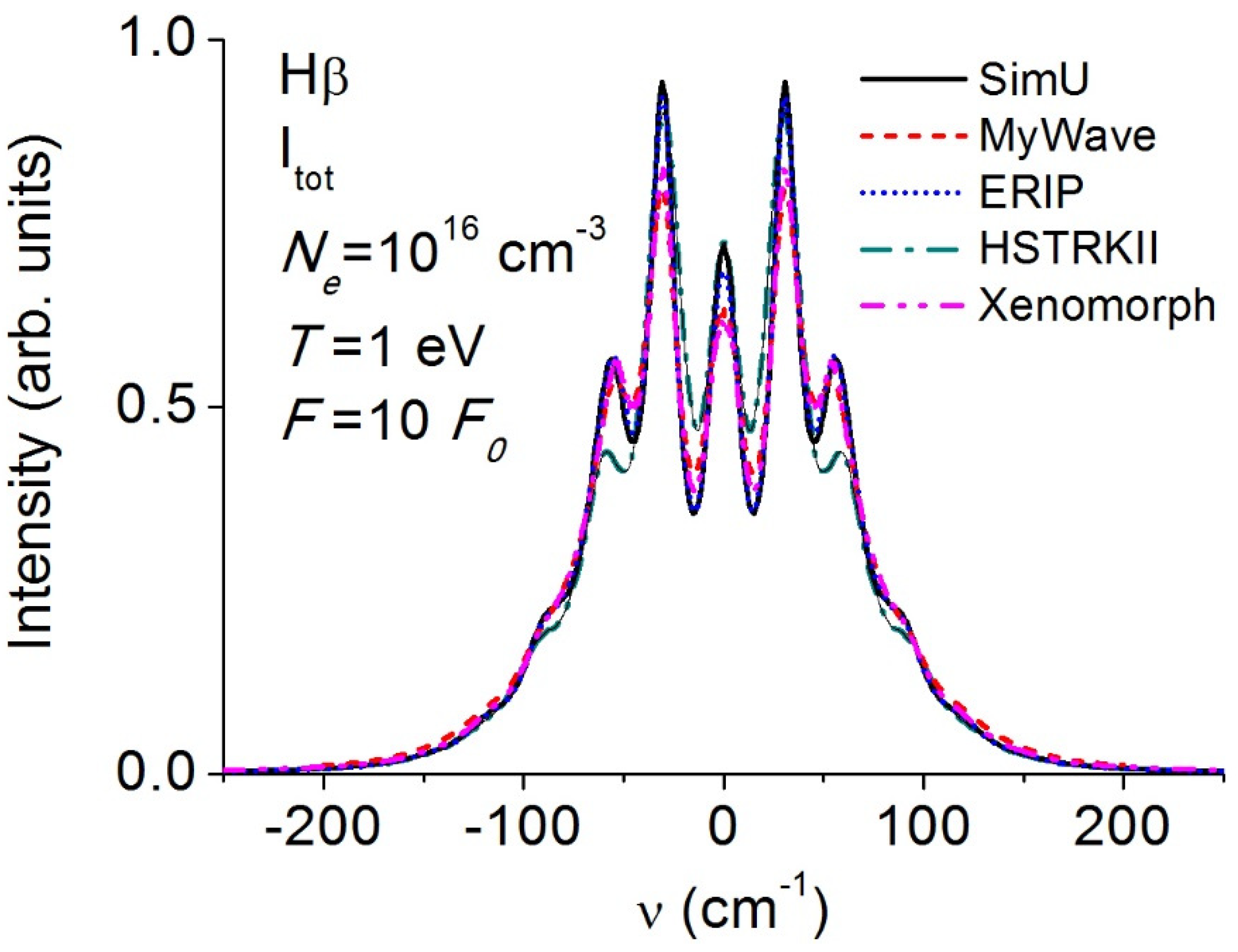
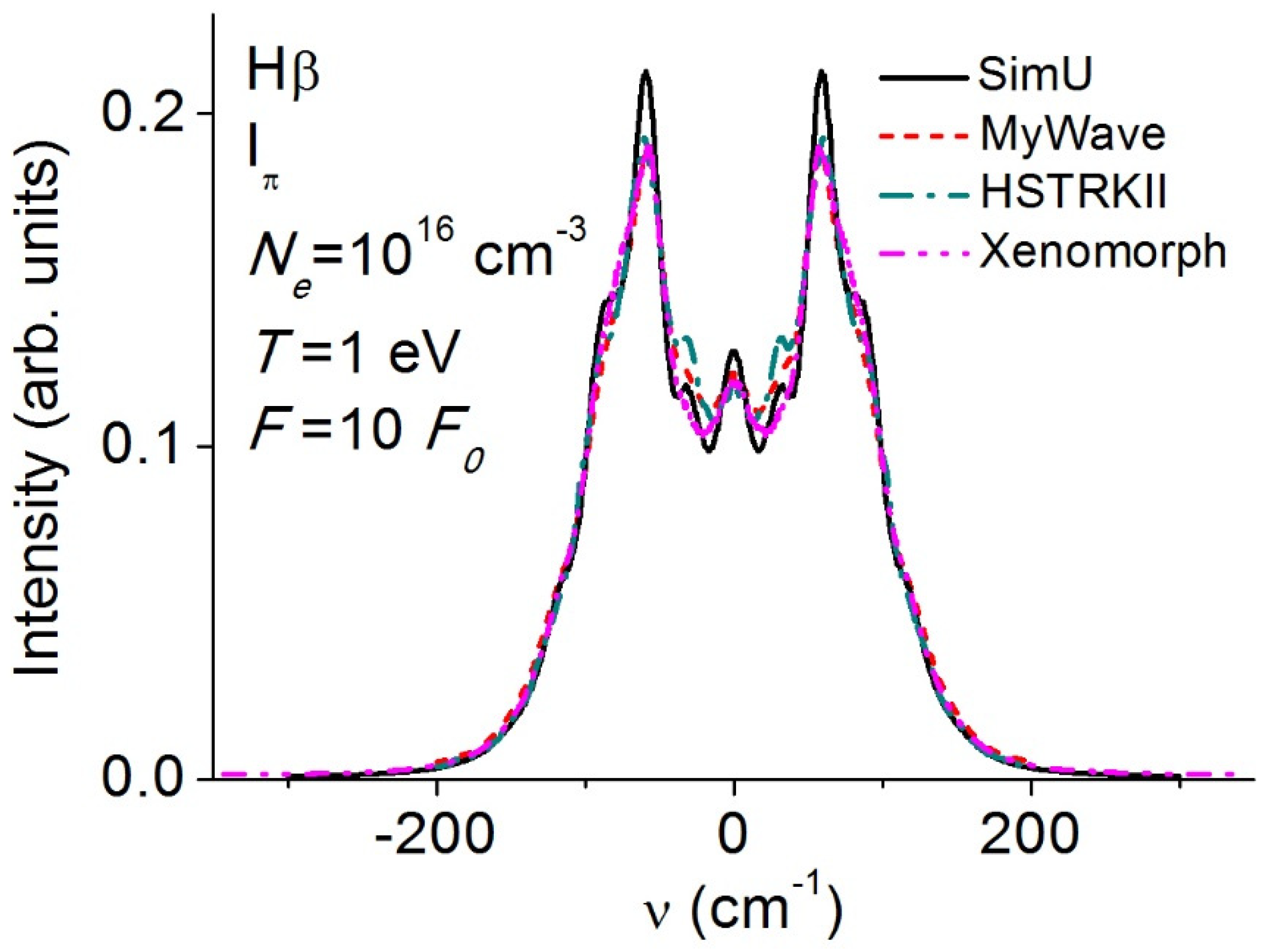
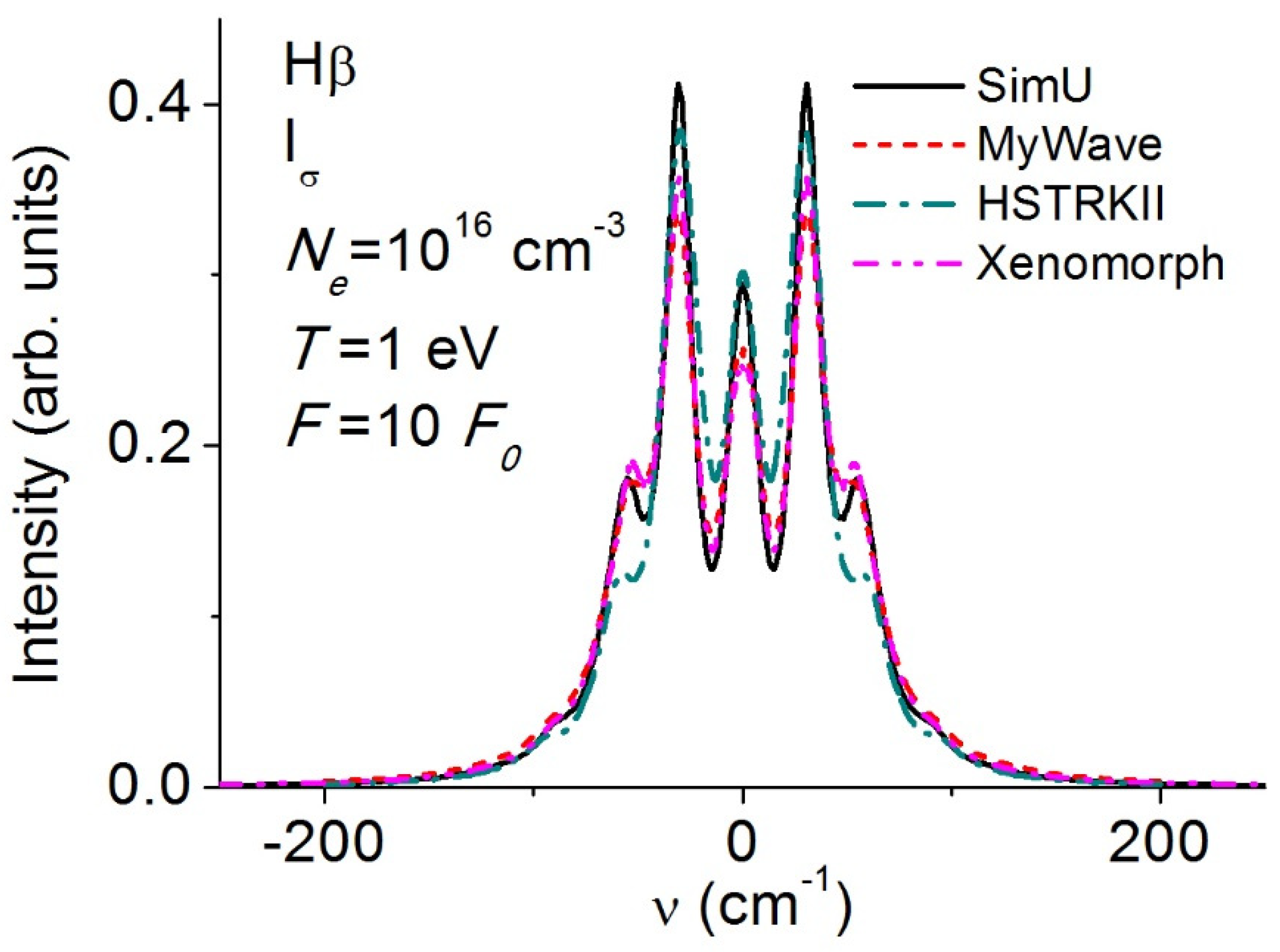
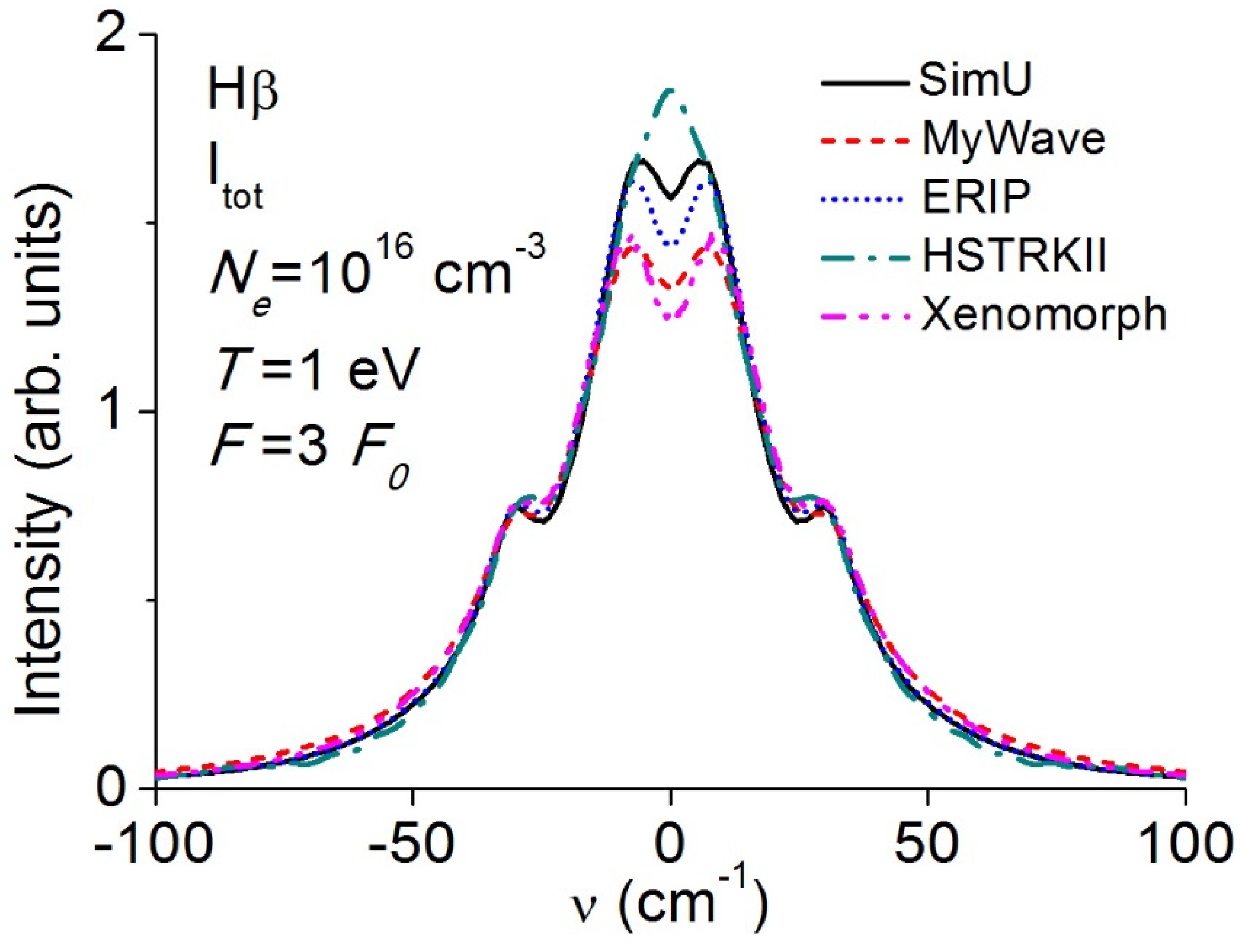
3.5. Balmerβ (Hβ)
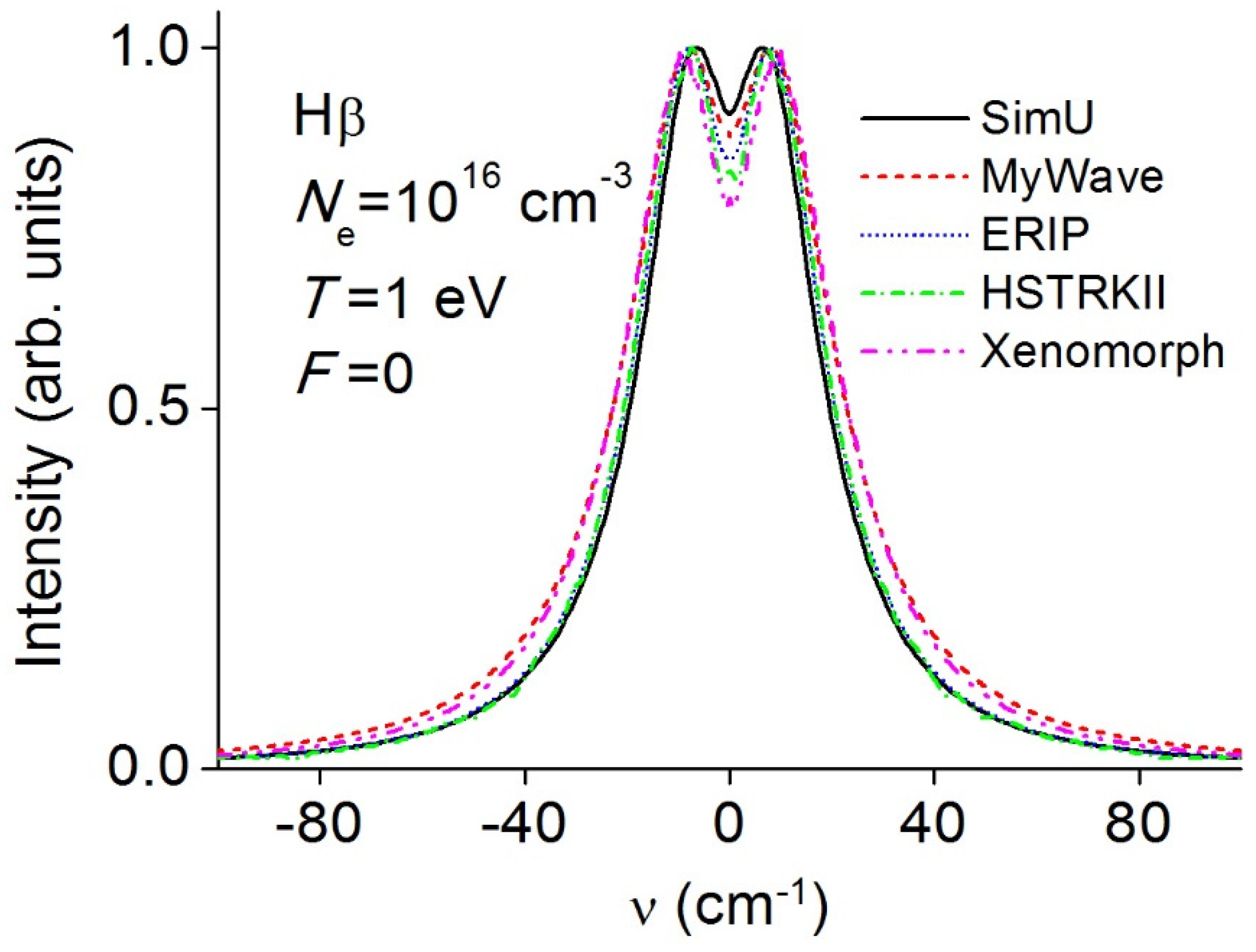
3.6. Line Shapes in Absence of Oscillating Electric Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stambulchik, E. Review of the 1st Spectral Line Shapes in Plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528–534. [Google Scholar] [CrossRef]
- Stambulchik, E.; Iglesias, C. Full radiator-perturber interaction in computer simulations of hydrogenic spectral line broadening by plasmas. Phys. Rev. E 2022, 105, 055210. [Google Scholar] [CrossRef]
- Gomez, T.; Nagayama, T.; Cho, P.; Zammit, M.; Fontes, C.; Kilcrease, D.; Bray, I.; Hubeny, I.; Dunlap, B.; Montgomery, M.; et al. All-order full-Coulomb quantum spectral line-shape calculations. Phys. Rev. Lett. 2021, 127, 235001. [Google Scholar] [CrossRef] [PubMed]
- Rosato, J.; Marandet, Y.; Stamm, R. A new table of Balmer line shapes for the diagnostic of magnetic fusion plasmas. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 333–337. [Google Scholar] [CrossRef]
- Ferri, S.; Peyrusse, O.; Calisti, A. Stark–Zeeman line-shape model for multielectron radiators in hot dense plasmas subjected to large magnetic fields. Matter Radiat. Extrem. 2022, 7, 015901. [Google Scholar] [CrossRef]
- Baranger, M.; Mozer, B. Light as a plasma probe. Phys. Rev. 1961, 123, 25–28. [Google Scholar] [CrossRef]
- Lisitsa, V. Atoms in Plasmas; Springer: Berlin/Heidelberg, Germany, 1994; ISBN 3-540-57580-4. [Google Scholar]
- Oks, E. Plasma Spectroscopy; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 3-540-54100-4. [Google Scholar]
- Griem, H. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997; ISBN 0-521-45504-9. [Google Scholar]
- Wiese, W.; Kelleher, D.; Paquette, D. Detailed study of the Stark broadening of Balmer lines in a high density plasma. Phys. Rev. A 1972, 6, 1132–1153. [Google Scholar] [CrossRef]
- Gallagher, C.; Levine, M. Observation of Hβ satellites in the presence of turbulent electric fields. Phys. Rev. Lett. 1971, 27, 1693–1696. [Google Scholar] [CrossRef]
- Rose, S. A review of opacity workshops. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 317–318. [Google Scholar] [CrossRef]
- Gigosos, M.; Fraile, J.; Torres, F. Hydrogen Stark profiles: A simulation-oriented mathematical simplification. Phys. Rev. A 1985, 31, 3509–3511. [Google Scholar] [CrossRef]
- Alexiou, S. Methods for Line Shapes in Plasmas in the Presence of External Electric Fields. Atoms 2021, 9, 30. [Google Scholar] [CrossRef]
- Hegerfeld, G.; Kesting, V. Collision time simulation technique for pressure-broadened spectral lines with applications to Ly-α. Phys. Rev. A 1988, 37, 1488–1496. [Google Scholar] [CrossRef]
- Tuck, E. A simple “Filon-trapezoidal” rule. Math. Comput. 1967, 21, 239–241. [Google Scholar]
- Blokhintsev, D. Theory of the Stark effect in a time-dependent field. Phys. Z. Sow. Union 1933, 4, 501–515. [Google Scholar]
- Griem, H.; Kolb, A.; Shen, K. Stark broadening of hydrogen lines in a plasma. Phys. Rev. 1959, 116, 4–16. [Google Scholar] [CrossRef]
- Hannachi, I.; Stamm, R.; Rosato, J.; Marandet, Y. Calculating the simultaneous effect of ion dynamics and oscillating electric fields on Stark profiles. Adv. Space Res. 2023, 71, 1269–1274. [Google Scholar] [CrossRef]
- Hannachi, I.; Stamm, R.; Rosato, J.; Marandet, Y. Spectroscopic diagnostic of oscillating electric fields in edge plasmas. Contrib. Plasma Phys. 2022, 62, e202100168. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Stambulchik, E.; Alexiou, S.; Griem, H.; Kepple, P. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. E 2007, 75, 016401. [Google Scholar] [CrossRef] [PubMed]
- Cho, P.; Gomez, T.; Montgomery, M.; Dunlap, B.; Fitz Axen, M.; Hobbs, B.; Hubeny, I.; Winget, D. Simulation of Stark-broadened hydrogen Balmer-line shapes for DA white dwarf synthetic spectra. ApJ 2022, 927, 70. [Google Scholar] [CrossRef]
- SLSP Browser Extension. Available online: https://plasma-gate.weizmann.ac.il/slsp/xul/ (accessed on 1 December 2022).
- Ramette, J.; Drawin, H. Structure of Stark Broadened Hβ Lines at low Electron Densities. Z. Naturforschung A 1976, 31, 401–407. [Google Scholar] [CrossRef]
- Rutgers, W.; de Kluiver, H. The dynamic Stark-effect in a turbulent hydrogen plasma. Z. Naturforschung A 1974, 29, 42–44. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.; Gonzales, M.; Gonzales-Herrero, D.; Lara, N.; et al. Ion dynamics effect on Stark-broadened line shapes: A cross-comparison of various models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
| Code | Stationarity | Simulation Technique | Schrödinger Solver | Fourier Transform |
|---|---|---|---|---|
| ERIP | Yes | Reinjection | Euler–Rodrigues and Runge–Kutta in this case | Fast Fourier Transform |
| HSTRKII | No | Collision-time Statistics | Stiff Solver for 0th order plus predictor corrector for plasma14 | Filon |
| MyWave | Yes | Reinjection | Implicit scheme | Filon |
| SimU | Yes | Reinjection | Runge–Kutta | Fast Fourier Transform |
| Xenomorph | Yes | Reinjection | Exponential scheme | Fast Fourier Transform |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hannachi, I.; Alexiou, S.; Stamm, R. Line Shape Code Comparison of the Effect of Periodic Fields on Hydrogen Lines. Atoms 2024, 12, 19. https://doi.org/10.3390/atoms12040019
Hannachi I, Alexiou S, Stamm R. Line Shape Code Comparison of the Effect of Periodic Fields on Hydrogen Lines. Atoms. 2024; 12(4):19. https://doi.org/10.3390/atoms12040019
Chicago/Turabian StyleHannachi, Ibtissem, Spiros Alexiou, and Roland Stamm. 2024. "Line Shape Code Comparison of the Effect of Periodic Fields on Hydrogen Lines" Atoms 12, no. 4: 19. https://doi.org/10.3390/atoms12040019
APA StyleHannachi, I., Alexiou, S., & Stamm, R. (2024). Line Shape Code Comparison of the Effect of Periodic Fields on Hydrogen Lines. Atoms, 12(4), 19. https://doi.org/10.3390/atoms12040019








