Abstract
The electron transitions in atoms caused by charged particle impact are benchmarks for the study of electron dynamics. In the present paper we focus on the excitation of helium by proton and antiproton impact. We perform both ab initio and perturbational calculations, revealing the importance of electron correlations and higher-order effects. The influence of the projectile charge sign on the excitation cross section is also studied.
1. Introduction
Cross sections of the excitation of helium via proton impact have been experimentally measured and calculated since the 1960’s; for example, see the articles by Thomas [1,2] and the references therein. Obtaining these data has been particularly interesting for modelling fusion plasma, which was still a focus within the field in the 1990s [3,4]. On the other hand, to our knowledge there are no experimental data on the excitation of helium by antiproton projectiles. However, since 1987 several measurements have been made for the single and double ionization of helium by antiproton impact and the cross sections obtained have been compared with the corresponding proton data [5]. In the case of single ionization, as expected, the effect of the projectile’s charge sign on the result was small, but for double ionization, the cross section of the antiproton’s impact showed a much higher impact than the corresponding proton impact. This result explained the previously observed Barkas effect for the stopping power of positively and negatively charged projectiles in matter. An explanation for the charge sign’s dependence on the double ionization cross section was found in the importance of electron correlation and the interference between first-order and second-order contributions [6,7,8]. Since then, several more precise experimental measurements and calculations have been performed for the ionization of helium by antiproton impact [9,10,11,12,13,14,15,16,17,18,19,20], but the excitation process has generally been neglected. Some calculations were published for proton impact [21,22,23], and even for antiproton impact [24,25,26,27], the focus was not on the excitation processes. As such, we have no knowledge about experimental cross sections for antiproton impact.
In the present paper we calculate excitation cross sections of helium atoms in collision with proton and antiproton projectiles. We perform an ab initio, time-dependent close-coupling (TDCC) calculation, based on the numerical solution of the time-dependent Schrödinger equation for two electrons, and also a simpler, first-order calculation. A comparison of the different results can reveal the importance of higher-order and electron correlation effects in these excitation processes, and clearly show the limits of the applicability of the first-order calculations for different excited states in different energy impact regions. While the first-order calculation leads to the same cross section for protons and antiprotons, the ab initio calculation shows that the excitation cross section depends on the sign of the projectile charge, and can reveal the cause of these differences (higher-order effects such as target polarization, electron correlation). We compare our results for proton impact with previous calculations and the existing experimental data, while for the antiproton impact, a comparison is made with the few existing theoretical excitation cross sections. This study intends to contribute to a better understanding of two-electron dynamics in the ion–atom collision processes.
2. Theory
In our calculations, we use the semi-classical impact parameter approximation, which assumes a classical straight-line trajectory for the projectile, and only the electron system of the target is treated using quantum mechanics. This approach is valid for fast heavy projectiles, such as protons or antiprotons. Deviations from the straight-line trajectory because of Coulomb deflection from the nucleus are negligible. In the case of the lowest considered projectile energy (100 keV), the deviation is only larger than 1° for impact parameters lower than 0.05 atomic units. This region contributes to a cross section of less than 0.1%. Furthermore, the validity of the straight-line trajectory model was also demonstrated by Classical Trajectory Monte Carlo (CTMC) calculations for projectiles with even lower energies, down to 3 keV [19]. This semi-classical model cannot be applied to equivelocity light projectiles (electrons and positrons). In those cases, the de Broglie wavelength associated with the projectile is close to atomic dimensions, so a classical description would be incorrect, and a quantum description is needed, as in [28].
The cross section for the excitation process can be written as an integral over the impact parameter
where is the transition probability amplitude, while i and f are the initial and the final states, respectively (eigenstates of the unperturbed Hamiltonian of the atomic system with energies and ).
2.1. Perturbational Method
The simplest way to calculate the excitation cross section is the application of one active electron and first-order perturbation approximation. The projectile trajectory is assumed to be along the axis. In this framework the first-order transition amplitude is calculated as the integral of the matrix element of the projectile–electron interaction (multiplied by an oscillating factor) over the z coordinate (the trajectory) of the projectile
Here, is the position vector of the projectile and is the position vector of the active electron. is the charge and v is the velocity of the projectile.
For the single-electron wave functions i and f, the radial and orbital parts are separated
Here, , , and are the orbital and magnetic quantum numbers of the active electron in the initial and final states, respectively.
The interaction potential is expanded using the multipole series
where the Legendre polynomial depends on the mutual angle between and , while and .
In order to perform the integral according to the orbital coordinates of the electron, we make use of the expression of the Legendre polynomials as a function of spherical harmonics
Substituting (3)–(6) into expression (2) of the transition amplitude, we perform the integration over using the equation
where and are the Clebsch–Gordan coefficients. For the first-order excitation amplitude, we obtain
2.2. The Time-Dependent Close-Coupling Method
In our ab initio approach, the quantum dynamics of the two active electrons driven by the time-dependent Coulomb field of the classical projectile are solved numerically using the TDCC method [18]. The fully correlated two-electron wave function is represented as the basis of symmetrized coupled spherical harmonics [19,20]
For the radial partial wave functions we have used the finite element discrete variable representation (FEDVR) [29,30], where each radial coordinate is divided into finite elements (i.e., segments with finite length) and inside each finite element the wave function is represented on a local polynomial basis. For the time propagation of the wave function, the short iterative Lanczos method [31,32] with adaptive time step control was implemented.
The time evolution of the wave function was started from the ground state of He, which in turn was obtained by performing the negative imaginary time propagation () of an initial guess wave function.
The excitation probability amplitudes were calculated directly from the time-dependent wave function by projecting it onto eigenstates of the He target obtained by directly diagonalizing the discretized Hamiltonian using the Scalable Library for Eigenvalue Problem Computations (SLEPc) package [33]. The accuracy of the obtained results was ensured by convergence tests with respect to the numerical parameters of the model. More details on these convergence tests and on the present implementation of the TDCC model can be found in our earlier publications [19,20].
3. Results and Discussion
We have performed calculations for the excitation of helium by proton and antiproton impact in the projectile energy region between 100 and 1000 keV. In the case of the ab initio calculations, the two-electron wave functions for the initial and final states were obtained by our code, but for the perturbational calculations we have used one-electron variational wavefunctions from the literature. The ground state is taken from the basic configuration of the wavefunction of Nesbet and Watson [34], while for the and excited states we have used the wavefunctions given in [35]. The excited state is taken to be simply a hydrogenlike function. The wavefunction is orthogonalized onto the ground state using the Gram–Schmidt method.
In addition to excitation cross sections (comparable with experiments), we also show transition probabilities as a function of the impact parameter in order to identify the impact parameter regions in which the first-order calculations fail.
The impact parameter dependence on the excitation probabilities in the state obtained from the perturbational method and the ab initio calculations are presented in Figure 1, where the impact parameter is in atomic units (a.u.).
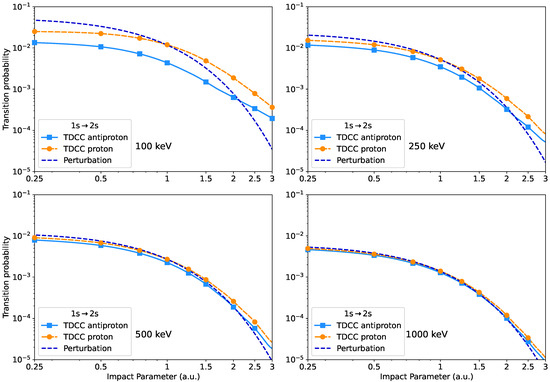
Figure 1.
Transition probabilities for the excitation process of helium as a function of the impact parameter for proton and antiproton projectiles in the case of different impact energies. The results obtained from the ab initio TDCC calculations are presented compared to the first-order perturbational approximation.
For the highest projectile energy (1000 keV), as expected, the results obtained with the perturbational method are in good agreement with the TDCC calculations, and there is no significant difference between the transition probabilities for protons and antiprotons. For lower impact energies, the higher-order and electron correlation effects become more and more important, and the difference between the two methods increases. We obtained higher transition probabilities for protons than for antiprotons for all impact parameters. This may be caused by the fact that the protons attract the electrons, resulting in a smaller average electron–projectile distance during the collision, and a stronger interaction. The first-order results are higher than the ab initio data for small impact parameters in the case of both projectiles.
The excitation probabilities calculated with the perturbational approximation and the TDCC method are shown in Figure 2. Similar to the excitation, for the highest impact energy the transition probability practically does not depend on the charge sign of the projectile, and the perturbational approach gives comparable results. For lower impact energies, the difference between the three curves increases, particularly for small impact parameters. In the case of large impact parameters, where the distant collision mechanism is dominant [36], the perturbational result reproduces those obtained from the ab initio calculations very well. This suggests that, in this impact parameter region, the excitation is mainly a single-electron process and the electron correlation effects can be neglected, even at a 100 keV projectile energy. In contrast, at small impact parameter values, significant difference between the proton- and antiproton-induced transition probabilities is observed. This indicates that in the excitation process the correlated multi-particle quantum dynamics plays an important role, which is the fingerprint of the close collision mechanism [36]. An important difference relative to the excitation is that, in the present case, the transition probabilities for antiprotons and for small impact parameters (below 1 a.u.) are much higher than for protons. For impact parameters above 2 a.u., the transition probabilities for antiprotons are slightly smaller compared to proton projectiles.
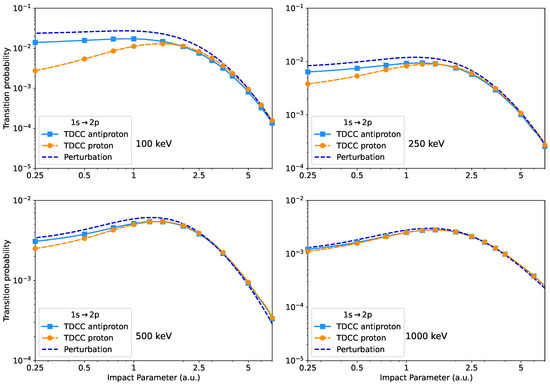
Figure 2.
Same as Figure 1 but for the transition.
The excitation probabilities calculated using the TDCC and the perturbational method are shown in Figure 3. Similarly to the previous cases, for a 1000 keV projectile energy the transition probabilities are practically the same for protons and antiprotons, and the first-order approximation reproduces the TDCC results well. For lower-impact energies, the TDCC method leads to higher excitation probabilities for antiprotons below the impact parameter than for proton projectiles, and higher transition probabilities for protons at larger impact parameters. The perturbational method underestimates the results especially for small impact parameters, and at 100 and 250 keV projectile energies.
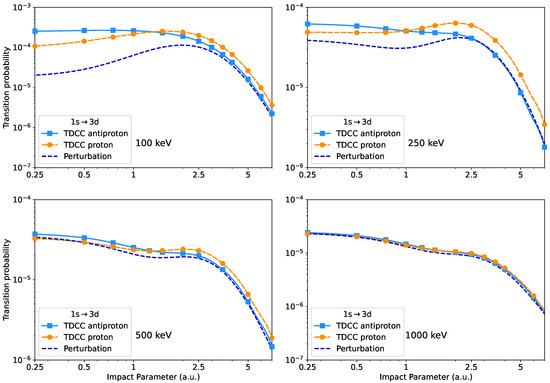
Figure 3.
Same as Figure 1 but for the transition.
The excitation cross sections for the transition are presented in Figure 4 for proton (left panel) and antiproton (right panel) projectiles as a function of impact energy. Our TDCC and perturbational results are compared with the theoretical calculations for protons by Alladustov et al. [22], and for antiprotons with the calculations by Igarashi et al. [26] and the coupled pseudostate (CP) results of McGovern et al. [27]. We also show the recommended values proposed for proton projectiles by Heer et al. [4]. Our TDCC results show a good overall agreement with these data for both projectiles, but for lower proton energies we obtain up to 10% smaller cross sections than the recommended values. The first-order results are close to the ab initio ones for proton projectiles even at the lowest energy, while they overestimate the cross sections obtained with antiprotons up to a factor of 2.2 at 100 keV. This observation suggests that, for this transition, electron correlation and higher-order effects are more important for antiprotons than for protons.
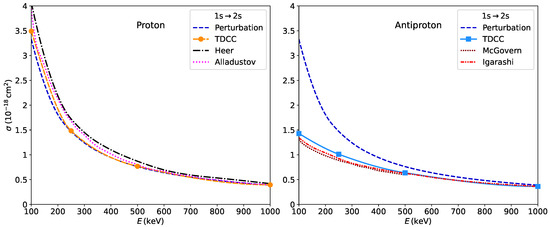
Figure 4.
Excitation cross sections of helium for the transition as a function of the projectile energy for proton (left panel) and antiproton (right panel) projectiles. The results of the first-order perturbation approximation and the TDCC method are compared with the recommended values given by Heer et al. [4] and the theoretical results of Alladustov et al. [22] for proton projectiles, and the calculations of Igarashi et al. [26] and McGovern et al. [27] for antiproton projectiles.
The excitation cross sections for the transition obtained with proton and antiproton projectiles are shown in Figure 5 as a function of projectile energy, in comparison with other theoretical calculations and experimental and recommended data (for proton impact). In this case, our TDCC method leads to slightly lower values relative to the recommended and experimental ones for protons and both theoretical calculations for antiprotons, for all energies. However, for proton projectiles we have obtained good agreement with the most recent calculations of Alladustov et al. [22]. Our perturbational results are higher than the TDCC ones for both projectiles. These show good agreement with other theories for antiprotons and the experimental data for protons above a 500 keV projectile energy, but below this energy, they overestimate all of the other data.
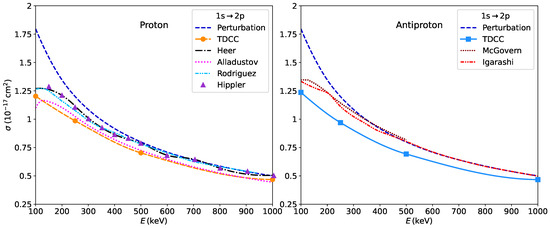
Figure 5.
Same as Figure 4, but for the transition. The results for protons are compared in addition to the calculation of Rodriguez et al. [21] and the experimental data of Hippler et al. [37].
The excitation cross sections calculated for the transition are presented in Figure 6 in comparison with the available recommended and experimental values for proton impact and theoretical calculations for antiproton impact. In the case of protons, the TDCC results agree well with the recommended values for energies above 500 keV, while for the low energies (below 200 keV) the agreement is good with the experimental data of Van den Bos et al. [38]. Here, the recommended values are lower. In contrast with the other two excitations in this case the first-order results are lower than the ab initio ones. In the case of antiprotons, our TDCC results are lower than the other two calculations of Igarashi et al. [26] and McGovern et al. [27]. Surprisingly, our first-order results are in perfect agreement with the ab initio ones above 250 keV. Below this energy the first-order calculations underestimate the TDCC ones.
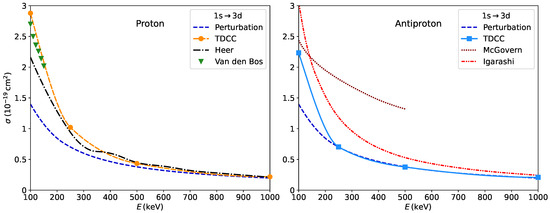
Figure 6.
Same as Figure 4, but for the transition. The results for protons are compared in addition to the experimental results of Van den Bos et al. [38].
The present TDCC results are in good agreement with the recent convergent close-coupling (CCC) calculations of Alladustov et al. [22], which is not a surprise since both approaches use a relatively large basis set during the solution of the time-dependent Schrödinger equation. In contrast, there is noticeable difference between the present TDCC results and previous calculations [26,27], which can be attributed to the smaller basis sets used in those calculations.
Finally, in Figure 7 we show a comparison of the obtained excitation cross sections with proton and antiproton projectiles by the TDCC method and the first-order approximation, for all three studied excited states. One may observe that, for the excitation of the state, the cross sections for protons and antiprotons are almost identical. This does not mean that higher-order effects are not important, because, as we have seen in Figure 2, transition probabilities depending on the impact parameter differ for the two projectiles. For this excitation, the effects for small and large impact parameters cancel each other out. The first-order perturbational results overestimate the TDCC ones for all energies, especially on the lower side. In the case of the other two studied excitations’ cross sections, the results for protons are comparatively higher than those for antiproton projectiles. As expected, the difference increases for lower impact energies, because here, higher-order effects, responsible for the Barkas effect, are more important. The perturbational results reproduce the TDCC cross sections for the excitation of the state by proton impact almost exactly, and for the excitation of the they are in very good agreement with the TDCC results for antiprotons above 250 keV. Looking at Figure 1, Figure 2 and Figure 3, this agreement is also a result of the cancellation of differences in transition probabilities for small and large impact parameters. It can be also observed, that the difference between proton and antiproton excitation cross sections is significantly larger in the case of dipole-forbidden transitions compared to the dipole-allowed transitions. This behaviour was also observed in the case of the H target [7].
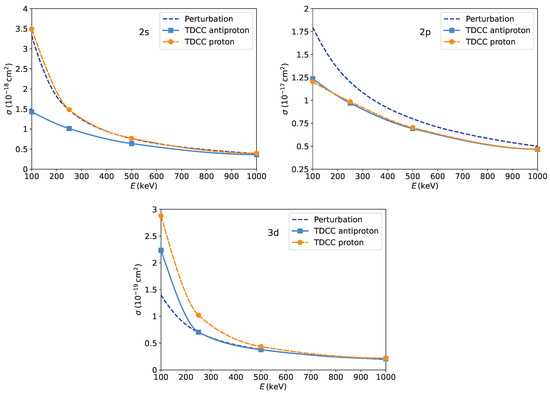
Figure 7.
Comparison of excitation cross sections for helium obtained with proton and antiproton projectiles (TDCC calculations) and the perturbational approximation. Excitation to the , and states are presented as a function of projectile energy.
4. Conclusions
We have performed perturbational and ab initio TDCC calculations for the excitation of helium by proton and antiproton impact. Studying the impact parameter dependence of the transition probabilities, we have observed that these behave differently for the three studied excitations. For the state transition, the probabilities for antiprotons are higher relative to protons for all impact parameters. In the case of the excitation of the and states for small impact parameters, the transition probabilities for antiproton projectiles are higher, while for larger impact parameters the proton projectiles induce the transition with a higher probability.
Concerning the excitation cross sections as a function of the impact energy, the results for proton and antiproton projectiles are practically equal for the highest considered energy, 1000 keV. This suggests that higher-order effects, responsible for the dependence of the cross section on the projectile charge sign, can be neglected in this case. Consequently, the first-order perturbational calculations reproduce the TDCC results well at this energy. For lower impact energies, in the case of the excitation of the and states, higher cross sections are obtained for protons than for antiprotons. For the excitation of the state, the cross sections obtained with proton and antiproton projectiles are almost the same. Concerning the perturbational results, these overestimate the TDCC ones for the state, while in the case of they reproduce the cross sections obtained with protons almost exactly. As for the state, the perturbational result is below the TDCC ones for the lowest impact energy (100 keV), while for higher energies follow the TDCC data for antiprotons.
Comparing our results with other calculations, and in the case of the proton impact on the recommended and experimental cross sections (excitation of the ), the agreement is very good. In other cases, such as the excitation of the state by proton impact, our TDCC result is in good agreement with other elaborate calculations [22] but are below the experimental and recommended cross sections. For the excitation of the with the same projectile, the agreement with the experimental data (small impact energies) or the recommended values (higher energies) is good. While in case of the excitation of the and states by antiproton projectiles, our TDCC results are below the other two available calculations, which can be attributed to the relatively small configuration space on which the Schrödinger equation was solved in those studies.
Author Contributions
Conceptualization, L.N.; methodology, L.N. and S.B.; software, Z.B. and S.B.; validation, L.N.; writing—original draft preparation, Z.B., S.B. and L.N.; writing—review and editing, L.N. and S.B.; supervision, L.N. All authors have read and agreed to the published version of the manuscript.
Funding
Z.B. was funded by the student research scholarship of the Babeş-Bolyai University, the Hungarian University Federation of Cluj-Napoca and the Bethlen Gábor Alapkezelő Zrt.
Data Availability Statement
The data produced by both models is available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thomas, E.W.; Bent, G.D. Formation of Excited States in a Helium Target by the Impact of 0.15- to 1.0-MeV Protons and Deuterons. I. Experimental. Phys. Rev. 1967, 164, 143–150. [Google Scholar] [CrossRef]
- Thomas, E.W. Cross Sections for the Formation of Excited States in a Helium Target by the Impact of 0.15- to 1.0-MeV Protons and Deuterons. II. Comparison with Theory. Phys. Rev. 1967, 164, 151–155. [Google Scholar] [CrossRef]
- Fritsch, W. Helium Excitation in Heavy Particle Collisions. In Atomic and Plasma–Material Interaction Data for Fusion; IAEA: Vienna, Austria, 1992; Volume 3, pp. 41–46. [Google Scholar]
- De Heer, F.; Hoekstra, R.; Summers, H.P.; Undertaking, J.J. New Assessment of Cross-Section Data for Helium Excitation by Protons. In Atomic and Plasma–Material Interaction Data for Fusion; IAEA: Vienna, Austria, 1992; Volume 3, pp. 47–50. [Google Scholar]
- Andersen, L.H.; Hvelplund, P.; Knudsen, H.; Moller, S.P.; Sorensen, A.H.; Elsener, K.; Rensfelt, K.-G.; Uggerhoj, E. Multiple ionization of He, Ne, and Ar by fast protons and antiprotons. Phys. Rev. A 1987, 36, 3612–3629. [Google Scholar] [CrossRef] [PubMed]
- Reading, J.F.; Ford, A.L. The forced impulse method applied to the double ionisation of helium by collision with high-energy protons, antiprotons and alpha particles. J. Phys. B Atom. Mol. Phys. 1987, 20, 3747–3769. [Google Scholar] [CrossRef]
- Knudsen, H.; Reading, J. Ionization of atoms by particle and antiparticle impact. Phys. Rep. 1992, 212, 107–222. [Google Scholar] [CrossRef]
- Nagy, L. Two-electron processes in fast collisions with charged particles. Nucl. Instrum. Methods Phys. Res. B 1997, 124, 271–280. [Google Scholar] [CrossRef]
- Andersen, L.H.; Hvelplund, P.; Knudsen, H.; Mo, S.P.; Pedersen, J.O.P.; Tang-Petersen, S.; Uggerho, E.; Elsener, K.; Morenzoni, E. Single ionization of helium by 40–3000-keV antiprotons. Phys. Rev. A 1990, 41, 6536–6539. [Google Scholar] [CrossRef]
- Hvelplund, P.; Knudsen, H.; Mikkelsen, U.; Morenzoni, E.; Moller, S.P.; Uggerhoj, E.; Worm, T. Ionization of helium and molecular hydrogen by slow antiprotons. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 925. [Google Scholar] [CrossRef]
- Knudsen, H.; Kristiansen, H.-P.E.; Thomsen, H.D.; Uggerhøj, U.I.; Ichioka, T.; Møller, S.P.; Hunniford, C.A.; McCullough, R.W.; Charlton, M.; Kuroda, N.; et al. Ionization of Helium and Argon by Very Slow Antiproton Impact. Phys. Rev. Lett. 2008, 101, 043201. [Google Scholar] [CrossRef]
- Knudsen, H.; Kristiansen, H.-P.E.; Thomsen, H.D.; Uggerhøj, U.I.; Ichioka, T.; Møller, S.P.; Hunniford, C.A.; McCullough, R.W.; Charlton, M.; Kuroda, N.; et al. On the double ionization of helium by very slow antiproton impact. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 244. [Google Scholar] [CrossRef]
- Khayyat, K.; Weber, T.; Dörner, R.; Achler, M.; Mergel, V.; Spielberger, L.; Jagutzki, O.; Meyer, U.; Ullrich, J.; Moshammer, R.; et al. Differential cross sections in antiproton- and proton-helium collisions. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L73. [Google Scholar] [CrossRef]
- Kirchner, T.; Knudsen, H. Current status of antiproton impact ionization of atoms and molecules: Theoretical and experimental perspectives. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 122001. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Lee, T.G.; Colgan, J. Antiproton-impact ionization of H, He and Li. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 205204. [Google Scholar] [CrossRef]
- Guan, X.; Bartschat, K. Complete Breakup of the Helium Atom by Proton and Antiproton Impact. Phys. Rev. Lett. 2009, 103, 213201. [Google Scholar] [CrossRef]
- Abdurakhmanov, I.B.; Kadyrov, A.S.; Fursa, D.V.; Bray, I.; Stelbovics, A.T. Convergent close-coupling calculations of helium single ionization by antiproton impact. Phys. Rev. A 2011, 84, 062708. [Google Scholar] [CrossRef]
- Foster, M.; Colgan, J.; Pindzola, M.S. Fully Correlated Electronic Dynamics for Antiproton Impact Ionization of Helium. Phys. Rev. Lett. 2008, 100, 033201. [Google Scholar] [CrossRef]
- Borbély, S.; Feist, J.; Tőkési, K.; Nagele, S.; Nagy, L.; Burgdörfer, J. Ionization of helium by slow antiproton impact: Total and differential cross sections. Phys. Rev. A 2014, 90, 052706. [Google Scholar] [CrossRef]
- Borbély, S.; Tong, X.-M.; Nagele, S.; Feist, J.; Březinová, I.; Lackner, F.; Nagy, L.; Tőkési, K.; Burgdörfer, J. Electron correlations in the antiproton energy-loss distribution in He. Phys. Rev. A 2018, 98, 012707. [Google Scholar] [CrossRef]
- Rodríguez, V.D.; Ramírez, C.A.; Rivarola, R.D.; Miraglia, J.E. Helium excitation by protons and highly-charged-ion impact. Phys. Rev. A 1997, 55, 4201–4208. [Google Scholar] [CrossRef]
- Alladustov, S.U.; Abdurakhmanov, I.B.; Kadyrov, A.S.; Bray, I.; Bartschat, K. Wave-packet continuum-discretization approach to proton collisions with helium. Phys. Rev. A 2019, 99, 052706. [Google Scholar] [CrossRef]
- Spicer, K.H.; Plowman, C.T.; Abdurakhmanov, I.B.; Kadyrov, A.S.; Bray, I.; Alladustov, S.U. Differential study of proton-helium collisions at intermediate energies: Elastic scattering, excitation, and electron capture. Phys. Rev. A 2021, 104, 032818. [Google Scholar] [CrossRef]
- Hall, K.A.; Reading, J.F.; Ford, A.L. Excitation and ionization of atomic hydrogen by antiprotons. J. Phys. B 1996, 29, 6123. [Google Scholar] [CrossRef]
- Kirchner, T.; Lüdde, H.J.; Kroneisen, O.J.; Dreizler, R.M. New trends in the description of ion–atom collisions by time-dependent quantum methods. Nucl. Instrum. Methods Phys. Res. B 1999, 154, 46–53. [Google Scholar] [CrossRef]
- Igarashi, A.; Ohsaki, A.; Nakazaki, S. Single ionization of helium by antiproton impact. Phys. Rev. A 2000, 62, 052722. [Google Scholar] [CrossRef]
- McGovern, M.; Assafrão, D.; Mohallem, J.R.; Whelan, C.T.; Walters, H.R.J. Differential and total cross sections for antiproton-impact ionization of atomic hydrogen and helium. Phys. Rev. A 2009, 79, 042707. [Google Scholar] [CrossRef]
- Nagy, L.; Tóth, I.; Campeanu, R.I. Electron and Positron Impact Ionization of Molecules. Atoms 2024, 12, 38. [Google Scholar] [CrossRef]
- Schneider, B.I.; Collins, L.A. The discrete variable method for the solution of the time-dependent Schrödinger equation. J. Non-Cryst. Solids 2005, 351, 1551–1558. [Google Scholar] [CrossRef]
- Rescigno, T.N.; McCurdy, C.W. Numerical grid methods for quantum-mechanical scattering problems. Phys. Rev. A 2000, 62, 032706. [Google Scholar] [CrossRef]
- Park, T.J.; Light, J.C. Unitary quantum time evolution by iterative Lanczos reduction. J. Chem. Phys. 1986, 85, 5870–5876. [Google Scholar] [CrossRef]
- Schneider, B.I.; Feist, J.; Nagele, S.; Pazourek, R.; Hu, S.; Collins, L.A.; Burgdörfer, J. Recent Advances in Computational Methods for the Solution of the Time-Dependent Schrödinger Equation for the Interaction of Short, Intense Radiation with One and Two Electron Systems. In Quantum Dynamic Imaging: Theoretical and Numerical Methods; Bandrauk, A.D., Ivanov, M., Eds.; Springer: New York, NY, USA, 2011; pp. 149–208. [Google Scholar]
- Hernandez, V.; Roman, J.E.; Vidal, V. SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 2005, 31, 351–362. [Google Scholar] [CrossRef]
- Nesbet, R.K.; Watson, R.E. Approximate Wave Functions for the Ground State of Helium. Phys. Rev. 1958, 110, 1073–1076. [Google Scholar] [CrossRef]
- Bransden, B.H.; Joachain, C.J. Physics of Atoms and Molecules; Longman & Scientific Technical: New York, NY, USA, 1983; pp. 139, 275, 285. [Google Scholar]
- Bohr, N., II. On the theory of the decrease of velocity of moving electrified particles on passing through matter. Philos. Mag. 1913, 25, 10–31. [Google Scholar] [CrossRef]
- Hippler, R.; Schartner, K.H. Absolute cross sections for the excitation of n1P-levels of helium by proton impact (150–1000 keV). J. Phys. B Atom. Mol. Phys. 1974, 7, 618. [Google Scholar] [CrossRef]
- Van den Bos, J.; Winter, G.J.; De Heer, F.J. Excitation of helium by protons in the 1–150 keV region. Physica 1968, 40, 357–384. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).