Measurement of the Tensor-Analyzing Power Component T20 for Incoherent Negative Pion Photoproduction on a Deuteron
Abstract
1. Introduction
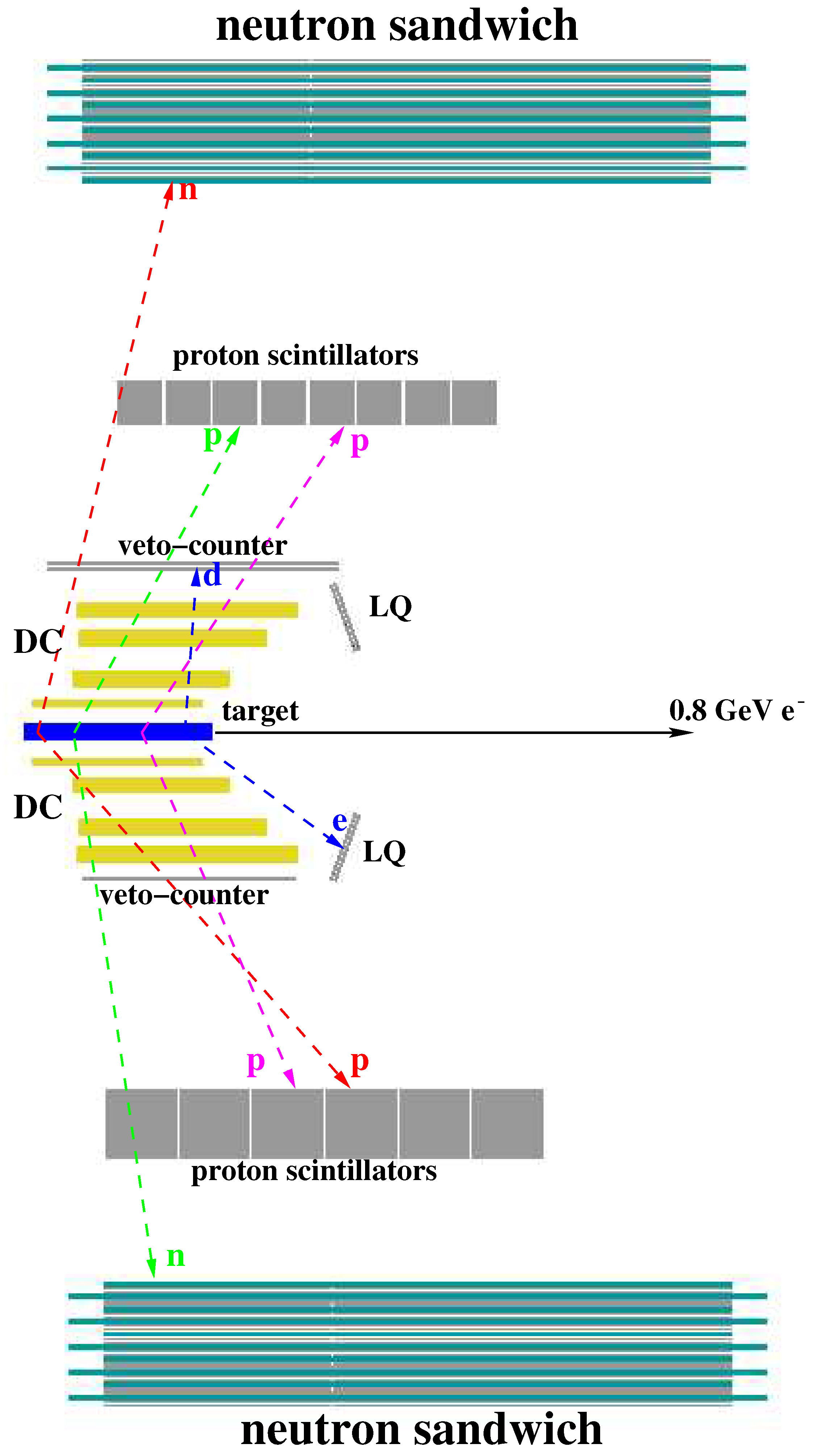
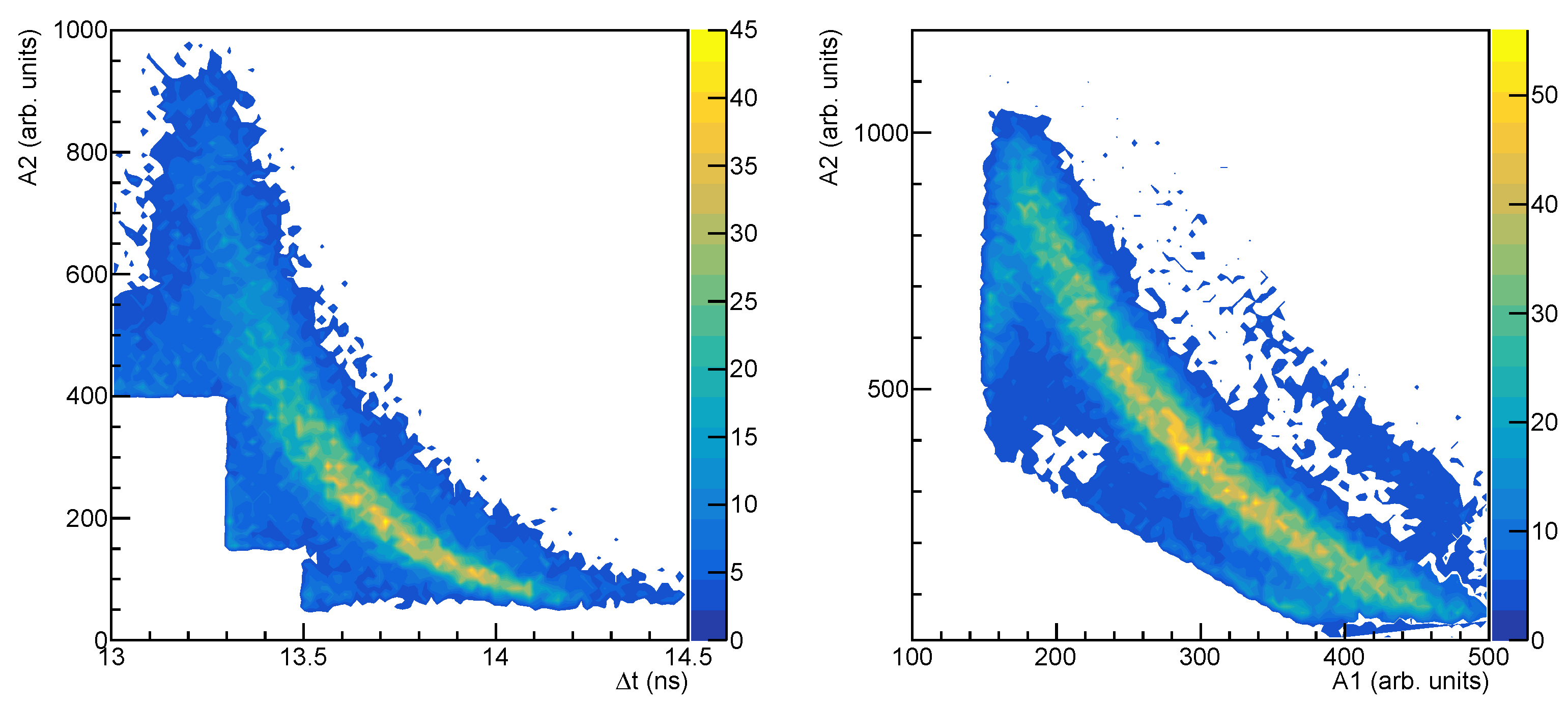
2. Experiment
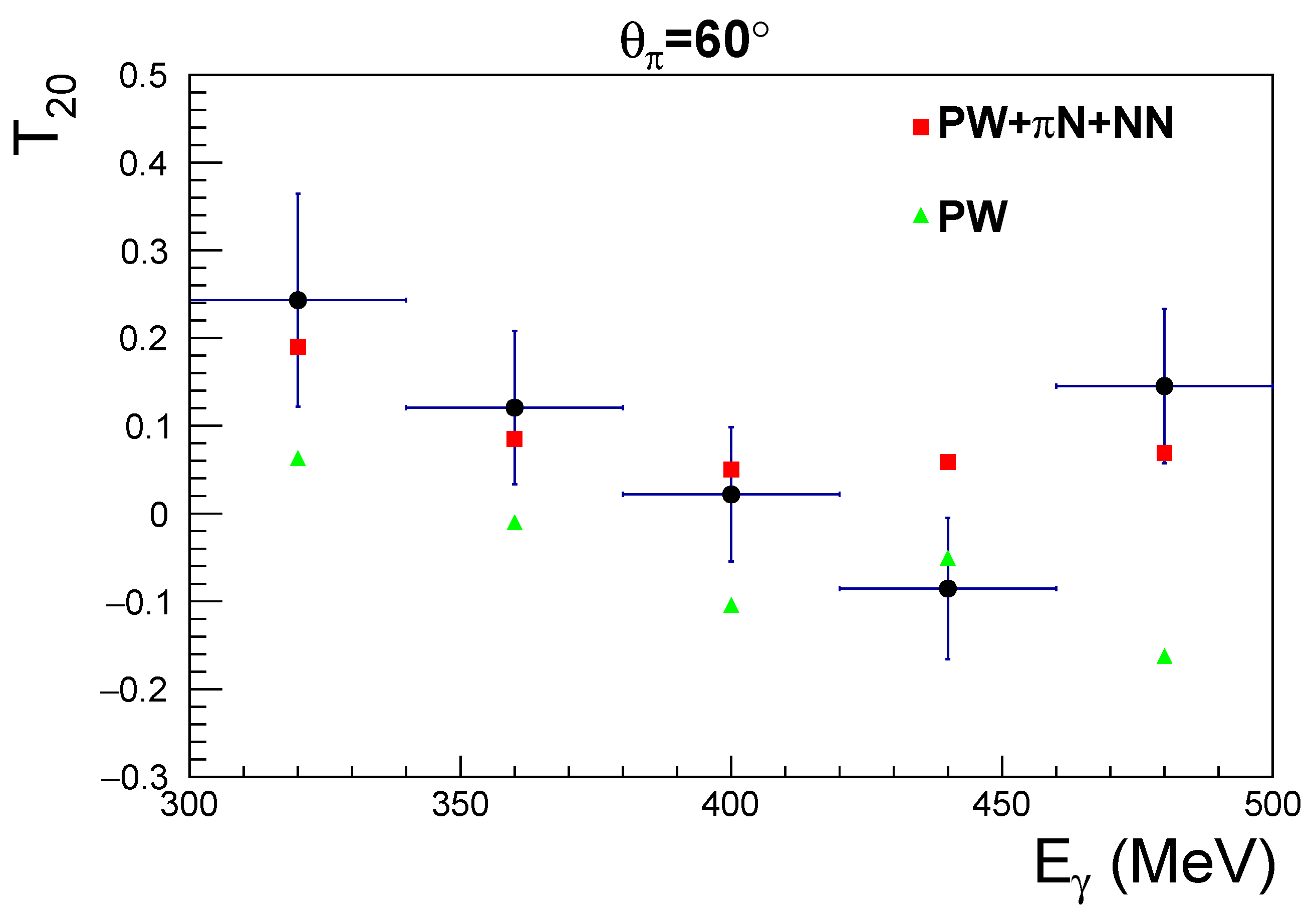
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Levchuk, M.I.; Loginov, A.Y.; Sidorov, A.A.; Stibunov, V.N. Incoherent pion photoproduction on the deuteron in the first resonance region. Phys. Rev. C 2006, 74, 014004. [Google Scholar] [CrossRef]
- Laget, J.M. Pion photoproduction on few body systems. Phys. Rep. 1981, 69, 1–84. [Google Scholar] [CrossRef]
- Fix, A.I.; Arenhövel, H. Incoherent pion photoproduction on the deuteron with polarization observables. II. Influence of final state rescattering. Phys. Rev. C 2005, 72, 064004. [Google Scholar] [CrossRef]
- Briscoe, W.J.; Kudryavtsev, A.E.; Strakovsky, I.I.; Tarasov, V.E.; Workman, R.L. On the photoproduction reactions γd→πNN. Eur. Phys. J. A 2022, 58, 23. [Google Scholar] [CrossRef]
- Strandberg, B.; Fissum, K.G.; Annand, J.R.M.; Briscoe, W.J.; Brudvik, J.; Cividini, F.; Clark, L.; Downie, E.J.; England, K.; Feldman, G.; et al. Near-threshold π− photoproduction on the deuteron. Phys. Rev. C 2020, 101, 035207. [Google Scholar] [CrossRef]
- Nikolenko, D.M.; Barkov, L.M.; Dmitriev, V.F.; Dyug, M.V.; Isaeva; Lazarenko, B.A.; Mishnev, S.I.; Rachek, I.A.; Shestakov, Y.V.; Toporkov, D.K.; et al. Measurement of polarization observables in elastic and inelastic electron-deuteron scattering at the VEPP-3 storage ring. Nucl. Phys. A 2001, 684, 77–85. [Google Scholar] [CrossRef]
- Nikolenko, D.M.; Arenhövel, H.; Barkov, L.M.; Belostotsky, S.L.; Dmitriev, V.F.; Dyug, M.V.; Gilman, R.; Holt, R.J.; Isaeva, L.G.; De Jager, C.W.; et al. Measurement of the tensor analyzing powers T20 and T21 in elastic electron deuteron scattering. Phys. Rev. Lett. 2003, 90, 072501. [Google Scholar] [CrossRef]
- Rachek, I.A.; Barkov, L.M.; Belostotsky, S.L.; Dmitriev, V.F.; Dyug, M.V.; Gilman, R.; Holt, R.J.; Lazarenko, B.A.; Mishnev, S.I.; Nelyubin, V.V.; et al. Measurement of Tensor Analyzing Powers in Deuteron Photodisintegration. Phys. Rev. Lett. 2007, 98, 182303. [Google Scholar] [CrossRef]
- Loginov, A.Y.; Osipov, A.V.; Sidorov, A.A.; Stibunov, V.N.; Voitsekhovskii, B.B.; Nikolenko, D.M.; Popov, S.G.; Rachek, I.A.; Toporkov, D.K.; Tsentalovich, E.P. Investigation of the reaction D(e,pp)e′π− on a tensor polarized deuterium target at high proton momenta. JETP Lett. 1998, 67, 770–776. [Google Scholar] [CrossRef]
- Gauzshtein, V.V.; Gramolin, A.V.; Lazarenko, B.A.; Loginov, A.Y.; Mishnev, S.I.; Nikolenko, D.M.; Rachek, I.A.; Sadykov, R.S.; Shestakov, Y.V.; Toporkov, D.K.; et al. Measurement of tensor analyzing powers of the incoherent pion photoproduction on a deuteron. Nucl. Phys. A 2017, 968, 23–30. [Google Scholar] [CrossRef]
- Lukonin, S.E.; Gauzshtein, V.V.; Levchuk, M.I.; Loginov, A.Y.; Nikolenko, D.M.; Rachek, I.A.; Sadykov, R.S.; Shestakov, Y.V.; Toporkov, D.K.; Zevakov, S.A. Measurement of tensor analyzing power components for the incoherent π0-meson photoproduction on a deuteron. Nucl. Phys. A 2019, 986, 75–84. [Google Scholar] [CrossRef]
- Vasilishin, B.I.; Fix, A.I.; Gauzshtein, V.V.; Darwish, E.M.; Kuzin, M.Y.; Levchuk, M.I.; Loginov, A.Y.; Nikolenko, D.M.; Rachek, I.A.; Shestakov, Y.V.; et al. Measurement of the tensor analyzing power component T20 for the incoherent neutral-pion photoproduction on a deuteron. Phys. Rev. C 2022, 106, 024003. [Google Scholar] [CrossRef]
- Dyug, M.V.; Isaeva, L.G.; Lazarenko, B.A.; Mishnev, S.I.; Nikolenko, D.M.; Rachek, I.A.; Shestakov, Y.V.; Sadykov, R.S.; Toporkov, D.K.; Zevakov, S.A.; et al. Internal polarized deuterium target with cryogenic atomic beam source. Nucl. Instrum. Methods A 2002, 495, 8–19. [Google Scholar] [CrossRef]
- Dyug, M.V.; Lazarenko, B.A.; Mishnev, S.I.; Nikolenko, D.M.; Rachek, I.A.; Shestakov, Y.V.; Sadykov, R.S.; Toporkov, D.K.; Zevakov, S.A.; Osipov, A.N.; et al. Deuterium Target Polarimeter at the VEPP-3 Storage Ring. Nucl. Instrum. Methods A 2005, 536, 344–349. [Google Scholar] [CrossRef]
- Iljinov, A.S.; Pshenichnov, I.A.; Bianchi, N.; De Sanctis, E.; Muccifora, V.; Mirazita, M.; Rossi, P. Extension of the intranuclear cascade model for photonuclear reactions at energies up to 10 Gev. Nucl. Phys. A 1997, 616, 575–592. [Google Scholar] [CrossRef]
- Loginov, A.Y.; Sidorov, A.A.; Stibunov, V.N. Effect of rescattering on polarization observables of the reaction γd→ppπ− in the delta-resonance region. Phys. At. Nucl. 2000, 63, 391–398. [Google Scholar] [CrossRef]
- Garcilazo, H.; Moya de Guerra, E. A model for pion electro- and photo-production from threshold up to 1 GeV. Nucl. Phys. A 1993, 562, 521–568. [Google Scholar] [CrossRef]
- Olsson, M.G.; Osipowski, E.T. Systematics of low-energy πN scattering. Nucl. Phys. B 1975, 101, 136–158. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Plessas, W. Separable representation of the Paris nucleon-nucleon potential. Phys. Rev. C 1984, 30, 1822–1839. [Google Scholar] [CrossRef]
- Smirnov, Y.F.; Tchuvil’sky, Y.M. Isobaric component of deuteron in the quark model. J. Phys. G 1978, 4, L1. [Google Scholar] [CrossRef]
- Kukulin, V.I.; Obukhovsky, I.T.; Pomerantsev, V.N.; Faessler, A. New mechanism for intermediate- and short-range nucleon-nucleon interaction. J. Phys. G 2001, 27, 1851–1864. [Google Scholar] [CrossRef]
- Kukulin, V.I.; Obukhovsky, I.T.; Grabmayr, P.; Faessler, A. Isoscalar short-range current in the deuteron induced by an intermediate dibaryon. Phys. Rev. C 2006, 74, 064005. [Google Scholar] [CrossRef]
- Kukulin, V.I.; Rubtsova, O.A.; Platonova, M.N.; Pomerantsev, V.N.; Clement, H.; Skorodko, T. Nature of S-wave NN interaction and dibaryon production at nucleonic resonance thresholds. Eur. Phys. J. A 2020, 56, 229. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuzmenko, A.; Gauzshtein, V.; Darwish, E.; Fix, A.; Kuzin, M.; Levchuk, M.; Loginov, A.; Nikolenko, D.; Rachek, I.; Shestakov, Y.; et al. Measurement of the Tensor-Analyzing Power Component T20 for Incoherent Negative Pion Photoproduction on a Deuteron. Atoms 2023, 11, 99. https://doi.org/10.3390/atoms11060099
Kuzmenko A, Gauzshtein V, Darwish E, Fix A, Kuzin M, Levchuk M, Loginov A, Nikolenko D, Rachek I, Shestakov Y, et al. Measurement of the Tensor-Analyzing Power Component T20 for Incoherent Negative Pion Photoproduction on a Deuteron. Atoms. 2023; 11(6):99. https://doi.org/10.3390/atoms11060099
Chicago/Turabian StyleKuzmenko, Anna, Vyacheslav Gauzshtein, Eed Darwish, Alexander Fix, Matvey Kuzin, Michael Levchuk, Alexey Loginov, Dmitriy Nikolenko, Igor Rachek, Yuriy Shestakov, and et al. 2023. "Measurement of the Tensor-Analyzing Power Component T20 for Incoherent Negative Pion Photoproduction on a Deuteron" Atoms 11, no. 6: 99. https://doi.org/10.3390/atoms11060099
APA StyleKuzmenko, A., Gauzshtein, V., Darwish, E., Fix, A., Kuzin, M., Levchuk, M., Loginov, A., Nikolenko, D., Rachek, I., Shestakov, Y., Toporkov, D., Yurchenko, A., Vasilishin, B., & Zevakov, S. (2023). Measurement of the Tensor-Analyzing Power Component T20 for Incoherent Negative Pion Photoproduction on a Deuteron. Atoms, 11(6), 99. https://doi.org/10.3390/atoms11060099





