Abstract
We considered the resonance scattering of ultrashort laser pulses (USLP) on the bound electrons of hydrogen-like ions in a dense plasma. A process description was proposed in terms of full scattering probability during the time of pulse action. Dense plasma’s effect was demonstrated at the resonance scattering cross-section spectrum, and the probability dependence on USLP carrier frequency and duration was obtained for the cases of isolated ions and ions in a dense plasma.
1. Introduction
Plasma physics operates according to the statistical properties of systems consisting of many charged particles, where Coulomb forces on collective effects play a significant role [1]. With increasing electron density, plasma acquires the properties of condensed matter, and the neglection of short-distance forces becomes incorrect. Thus, the subject of consideration is a strongly correlated Coulomb system in which quantum statistics, as well as dynamic effects, should be taken into account [2,3]. Hence, building a proper theoretical model describing dense plasma processes can address problems related to nuclear, atomic, and molecular physics. The solution to this issue demands lots of experimental data. One of the most efficient methods for studying classic plasma parameters is laser diagnostics. For high-density matter sensing with the appropriate spatial and time resolution, ultrashort x-ray pulse generation is essential [4]. USLP’s duration is too small to consider it monochromatic. Generally, the probabilistic models of laser–matter interaction operate according to the notion of probability per unit of time with monochromatic and stationary photon flux [5]. Thus, these models should be reconsidered.
Works describing ultrashort-pulse interactions with atomic systems in terms of probability and full probability during the pulse action exist. For example, in [6], the authors dealt with quasi-stationary non-monochromatic radiation that made it possible to introduce probability per unit of time and consider constant energy flux. Thus, the description of the interaction in terms of the scattering of the cross-section normalized on the spectral width of the non-monochromatic radiation is valid. However, such an approach does not consider pulse duration. Our model considers non-stationary radiation flux and allows researching the dependencies of photoprocessing characteristics on the pulse duration. The authors of [7,8,9] studied the interaction of subcycle pulses with quantum systems at durations much less than the characteristic time of electron oscillations. Photoprocesses’ probability dependence on pulse duration was described in detail. Another work dealing with sudden perturbation approximation proposed a description of a wide class of photoprocesses in the field of USLP [10,11]. Nevertheless, the approach presented in [7,8,9] is applicable only for subcycle pulses as well as sudden perturbation approximation, upon which the work carried out in [10,11] rely, and is valid for USLP durations much lower than the inner atomic process time. The model we suggest has no restriction in terms of the cycle number or duration of USLP and could be universalized in various systems.
The general formulas of ultrashort laser pulse (USLP) scattering on atoms were obtained in [12]. A later work [13] was devoted to the consideration of femtosecond pulse resonance scattering on atoms in plasma. In the present paper, we presented a model of ultrashort laser pulse (USLP) resonance scattering on bound electrons in dense plasma, which was formulated in terms of the full probability during the time of pulse action. We assessed the full probability dependence on USLP carrier frequency and duration. Special attention was paid to the particularities of dependencies defined by high plasma density.
2. General Formulas
To calculate the full probability of photoprocessing in the field of USLP during pulse action, we used the following Formula [12]:
where c—speed of light in vacuum and ℏ—Planck constant. We consider the Gauss shape of USLP electric field strength Fourier transform E(ω,ωc,τ):
where E0—electric field amplitude, and ωc, τ—carrier frequency and duration of USLP, respectively.
Equation (1) enables a connection between the full probability and scattering cross-section σsc. In the framework of dipole approximation, the scattering cross-section could be expressed through dynamic polarizability β [5]:
The scope of the present work determining the scattering of bound electrons. The Feynman diagram, illustrating this process, is presented in Figure 1 [14].
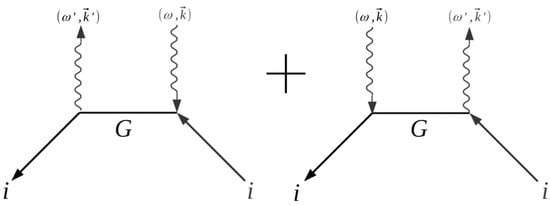
Figure 1.
Feynman diagram of scattering of bound electrons.
An absorbing photon with a four-wavevector (ω,k) electron is transmitted from the state |i> into the virtual state |j>, after which it returns to the initial state |i>, reradiating the absorbed photon with four-wavevector (ω′,k′). In the case of resonance scattering, only resonance virtual states |j> contribute to the Green function of a bound electron.
In the present paper, we considered resonance transitions from the ground state 1s to np-shells in hydrogen-like ions, taking into account their fine structure.
The dependence of dynamic polarizability on the frequency of transition 1s → np with the allowance of fine-structure splitting could be described by the following formula [13]:
where e—electron charge and me—electron mass. The spectral line of an atom is determined by three parameters: oscillator strength fij, transition frequency ωij, and Einstein coefficient of spontaneous transition Aij.
As ions are involved in thermal motion, spectral lines are subjected to Doppler broadening. To consider this fact, we average |β(ω)|2 over the ion velocity projections υx on the direction of the wave vector of the incident photon following the Maxwell distribution [13]:
where Ti—ion temperature in eV. In the present work, we consider equilibrium plasma (Te = Ti).
The final formula for the scattering cross-section on bound electrons for ions involved in chaotic thermal motion is as follows:
Thus, the knowledge of atomic transition parameters and USLP parameters along with Formulas (1), (2), (5), and (6) provide descriptions of USLP scattering on bound electrons in terms of the full probability during pulse action.
In the case of isolated hydrogen-like ions, line parameters could be calculated by simple analytical Expressions (7)–(9).
A rigorous formula for oscillator strength is as follows [14]:
where gj is the statistical weight of the state with the full electron momentum equal to j.
The strict quantum mechanical description of motion in the centrally symmetric field gives the formula for transition frequency [14]:
where α—fine structure constant and Z—the atomic number.
The Einstein coefficient for a spontaneous transition between the state with the main quantum number n and the ground state is described by the following rigorous formula [14]:
where Ry—Rydberg.
In the case of dense plasma, delocalized electron shielding has a sufficient impact on the parameters of the spectral line. Using the finite temperature ion sphere model, the authors of [15] investigated how plasma screening affects the parameters of atomic electron transitions. In particular, under the dipole approximation, they calculated spectral radiative transition rates and oscillator strengths as well as estimated correction terms to transition frequencies. Spectral line parameters for 1s → npj transitions in Si13+ ion, published in [15], are presented in Table 1 for n = {2, 3, 4} and j = {1/2, 3/2} for dense plasma. Besides, for comparison, it contains line parameters for isolated ions calculated by Formulas (7)–(9).

Table 1.
Spectral line parameters for 1s→np transitions (fnpj1s, ωnpj1s, An1) in Si13+ ions for the case of dense plasma at different values of plasma electron density and temperatures [15] as well as for isolated ions.
The advantage of the described method is the simplicity of the numerical calculations. The simulations do not require any sophisticated algorithms and could be performed with the use of an ordinary PC.
3. Results and Discussion
Figure 2 demonstrates the scattering cross-section calculated with the use of data presented in Table 1. Among the all considered plasma conditions, only in the case of 1s→2p transition was fine splitting distinguishable (Figure 2a). In cases 1s→3p and 1s→4p, the fine structure blurred as the gap between the peaks of the fine structure was commensurable with Doppler broadening .
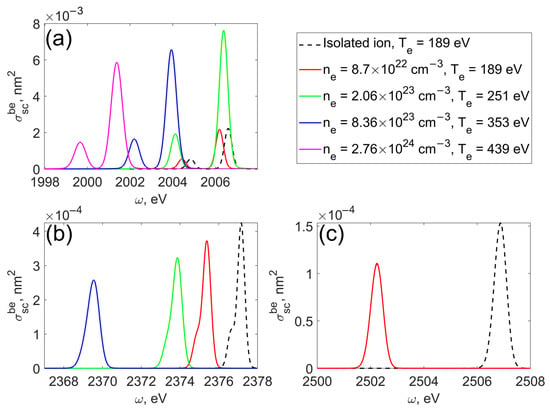
Figure 2.
Resonance scattering cross-section spectrum for electron transition in Si13+ ion: 1s→2p (a), 1s→3p (b), and 1s→4p (c). Solid lines correspond to calculations for ions shielded by dense plasma, and dashed lines represent the calculations for isolated ions.
The screening of Coulomb interactions induced by the plasma environment affects the atomic structure and radiative atomic data. Hence, the phases and amplitudes of continuum wave functions change. Thus, according to the configuration interaction method, the energy of considered levels decreases. The latter is clearly expressed by the red shift of spectral peaks at the electron density increase in relation to the graphs plotted for isolated ions in accordance with Formulas (5)–(9). Exclusion is the 1s1/2→2p3/2 transition, whose frequency increases at the density increase from 8.7·1022 cm−3 to 2.06·1023 cm−3 (green spectral peak with higher frequency in Figure 2). In this case, level 2s1/2 undergoes a larger energy shift than other levels as its wavefunction is more sensitive to changes in the plasma shield. Configuration interaction of 1s1/2 and 2s1/2 leads to a more significant energy decrease of 1s1/2 energy than 2p1/2 and 2p3/2. As a result, the energy gap between 1s1/2 and 2p3/2 is greater than for other transitions [16].
Figure 3a demonstrates the dependence of the resonance scattering probability by bound electron on USLP carrier frequency at the variation of electron plasma density. It is clearly seen that the dynamics of the Wsc(ωc) profile are identical to the cross-section dynamic illustrated in Figure 2. Figure 3b demonstrates how the Wsc(ωc) profile changes according to pulse duration variation. At durations in order of 0.1 fs, dependence had a bell-shaped curve, almost symmetric about the frequency of the 1s1/2→2p3/2 transition. With the increase in the pulse duration, the USLP spectrum narrowed, and for carrier frequencies near the 1s1/2→2p1/2 transition frequency, the scattering probability component corresponding to transition 1s1/2→2p3/2 decreased. Thus, with an increase in the pulse duration, the maximum corresponding to 1s1/2→2p1/2 appeared.
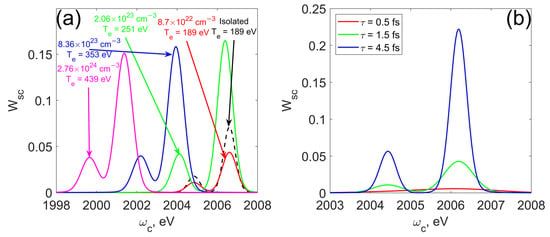
Figure 3.
Dependence of resonance USLP scattering probability on carrier frequency in the vicinity of 1s→2p transition frequency at various plasma densities for τ = 1.5 fs (a) and USLP durations (b) for ne = 8.7·1022 cm−3, Te = 189 eV (b). E0 = 1 a.u.
The probability dependence on the USLP duration (τ-dependence) had different trends at durations τ ~ 1 fs, including non-monotonic (Figure 4). When carrier frequency was in the vicinity of spectral maximum (green line in Figure 4), the τ-dependence monotonically grew. Greater corresponds to a greater steepness of Wsc(τ). From a certain detuning of ωc from a maximum of , the τ-dependence became non-monotonic. In the vicinity of τ~1 fs, the maximum and minimum appeared (i.e., the magenta curve in Figure 4). The mechanism of non-monotonic dependence at small τ USLP comprises non-monotonic changes of the integral value to which probability (1) is proportional, due to the commensurability of the scattering cross-section and USLP spectral width. When the carrier frequency was out of the spectral maximum vicinity and the scattering cross-section was negligibly small, the probability was nonzero at small durations (cyan line in Figure 4) as the USLP spectral width was large enough to overlap with the scattering cross-section maxima. As the USLP duration increased, the overlapping degree of and decreased, and the τ-dependence tended to zero.
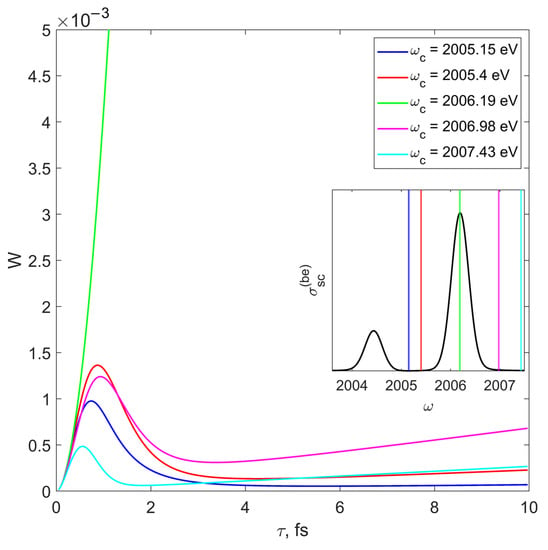
Figure 4.
τ-dependence of USLP scattering probability on bound electrons in dense plasma for carrier frequencies in the vicinity of 1s→2p transition frequency. The subplot illustrates carrier frequency positions in relation to the scattering cross-section spectra. ne = 8.7·1022 cm−3, Te = 189 eV, E0 = 1 a.u.
Density affects the τ-dependency trend (Figure 5). As discussed above, as the density increased, peaks of Wsc(ωc) shifted. Thus, nonmonotonic trends are shown. Greater plasma density corresponds to less τmax and τmin values according to the local maximum and minimum of τ-dependence. As the peak of Wsc(ω), to which the isolated case ωc is oriented, shifted, the magnitude of τ-dependence decreased.
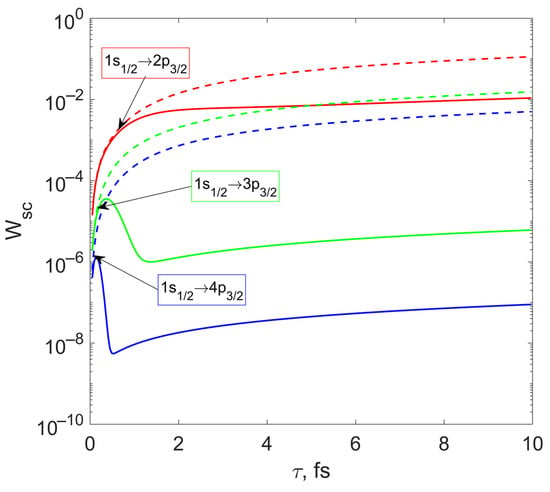
Figure 5.
τ-dependence of the scattering probability on bound electrons of ions in dense plasma (solid lines) and for isolated ions (dashed lines). Transitions 1s1/2→np3/2 are considered at Te = 189 eV and in the case of the shield ion at electron density ne = 8.7·1022 cm−3. USLP carrier frequency corresponds to the maximum of W(ωc) dependence in the case of isolated ions.
4. Conclusions
In the present paper, we studied the particularities of resonance ultrashort laser pulse scattering on bound electrons in dense plasma. Studying the cross-section spectra and dependency of resonance scattering probability on USLP carrier frequency and duration, we determined the effects of dense plasma.
Due to dense plasma screening, cross-section spectrum and probability dependence on the carrier frequency, in general, had a redshift as the density increased. We considered the dependence of scattering probability on USLP duration (τ-dependence) and demonstrated that. in general, it is not a monotonic function. Separately, we showed that as the plasma density increased, the τ-dependence trend became non-monotonic and USLP durations, corresponding to extremums, decreased. Along with this, the scattering probability magnitude radically decreased.
Typical trends of τ-dependence were herein assessed. We demonstrated that for carrier frequency in the vicinity of spectral maximum, τ-dependence monotonically rises, and the greater the scattering of the cross-section, the greater the steepness of τ-dependence. At the carrier frequencies detuned from the the spectral maximum for a certain value, the local maximum and minimum of the considered function appeared due to the complex τ-dependence of the overlapping area between the scattering cross-section and the USLP spectrum. If the cross-section value at the carrier frequency was negligibly small, τ-dependence was nonzero at low pulse durations due to the broad USLP spectrum.
In the example 1s→2p transition in Si13+ ions, we assessed full scattering probability as a function of carrier frequency and established that as the USLP duration decreases, the dependence profile broadens and at after a certain duration, the fine splitting of the atomic energy level becomes indistinguishable.
Author Contributions
Writing—original draft preparation, E.S.K.; writing—review and editing, V.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation, Agreement No. 22-22-00537.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, F.F. Plasma Physics and Controlled Fusion; Plenum Press: New York, NY, USA; London, UK, 1984; p. 421. [Google Scholar]
- Kraeft, W.D.; Kremp, D.; Ebeling, W.; Ropke, G. Quantum Statistics of Charged Particle Systems; Akademie-Verlag: Berlin, Germany, 1986; p. 298. [Google Scholar]
- Ichmaru, S. Statistical Plasmas Physics: Condensed Plasmas; Westview Press: Oxford, UK, 2004; p. 304. [Google Scholar]
- Lindroth, E.; Calegari, F.; Young, L.; Harmand, M.; Dudovich, N.; Berrah, N.; Smirnova, O. Challenges and opportunities in attosecond and XFEL science. Nat. Rev. Phys. 2019, 1, 107–111. [Google Scholar] [CrossRef]
- Rosmej, F.B.; Astapenko, V.A.; Lisitsa, V.S. Plasma Atomic Physics; Springer International Publishing: Berlin, Germany, 2021; p. 650. [Google Scholar]
- Gorbunov, L.; Salikhov, D. Scattering of nonmonochromatic radiation. Radiophys. Quantum Electron. 1981, 24, 759–763. [Google Scholar] [CrossRef]
- Arkhipov, R.; Pakhomov, A.; Arkhipov, M.; Demircan, A.; Morgner, U.; Rosanov, N.; Babushkin, I. Selective ultrafast control of multi-level quantum systems by subcycle and unipolar pulses. Opt. Express 2020, 28, 17020–17034. [Google Scholar] [CrossRef] [PubMed]
- Pakhomov, A.; Arkhipov, M.; Rosanov, N.; Arkhipov, R. Ultrafast control of vibrational states of polar molecules with subcycle unipolar pulses. Phys. Rev. A 2022, 105, 043103. [Google Scholar] [CrossRef]
- Arkhipov, R.M.; Pakhomov, A.V.; Arkhipov, M.V.; Babushkin, I.; Demircan, A.; Morgner, U.; Rosanov, N.N. Unipolar subcycle pulse-driven nonresonant excitation of quantum systems. Opt. Lett. 2019, 44, 1202–1205. [Google Scholar] [CrossRef]
- Matveev, V.I. Emission and electron transitions in an atom interacting with an ultrashort electromagnetic pulse. J. Exp. Theor. Phys. 2003, 97, 915–921. [Google Scholar] [CrossRef]
- Makarov, D.N.; Matveev, V.I. Spectra for the reemission of attosecond and shorter electromagnetic pulses by multielectron atoms. J. Exp. Theor. Phys. 2017, 125, 189–194. [Google Scholar] [CrossRef]
- Astapenko, V.A. Scattering of an ultrashort electromagnetic radiation pulse by an atom in a broad spectral range. J. Exp. Theor. Phys. 2011, 112, 193–198. [Google Scholar] [CrossRef]
- Rosmej, F.B.; Astapenko, V.A.; Lisitsa, V.S.; Moroz, N.N. Nonlinear resonance scattering of femtosecond X-ray pulses on atoms in plasmas. Phys. Lett. A 2017, 381, 3576–3579. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamic; Butterworth-Heinemann: Oxford, UK, 1982; Volume 4. [Google Scholar]
- Zeng, J.; Li, Y.; Yuan, J. Effects of plasma screening on radiative transition and photoionization of Si10+–Si13+ in a dense plasma environment. J. Quant. Spectrosc. Radiat. Transf. 2021, 272, 107777. [Google Scholar] [CrossRef]
- Zeng, J.; (College of Science, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China). Private Communication, 2022.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).