Simple Summary
Tetra-coordinated carbon-containing molecules generally form tetrahedral carbon geometries. However, there are continuous searches for other possible geometries of tetra-coordinated carbon which are non-classical in nature. However, planar tetra-coordinated carbon (ptC), where all four bonds of the carbon atom are in the same plane or the pyramidane structure in which tetra-coordinated carbon with all four bonds are on the same side of a plane, are good examples of non-classical structures. However, synthesis and experimental realization of these molecules are very challenging in the laboratory. In this paper, we have theoretically investigated nine unusual isomers of the molecular formula C5H4 and studied their stability and novel bonding patterns. One of the ptC compounds has been found to be thermodynamically more stable compared to its tetrahedral counterpart with a high value of dipole moment (μ = 4.64 D), which may be helpful for experimental detection in the laboratory or in the low-temperature regions of the interstellar medium.
Abstract
We have theoretically investigated nine unusual isomers of the molecular formula C5H4 using coupled cluster (CC) and density functional theory (DFT) methods. These molecules possess non-classical structures consisting of two pyramidanes, three planar tetracoordinate carbon (ptC), and four spiro types of isomers. Both the pyramidanes (tetracyclo-[2.1.0.01,3.02,5]pentane; py-1 and tricyclo-[2.1.0.02,5]pentan-3-ylidene; py-2) are minima on the potential energy surface (PES) of C5H4. Among the three isomers containing ptC, (SP4)-spiro [2.2]pent-1-yne (ptC-2) is a minimum, whereas isomer, (SP4)-spiro [2.2]pent-1,4-diene (ptC-1) is a fourth-order saddle point, and (SP4)-sprio[2.2]pent-1,4-diylidene (ptC-3) is a transition state. The corresponding spiro isomers spiro[2.2]pent-1,4-diene (spiro-1), sprio[2.2]pent-1,4-diylidene (spiro-3) and spiro[2.2]pent-4-en-1-ylidene (spiro-4) are local minima, except spiro[2.2]pent-1-yne (spiro-2), which is a second-order saddle point. All relative energies are calculated with respect to the global minimum (pent-1,3-diyne; 1) at the CCSD(T)/cc-pVTZ level of theory. Quantum chemical calculations have been performed to analyze the bonding and topological configurations for all these nine isomers at the B3LYP/6-311+G(d,p) level of theory for a better understanding of their corresponding electronic structures. ptC-2 was found to be thermodynamically more stable than its corresponding spiro counterpart (spiro-2) and possesses a high dipole moment (μ = 4.64 D). The stability of the ptC structures with their higher spin states has been discussed.
1. Introduction
Tetrahedral carbon is the fundamental paradigm of organic chemistry introduced independently by van’t Hoff and Le-Bel in 1874 [1,2]. However, with the development of different experimental and theoretical margins, scientists have widely explored the possibility of non-classical proclivities (i.e., anti-van’t Hoff and Le Bel molecules) with unusual bonding features of the tetracoordinate carbon or silicon atoms [3,4,5,6]. Planar tetra-coordinated carbon (ptC), where all four bonds of the carbon atom are in the same plane or the pyramidane structure in which tetra-coordinated carbon with all four bonds are on the same side of a plane, are good examples of non-classical structures. Along with these structures, spiro compounds with tetrahedral carbon centers have also become esoteric targets for organic chemists to design and synthesize in the laboratory [7,8,9,10].
Although simple hydrocarbons with ptC moiety have not been experimentally detected in the laboratory to date, many theoretical and experimental research groups have designed such molecules [4,5,9,10,11,12,13,14,15,16,17]. Hoffmann et al. explored the stability of planar methane and its derivatives for the first time in 1970 [18]. Based on their calculations, they have suggested a few rules to stabilize molecules with ptC, such as to include the lone pair in the bonding framework by replacing one or more hydrogen atoms with good σ-donor/π-acceptor ligands or, alternatively, by incorporating the lone pair into a (4n + 2) π delocalized system. Commonly, two approaches have been used to design ptC structures: the first is to obtain the planar structure under forcible structural constraints from supporting fragments [19,20,21], and the second is through electronic stabilization of the ptC center using σ-donor and π-accepting groups by employing transition metal fragments or main group elements and controlling suitable charge on the skeleton [14,17,19,21,22,23,24,25,26,27,28,29,30,31,32]. Rasmussen and Radom discussed the evolution of the potential solution of this problem by considering ptC in the cycloalkane systems [33].
Despite being challenging, molecules with a ptC atom among hydrocarbons have been drawing huge attention from theoretical scientists. Sastry et al. theoretically designed several neutral hydrocarbons with ptCs and discussed the stabilization of the planar arrangements through the negative of the absolute shielding nucleus independent chemical shift (NICS) values and suggested the unique bonding mode of the planar arrangements, which is stabilized through high delocalization of π –framework or aromatization of the rings [34]. Thimmakondu et al. have theoretically shown that two isomers of C5H2 with ptC atom, (SP-4)-spiro[2.2]pent-1,4-dien-1,4-diyl and (SP-4)-spiro[2.2]pent-1,4-dien-1,5-diyl [35] that can act as reactive intermediates for the formation of ethynylcyclopropenylidene, which had been astronomically identified in Taurus Molecular Cloud-1 (TMC-1) [36,37] as well as in the laboratory [38,39,40]. The Vennapusa group has recently considered the semi-saturated planar tetracoordinate carbon molecule of C7H4 molecular formula and studied the nonadiabatic relaxation dynamics [41]. Priyakumar et al. have studied the stereomutation between [R]- and [S]-stereoisomers of tetrahedral centers via the planar tetracoordinate atoms [42].
Apart from ptCs, pyramidane structures have also shown unusual bonding patterns. In chemistry, the compound possessing the shape of a square pyramid is called pyramidane. Four bonds are symmetrically oriented around a central axis when the pyramidal carbon lies on a C4v axis. Stohrer and Hoffman had first introduced the stable pyramidal structure for (CH)5+ in 1972 followed by several other groups over the years [43,44,45]. Schaefer et al. explored the potential energy surface of the molecular formula of C5H4 around the pyramidane isomers [46]. Errol Lewars theoretically studied the pyramidane, tetracyclo[2.1.0.01,302,5]pentane, a neutral minima isomer in the potential energy surface of C5H4 at the QCISD(T)/6-31G*//MP2(FC)/6-31G* level of theory [47]. Besides the pyramidane in hydrocarbons, few silicon analogues of similar structures have been studied theoretically where stable pyramidal structures had been reported with the bare apical silicon atoms [48,49,50].
A comprehensive knowledge of the electronic structures of these hydrocarbons can provide valuable insights into the principles of non-classical bonding and can have practical implications in designing new materials with specific electronic properties. In this paper, we endeavor to the electronic structures of the possible ptC, pyrimidine, and spiro type of isomers of the molecular formula C5H4 using density functional theory (DFT) and coupled cluster (CC) methods. C5H4 is one of the simplest structures where all these stereochemical proclivities are possible. Considering the different types of unusual bonding patterns in the non-classical molecules, nine hydrocarbons with molecular formula C5H4 have been considered for the present study. Among the nine isomers, two pyramidane structures are tetracyclo-[2.1.0.01,3.02,5]pentane (py-1) and tricyclo-[2.1.0.02,5]pentan-3-ylidene (py-2); three ptCs are (SP4)-spiro[2.2]pent-1,4-diene (ptC-1), (SP4)-sprio[2.2]pent-1-yne (ptC-2), (SP4)-sprio[2.2]pent-1,4-diylidene (ptC-3); and rest of the four isomers are spiro compounds: spiro[2.2]pent-1,4-diene (spiro-1), spiro[2.2]pent-1-yne (spiro-2), sprio[2.2]pent-1,4-diylidene (spiro-3), and spiro[2.2]pent-4-en-1-ylidene (spiro-4). Different bonding topologies have been discussed to get an insight of the non-classical nature of these molecules and to explain the bonding patterns of these isomers. Among the three ptCs, the ptC-2 is the only isomer which is at a minimum on the C5H4 PES and more stable than the corresponding tetrahedral form (spiro-2). The kinetic stability of these non-classical structures has been also studied using ab initio molecular dynamics (AIMD) simulations.
2. Computational Methodology
Initially, we designed 13 possible geometries of molecular formula C5H4 consisting of three pyramidanes, five ptCs, and five spiro molecules (Figure S1). These structures were subjected to geometry optimization using DFT at the B3LYP [51,52] /6-311+G(d,p) [53,54] level of theory without applying any geometrical or symmetry constraints. Some initial structures did not converge to the desired geometry; however, after multiple trials we could optimize two pyramidanes, three ptCs, and four spiro structures. These optimized structures were then subjected to frequency calculation to check the number of imaginary frequencies (NImag) and to ascertain whether the isomer is a minimum or higher-order saddle point or transition state on the C5H4 PES.
Furthermore, the structures of all nine isomers have been optimized and frequencies have been calculated using the Møller–Plesset perturbation theory (MP2) [55] and also at the ωB97XD [56,57] /6-311+G(d,p) level that incorporates the empirical dispersion corrections [56]. Further, considering the DFT-optimized geometries as initial guess structures, geometry optimization has been carried out at the coupled-cluster singles and doubles with quasi-perturbative triple excitation [CCSD(T)] methods [58,59,60] using Dunning’s correlation-consistent polarized valence triple-zeta basis set (cc-pVTZ) [61,62,63] for all isomers. After geometry optimization, harmonic vibrational frequencies were computed at the fc-CCSD(T)/cc-pVTZ level of theory. NICS calculations have been carried out to evaluate the aromatic nature of molecules at the B3LYP/6-311+G(d,p) level. All DFT calculations were performed using the Gaussian 09 suite of programs [64] and all CC calculations have been carried out using CFOUR program package [65] and ORCA [66]. The nature of bonding between the C-C and C-H atoms have been studied using the topological analysis of ‘atoms in molecule’ (AIM) formalism employing the multifunctional wavefunction analyzer program, Multiwfn [67]. AIMD simulation calculations have been performed to check the kinetic stability of these isomers under different thermal conditions [68].
3. Results and Discussions
All nine isomers considered in the present study are shown in Figure 1 and 3D ball-stick models of the optimized geometries, along with the atom numbers, of all the isomers are shown in Figure 2. The relative energies of these isomers are calculated with respect to the most stable isomer, pent-1,3-diyne (1), which is the global minimum on the C5H4 PES. Here we note that, 1 had been detected in the dark dust cloud of TMC-1 and in the interstellar medium (ISM) back in 1984 [69,70]. The detection of this molecule in astrophysical environments highlights its importance and motivates the current study. Later, in 2017, M. Araki et al. identified the same molecule in the low-mass star-forming region L1527 [71]. Very recently, J. Cernicharo et al. identified the deuterated species of global minima (CH2DC4H) in TMC-1 with the help of the QUIJOTE line survey [72], which underscores the relevance of investigating the electronic structures of these hydrocarbons in the context of astrophysical chemistry.
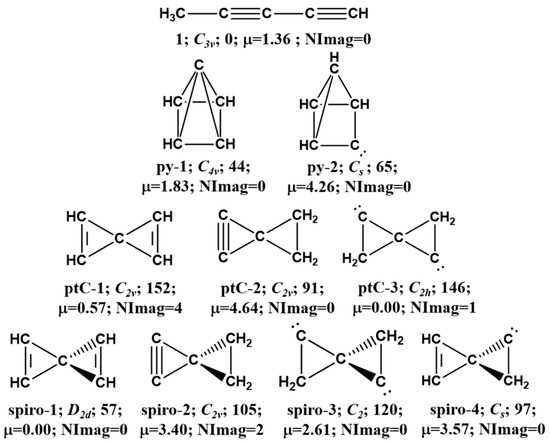
Figure 1.
Electronic structure of nine unusual high energy isomers of molecular formula C5H4. Point group symmetry, ZPVE-corrected relative energies (in kcal mol−1), absolute dipole moment values (in Debye) and number of imaginary frequencies (NImag) are calculated at the fc-CCSD(T)/cc-pVTZ level of theory.
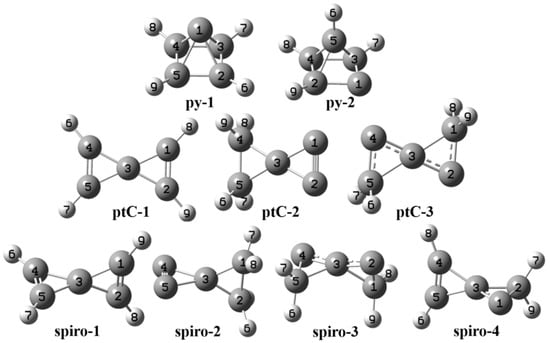
Figure 2.
3D ball-stick models of the same molecules along with the atom numbers are shown in Figure 1.
In Table 1, we present the zero-point vibrational energy (ZPVE) corrected relative energies (ΔE0; in kcal mol−1), point group symmetry, numbers of imaginary frequencies (NImag), and the total dipole moment (μ; in Debye) at various levels of theory for all the isomers. However, we have considered the relative energy values calculated at the fc-CCSD(T)/cc-pVTZ level of theory in all our further discussion as they are much more accurate and reliable than the DFT method employed here. The Wiberg bond indices (WBIs) for the different C-C bonds in each isomer, obtained from natural bond orbital (NBO) analysis, are calculated at the ωB97XD/6-311+G(d,p) level and listed in Table 2. These WBIs serve as indicators of the relative bond strengths between carbon atoms in the respective isomers.

Table 1.
ZPVE-corrected relative energies (ΔE0; in kcal mol−1), points groups, numbers of imaginary frequencies, and the total dipole moments (μ; in Debye) of the isomers of molecular formula C5H4 calculated at different levels of theory.

Table 2.
WBI indices for all nine isomers calculated at ωB97XD/6-311+G(d,p) level of theory.
The electronic distribution in the frontier molecular orbitals is analyzed by examining the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) for each isomer calculated at the ωB97XD/6-311+G(d,p) level, which are depicted in Figure 3. Here we note that, as reported earlier, the B3LYP functional without dispersion correction may not be able to reproduce accurate orbital energies for the simple hydrocarbon molecules [73]. However, the results obtained using the B3LYP density functional have been included in the ESI for reference. The electron localization function (ELF) analysis is carried out to assess the extent of electron delocalization in the molecular systems at the same level of theory. Figure 4 presents the color-filled ELF plots of nine isomers being studied. The bond critical points (BCPs) and ring critical points (RCPs) calculated at the ωB97XD/6-311+G(d,p) level of theory are listed in Figure 5. Electron density descriptors (in a.u.) at the (3, –1) bond critical points (BCP) are calculated for all nine isomers along with the topological parameters such as Hamiltonian kinetic energy K(rc), electron density ρ(rc), Laplacian electron density ∇2 ρ(rc), Lagrangian kinetic energy G(rc), potential energy density V(rc), total energy density E(rc) or H(rc), ELF, G(rc)/V(rc), and G(rc)/ρ(rc) and listed in Table 3. The spectroscopic parameters such as inertial axis dipole moments along with their components, rotational constants and the centrifugal distortion constants, and the final optimized Cartesian coordinates are given in the Supporting Information.
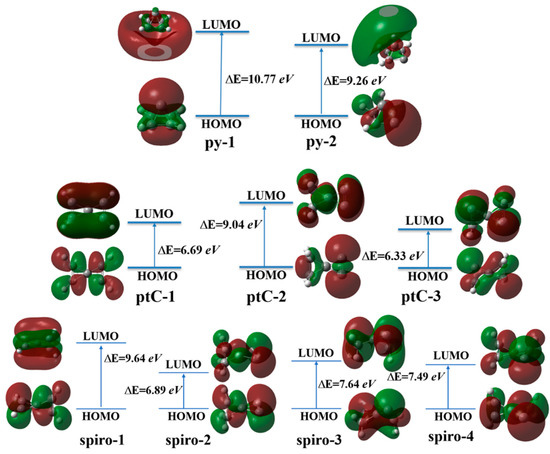
Figure 3.
Molecular orbitals (HOMO and LUMO) and their energy gap of all nine isomers calculated at the ωB97XD/6-311+G(d,p) level of theory.
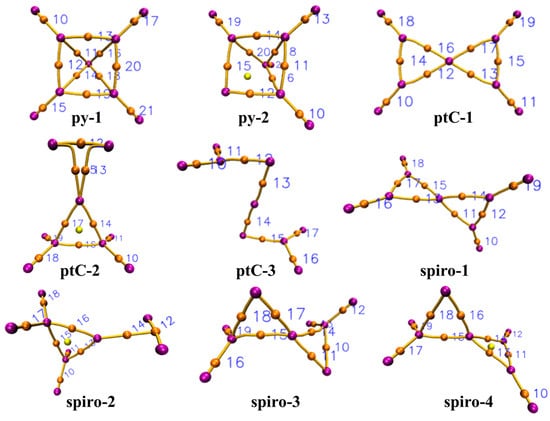
Figure 4.
Molecular graph representation of the pyramidane, ptC and spiro isomers of C5H4. Atoms are shown in violet color, bond critical points in orange color, and ring critical points in yellow color calculated at the ωB97XD /6-311+G(d,p) level of theory.
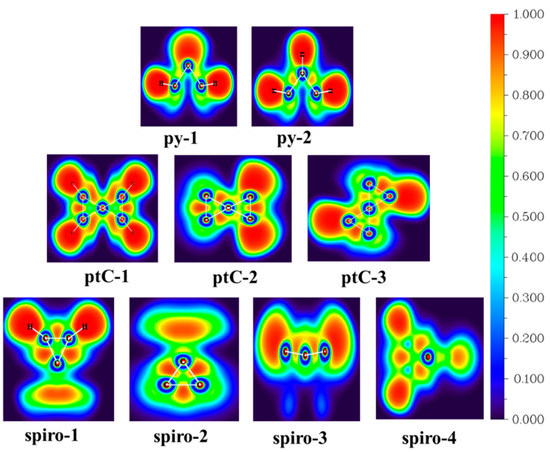
Figure 5.
Color-filled electron localization function (ELF) plots of all nine isomers calculated at the ωB97XD/6-311+G(d,p) level of theory.

Table 3.
Electron density descriptors (in a.u.) at the (3, –1) bond critical points (BCP) obtained from the ωB97XD/6-311+G(d,p) level for all the nine isomers. The topological parameters such as Hamiltonian kinetic energy K(rc), ρ(rc), Laplacian electron density (∇2ρ(rc)), Lagrangian kinetic energy G(rc), potential energy density V(rc), energy density E(rc) or H(rc), ELF, G(rc)/V(rc), and G(rc)/ρ(rc) at the critical points are also given.
The detailed structural studies of these nine unusual C5H4 isomers are discussed in the following sub-sections.
3.1. Pyramidane
The simplest possible hydrocarbon molecule with one pyramidal C atom can be represented by isomers tetracyclo-[2.1.0.01,3.02,5]pentane (py-1) and tricyclo-[2.1.0.02,5]pentan-3-ylidene (py-2) (Figure 1). These molecules pose inverted tetrahedral geometry (so-called “umbrella”) configurations of the tetra-coordinated C atom. Although a fascinating target for synthetic chemists, to the best of our knowledge, no pyramidane hydrocarbon molecule and its structural isomers has been isolated as a stable compound to date. Both the pyramidane structures (py-1 and py-2) are minima on the C5H4 PES, having no imaginary frequency at the fc-CCSD(T)/cc-pVTZ level of theory. py-1 and py-2 are found to be 44 and 65 kcal mol−1 higher in energy than the global minima 1, respectively.
In py-1, one carbon atom is on top of the pyramid, which is attached to the base with the four carbon atoms in a cyclobutene ring. The ground electronic state of py-1 is 1A1 (C4v symmetry) with the electronic configuration (1a1)2(1e)4(1b2)2(2a1)2(3a1)2(2e)4(4a1)2(5a1)2(2b2)2(1b1)2(3e)4(4e)4(6a1)2. From the electronic configuration, it is clear that the overall stabilization of py-1 is due to the formation of two doubly degenerated frontier occupied molecular orbitals, HOMO-1 (4e) and HOMO-2 (3e); the HOMO (6a1) possess a lone pair of electrons (Figure 3). This is due to the strong overlap between the π-orbital of the cyclobutadiene ring and the apical carbon , , and orbitals. This observation is also supported by the high energy gap between the HOMO-LUMO (∆EHOMO-LUMO = 10.77 eV) of py-1 at the ground (singlet) electronic state compared to other isomers. Based on the WBIs (Table 2), it can be inferred Capical-Cbasal (bond order 0.70) is weaker than Cbasal-Cbasal (bond order 1.10) and Cbasal-H (bond order 0.91). There is a possibility of formation of an aromatic C4H42- ring (cycobutadienyl dianion) in the base with a capping C2+ moiety; however, this aspect has not been considered in the present study.
In the case of the py-2, the top carbon atom is attached to one hydrogen atom and the base consists of a four-membered ring containing three -CH groups and one carbene carbon. The ground electronic state of py-2 is 1A′ (Cs symmetry) with electronic configuration (1-3a′)2(1a′′)2(4-5a′)2(2a′′)2(6-10a′)2(3-4a′′)2(11a′)2(5a′′)2(12a′)2. The observed HOMO-LUMO energy gap for py-2 is also high (∆EHOMO-LUMO = 9.26 eV). The WBI value for py-2 of Capical-Cbasal(attached to hydrogen) is 0.81, whereas Capical-Cbasal(carbene carbon) is 0.59 which implies more electrostatic interaction between the apical carbon and the basal carbene carbon. Again, the WBI value for Cbasal-Cbasal bond is 1.06, which indicates a possible single-bond character.
3.2. Planar Tetracoordinate Carbon (ptC)
The (SP4)-spiro[2.2]pent-1,4-diene (ptC-1) refers to the molecule where the central carbon atom is attached to four other carbon atoms in one plane. However, the hydrogen atoms attached to the four terminal carbon atoms are not in the same plane. Therefore, the point group symmetry for this molecule is C2v. ptC-1 is a fourth-order saddle point on the C5H4 PES having four imaginary frequencies. Here we note that if all four hydrogen atoms are forced to remain in the same plane of the carbon atoms, the molecule becomes a fifth-order saddle point with D2h molecular symmetry. However, if we remove two electrons from the planar form, the dicationic form of the molecule becomes a minimum energy isomer on the C5H4 PES. The above phenomenon can be explained by looking into the electronic structure of both systems. The removal of the electron pair from the ptC-1 leads to the delocalization of the electrons and the formation of two aromatic cyclopropenyl rings containing two electrons each.
The ground electronic state of ptC-1 is 1A2 with the electronic configuration (1a1)2(1b1)2(2a1)2(1a2)2(1b2)2(3a1)2(2b1)2(4a1)2(2b2)2(2a2)2(3b1)2(5-6a1)2(3b2)2(4b1)2(3a2)2. This isomer is 152 kcal mol−1 higher in energy compared to 1. However, the HOMO-LUMO energy gap (∆EHOMO-LUMO = 6.69 eV) is relatively low. The WBI value of Cterminal-Cterminal is 1.66, indicating double bonding character, whereas the WBI bond order for Ccentral-Cterminal is 0.98, which signifies a C-C single bond.
The (SP4)-sprio[2.2]pent-1-yne (ptC-2) refers to the ptC moiety where one side of the ring is attached to two sp3 hybridized carbon atoms and the other side is attached to two sp-hybridized carbon atoms (Figure 1). Therefore, all the four hydrogen atoms are attached to the side of the sp3-hybridized carbon atoms. The point group symmetry for this molecule is C2v. ptC-2 is found to be the only planar tetracoordinate carbon which is a minimum on the C5H4 PES. It is 91 kcal mol−1 higher in energy compared to the global minimum. It is worth mentioning here that this isomer is 14 kcal mol−1 lower in energy compared to the corresponding tetrahedral form (spiro-2). However, ptC-2 has a substantial HOMO-LUMO energy gap (∆EHOMO-LUMO = 9.04 eV) compared to spiro-2 (∆EHOMO-LUMO = 6.89 eV). The dicationic form of ptC-2 is also a planar tetracoordinate carbon and a minimum energy structure on the C5H4 PES.
The ground electronic state of ptC-2 is 1A1 with the electronic configuration (1a1)2(2a1)2(1b2)2(3a1)2(2b2)2(4a1)2(5a1)2(3b2)2(6a1)2(1b1)2(4b2)2(7a1)2(1a2)2(8a1)2(2b1)2(5b2)2(9a1)2. The WBI value of ptC-2 for Ccentral-Cterminal(no hydrogen) is 1.13, Ccentral-Cterminal(attached hydrogen) is 0.87 which indicates the stronger C-C between the central carbon atom and terminal carbon atoms having no hydrogen. Again, WBI value for Cterminal(attached hydrogen)-Cterminal (attached hydrogen) is 1.02 indicating C-C single bond character. However, Cterminal(no hydrogen)-Cterminal(no hydrogen) has WBI value of 1.56 which corresponds closely to a double bond instead of triple bond. This anomaly is also evident from the molecular graph representation (Figure 5), and the ELF value (0.66) between Ccentral-Cterminal(no hydrogen) bond.
The (SP4)-sprio[2.2]pent-1,4-diylidene (ptC-3) refers to the molecule where one carbon is in the center attached to the four carbon atoms in the same plane. Among the four carbon atoms, two carbon atoms are carbene in nature and lie opposite to each other. The other two carbon atoms are sp3-hybridized and have two hydrogen molecules attached to them. The point group symmetry for this molecule is C2h. ptC-3 is 146 kcal mol−1 higher in energy compared to the corresponding global minima. However, ptC-3 is a transition state, having an imaginary frequency on the C5H4 PES. An intrinsic reaction coordinate (IRC) calculation reveals ptC-3 connects the stereomutation of the spiro-3 molecules at both ends of the reaction coordinates, as shown in Figure S1.
The ground electronic state of ptC-3 is 1Bu with the electronic configuration (1ag)2(1bu)2(2ag)2(2bu)2(3ag)2(4ag)2(3bu)2(4bu)2(5ag)2(1au)2(1bg)2(6ag)2(5bu)2(6bu)2(7ag)2(2au)2(7bu)2. The WBI value for Ccentral-Cterminal(no hydrogen) = 1.23, Ccentral-Cterminal(attached hydrogen) = 0.70, and Cterminal(no hydrogen)-Cterminal(attached hydrogen) = 1.12 designates to the stronger C-C bond between the central carbon and the terminal carbon having no attached hydrogen.
3.3. Spiro
In the case of the spiro[2.2]pent-1,4-diene (spiro-1) molecule, the central carbon atom is attached to the four CH groups in a tetrahedral manner with the molecular symmetry of D2d. The tetrahedral form (spiro-1) is a minimum on the PES of the molecular formula C5H4. spiro-1 is 57 kcal mol−1 higher than 1. Removing two electrons from spiro-1 leads to the dicationic form of spiropentadiene at a higher-order saddle point. The delocalized rings of the dication of the spiropentadiene bring the aromatic character and explain the stability of the molecules. The ground electronic state of spiro-1 is 1E with the electronic configuration (1a1)2(1b2)2(2a1)2(1e)4(3a1)2(2b2)2(2e)4(4a1)2(3b2)2(5a1)2(3e)4(4b2)2(4e)4. This molecule possesses a higher HOMO-LUMO energy gap (∆EHOMO-LUMO = 9.64 eV) than the corresponding ptC-1 (∆EHOMO-LUMO = 6.69 eV). The WBI value of spiro-1 for Cterminal-Cterminal = 1.88 and Ccentral-Cterminal = 0.97 indicates the double bond and single bond characters, respectively.
In the spiro[2.2]pent-1-yne (spiro-2) molecule, the central carbon atom is attached to the two -CH2 groups and two sp-hybridized carbon atoms in a tetrahedral manner with the molecular symmetry of C2v. The tetrahedral form (spiro-2) is not a minimum on the PES, as it corresponds to a second-order saddle point on C5H4 PES having two imaginary frequencies. The ground electronic state of this molecule is 1B2 with the electronic configuration (1a1)2(2a1)2(1b2)2(3a1)2(1b1)2(4a1)2(5a1)2(2b2)2(6a1)2(2b1)2(7a1)2(3b1)2(1a2)2(3b2)2(8a1)2(9a1)2(4b2)2. The WBI value of spiro-2 for Cterminal(no attached hydrogen)-Cterminal(no attached hydrogen) = 2.44, Cterminal(attached hydrogen)-Cterminal(attached hydrogen) = 0.96, Ccentral-Cterminal(no attached hydrogen) = 0.97, and Ccentral-Cterminal(attached hydrogen) =1.01 indicates triple bond, single bond, single bond and single bond characters, respectively.
In spiro[2.2]pent-1,4-diylidene (spiro-3), the central carbon atom is attached to the two carbene carbon, forming the allene-type molecules in a tetrahedral manner with the molecular symmetry of C2 and a minimum energy isomer in C5H4 PES. The ground electronic state of spiro-3 is 1B with the electronic configuration (1a)2(1b)2(2a)2(2b)2(3a)2(4a)2(3b)2(4b)2(5a)2(6a)2(5b)2(7a)2(6b)2(8a)2(7b)2(9a)2(8b)2. The WBI value of this molecule for Cterminal(no attached hydrogen)-Cterminal(attached hydrogen) = 1.07, Ccentral-Cterminal(no attached hydrogen) = 1.18, and Ccentral-Cterminal(attached hydrogen) = 0.77 represents all single bond character.
Again, in the case of spiro[2.2]pent-4-en-1-ylidene (spiro-4), the central atom is attached with a carbene carbon, two sp2-hybridized carbon atom, and one sp3-hybridized carbon atom. This molecule is 97 kcal mol−1 higher in energy than 1 and a minima on the C5H4 PES. The corresponding ptC structure is unstable with respect to isomerization process. The ground electronic state of this isomer is 1A′ (Cs molecular symmetry) with the electronic configuration (1a′)2(1a′′)2(2-6a′)2(2a′′)2(7-9a′)2(3a′′)2(10-11a′)2(4a′′)2(12-13a′)2. The WBI indices of spiro-4 predict that C1-C2, C1-C3, C2-C3, C3-C4, and C3-C5 have a single bonding character, whereas C4-C5 bond possess a double bonding character.
3.4. Topological Analysis using AIM Theory
The presence of interatomic bonding interactions has been observed between the nuclei through careful analysis of the electron density distribution using topological methods. This is indicated by the existence of a (3, -1) critical point, and these interactions are characterized by their partial covalent behavior, as suggested by the negative H(rc) values in accordance with Bader’s theory. According to this theory, interatomic states can be classified based on the magnitude of the Laplacian of the electron density, represented by |V(rc)|. Bonds are classified as electrostatic if |V(rc)| < G(rc), covalent if |V(rc)| > G(rc), and partially covalent in the intermediate range of G(rc) < |V(rc)| < 2G(rc).
The AIM theory was used to investigate the electronic structure of pyramidal, spiro, and planar tetracoordinate geometries. The theory is based on the analysis of the electronic density distribution, ρ(rc), which provides much information such as the critical points related to bonds and rings and their respective eigenvalues and ellipticities. Another important analysis from the AIM theory is the Laplacian of the charge density, ∇2 ρ(rc), which is defined as the sum of the three principal curvatures of the function at each point of space. The density is locally concentrated in regions where ∇2 ρ(rc) < 0 and ρ(rc) is a local maximum, and locally depleted in regions where ∇2 ρ(rc) > 0 and ρ(rc) is a local minimum. In the molecular graph representing the pyramidane geometry (Figure 4), atoms are shown in violet, bond critical points in orange, and ring critical points in yellow. There are two types of bonds throughout the analysis: C-C bonds and C-H bonds. From the geometrical point of view, the py-1 structure has 12 bond critical points, and the py-2 structure has 11 bond critical points. This indicates all the bond paths. For py-1, index number 10, 11, and 12 correspond to bond critical points in 8(H)--4(C), 4(C)--1(C), and 4(C)--3(C), respectively. In contrast, in py-2, index number 10, 11, and 12 represent the same in 9(H)--2(C), 2(C)--4(C), and 2(C)--1(C) bonds, respectively. From the above table, the values of H(rc) and |V(rc)| > G(rc) indicate that all the bonds are covalent in nature. Regarding the planar tetracoordinate geometry, ptC-1 contains the three distinct index numbers 10, 12, and 14 for the bonds 7(H)--5(C), 5(C)--3(C), and 5(C)--4(C), respectively. It shows all the possible bond critical points in the above figure. The same is true for ptC-2, where index numbers 10, 12, 13, 14, and 16 represent the bonds between 6(H)--5(C), 2(C)--1(C), 2(C)--3(C), 5(C)--3(C), and 5(C)--4(C), respectively. However, ptC-3 shows eight bond critical points (BCPs), indicating that the initial structure is not stable and the ring is broken. The analysis of four plausible neutral geometries of spiro compounds revealed interesting results. AIM analysis showed that spiro-1 and spiro-4 both had 10 bond critical points. For spiro-1, index numbers 10, 11, and 12 were distinct and represented the bonds between 8(H)--2(C), 2(C)--3(C), and 2(C)--1(C), respectively. Similarly, for spiro-4, index numbers 10, 11, 13, 15, 16, and 18 were distinct and represented the bonds between 8(H)--4(C), 4(C)--5(C), 4(C)--3(C), 3(C)--2(C), 3(C)--1(C), and 2(C)--1(C), respectively. However, the geometries of spiro-2 and spiro-3 were found to be unstable. In the case of spiro-2, the three-membered ring towards the alkyne moiety was cleaved, resulting in a linear structure. Meanwhile, spiro-3 had two three-membered rings that broke due to rupturing of the 1(C)--3(C) and 3(C)--5(C) bonds.
The stability of the ptC-containing molecules can be understood from the nature of the loan pairs located on the central carbon atom. The topology of the electron density provides a consistent mapping of the bonded and nonbonded electron pairs through analysis of the Laplacian of the electron density. One possibility to complement the nonempirical connectivity provided by the electron density is to use the electron localization function, ELF(r), proposed by Becke and Edgecombe [74]. The color-filled ELF plot in Figure 5 visually represents the degree of electron localization in a molecule, which is measured by the ELF value. This quantum chemical property ranges from 0 to 1, where 0 signifies a fully delocalized electron cloud and 1 signifies a fully localized electron cloud. The color gradients used in the plot highlights high electron density with bright red and low electron density with dark blue. This plot specifically demonstrates the significant localization between the C-H and C-C bonds of the molecule.
In accordance with the WBIs, the electron localization function (ELF) values in Table 3 (Column 10) suggest, for isomer py-1 and py-2, the hydrogen atoms (H) bonded to the base carbon atoms (C) have a higher covalency than the C-C bonds between the apical positions. However, the covalency of all C-H bonds decreases going from py-1 to py-2, while the covalency of C1-C3 and C1-C2 bonds increases going from py-1 to py-2. The electron density between the C-C and C-H bonds is in the range of 0.69-0.99 (Table 3, column 6) indicating the strong localization of electrons. Similarly, the ELF analysis for the spiro compounds predicts that the covalency order for the C-H bonds is more comparable with the C-C bonds.
The bonding properties in three planar tetracoordinate geometries ptC-1, ptC-2, and ptC-3 are discussed in detail in the following section. The ELF analysis of ptC-1 predicts the covalency order as C5-H7 = C2-H9 = C4-H6 = C1-H8 > C5-C4 = C1-C2 > C3-C5 = C3-C2 = C2-C1 = C3-C4. It can be observed that the covalent bond between carbon and hydrogen atoms (C-H bond) is predominant over the bonds between carbon atoms (C-C bond). From the ELF analysis of ptC-2, the covalency order is found to be C5-H6 = C5-H7 = C4-H9 = C4-H8 > C1-C2 > C4-C5 > C3-C5 = C3-C4 > C2-C3 = C1-C3. Here, the covalency order of all the C-H bonds increase compared to ptC-1. Furthermore, the C4-C5 and C1-C2 bonds in ptC-2 are less covalent than in ptC-1. However, they are more covalent than the C3-C4, C3-C5, C1-C3, and C2-C3 bonds but less covalent than the C-H bonds. In case of ptC-3, the ELF analysis predicts the covalency order as C5-H6 = C5-H7 = C1-H9 = C1-H8 > C4-C5 = C1-C2 > C4-C3 = C3-C2. The covalency of all C-H bonds decreases slightly compared to ptC-2. The C4-C5 and C1-C2 bonds are less covalent than in ptC-2, but they are more covalent than the C3-C4, C3-C5, C1-C3, and C2-C3 bonds. The covalency of the C2-C3 bond increases compared to ptC-2.
In summary, the covalency of the C-H bonds increases from ptC-1 to ptC-2, then slightly decreases to ptC-3. The covalency of the C4-C5 and C1-C2 bonds decreases from ptC-1 to ptC-3, then increases from ptC-2 to ptC-3. The C3-C4 bond becomes more covalent from ptC-1 to ptC-3, while the C2-C3 bond becomes less covalent from ptC-1 to ptC-2. The C5-C3 and C1-C3 bonds decrease in covalency from ptC-1 to ptC-2.
3.5. Structural Comparison between Different Spin States
We have extended our calculations to investigate the structural changes with respect to the change in the spin state of the molecules. Though the feasibility of different spin states cannot be explained through single reference theory, for brevity all the isomers have been geometrically optimized in their triplet spin state using DFT at the ωB97XD /6-3111+G(d,p) level of theory and the harmonic vibrational frequencies have been calculated. The singlet-triplet energy gaps for all the molecules have been listed in Table S4. We have found that the ptC-1 is a fourth-order saddle point on the PES of C5H4 in its singlet spin state. However, the corresponding tetrahedral form, spiro-1, is a minimum energy structure. While analyzing the geometry in its triplet state, we observed that the central carbon of ptC-1 is no longer in the same plane with the other four carbon atoms (Figure S3). The dihedral angle between any three-terminal carbon and the central carbon has become 11.90° and the positions of the hydrogen atoms have shifted downwards by 40° with respect to the plan of the four terminal carbon atoms. The triplet state of the ptC-1 becomes a second-order saddle point. The singlet state is marginally stable compared to the triplet state (ΔES-T = 1.51 kcal mol−1). Here we note that the corresponding tetrahedral form (spiro-1) becomes a third-order saddle point in the triplet spin state, having three negative vibrational frequencies. The optimized geometry of ptC-1 in the quintet spin state is a minimum energy structure on the C5H4 PES, having no imaginary frequency at the same level of theory. However, the optimized structure in the quintet state converges more towards the pyramidane structure, as the hydrogen atoms are shifted downwards and the central carbon atom is being uplifted by 44.5° from the plane of the terminal carbon atoms.
The ptC-2 is the only minimum isomer on the PES of C5H4, which possesses a planar tetracoordinate carbon in the singlet spin state. The molecule becomes a second-order saddle point in its triplet spin state. The positive singlet-triplet energy gap (ΔES-T = 60.69 kcal mol−1) suggests the molecule is more stable in the singlet spin state. However, the spiro-2 is a minimum structure. In the case of the ptC-3 as well as the spiro-3, both isomerize to the more stable allene isomer (pent-1,2,3,4-tetraene) in their triplet electronic spin state.
3.6. Ab Initio Molecular Dynamics
The ab initio molecular dynamics simulations (AIMD) [68] have been carried out for all nine isomers at different temperatures to confirm their kinetic stability in their respective singlet ground electronic states. Atom-centered density matrix propagation (ADMP) is an extended Lagrangian molecular dynamics method which has been used to employ the atom-centered Gaussian basis functions and one-particle density matrix propagation. These simulations were executed in Gaussian 09 software at 1 atm pressure and temperatures of 10 K, 60 K, 120 K, and 29 8 K for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory. The time evolution of the total energy of the minimum energy ptC isomer (ptC-2) at different temperatures is shown in Figure 5. AIMD results for other isomers at different temperatures are shown in the Supporting Information.
Again, most of the molecular geometry breaks at the room temperature (298 K). Figure 6 shows the energy oscillations and the geometrical changes of ptC-2 happening within a 10,000 fs time scale at different temperatures (10 K, 60 K, 120 K, and 298 K). This analysis concludes that ptC-2 is kinetically stable. Furthermore, most of the minimum energy isomers (py-1, py-2, spiro-1, spiro-3, and spiro-4) are kinetically stable at low temperatures (10 K, 60 K, and 120 K). Only spiro-1 is kinetically stable at 298 K.
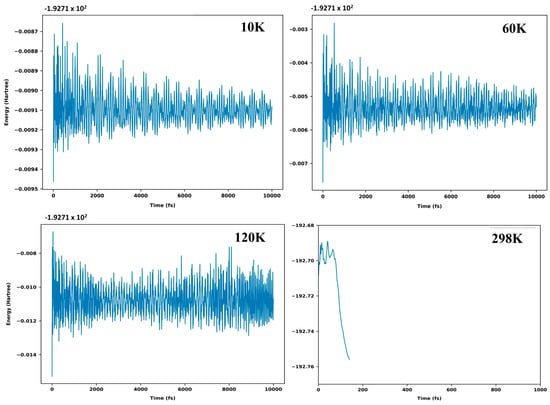
Figure 6.
Energy evolution of isomer ptC-2 (1A1) of C5H4 obtained from the AIMD simulation carried out at different temperatures (10 K, 60 K, 120 K, and 298 K) and 1 atm pressure for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory.
3.7. Aromatic Characteristics and Relative Stability of the Molecules
To gain a better understanding of these molecules, NICS values have been calculated. It is well known that NICS value provides the information about the aromaticity of the ring. The NICS(1Å) values for all molecules have been calculated at the B3LYP/6-311+G(d,p) level of theory and listed in Table 4. One ghost atom is placed in the center of the ring and another one is placed perpendicular to it at 1Å distance. The negative NICS value indicates the aromatic character present in the molecules whereas positive value corresponds to the antiaromatic character. All the molecules possess negative NICS(1Å) (except ptC-1 and spiro-2) which represent their aromatic characteristics. Pyramidane (py-1 and py-2) structures consist of two different type of rings (four-membered and three-membered rings). In case of py-1, both the rings are aromatic in nature (−9.14 ppm (four-membered ring); −10.43 ppm (three-membered ring)), whereas the four-membered ring (−4.72 ppm) of py-2 is less aromatic compared to the three-membered ring (−10.00 ppm). From the above observation, it can be clearly defined that py-1 is more aromatic than py-2, justifying more stability. This fact can be verified through the electron delocalization in the HOMO of both pyramidane structures. The HOMO of the py-1 is mainly delocalized in the apical carbon and the basal four-membered ring. In contrast, the HOMO of py-2 is mainly localized at the carbene carbon.

Table 4.
NICS(1Å) values (in ppm) for all the nine isomers calculated at B3LYP/6-311+G(d,p) level of theory. a represents the NICS value for the four-membered ring and b represents the value for the three-membered ring.
The positive NICS value (11.20 ppm) of ptC-1 indicates its antiaromatic character. The HOMO picture reflects that the electrons are spread all over and the removal of the two electrons leads to the stabilization of the molecule by forming the two aromatic rings on both sides. The NICS value becomes −40.17 ppm, which specifies the high aromatic character of the system. For ptC-2, it was found that the NICS value is −18.87 ppm, which indicates the planar structure is aromatic in nature. It can be noted that in the HOMO, the electrons are delocalized mainly at the ethylene moiety, which stabilizes the molecule and widens the HOMO-LUMO energy gap. The electron delocalization can also be seen from the color-filled ELF graph where bright red colors indicate the same. This confirms the better stability and the reason to be a minimum on the C5H4 PES. The corresponding tetrahedral form of ptC-2 (spiro-2) possesses a positive NICS value of 14.40 ppm, which is not a minimum energy isomer on the C5H4 PES. The NICS values for other spiro isomers are found to be negative, indicating the stability of the molecules.
4. Conclusions
For many years, researchers have been searching for the planar tetracoordinated carbon atoms as a minimum on various potential energy surfaces. Though the neutral form of ptC-1 is a fourth-order saddle point, the dication form is a minimum on the PES of C5H4 as it gains the aromatic character by forming the two cyclopropenyl rings. Among the three ptCs, the ptC-2 has been found to be a minimum on the PES of C5H4. It is energetically 14 kcal mol−1 more stable than the corresponding tetrahedral form (spiro-2). The electron distributions of HOMO and the negative NICS value indicate the greater stability of the ptC-2 molecule and its aromatic nature. On the other hand, spiro-2 has a positive NICS value reflecting its antiaromatic nature. The significant HOMO-LUMO energy gap of ptC-2 (∆EHOMO-LUMO = 9.04 eV), compared to spiro-2 (∆EHOMO-LUMO = 6.89 eV), might correlate to the higher stability of the planar form. In addition, the high dipole moment value (μ = 4.64 D) of ptC-2 might help to detect this molecule in ISM or in laboratory. The ptC-3 (a transition state) connects the stereomutation of spiro-3. The spiro-1, spiro-3, and spiro-4 are minima on the C5H4 PES but the spiro-2 is a second-order saddle point. The WBIs and the topological analysis of AIM calculations reveal the bond order and the bonding patterns between different C-C and C-H bonds. Along with this, AIMD calculations have been performed at different temperatures. This study reveals that all the molecules are kinetically unstable at 298 K except spiro-1, but the stationary points that are minima are stable at low temperature (10 K, 60 K, 120 K) conditions. It can be concluded that these molecules may be unstable in room temperature but stable in the exotic conditions like the interstellar medium.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atoms11060096/s1, Figure S1: Possible 2D structure of initial guess isomers; Figure S2: Optimized geometries of all nine isomers in their triplet spin state calculated at the B3LYP/6-311+G(d,p) level of theory; Figure S3: Energy profile and the structural changes of ptC-1 with respect to the change in spin state with the ground state molecular term symbol and number of imaginary frequencies; Figure S4: Intrinsic Reaction Coordinate (IRC) for the transition state ptC-3 calculated at B3LYP/6-311+G(d,p) level of theory; Figure S5: Energy evolution of isomer py-1 (1A1) of C5H4 obtained from the AIMD simulation carried out at different temperature (10K, 60 K and 120 K) and 1 atm pressure for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory; Figure S6: Energy evolution of isomer py-2 (1A′) of C5H4 obtained from the AIMD simulation carried out at different temperature (10 K, 60 K and 120 K) and 1 atm pressure for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory; Figure S7: Energy evolution of isomer spiro-1 (1E) of C5H4 obtained from the AIMD simulation carried out at different temperature (10 K, 60 K, and 298 K) and 1 atm pressure for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory; Figure S8: Energy evolution of isomer spiro-3 (1B) of C5H4 obtained from the AIMD simulation carried out at different temperature (10 K, 60 K and 120 K) and 1 atm pressure for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory; Figure S9: Energy evolution of isomer spiro-4 (1A′) of C5H4 obtained from the AIMD simulation carried out at different temperature (10 K, 60 K and 120 K) and 1 atm pressure for 10,000 fs at the B3LYP/6-311+G(d,p) level of theory; Table S1: Optimized geometries of the C5H4 isomers in singlet ground electronic state in Cartesian coordinates (in Angstrom units) obtained at CCSD(T)/cc-pVTZ level of theory; Table S2: Optimized geometries of the C5H4 isomers in triplet ground electronic state and quintet electronic state of ptC-1 in Cartesian coordinates (in Angstrom units) obtained at B3LYP/6-311+G(d,p) level of theory; Table S3: Dipole moments in different axis (in Debye), total dipole moment (in Debye), Centrifugal distortion constants, and rotational constants (in MHz) of C5H4 isomers in their ground electronic states calculated at the CCSD(T)/cc-pVTZ level of theory; Table S4: The energy gap between singlet and triplet spin state of all nine isomers of C5H4 at B3LYP/6-311+G(d,p) level of theory; Table S5: The energy gap between singlet and triplet spin state (ΔEst in kcal mol-1), number of imaginary frequencies (NImag), and dipole moment (|μ| in Debye) of all nine isomers of C5H4 at ωB97XD/6-311+G(d,p) level of theory; Table S6: Electron density descriptors (in a.u.) at the (3, –1) bond critical points (BCP) obtained from the B3LYP/6-311+G(d,p) level for all the nine isomers. The topological parameters such as Hamiltonian Kinetic Energy K(rc), ρ(rc), Laplacian Electron Density (∇2ρ(rc)), Lagrangian Kinetic Energy G(rc), Potential Energy Density V(rc), Energy Density E(rc) or H(rc), ELF, G(rc )/V(rc ), and G(rc)/ρ(rc) at the critical points are also given; Table S7: WBI Indices for all nine isomers calculated at B3LYP/6-311+G(d,p) level of theory.
Author Contributions
Conceptualization, S.G. (Subhas Ghosal); methodology, A.A., V.S.T. and S.G. (Subhas Ghosal); software, S.S., T.R. and S.G. (Sandip Giri); validation, S.G. (Subhas Ghosal), V.S.T. and A.A.; formal analysis, S.S., T.R. and S.G. (Sandip Giri); investigation, S.S., T.R. and S.G. (Sandip Giri); resources, S.G. (Subhas Ghosal), A.A. and V.S.T.; data curation, S.S., T.R. and S.G. (Sandip Giri); writing—original draft preparation, S.S., T.R., S.G. (Sandip Giri) and S.G. (Subhas Ghosal); writing—review and editing, S.G. (Subhas Ghosal), A.A. and V.S.T.; visualization, S.S., T.R., S.G. (Subhas Ghosal), A.A. and V.S.T.; supervision, S.G. (Subhas Ghosal), A.A. and V.S.T.; project administration, S.G. (Subhas Ghosal), A.A. and V.S.T. All authors have read and agreed to the published version of the manuscript.
Funding
S.G. and A.A. thanks Govt. of India (GoI) for grant No. DST/NSM/R&D_HPC_Applications/2021/21 for the Paramshakti HPC facilities at IIT Kharagpur. S.G. thanks for the computational facilities in NITD supported by EMR/2017/002653 and V.S.T. thanks U.S. Department of Defense for DURIP grant W911NF-10-1-0157 and NSF CRIF grant CHE-0947087 at SDSU.
Data Availability Statement
Data available in the article or Supplementary Materials.
Acknowledgments
Subhas Ghosal and Anakuthil Anoop thanks Govt. of India (GoI) for grant no. DST/NSM/R&D_HPC_Applications/2021/21 for the Paramshakti HPC facilities at IIT Kharagpur and the doctoral fellowship for Sayon Satpati Computational facilities in NITD supported by EMR/2017/002653. Support provided at SDSU (for Venkatesan S. Thimmakondu) by DURIP grant W911NF-10-1-0157 from the U.S. Department of Defense and NSF CRIF grant CHE-0947087 are gratefully acknowledged. Tarun Roy thanks NITD for the doctoral fellowship. Sandip Giri thanks IITKGP for the doctoral fellowship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- van’t Hoff, J.H. A suggestion looking to the extension into space of the structural formulas at present used in chemistry, and a note upon the relation between the optical activity and the chemical constitution of organic compounds. Arch. Neerl. Sci. Exactes Nat. 1874, 9, 445–454. [Google Scholar]
- Le Bel, J.A. Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions. Bull. Soc. Chim. Fr. 1874, 22, 337–347. [Google Scholar]
- Minkin, V.I.; Minyaev, R.M.; Hoffmann, R. Non-classical structures of organic compounds: Unusual stereochemistry and hypercoordination. Russ. Chem. Rev. 2002, 71, 869–892. [Google Scholar] [CrossRef]
- Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar pentacoordinate carbons. Nat. Rev. Chem. 2018, 2, 0114. [Google Scholar] [CrossRef]
- Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P.V.R. Four decades of the chemistry of planar hypercoordinate compounds. Angew. Chem. Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef] [PubMed]
- Shan, C.; Dong, S.; Yao, S.; Zhu, J.; Driess, M. Synthesis and Reactivity of an Anti-van’t Hoff/Le Bel Compound with a Planar Tetracoordinate Silicon(II) Atom. J. Am. Chem. Soc. 2023, 145, 7084–7089. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Xia, D.; Baumgarten, M. Rigidly Fused Spiro-Conjugated π-Systems. ChemPlusChem 2021, 86, 36–48. [Google Scholar]
- Randić, M.; Rubčić, A.; Klasinc, L. Hybridization in highly strained small ring hydrocarbons—III: Unsaturated spiro-compounds. Tetrahedron 1971, 27, 5771–5777. [Google Scholar] [CrossRef]
- Delouche, T.; Hissler, M.; Bouit, P.-A. Polycyclic aromatic hydrocarbons containing heavy group 14 elements: From synthetic challenges to optoelectronic devices. Coord. Chem. Rev. 2022, 464, 214553. [Google Scholar] [CrossRef]
- Firme, C.L. Cycloalkanes, Bicyclic, and Caged Hydrocarbons. In Introductory Organic Chemistry and Hydrocarbons; CRC Press: Boca Raton, FL, USA, 2019; pp. 241–266. [Google Scholar]
- Leyva-Parra, L.; Inostroza, D.; Yañez, O.; Cruz, J.C.; Garza, J.; García, V.; Tiznado, W. Persistent planar tetracoordinate carbon in global minima structures of silicon-carbon clusters. Atoms 2022, 10, 27. [Google Scholar] [CrossRef]
- Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar tetracoordinate carbon in extended systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef] [PubMed]
- Thirumoorthy, K.; Thimmakondu, V.S. Flat crown ethers with planar tetracoordinate carbon atoms. Int. J. Quantum. Chem. 2021, 121, e26479. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Karton, A.; Thimmakondu, V.S. From High-Energy C7H2 Isomers with A Planar Tetracoordinate Carbon Atom to An Experimentally Known Carbene. J. Phys. Chem. A 2018, 122, 9054–9064. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-S.; Boldyrev, A.I.; Li, X.; Simons, J. Experimental Observation of Pentaatomic Tetracoordinate Planar Carbon-Containing Molecules. J. Am. Chem. Soc. 2000, 122, 7681–7687. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Yu, S.; Ding, Y.-H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef]
- Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. 1997, 36, 812–827. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F., Jr. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- McGrath, M.P.; Radom, L. Alkaplanes: A Class of Neutral Hydrocarbons Containing a Potentially Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1993, 115, 3320–3321. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Schleyer, P.v.R. The theoretical design of neutral planar tetracoordinate carbon molecules with C (C) 4 substructures. J. Am. Chem. Soc. 2002, 124, 11979–11982. [Google Scholar] [CrossRef]
- Wang, Z.-X.; Schleyer, P.v.R. A new strategy to achieve perfectly planar carbon tetracoordination. J. Am. Chem. Soc. 2001, 123, 994–995. [Google Scholar] [CrossRef]
- Sorger, K.; Ragué; Schleyer, P.V. Planar and inherently non-tetrahedral tetracoordinate carbon: A status report. J. Mol. Struct. 1995, 338, 317–346. [Google Scholar] [CrossRef]
- Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371. [Google Scholar] [CrossRef]
- Rasmussen, D.R.; Radom, L. Planar-Tetracoordinate Carbon in a Neutral Saturated Hydrocarbon: Theoretical Design and Characterization. Angew. Chem. Int. Ed. 1999, 38, 2875–2878. [Google Scholar] [CrossRef]
- Das, P.; Khatun, M.; Anoop, A.; Chattaraj, P.K. CSinGe4−n2+ (n = 1–3): Prospective systems containing planar tetracoordinate carbon (ptC). Phys. Chem. Chem. Phys. 2022, 24, 16701–16711. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.X.; Von Ragué Schleyer, P. Construction principles of "Hyparenes": Families of molecules with planar pentacoordinate carbons. Science 2001, 292, 2465–2469. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. N. J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Wang, M.-H.; Orozco-Ic, M.; Leyva-Parra, L.; Tiznado, W.; Barroso, J.; Ding, Y.-H.; Cui, Z.-H.; Merino, G. Planar Tetracoordinate Carbons in Allene-Type Structures. J. Phys. Chem. A 2021, 125, 3009–3014. [Google Scholar] [CrossRef] [PubMed]
- Job, N.; Khatun, M.; Thirumoorthy, K.; CH, S.S.R.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. CAl4Mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
- Sateesh, B.; Srinivas Reddy, A.; Narahari Sastry, G. Towards design of the smallest planar tetracoordinate carbon and boron systems. J. Comput. Chem. 2007, 28, 335–343. [Google Scholar] [CrossRef]
- Suresh, C.H.; Frenking, G. Direct 1−3 Metal−Carbon Bonding and Planar Tetracoordinated Carbon in Group 6 Metallacyclobutadienes. Organometallics 2010, 29, 4766–4769. [Google Scholar] [CrossRef]
- Thirumoorthy, K.; Chandrasekaran, V.; Cooksy, A.L.; Thimmakondu, V.S. Kinetic Stability of Si2C5H2 Isomer with a Planar Tetracoordinate Carbon Atom. Chemistry 2020, 3, 13–27. [Google Scholar] [CrossRef]
- Rasmussen, D.R.; Radom, L. Hemispiroalkaplanes: Hydrocarbon Cage Systems with a Pyramidal-Tetracoordinate Carbon Atom and Remarkable Basicity. Chem. Eur. J. 2000, 6, 2470–2483. [Google Scholar] [CrossRef] [PubMed]
- Priyakumar, U.D.; Reddy, A.S.; Sastry, G.N. The design of molecules containing planar tetracoordinate carbon. Tetrahedron Lett. 2004, 45, 2495–2498. [Google Scholar] [CrossRef]
- Karton, A.; Thimmakondu, V.S. From Molecules with a Planar Tetracoordinate Carbon to an Astronomically Known C5H2 Carbene. J. Phys. Chem. A 2022, 126, 2561–2568. [Google Scholar] [CrossRef]
- Cabezas, C.; Tercero, B.; Agúndez, M.; Marcelino, N.; Pardo, J.; de Vicente, P.; Cernicharo, J. Cumulene carbenes in TMC-1: Astronomical discovery of l-H2C5. Astron. Astrophys. 2021, 650, L9. [Google Scholar] [CrossRef]
- Cernicharo, J.; Agúndez, M.; Cabezas, C.; Tercero, B.; Marcelino, N.; Pardo, J.R.; de Vicente, P. Pure hydrocarbon cycles in TMC-1: Discovery of ethynyl cyclopropenylidene, cyclopentadiene, and indene. Astron. Astrophys. 2021, 649, L15. [Google Scholar] [CrossRef]
- Blanksby, S.J.; Dua, S.; Bowie, J.H.; Schröder, D.; Schwarz, H. Gas-phase syntheses of three isomeric C5H2 radical anions and their elusive neutrals. a joint experimental and theoretical study. J. Phys. Chem. A 1998, 102, 9949–9956. [Google Scholar] [CrossRef]
- He, C.; Galimova, G.R.; Luo, Y.; Zhao, L.; Eckhardt, A.K.; Sun, R.; Mebel, A.M.; Kaiser, R.I. A chemical dynamics study on the gas-phase formation of triplet and singlet C5H2 carbenes. Proc. Natl. Acad. Sci. USA 2020, 117, 30142–30150. [Google Scholar] [CrossRef]
- Sun, Y.-L.; Huang, W.-J.; Lee, S.-H. Formation of C3H2, C5H2, C7H2, and C9H2 from reactions of CH, C3H, C5H, and C7H radicals with C2H2. Phys. Chem. Chem. Phys. 2016, 18, 2120–2129. [Google Scholar] [CrossRef]
- Jayakumari, C.M.; Nag, P.; Isukapalli, S.V.K.; Vennapusa, S.R. Exploring the Excited-State Nonadiabatic Effects in the Semisaturated Planar Tetracoordinated Carbon Molecule C7H4. Atoms 2022, 10, 10. [Google Scholar] [CrossRef]
- Yadav, K.; Lourderaj, U.; Priyakumar, U.D. Stereomutation in Tetracoordinate Centers via Stabilization of Planar Tetracoordinated Systems. Atoms 2021, 9, 79. [Google Scholar] [CrossRef]
- Stohrer, W.D.; Hoffmann, R. Bond-stretch isomerism and polytopal rearrangements in (CH)5+, (CH)5−, and (CH)4CO. J. Am. Chem. Soc. 1972, 94, 1661–1668. [Google Scholar] [CrossRef]
- Minkin, V.; Zefirov, N.; Korobov, M.; Averina, N.; Boganov, A.; Nivorozhkin, L. 1,3,5-Trimethyl Derivative of the Square Pyramidal Cation (Ch) 5+. Chem. Inf. Dienst. 1981, 12, 2616–2618. [Google Scholar]
- Krogh-Jespersen, K.; Chandrasekhar, J.; Schleyer, P.V.R. Geometries and relative energies of some C6H5+ and C5H5Si+ isomers. Pyramidal (nido) vs. planar, cyclic structures. J. Org. Chem. 1980, 45, 1608–1614. [Google Scholar] [CrossRef]
- Kenny, J.P.; Krueger, K.M.; Rienstra-Kiracofe, J.C.; Schaefer, H.F. C5H4: Pyramidane and its low-lying isomers. J. Phys. Chem. A 2001, 105, 7745–7750. [Google Scholar] [CrossRef]
- Lee, V.Y.; Gapurenko, O.A.; Ito, Y.; Meguro, T.; Sugasawa, H.; Sekiguchi, A.; Minyaev, R.M.; Minkin, V.I.; Herber, R.H.; Gornitzka, H. Pyramidanes: The Covalent Form of the Ionic Compounds. Organometallics 2016, 35, 346–356. [Google Scholar] [CrossRef]
- Gapurenko, O.A.; Minyaev, R.M.; Minkin, V.I. Silicon analogues of pyramidane: A quantum-chemical study. Mendeleev. Commun. 2012, 22, 8–10. [Google Scholar] [CrossRef]
- Moreno-Armenta, M.G.; Pearce, H.R.; Winter, P.; Cooksy, A.L. Computational search for metastable high-spin C5Hn (n = 4, 5, 6) species. Comput. Theor. Chem. 2018, 1140, 1–6. [Google Scholar] [CrossRef]
- Adewale, R.; da Silva, G. Kinetics of C5H4 isomer + H reactions and incorporation of C5Hx (x = 3–5) chemistry into a detailed chemical kinetic model. Combust. Flame 2021, 227, 227–237. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+ G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Frisch, M.J.; Head-Gordon, M.; Pople, J.A. A direct MP2 gradient method. Chem. Phys. Lett. 1990, 166, 275–280. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Purvis, G.D. Many-body perturbation theory, coupled-pair many-electron theory, and the importance of quadruple excitations for the correlation problem. Int. J. Quantum. Chem. 1978, 14, 561–581. [Google Scholar] [CrossRef]
- Pople, J.; Krishnan, R.; Schlegel, H.; Binkley, J. Electron correlation theories and their application to the study of simple reaction potential surfaces. Int. J. Quantum. Chem. 1978, 14, 545–560. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Peterson, K.A.; Dunning, T.H., Jr. Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited. J. Chem. Phys. 2002, 117, 10548–10560. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. V. Core-valence basis sets for boron through neon. J. Chem. Phys. 1995, 103, 4572–4585. [Google Scholar] [CrossRef]
- Frisch, M.J.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Matthews, D.A.; Cheng, L.; Harding, M.E.; Lipparini, F.; Stopkowicz, S.; Jagau, T.-C.; Szalay, P.G.; Gauss, J.; Stanton, J.F. Coupled-cluster techniques for computational chemistry: The CFOUR program package. J. Chem. Phys. 2020, 152, 214108. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system, version 4.0. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Schlegel, H.B.; Millam, J.M.; Iyengar, S.S.; Voth, G.A.; Daniels, A.D.; Scuseria, G.E.; Frisch, M.J. Ab initio molecular dynamics: Propagating the density matrix with Gaussian orbitals. J. Chem. Phys. 2001, 114, 9758–9763. [Google Scholar] [CrossRef]
- Walmsley, C.M.; Jewell, P.R.; Snyder, L.E.; Winnewisser, G. Detection of interstellar methyldiacetylene (CH3C4H) in dark dust cloud TMC1. Astron. Astrophys. 1984, 134, L11–L14. [Google Scholar]
- MacLeod, J.M.; Avery, L.W.; Broten, N.W. The detection of interstellar methyldiacetylene (CH3C4H). Astrophys. J. 1984, 282, L89–L92. [Google Scholar] [CrossRef]
- Araki, M.; Takano, S.; Sakai, N.; Yamamoto, S.; Oyama, T.; Kuze, N.; Tsukiyama, K. Long Carbon Chains in the Warm Carbon-chain-chemistry Source L1527: First Detection of C7H in Molecular Clouds. Astrophys. J. 2017, 847, 51. [Google Scholar] [CrossRef]
- Cabezas, C.; Fuentetaja, R.; Roueff, E.; Agúndez, M.; Tercero, B.; Marcelino, N.; Pardo, J.R.; de Vicente, P.; Cernicharo, J. New deuterated species in TMC-1: Detection of CH2DC4H with the QUIJOTE line survey. Astron. Astrophys. 2022, 657, L5. [Google Scholar] [CrossRef]
- Tsuneda, T.; Song, J.-W.; Suzuki, S.; Hirao, K. On Koopmans’ theorem in density functional theory. J. Chem. Phys. 2010, 133, 174101. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Méndez-Rojas, M.A.; Beltrán, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical Analysis of the Smallest Carbon Cluster Containing a Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 2004, 126, 16160–16169. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).