The Vortex Surface in a Three-Body Quantum System

Abstract

Vortices are structures known in our daily lives and observed in a wide variety of systems, from cosmic to microscopic scales. Relatively recent studies showed that vortices could also appear in simple quantum systems. For instance, they were observed experimentally and theoretically as isolated zeros in the differential cross section in atomic ionization processes by the impact of charged particles. In this work, we show that the appearance of these quantum vortices as point structures was not due to any intrinsic property of them, but to the use of restrictive geometries in their visualization. In particular, we show that by studying the fully differential cross section for hydrogen ionization by positron impact, these vortex points are actually a manifestation of a more complex and hitherto unexplored structure, a 3D “vortex surface”.

1. Introduction

This article is about vortices. We have all experienced them in our daily lives; for example, when we stir the coffee in our cup during breakfast. And we also have a pretty precise idea of how to define a vortex as a fluid rotating around an axis.

This is a ubiquitous effect not only in classical physics, but also in other areas, most notably quantum physics. In all these cases, it is associated with many-body systems, describable by means of a fluid–dynamic theory. However, as we will see in this article, it can also occur in simple quantum systems, in fact, as simple as those composed of only two or three bodies. Naturally, this raises an obvious question: if vortices are effects that, as far as our common knowledge dictates, occur in a fluid, how can vortices exist in the absence of a fluid?

As if this were not enough, we will also see that, vortices, which we usually associate with a rotational movement around a point or a line, can occur around a surface. The very existence of vortex surfaces seems to go against intuition, since there would not be enough “space” (i.e., spatial dimensions) to trace closed flow circuits around them.

If we wanted to condense the content of this article in a single and brief sentence, which also puts in focus the two apparent paradoxes that we have just mentioned, we would say neither more nor less than “we will study the formation of vortex surfaces in a three-body quantum system”.

In the next section, we will describe the background of this work, both in the broader contexts of fluid physics and many-body quantum mechanics, to arrive at simple few-body quantum systems, in which we are interested. In this area, we will focus in more detail on the existing results, as well as their various findings and future hypotheses.

Next, we will review the concept of a quantum vortex, and its intimate relationship with the geometry of the problem under study, thus providing the conceptual basis for understanding the existence of vortex surfaces in simple quantum systems.

We will also give a description of the theoretical model used to calculate the fully differential cross section (FDCS) in the simple ionization of atoms by positron impact of energies in the range of tens of electron volts.

Finally, we will show the results obtained, which constitute the first complete calculation made so far of a vortex surface in a three-body quantum system. We will show that, when analyzed in the framework of restricted geometries, this vortex surface gives rise to lines or rings in a 3D space or isolated point vortices in a 2D space, such as those observed by other authors in previous works.

2. A World of Vortices

Vortices are well-known and thoughtfully studied structures in fluid physics. Also, we all know from experience that these flows are in rotation around an axis, since they can be found frequently and naturally in the most diverse systems. For instance, vortices are well-known and frequent effects on atmospheric and aquatic dynamics, in the form of dust devils, tornadoes, waterspouts, mesocyclones, hurricanes, and cyclones. On a smaller scale, we can mention the smoke rings that smokers can create, or the bubble rings blown by divers and cetaceans.

At the planetary level, we can highlight the intermittent Dark Spot of Neptune, the polar vortices of Mars, Earth, Venus, Jupiter, and Titan, and the strange hexagonal vortex in the north pole of Saturn.

The eddies that usually appear in rivers and the sea are easily recognizable, and in some cases have given rise to mythical narratives and artistic representations.

In classical physics, we recognize examples such as the Taylor–Couette flow, and those generated with airfoils and electromagnetic fields.

Vortices are also ubiquitous structures in many-body quantum systems. For example, Nobel laureates Lars Onsager in 1949 [1] and Alexei Alexeyevich Abrikosov [2] in 1957 predicted their presence in superfluids, and type-II superconductors, respectively.

2.1. Vortex Atom

In 1858, Hermann von Helmholtz made the first mathematical study of vortex rings [3]. A few years later, William Thomson read before the Royal Society of Edinburgh a work entitled “Vortex Atoms” [4], postulating that “Helmholtz’s rings are the only true atoms”. This model was further developed by Joseph John Thomson [5]. On discovering the electron in 1897, J. J. Thomson himself initiated the abandonment of this model [6]. However, as we will see below, more than a century later, we know that quantum vortices are ubiquitous in atomic physics. Nevertheless, the concepts we now know as atoms and (quantum) vortices had to evolve significantly to establish that link.

2.2. Vortices in Quantum Few-Body Systems

Let us consider one of the simplest quantum systems, such as the stationary bound state of a hydrogenic atom of reduced mass $\mu$, and of principal, angular, and magnetic quantum numbers $n$, $\mathcal{l}$, and $m$, respectively, and with wave function, ${\psi }_{n\mathcal{l}m}\left(r,\theta ,\phi \right)$ As we will see later, it can be shown that this very basic quantum system has a vortex around the quantization axis with circulation $\Gamma =h m⁄\mu$. This simple example shows that it is not necessary to resort to highly complex or many-body quantum systems to observe vortices. In fact, they appear even in a two-body system, reducible to the problem of a particle of reduced mass μ in the presence of a central potential, as is the case of the hydrogen atom.

However, despite their ubiquity, even in the simplest quantum systems, vortices are not only not treated but not even mentioned in quantum physics textbooks. Except for error or omission, an exhaustive search in more than fifty of the best-known books used in academic courses, from the most basic to the most advanced, shows that the words vortex or vortices do not even appear in the alphabetical indexes. Only two books [7,8] make a presentation of this concept, although not exhaustively. However, it should be noted that both books, being based on either the de Broglie–Bohm pilot wave or the Madelung Hydrodynamics interpretations, respectively, were not intended for their use in quantum physics courses.

To find a complete analysis of these structures, it is necessary to turn to, for example, the following articles by Białynicki-Birula et al. [9,10]. Furthermore, a review of their citations might serve to put into context the impact that this initially marginal topic is having on the study of various few-body processes such as, for example, the simple ionization of atoms, as we will see in this article.

3. Quantum Vortex

Let us consider a quantum system characterized by a wave function, $\psi (\mathbf{r},t)$. For simplicity in what follows, we will consider the case of a single particle, although the calculation and its conclusions can easily be generalized to systems of more particles. We define the amplitude $A$ and the action $S$, real quantities that verify

$$\psi \left(\mathbf{r},t\right)=A\left(\mathbf{r},t\right)\exp [\frac{i}{\hslash }S\left(\mathbf{r},t\right)],$$

(1)

from which we obtain the probability density and the velocity field,

$$\rho \left(\mathbf{r},t\right)={A\left(\mathbf{r},t\right)}^2,$$

(2)

$$\mathbf{u}\left(\mathbf{r},t\right)=\nabla S\left(\mathbf{r},t\right)/\mu .$$

(3)

These two “fields” verify the continuity equation [11] (pp. 26–27),

$$\frac{\partial \rho }{\partial t}+\nabla \cdot \rho \mathbf{u}=0.$$

(4)

Now, since the velocity is defined from a gradient according to Equation (3), then its rotor is zero, and therefore we obtain a vorticity equal to zero regardless of position and time,

$$\mathit{\omega }\left(\mathit{r},t\right)=\nabla \times \mathbf{u}=\mathbf{0}.$$

(5)

In this sense, we see that the concept of a vortex system may not be associated with the wave function of a pure quantum system, when interpreted in hydrodynamic terms [8,12]. However, this is not the case. Let us consider, for example, the state ${\psi }_{n\mathcal{l}m}\left(r,\theta ,\phi \right)$ of a hydrogenic atom. We write its wave function as

$${\psi }_{n\mathcal{l}m}\left(r,\theta ,\phi \right)=R_{n\mathcal{l}}\left(r\right) N_{\mathcal{l}m} P_{\mathcal{l}}^m\left(\cos \theta \right) e^{im\phi },$$

(6)

where $R_{n\mathcal{l}}\left(r\right)$ is a radial function, $P_{\mathcal{l}}^m$ are the associated functions of Legendre, and $N_{\mathcal{l}m}$ is a constant of normalization [11], all real quantities. We see that

$$\mathbf{u}\left(\mathbf{r},t\right)=\frac{\hslash m}{\mu }\nabla \phi =\frac{\hslash m}{\mu }\frac{1}{r\sin \theta }\widehat{\phi }.$$

(7)

and, therefore, the circulation through any circuit around the axis $\widehat{\mathit{z}}$ is equal to

$$\Gamma =\frac{h}{\mu } m.$$

(8)

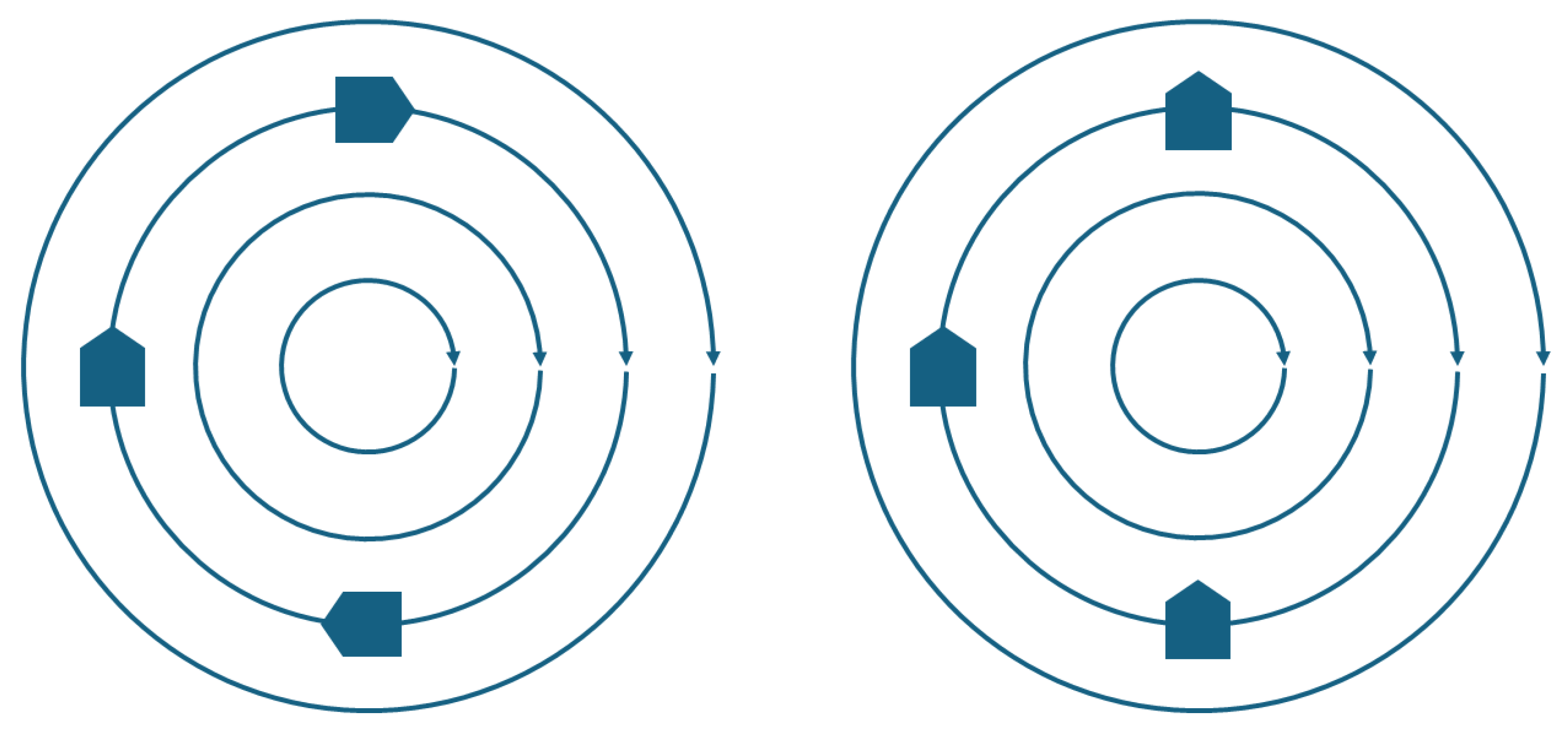
We see that the circulation around the quantization axis is nonzero (except for $m=0$). This makes sense, since the action $S$ must be well defined, except for an integer multiple of 2π. In addition, the velocity diverges as $1/r\sin \theta$, and the only way this is not absurd is that $\rho \left(\mathbf{r},t\right)$ is zero on that axis, which indeed happens. But the most important conclusion of this example is that there can indeed be vortices associated with pure quantum systems, where the vorticity is zero along any closed contour that does not contain the zone where the probability density is canceled and around which the circulation is nonzero and quantized. Unlike the vortices typically found in macroscopic systems, called “rotational” vortices (see Figure 1, left), these types of vortices, which we have described here, are called “irrotational or free” vortices (see Figure 1, right).

The previous calculation was restricted to a reduced quantum (three-dimensional) system of one particle but can be extended to systems of more particles and therefore of greater dimension. In such a case, since the quantum vortex is characterized by the locus where the probability density cancels out (that is, where the real and imaginary parts of the wave function are zero simultaneously), it must have a dimension twice as small as the dimension of the system. It is said, then, that quantum vortices have codimension 2.

4. Quantum Vortex in Atomic Collisions

Studies based on the numerical resolution of the time-dependent Schrödinger equation (TDSE) for the evolution of the wave function of a hydrogen atom subject to interaction with charged protons [13,14,15] or antiprotons [16] following classical rectilinear and uniform motion show that quantum vortices can appear, evolve in different ways, and even disappear in time. More specifically, these theoretical studies analyzed the temporal evolution of the wave function,

$$\psi \left({\mathbf{r}}_p, {\mathbf{r}}_n, {\mathbf{r}}_e, t\right),$$

(9)

where ${\mathbf{r}}_p$, ${\mathbf{r}}_n$, and ${\mathbf{r}}_e$ represent the positions of the projectile, and of the nucleus and electron, of the target atom (of masses $m_p$, $m_n$, and $m_e$), respectively. In addition, an impact parameter approximation was applied to the motion of the projectile, which was classically described by means of the equation ${\mathbf{r}}_p=\mathbf{v}t+\mathit{b}$, with v being the velocity and b being the impact parameter. While convincingly demonstrating the emergence and evolution of quantum vortices in collision processes, and even that some of these vortices can stabilize and remain even at very large times and macroscopic distances, these studies did not indicate how it would be possible to detect their presence in the corresponding cross sections. To establish this link, we must apply the following theorem.

4.1. Imaging Theorem

Let us consider a simple ionization process, where a projectile p ionizes an atom that separates into a residual nucleus $n$ and an electron $e$. From a theorem proved by John Dollard in 1971 [17], we have that, in the asymptotic limit,

$$\underset{t\to \infty }{\lim }{\left|\psi \left({\mathbf{r}}_p, {\mathbf{r}}_n, {\mathbf{r}}_e, t\right)\right|}^2 d{\mathbf{r}}_{p}d{\mathbf{r}}_{n}d{\mathbf{r}}_e \propto {\left|T\left({\mathbf{k}}_p, {\mathbf{k}}_n, {\mathbf{k}}_e\right)\right|}^2 d{\mathbf{k}}_{p}d{\mathbf{k}}_{n}d{\mathbf{k}}_e$$

(10)

where ${\mathbf{k}}_j=m_j{\mathit{r}}_j/t$ are the momentum of the particles $j=p$, $n$, and $e$ in the three-body final state. Here, $T\left({\mathbf{k}}_p, {\mathbf{k}}_n, {\mathbf{k}}_e\right)$ is the transition matrix element, which is related to the fully differential cross section (FDCS) by means of the following equation:

$$\begin{gathered} \frac{d\sigma }{d{\mathbf{k}}_{p}d{\mathbf{k}}_{n}d{\mathbf{k}}_e}=\frac{{\left(2\pi \right)}^4}{\mathrm{v}} {\left|T\left({\mathbf{k}}_p, {\mathbf{k}}_n, {\mathbf{k}}_e\right)\right|}^2 \\ \times \delta \left({\mathbf{k}}_p+{\mathbf{k}}_n+{\mathbf{k}}_e-m_p\mathbf{v}\right) \delta \left(\frac{k_p^2}{2m_p}+\frac{k_n^2}{2m_n}+\frac{k_e^2}{2m_e}-\frac{1}{2}{m}_p{\mathrm{v}}^2+\epsilon \right). \end{gathered}$$

(11)

Here, $\epsilon$ is the single ionization energy of the atom in its initial state. In the above equation and in the rest of this article, we will use Hartree’s atomic units [18]; that is, the mass and unit charge of the electron are taken as equal to one, as is Planck’s reduced constant, $\hslash =1$, and the Bohr radius (i.e., the average radius of the orbit of the fundamental state of the hydrogen atom).

Finally, it should be mentioned that although in this section we have been studying a collision process characterized by a three-body final state, the conclusions obtained are not limited to this system, and can be extended to other collision processes with ease.

4.2. Reduction in the Number of Variables with Conservation and Symmetry Laws

The Dirac deltas due to the conservation of linear momentum and energy allow for reducing the dependence of the cross section on the nine components of ${\mathbf{k}}_p$ ${\mathbf{k}}_n$ y ${\mathbf{k}}_e$ to only five. Furthermore, due to the rotation symmetry around the collision axis determined with $\mathbf{v}$, it is possible to eliminate one more variable, and be left with only four. Therefore, we write

$$\frac{d\sigma }{d{q}_{1}d{q}_{2}d{q}_{3}d{q}_4}=N {\left|T\left(q_1,q_2,q_3,q_4\right)\right|}^2,$$

(12)

where $N$ is a normalization factor that depends on the set of variables chosen. There is complete freedom in the choice of these four variables, and different authors have chosen different sets to represent their results, with the only requirement that any of these choices should be complete, in the sense that any other set of four independent variables can be written in terms of them.

4.2.1. Rochester Geometry

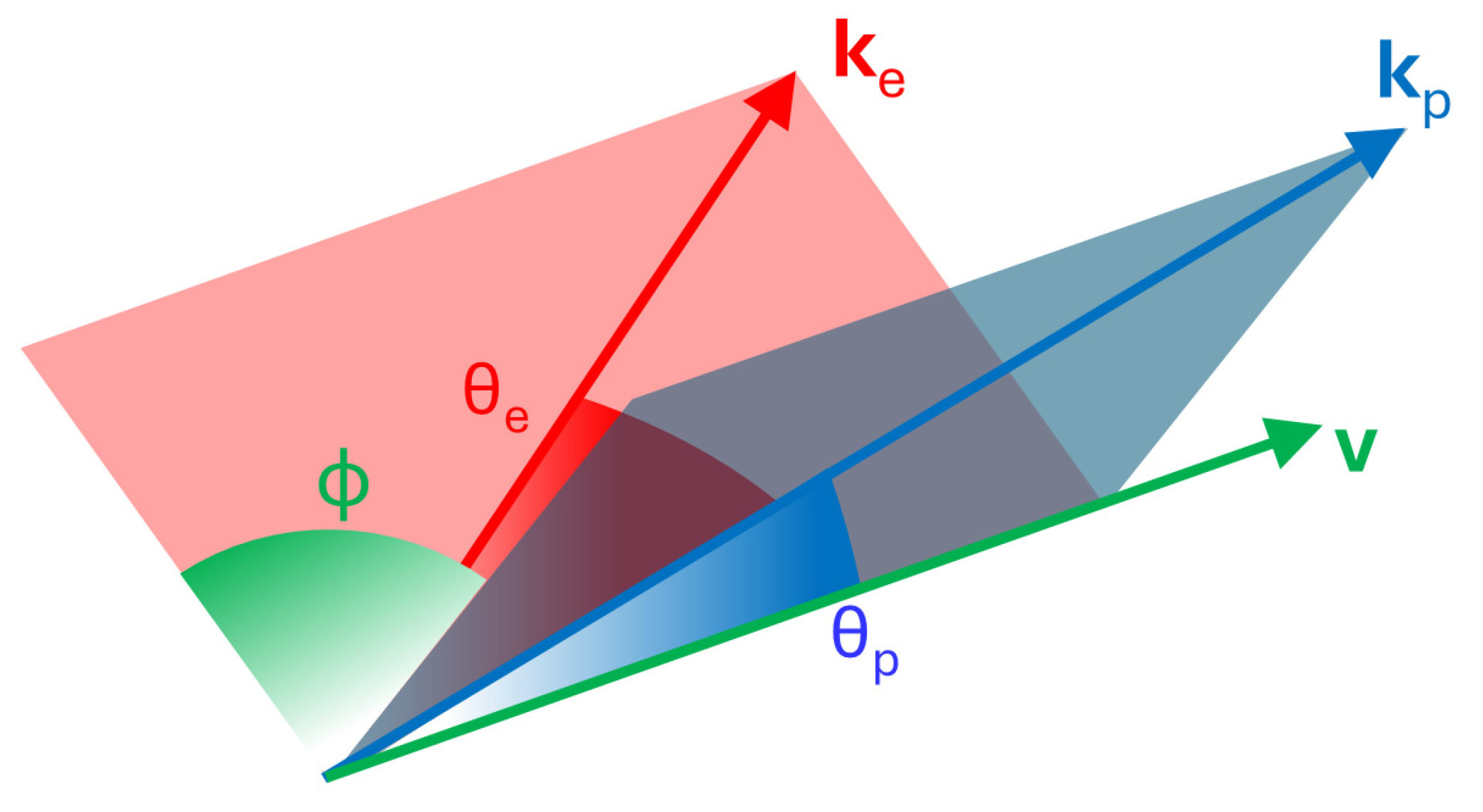
One of the most used options is the so-called Rochester geometry [19], which chooses the polar angles of two particles (usually the projectile and the electron), their relative azimuthal angle, and the energy of one of them (see Figure 2).

4.2.2. Harvard Geometry

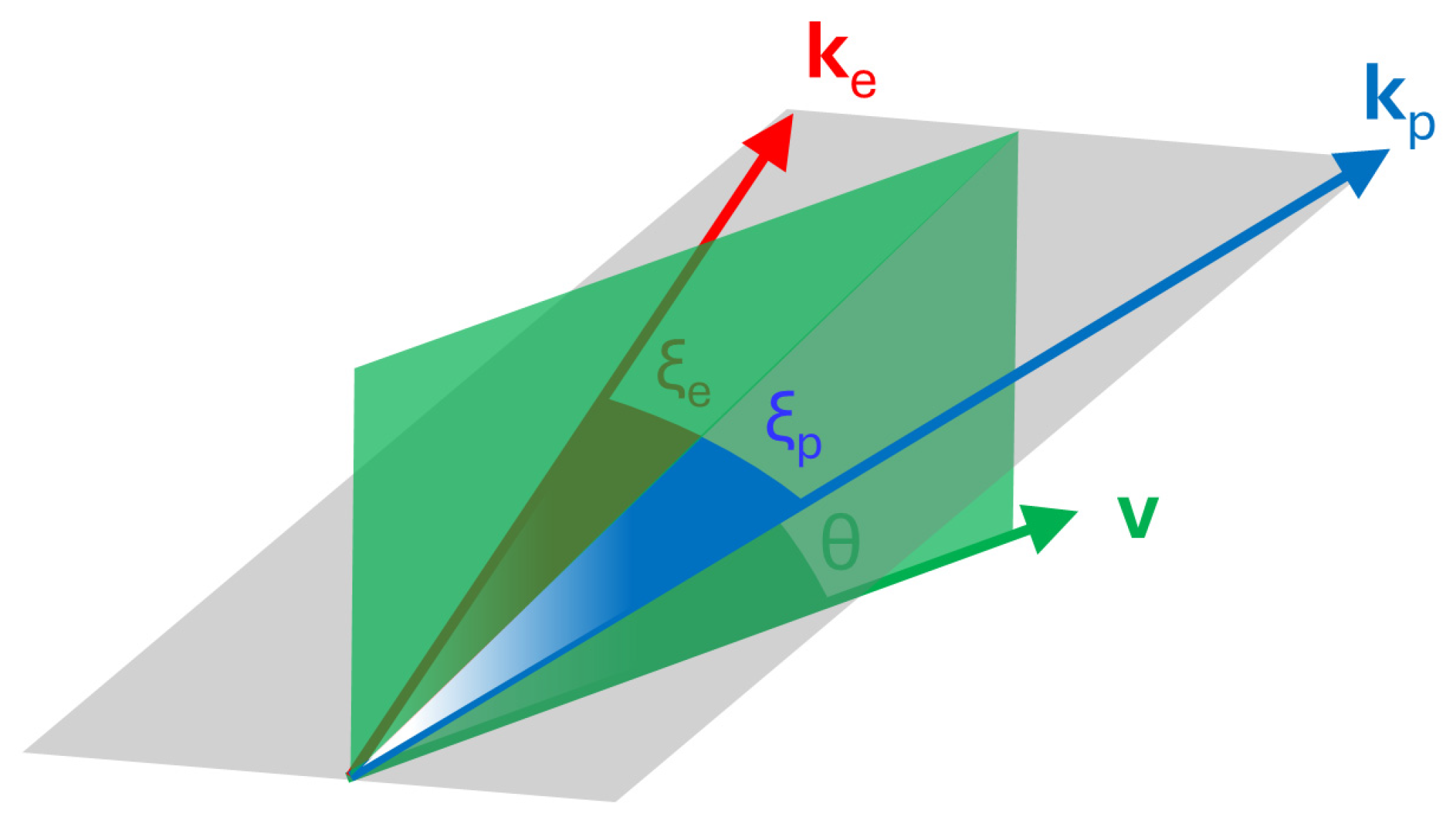
Unlike the previous geometry, in the so-called Harvard geometry [19], the “gun angle” $\theta$ between the initial direction of the projectile and the plane formed with the particles $p$ and $e$, the relative angles on that plane, as shown in Figure 3, and the energy of one of them are chosen as relevant variables.

4.3. Restrictive Geometries

Naturally, since the FDCS in a simple ionization process depends on four variables, there is an inherent difficulty in its visualization, since this would require a reduction in at least one variable to be represented graphically in our three-dimensional world. It is for this reason that restrictive geometries are usually used, where one or more conditions are imposed on the four variables chosen.

5. Vortex Points in Simple Impact Ionization of Charged Particles

5.1. Electron Impact

One of the first experimental pieces of evidence of the presence of vortices in a simple quantum system was obtained by Murray and Read in 1993 [20,21] in the single ionization of helium by an electron impact of 64.6 eV. It appeared in the form of a deep minimum in the FDCS in a “symmetric” variant of Harvard geometry [22], where it is imposed that the angles ${\xi }_p$ y ${\xi }_e$ should be equal (i.e., ${\xi }_p={\xi }_e=\xi$), which reduces the number of variables by one. Plotting the FDCS as a function of the scattering angle $\xi$ for fixed values of the Gun Angle $\theta$ and the final energy $E_p$ or $E_e$ (in this case, interchangeable), the authors observed the presence of a minimum when $\theta =67.5$ degrees and $E_p=E_e=20$ eV, for a symmetric scattering angle $\xi$ equal to 70 degrees.

Initially, this minimum was attributed to the “interference between the scattering amplitudes for the forward- and backward-scattering processes”. Using a three-body distorted wave (3DW) approximation, but modified to allow for three-body effects, this minimum could theoretically be reproduced a year later [23]. In addition, it was theoretically shown that this deep minimum was an isolated zero in the restricted FDCS, thus constituting a novel and hitherto unknown structure. It took 16 years before Macek et al. [24] concluded that this zero could be traced to the presence of an isolated quantum vortex in the atomic wave function. Subsequent theoretical studies also observed the presence of an isolated vortex point in the restricted FDCS for (e,2e) collisions with other targets. For example, with (K-shell) carbon [25] in a Coulomb–Born (CB1) approximation, oriented molecular hydrogen [3,26] by means of a time-dependent close-coupling (TDCC) approach, and atomic hydrogen [22,27,28] using 3DW TDCC, and different types of modified-CB1 approximations [22].

5.2. Positron Impact

In 1991, 2 years before the Murray and Read experiment, Braunner and Briggs [29], using a 3DW approximation, theoretically discovered a minimum in the TDCS for atomic hydrogen ionization by a positron impact of 10 and 100 keV.

Using a collinear geometry, which can be achieved either by fixing $\varphi =0$ and ${\theta }_p={\theta }_e=\theta$ in Rochester geometry or ${\xi }_p={\xi }_e=0$ in Harvard geometry, they observed that for $\theta =45$ degrees, a deep minimum was generated when $E_e\approx 4.76$ keV and $E_e\approx 49$ keV, for impact energies of 10 keV and 100 keV, respectively.

The appearance of this minimum at an emission angle of 45 degrees was initially attributed to some kind of interference between two Thomas double-binary scattering mechanisms.

In 2003, it was demonstrated [30] that, using the same collinear geometry, an isolated zero was also observed at impact energies of the order of 100 eV, that is, in a plausible range of experimental study, well below the excessively high energies analyzed by Brauner and Briggs. This zero was at an emission angle of about 22.5 degrees and was therefore associated with a saddle-point mechanism.

Later it was found that, as the impact energy increased, two other zeros at 45 degrees also began to be observed [31], as shown in Figure 4. These zeros are compatible with the minimum reported years earlier by Brauner and Briggs [29], this being the first evidence of the coexistence of more than one isolated zero in the doubly restricted FDCS corresponding to the same collision.

Finally, in 2013, as shown in Figure 4, these isolated zeros were shown to be manifestations of quantum vortices [32]. In particular, the two zeros observed at an angle of 45 degrees had opposite vorticities. This was compatible with one of the mechanisms for vortex appearance identified by Białynicki-Birula et al. [9,10].

Moreover, it was observed that the vortex at 22.5 degrees could exist at impact energies of a few tens of eV [33], being therefore accessible to experimental observation. Although in 2015 a technique was proposed [34] to facilitate the identification of vortices in positron impact ionization experiments, an experimental confirmation such as the one that has existed for three decades in the case of processes (e,2e) has not yet been achieved.

6. Vortex Lines

In 2017, it was discovered that the three isolated vortices shown in Figure 4 for the ionization of atomic hydrogen by the impact of positrons of 275 eV were part of a single structure, a vortex line [35]. This can be clearly seen in Figure 5, corresponding to a Rochester geometry with $\varphi =0$ where the vortex line cuts the plane of collinear geometry three times, thus forming the three vortex points observed in Figure 4.

That the presence of this structure was not previously observed was due to simple reasons; basically, with a few exceptions, FDCSs are usually represented in 2D restricted geometries. Therefore, since vortices are codimension 2 structures, they can only appear as isolated points. When moving to 3D constrained geometry, vortices become visible as one-dimensional structures, that is, as vortex lines.

7. Vortex Rings

A subsequent study [36] showed that, by using an appropriate set of coordinates (in this case, Cartesian), but without departing from the restrictive geometry described in the previous section, the vortex line shown in Figure 5 closes on itself, constituting a vortex ring, as it is seen in Figure 6.

8. Vortex Surface

In all the previous examples, some kind of constraint is used on the four variables that define the final state of the three-body system. The question naturally arises as to what would happen if we calculated the FDCS completely and without any restriction, that is, for all kinematically accessible values in a four-dimensional space. As mentioned in the introduction, this is precisely the central objective of this article.

We will use the same C3 model used in the previous calculations, where the final state in the ionization of atomic hydrogen by positron impact is described with the following correlated wave function [32]:

$$\psi ={\phi }_{-1}\left({\mathbf{k}}_{\mathrm{p}},{\mathbf{r}}_{\mathrm{p}}\right)\times {\phi }_1\left({\mathbf{k}}_{\mathrm{e}},{\mathbf{r}}_{\mathrm{e}}\right)\times {\phi }_{1/2}\left({\mathbf{k}}_{\mathrm{e}}-{\mathbf{k}}_{\mathrm{p}},{\mathbf{r}}_{\mathrm{e}}-{\mathbf{r}}_{\mathrm{p}}\right)\times {\left(2\mathsf{\pi }\right)}^{3/2}\exp \left(\mathrm{i}\mathbf{k}\cdot \mathbf{r}\right),$$

(13)

where

$${\phi }_{\alpha }\left(\mathbf{k},\mathbf{r}\right)={\left(2\pi \right)}^{-3/2}\Gamma \left(1+i\frac{\alpha }{k}\right)\exp \left(\frac{\pi \alpha }{2k}+i\mathbf{k}\cdot \mathbf{r}\right){}_1{F}_1\left(-i\frac{\alpha }{k},1;-i\left(kr+\mathbf{k}\cdot \mathbf{r}\right)\right),$$

(14)

is the continuum state for a two-body system of relative position $\mathbf{r}$ and momentum $\mathbf{k}$, unit reduced mass, and interacting by means of a Coulomb potential, $V\left(r\right)=-\alpha /r$. The reader can refer to article [32] to find a detailed description of this theory, its advantages, limitations, and previous applications.

If we look at Figure 5 and Figure 6, it is obvious that the geometries used so far do not seem to be adequate for the representation of vortex structures. Obviously, the intricate aspect of the vortex ring will also be observed in the vortex surface (of which the above is a cut for a fixed value of the perpendicular component of the positron’s final moment). This will not only make it very difficult to represent the vortex surface, but also to identify its fundamental characteristics. To avoid this conundrum, we will use a different geometry than those used or referred to so far in this article and by other authors. In what follows, we will represent the FDCS without any restrictions whatsoever, using as its four representative variables the three Cartesian components of the electron momentum and the exit angle $\theta$ of the positron with respect to its initial velocity $\mathbf{v}$.

It should be mentioned that these calculations are very time-consuming, since to locate the vortices, it is necessary to explore the entire variable space of the FDCS looking for those points where both the real part and the imaginary part of the transition matrix are simultaneously equal to zero, namely $\mathrm{Im}T=\mathrm{Re}T=0$. The technique to do so consists of tracking the regions where the imaginary and real parts of $T$ cancel out separately, and then where they cross, as described in detail in article [32]. Each point on the following figures represents a match, $\mathrm{Im}T=\mathrm{Re}T=0$. The set of these points will thus define the vortex lines. For calculating each point of a vortex ring, we calculate FDCS on a grid equally spaced in the modulus of momentum (50 points) and final angle of the electron (180 points). The crossings of the real and imaginary lines are estimated using the bisection. Each ring in the end is composed of 90 points (by symmetry considerations, only 45 are calculated), then implies the calculation of 405,000 cross sections.

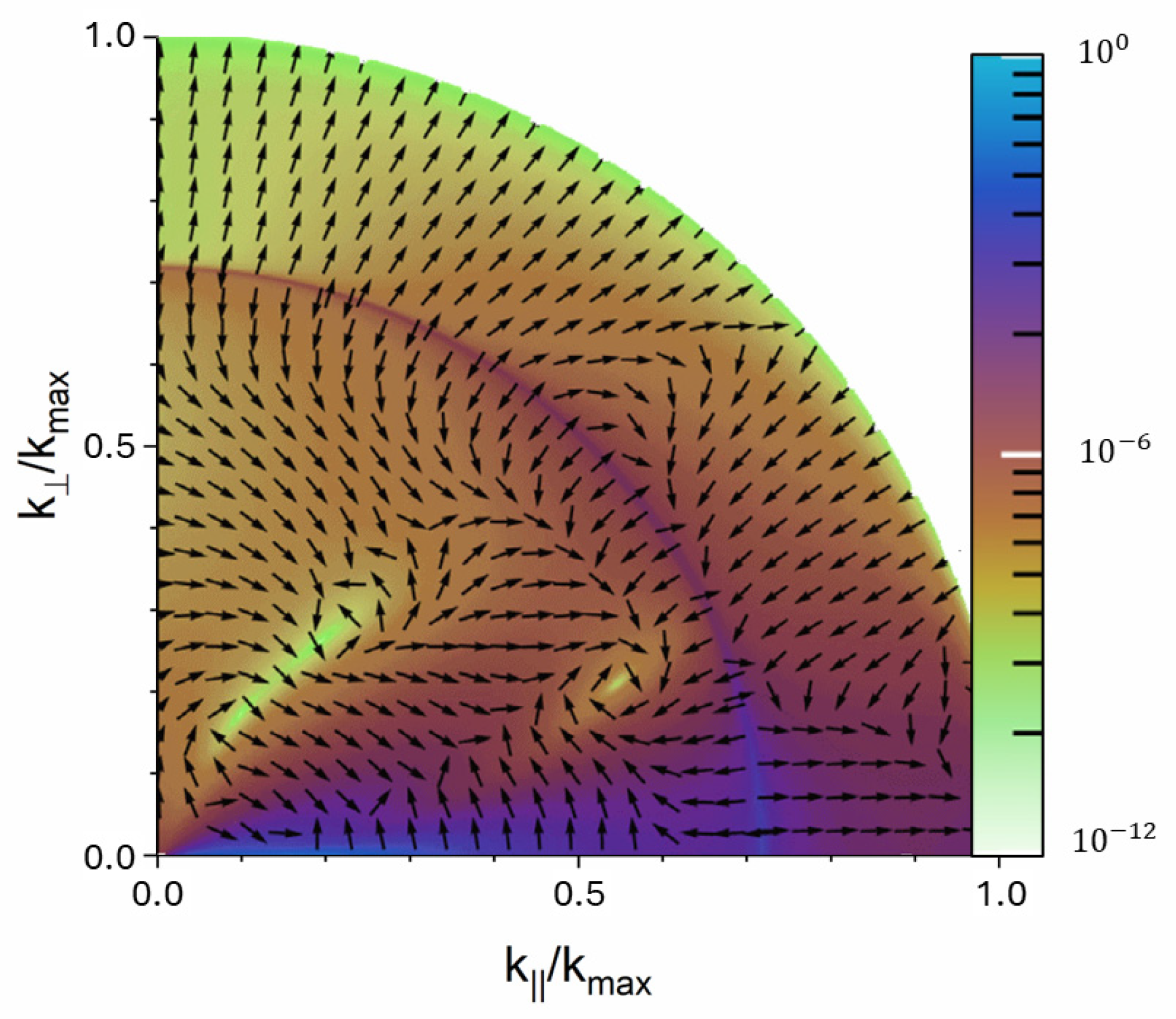
In Figure 7, we see that for $\theta =0$, two vortex rings (of opposite vorticity) are observed around $\mathbf{v}$, which we take as axis $\mathit{z}$. The symmetry of rotation around this axis is reflected in the circular shape of both vortices.

In Figure 8 below, the positron is deflected at an angle of 5 degrees, which produces several effects on the vortex structures. First, the rotational symmetry is broken around the z-axis, but a reflection symmetry remains with respect to the collision plane ($k_y=0$) formed with the initial and final directions of motion of the projectile. On the other hand, the lower vortex ring has been deformed in the direction of the exit of the positron. Finally, the top vortex ring has been opened into a vortex line that starts and ends at the kinematic limit. This boundary forms a sphere of radius $k_{\mathrm{m}\mathrm{a}\mathrm{x}}=\sqrt{{\mathrm{v}}^2-2\epsilon }$ around $\mathbf{k}=0$, which, for simplicity, is not shown in the figure. Here, it is worth highlighting that reaching the kinematic limit in momentum space is equivalent to reaching infinity in coordinate space, because the distance between an electron escaping with the maximum allowed kinetic energy and any other with a smaller speed grows linearly with time.

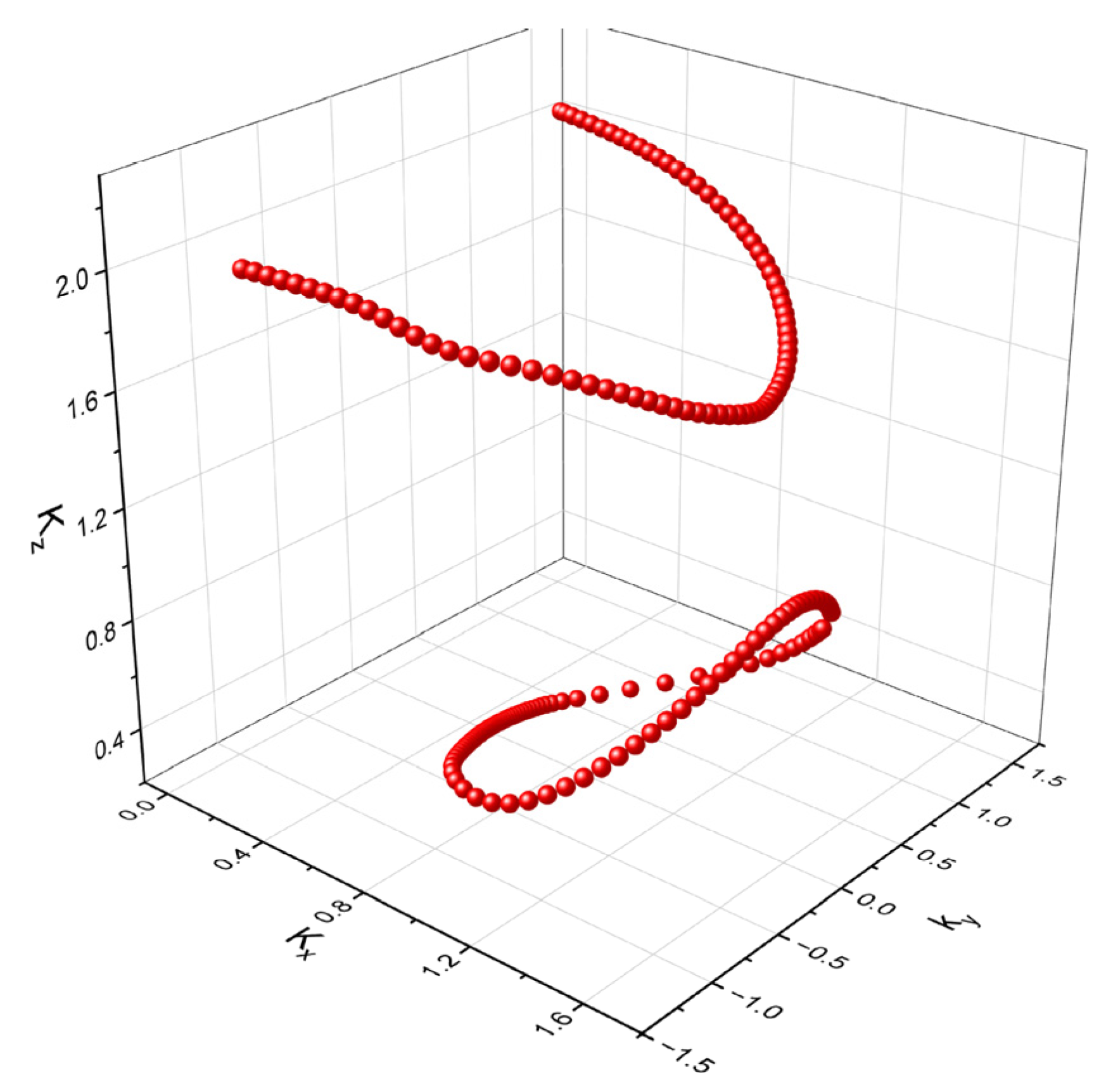
As the deflection angle $\theta$ of the positron increases, the ends of both vortices get closer together, until they join to form a single line as shown in the Figure 9, in one of the forms of vortex evolution studied by Białynicki-Birula [9,10].

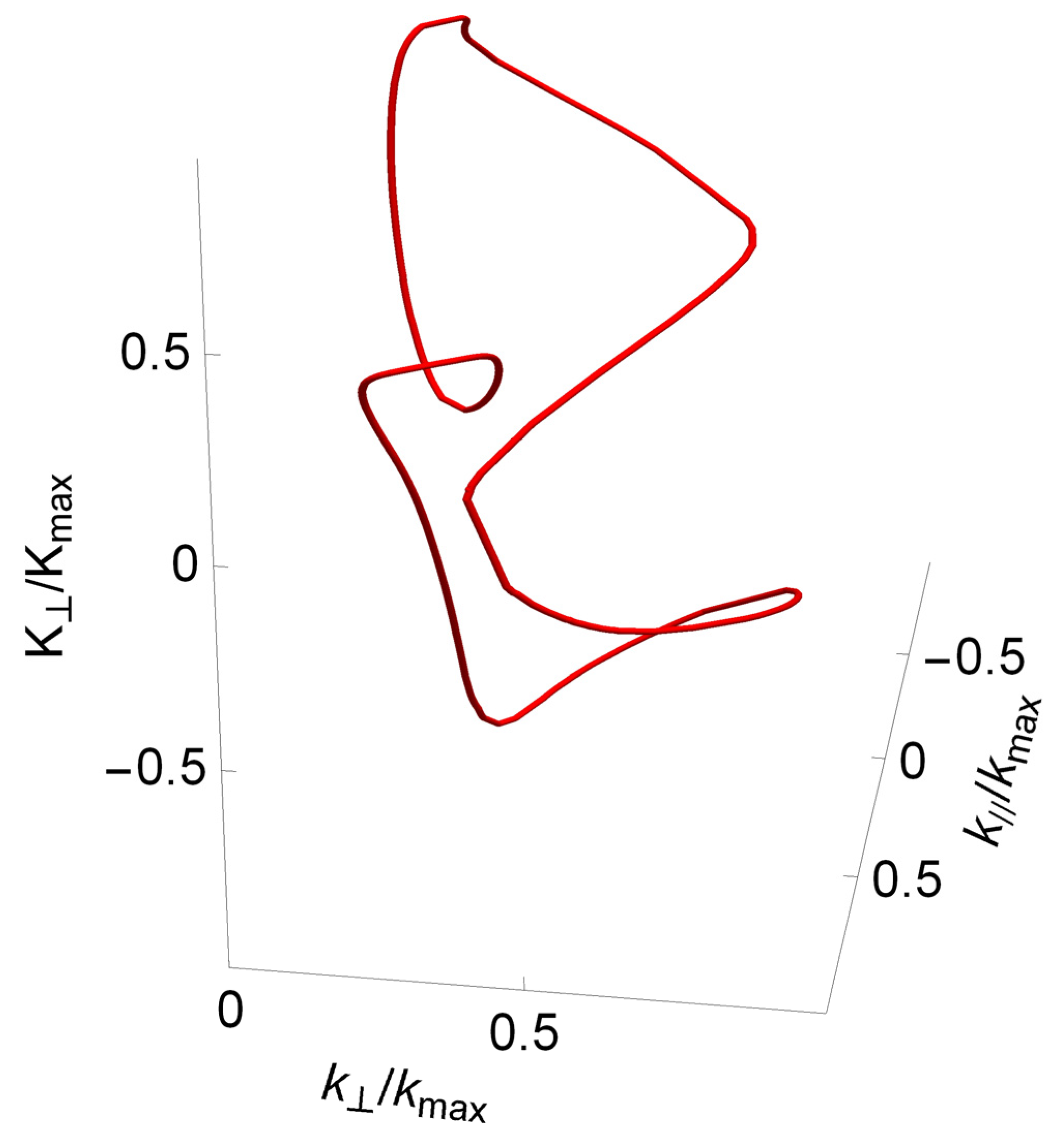
If the deflection angle of the positron continues to increase, this vortex line is deformed until, in an inverse process to that observed in the previous figure, it separates into a line and a ring, as shown in Figure 10 for $\theta =120°$.

Finally, by continuing to increase $\theta$, the vortex ring closes on itself, while the vortex line vanishes over the kinematic limit, thus closing the vortex surface of which the lines shown in Figure 7, Figure 8, Figure 9 and Figure 10 are only cuts for certain values of $\theta$. Indeed, plotting together the set of these different cuts gives a representation of the vortex surface itself. For simplicity, we only show a fragment of this surface (Figure 11), limited to the range $0°\le \theta \le 25°$.

9. Conclusions

In this work, we have made a complete calculation of the vortex surface for a process of atomic ionization by impact of positrons. We showed not only that the vortex points observed previously in the FDCS by different authors and in different ionization processes using restrictive 2D geometries seem to correspond to a single vortex line when one of the variables is relaxed, i.e., moving to a 3D geometry, but that these vortex lines are only cuts of a single vortex surface in the complete FDCS with no geometric restrictions.

From an exhaustive bibliographic search, we believe our study might be relevant to explore this type of structures in other fields of physics where vortices arise. Moreover, it is important to highlight again that these vortex surfaces appear in an extremely simple quantum process, characterized by a final three-body state consisting of an electron, a positron, and a proton. Preliminary calculations seem to indicate that a similar structure would exist in ion impact ionization processes.