Abstract
We present a theoretical investigation of the elastic Rayleigh scattering of X-rays by atomic targets. Special attention is paid to the question of how the polarization of the scattered photons is affected if the incident light is itself polarized. In particular, we found that the circular polarization of the incoming X-rays may lead to a remarkable modification of the linear polarization of the scattered photons. Based on this ’circular-to-linear-polarization-transfer’ and on the fact that the linear polarization of X-rays can be conveniently observed by solid-state Compton detectors, we argue that Rayleigh scattering may be used as a tool for circular polarimetry of hard X-rays. To illustrate our proposal, we performed detailed calculations of 145 and 500 keV circularly polarized photons scattered by lead atoms. Based on these calculations, we found that the photon scattering under large angles with respect to the incident beam direction is most favorable for the circular polarimetry of hard X-rays. In particular, for 500 keV photon energy and scattering angles around 70 deg we found a remarkable modification of the linear polarization of scattered light for the case when the incident radiation is circularly polarized.
Keywords:
elastic scattering; X-rays; Rayleigh; circular polarization; polarimetry; Compton detector 1. Introduction
Recently, great progress has been achieved in the development of polarization-sensitive X-ray detectors. In particular, state-of-the-art solid-state Compton scatterers allow for a highly precise determination of the linear polarization of photons in the energy range between about 60 keV up to 1 MeV [1,2]. It was shown that the uncertainty of the polarization reconstruction using such polarimeters is mainly limited by the statistics of registered Compton scattering events in the detector and can be reduced to below [3]. These polarimeters were successfully used to investigate fundamental processes that occur in collisions of highly charged ions with photons, electrons and atoms. In particular, the polarization properties of X-rays emitted in radiative electron capture, dielectronic recombination, bremsstrahlung and Rayleigh scattering were analyzed using Compton detectors [4,5,6,7,8,9]. These polarization measurements gained valuable information about the physics of electronic systems in the presence of strong electromagnetic fields.
In contrast to linear polarization, much less progress has been made so far in the development of circular X-ray polarimetry techniques. Some proposals based on Compton scattering off polarized electrons were made in the past [10,11,12,13,14,15] but the drawbacks of this method, such as the need for magnetized targets and the rivalry between solid-angle coverage and angular resolution, were not yet overcome [16]. Recently, another proposal was made, based on the spin transfer from the photon to the electron during Compton scattering [16] but this proposal was not yet realized in practice.
In this contribution, we propose yet another approach to measure the circular polarization of X-rays and discuss its feasibility. This approach is based on the application of the elastic Rayleigh scattering of X-rays by atomic targets. During the recent years, Rayleigh scattering has been studied in detail for the energy range from 17 to 889 keV and for various target atoms both in low-Z and high-Z domains [17,18,19,20]. These studies focused on the linear polarization of the elastically scattered photons which were measured by means of Compton detectors. In the present work we show that Rayleigh scattering may also lead to the partial transfer of the circular polarization of incident X-rays to linear polarization of the scattered photons, where the latter can be measured by conventional Compton detectors.
The article is organized as follows. In Section 2, we first introduce the geometry of the process. Then, we discuss the Rayleigh scattering amplitudes and introduce the Stokes parameters in order to describe the polarization transfer between incident and outgoing photons. In Section 3, we use the derived formulas to analyze the scattering of 145 and 500 keV photons by a lead atom. We show, in particular, that the linear polarization of the scattered photons can be remarkably affected if the incoming light is circularly polarized and that this effect can be observed with current Compton scatterers. A brief summary of our results is given finally in Section 4. Atomic units () are used throughout this article unless stated otherwise.
2. Theoretical Background
2.1. Geometry
To provide a description of the polarization transfer in Rayleigh scattering, we first discuss the geometry of the process. For the theoretical analysis, it is convenient to define the so-called scattering () plane, spanned by the wave vectors and of the incoming and outgoing photons, see Figure 1. The propagation direction of the initial photon is chosen parallel to the z axis and the scattered photon is emitted under the polar angle . In our study, we focus on the case when the incident light is circularly polarized, while the linear polarization of the scattered radiation is detected. The linear polarization vector of the outgoing photon does not necessarily lie in the scattering plane. It can be tilted with respect to this plane by an angle .
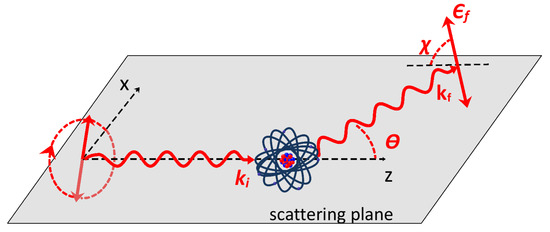
Figure 1.
The geometry of the elastic photon-atom scattering. The scattering plane, chosen as plane, is defined by the wave vectors of the incoming and outgoing photons. The propagation direction of the incident photon is taken along the z axis. We are interested especially in the case when incident light is circularly polarized, and the linear polarization of the scattered radiation is detected.
2.2. Scattering Amplitudes
The main ‘building block’ to describe the Rayleigh scattering is the scattering amplitude. Within the framework of second-order perturbation theory, this amplitude can be written as:
where is the fine structure constant and and are the vector of Dirac matrixes and the coordinate vector of the jth electron in a target atom [21]. The polarization vectors and energies of the incoming and outgoing photon are denoted as and . The initial, intermediate and final atomic states and their energies E are identified by the indices i, and f, respectively.
In our study, we will focus on scattering off closed-shell atoms. The scattering amplitudes for such systems provide a crucial symmetry property: The entire scattering process can be described by only two linearly independent amplitudes. Due to historical reasons, the amplitudes for parallel and perpendicular linear polarizations with respect to the scattering plane are used [17]. They are usually denoted as and . The ratio of these two amplitudes is a very practical quantity to describe many properties of the process see for instance Ref. [22] for further details.
For many-electron systems, the evaluation of the scattering amplitude (1) is a very complicated task. In our calculations, we approach this issue using the independent particle approximation (IPA) which is known to work very well in the high energy regime [23]. In the IPA, we calculate first the single-electron amplitudes assuming that only one electron interacts with the photon while the others remain ’frozen’. The many-electron amplitude is then the sum over the single-electron amplitudes, including all occupied electron shells. We do not discuss the further details for the evaluation of the scattering amplitude here as it was described in our previous works [22,24] as well as in the literature [17,25,26,27].
2.3. Stokes Parameters
With the help of the scattering amplitude (1), we are able to investigate all the properties of the scattering process. In this work in particular, we are interested to study how the polarizations of incoming and outgoing photons are related to each other. Such a polarization transfer can be described most conveniently with the Stokes parameters. For linear polarization of light, the Stokes parameters are defined as
In these equations, describes the intensity of light linearly polarized under a certain angle with respect to the plane. Similarly, we can define the degree of circular polarization
with I being the intensity of right- () or left-handed () circularly polarized light. In our recent study [24], we derived equations which relate the Stokes parameters of the incoming light (denoted by index i below) to their counterparts of the scattered light (index f):
where S is the ratio of the scattering amplitudes as mentioned above. Here we restricted our analysis to the parameters and which describe the linear polarization of the scattered light. We did not include a consideration of the circular polarization of the scattered light (), as modern Compton polarimeters are insensitive to this parameter.
As seen from Equations (5) and (6), the Stokes parameters of the scattered light and exhibit a qualitatively different sensitivity to the circular polarization of the incident light. While is independent on , the second Stokes parameter is proportional to the circular polarization component (if ). As we will see below, this sensitivity opens a way for circular polarimetry with the help of Rayleigh scattering.
Another important observable of the Rayleigh scattering process is the differential cross section. If the outgoing polarization is not observed, it is given by
and is independent on the circular polarization of the incoming photon [25].
2.4. Competing Processes
In experiments, Rayleigh scattering cannot be separated from the two other elastic channels, Delbrück and nuclear Compton scattering. Nevertheless, in this work we will not consider these two competing processes, since their contribution to the cross section is negligible for the parameter space considered here. For example, using the Delbrück amplitudes obtained in Refs. [28,29] and the low-energy scaling, we estimate that the Delbrück contribution to the cross section is in the order of less than for 145 keV and approximately for 500 keV. Moreover, using analytical formulas for nuclear Compton scattering [30], we find that its contribution is smaller than 0.01%.
3. Results
By making use of Equations (5)–(7), we are ready to investigate the Rayleigh scattering of circularly polarized X-rays by an atomic target. In this work, we performed calculations for the scattering of photons with energies of 145 keV and 500 keV by a lead atom. This particular choice of energies and target was proposed by previous theoretical and experimental studies [6,17,31]. To find the scattering amplitudes and hence, the amplitude ratio S, we employed the IPA as discussed in Section 2.2 and restricted our calculations to the scattering from K and L shells only. Such an approximation is well justified since the scattering by higher shells is known to contribute only for very small scattering angles which are typically not approached in modern experiments [6,27,32].
In Figure 2, we display the differential cross sections as well as the Stokes parameters and for the case when the incident light is completely right-handed circularly polarized (). As we mentioned already above, only the second Stokes parameter is sensitive to the incident circular polarization and, hence, can be used to measure . As seen from the figure, reaches the maximum value 0.112 for the energy 145 keV and 0.142 for 500 keV photons. To observe these rather remarkable values of , one needs to place the Compton detectors at the angles and , respectively. As seen from the left panel of Figure 2, the Rayleigh scattering cross section reaches 0.16 barn and barn at these angles and for the energies 145 keV and 500 keV. These relatively large cross sections make the measurement of the polarization Stokes parameter feasible. Please note that for higher photon energies, larger values of the second Stokes parameter are achieved, and this might even partially compensate for the reduced statistics due to the lower differential cross section.
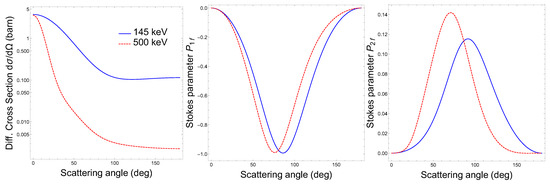
Figure 2.
Rows from left to right: Differential cross sections and Stokes parameters and for the Rayleigh scattering of 145 keV (red dashed line) and 500 keV (blue solid line) circularly polarized photons off a lead target atom. The theoretical predictions are presented as a function of the polar photon scattering angle .
To study the sensitivity of to the initial circular polarization, we show in Figure 3 the second Stokes parameter of the outgoing photons for . As seen from the figure, we observe a strong dependence , for example if is varied from 1 to 0.4, the Stokes parameter changes from 0.142 to 0.05. This modification can be measured by state-of-the-art Compton polarimeters which makes the Rayleigh scattering a promising tool for circular polarimetry, when taking also the theoretically calculated amplitude ratio into account.
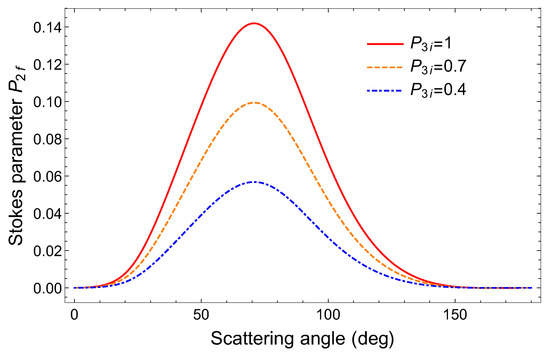
Figure 3.
The second Stokes parameter of the outgoing photons for the Rayleigh scattering of circularly polarized 500 keV photons by a lead atom. Calculations were performed for different degrees of circular polarization of the incident light: (red solid line), (orange dashed line), (blue dash-dotted line).
4. Conclusions
We re-investigated the elastic Rayleigh scattering of X-rays by atomic targets. We paid special attention to the polarization transfer between the incident and the outgoing photons. In particular, we found that the circular polarization of incident light can result in a non-zero linear polarization of the scattered light, orientated in such a way that the polarization vector points out of the scattering plane. To illustrate this ‘circular-to-linear-polarization-transfer’ effect, we performed calculations for 145 keV and 500 keV photons, scattered by lead atoms. For the case of a fully right-handed circularly polarized 500 keV photon beam, the second Stokes parameter that characterizes the out-of-plane linear polarization of the scattered photons can reach 0.142 which can be detected by modern Compton detectors. Thus, we show that elastic X-ray scattering can be potentially used for circular polarimetry in the previously problematic region of few hundred keV.
Author Contributions
Conceptualization, S.S., J.S., V.Y., W.M., T.S. and A.S.; methodology, S.S., J.S., V.Y., W.M., T.S. and A.S.; software, S.S., J.S. and V.Y.; validation, S.S., J.S., V.Y., W.M., T.S. and A.S.; formal analysis, S.S., J.S., V.Y., W.M., T.S. and A.S.; investigation, S.S., J.S., V.Y., W.M., T.S. and A.S.; data curation, S.S., J.S., V.Y., W.M., T.S. and A.S.; writing—original draft preparation, S.S., J.S., V.Y., W.M., T.S. and A.S.; writing—review and editing, S.S., J.S., V.Y., W.M., T.S. and A.S.; visu-alization, S.S., J.S., V.Y., W.M., T.S. and A.S.; supervision, S.S., J.S., V.Y., W.M., T.S. and A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the GSI Helmholtz Centre for Heavy Ion Research under the Project No. BSSURZ1922.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work has been supported by the GSI Helmholtz Centre for Heavy Ion Research under the Project No. BSSURZ1922.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Middents, W.; Weber, G.; Spillmann, U.; Krings, T.; Vockert, M.; Volotka, A.; Surzhykov, A.; Stöhlker, T. Possible Polarization Measurements in Elastic Scattering at the Gamma Factory Utilizing a 2D Sensitive Strip Detector as Dedicated Compton Polarimeter. Ann. Phys. 2022, 534, 2100285. [Google Scholar] [CrossRef]
- Weber, G.; Bräuning, H.; Hess, S.; Märtin, R.; Spillmann, U.; Stöhlker, T. Performance of a position sensitive Si(Li) x-ray detector dedicated to Compton polarimetry of stored and trapped highly-charged ions. J. Instrum. 2010, 5, C07010. [Google Scholar] [CrossRef]
- Vockert, M.; Weber, G.; Spillmann, U.; Krings, T.; Stöhlker, T. Polarization reconstruction algorithm for a Compton polarimeter. J. Phys. Conf. Ser. 2018, 1024, 012041. [Google Scholar] [CrossRef]
- Hess, S.; Bräuning, H.; Spillmann, U.; Brandau, C.; Geyer, S.; Hagmann, S.; Hegewald, M.; Kozhuharov, M.; Krings, T.; Kumar, A.; et al. Polarization studies of radiative electron capture into highly-charged uranium ions. J. Phys. Conf. Ser. 2009, 163, 012072. [Google Scholar] [CrossRef]
- Märtin, R.; Weber, G.; Barday, R.; Fritzsche, Y.; Spillmann, U.; Chen, W.; DuBois, R.D.; Enders, J.; Hegewald, M.; Hess, S.; et al. Polarization Transfer of Bremsstrahlung Arising from Spin-Polarized Electrons. Phys. Rev. Lett. 2012, 108, 264801. [Google Scholar] [CrossRef]
- Blumenhagen, K.H.; Fritzsche, S.; Gassner, T.; Gumberidze, A.; Märtin, R.; Schell, N.; Seipt, D.; Spillmann, U.; Surzhykov, A.; Trotsenko, S.; et al. Polarization transfer in Rayleigh scattering of hard x-rays. New J. Phys. 2016, 18, 103034. [Google Scholar] [CrossRef]
- Jörg, H.; Hu, Z.; Bekker, H.; Blessenohl, M.A.; Hollain, D.; Fritzsche, S.; Surzhykov, A.; López-Urrutia, J.R.C.; Tashenov, S. Linear polarization of x-ray transitions due to dielectronic recombination in highly charged ions. Phys. Rev. A 2015, 91, 042705. [Google Scholar] [CrossRef]
- Tsuzuki, Y.; Watanabe, S.; Oishi, S.; Nakamura, N.; Numadate, N.; Odaka, H.; Uchida, Y.; Yoneda, H.; Takahashi, T. An application of a Si/CdTe Compton camera for the polarization measurement of hard x rays from highly charged heavy ions. Rev. Sci. Instrum. 2021, 92, 063101. [Google Scholar] [CrossRef]
- Numadate, N.; Oishi, S.; Odaka, H.; Sakurai, M.; Takahashi, T.; Tsuzuki, Y.; Uchida, Y.; Watanabe, H.; Watanabe, S.; Yoneda, H.; et al. Polarization measurement of L-shell radiative recombination x rays from highly charged bismuth ions. Phys. Rev A 2022, 105, 023109. [Google Scholar] [CrossRef]
- Steffen, R.M. Beta-Gamma Angular Correlation Measurements on Au198. I. Directional and Circular Polarization Correlation. Phys. Rev. A 1960, 118, 763. [Google Scholar] [CrossRef]
- Pechacek, R.E.; Mann, L.G.; Bloom, S.D.; Rodrigues, R.M. Gamma-Ray Circular Polarization Analyzer Using a Rapidly Alternating Magnetic Field. Rev. Sci. Instrum. 1964, 35, 58. [Google Scholar] [CrossRef]
- Mackie, R.D.L.; Byrne, J. An experimental test of a proposal for determining the absolute efficiency of a γ-ray transmission circular polarimeter. Nucl. Instrum. Methods 1969, 76, 241. [Google Scholar] [CrossRef]
- Trautmann, W.; De Boer, J.; Dünnweber, W.; Graw, G.; Kopp, R.; Lauterbach, C.; Puchta, H.; Lynen, U. Evidence for Negative Deflection Angles in 40Ar + Ag Deep-Inelastic Reactions from γ-Ray Circular Polarization Measurements. Phys. Rev. Lett. 1977, 39, 1062. [Google Scholar] [CrossRef]
- Fazzini, T.F.; Maurenzig, P.R.; Sona, P.; Stefanini, A.; Taccetti, N. Measurement of the analyzing power of a transmission-type polarimeter. Nucl. Instrum. Methods Phys. Res. 1982, 192, 287. [Google Scholar] [CrossRef]
- Knyaz’kov, V.A.; Kolomenskii, E.A.; Lobashov, V.M.; Nazarenko, V.A.; Pirozhkov, A.N.; Shablii, A.I.; Shul’gina, E.V.; Sobolev, Y.V.; Yegorov, A.I. A new experimental study of the circular polarization of np capture γ-rays. Nucl. Phys. A 1984, 417, 209. [Google Scholar] [CrossRef]
- Tashenov, S. Circular polarimetry with gamma-ray tracking detectors. Nucl. Instrum. Methods Phys. Res. Sect. A 2011, 640, 164–169. [Google Scholar] [CrossRef]
- Johnson, W.R.; Cheng, K. Elastic scattering of 0.1–1-MeV photons. Phys. Rev. A 1976, 13, 692. [Google Scholar] [CrossRef]
- Manakov, N.L.; Meremianin, A.V.; Maquet, A.; Carney, J.P.J. Photon-polarization effects and their angular dependence in relativistic two-photon bound-bound transitions. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 4425. [Google Scholar] [CrossRef]
- Surzhykov, A.; Yerokhin, V.A.; Jahrsetz, T.; Amaro, P.; Stöhlker, T.; Fritzsche, S. Polarization correlations in the elastic Rayleigh scattering of photons by hydrogenlike ions. Phys. Rev. A 2013, 88, 062515. [Google Scholar] [CrossRef]
- Ice, G.E.; Chen, M.H.; Crasemann, B. Photon-scattering cross sections of H2 and He measured with synchrotron radiation. Phys. Rev. A 1978, 17, 2. [Google Scholar] [CrossRef]
- Kane, P.P.; Kissel, L.; Pratt, R.H.; Roy, S.C. Elastic scattering of γ-rays and X-rays by atoms. Phys. Rep. 1986, 140, 75. [Google Scholar] [CrossRef]
- Surzhykov, A.; Yerokhin, V.A.; Fritzsche, S.; Volotka, A.V. Diagnostics of polarization purity of x rays by means of Rayleigh scattering. Phys. Rev. A 2018, 98, 053403. [Google Scholar] [CrossRef]
- Pratt, R.H. Tutorial on fundamentals of radiation physics: Interactions of photons with matter. Radiat. Phys. Chem. 2004, 70, 595. [Google Scholar] [CrossRef]
- Strnat, S.; Yerokhin, V.A.; Volotka, A.V.; Weber, G.; Fritzsche, S.; Müller, R.A.; Surzhykov, A. Polarization studies on Rayleigh scattering of hard x rays by closed-shell atoms. Phys. Rev. A 2021, 103, 012801. [Google Scholar] [CrossRef]
- Roy, S.C. Polarization effects in elastic photon-atom scattering. Phys. Rev. A 1986, 34, 1178. [Google Scholar] [CrossRef]
- Goldman, S.P. Relativistic two-photon decay rates of 2s1/2 hydrogenic ions. Phys. Rev. A 1981, 24, 183. [Google Scholar] [CrossRef]
- Surzhykov, A.; Yerokhin, V.A.; Stöhlker, T.; Fritzsche, S. Rayleigh x-ray scattering from many-electron atoms and ions. J. Phys. At. Mol. Opt. Phys. 2015, 48, 144015. [Google Scholar] [CrossRef]
- Falkenberg, H.; Hünger, A.; Rullhusen, P.; Schumacher, M.; Milstein, A.I.; Mork, K. Amplitudes for Delbrück scattering. At. Data Nucl. Data Tables 1992, 50, 1–27. [Google Scholar] [CrossRef]
- Sommerfeldt, J.; Yerokhin, V.A.; Müller, R.A.; Zaytsev, V.A.; Volotka, A.V.; Surzhykov, A. Calculations of Delbrück scattering to all orders in αZ. Phys. Rev. A 2022, 105, 022804. [Google Scholar] [CrossRef]
- Rullhusen, P.; Mückenheim, W.; Smend, F.; Schumacher, M.; Berg, G.P.A.; Mork, K.; Kissel, L. Test of vacuum polarization by precise investigation of Delbrück scattering. Phys. Rev. C 1981, 23, 1375. [Google Scholar] [CrossRef]
- Roy, S.C.; Pratt, R.H.; Kissel, L. Rayleigh Scattering by energetic photons: Development of Theory and current Status. Radiat. Phys. Chem. 1993, 41, 725–738. [Google Scholar] [CrossRef]
- Middents, W.; Weber, G.; Spillmann, U.; Gumberidze, A.; Pfäfflein, P.; Vockert, M.; Schell, N.; Krings, T.; Kurz, N.; Hahn, C.; et al. Cross section measurements in Rayleigh scattering of highly linearly polarized hard x-rays on Atoms. 2022; submitted. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).