Abstract
In this work, we present a scheme of a two-photon interaction to calculate magic wavelengths for the 6 − 5 clock transitions of Ba ion employing the relativistic coupled-cluster method. These magic wavelengths can be essential inputs to achieve better accuracy in the future ionic clock experiments. In this paper, we further show an application of a two-photon interaction to the spin-mixing processes, ↔ and ↔, of an ultra-cold spin-1 mixture of Ba ions and Rb atoms. We determine the protocols for selecting these spin-mixing oscillations by changing the strength and frequencies of the externally applied magnetic field and laser beams, respectively.
1. Introduction
Theoretical advancements toward achieving high accuracy have led to reliable experimental explorations on optical clocks [1,2], the processing of quantum information [3,4] and measurements of fundamental constants and other atomic properties [4,5,6,7,8]. Singly charged barium, or Ba, is one of the promising candidates for these experiments. It has well-understood energy levels and long-lived 5 states as the first two excited states. This ion has drawn the attention of several theorists and experimenters over the last two decades.
Recent theoretical and experimental ventures [1,2,9] proved the extant significance of this ion in the advances of science and technology. A laser, which can be used to control this ion for experimental purposes, shifts the energy levels of this ion due to the Stark effect. Consequently, these Stark shifts give rise to uncertainty in the frequency measurements of the 6 − 5 optical clock transitions of this ion. To eliminate this uncertainty, one needs to know the accurate dynamic or frequency-dependent profiles for the polarizabilities [10,11] for the clock states 6 and 5.
The intersections between the polarizability profiles of the 6 and 5 states provide the values of the magic wavelengths [10,11]. If the wavelength of the laser light is tuned to a magic wavelength, the differential Stark shift between the clock states vanishes.
Moreover, the static scalar part of this differential Stark shift can measure of the black-body radiation (BBR) shift [2,12,13] of the clock frequency. The BBR shift is reported as one of the most significant systematic uncertainties for the present-day International System of Units (SI) [14].
Two-photon spectroscopy is beneficial compared to single-photon spectroscopy in many aspects. A two-photon optical clock [15,16,17,18,19,20] with a pair of counter-propagating laser beams is advantageous over a single-photon clock. Two-photon direct frequency comb spectroscopy (DFCS) enables detailed and precise studies of simultaneous investigation of the time-resolved atomic dynamic, spectral probing in the frequency domain, coherent accumulation and interference as well as coherent control [21,22]. Together, these photons enable supreme control over the ions used as quantum gates or registers [23].
Therefore, it can be a matter of significant research interest to explore how the dynamic polarizabilities, and hence magic wavelengths, for Ba respond to a two-photon interaction. In particular, our interest is in minimizing the error budget in the frequency measurements on the optical clock transitions, 6 − 5, of this ion due to the two-photon interaction. The three low-lying states of the Ba ion form ∧-shaped two-photon transitions between the 6 and 5 states are depicted in Figure 1.
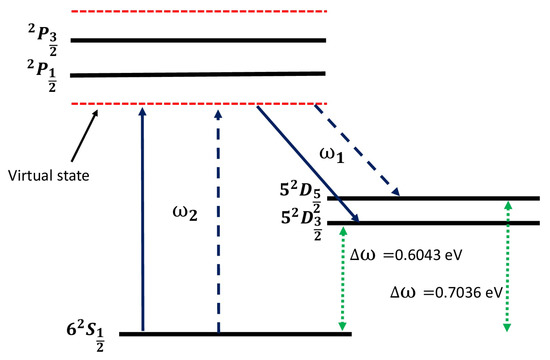
Figure 1.
A schematic energy-level diagram for the ground and first few low-lying excited states (indicated by solid horizontal black line) of Ba ion. The two-photon 6 − 5 (indicated by solid indigo arrow) and 6 − 5 (indicated by dotted indigo arrow) transitions are shown. The red dotted lines indicate the virtual states, which can have different positions depending on the magic wavelengths. The green dotted lines with arrows in both directions indicate the frequencies of the clock transitions.
We also demonstrate a distinct application of the two-photon dynamic polarizability in the spin-mixing processes [24] of trapped atoms/ions inside spinor Bose–Einstein condensate (BEC). This type of condensate has been experimentally realized and theoretically investigated in different atom–atom [25,26,27,28,29,30,31,32,33,34,35,36] and ion–atom mixtures [37,38]. For instance, spin oscillation is studied in an Rb − Na mixture [34,35] under the influence of a linearly polarized light. However, our curiosity is regarding two-photon-induced spin-mixing processes in an ion–atom heteronuclear mixture, Ba − Rb.
This mixture can be a potential candidate in ultra-cold chemistry and promises to reach the s-wave scattering regime with state-of-the-art experimental techniques [39,40]. In general, in a binary species (X, Y) with the hyperfine quantum numbers (, ) = (1, 1), the spin-dependent inter-species interaction [41] can induce different spin-mixing processes. For example, and , where the subscripts 0, and stand for the magnetic quantum numbers of the hyperfine levels.
We recently showed that only one of these two processes could be achieved using a single linearly polarized focused vortex beam [42]. However, the two-photon model can bring an exciting consequence in the controlling mechanism of both the spin-oscillation processes. Our strategy to calculate the frequency-dependent or dynamic polarizability of an atomic state is described in detail in some of our earlier publications [43,44]. The accuracy of the calculated polarizability value depends mainly on the exhaustiveness of the many-body methods used to evaluate the essential electric dipole (E1) matrix elements.
These matrix elements appeared in the sum-over-states expression of the polarizability [43,44]. This work employs a highly accurate relativistic coupled-cluster method with single, double and valence triple excitations (RCCSD(T)) [45,46,47,48,49,50,51,52] to compute the crucial matrix elements [43,44]. The rest of the important matrix elements are calculated using the second-order relativistic many-body perturbation theory (RMBPT(2)) [53,54,55].
Section 2 of this paper discusses a brief formalism to calculate the dynamic polarizability of a single valence atomic state using the sum-over-states approach, including RCCSD(T), RMBPT(2) and Dirac–Fock (DF) E1 matrix elements. In Section 3, we graphically depict and analyze our calculated dynamic polarizability values for Ba considering both the single-photon and two-photon interaction cases.
Subsequently, we provide the two-photon magic wavelengths for the clock transitions. Following this, we illustrate the role of the two-photon polarizability in the controlling mechanism of the spin-oscillation processes for a trapped Ba − Rb mixture. In Section 4, we conclude by highlighting the most important findings of this work and their applications.
2. Theory
The Stark shift of an atomic state in the presence of an external electric field is represented by using the second-order perturbation theory:
Here, and represent the dynamic polarizability and the applied field strength, respectively. ‘v’ at the subscript indicates the single-valence atomic state withand and and valence electron at the ‘v’th orbital. is comprised of three parts: the valence part (), core part ()) and core-valence part () [44,56]. Accordingly, one can write = . Brief descriptions of all these three parts are given in Ref. [43]. The most crucial part in computing is . The other two parts do not contribute significantly to the polarizability in general.
Furthermore, the core part of the polarizability is independent of any valence configuration. Therefore, in the determination of a magic wavelength, the values of or comprehensively are canceled mutually between the transition states. However, the values of ) are not the same for the transition states and, hence, can contribute by a tiny amount to a magic wavelength. Nevertheless, of the transition states play the determinant role in locating the position of a magic wavelength and, thus, are calculated with appropriate accuracy.
For a linearly polarized light, the valence part of the dynamic polarizability can be expressed in terms of the scalar () and tensor () components as [43,44,56]
where
Here, ‘n’ under the summation symbol indicates the different intermediate states. is the reduced matrix element of the E1 operator between the atomic states and . is the excitation energy between these two states. Including the contributions of and , the total scalar polarizability becomes = ++. The BBR shift between the transition states can be estimated from the differential Stark shift for the total scalar polarizabilities of the states at [11,13].
The vector component () appears in the valence part of the dynamic polarizability when a circularly polarized light is considered. Adding this component, the resultant expression for the valence polarizability becomes [44]
with
The value of A is 0 for a linearly polarized light, +1 for a left circularly polarized light and −1 for a right circularly polarized light.
In the presence of two counter-propagating laser beams with frequency and , the Stark shift of the atomic state can be represented by
Here, we assume that the two fields of the laser beams with intensities and , respectively, act on the atom or ion independently. Here, is defined as the two-photon polarizability.
3. Results Furthermore, Discussions
The precursor of employing any correlated many-body method to an atomic system is to construct accurate Dirac–Fock (DF) orbital wavefunctions. In this work, we use Gaussian type orbital (GTO) basis functions [46,57] with optimized [58] even-tempered exponents [59,60] to generate the DF wavefunctions. These exponents, optimized for all the relativistic symmetries, are presented in Table 1. The number of GTO basis functions used in our calculations for the s-, p-, d-, f-, g- and h-type symmetries are 33, 30, 28, 25, 21 and 20, respectively. The numbers of active DF orbitals chosen for our correlated many-body calculations using the RMBPT(2) and the RCCSD(T) methods are considered as 12, 12, 13, 10, 6 and 6, respectively, for the above-mentioned orbital symmetries.

Table 1.
Even-tempered exponents are used in our relativistic calculations. We extend Huzinaga’s non-relativistic exponents [60] for relativistic symmetries.
3.1. Electric Dipole Reduced Matrix Elements of Ba
In Table 2, we present the absolute values of a few E1 reduced matrix elements computed using the RCCSD(T) method and compare these values with some earlier results. All these reduced matrix elements can be crucial in computing the dynamic polarizabilities of 6, 5 and 5 states, which is indicated in the next subsection. The SD and SDpT values are calculated by Safronova [61] and Barrett et al. [62]. The SD method is a linearized approximation of the coupled-cluster method with single and double excitations.
In contrast, SDpT is an extension of the SD method to include partial triple excitations. Safronova did not present the SD and SDpT reduced matrix elements associated with the n states in her paper due to some convergence issue [61]. Therefore, she presented the third-order relativistic perturbation theory results () for the matrix elements associated with these states. This convergence issue was resolved later in the work of Barrett et al. [62]. Sahoo et al. [63] employed a similar RCCSD(T) method to the one used by us. However, they used different sets of basis parameters and active orbitals.
The dipole matrix elements for Ba were calculated by Jian et al. using the relativistic configuration interaction plus core polarization (RCICP) method [64]. Due to single-photon interaction, they used these matrix elements to compute dynamic polarizabilities and magic wavelengths for this ion. As found in the literature, all these accurate theoretical values and some experimental results can reveal a better understanding of the precision of our calculated polarizability values and, hence, magic wavelengths. The agreements between our values and the other values are excellent for the E1 matrix elements associated with the lower states.
However, the E1 matrix elements corresponding to some of the higher states agree poorly. Even mutual agreements among these latter matrix elements, calculated using different theoretical approaches, are poor. Fortunately, such matrix elements have little contribution to the dynamic polarizabilities. Therefore, the accuracy of these matrix elements hardly has any impact on our estimated magic wavelengths, which are discussed later.
3.2. Strategy for Calculating Frequency-Dependent or Dynamic Dipole Polarizabilities of Ba
As mentioned in Section 2, the calculation of the polarizability can be divided into three parts: , and . Our calculation strategy for these parts for an alkali-metal-like system is described in one of our recent works Ref. [44]. , which is calculated by using the third-order relativistic many-body perturbation theory (RMBPT(3)) [43,44,65], varies slowly with the frequency within the frequency region considered here. The static value of the core polarizability () is calculated to be 10.79 a.u.
The dynamic core polarizability reaches the maximum with a value of 11.10 a.u. at the highest frequency ( = 0.18 a.u.) in this region. is almost insensitive to the frequency of the external field. Its values are calculated to be −0.48 a.u., −0.69 a.u. and −0.82 a.u. for the 6, 5 and 5 states, respectively, and are kept fixed within the entire frequency region. However, , which contributes mostly to the polarizability, is much sensitive to the frequency in this region. Therefore, the calculation of this part for the 6, 5 and 5 states should be performed with utmost care to accurately determine the frequency dependence of the polarizability values.
The most dominant contributions to the appear from the sum of the terms having matrix elements associated with the intermediate states 6–9 and 4–6. Here, we use the RCCSD(T) method to calculate these matrix elements. The next significant contributions arise from the intermediate states 10–15 and 7–15, where the matrix elements are calculated using the RMBPT(2) method. The excitation energies associated with all these low-lying states are extracted from the website of NIST atomic database [66].
The remaining contributions, which are relatively small, include the sum of the terms with intermediate states 16–25 and 16–25 and are calculated using the DF method. We do not consider any intermediate state beyond 25 and 25 due to almost negligible contributions from these.
3.3. Differential Scalar Polarizabilities of Ba
As a preliminary test of the quality of our calculations aiming at magic wavelengths, we compare our differential scalar polarizability values for the clock transitions with the corresponding other values as available in the literature. Figure 2 displays the variations of the dynamic scalar polarizabilities () with wavelength for 6, 5 and 5 states. The crossing points between the polarizability curves of 6 and 5 states indicate the positions of zero differential scalar polarizabilities ( = 0) for the 6 − 5 transitions.
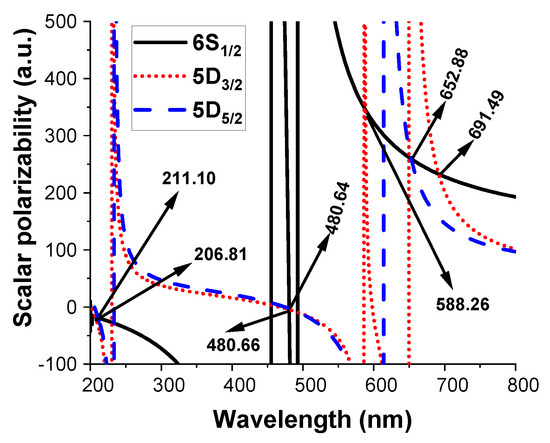
Figure 2.
Scalar dynamic polarizabilities of 6, 5 and 5 states of Ba. Here, the different n states are indicated by nL. The positions of the crossing points between the polarizability curves for 6 and 5 states provide the values of wavelengths (indicated in the panels in the unit of nm), which yield zero differential scalar polarizabilities for the 6 − 5 clock transitions.
In Table 3, we report the differential static scalar polarizabilities (), which can provide estimations of the BBR shifts in the clock transitions. These values are compared with the corresponding recent estimations of Barrett et al. [62], Chanu et al. [2] and Sahoo et al. [67]. This comparison shows a good agreement between our values and their values. This table also contains the positions of the crossing points (wavelengths indicated by ) as mentioned above.
Barrett et al. and Chanu et al. reported only one such crossing point for the 6 − 5 clock transition, which is located near 653 nm. This result matches excellently with our estimation of 652.88 nm. However, the table contains a few additional values of for this clock transition as well as the values for the 6 − 5 clock transition.
3.4. Single-Photon Dynamic Polarizabilities and Magic Wavelengths of Ba
Figure 3 represents the dynamic polarizability profiles for the 6 ( = ), 5(= ,) and 5( = ,,) states in the presence of a single linearly polarized laser light. The crossing points between the two profiles for the 6 and 5 states indicate the positions of magic wavelengths for the transitions between them. The magic wavelengths (in nm) in the optical region are highlighted in the figure and also tabulated in Table 4. We do not highlight and tabulate any magic wavelength obtained on a sharp (vertical) line of the polarizability profile.
The magic wavelengths on these lines are of no practical use. The magic wavelengths in the optical region can be favored due to the easy availability of lasers operated in this region. However, the magic wavelengths, which occur with high polarizability values, can be the candidates of optimal choice. Table 4 shows that our calculated magic wavelengths agree excellently on average with the corresponding magic wavelengths reported in Refs. [64,68]. This agreement can indicate the reliability of our computed two-photon magic wavelengths, which are described in the following subsection.
3.5. Two-Photon Dynamic Polarizabilities and Magic Wavelengths of Ba
The primary objective of the present work is to estimate the two-photon magic wavelengths accurately. The estimated values of these wavelengths are tabulated in Table 5 for the 6 − 5 clock transitions. Here, we assume that both the counter-propagating laser beams have linear polarization. We fix the difference ( = ) between the frequencies of the two beams at the frequency of the corresponding clock transition. Accordingly, the value of is 0.022206903 a.u. [8] for the 6 − 5 clock transition and 0.025856323 a.u. [66] for the 6 − 5 clock transition.
The intensities of the two laser beams at the position of the Ba ion are considered to be the same (). Therefore, following Equation (6), the effective or two-photon polarizability of a state can be written as the sum of the independent polarizabilities caused by each of the two laser beams: . We also plot the variations of the two-photon polarizabilities with (in a.u.) for the clock states in Figure 4. These plots reveal the values of the two-photon magic wavelengths shown in the figure.
Few of these magic wavelengths with high polarizability values appeared in the optical region and, hence, are significant for experiments. A comparison between Table 4 and Table 5 reveals the availability of more number of magic wavelengths in the optical region in the two-photon case compared to the single-photon case. Therefore, one can have more choices in conducting the field-free clock experiments at the cost of one more laser source.
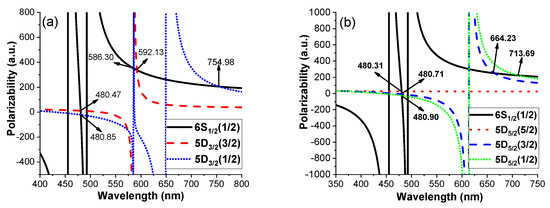
Figure 3.
Variations in the polarizabilities (single-photon) with wavelength for the transitions among (a) 6 and 5 and (b) 6 and 5 states are plotted to extract the magic wavelengths (indicated in the panels in the unit of nm) in the presence of a linearly polarized light source. Here, in the inset, the different levels of the state n are indicated by nL.
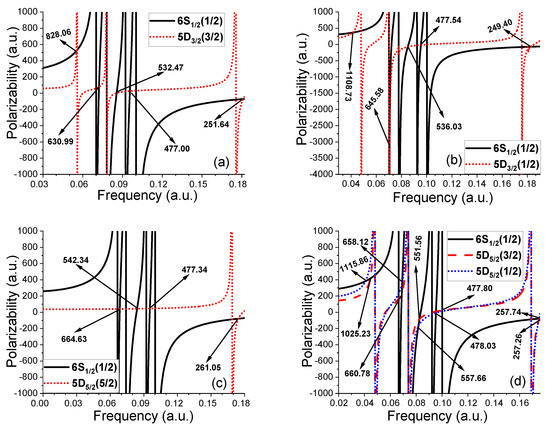
Figure 4.
Variations in the polarizabilities (two-photon) with frequency () to extract the magic wavelengths (indicated in the panels in the unit of nm) in the presence of two counter-propagating linearly polarized lights with frequencies and . (a,b) represent transition among the states 6 and 5, and (c,d) represent transition among 6 and 5. Here, the different levels of the state n are indicated by nL.

Table 2.
The absolute values of our calculated reduced electric dipole matrix elements (indicated by ‘Our’) in a.u. are compared with few other theoretical and experimental (Expt.) values. Uncertainties of the results are mentioned in the parenthesis for the last digits.
Table 2.
The absolute values of our calculated reduced electric dipole matrix elements (indicated by ‘Our’) in a.u. are compared with few other theoretical and experimental (Expt.) values. Uncertainties of the results are mentioned in the parenthesis for the last digits.
| Transition | RCCSD(T) [63] | RCICP [64] | SD [61] | SDpT [61] | Our | Expt. |
|---|---|---|---|---|---|---|
| 5 → 6 | 3.11(3) | 3.033(29) | 3.0503 | 3.0957 | 3.0641 | 3.03(9) , 2.90(9) , 3.034 |
| →6 | 1.34(2) | 1.336(13) | 1.3324 | 1.3532 | 1.3335 | 1.36(4) , 1.54(19) , 1.325 1.349(36), 1.33199(96) e |
| →7 | 0.28(2) | 0.23(3) | 0.2792 | 0.2775 | 0.3336 | 0.42(11) |
| →7 | 0.16(1) | 0.14(2) | 0.1555 | 0.1548 | 0.1797 | 0.19(5) |
| →8 | 0.07(2) | 0.10(5) | 0.1346 | 0.1349 | 0.1527 | 0.23(6) |
| →8 | 0.07(2) | 0.07(3) | 0.0768 | 0.0769 | 0.0867 | 0.10(3) |
| 5 → 6 | 4.02(7) | 4.105(39) | 4.1032 | 4.1631 | 4.1368 | 4.080 , 4.1028(25) e |
| 7 | 0.46(1) | 0.39(6) | 0.4513 | 0.4500 | 0.5123 | |
| 8 | 0.21(2) | 0.18(3) | 0.2232 | 0.2239 | 0.2457 | |
| 6 → 6 | 3.36(1) | 3.275(47) | 3.3380 | 3.3710 | 3.4082 | 3.36(16) , 3.36(4) , 3.3357 |
| →6 | 4.73(3) | 4.637(67) | 4.7097 | 4.7569 | 4.8103 | 4.45(19) , 4.55(10) , 4.72(4) 4.7065 |
| →7 | 0.10(1) | 0.10(5) | 0.0605 | 0.0607 | 0.0350 | 0.24(3) |
| →7 | 0.17(5) | 0.04(2) | 0.0870 | 0.0858 | 0.1337 | 0.33(4) |
| →8 | 0.11(5) | 0.11(6) | 0.0868 | 0.0866 | 0.0426 | 0.10(1) |
| →8 | 0.11(5) | 0.06(3) | 0.0331 | 0.0334 | 0.0400 | 0.15(2) |
| Transition | RCCSD(T) [63] | RCICP [64] | SD [62] | SDpT [62] | Our | Z [61] |
| 5 →4 | 3.75(11) | 3.671(35) | - | - | 3.6370 | 3.6216 |
| →5 | 1.59(8) | - | - | - | 1.9454 | 1.8513 |
| →6 | 0.17(2) | - | - | - | 1.15358 | 0.9208 |
| 5 →4 | 1.08(4) | 1.002(9) | 0.998 | 1.012 | 1.0044 | 0.9951 |
| →4 | 4.84(5) | 4.500(42) | 4.475 | 4.540 | 4.5017 | 4.4504 |
| →5 | 0.45(7) | - | 0.016 | 0.210 | 0.5255 | 0.5005 |
| →5 | 2.47(6) | - | 0.130 | 1.049 | 2.4283 | 2.2445 |
| →6 | 0.15(2) | - | 0.236 | 0.018 | 0.2996 | 0.2449 |
| →6 | 1.04(7) | - | 0.961 | 0.170 | 1.3690 | 1.1160 |
a → Ref. [69], b → Refs. [70,71], c → Ref. [72], d → Ref. [73], e → Ref. [9].

Table 3.
Comparisons of our (‘Our’) calculated differential static scalar polarizabilities, i.e., for the clock transitions with the corresponding other (‘Other’) values as found in the literature. The last two columns highlight the comparison of at which .
Table 3.
Comparisons of our (‘Our’) calculated differential static scalar polarizabilities, i.e., for the clock transitions with the corresponding other (‘Other’) values as found in the literature. The last two columns highlight the comparison of at which .
| Clock Transition | (a.u.) | (nm) | ||
|---|---|---|---|---|
| Our | Other | Our | Other | |
| 6–5 | −71.39 | −73.1(1.3) [62], | 652.88, | 653(near) [2,62] |
| −73.56(0.21) [2], | 480.64, 211.10 | − | ||
| −73.59 [67] | ||||
| 6–5 | −77.64 | −75.45 [67] | 691.49, 588.26, | − |
| 480.66, 206.81 | − | |||

Table 4.
Single-photon magic wavelengths () in nm and the corresponding polarizabilities () in a.u. for the clock transitions 6− 5 are presented. Our estimated magic wavelengths (‘Our’) are also compared with the corresponding values in Ref. [68] and Ref. [64].
Table 4.
Single-photon magic wavelengths () in nm and the corresponding polarizabilities () in a.u. for the clock transitions 6− 5 are presented. Our estimated magic wavelengths (‘Our’) are also compared with the corresponding values in Ref. [68] and Ref. [64].
| States | ||||
|---|---|---|---|---|
| (,) | Our | Ref. [68] | Ref. [64] | |
| () | 592.13 | 592.46 | 592.39(14) | 337.27 |
| 480.47 | 480.44 | 480.539(14) | 12.03 | |
| () | 754.98 | 767.81 | 757.7(3.9) | 337.27 |
| 586.30 | 585.98 | 585.982(10) | 348.92 | |
| 480.85 | 480.81 | 480.93(3) | −21.13 | |
| () | 480.31 | 480.26 | 480.38(2) | 26.30 |
| () | 664.23 | 666.64 | 663.6(1.4) | 250.17 |
| 480.71 | 480.71 | 480.86(2) | −8.58 | |
| () | 713.69 | 718.18 | 707.9(3.3) | 221.45 |
| 480.90 | 480.93 | 481.10(2) | −26.17 | |

Table 5.
Two-photon magic wavelengths ( and ) in nm with two-photon polarizability values () in a.u. for the 6 − 5 clock transitions of Ba ion. The intensities of the two laser beams are considered to be same at the position of Ba.
Table 5.
Two-photon magic wavelengths ( and ) in nm with two-photon polarizability values () in a.u. for the 6 − 5 clock transitions of Ba ion. The intensities of the two laser beams are considered to be same at the position of Ba.
| 6 − 5 | 6 − 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (,) | (,) | ||||||||||
| () | 0.055024 | 0.077231 | 528.21 | 828.06 | 589.96 | () | 0.068554 | 0.094410 | 51.02 | 664.64 | 482.61 |
| 0.072209 | 0.094416 | 85.56 | 630.99 | 482.58 | 0.084010 | 0.109867 | 53.61 | 542.35 | 414.72 | ||
| 0.085568 | 0.107774 | 12.66 | 532.48 | 422.77 | 0.095452 | 0.121308 | 56.25 | 477.34 | 375.60 | ||
| 0.095519 | 0.117726 | 36.17 | 477.01 | 387.03 | 0.174544 | 0.200400 | −68.45 | 261.04 | 227.36 | ||
| 0.181074 | 0.203281 | −61.64 | 251.63 | 224.14 | () | 0.044445 | 0.070301 | 424.78 | 1025.16 | 648.12 | |
| () | 0.041102 | 0.063309 | 374.78 | 1108.54 | 719.70 | 0.068954 | 0.094810 | 255.99 | 660.78 | 480.57 | |
| 0.070577 | 0.092784 | −3433.52 | 645.58 | 491.07 | 0.082605 | 0.108462 | −73.92 | 551.58 | 420.09 | ||
| 0.085000 | 0.107207 | −63.55 | 536.04 | 425.00 | 0.095360 | 0.121216 | 19.86 | 477.80 | 375.89 | ||
| 0.095412 | 0.117619 | −6.14 | 477.54 | 387.38 | 0.176783 | 0.202639 | −65.40 | 257.74 | 224.85 | ||
| 0.182695 | 0.204902 | −59.68 | 249.40 | 222.37 | () | 0.040841 | 0.066697 | 393.14 | 1115.64 | 683.14 | |
| 0.069232 | 0.095088 | 378.05 | 658.13 | 479.17 | |||||||
| 0.081702 | 0.107559 | −163.43 | 557.68 | 423.61 | |||||||
| 0.095314 | 0.121170 | 1.45 | 478.03 | 376.03 | |||||||
| 0.177112 | 0.202968 | −64.97 | 257.26 | 224.49 | |||||||
3.6. Uncertainty in the Estimated Magic-Wavelengths
We follow two procedures to estimate the maximum deviations of our computed magic wavelengths to estimate an approximate uncertainty in the magic wavelength values. First, we consider Table 4, where our calculated magic wavelengths are compared with the values of Refs. [64,68]. It is evident that our magic wavelengths agree excellently (maximum deviation of 0.1%) with the corresponding wavelengths of Refs. [64,68] when one of the two intersecting curves, as shown in Figure 3, is almost vertical at the point of intersection. We indicate this type of magic wavelengths as category-I.
On the other hand, the magic wavelengths 754.98, 664.23 and 713.69 nm, which appear on the intersections of almost horizontally flat portions of the curves, differ by a maximum amount of 0.8% from the corresponding magic wavelengths of Ref. [64] and 1.7% from the corresponding magic wavelengths of Ref. [68]. We indicate this latter type of magic wavelengths as category-II. This comparison shows that category-I magic wavelengths are expected to be more accurate than category-II. We re-evaluate all the single-photon magic wavelengths in the second procedure by replacing our RCCSD(T) matrix elements with the less-precise SD matrix elements [61,62].
Then, we further reevaluate these magic wavelengths by replacing our RCCSD(T) matrix elements with the highly accurate RCCSD(T) matrix elements of Sahoo et al. [67]. These re-evaluated magic wavelengths using these approaches differ by a maximum amount of 0.2% from our presented magic wavelengths in Table 4. Therefore, following both procedures, one can say that the maximum deviation for the category-I magic wavelengths can be 0.2%. In contrast, the maximum deviation for the category-II magic wavelengths can be 1.7%.
Consequently, we conclude that our calculated single-photon category-I magic wavelengths may not have uncertainty by more than 0.5%, and category-II magic wavelengths may not have uncertainty by more than 2%. These estimates of uncertainty for both these categories can also be valid for the two-photon magic wavelengths in Table 5, as similar approaches are followed to evaluate both the single-photon and two-photon magic wavelengths.
3.7. Application of Two-Photon Polarizability: Spin-Mixing in Ba − Rb Mixture
As an exclusive application of the presented theory of dipole polarizability for a two-photon mechanism, we investigate the importance of this polarizability on an ion–atom mixture of a hetero-nuclear binary system. We consider a mixture of Ba and Rb with their hyperfine ground states and , respectively.
According to the multichannel quantum defect theory calculation, this particular choice of ion–atom pair can be made as a promising candidate for ultra-cold chemistry [39,40,74]. The composite sublevels (spin states) consisting of the magnetic sublevels of the hyperfine ground states of the ion and the atom are represented by . Accordingly, the spin states of the binary mixture of Ba and Rb can be , and (see Figure 5), conserving the total (here, we ignore the spin–spin interaction between the ion and the atom).
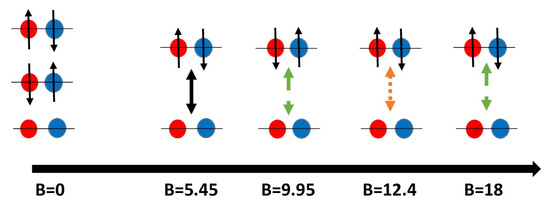
Figure 5.
Spin-oscillation processes between the spin states for the Ba ion and Rb atom mixture are shown schematically at different magnetic fields (in Gauss). The red ball (on the left) and blue ball (on the right) represent the Ba ion and Rb atom, respectively. The balls with upward, downward and no arrows represent , and spin states, respectively, for both the atom and the ion. Solid black, orange dotted and green dashed arrows represent the spin-changing processes for the no-light, single-photon and two-photon, respectively, cases. In the single-photon case, we assume a left circularly polarized light. In the two-photon case, we assume a left circularly polarized light and a linearly polarized light.
The magnetic sublevels of the Rb atom or the Ba ion are degenerate in the absence of an external magnetic field or a circularly polarized light. A circularly polarized light can create additional Stark shifts in opposite directions to and levels ( 1 or 2) by inducing the vector part of the polarizability and, hence, can break this degeneracy completely (see Equation (4) and the description there). In general, this vector part can not be induced by a linearly polarized light. However, in a two-photon process, when a linearly polarized and a circularly polarized lights interact with the atom or the ion, the vector part can be induced into the two-photon polarizability by the latter light.
Nevertheless, the additional energy shifts to the atom or ion either by the circularly polarized light or by the combination of the linearly and circularly polarized lights can provide a fictitious magnetic field at the tune-out wavelength for state [75]. The tune-out wavelength for a state is the externally applied laser light wavelength for which the dipole polarizability of the state becomes zero. However, for a two-photon process, it is an appropriate combination of the wavelengths of the two externally applied laser lights for which the two-photon polarizability of the state vanishes.
For instance, we can extract the single-photon (480.61 nm) and two-photon (632.21 and 533.08 nm) tune-out wavelengths for the 6() state of Ba from Figure 6. In Appendix A, we show the conversion of the dynamic polarizability expression from fine-structure sublevels to hyperfine sublevels. The degeneracy among the , and spin states can also be broken by applying an arbitrary external magnetic field of suitable strength through the Zeeman effect.
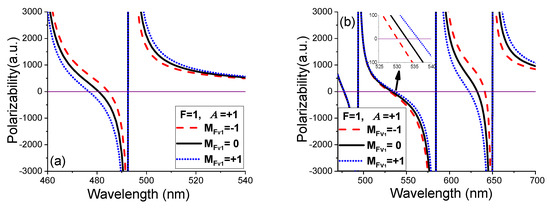
Figure 6.
Variations in (a) single-photon and (b) two-photon polarizabilities with wavelength for the state of Ba ion. In the single-photon case, we assume a left circularly polarized light. In the two-photon case, we assume a left circularly polarized light and a linearly polarized light. In the inset of the panel in (b), we display the enlarged version of the plot around the wavelength 533.08 nm.
This lifting of degeneracy is also possible by a circularly polarized light or a combination of a linearly and circularly polarized lights. Therefore, it will be significantly interesting to see the interplay between the external magnetic field and these polarized lights on the degeneracy of the spin states and, hence, on the spin oscillations and .
We indicate the energy difference between the composite levels by = and = . The magnetic energy for the mixture of Ba and Rb is determined using the Hamiltonian , where and are the linear and quadratic Zeeman shifts, respectively. represents the z-component of the external magnetic field. The coefficients and can be evaluated from the power series expansion of the Breit–Rabi formula [76,77].
In this analysis, we consider the ground state magnetic dipole hyperfine coupling constant for Ba as 4.0189 GHz [78]. Nevertheless, in the absence of any light, as we increase the magnetic field from zero, the values of shift from zero, shown in Figure 7a. becomes zero again at B = 5.45 G indicating the fact that spin oscillation is also possible between and states at some non-zero magnetic field (see also Figure 5). However, the other spin oscillation, , does not seem to be taken place at a finite non-zero magnetic field.
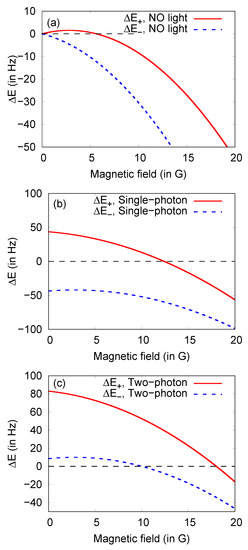
Figure 7.
Magnetic energy diagram for the two heteronuclear spin-oscillation processes in the spin-1 Ba and Rb mixture (a) without light shift, (b) with light shift by single-photon interaction ( nm) and (c) with light shift by two-photon interaction (632.21 and 493.30 nm) and (533.08 and 423.14 nm).
Figure 7b indicates that the two spin-mixing processes cannot occur at zero magnetic field when the binary system is exposed under a left circularly polarized light with a wavelength of 480.61 nm. Here, we consider the intensity of the external light beam is 10 W/m. The tune-out wavelength of 480.61 nm is close to the first resonance line of Ba ion and far away from the resonance lines of Rb atom. Therefore, the light affects the Ba ion; however, the Rb atom remains almost unaffected.
As the light is circularly polarized, the dipole polarizability induced by this light has a non-zero vector part. This vector part leads to a fictitious magnetic field felt only by the Ba ion. Figure 7b reveals that and split away for this fictitious magnetic field when the external magnetic field is zero. Therefore, the spin oscillation is suppressed forever as the external magnetic field increases from zero.
Whereas the spin oscillation becomes feasible at the magnetic field of 12.40 G (see also Figure 5). This shift of the external magnetic field from 5.45 (without light) to 12.40 G (single-photon interaction) is a manifestation of the vector polarizability created by the circularly polarized light. Therefore, by tuning the light to an appropriate wavelength, one can switch on the spin oscillation at a desired non-zero magnetic field. Nevertheless, the spin oscillation cannot be achieved unless we change the direction of the circular polarization of the light.
In the two-photon case, one of the laser lights with frequency (wavelength ) is considered to have left circular polarization, and another with frequency (wavelength ) is considered to have linear polarization. Both the laser lights have intensities of 10 W/m.
The frequency difference between the two lights is considered to be a.u., which corresponds to the frequency of − transition. Here, we obtain two sets of tune-out wavelengths at () = (632.21 and 493.30 nm) and (533.08 and 423.14 nm) for the 6 state of Ba as depicted in Figure 6b. Here, the Rb atom also behaves as almost transparent for these two sets of tune-out wavelengths.
Figure 7c shows the external magnetic field variation of = for lights with wavelengths (632.21 and 493.30 nm) and = for lights with wavelengths (533.08 and 423.14 nm). Here, indicates the light shift due to the two-photon interaction. This figure shows that, by proper choice of wavelengths of the lights and the external magnetic field (9.95 G), can be made zero to switch on the spin oscillation.
This particular spin oscillation is not observed in no-light conditions and the single-photon case with left circularly polarized light. One must look at Figure 6b to understand its possibility in a two-photon case. This figure shows that the two-photon polarizabilities of and for Ba ion are positive and negative, respectively, at nm. However, the signs of these polarizabilities are reversed at the other wavelength, nm. Therefore, the signs of the fictitious magnetic fields are changed accordingly between these two wavelengths. As a consequence, the spin oscillation is achievable at 9.95 G for nm and nm.
The spin oscillation can occur at 18 G for nm and nm (see also Figure 5). On this account, we can say that, by changing the wavelengths of the two counter-propagating lights, one can control both the spin-oscillation processes of the heteronuclear spin-1 mixture of Ba and Rb. Both these spin-oscillation processes can also be achieved at different magnetic fields if we consider a.u., which corresponds to the frequency of the − transition.
4. Conclusions
This work showed the frequency or wavelength dependence of dipole polarizabilities of a few low-lying states of singly ionized barium atom. These low-lying states, , and , are associated with the proposed optical clock transitions − of Ba.
From the profiles of these polarizabilities, we extracted the magic wavelengths for the zero differential Stark shifts in the clock transitions due to the single-photon and two-photon interactions. The single-photon differential polarizabilities and the magic wavelength values were compared with the relevant other theoretical and experimental values to calibrate our calculations. The excellent agreements in this comparison give an indication of the accuracy of our two-photon calculations, which are the primary objective of this work. We found a few two-photon magic wavelengths in the optical region providing high polarizability values to the clock states. These magic wavelengths can be advantageous in conducting clock experiments on Ba with minimal errors.
In addition to the clock-related experiments, the most important advantage of using a two-photon mechanism is highlighted here in the spin-oscillation processes of a spin-1 mixture of Ba ion and Rb atom in the presence of an external magnetic field. The spin states of this binary mixture, , and , act as degenerate states in no-light and no-magnetic-field conditions. However, when a single circularly polarized laser light is applied, this degeneracy is lifted completely. In this situation, a non-zero magnetic field is required to maintain the degeneracy between the state and one of the two states, and , depending on the direction of circular polarization.
Consequently, such a magnetic field can activate only one of the two spin-oscillation processes, ↔ and ↔. In this work, we demonstrated that a two-photon interaction using a circularly polarized light and a linearly polarized light can activate both spin-oscillation processes without changing the direction of the circular polarization. However, each of these processes requires an appropriate combination of wavelengths of the lights and accordingly, an appropriate external magnetic field. The triggering of both the spin oscillation processes by tuning the wavelength of the two laser lights and the strength of the magnetic field is a manifestation of the fictitious magnetic field generated by the vector component of the dipole polarizability.
Therefore, the two-photon model can induce coherent heteronuclear spin-mixing dynamics and significantly influence the quantum phases of the binary-species spin-1 BEC. Our model can be applied to other atomic mixtures to generate entanglement between two different atoms [79,80] and control the singlet-pairing process [81].
Author Contributions
Conceptualization, A.D., A.B. and S.M.; Data curation, A.D.; Formal analysis, A.D., A.B., N.N.D. and S.M.; Investigation, A.D., A.B. and N.N.D.; Methodology, A.B. and N.N.D.; Software, N.N.D.; Supervision, S.M.; Validation, N.N.D.; Visualization, A.B. and S.M.; Writing—original draft, A.D., A.B., N.N.D. and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are computed from self-developed program.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Valence Dynamic Polarizability at the Hyperfine Level
The scalar , vector and tensor components of valence polarizability at a hyperfine level can be related to the corresponding polarizability at the fine-structure level by [44,82,83]
and
Here, () and represent a hyperfine quantum number and its magnetic component, respectively. Hence, the valence polarizability at a hyperfine level can be written as
where
References
- Arnold, K.J.; Kaewuam, R.; Chanu, S.R.; Tan, T.R.; Zhang, Z.; Barrett, M.D. Precision Measurements of the 138Ba+6s2S1/2 − 5d2D5/2 Clock Transition. Phys. Rev. Lett. 2020, 124, 193001. [Google Scholar] [CrossRef]
- Chanu, S.; Koh, V.P.W.; Arnold, K.J.; Kaewuam, R.; Tan, T.R.; Zhang, Z.; Safronova, M.S.; Barrett, M.D. Magic wavelength of the 138Ba+6s2S1/2 − 5d2D5/2 clock transition. Phys. Rev. A 2020, 101, 042507. [Google Scholar] [CrossRef]
- Inlek, I.V.; Crocker, C.; Lichtman, M.; Sosnova, K.; Monroe, C. Multispecies Trapped-Ion Node for Quantum Networking. Phys. Rev. Lett. 2017, 118, 250502. [Google Scholar] [CrossRef] [PubMed]
- Hucul, D.; Christensen, J.E.; Hudson, E.R.; Campbell, W.C. Spectroscopy of a Synthetic Trapped Ion Qubit. Phys. Rev. Lett. 2017, 119, 100501. [Google Scholar] [CrossRef]
- Dutta, N.N.; Majumder, S. E1 parity-nonconserving transition amplitudes of the hyperfine components for 2S1/2 − 2D3/2 transitions of 137Ba+ and 87Sr+. Phys. Rev. A 2014, 90, 012522. [Google Scholar] [CrossRef]
- Kozlov, M.G.; Safronova, M.S.; Crespo López-Urrutia, J.R.; Schmidt, P.O. Highly charged ions: Optical clocks and applications in fundamental physics. Rev. Mod. Phys. 2018, 90, 045005. [Google Scholar] [CrossRef]
- De Munshi, D.; Dutta, T.; Rebhi, R.; Mukherjee, M. Precision measurement of branching fractions of 138Ba+: Testing many-body theories below the 1% level. Phys. Rev. A 2015, 91, 040501(R). [Google Scholar] [CrossRef]
- Dijck, E.A.; Nuñez Portela, M.; Grier, A.T.; Jungmann, K.; Mohanty, A.; Valappol, N.; Willmann, L. Determination of transition frequencies in a single 138Ba+ ion. Phys. Rev. A 2015, 91, 060501(R). [Google Scholar] [CrossRef]
- Zhang, Z.; Arnold, K.J.; Chanu, S.R.; Kaewuam, R.; Safronova, M.S.; Barrett, M.D. Branching fractions for P3/2 decays in Ba+. Phys. Rev. A 2020, 101, 062515. [Google Scholar] [CrossRef]
- Tang, Y.-B.; Qiao, H.-X.; Shi, T.-Y.; Mitroy, J. Dynamic polarizabilities for the low-lying states of Ca+. Phys. Rev. A 2013, 87, 042517. [Google Scholar] [CrossRef]
- Mitroy, J.; Safronova, M.S.; Clark, C.W. Theory and applications of atomic and ionic polarizabilities. J. Phys. B 2010, 43, 202001. [Google Scholar] [CrossRef]
- Gallagher, T.F.; Cooke, W.E. Interactions of Blackbody Radiation with Atoms. Phys. Rev. Lett. 1979, 42, 835–839. [Google Scholar] [CrossRef]
- Porsev, S.G.; Derevianko, A. Multipolar theory of blackbody radiation shift of atomic energy levels and its implications for optical lattice clocks. Phys. Rev. A 2006, 74, 020502(R), Erratum in Phys. Rev. A 2012, 86, 029904. [Google Scholar] [CrossRef]
- Jefferts, S.R.; Heavner, T.P.; Parker, T.E.; Shirley, J.H.; Donely, E.A.; Ashby, N.; Levi, F.; Calonico, D.; Costanzo, G.A. High-Accuracy Measurement of the Blackbody Radiation Frequency Shift of the Ground-State Hyperfine Transition in 133Cs. Phys. Rev. Lett. 2014, 112, 050801. [Google Scholar] [CrossRef]
- Gerginov, V.; Beloy, K. Two-photon Optical Frequency Reference with Active ac Stark Shift Cancellation. Phys. Rev. Appl. 2018, 10, 014031. [Google Scholar] [CrossRef]
- Martin, K.W.; Stuhl, B.; Eugenio, J.; Safronova, M.S.; Phelps, G.; Burke, J.H.; Lemke, N.D. Frequency shifts due to Stark effects on a rubidium two-photon transition. Phys. Rev. A 2019, 100, 023417. [Google Scholar] [CrossRef]
- Perrella, C.; Light, P.S.; Anstie, J.D.; Baynes, F.N.; White, R.T.; Luiten, A.N. Dichroic Two-Photon Rubidium Frequency Standard. Phys. Rev. Appl. 2019, 12, 054063. [Google Scholar] [CrossRef]
- Jackson, S.; Vutha, A.C. Magic polarization for cancellation of light shifts in two-photon optical clocks. Phys. Rev. A 2019, 99, 063422. [Google Scholar] [CrossRef]
- Martin, K.W.; Phelps, G.; Lemke, N.D.; Bigelow, M.S.; Stuhl, B.; Wojcik, M.; Holt, M.; Coddington, I.; Bishop, M.W.; Burke, J.H. Compact Optical Atomic Clock Based on a Two-Photon Transition in Rubidium. Phys. Rev. Appl. 2018, 9, 014019. [Google Scholar] [CrossRef]
- Hall, J.L.; Zhu, M.; Buch, P. Prospects for using laser-prepared atomic fountains for optical frequency standards applications. JOSA B 1989, 6, 2194–2205. [Google Scholar]
- Marian, A.; Stowe, M.C.; Lawall, J.R.; Felinto, D.; Ye, J. United Time-Frequency Spectroscopy for Dynamics and Global Structure. Science 2004, 306, 2063–2068. [Google Scholar] [CrossRef] [PubMed]
- Diddams, S.A.; Vahala, K.; Udem, T. Optical frequency combs: Coherently uniting the electromagnetic spectrum. Science 2020, 369, 6501. [Google Scholar] [CrossRef]
- Kang, Y.H.; Xia, Y.; Lu, P.M. Two-photon phase gate with linear optical elements and atom–cavity system. Quantum Inf. Process 2016, 15, 4521–4535. [Google Scholar] [CrossRef]
- Xu, Z.F.; Wang, D.J.; You, L. Quantum spin mixing in a binary mixture of spin-1 atomic condensates. Phys. Rev. A 2012, 86, 013632. [Google Scholar] [CrossRef]
- Zhang, J.; Li, T.; Zhang, Y. Interspecies singlet pairing in a mixture of two spin-1 Bose condensates. Phys. Rev. A 2011, 83, 023614. [Google Scholar] [CrossRef]
- Li, Z.B.; Liu, Y.M.; Yao, D.X.; Bao, C.G. Two types of phase diagrams for two-species Bose–Einstein condensates and the combined effect of the parameters. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 135301. [Google Scholar] [CrossRef]
- Xu, Z.F.; Zhang, J.; Zhang, Y.; You, L. Quantum states of a binary mixture of spinor Bose–Einstein condensates. Phys. Rev. A 2010, 81, 033603. [Google Scholar] [CrossRef]
- Modugno, G.; Modugno, M.; Riboli, F.; Roati, G.; Inguscio, M. Two Atomic Species Superfluid. Phys. Rev. Lett. 2002, 89, 190404. [Google Scholar] [CrossRef] [PubMed]
- Thalhammer, G.; Barontini, G.; De Sarlo, L.; Catani, J.; Minardi, F.; Inguscio, M. Double Species Bose–Einstein Condensate with Tunable Interspecies Interactions. Phy. Rev. Lett. 2008, 100, 210402. [Google Scholar] [CrossRef] [PubMed]
- McCarron, D.J.; Cho, H.W.; Jenkin, D.L.; Köppinger, M.P.; Cornish, S.L. Dual-species Bose–Einstein condensate of 87Rb and 133Cs. Phys. Rev. A 2011, 84, 011603. [Google Scholar] [CrossRef]
- Roy, A.; Angom, D. Thermal suppression of phase separation in condensate mixtures. Phy. Rev. A 2015, 92, 011601(R). [Google Scholar] [CrossRef]
- Li, X.; Zhu, B.; He, X.; Wang, F.; Guo, M.; Xu, Z.-F.; Zhang, S.; Wang, D. Coherent Heteronuclear Spin Dynamics in an Ultracold Spinor Mixture. Phys. Rev. Lett. 2015, 114, 255301. [Google Scholar] [CrossRef]
- Mil, A.; Zache, T.V.; Hegde, A.; Xia, A.; Bhatt, R.P.; Oberthaler, M.K.; Hauke, P.; Berges, J.; Jendrzejewski, F.A. scalable realization of local U(1) gauge invariance in cold atomic mixtures. Science 2020, 367, 1128–1130. [Google Scholar] [CrossRef]
- Chen, J.-J.; Xu, Z.-F.; You, L. Resonant spin exchange between heteronuclear atoms assisted by periodic driving. Phys. Rev. A 2018, 98, 023601. [Google Scholar] [CrossRef]
- Li, L.; Zhu, B.; Lu, B.; Zhang, S.; Wang, D. Manipulation of heteronuclear spin dynamics with microwave and vector light shift. Phys. Rev. A 2020, 101, 053611. [Google Scholar] [CrossRef]
- Fang, F.; Wu, S.; Smull, A.; Isaacs, J.A.; Wang, Y.; Greene, C.H.; Stamper-Kurn, D.M. Cross-dimensional relaxation of 7Li − 87Rb atomic gas mixtures in a spherical-quadrupole magnetic trap. Phys. Rev. A 2020, 101, 012703. [Google Scholar] [CrossRef]
- Hirzler, H.; Feldker, T.; Fürst, H.; Ewald, N.V.; Trimby, E.; Lous, R.S.; Arias Espinoza, J.D.; Mazzanti, M.; Joger, J.; Gerritsma, R. Experimental setup for studying an ultracold mixture of trapped Yb+ − 6Li. Phys. Rev. A 2020, 102, 033109. [Google Scholar] [CrossRef]
- Tomza, M.; Jachymski, K.; Gerritsma, R.; Negretti, A.; Calarco, T.; Idziaszek, Z.; Julienne, P.S. Cold hybrid ion-atom systems. Rev. Mod. Phys. 2019, 91, 035001. [Google Scholar] [CrossRef]
- Huber, T. Optical Trapping of Barium Ions- Towards Ultracold Interactions in Ion-Atom Ensembles. Ph.D. Thesis, Albert-Ludwigs-Universität Freiburg, Freiburg im Breisgau, Germany, 2014. Available online: https://d-nb.info/1123480699/34 (accessed on 7 September 2022).
- Krych, M.; Skomorowski, W.; Pawlowski, F.; Moszynski, R.; Idziaszek, Z. Sympathetic cooling of the Ba+ ion by collisions with ultracold Rb atoms: Theoretical prospects. Phys. Rev. A 2011, 83, 032723. [Google Scholar] [CrossRef]
- Widera, A.; Gerbier, F.; Fölling, S.; Gericke, T.; Mandel, O.; Bloch, I. Coherent Collisional Spin Dynamics in Optical Lattices. Phys. Rev. Lett. 2005, 95, 190405. [Google Scholar] [CrossRef]
- Bhowmik, A.; Dutta, N.N.; Majumder, S. Vector polarizability of an atomic state induced by a linearly polarized vortex beam: External control of magic, tune-out wavelengths, and heteronuclear spin oscillations. Phys. Rev. A 2020, 102, 063116. [Google Scholar] [CrossRef]
- Dutta, N.N.; Roy, S.; Deshmukh, P.C. Dynamic polarizabilities and hyperfine-structure constants for Sc2+. Phys. Rev. A 2015, 92, 052510. [Google Scholar] [CrossRef]
- Das, A.; Bhowmik, A.; Dutta, N.N.; Majumder, S. Many-body calculations and hyperfine-interaction effect on dynamic polarizabilities at the low-lying energy levels of Y2+. Phy. Rev. A 2020, 102, 012801. [Google Scholar] [CrossRef]
- Chaudhuri, R.K.; Sahoo, B.K.; Das, B.P.; Merlitz, H.; Mahapatra, U.S.; Mukherjee, D. Relativistic coupled cluster calculations of the energies for rubidium and cesium atoms. J. Chem. Phys. 2003, 119, 10633–10637. [Google Scholar] [CrossRef]
- Dutta, N.N.; Majumder, S. Ab initio calculations of spectroscopic properties of Cr5+ using coupled-cluster theory. Indian J. Phys. 2016, 90, 373–380. [Google Scholar] [CrossRef]
- Dutta, N.N.; Roy, S.; Dixit, G.; Majumder, S. Ab initio calculations of transition amplitudes and hyperfine A and B constants of Ga iii. Phys. Rev. A 2013, 87, 012501. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musial, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
- Biswas, S.; Das, A.; Bhowmik, A.; Majumder, S. Accurate estimations of electromagnetic transitions of Sn IV for stellar and interstellar media. Mon. Not. R. Astron. Soc. 2018, 477, 5605–5611. [Google Scholar] [CrossRef]
- Majumder, S.; Gopakumar, G.; Merlitz, H.; Das, B.P. Relativistic coupled cluster calculations using hybrid basis functions. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 4821–4829. [Google Scholar] [CrossRef]
- Bhowmik, A.; Roy, S.; Dutta, N.N.; Majumder, S. Study of coupled-cluster correlations on electromagnetic transitions and hyperfine structure constants of W VI. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 125005. [Google Scholar] [CrossRef]
- Das, A.; Bhowmik, A.; Dutta, N.N.; Majumder, S. Electron-correlation study of Y iii-Tc vii ions using a relativistic coupled-cluster theory. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 025001. [Google Scholar] [CrossRef]
- Lindgren, I.; Morrison, J. Atomic Many-Body Theory; Springer: Berlin/Heidelberg, Germany, 1986; Volume 3. [Google Scholar] [CrossRef]
- Boyle, J.; Pindzola, M.S. Many-Body Atomic Physics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Johnson, W.R.; Liu, Z.W.; Sapirstein, J. Transition rates for lithium-like ions, sodium-like ions, and neutral alkali-metal atoms. At. Data Nucl. Data Tables 1996, 64, 279–300. [Google Scholar] [CrossRef]
- Bhowmik, A.; Dutta, N.N.; Majumder, S. Tunable magic wavelengths for trapping with focused Laguerre–Gaussian beams. Phys. Rev. A 2018, 97, 022511. [Google Scholar] [CrossRef]
- Clementi, E. (Ed.) Modern Techniques in Computational Chemistry: MOTECC-90; Springer: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Roy, S.; Majumder, S. Ab initio estimations of the isotope shift for the first three elements of the K isoelectronic sequence. Phys. Rev. A 2015, 92, 012508. [Google Scholar] [CrossRef]
- Huzinaga, S.; Klobukowski, M. Well-tempered Gaussian basis sets for the calculation of matrix Hartree—Fock wavefunctions. Chem. Phys. Lett. 1993, 212, 260–264. [Google Scholar] [CrossRef]
- Huzinaga, S.; Klobukowski, M.; Tatewaki, H. The well-tempered GTF basis sets and their applications in the SCF calculations on N2, CO, Na2, and P2. Can. J. Chem. 1985, 63, 1812–1828. [Google Scholar] [CrossRef]
- Safronova, U.I. Relativistic many-body calculation of energies, lifetimes, hyperfine constants, multipole polarizabilities, and blackbody radiation shift in 137Ba ii. Phys. Rev. A 2010, 81, 052506. [Google Scholar] [CrossRef]
- Barrett, M.D.; Arnold, K.J.; Safronova, M.S. Polarizability assessments of ion-based optical clocks. Phys. Rev. A 2019, 100, 043418. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Wansbeek, L.W.; Jungmann, K.; Timmermans, R.G.E. Light shifts and electric dipole matrix elements in Ba+ and Ra+. Phys. Rev. A 2009, 79, 052512. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, Y.; Wang, X.; Dong, C.-Z.; Wu, Z.W. Tune-out and magic wavelengths of Ba+ ions. Phys. Rev. A 2021, 103, 032803. [Google Scholar] [CrossRef]
- Dutta, N.N. Trend of Gaunt interaction contributions to the electric dipole polarizabilities of noble gas, alkaline-earth, and a few group-12 atoms. Chem. Phys. Lett. 2020, 758, 137911. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.9), [Online]. National Institute of Standards and Technology, Gaithersburg, MD. 2021. Available online: https://physics.nist.gov/asd (accessed on 7 September 2022).
- Sahoo, B.K.; Timmermans, R.G.E.; Das, B.P.; Mukherjee, D. Comparative studies of dipole polarizabilities in Sr+, Ba+, and Ra+ and their applications to optical clocks. Phys. Rev. A 2009, 80, 062506. [Google Scholar] [CrossRef]
- Kaur, J.; Singh, S.; Arora, B.; Sahoo, B.K. Magic wavelengths in the alkaline-earth-metal ions. Phys. Rev. A 2015, 92, 031402(R). [Google Scholar] [CrossRef]
- Kastberg, A.; Villemoes, P.; Arnesen, A.; Heijkenskjöld, F.; Langereis, A.; Jungner, P.; Linnæus, S. Measurements of absolute transition probabilities in Ba ii through optical nutation. J. Opt. Soc. Am. B 1993, 10, 1330–1336. [Google Scholar] [CrossRef]
- Klose, J.Z.; Fuhr, J.R.; Wiese, W.L. Critically Evaluated Atomic Transition Probabilities for Ba I and Ba II. J. Phys. Chem. Ref. Data 2002, 31, 217–230. [Google Scholar] [CrossRef]
- Davidson, M.D.; Snoek, L.C.; Volten, H.; Doenszelmann, A. Oscillator strengths and branching ratios of transitions between low-lying levels in the barium II spectrum. Astron. Astrophys. 1992, 255, 457–458. [Google Scholar]
- Woods, S.L.; Hanni, M.E.; Lundeen, S.R.; Snow, E.L. Dipole transition strengths in Ba+ from Rydberg fine-structure measurements in Ba and Ba+. Phys. Rev. A 2010, 82, 012506. [Google Scholar] [CrossRef]
- Kurz, N.; Dietrich, M.R.; Shu, G.; Bowler, R.; Salacka, J.; Mirgon, V.; Blinov, B.B. Measurement of the branching ratio in the 6P3/2 decay of Ba II with a single trapped ion. Phys. Rev. A 2008, 77, 060501(R). [Google Scholar] [CrossRef]
- Da Silva, H., Jr.; Raoult, M.; Aymar, M.; Dulieu, O. Formation of molecular ions by radiative association of cold trapped atoms and ions. New J. Phys. 2015, 17, 045015. [Google Scholar] [CrossRef]
- Kien, F.L.; Schneeweiss, P.; Rauschenbeute, A. Dynamical polarizability of atoms in arbitrary light fields: General theory and application to cesium. Eur. Phys. J. D 2013, 67, 92. [Google Scholar] [CrossRef]
- Vanier, J.; Audoin, C. The Quantum Physics of Atomic Frequency Standards, 1st ed.; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, D.L.; Chang, M.-S.; Chapman, M.S.; You, L. Coherent spin mixing dynamics in a spin-1 atomic condensate. Phys. Rev. A 2005, 72, 013602. [Google Scholar] [CrossRef]
- Trapp, S.; Marx, G.; Tommaseo, G.; Klaas, A.; Drakoudis, A.; Revalde, G.; Szawiola, G.; Werth, G. Hyperfine structure and g factor measurements on Ba+ and Eu+ isotopes. Hyperfine Interact. 2000, 127, 57–64. [Google Scholar] [CrossRef]
- Luo, X.-Y.; Zou, Y.-Q.; Wu, L.-N.; Liu, Q.; Han, M.-F.; Tey, M.K.; You, L. Deterministic entanglement generation from driving through quantum phase transitions. Science 2017, 355, 620–623. [Google Scholar] [CrossRef]
- Zou, Y.-Q.; Wu, L.-N.; Liu, Q.; Luo, X.-Y.; Guo, S.-F.; Cao, J.-H.; Tey, M.K.; You, L. Beating the classical precision limit with spin-1 Dicke states of more than 10,000 atoms. Proc. Natl. Acad. Sci. USA 2018, 115, 6381–6385. [Google Scholar] [CrossRef]
- Jie, J.; Yu, Y.; Wang, D.; Zhang, P. Laser control of the singlet-pairing process in an ultracold spinor mixture. Phys. Rev. A 2021, 103, 053321. [Google Scholar] [CrossRef]
- Beloy, K. Theory of the Ac Stark Effect on the Atomic Hyperfine Structure and Applications to Microwave Atomic Clocks. Ph.D. Dissertation, University of Nevada, Reno, NV, USA, 2009. [Google Scholar]
- Dzuba, V.A.; Flambaum, V.V.; Beloy, K.; Derevianko, A. Hyperfine-mediated static polarizabilities of monovalent atoms and ions. Phys. Rev. A 2010, 82, 062513. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).