nl-Selective Classical Charge-Exchange Cross Sections in Be⁴⁺ and Ground State Hydrogen Atom Collisions

Abstract

Charge-exchange cross sections in Be⁴⁺ + H(1s) collisions are calculated using the three-body classical trajectory Monte Carlo method (CTMC) and the quasi-classical trajectory Monte Carlo method of Kirschbaum and Wilets (QCTMC) for impact energies between 10 keV/amu and 300 keV/amu. We present charge-exchange cross sections in the projectile n = 2 and nl = 2s, 2p states. Our results are compared with the previous quantum-mechanical approaches. We found that the QCTMC model is a powerful classical model to describe the state-selective charge-exchange cross sections at lower impact energies and the QCTMC results are in good agreement with previous observations.

1. Introduction

In recent decades, efforts have been made to take a significant step in supplying energy cleanly and safely by developing power plants that produce energy by the nuclear fusion process. Reactors have been developed in this regard, such as the International Thermonuclear Experimental Reactor (ITER). Due to the unique thermophysical properties and low atomic number, beryllium (Be) is defined as a plasma-facing material [1]. Therefore, it plays a key role in the wall structure of next-generation fusion reactors. On the other hand, impurities are one of the main problems in controlled thermonuclear fusion plasmas. As a common plasma impurity, Be ions also play a role in the loss of radiant energy that causes the plasma to cool when colliding with the primary plasma components, such as neutral hydrogen (H) atoms [2]. Therefore, it is necessary to know how beryllium ions behave in collisions with hydrogen atoms. To determine the Be impurities in the plasma, knowledge of the charge-exchange cross section is very important, because the deexcitation radiation of fully striped Be ions after the charge-exchange process can be detected by charge-exchange recombination spectroscopy (CXRS) [3].

Although the importance of charge-exchange processes for the Be⁴⁺ projectile is evident in fusion research, experimental data are still missing. In contrast, different theoretical methods have been studied for this collision system. For example, the classical trajectory Monte Carlo (CTMC) method has been used by Olson and Salop [4], Schultz et al. [5], and Minami et al. [6] to calculate the state-selective charge-exchange cross sections for the interaction of Be⁴⁺ with H in the wide range of impact energies. On the other hand, quantum-mechanical methods have been used to calculate the total, shell- and subshell-selective charge-exchange cross sections in Be⁴⁺ + H(1s) collisions, including:

• One electron diatomic molecule (OEDM) [7],
• Molecular orbital close-coupling (MOCC) [8],
• Continuum distorted wave (CDW) [9],
• Boundary-corrected continuum intermediate state (BCCIS) approximation [10],
• Lattice time-dependent Schrödinger equation (LTDSE) [6],
• Atomic-orbital close-coupling (AOCC) [6], and
• Semiclassical two-center wave-packet convergent close-coupling (WP-CCC) [11].

Quantum mechanical models are known to be potent candidates for performing the simulations but the analyses of equations to describe atomic collisions are, in many cases, very complicated and time-consuming. Therefore, classical theories, such as the trajectory Monte Carlo method, can be a good alternative. The CTMC method is a non-perturbative method, via which classical equations of motion are solved numerically with randomly selected initial conditions [4,12,13]. A consideration of the many-body interactions during collisions is one of the benefits of the CTMC method.

The quasi-classical trajectory Monte Carlo (QCTMC) method was proposed by Kirschbaum and Wilets in 1980 [14]. This method has been applied to calculate various cross sections in the number of collision systems [15,16,17,18,19]. According to the model, two basic requirements for improving the standard CTMC method are that the electrons cannot collapse into the nucleus and that the two identical electrons cannot occupy the same level of energy. The effective potential was introduced along this line to mimic the Heisenberg uncertainty principle and the Pauli constraints.

In this work, we use the QCTMC method to show the charge-exchange cross sections in n = 2 and nl = 2s, 2p states of the projectile in Be⁴⁺ + H(1s). For comparison, we computed the corresponding cross sections using the standard three-body CTMC model. The calculations were made for impact energies between 10 keV/amu and 300 keV/amu. Furthermore, since there are no experimental data for a Be⁴⁺ and H(1s) collision system, we compared our classical results with the previous results obtained by quantum-mechanics methods, such as AOCC [6,20], MOCC [8], LTDSE [6], OEDM [7], CDW [9], and WP-CCC [11].

2. Theory

In the present work, we performed our calculations in the framework of the three-body CTMC model. We solved the equation of motions according to relative position vectors of three bodies (projectile, electron, target), based on Hamiltonian mechanics. The interaction among the particles was the pure Coulomb interaction. The initial conditions, such as electron position, velocity, and the impact parameter, were chosen randomly from the microcanonical ensemble [12,13].

In the next step, to improve the results of the classical simulations, we considered the Heisenberg uncertainty principle by adding effective potential to our calculations. Because the hydrogen atom, as a target, has only one electron, we did not need to consider the Pauli constraints. To perform the QCTMC model calculations, we numerically solved the equations of motion by considering the correction term. The starting point of theoretical calculations was to define the Hamiltonian equation. Quasi-classical Hamiltonian mechanics consist of constraining potential, V_H, inspired by the Heisenberg principles, and the Hamiltonian H₀. Thus

$$H_{QCTMC}=H_0+V_H$$

(1)

where

$$H_0=T+V_{Coul}$$

(2)

T and V_Coul are the total kinetic potential and the pure Coulomb potential between the particles, respectively. V_H can be written as:

$$V_H={{\displaystyle \sum }}_{n=a,b}{{\displaystyle \sum }}_{i=1}^{N_e}f(r_{ni},p_{ni};{\xi }_H,{\alpha }_H),$$

(3)

where a and b signify the nuclei, and the i represents the electron. In addition, ${\alpha }_H$ and ${\xi }_H$ are the Heisenberg adjustable hardness and dimensionless parameters, respectively. $r_{\alpha \beta }=r_{\beta }-r_{\alpha }$, and the relative momenta is defined as:

$$p_{\alpha \beta }=\frac{m_{\alpha }{p}_{\beta }-m_{\beta }{p}_{\alpha }}{m_{\alpha }+m_{\beta }}$$

(4)

The function f mimicking the Heisenberg principle is written as [14]:

$$f\left(r_{\lambda \nu }, p_{\lambda \nu };{\xi }_H , {\alpha }_H\right)=\frac{{\xi }_H}{4{\alpha }_H{r}_{\mathsf{\lambda }\nu }^2{\mu }_{\lambda \nu }}exp\left\{\alpha \left[1-{\left(\frac{r_{\lambda \nu }{p}_{\lambda \nu }}{{\xi }_H}\right)}^4\right]\right\}$$

(5)

where ${\mu }_{\lambda \nu }$ is the reduced mass of particles $\lambda$ and $\nu$.

In this work, we used ${\alpha }_H$ = 4 and ${\xi }_H$ = 0.9428 [17,18,19], respectively. We used the target-projectile-centered scheme, in which the correction term is taken into account between the target electron and both the target nucleus and the projectile, as follows:

$$f\left({\overrightarrow{r}}_{pe} ,{\overrightarrow{P}}_{pe};{\xi }_H , {\alpha }_H\right)=\frac{{\xi }_H{}^2}{4{\alpha }_H{\overrightarrow{r}}_{pe}^2{\mu }_{pe}}exp\left\{{\alpha }_H\left[1-{\left(\frac{{\overrightarrow{r}}_{pe}{\overrightarrow{P}}_{pe}}{{\xi }_H}\right)}^4\right]\right\}$$

(6)

$$f\left({\overrightarrow{r}}_{Te} ,{\overrightarrow{P}}_{Te};{\xi }_H , {\alpha }_H\right)=\frac{{\xi }_H{}^2}{4{\alpha }_H{\overrightarrow{r}}_{Te}^2{\mu }_{Te}}exp\left\{{\alpha }_H\left[1-{\left(\frac{{\overrightarrow{r}}_{Te}{\overrightarrow{P}}_{Te}}{{\xi }_H}\right)}^4\right]\right\}$$

(7)

where T, p, and e stand for the target, the projectile, and the electron, respectively.

The equations to be solved within the framework of the QCTMC method, by considering the Hamiltonian mechanics, were as follows:

$$\begin{gathered} {\dot{\overrightarrow{P}}}_e=-\frac{\delta H_{QCTMC}}{\delta {\overrightarrow{r}}_e}=-\frac{Z_p{Z}_e}{{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right|}^3}\left({\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right)+\frac{Z_e{Z}_T}{{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}^3}\left({\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right)+ \\ \left(\frac{{\xi }_H{}^2}{2{\alpha }_H{\mu }_{Te}{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}^4}+\frac{{\overrightarrow{P}}_{Te}^4}{{\xi }_H{}^2{\mu }_{Te}}\right)e^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|\left|{\overrightarrow{P}}_{Te}\right|}{{\xi }_H}\right)}^4\right]}\left({\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right)+ \\ \left(\frac{{\xi }_H{}^2}{2{\alpha }_H{\mu }_{pe}{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_p\right|}^4}+\frac{{\overrightarrow{P}}_{pe}^4}{{\xi }_H{}^2{\mu }_{pe}}\right)e^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_p\right|\left|{\overrightarrow{P}}_{pe}\right|}{{\xi }_H}\right)}^4\right]}\left({\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right) \end{gathered}$$

(8)

$$\begin{gathered} {\overrightarrow{\dot{r}}}_e=\frac{\partial H_{QCTMC}}{\partial {\overrightarrow{P}}_e}=N_e{\overrightarrow{P}}_e-\frac{N_e{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}^2{\left|{\overrightarrow{P}}_{Te}\right|}^2}{{\xi }_H{}^2}{e}^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|\left|{\overrightarrow{P}}_{Te}\right|}{{\xi }_H}\right)}^4\right]}{\overrightarrow{P}}_{Te}+ \\ \frac{N_e{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right|}^2{\left|{\overrightarrow{P}}_{pe}\right|}^2}{{\xi }_H{}^2}{e}^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right|\left|{\overrightarrow{P}}_{pe}\right|}{{\xi }_H}\right)}^4\right]}{\overrightarrow{P}}_{pe} \end{gathered}$$

(9)

$$\begin{gathered} {\dot{\overrightarrow{P}}}_T=-\frac{\delta H_{QCTMC}}{\delta {\overrightarrow{r}}_T}=-\frac{Z_p{Z}_T}{{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_T\right|}^3}\left({\overrightarrow{r}}_p-{\overrightarrow{r}}_T\right)-\frac{Z_e{Z}_T}{{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}^3}\left({\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right)+ \\ \left(\frac{{\xi }_H{}^2}{2{\alpha }_H{\mu }_{Te}{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}^4}+\frac{{\overrightarrow{P}}_{Te}^4}{{\xi }_H{}^2{\mu }_{Te}}\right)e^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|\left|{\overrightarrow{P}}_{Te}\right|}{{\xi }_H}\right)}^4\right]}\left({\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right) \end{gathered}$$

(10)

$${\overrightarrow{\dot{r}}}_T=\frac{\partial H_{QCTMC}}{\partial {\overrightarrow{P}}_p}=N_T{\overrightarrow{P}}_T-\frac{N_T{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|}^2{\left|{\overrightarrow{P}}_{Te}\right|}^2}{{\xi }_H{}^2}{e}^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_T\right|\left|{\overrightarrow{P}}_{Te}\right|}{{\xi }_H}\right)}^4\right]}{\overrightarrow{P}}_{Te}.$$

(11)

$$\begin{gathered} {\dot{\overrightarrow{P}}}_p=-\frac{\delta H_{QCTMC}}{\delta {\overrightarrow{r}}_p}=\frac{Z_p{Z}_e}{{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right|}^3}\left({\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right)+\frac{Z_p{Z}_T}{{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_T\right|}^3}\left({\overrightarrow{r}}_p-{\overrightarrow{r}}_T\right)- \\ \left(\frac{{\xi }_H{}^2}{2{\alpha }_H{\mu }_{pe}{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_p\right|}^4}+\frac{{\overrightarrow{P}}_{pe}^4}{{\xi }_H{}^2{\mu }_{pe}}\right)e^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_e-{\overrightarrow{r}}_p\right|\left|{\overrightarrow{P}}_{pe}\right|}{{\xi }_H}\right)}^4\right]}\left({\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right) \end{gathered}$$

(12)

$${\overrightarrow{\dot{r}}}_p=\frac{\partial H_{QCTMC}}{\partial {\overrightarrow{P}}_p}=N_p{\overrightarrow{P}}_p+\frac{N_p{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right|}^2{\left|{\overrightarrow{P}}_{pe}\right|}^2}{{\xi }_H{}^2}{e}^{{\alpha }_H\left[1-{\left(\frac{\left|{\overrightarrow{r}}_p-{\overrightarrow{r}}_e\right|\left|{\overrightarrow{P}}_{pe}\right|}{{\xi }_H}\right)}^4\right]}{\overrightarrow{P}}_{pe}$$

(13)

where $\overrightarrow{r}$, $\overrightarrow{p}$, Z, and m are the position vector, the momentum vector, the charge, and the mass of the given particles; p is the projectile; e is the electron; and T is the target nucleus, respectively. In addition, we used $N_i=\frac{1}{m_i}$.

The total cross sections were estimated as follows:

$$\sigma =\frac{2\pi b_{max}}{T_N}{{\displaystyle \sum }}_j{b}_j^{\left(i\right)}$$

(14)

where T_N is the total number of trajectories computed for the impact parameters less than b_max and b_j⁽ⁱ⁾ is the actual impact parameter for the trajectory corresponding charge-exchange processes. The statistical uncertainty of the cross sections is given by:

$$\Delta \sigma =\sigma {\left(\frac{T_N-T_N^{\left(i\right)}}{T_N{T}_N^{\left(i\right)}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.$$

(15)

where $T_N^{(i)}$ is the number of trajectories that fulfill the corresponding final channels (charge exchange).

3. Results

To study the state-selective charge-exchange cross sections in the n = 2 and nl = 2s, 2p states of the projectile in Be⁴⁺ and ground-state hydrogen atom collisions, we used both the standard three-body CTMC and the QCTMC models. The calculations were performed in the impact energy range between 10 keV/amu and 300 keV/amu. Because the higher trajectories provide higher accuracy in classical trajectory Monte Carlo approaches, we took into account 5 × 10⁶ individual trajectories in the CTMC and QCTMC models for each impact energy. According to a large number of primary histories, the estimated uncertainties (see Equation (15)) of the cross sections in the CTMC and QCTMC models are approximately 0.6%.

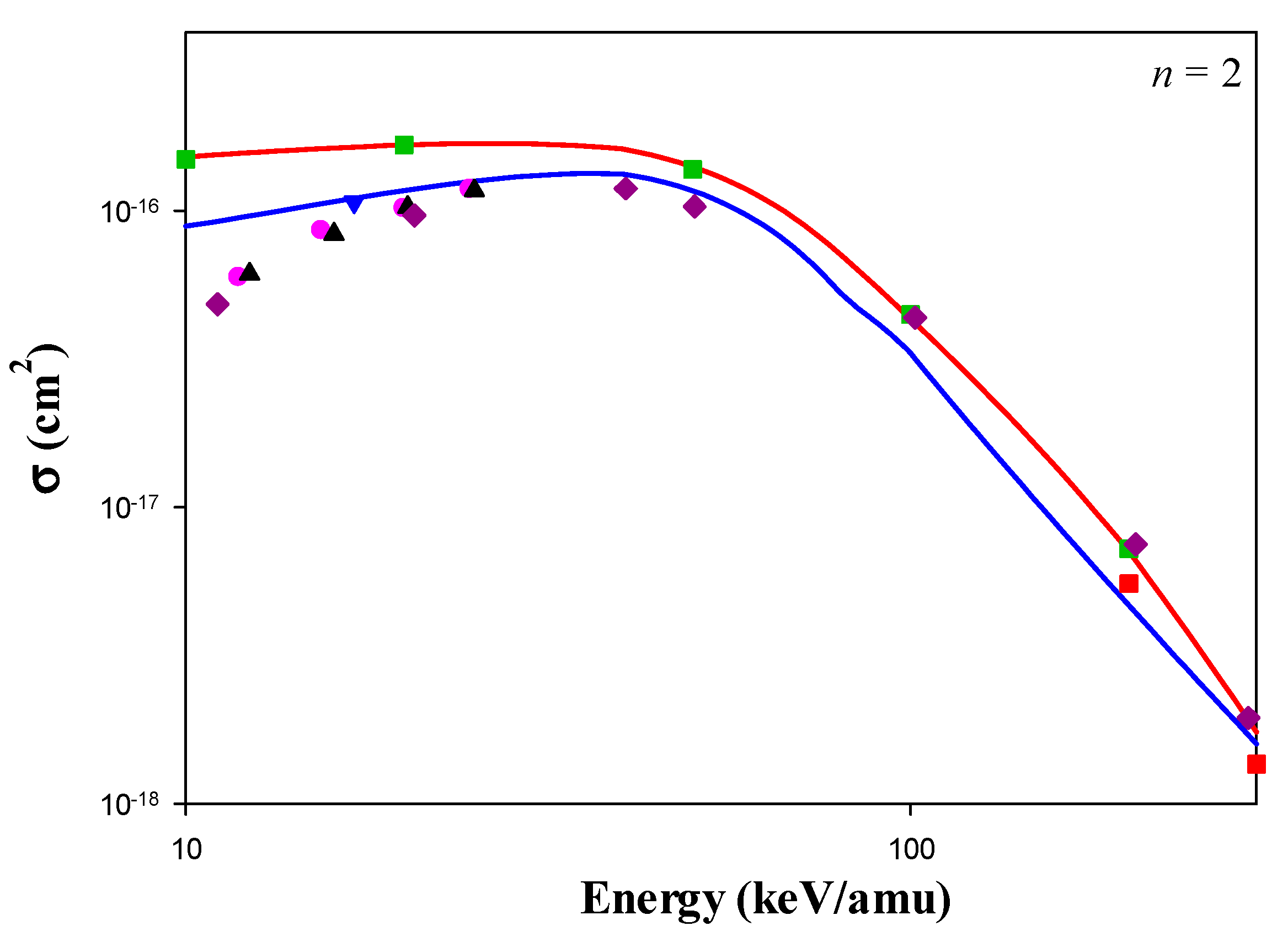
Figure 1 shows the present CTMC and QCTMC results of the charge exchange in the n = 2 state of the projectile in Be⁴⁺ + H(1s), as a function of the impact energy. We compared our present results with the quantum-mechanical approaches, based on the AOCC [20], MOCC [8], OEDM [7], CDW [9], and WP-CCC [11]. To evaluate the validity of our CTMC results, we also compared our results with the CTMC results of Schultz et al. [5].

Figure 1. Charge-exchange cross sections in the n = 2 state of the projectile in Be⁴⁺ + H(1s) collision, as a function of the impact energy. Solid red line: present CTMC results; solid blue line: present QCTMC results; blue inverse triangle: AOCC results of Fritsch et al. [20]; pink circles: MOCC results of Harel et al. [8]; black triangles: OEDM results of Errea et al. [7]; red diamonds: CDW results of Belkic et al. [9]; purple diamonds: WP-CCC results of Antonio et al. [11]; green squares: CTMC results of Schultz et al. [5].

We found that the QCTMC results were significantly closer to the quantum-mechanics results, such as the AOCC results of Fritsch et al. [20], the OEDM results of Errea et al. [7], the MOCC results of Harel et al. [8], and the WP-CCC results of Antonio et al. [11], compared with the CTMC results in the lower-energy range (≤ 50 keV/amu). Our CTMC results matched well with the WP-CCC results of Antonio et al. [11], above 100 keV/amu impact energies. The present CTMC cross sections were higher than the QCTMC cross sections in the entire range of the impact energies.

Physically, in the QCTMC model, the Heisenberg correction term represents the repulsive force between the electron and both the target nucleus and the projectile. This repulsive force affects the attractive Coulomb force between the electron and the target nucleus. On the other hand, at a lower-impact energy range, the projectile spent more time in the vicinity of the target. Therefore, the effect of the correction term on the electron-capture cross sections was more significant at the lower-projectile energy range (≤50 keV/amu) in the QCTMC model. The correction term lost its effect at higher-impact energies, and the standard CTMC method described the cross sections reasonably well. As shown in Figure 1, the present QCTMC results are in good agreement with the CDW results of Belkic et al. [9] above 100 keV/amu impact energies.

Figure 2a shows the charge-exchange cross sections in the 2s state of the projectile in Be⁴⁺ + H(1s) as a function of the impact energy. The LTDSE results of Minami et al. [6] are in better agreement with the present QCTMC results in the lower-energy range (≤30 keV/amu). In addition, the AOCC results of Minami et al. [6], and WP-CCC results of Antonio et al. [11] agreed with QCTMC results at an entire range of energies, compared with CTMC results. The present CTMC and QCTMC results were very close to each other at low-impact energies, and they agreed with the MOCC results of Harel et al. [7]. In addition, one can see the excellent agreement between the CDW results of Belkic [9] and the present QCTMC results above 200 keV/amu impact energies.

Figure 2. Charge-exchange cross sections in (a) 2s, (b) 2p states of the projectile in Be⁴⁺ + H(1s) collisions as a function of the impact energy. Solid red line: present CTMC results; solid blue line: present QCTMC results; blue inverse triangles: AOCC results of Minami et al. [6]; pink circles: MOCC results of Harel et al. [8]; black triangles: LTDSE results of Minami et al. [6]; red diamonds: CDW results of Belkic et al. [9]; purple diamonds: WP-CCC results of Antonio et al. [11]; green squares: CTMC results of Schultz et al. [5].

Figure 2b shows the charge-exchange cross sections in the 2p state of the projectile in Be⁴⁺ + H(1s) as a function of the impact energy. The QCTMC results dropped more than the CTMC results in the lower-energy range (≤50 keV/amu), which agreed with quantum-mechanical approaches, such as AOCC [6], MOCC [8], LTDSE [6], and WP-CCC [11]. In addition, the present QCTMC results were in good agreement with the obtained results based on CDW approximation [9] at intermediate impact energies.

4. Conclusions

We calculated the charge-exchange cross sections in n = 2, and nl = 2s, 2p states of the projectile in the collision between Be⁴⁺ and ground-state hydrogen atoms in a wide-impact-energies range based on the CTMC and QCTMC models. The CTMC model cannot compete with quantum calculation in many respects, because it lacks the quantum feature of the collisions. Therefore, we developed a three-body QCTMC model that takes into account the quantum features of the collision system, in which the Heisenberg correction term was added to the standard three-body CTMC model. For the determination of the cross sections, 5 × 10⁶ trajectories were calculated for each impact energy. Comparisons were made with the available quantum-mechanical approaches, such as MOCC, AOCC, OEDM, CDW, WP-CCC, and previous classical simulations. We found that the QCTMC method can reasonably describe the state-selective cross sections, especially at a lower-projectile energy range (≤50 keV/amu). Our calculations provide a fast and reliable estimation of fusion-related state-selective cross sections, in both low- and intermediate-impact energies. We showed that the QCTMC model may provide an alternative to the quantum-mechanical models, especially at low-impact energies, possibly providing the same results with low-computation efforts.