Probing the Atomic Structure of Californium by Resonance Ionization Spectroscopy
Abstract
1. Introduction
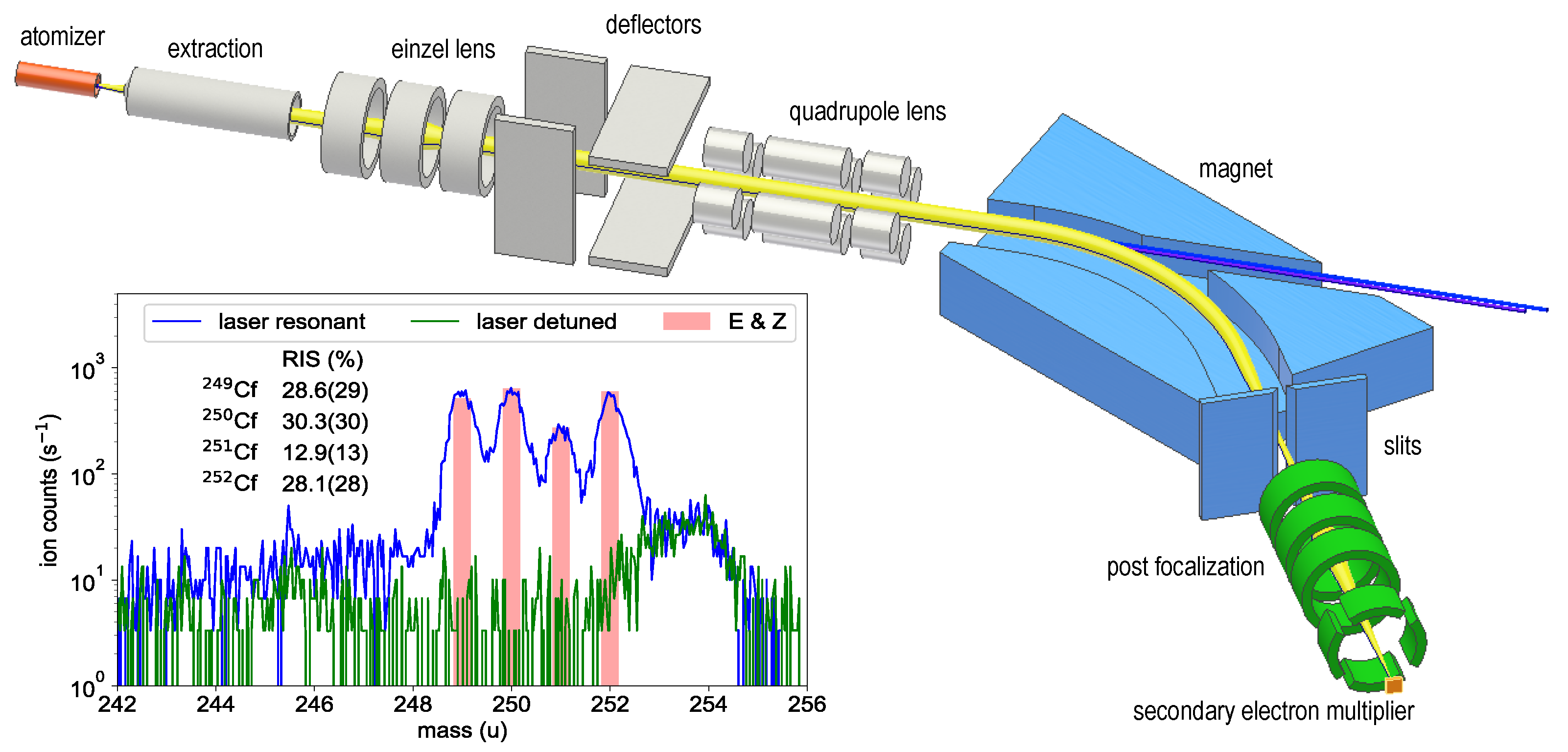
2. Experimental Setup
3. Laser Spectroscopic Investigations
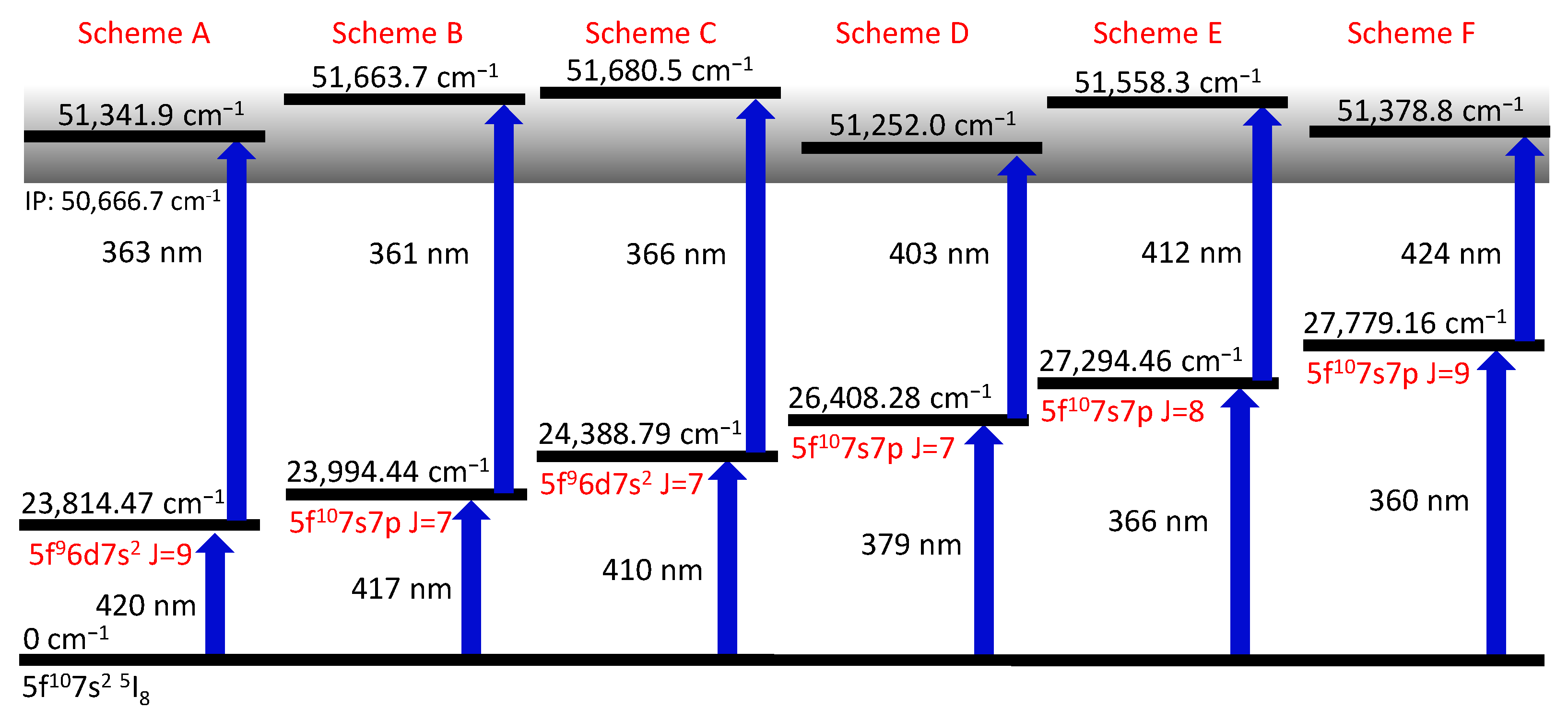
3.1. Ionization Schemes
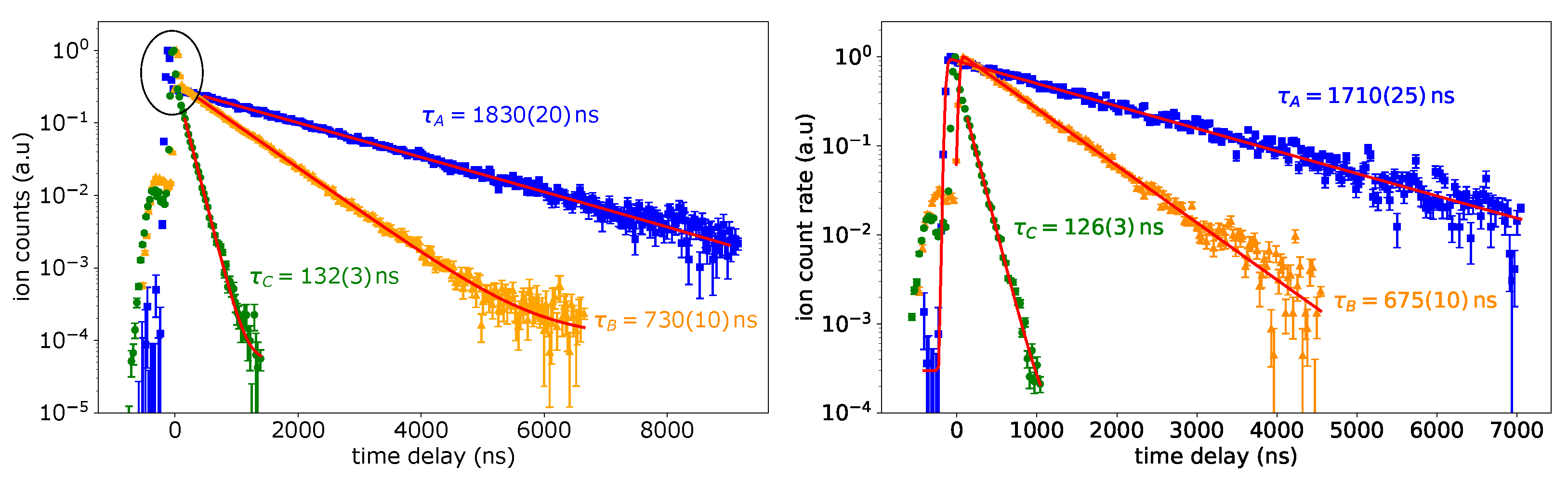
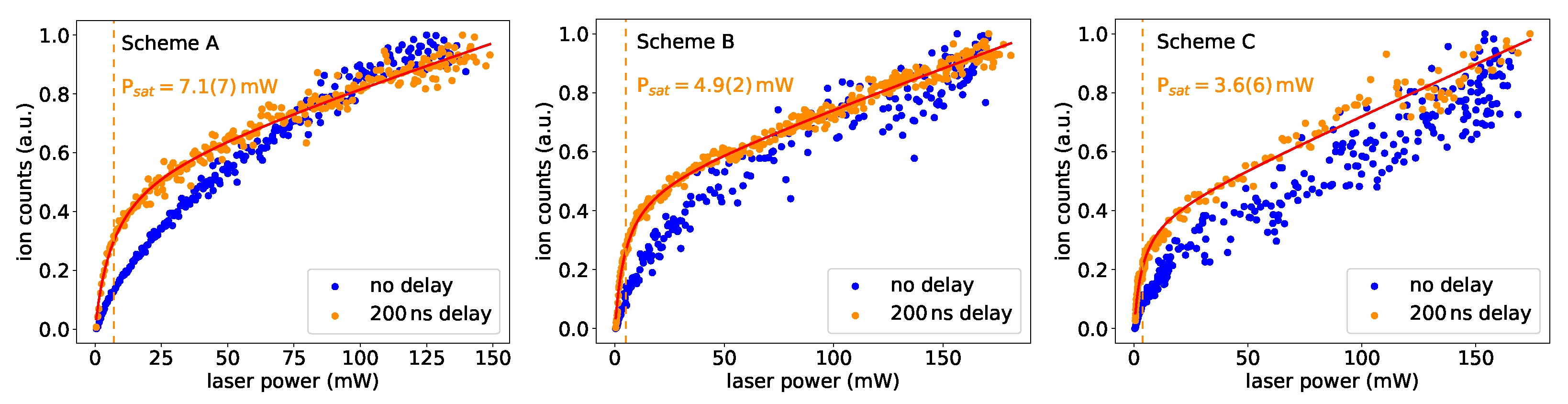
3.2. Lifetime and Saturation
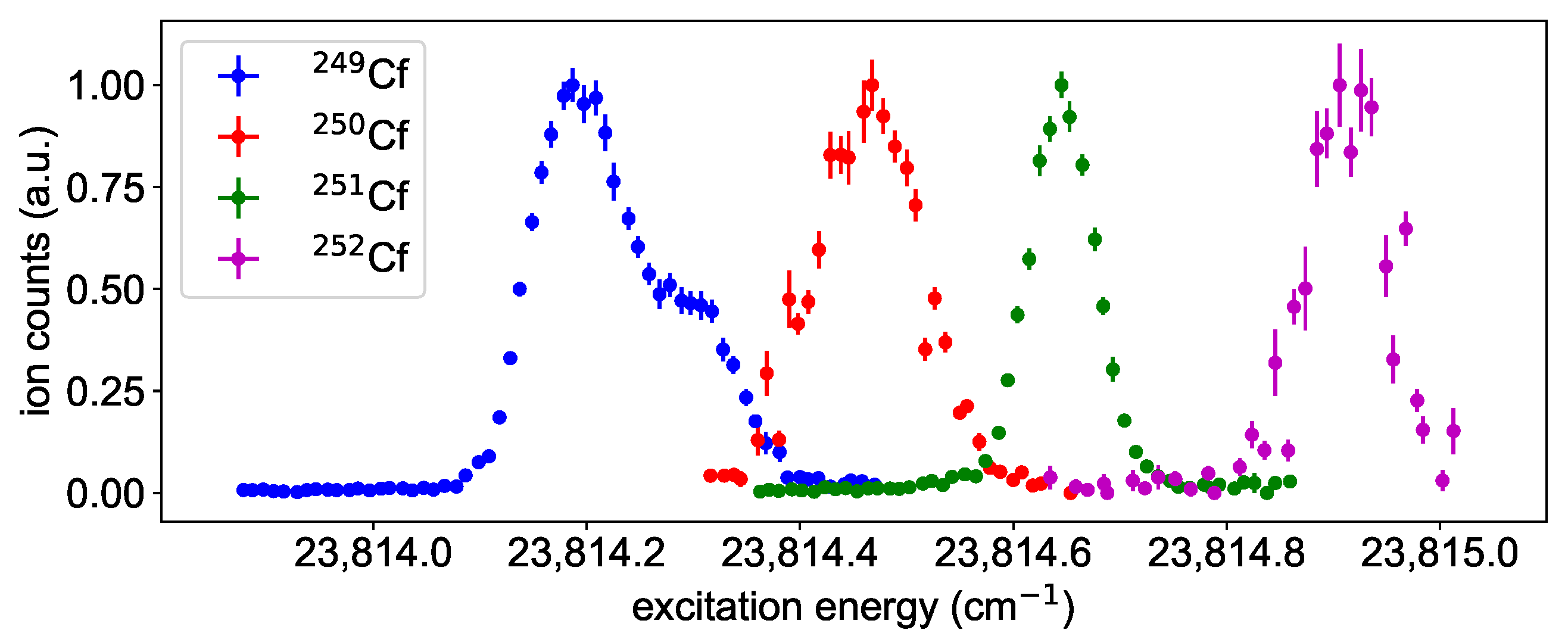
3.3. Isotope Shift
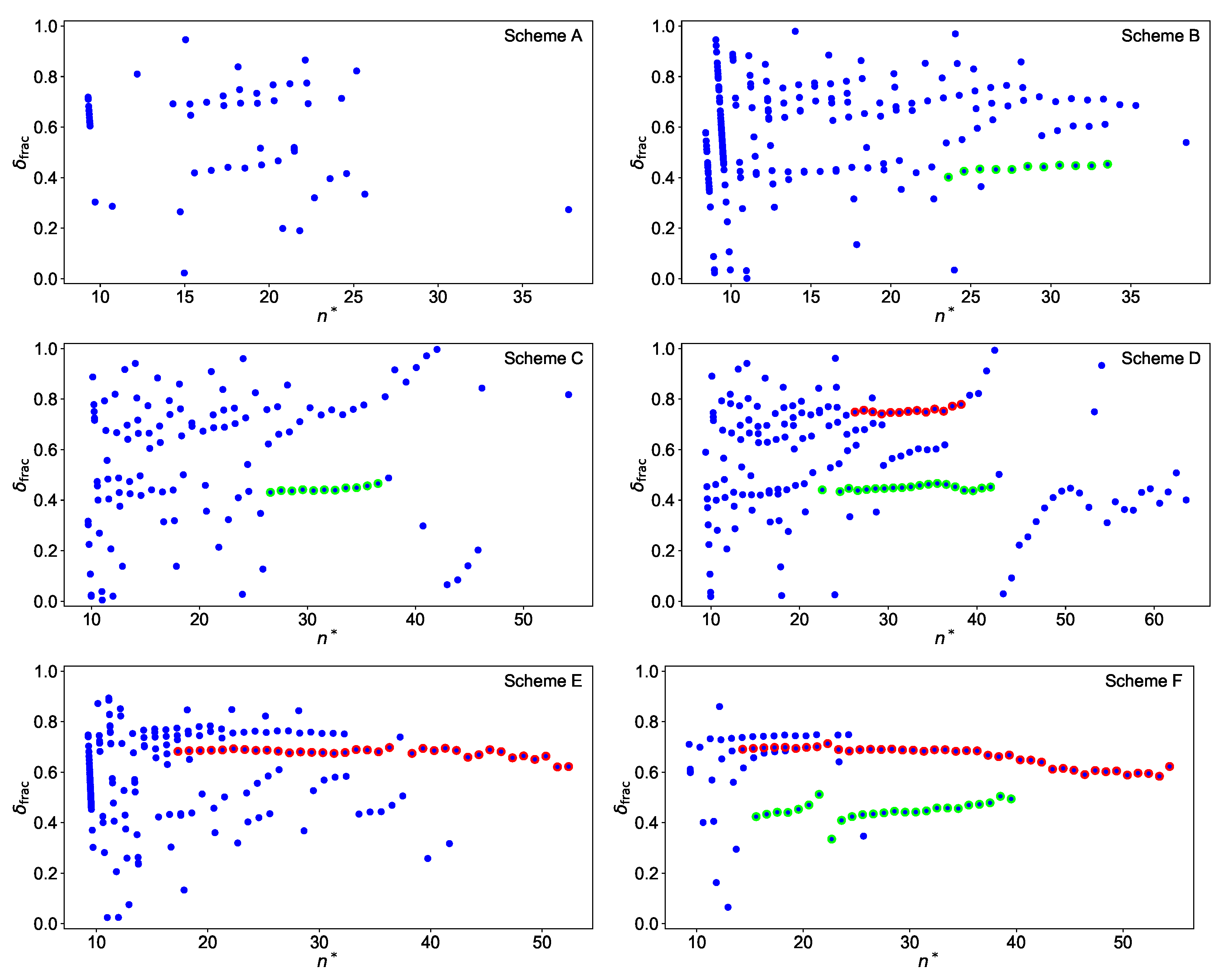
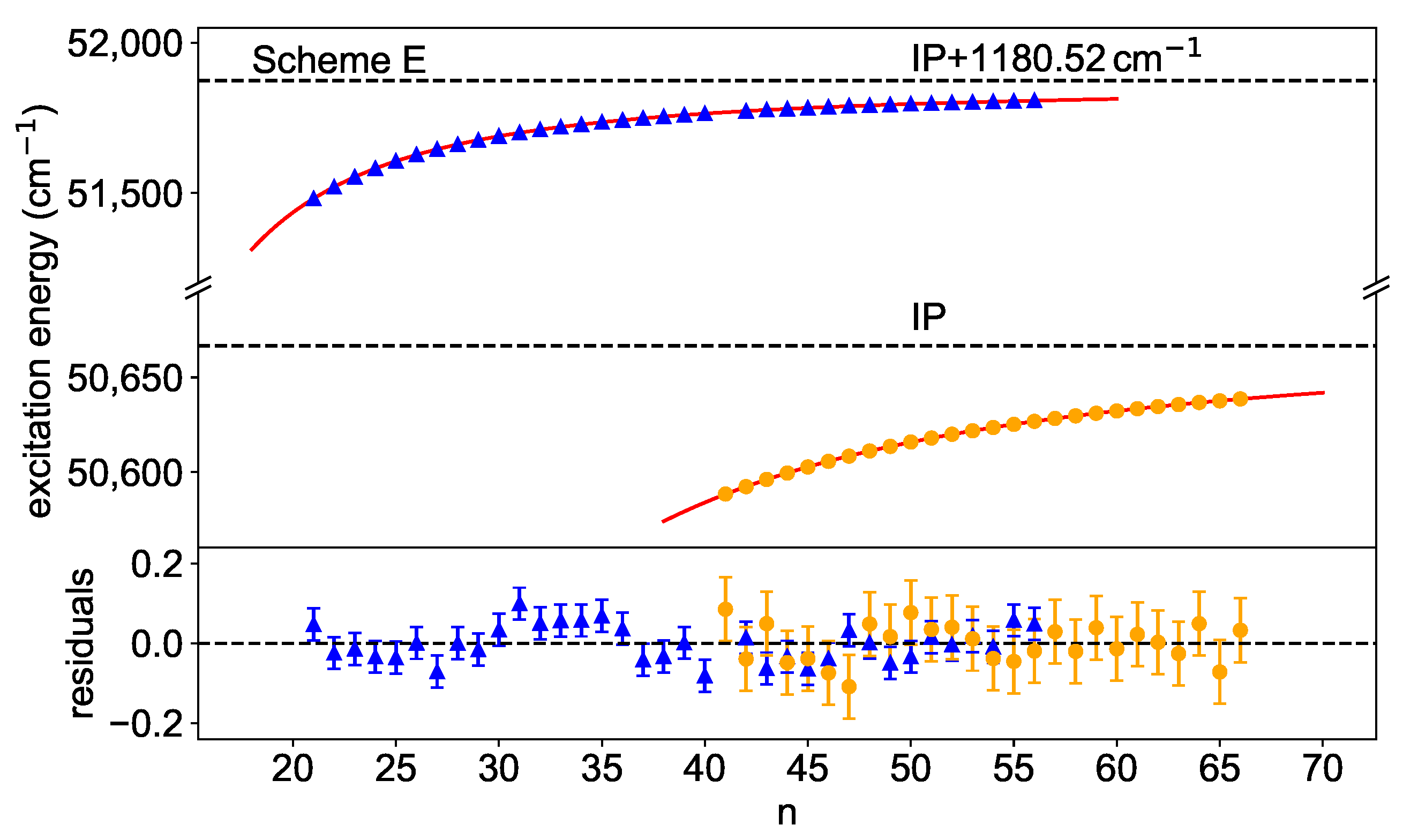
3.4. Ionization Potential
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Conway, J.G.; Worden, E.F.; Blaise, J. Energy levels of neutral californium (249Cf I) and singly ionized californium (249Cf II). J. Opt. Soc. Am. B 1995, 12, 1186–1202. [Google Scholar] [CrossRef]
- Bosco, H.; Hamann, L.; Kneip, N.; Raiwa, M.; Weiss, M.; Wendt, K.; Walther, C. New horizons in microparticle forensics: Actinide imaging and detection of 238Pu and 242mAm in hot particles. Sci. Adv. 2021, 7, eabj1175. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, R.; Barzakh, A.; Bastin, B.; Beerwerth, R.; Block, M.; Creemers, P.; Grawe, H.; de Groote, R.; Delahaye, P.; Fléchard, X.; et al. Towards high-resolution laser ionization spectroscopy of the heaviest elements in supersonic gas jet expansion. Nat. Commun. 2017, 8, 14520. [Google Scholar] [CrossRef] [PubMed]
- Campbell, P.; Moore, I.D.; Pearson, M.R. Laser spectroscopy for nuclear structure physics. Prog. Part. Nucl. 2016, 86, 127–180. [Google Scholar] [CrossRef]
- Seaborg, G.T. Transuranium isotopes—An overview. Trans. Am. Nucl. Soc. 1989, 60, 275–276. [Google Scholar]
- Ramirez, E.M.; Ackermann, D.; Blaum, K.; Block, M.; Droese, C.; Düllmann, C.E.; Dworschak, M.; Eibach, M.; Eliseev, S.; Haettner, E.; et al. Direct mapping of nuclear shell effects in the heaviest elements. Science 2012, 337, 1207–1210. [Google Scholar] [CrossRef]
- Ackermann, D. Nuclear structure of superheavy nuclei—State of the art and perspectives (@ S3). EPJ Web Conf. 2018, 193, 04013. [Google Scholar] [CrossRef][Green Version]
- Block, M.; Giacoppo, F.; Heßberger, F.-P.; Raeder, S. Recent progress in experiments on the heaviest nuclides at SHIP. Riv. Nuovo C. 2022, 45, 279–323. [Google Scholar] [CrossRef]
- Ferguson, D.E. ORNL transuranium program—The production of transuranium elements. Nucl. Sci. Eng. 1963, 17, 435–437. [Google Scholar] [CrossRef]
- Martin, R.C.; Knauer, J.B.; Balo, P.A. Production, distribution and applications of californium-252 neutron sources. Appl. Radiat. Isot. 2000, 53, 785–792. [Google Scholar] [CrossRef]
- Boulogne, A.R.; Faraci, J.P. Californium-252 neutron sources for industrial applications. Nucl. Technol. 1971, 11, 75–83. [Google Scholar] [CrossRef]
- Thompson, S.G.; Street, K., Jr.; Ghiorso, A.; Seaborg, G.T. The new element californium (atomic number 98). Phys. Rev. 1950, 80, 790. [Google Scholar] [CrossRef]
- Conway, J.G.; Hulet, E.K.; Morrow, R.J. Emission spectrum of californium. J. Opt. Soc. Am. 1962, 52, 222. [Google Scholar] [CrossRef]
- Worden, E.F.; Conway, J.G. Ground states and normal electronic configurations of californium I and II. J. Opt. Soc. Am. 1970, 60, 1144–1145. [Google Scholar] [CrossRef]
- Conway, J.G.; Worden, E.F.; Blaise, J.; Vergfàs, J. The infrared spectrum of californium-249. Spectrochim. Acta B 1977, 32, 97–99. [Google Scholar] [CrossRef]
- Hurst, G.S.; Payne, M.G.; Kramer, S.D.; Young, J.P. Resonance ionization spectroscopy and one-atom detection. Rev. Mod. Phys. 1979, 51, 767–819. [Google Scholar] [CrossRef]
- Letokhov, V.S.; Mishin, V.I. Highly selective multistep ionization of atoms by laser radiation. Opt. Commun. 1979, 29, 168–171. [Google Scholar] [CrossRef]
- Raeder, S.; Kneip, N.; Reich, T.; Studer, D.; Trautmann, N.; Wendt, K. Recent developments in resonance ionization mass spectrometry for ultra-trace analysis of actinide elements. Radiochim. Acta 2019, 107, 645–652. [Google Scholar] [CrossRef]
- Köhler, S.; Erdmann, N.; Nunnemann, M.; Herrmann, G.; Huber, G.; Kratz, J.V.; Passler, G.; Trautmann, N. First experimental determination of the ionization potentials of berkelium and californium. Chem. Int. Ed. 1996, 35, 2856–2858. [Google Scholar] [CrossRef]
- Fritzsche, S. Level structure and properties of open f-shell elements. Atoms 2022, 10, 7. [Google Scholar] [CrossRef]
- Naubereit, P.; Gottwald, T.; Studer, D.; Wendt, K. Excited atomic energy levels in protactinium by resonance ionization spectroscopy. Phys. Rev. A 2018, 98, 022505. [Google Scholar] [CrossRef]
- Studer, D.; Heinitz, S.; Heinke, R.; Naubereit, P.; Dressler, R.; Guerrero, C.; Köster, U.; Schumann, D.; Wendt, K. Atomic transitions and the first ionization potential of promethium determined by laser spectroscopy. Phys. Rev. A 2019, 99, 062513. [Google Scholar] [CrossRef]
- Kieck, T.; Biebricher, S.; Düllmann, C.E.; Wendt, K. Optimization of a laser ion source for 163Ho isotope separation. Rev. Sci. Instrum. 2019, 90, 053304. [Google Scholar] [CrossRef]
- Eichler, B.; Hübener, S.; Erdmann, N.; Eberhardt, K.; Funk, H.; Herrmann, G.; Köhler, S.; Trautmann, N.; Passler, G.; Urban, F.-J. An atomic beam source for actinide elements: Concept and realization. Radiochim. Acta 1997, 79, 221–234. [Google Scholar] [CrossRef][Green Version]
- Raiwa, M.; Büchner, S.; Kneip, N.; Weiß, M.; Hanemann, P.; Fraatz, P.; Heller, M.; Bosco, H.; Weber, F.; Wendt, K.; et al. Actinide imaging in environmental hot particles from Chernobyl by rapid spatially resolved resonant laser secondary neutral mass spectrometry. Spectrochim. Acta B 2022, 190, 106377. [Google Scholar] [CrossRef]
- King, G.C.; Read, F.H.; Imhof, R.E. The measurement of molecular lifetimes by the photon-photon delayed coincidence method. J. Phys. B 1975, 8, 665–673. [Google Scholar] [CrossRef]
- Schneider, F.; Chrysalidis, K.; Dorrer, H.; Düllmann, C.E.; Eberhardt, K.; Haas, R.; Kieck, T.; Mokry, C.; Naubereit, P.; Schmidt, S.; et al. Resonance ionization of holmium for ion implantation in microcalorimeters. Nucl. Instrum. Methods Phys. Res. B 2016, 376, 388–392. [Google Scholar] [CrossRef]
- Fano, U. Effects of configuration interaction on intensities and phase shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Fano, U.; Theodosiou, C.E.; Dehmer, J.L. Electron-optical properties of atomic fields. Rev. Mod. Phys. 1976, 48, 49–68. [Google Scholar] [CrossRef]
- Birge, R.T. Probable values of the general physical constants. Rev. Mod. Phys. 1929, 1, 1–73. [Google Scholar] [CrossRef]
- Bodnar, O.; Elster, C. On the adjustment of inconsistent data using the Birge ratio. Metrologia 2014, 51, 516–521. [Google Scholar] [CrossRef]
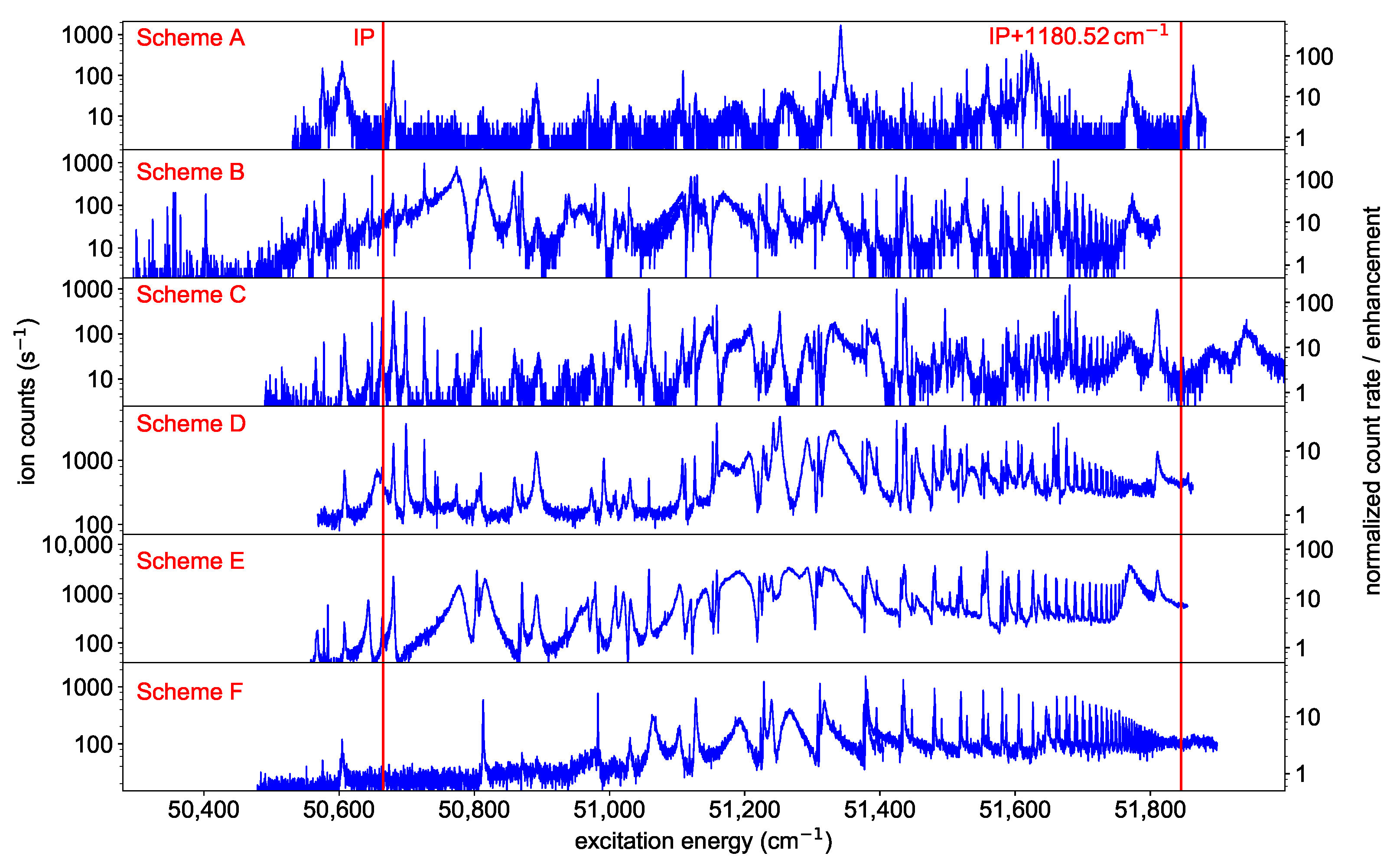
| (cm) | n | () | IP () | |||
|---|---|---|---|---|---|---|
| 23,994.44(1) | 41–70 | 3.64(2) | - | 50,666.75(11) | 50,666.75(11) | 0.99 |
| 23,994.44(1) | 29–39 * | 5.42(4) | - | 51,847.04(34) | 50,666.52(34) | 0.41 |
| 24,388.79(1) | 32–42 | 5.42(1) | - | 51,847.04(16) | 50,666.52(16) | 0.45 |
| 26,408.28(1) | 30–42 | 3.74(2) | - | 51,847.13(24) | 50,666.61(24) | 0.35 |
| 26,408.28(1) | 28, 30–47 | 5.44(1) | - | 51,847.14(16) | 50,666.62(16) | 0.25 |
| 27,294.46(1) | 41–66 | 3.61(2) | - | 50,666.78(13) | 50,666.78(13) | 0.39 |
| 27,294.46(1) | 21–40, 42–56 * | 3.70(4) | −3.6(13) | 51,847.28(8) | 50,666.76(8) | 1.42 |
| 27,779.16(1) | 18–58 * | 3.72(1) | −4.5(6) | 51,847.42(8) | 50,666.90(8) | 0.71 |
| 27,779.16(1) | 21–43 * | 5.46(1) | −10.0(15) | 51,847.17(16) | 50,666.65(16) | 0.68 |
| weighted mean value | 50,666.76(5) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, F.; Düllmann, C.E.; Gadelshin, V.; Kneip, N.; Oberstedt, S.; Raeder, S.; Runke, J.; Mokry, C.; Thörle-Pospiech, P.; Studer, D.; et al. Probing the Atomic Structure of Californium by Resonance Ionization Spectroscopy. Atoms 2022, 10, 51. https://doi.org/10.3390/atoms10020051
Weber F, Düllmann CE, Gadelshin V, Kneip N, Oberstedt S, Raeder S, Runke J, Mokry C, Thörle-Pospiech P, Studer D, et al. Probing the Atomic Structure of Californium by Resonance Ionization Spectroscopy. Atoms. 2022; 10(2):51. https://doi.org/10.3390/atoms10020051
Chicago/Turabian StyleWeber, Felix, Christoph Emanuel Düllmann, Vadim Gadelshin, Nina Kneip, Stephan Oberstedt, Sebastian Raeder, Jörg Runke, Christoph Mokry, Petra Thörle-Pospiech, Dominik Studer, and et al. 2022. "Probing the Atomic Structure of Californium by Resonance Ionization Spectroscopy" Atoms 10, no. 2: 51. https://doi.org/10.3390/atoms10020051
APA StyleWeber, F., Düllmann, C. E., Gadelshin, V., Kneip, N., Oberstedt, S., Raeder, S., Runke, J., Mokry, C., Thörle-Pospiech, P., Studer, D., Trautmann, N., & Wendt, K. (2022). Probing the Atomic Structure of Californium by Resonance Ionization Spectroscopy. Atoms, 10(2), 51. https://doi.org/10.3390/atoms10020051






