Inelastic Processes in Strontium-Hydrogen Collisions and Their Impact on Non-LTE Calculations
Abstract
1. Introduction
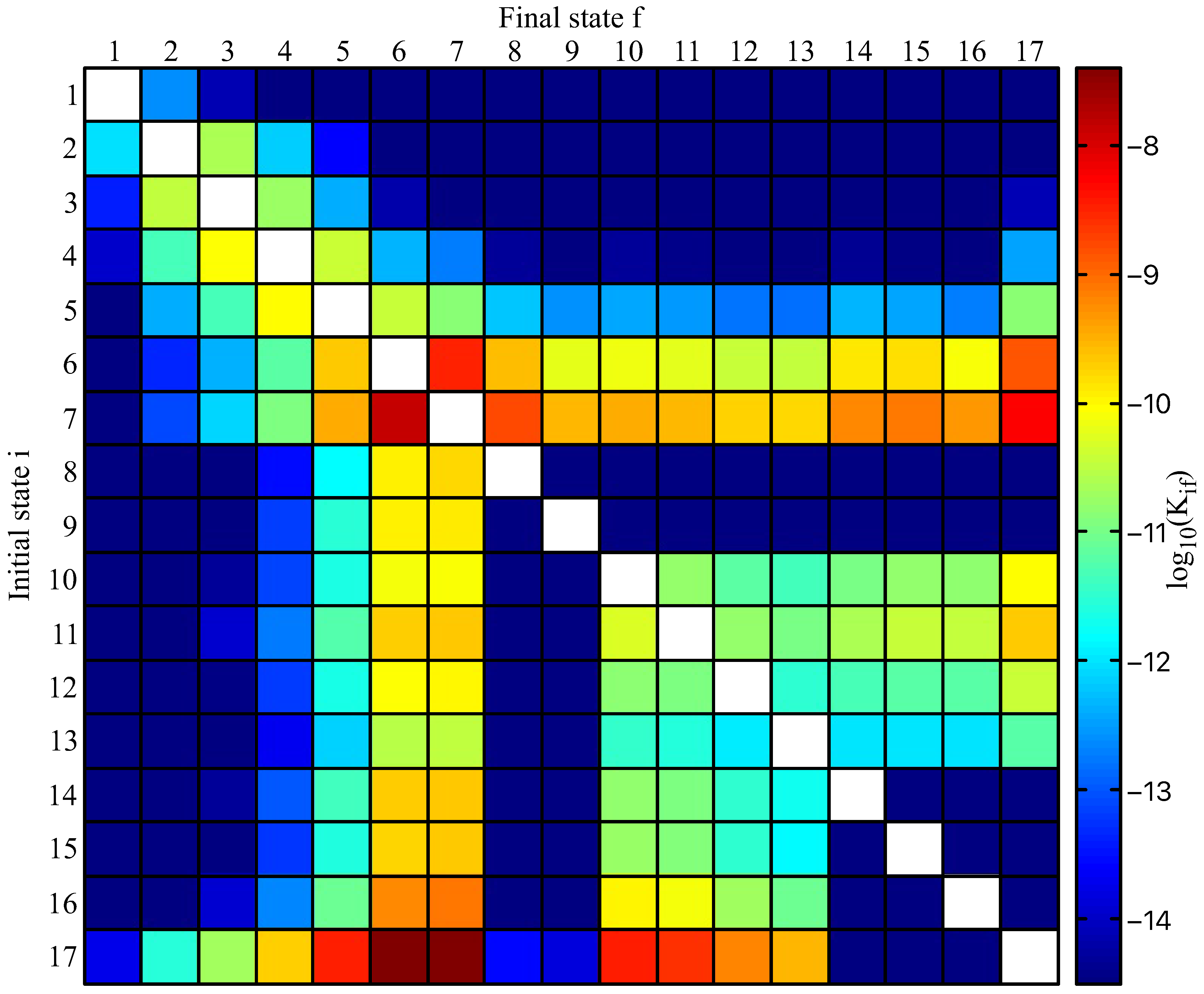
2. Atomic Data Calculations
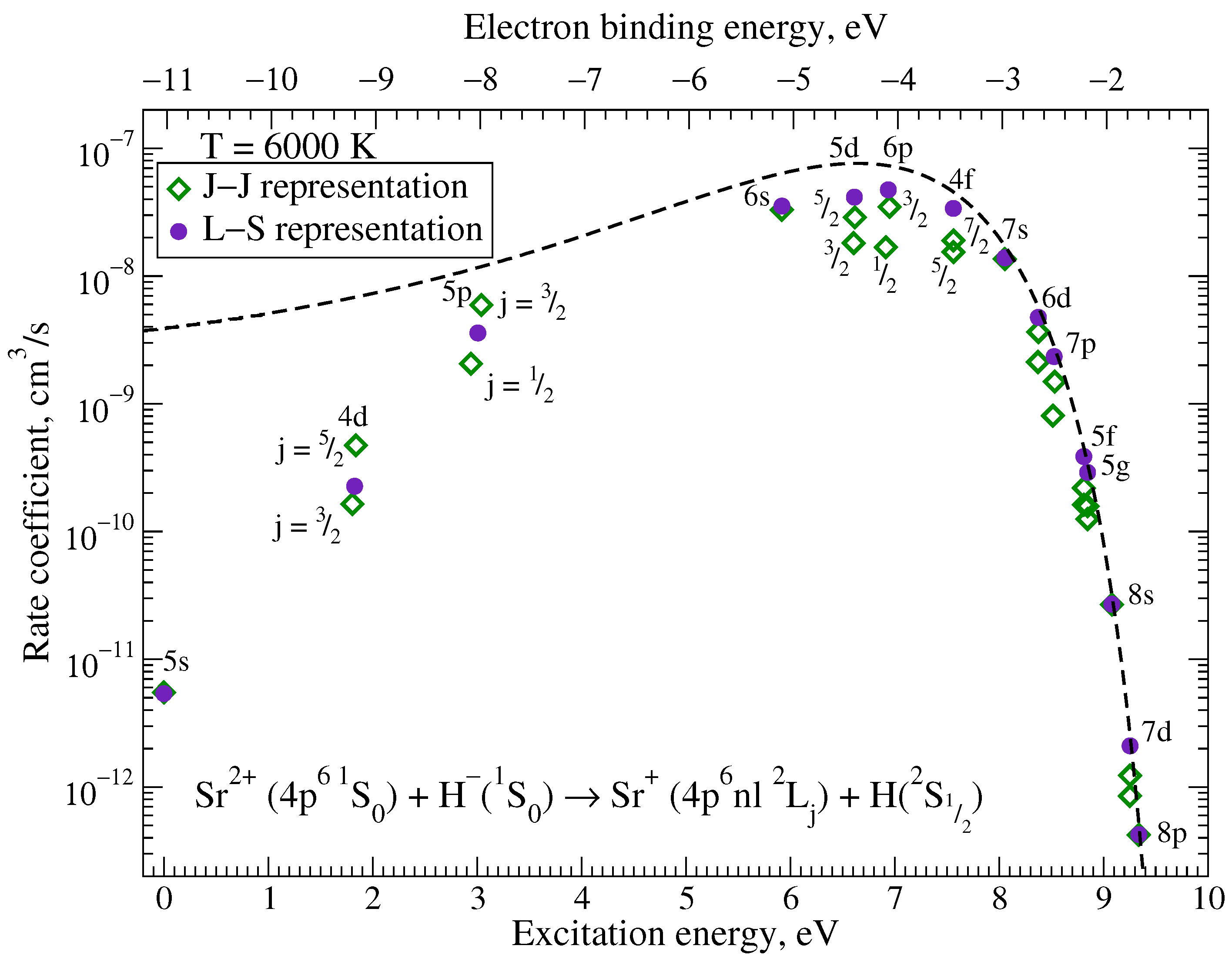
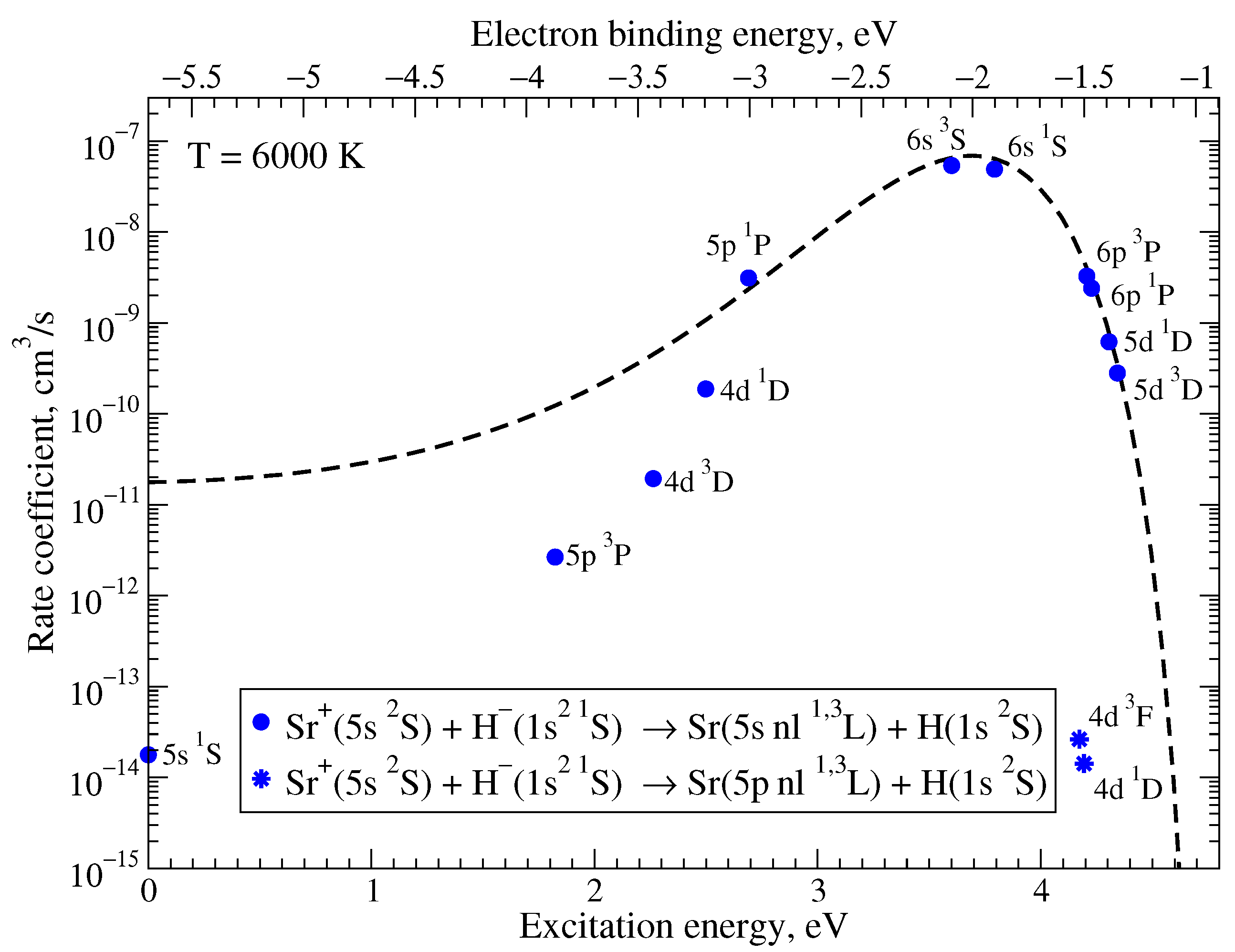
2.1. Processes in Sr + H and Sr + H Collisions
2.2. Processes in Sr + H and Sr + H Collisions
3. Non-LTE Calculations for Sr ii
3.1. Model Atom of Sr ii and Method of Calculations
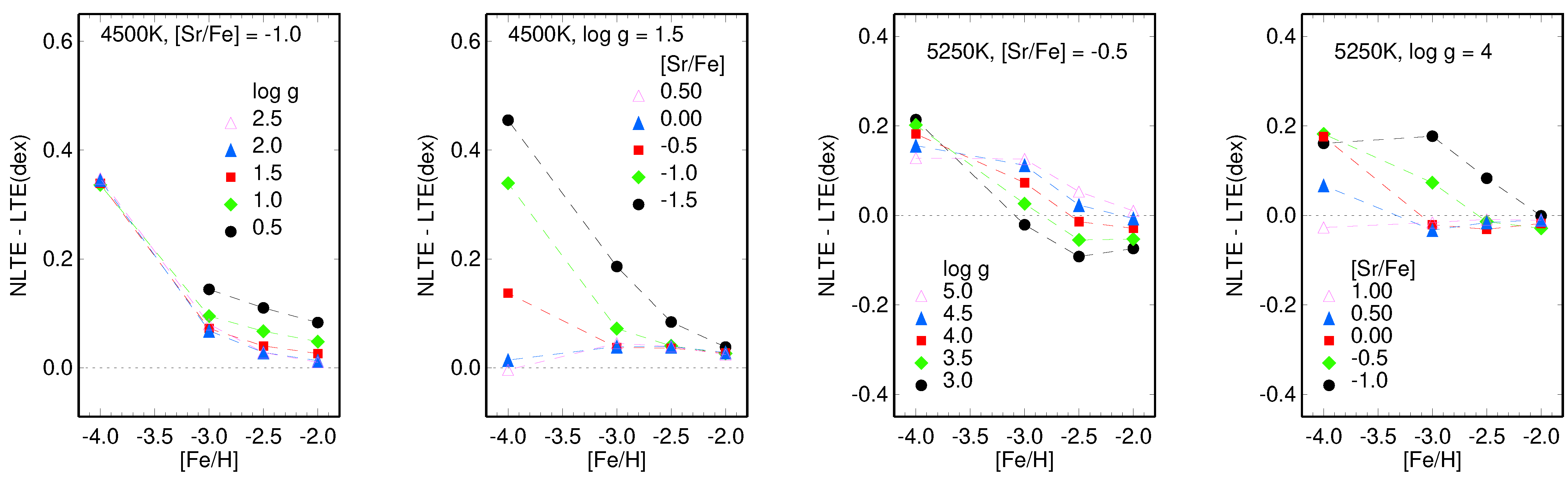
3.2. Non-LTE Effects for Lines of Sr ii
- Grid I:
- = 5000 to 6500 K, with a step of 250 K; = 3.0 to 5.0, with a step of 0.5; [Fe/H] = , , , and ; [Sr/Fe] = to +1.0, with a step of 0.5.
- Grid II:
- = 4000 to 5000 K, with a step of 250 K; = 0.5 to 2.5, with a step of 0.5; [Fe/H] = , , , and ; [Sr/Fe] = to +0.5, with a step of 0.5.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LTE | Local thermodynamic equilibrium |
| NLTE | Non-local thermodynamic equilibrium |
| SN | Supernova |
| dSph galaxy | dwarf spheroidal galaxy |
Appendix A
| k | Scattering Channels | Asymptotic |
|---|---|---|
| Energies (eV) | ||
| 1 | 0.0 | |
| 2 | 1.8047016 | |
| 3 | 1.8394593 | |
| 4 | 2.9403088 | |
| 5 | 3.0396772 | |
| 6 | 5.9185754 | |
| 7 | 6.6066604 | |
| 8 | 6.6174048 | |
| 9 | 6.91456 | |
| 10 | 6.95029 | |
| 11 | 7.561801 | |
| 12 | 7.561962 | |
| 13 | 8.0545218 | |
| 14 | 8.3717688 | |
| 15 | 8.3767629 | |
| 16 | 8.515153 | |
| 17 | 8.532235 | |
| 18 | 8.811036 | |
| 19 | 8.811036 | |
| 20 | 8.847240 | |
| 21 | 8.847240 | |
| 22 | 9.080243 | |
| 23 | 9.251862 | |
| 24 | 9.254565 | |
| 25 | 9.337473 | |
| 26 | 9.491412 | |
| 27 | 9.491412 | |
| 28 | 9.514262 | |
| 29 | 9.514262 | |
| 30 | 9.653112 | |
| 31 | 10.2762764 |
| k | Scattering Channels | Asymptotic |
|---|---|---|
| Energies (eV) | ||
| 1 | 0.0 | |
| 2 | 1.8228877 | |
| 3 | 2.2631734 | |
| 4 | 2.4982425 | |
| 5 | 2.6902652 | |
| 6 | 3.600349 | |
| 7 | 3.7929029 | |
| 8 | 4.1725763 | |
| 9 | 4.1940009 | |
| 10 | 4.2061469 | |
| 11 | 4.2276633 | |
| 12 | 4.3056546 | |
| 13 | 4.3431318 | |
| 14 | 4.4051164 | |
| 15 | 4.5181299 | |
| 16 | 4.6400683 | |
| 17 | 4.9408674 |
References
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef]
- Bisterzo, S.; Travaglio, C.; Gallino, R.; Wiescher, M.; Käppeler, F. Galactic Chemical Evolution and Solar s-process Abundances: Dependence on the 13C-pocket Structure. Astrophys. J. 2014, 787, 10. [Google Scholar] [CrossRef]
- Sneden, C.; Cowan, J.J.; Gallino, R. Neutron-Capture Elements in the Early Galaxy. Annu. Rev. Astron. Astrophys. 2008, 46, 241–288. [Google Scholar] [CrossRef]
- McWilliam, A.; Preston, G.W.; Sneden, C.; Searle, L. Spectroscopic Analysis of 33 of the Most Metal Poor Stars. II. Astron. J. 1995, 109, 2757. [Google Scholar] [CrossRef]
- Honda, S.; Aoki, W.; Kajino, T.; Ando, H.; Beers, T.C.; Izumiura, H.; Sadakane, K.; Takada-Hidai, M. Spectroscopic Studies of Extremely Metal-Poor Stars with the Subaru High Dispersion Spectrograph. II. The r-Process Elements, Including Thorium. Astrophys. J. 2004, 607, 474–498. [Google Scholar] [CrossRef]
- François, P.; Depagne, E.; Hill, V.; Spite, M.; Spite, F.; Plez, B.; Beers, T.C.; Andersen, J.; James, G.; Barbuy, B.; et al. First stars. VIII. Enrichment of the neutron-capture elements in the early Galaxy. Astron. Astrophys. 2007, 476, 935–950. [Google Scholar] [CrossRef]
- Mashonkina, L.; Jablonka, P.; Sitnova, T.; Pakhomov, Y.; North, P. The formation of the Milky Way halo and its dwarf satellites; a NLTE-1D abundance analysis. II. Early chemical enrichment. Astron. Astrophys. 2017, 608, A89. [Google Scholar] [CrossRef]
- Barklem, P.S.; Christlieb, N.; Beers, T.C.; Hill, V.; Bessell, M.S.; Holmberg, J.; Marsteller, B.; Rossi, S.; Zickgraf, F.J.; Reimers, D. The Hamburg/ESO R-process enhanced star survey (HERES). II. Spectroscopic analysis of the survey sample. Astron. Astrophys. 2005, 439, 129–151. [Google Scholar] [CrossRef]
- Rizzuti, F.; Cescutti, G.; Matteucci, F.; Chieffi, A.; Hirschi, R.; Limongi, M. The contribution from rotating massive stars to the enrichment in Sr and Ba of the Milky Way. Mon. Not. R. Astron. Soc. 2019, 489, 5244–5255. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Yakovleva, S.A. Data on inelastic processes in low-energy collisions of barium atoms and ions with hydrogen atoms and anions. Mon. Not. R. Astron. Soc. 2018, 478, 3952–3960. [Google Scholar] [CrossRef]
- Mashonkina, L.I.; Belyaev, A.K. Even-to-Odd Barium Isotope Ratio in Selected Galactic Halo Stars. Astron. Lett. 2019, 45, 341–352. [Google Scholar] [CrossRef]
- Gallagher, A.J.; Bergemann, M.; Collet, R.; Plez, B.; Leenaarts, J.; Carlsson, M.; Yakovleva, S.A.; Belyaev, A.K. Observational constraints on the origin of the elements. II. 3D non-LTE formation of Ba II lines in the solar atmosphere. Astron. Astrophys. 2020, 634, A55. [Google Scholar] [CrossRef]
- Belyakova, E.V.; Mashonkina, L.I. Statistical equilibrium of Sr II in the atmospheres of F and G stars. Astron. Rep. 1997, 41, 530–536. [Google Scholar]
- Andrievsky, S.M.; Spite, F.; Korotin, S.A.; François, P.; Spite, M.; Bonifacio, P.; Cayrel, R.; Hill, V. NLTE strontium abundance in a sample of extremely metal poor stars and the Sr/Ba ratio in the early Galaxy. Astron. Astrophys. 2011, 530, A105. [Google Scholar] [CrossRef]
- Bergemann, M.; Hansen, C.J.; Bautista, M.; Ruchti, G. NLTE analysis of Sr lines in spectra of late-type stars with new R-matrix atomic data. Astron. Astrophys. 2012, 546, A90. [Google Scholar] [CrossRef]
- Steenbock, W.; Holweger, H. Statistical equilibrium of lithium in cool stars of different metallicity. Astron. Astrophys. 1984, 130, 319–323. [Google Scholar]
- Drawin, H.W. Influence of atom-atom collisions on the collisional-radiative ionization and recombination coefficients of hydrogen plasmas. Z. Phys. 1969, 225, 483–493. [Google Scholar] [CrossRef]
- Barklem, P.S.; Belyaev, A.K.; Guitou, M.; Feautrier, N.; Gadéa, F.X.; Spielfiedel, A. On inelastic hydrogen atom collisions in stellar atmospheres. Astron. Astrophys. 2011, 530, A94. [Google Scholar] [CrossRef]
- Aymar, M.; Dulieu, O. The electronic structure of the alkaline-earth-atom (Ca, Sr, Ba) hydride molecular ions. J. Phys. At. Mol. Opt. Phys. 2012, 45, 215103. [Google Scholar] [CrossRef]
- Mejrissi, L.; Habli, H.; Oujia, B.; Gadéa, F.X. Charge transfer ionic character illustration for strontium hydride ion through a diabatic investigation. Int. J. Quantum Chem. 2018, 118, e25680. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Voronov, Y.; Yakovleva, S. Inelastic processes in calcium-hydrogen ionic collisions with account for fine structure. Phys. Rev. A 2019, 100, 062710. [Google Scholar] [CrossRef]
- Olson, R.E.; Smith, F.T.; Bauer, E. Estimation of the Coupling Matrix Elements for One-Electron Transfer Systems. Appl. Opt. 1971, 10, 1848. [Google Scholar] [CrossRef] [PubMed]
- Belyaev, A.K. Model approach for low-energy inelastic atomic collisions and application to Al+H and Al+ + H−. Phys. Rev. A 2013, 88, 052704. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Yakovleva, S.A.; Barklem, P.S. Inelastic silicon-hydrogen collision data for non-LTE applications in stellar atmospheres. Astron. Astrophys. 2014, 572, A103. [Google Scholar] [CrossRef]
- Yakovleva, S.A.; Voronov, Y.V.; Belyaev, A.K. Atomic data on inelastic processes in low-energy beryllium-hydrogen collisions. Astron. Astrophys. 2016, 593, A27. [Google Scholar] [CrossRef][Green Version]
- Landau, L.D. Zur Theorie der Energieübertragung bei Stössen. Phys. Z. Sowietunion 1932, 1, 88. [Google Scholar]
- Landau, L.D. Zur Theorie der Energieübertragung bei Stössen. II. Phys. Z. Sowietunion 1932, 2, 46. [Google Scholar]
- Zener, C. Non-adiabatic crossing of energy levels. Proc. R. Soc. A 1932, 137, 696. [Google Scholar]
- Belyaev, A.K.; Lebedev, O.V. Nonadiabatic nuclear dynamics of atomic collisions based on branching classical trajectories. Phys. Rev. A 2011, 84, 014701. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Yakovleva, S.A. Estimating Inelastic Heavy-Particle-Hydrogen Collision Data. II. Simplified Model for Ionic Collisions and Application to Barium-Hydrogen Ionic Collisions. Astron. Astrophys. 2017, 608, A33. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.9); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2021. Available online: https://physics.nist.gov/asd (accessed on 23 January 2022).
- Belyaev, A.K.; Yakovleva, S.A. Estimating Inelastic Heavy-Particle-Hydrogen Collision Data. I. Simplified Model and Application to Potassium-Hydrogen Collisions. Astron. Astrophys. 2017, 606, A147. [Google Scholar] [CrossRef]
- Bautista, M.A.; Gull, T.R.; Ishibashi, K.; Hartman, H.; Davidson, K. Excitation of Srii lines in Eta Carinae. Mon. Not. R. Astron. Soc. 2002, 331, 875–879. [Google Scholar] [CrossRef]
- Reader, J.; Corliss, C.H.; Wiese, W.L.; Martin, G.A. Wavelengths and Transition Probabilities for Atoms and Atomic Ions: Part 1. Wavelengths, Part 2. Transition Probabilities; NIST: Gaithersburg, MD, USA, 1980.
- Lindgård, A.; Nielson, S.E. Transition Probabilities for the Alkali Isoelectronic Sequences. At. Data Nucl. Data Tables 1977, 19, 533. [Google Scholar] [CrossRef]
- Peach, G. A revised general formula for the calculation of atomic photoionization cross sections. Mem. R. Astron. Soc. 1967, 71, 13. [Google Scholar]
- van Regemorter, H. Rate of Collisional Excitation in Stellar Atmospheres. Astrophys. J. 1962, 136, 906. [Google Scholar] [CrossRef]
- Seaton, M.J. The Theory of Excitation and Ionization by Electron Impact. In Atomic and Molecular Processes; Bates, D.R., Ed.; Academic Press: New York, NY, USA, 1962; p. 375. [Google Scholar]
- Butler, K.; Giddings, J. Newsletter on Analysis of Astronomical Spectra; University of London: London, UK, 1985; No. 9. [Google Scholar]
- Mashonkina, L.; Gehren, T.; Shi, J.R.; Korn, A.J.; Grupp, F. A non-LTE study of neutral and singly-ionized iron line spectra in 1D models of the Sun and selected late-type stars. Astron. Astrophys. 2011, 528, A87. [Google Scholar] [CrossRef]
- Gustafsson, B.; Edvardsson, B.; Eriksson, K.; Jorgensen, U.G.; Nordlund, Å.; Plez, B. A grid of MARCS model atmospheres for late-type stars I. Methods and general properties. Astron. Astrophys. 2008, 486, 951–970. [Google Scholar] [CrossRef]
- Barklem, P.S.; O’Mara, B.J. Broadening of lines of Beii, Srii and Baii by collisions with hydrogen atoms and the solar abundance of strontium. Mon. Not. R. Astron. Soc. 2000, 311, 535–540. [Google Scholar] [CrossRef]
| 1 | http://kurucz.harvard.edu/atoms/3801/ (accessed on 1 October 1996). |
| 2 | http://marcs.astro.uu.se (accessed on 1 August 2019). |
| 3 | https://physics.nist.gov/PhysRefData/ASD (accessed on 1 October 1996). |
| 4 | http://www.inasan.ru/~lima/ (accessed on 21 August 2021). |

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakovleva, S.A.; Belyaev, A.K.; Mashonkina, L.I. Inelastic Processes in Strontium-Hydrogen Collisions and Their Impact on Non-LTE Calculations. Atoms 2022, 10, 33. https://doi.org/10.3390/atoms10010033
Yakovleva SA, Belyaev AK, Mashonkina LI. Inelastic Processes in Strontium-Hydrogen Collisions and Their Impact on Non-LTE Calculations. Atoms. 2022; 10(1):33. https://doi.org/10.3390/atoms10010033
Chicago/Turabian StyleYakovleva, Svetlana A., Andrey K. Belyaev, and Lyudmila I. Mashonkina. 2022. "Inelastic Processes in Strontium-Hydrogen Collisions and Their Impact on Non-LTE Calculations" Atoms 10, no. 1: 33. https://doi.org/10.3390/atoms10010033
APA StyleYakovleva, S. A., Belyaev, A. K., & Mashonkina, L. I. (2022). Inelastic Processes in Strontium-Hydrogen Collisions and Their Impact on Non-LTE Calculations. Atoms, 10(1), 33. https://doi.org/10.3390/atoms10010033







