Parameter Inference for Coalescing Massive Black Hole Binaries Using Deep Learning
Abstract
:1. Introduction
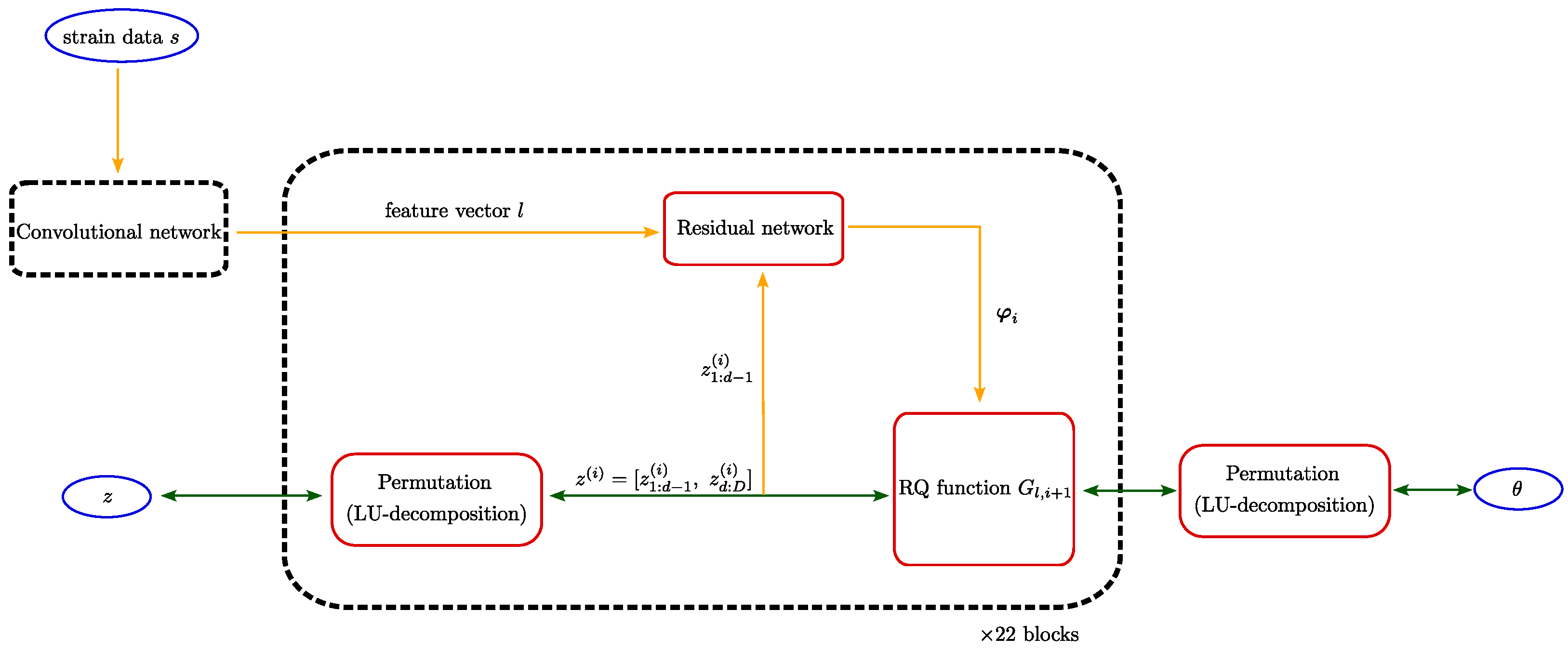
2. Model
3. Datasets
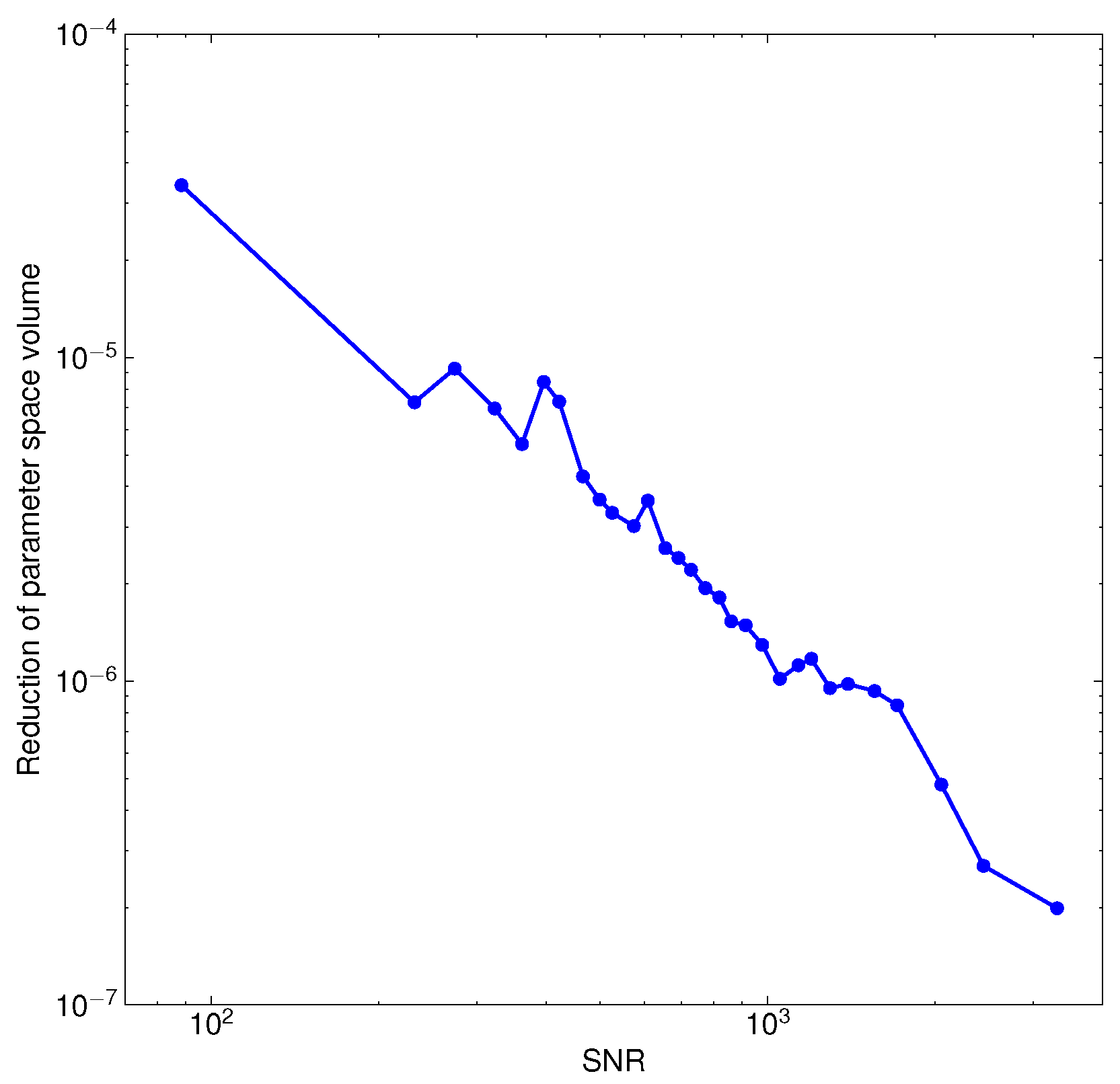
4. Results
5. Summary and Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Hu, W.-R.; Wu, Y.-L. The Taiji Program in Space for Gravitational Wave Physics and the Nature of Gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Luo, J.; Chen, L.-S.; Duan, H.-Z.; Gong, Y.-G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A Space-borne Gravitational Wave Detector. Class. Quantum Gravity 2016, 33, 035010. [Google Scholar] [CrossRef]
- Klein, A.; Barausse, E.; Sesana, A.; Petiteau, A.; Berti, E.; Babak, S.; Gair, J.; Aoudia, S.; Hinder, I.; Ohme, F.; et al. Science with the Space-based Interferometer eLISA: Supermassive Black Hole Binaries. Phys. Rev. D 2016, 93, 024003. [Google Scholar] [CrossRef]
- Owen, B.J.; Sathyaprakash, B.S. Matched Filtering of Gravitational Waves from Inspiraling Compact Binaries: Computational Cost and Template Placement. Phys. Rev. D 1999, 60, 022002. [Google Scholar] [CrossRef]
- Allen, B.; Anderson, W.G.; Brady, P.R.; Brown, D.A.; Creighton, J.D. FINDCHIRP: An Algorithm for Detection of Gravitational Waves from Inspiraling Compact Binaries. Phys. Rev. D 2012, 85, 122006. [Google Scholar] [CrossRef]
- Abbott, B.; Jawahar, S.; Lockerbie, N.; Tokmakov, K. GW150914: First Results from the Search for Binary Black Hole Coalescence with Advanced LIGO. Phys. Rev. D 2016, 93, 122003. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Tinto, M.; Dhurandhar, S.V. Time-Delay Interferometry. Living Rev. Relativ. 2014, 17, 1. [Google Scholar] [CrossRef]
- Cornish, N.J.; Crowder, J. LISA Data Analysis Using Markov Chain Monte Carlo Methods. Phys. Rev. D 2005, 72, 043005. [Google Scholar] [CrossRef]
- Littenberg, T.B.; Cornish, N.J.; Lackeos, K.; Robson, T. Global Analysis of the Gravitational Wave Signal from Galactic Binaries. Phys. Rev. D 2020, 101, 123021. [Google Scholar] [CrossRef]
- Littenberg, T.B.; Cornish, N.J. Prototype Global Analysis of LISA Data with Multiple Source Types. Phys. Rev. D 2023, 107, 063004. [Google Scholar] [CrossRef]
- George, D.; Huerta, E.A. Deep Learning for Real-time Gravitational Wave Detection and Parameter Estimation: Results with Advanced LIGO Data. Phys. Lett. B 2018, 778, 64. [Google Scholar] [CrossRef]
- Green, S.R.; Simpson, C.; Gair, J. Gravitational-wave Parameter Estimation with Autoregressive Neural Network Flows. Phys. Rev. D 2020, 102, 104057. [Google Scholar] [CrossRef]
- Krastev, P.G.; Gill, K.; Villar, V.A.; Berger, E. Detection and Parameter Estimation of Gravitational Waves from Binary Neutron-star Mergers in Real LIGO Data Using Deep Learning. Phys. Lett. B 2021, 815, 136161. [Google Scholar] [CrossRef]
- Green, S.R.; Gair, J. Complete Parameter Inference for GW150914 Using Deep Learning. Mach. Learn. Sci. Technol. 2021, 2, 03LT01. [Google Scholar] [CrossRef]
- Dax, M.; Green, S.R.; Gair, J.; Macke, J.H.; Buonanno, A.; Schölkopf, B. Real-time Gravitational Wave Science with Neural Posterior Estimation. Phys. Rev. Lett. 2021, 127, 241103. [Google Scholar] [CrossRef]
- Shen, H.; Huerta, E.; O’Shea, E.; Kumar, P.; Zhao, Z. Statistically-informed Deep Learning for Gravitational Wave Parameter Estimation. Mach. Learn. Sci. Technol. 2021, 3, 015007. [Google Scholar] [CrossRef]
- Schmidt, S.; Breschi, M.; Gamba, R.; Pagano, G.; Rettegno, P.; Riemenschneider, G.; Bernuzzi, S.; Nagar, A.; Del Pozzo, W. Machine Learning Gravitational Waves from Binary Black Hole Mergers. Phys. Rev. D 2021, 103, 043020. [Google Scholar] [CrossRef]
- Gabbard, H.; Messenger, C.; Heng, I.S.; Tonolini, F.; Murray-Smith, R. Bayesian Parameter Estimation Using Conditional Variational Autoencoders for Gravitational-wave Astronomy. Nat. Phys. 2022, 18, 112. [Google Scholar] [CrossRef]
- Langendorff, J.; Kolmus, A.; Janquart, J.; Van Den Broeck, C. Normalizing Flows as an Avenue to Studying Overlapping Gravitational Wave Signals. Phys. Rev. Lett. 2023, 130, 171402. [Google Scholar] [CrossRef]
- Chua, A.J.; Vallisneri, M. Learning Bayesian Posteriors with Neural Networks for Gravitational-wave Inference. Phys. Rev. Lett. 2020, 124, 041102. [Google Scholar] [CrossRef]
- Rezende, D.; Mohamed, S. Variational Inference with Normalizing Flows. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1530–1538. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based Learning Applied to Cocument Recognition. Proc. IEEE 1998, 86, 2278. [Google Scholar] [CrossRef]
- Durkan, C.; Bekasov, A.; Murray, I.; Papamakarios, G. Neural Spline Flows. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 7509–7520. [Google Scholar]
- Oliva, J.; Dubey, A.; Zaheer, M.; Poczos, B.; Salakhutdinov, R.; Xing, E.; Schneider, J. Transformation autoregressive networks. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, Stockholm, Sweden, 10–15 July 2018; pp. 3895–3904. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Annual Conference on Neural Information Processing Systems 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 8024–8035. [Google Scholar]
- Durkan, C.; Bekasov, A.; Murray, I.; Papamakarios, G. Nflows: Normalizing Flows in PyTorch; Zenodo: Geneva, Switzerland, 2020; p. 4296287. [Google Scholar]
- lfigw: Likelihood-Free Inference for Gravitational Waves. Available online: https://github.com/stephengreen/lfi-gw (accessed on 1 November 2022).
- Husa, S.; Khan, S.; Hannam, M.; Pürrer, M.; Ohme, F.; Forteza, X.J.; Bohé, A. Frequency-domain Gravitational Waves from Nonprecessing Black-hole Binaries. I. New Numerical Waveforms and Anatomy of the Signal. Phys. Rev. D 2016, 93, 044006. [Google Scholar] [CrossRef]
- Khan, S.; Husa, S.; Hannam, M.; Ohme, F.; Pürrer, M.; Forteza, X.J.; Bohé, A. Frequency-domain Gravitational Waves from Nonprecessing Black-hole Binaries. II. A Phenomenological Model for the Advanced Detector Era. Phys. Rev. D 2016, 93, 044007. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.; Barreiro, R.; Bartlett, J.; Bartolo, N.; et al. Planck 2015 Results. XIII. Cosmological Parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Prince, T.A.; Tinto, M.; Larson, S.L.; Armstrong, J. LISA Optimal Sensitivity. Phys. Rev. D 2002, 66, 122002. [Google Scholar] [CrossRef]
- The LISA Science Study Team, ESA-L3-EST-SCI-RS-001. 2018. Available online: https://atrium.in2p3.fr/f5a78d3e-9e19-47a5-aa11-51c81d370f5f (accessed on 1 November 2022).
- Babak, S.; Petiteau, A. LISA Data Challenge Manual. 2018. Available online: https://lisa-ldc.lal.in2p3.fr/static/data/pdf/LDC-manual-002.pdf (accessed on 1 November 2022).
- Nitz, A.; Harry, I.; Brown, D.; Biwer, C.M.; Willis, J.; Canton, T.D.; Capano, C.; Dent, T.; Pekowsky, L.; Williamson, A.R.; et al. 2021. Available online: https://gwastro/pycbc (accessed on 1 November 2022).
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic Gradient Descent with Warm Restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Massey, F.J., Jr. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68. [Google Scholar] [CrossRef]
- LISA Consortium’s LDC Working Group, LISA Data Challenges. 2019. Available online: https://lisa-ldc.lal.in2p3.fr (accessed on 1 November 2022).
- Cornish, N.J. Low Latency Detection of Massive Black Hole Binaries. Phys. Rev. D 2022, 105, 044007. [Google Scholar] [CrossRef]


| Parameter | Prior |
|---|---|
| M | |
| q | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, W.; Wang, H.; Liu, C.; Guo, Z. Parameter Inference for Coalescing Massive Black Hole Binaries Using Deep Learning. Universe 2023, 9, 407. https://doi.org/10.3390/universe9090407
Ruan W, Wang H, Liu C, Guo Z. Parameter Inference for Coalescing Massive Black Hole Binaries Using Deep Learning. Universe. 2023; 9(9):407. https://doi.org/10.3390/universe9090407
Chicago/Turabian StyleRuan, Wenhong, He Wang, Chang Liu, and Zongkuan Guo. 2023. "Parameter Inference for Coalescing Massive Black Hole Binaries Using Deep Learning" Universe 9, no. 9: 407. https://doi.org/10.3390/universe9090407
APA StyleRuan, W., Wang, H., Liu, C., & Guo, Z. (2023). Parameter Inference for Coalescing Massive Black Hole Binaries Using Deep Learning. Universe, 9(9), 407. https://doi.org/10.3390/universe9090407






