The Galactic Population of Pulsar Wind Nebulae and the Contribution of Its Unresolved Component to the Diffuse High-Energy Gamma-ray Emission

Abstract

In this work, we provide a phenomenological description of the population of galactic TeV pulsar wind nebulae (PWNe) based on suitable assumptions for their space and luminosity distribution. We constrain the general features of this population by assuming that it accounts for the majority of bright sources observed by H.E.S.S. Namely, we determine the maximal luminosity and fading time of PWNe (or, equivalently, the initial period and magnetic field of the pulsar powering the observed emission) by performing a statistical analysis of bright sources in the H.E.S.S. galactic plane survey. This allows us to estimate the total luminosity and flux produced by galactic TeV PWNe. We also evaluate the cumulative emission from PWNe that cannot be resolved by H.E.S.S., showing that this contribution can be as large as ∼40% of the total flux from resolved sources. We argue that also in the GeV domain, a relevant fraction of this population cannot be resolved by Fermi-LAT, providing a non-negligible contribution to the large-scale diffuse emission in the inner galaxy. This additional component could naturally account for a large part of the spectral index variation observed by Fermi-LAT, weakening the evidence of cosmic ray spectral hardening in the inner galaxy. Finally, the same result is obtained for PeV energy, for which the sum of the diffuse component, due to unresolved PWNe, and the truly diffuse emission well saturates the recent Tibet AS-$\gamma$ data, without the need to introduce a progressive hardening of the cosmic-ray spectrum toward the galactic centre.

1. Introduction

The field of TeV $\gamma$-ray astronomy is rapidly growing thanks to the observations made by recent experiments. Imaging Atmospheric Cherenkov Telescopes (IACTs), like H.E.S.S. [1], MAGIC [2] and VERITAS [3], and air shower arrays, such as Argo-YBJ [4], Milagro [5] and HAWC [6], have provided a detailed description of the $\gamma$-ray sky in the energy range $0.1–100\mathrm{TeV}$. Tibet AS$\gamma$ [7] and LAAHSO [8] have extended our knowledge to sub-PeV energies.

The TeV energy domain is particularly interesting for galactic studies. Indeed, the universe is not transparent in terms of radiation at these energies, and the observed $\gamma$-ray signal has predominantly a galactic origin. A guaranteed source of TeV radiation is the large-scale diffuse emission produced by the interaction of cosmic rays (CRs) with ∼$\mathrm{PeV}$ energies with the gas contained in the galactic disk. The detection of this component can provide information on the CR space and energy distributions and, thus, in turn, on the CR transport in the galactic magnetic field.

In addition to diffuse emission, there exists a comparable contribution from galactic $\gamma$-ray sources that can emit radiation up to the PeV energy. The H.E.S.S. detector has presented a survey of 78 extended and point-like TeV $\gamma$-ray sources, the so-called H.E.S.S. galactic plane survey (HGPS) [9] that includes a large part of the galactic plane. Recently, many galactic sources have been observed by Tibet AS$\gamma$ [7] and HAWC [10] that emit $\gamma$ rays above ∼50 TeV. Also, LHAASO-KM2A announced the detection of 530 photons in the energy range $100\mathrm{TeV}–1.4\mathrm{PeV}$ from 12 $\gamma$-ray sources [8].

The most intriguing scenario is that the TeV galactic sky is dominated by bright sources powered by pulsar activity, such as pulsar wind nebulae (PWNe) [9,11] or TeV halos [12,13,14]. These sources are composed of magnetised plasma of electrons and positrons escaping from the energetic wind of the pulsar. The observed high-energy gamma-ray radiation is due to synchrotron or inverse Compton (IC) emission and extends from GeV to sub-PeV energy [15]. The dominance of PWNe above 100 TeV was recently published also by the HAWC collaboration [16] and discussed also in other astrophysical contexts [17]. Moreover, the LAAHSO experiment confirmed the Crab Nebula as the first detected galactic PeVatron [18], highlighting the relevance of investigating the properties of these objects.

In this paper, following the lines of our previous works on this subject [19,20,21], we discuss the general properties of this source class. By assuming that TeV emission is proportional to the pulsar spin-down power, we model the luminosity function of galactic PWNe in terms of a few parameters, namely the PWNe maximal luminosity $L_{\max }$ and fading (or spin-down) time scale ${\tau }_{\mathrm{sd}}$ (or, equivalently, the initial pulsar period $P_0$ and magnetic field $B_0$). These parameters can be constrained by using the HGPS observations, allowing us to estimate with relatively good accuracy the total luminosity and flux produced by galactic TeV PWNe. This also permits us to evaluate the cumulative emission from PWNe that cannot be resolved by H.E.S.S. This is particularly important because unresolved PWNe contribution could contaminate the large-scale diffuse signal observed at TeV by H.E.S.S. [22], Milagro [23] and LHAASO [24]. Finally, since PWNe are expected to emit also at other energies (where, however, they can be less efficiently constrained, not being the dominant source class), we investigate the implications of our findings for the interpretation of Fermi-LAT and Tibet AS$\gamma$ diffuse flux determinations in the GeV and sub-PeV energy domains.

The plan of the paper is the following. In Section 2, after a brief description of the HGPS catalogue, we introduce our model for the galactic PWNe population. In Section 3, we present the constraints on the PWNe population parameters that are obtained by fitting the latitude, longitude and flux distribution of bright sources in the HGPS catalogue. We obtain a prediction for unresolved PWNe emission in the TeV energy domain, and we review the implications of our findings for the interpretations of experimental results at GeV and sub-PeV energies. A brief summary of our results is given in Section 4. We remark that our principal goal is to review and to present in a complete and consistent framework our previous results on galactic PWNe, mainly obtained in [19,20,21]. However, this paper also includes an original part devoted to discussing and estimating the relevance of statistical fluctuations of the (discrete) PWNe population. As a result of this discussion, we are able to improve the determination of the unresolved PWNe emission in the TeV regime. The estimate for this quantity presented in Section 3 should be considered more solid than that given in [19] because it is obtained by using theoretical and experimental quantities, which are more stable with respect to statistical fluctuations.

2. Materials and Methods

2.1. The H.E.S.S. Galactic Plane Survey

The HGPS provides optimal sky coverage to study the galactic population in the TeV energy domain. Indeed, its observational window (OW) $-{110}^{\circ }\le l\le {60}^{\circ }$ and $\left|b\right|<3^{\circ }$ includes about $80\%$ of potential sources located in the galactic plane, according to PWNe and SNR distributions parameterised by [25,26], respectively. As a comparison, we report the sky coverage of other TeV gamma-ray detectors. The HAWC experiment observes the galactic sky in the angular region $0^{\circ }<l<{180}^{\circ }$ and $\left|b\right|<2^{\circ }$ for a photon median energy $E_{\gamma }=7\mathrm{TeV}$ [27]. The Argo-YBJ experiment, instead, probes the region ${40}^{\circ }<l<{100}^{\circ }$ and $\left|b\right|<5^{\circ }$ for $E_{\gamma }=600\mathrm{GeV}$ [28]. At higher energy $E_{\gamma }=15\mathrm{TeV}$, the Milagro experiment probes the regions ${30}^{\circ }<l<{110}^{\circ }$ and ${136}^{\circ }<l<{216}^{\circ }$ and for latitudes $\left|b\right|<{10}^{\circ }$ [29]. The sky regions probed by Milagro, Argo-YBJ, and HAWC include ≃20%, ≃20%, and ≃40%, respectively, of the potential sources in the galactic plane. Therefore, this makes H.E.S.S. the best choice for our purposes.

The HGPS catalogue [30] includes 78 VHE sources measured with an angular resolution of $0.{08}^{\circ }$ and a sensitivity ≃1.5% Crab flux for point-like objects. The integral flux above 1 TeV of each source is obtained from the morphology fit of flux maps, assuming a power law index of $\beta =2.3$. In our work, we adopt the same assumption to describe the spectrum of galactic PWNe in the TeV domain to be consistent with the above procedure. The value $\beta =2.3$ is compatible with the average spectral index obtained by fitting HGPS sources using a power law or a power law with an exponential cut-off.

Most of the HGPS sources can be associated either with an energetic pulsar (47 of 78) or with shell-like SNRs (24). However, the set of firmly identified sources contains only 31 objects, among which include 3 binaries, 8 SNRs, 8 composite objects, and 8 PWNe. Further, we focus on the bright sources, whose $\gamma$-ray flux (above 1 TeV) is larger than $10\%$ of the Crab nebula flux. Above this threshold, the HGPS catalogue can be considered complete [30] and consists of 32 sources. By applying this selection, we are able to perform the analysis in full generality without the need for modelling H.E.S.S. sensitivity and the source size distribution (see also the discussion in Section 3.3). Indeed, the inclusion of sources below 10% of the Crab nebula flux requires the ability to correctly describe the H.E.S.S. sensitivity that, for this range of fluxes, is a non-trivial function of the sources’ angular size and sky position.

Moreover, we remove objects which are firmly associated with SNRs (i.e., Vela Junior, RCW 86, and RX J1713.7-3946) from the analysed sample and we treat the residual 29 sources listed in Table 3 as being pulsar powered. This assumption is justified by the fact that 22 of these sources have a clear identification or a potential association with PWNe. Indeed, the considered sample contains eight firmly identified PWNe and two composite objects, showing evidence of both shell and nebular emissions. Finally, 12 of the unidentified sources were considered candidate PWNe in recent studies on the basis of new data and/or phenomenological considerations [9,10,14,31]. The average spectral index of the considered sample of 29 HGPS sources is $2.34$, consistent with our assumption $\beta =2.3$.

2.2. PWNe Galactic Distribution

We consider high-energy gamma-ray galactic sources, such as PWNe [15] or TeV Halos [12], which are deeply connected to the explosion of core-collapse SN and powered by the central pulsar. For this reason, the birth rate of these objects R can be assumed to be proportional to that of SN explosions in our galaxy, i.e., $R=\epsilon R_{\mathrm{SN}}$ with $\epsilon \le 1$ and $R_{\mathrm{SN}}=0.019{\mathrm{yr}}^{-1}$ as recently measured by [32]. We assume that the spatial and intrinsic luminosity distributions of this population can be factorised as the product

$$\frac{dN}{d^{3}rdL}=\rho \left(\mathbf{r}\right)Y\left(L\right),$$

(1)

where $\mathbf{r}$ represents the position and L is the $\gamma$-ray luminosity integrated in the energy range $1–100\mathrm{TeV}$ constrained by H.E.S.S. The function $\rho \left(\mathbf{r}\right)$ is assumed to be proportional to the pulsar distribution in the galactic plane parameterised by [25] and is normalised to one when integrated in the entire galaxy. The source density along the direction perpendicular to the galactic plane is assumed to scale as $exp\left(-\left|z\right|/H\right)$ where $H=0.2\mathrm{kpc}$ is the galactic disk thickness.

Under the hypothesis that the TeV emission is powered by pulsar activity, the luminosity function $Y\left(L\right)$ is naturally expected to have a power law behaviour as it is explained in the following. It is quite reasonable to assume that the TeV luminosity is proportional to the pulsar spin-down power, i.e.,

$$L=\lambda \dot{E}$$

(2)

where $\lambda \le 1$. For energy losses dominated by magnetic dipole radiation (braking index $n=3$), the spin-down power decreases in time according to

$$\dot{E}={\dot{E}}_0{\left(1+\frac{t}{{\tau }_{\mathrm{sd}}}\right)}^{-2}$$

(3)

with

$$\begin{array}{ccc}\hfill {\dot{E}}_0& =& \frac{8{\pi }^4{B}_0^2{R}_{\mathrm{NS}}^6}{3c^3{P}_0^4},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\tau }_{\mathrm{sd}}& =& \frac{3I{c}^3{P}_0^2}{4{\pi }^2{B}_0^2{R}_{\mathrm{NS}}^6},\hfill \end{array}$$

(5)

where $P_0$ is the initial spin period, and $B_0$ is the constant magnetic field [33], while the inertial momentum is $I=1.4\times {10}^{45}{\mathrm{g}\mathrm{cm}}^2$ and the pulsar radius $R_{\mathrm{NS}}=12\mathrm{km}$ [34].

The parameter $\lambda$ in Equation (2) is highly uncertain, being determined by the conversion of the spin-down energy into $e^{\pm }$ pairs (which can be very efficient, see, for example, [13,35]) and the subsequent production of TeV photons. It can be observationally determined for firmly identified PWNe in the HGPS catalogue, obtaining values between $5\times {10}^{-5}$ and $6\times {10}^{-2}$ (see Table 1 of [9]). In case of the Geminga, the value of parameter $\lambda$ deduced by TeV observations is ∼$3\times {10}^{-3}$ [12]. This work considers $\lambda$ a free parameter, with $\lambda ={10}^{-3}$ being a reference value in numerical calculations. The possibility that $\lambda$ is correlated to the spin-down power, i.e.,

$$\lambda ={\lambda }_0{(\dot{E}/{\dot{E}}_0)}^{\delta }$$

(6)

was suggested by the results of [9] that found $L=\lambda \dot{E}\propto {\dot{E}}^{1+\delta }$ with $1+\delta =0.59\pm 0.21$ by studying a sample of PWNe in the HGPS catalogue.

By using Equations (2), (3) and (6), we conclude that the source intrinsic luminosity decreases over the time scale ${\tau }_{\mathrm{sd}}$ according to

$$L\left(t\right)=L_{\max }{\left(1+\frac{t}{{\tau }_{\mathrm{sd}}}\right)}^{-\gamma },$$

(7)

where $\gamma =2\left(1+\delta \right)$ and $L_{\max }={\lambda }_0{\dot{E}}_0$ is the initial luminosity. Assuming that the birth-rate $dN/dt=R$ of these sources in the galaxy is constant in time, we can calculate their luminosity distribution $dN/dL=Y\left(L\right)$ that is given by

$$Y\left(L\right)=\frac{R{\tau }_{\mathrm{sd}}(\alpha -1)}{L_{\max }}{\left(\frac{L}{L_{\max }}\right)}^{-\alpha }$$

(8)

where $\alpha =1/\gamma +1$. In the above relation, the luminosity is allowed to vary in the range $L_{\min }\le L\le L_{\max }$ with the lower bound given by $L_{\min }\equiv L\left(T_{\mathrm{d}}\right)$, where $T_{\mathrm{d}}$ is the total duration of the TeV emission.

The luminosity function in Equation (8) is obtained by assuming, for simplicity, that all sources have approximately the same values for the initial period $P_0$ and magnetic field $B_0$ (and, consequently, the same maximal luminosity $L_{\max }$ and spin-down time ${\tau }_{\mathrm{sd}}$). We can, however, modify it to include the effects of dispersion of these parameters around reference values indicated as ${\tilde{P}}_0$ and ${\tilde{B}}_0$. In this case, we obtain

$$Y\left(L\right)=\frac{R\tilde{\tau }(\alpha -1)}{\tilde{L}}{\left(\frac{L}{\tilde{L}}\right)}^{-\alpha }G\left(\frac{L}{\tilde{L}}\right)$$

(9)

where $\tilde{\tau }\equiv {\tau }_{\mathrm{sd}}({\tilde{B}}_0,{\tilde{P}}_0)$ and $\tilde{L}\equiv L_{\max }({\tilde{B}}_0,{\tilde{P}}_0)$ are the spin-down time scale and maximal luminosity for the reference values ${\tilde{P}}_0$ and ${\tilde{B}}_0$. The obtained luminosity distribution differs from Equation (8) for the presence of the function $G(L/\tilde{L})$ that is given by

$$G\left(x\right)\equiv \int dph\left(p\right)p^{6-4\alpha }\int dbg\left(b\right)b^{2\alpha -4}\theta \left(p^{-4}{b}^2-x\right)$$

(10)

where $p\equiv P_0/{\tilde{P}}_0$, $b\equiv B_0/{\tilde{B}}_0$, while $h\left(p\right)$ and $g\left(b\right)$ describe the probability distributions of the initial period and the magnetic field. We assume that these functions can be modelled as Gaussian distributions in ${log}_{10}\left(p\right)$ and ${log}_{10}\left(b\right)$, centred in zero and having widths given by ${\sigma }_{logP}={log}_{10}\left(f_p\right)$ and ${\sigma }_{logB}={log}_{10}\left(f_b\right)$, with the parameters $f_p$ and $f_b$ described in the next section. The important point to remark is that, when $f_p$ and $f_b$ are fixed, the luminosity distribution only depends on $\tilde{\tau }$ and $\tilde{L}$. These parameters can be observationally constrained by fitting the HGPS catalogue.

We note that a log-normal distribution for $B_0$ is also assumed by [10] (see also [36]), where, however, a Gaussian distribution for $P_0$ with fixed average $\langle P_0\rangle =50\mathrm{ms}$ and dispersion ${\sigma }_P=50/\sqrt{2}\mathrm{ms}$ is considered. We prefer to adopt a log-normal distribution also for $P_0$ because this choice naturally suppresses the very low values of the initial period that correspond to extremely large and unphysical values of ${\dot{E}}_0$1. If a Gaussian distribution for $P_0$ is used, the high-luminosity tail of the function $Y\left(L\right)$ is driven by the low-period tail of the $P_0$ distribution, and a slope $Y\left(L\right)\propto L^{-1.8}$ is obtained [10], almost irrespective of the assumed $B_0$ distribution and the adopted value for $\alpha$.

2.3. The Cumulative Emission of Resolved and Unresolved PWNe

The relation between the intrinsic luminosity L and the flux produced at Earth by a specific source can be generally written as

$$\varphi =\frac{L}{4\pi r^2\langle E\rangle },$$

(11)

where r is the source distance, and $\langle E\rangle$ is the average energy of photons emitted in the range $1–100\mathrm{TeV}$. We consider the average spectrum observed by HESS to be a reference [30], i.e., all sources in the energy range $1–100\mathrm{TeV}$ can be described by a power law with spectral index $\beta =2.3$ that corresponds to $\langle E\rangle =3.25\mathrm{TeV}$. The source flux distribution can be calculated as

$$\frac{dN}{d\varphi }=\int dr4\pi r^4\langle E\rangle Y\left(4\pi r^2\langle E\rangle \varphi \right)\overline{\rho }\left(r\right),$$

(12)

where $\overline{\rho }\left(r\right)\equiv {\int }_{\mathrm{OW}}d\Omega \rho (r,\mathbf{n})$ is the spatial distribution integrated over the longitude and latitude intervals probed by H.E.S.S.

The total TeV flux produced at Earth by the PWNe population of our galaxy can be calculated as

$${\mathsf{\Phi }}_{\mathrm{tot}}\equiv \int d\varphi \varphi \frac{dN}{d\varphi }=\xi \frac{{\mathcal{L}}^{\mathrm{MW}}}{4\pi \langle E\rangle }\langle r^{-2}\rangle ,$$

(13)

where the parameter $\xi$, defined as

$$\xi \equiv {\int }_{\mathrm{OW}}{d}^{3}r\rho \left(\mathbf{r}\right)=0.812,$$

(14)

represents the fraction of sources of the considered population, which are included in the H.E.S.S. OW, while

$$\langle r^{-2}\rangle \equiv \frac{1}{\xi }{\int }_{\mathrm{OW}}{d}^{3}r\rho \left(\mathbf{r}\right)r^{-2}=0.0176{\mathrm{kpc}}^{-2}$$

(15)

is the average value of their inverse square distance2. The quantity ${\mathcal{L}}^{\mathrm{MW}}$ is the total TeV luminosity produced by the considered population in the galaxy, and it is given by

$${\mathcal{L}}^{\mathrm{MW}}=\int dLY\left(L\right)L.$$

(16)

If we neglect $P_0$ and $B_0$ dispersions, all sources in the considered population have approximately the same maximal luminosity $L_{\max }$ and spin-down time ${\tau }_{\mathrm{sd}}$. These parameters can be determined by fitting the H.E.S.S. observational results, allowing us to calculate the total Milky Way luminosity, according to

$${\mathcal{L}}^{\mathrm{MW}}=R{\tau }_{\mathrm{sd}}{L}_{\max }\frac{(\alpha -1)}{(2-\alpha )}\left[1-{\mathsf{\Delta }}^{\alpha -2}\right]$$

(17)

where $\mathsf{\Delta }\equiv L_{\max }/L_{\min }$. The minimal luminosity $L_{\min }$ cannot be constrained by H.E.S.S. observations, and it is related to the temporal duration of the TeV PWNe emission, being that $L_{\min }\equiv L_{\max }{(1+T_{\mathrm{d}}/{\tau }_{\mathrm{sd}})}^{-\gamma }$ with $\gamma =1/(\alpha -1)$.

In the scientific literature, this quantity is assumed to be of the order $T_{\mathrm{d}}\sim {10}^5$ yr [37]. Considering that we find ${\tau }_{\mathrm{sd}}\sim {10}^3$ yr, we obtain $\mathsf{\Delta }\sim {10}^4$ ($\mathsf{\Delta }\sim {10}^3$) for $\alpha =1.5$ ($\alpha =1.8$). Taking into account that $\mathsf{\Delta }$ is expected to be large, unless otherwise specified, we quote the results for ${\mathcal{L}}^{\mathrm{MW}}$ and ${\mathsf{\Phi }}_{\mathrm{tot}}$ obtained for $\mathsf{\Delta }\to \infty$; these can be easily recalculated by using the above equations if finite values for $\mathsf{\Delta }$ are considered3.

If $P_0$ and $B_0$ dispersions are not negligible, one can still determine the average spin-down time $\tilde{\tau }$ and maximal luminosity $\tilde{L}$ of the PWNe population by fitting the H.E.S.S. observational results. In this case, the total Milky Way luminosity is obtained as

$${\mathcal{L}}^{\mathrm{MW}}=g\left(\alpha -1\right)R\tilde{\tau }\tilde{L}$$

(18)

where the parameter g is given by

$$g=\int dxG\left(x\right)x^{1-\alpha }.$$

(19)

As it will be discussed in the following, it is extremely important to evaluate the cumulative flux ${\mathsf{\Phi }}_{\mathrm{NR}}$ produced by sources that are too faint to be individually detected. Indeed, this quantity is not negligible and contaminates the observational determinations of diffuse gamma-ray galactic emissions. For this purpose, it is useful to split the total flux ${\mathsf{\Phi }}_{\mathrm{tot}}$ produced by the PWNe galactic population into the contributions produced by faint and bright sources, defined as

$${\mathsf{\Phi }}_{\mathrm{F}}\left({\varphi }_{\mathrm{th}}\right)\equiv {\int }_0^{{\varphi }_{\mathrm{th}}}d\varphi \varphi \frac{dN}{d\varphi }{\mathsf{\Phi }}_{\mathrm{B}}\left({\varphi }_{\mathrm{th}}\right)\equiv {\int }_{{\varphi }_{\mathrm{th}}}d\varphi \varphi \frac{dN}{d\varphi }$$

(20)

where the flux threshold ${\varphi }_{\mathrm{th}}$ is estimated by considering the performance results of the H.E.S.S. detector. We expect that the cumulative unresolved flux is included in the range

$${\mathsf{\Phi }}_{\mathrm{F}}\left(0.01{\varphi }_{\mathrm{Crab}}\right)\le {\mathsf{\Phi }}_{\mathrm{NR}}\le {\mathsf{\Phi }}_{\mathrm{F}}\left(0.1{\varphi }_{\mathrm{Crab}}\right)$$

(21)

as it can be understood by considering that $0.01{\varphi }_{\mathrm{Crab}}$ is the H.E.S.S. sensitivity limit (i.e., the flux level below which single sources cannot be detected) and $0.1{\varphi }_{\mathrm{Crab}}$ is the completeness threshold (i.e., the flux level above which all sources are resolved and the HGPS catalogue is complete). A more refined estimate of ${\mathsf{\Phi }}_{\mathrm{NR}}$ should take into account that some faint sources with flux below $0.1{\varphi }_{\mathrm{Crab}}$ are identified by H.E.S.S. and thus do not contribute to the unresolved contribution. In order to avoid including them, we subtract from the calculated value ${\mathsf{\Phi }}_{\mathrm{F}}\left(0.1{\varphi }_{\mathrm{Crab}}\right)$ the total flux ${\mathsf{\Phi }}_{\mathrm{F},\mathrm{HGPS}}$ produced by all the sources in the HGPS catalogue with flux below $0.1{\varphi }_{\mathrm{Crab}}$, obtaining the following expression:

$${\mathsf{\Phi }}_{\mathrm{NR}}={\mathsf{\Phi }}_{\mathrm{F}}\left(0.1{\varphi }_{\mathrm{Crab}}\right)-{\mathsf{\Phi }}_{\mathrm{F},\mathrm{HGPS}}$$

(22)

for the cumulative emission by unresolved PWNe in the 1–100 TeV energy range. This approach is conceptually equivalent to what is performed in [19], where the unresolved contribution is estimated as ${\mathsf{\Phi }}_{\mathrm{NR}}={\mathsf{\Phi }}_{\mathrm{tot}}-{\mathsf{\Phi }}_{\mathrm{HGPS}}$, and ${\mathsf{\Phi }}_{\mathrm{HGPS}}$ is the total flux produced by the 78 sources in the HGPS catalogue. However, as it is explained in Section 3.2, Equation (22) is expected to provide a more accurate result, being obtained from quantities which are more stable with respect to random fluctuations in the PWNe population.

3. Results

Flux, latitude, and longitude distributions of bright sources in the HGPS catalogue are fitted by using an unbinned likelihood with the goal of constraining the properties of the source population. Namely, we provide an observational determination of the maximal luminosity $L_{\max }$ and of the spin-down time ${\tau }_{\mathrm{sd}}$ of galactic PWNe, obtaining the results displayed in

Table 1. The best-fit values and the $1\sigma$ allowed ranges for the maximal luminosity ($L_{\max }$), the fading time scale (${\tau }_{\mathrm{sd}}$) and the total flux of PWNe population in the H.E.S.S. OW (${\mathsf{\Phi }}_{\mathrm{tot}}$); we also show the corresponding best-fit values for the initial spin-down period ($P_0$) and the pulsar magnetic field ($B_0$). The different cases are described in the text. $\mathsf{\Delta }{\chi }^2$ is calculated with respect to our reference case (first row in the table).

	${log}_{10}\left[\frac{{\mathit{L}}_{\mathbf{max}}}{\mathbf{erg}{\mathbf{s}}^{-1}}\right]$	${\mathit{\tau }}_{\mathbf{sd}}\left[\mathbf{kyr}\right]$	${\mathit{P}}_0\left[\mathbf{ms}\right]$	${\mathit{B}}_0\left[{10}^{12}\mathbf{G}\right]$	${\mathbf{\Phi }}_{\mathbf{tot}}\left[\frac{{10}^{-10}}{{\mathbf{cm}}^2\mathbf{s}}\right]$	$\mathbf{\Delta }{\mathit{\chi }}^2$
Ref.	$35.{69}_{-0.28}^{+0.21}$	$1.8_{-0.6}^{+1.5}$	$33.5_{-4.1}^{+5.0}$	$4.3_{-1.9}^{+2.0}$	$3.8_{-1.0}^{+1.0}$	−
SNR	$35.{69}_{-0.25}^{+0.22}$	$1.8_{-0.7}^{+1.6}$	$31.2_{-4.1}^{+4.9}$	$4.0_{-1.8}^{+2.0}$	$3.8_{-1.0}^{+1.0}$	$1.4$
$H=100\mathrm{pc}$	$35.{65}_{-0.27}^{+0.22}$	$1.6_{-0.6}^{+1.5}$	$35.1_{-4.6}^{+5.7}$	$4.9_{-2.2}^{+2.4}$	$4.1_{-1.0}^{+0.4}$	$-7.3$
$H=50\mathrm{pc}$	$35.{69}_{-0.26}^{+0.20}$	$2.9_{-1.4}^{+2.0}$	$37.0_{-4.7}^{+5.9}$	$3.8_{-1.5}^{+2.8}$	$4.4_{-0.9}^{+1.3}$	$-10.5$
$d=20\mathrm{pc}$	$35.{67}_{-0.25}^{+0.20}$	$1.9_{-0.7}^{+1.9}$	$31.2_{-4.0}^{+4.9}$	$3.9_{-1.9}^{+2.0}$	$3.9_{-1.0}^{+0.8}$	$-0.2$
$d=40\mathrm{pc}$	$35.{67}_{-0.25}^{+0.20}$	$2.2_{-0.8}^{+2.0}$	$29.5_{-4.0}^{+4.7}$	$3.5_{-1.7}^{+1.8}$	$4.4_{-1.1}^{+1.2}$	$-1.8$
$\alpha =1.3$	$35.{61}_{-0.27}^{+0.18}$	$4.3_{-1.5}^{+4.3}$	$21.8_{-4.0}^{+3.5}$	$1.8_{-0.8}^{+0.8}$	$3.5_{-0.9}^{+1.1}$	$0.0$
$\alpha =1.8$	$35.{83}_{-0.24}^{+0.29}$	$0.5_{-0.2}^{+0.4}$	$51.0_{-6.4}^{+8.1}$	$12.7_{-5.8}^{+9.6}$	$5.9_{-0.1}^{+1.8}$	$0.5$
$P_0$ and $B_0$ disp.	$35.{15}_{-0.23}^{+0.56}$	$6.7_{-4.8}^{+17.7}$	$30.2_{-3.8}^{+4.8}$	$2.0_{-1.3}^{+2.9}$	$4.1_{-1.0}^{+1.4}$	$-4.6$
$N_{\mathrm{obs}}=32$	$35.{71}_{-0.24}^{+0.22}$	−	−	−	$4.2_{-1.0}^{+1.3}$	−

. This permits us to estimate the initial period $P_0$ and magnetic field $B_0$ of PWNe by using

$$\begin{array}{ccc}\hfill \frac{P_0}{1\mathrm{ms}}& =& 94{\left(\frac{{\lambda }_0}{{10}^{-3}}\right)}^{1/2}{\left(\frac{{\tau }_{\mathrm{sd}}}{{10}^4\mathrm{yr}}\right)}^{-1/2}{\left(\frac{L_{\max }}{{10}^{34}{\mathrm{erg}\mathrm{s}}^{-1}}\right)}^{-1/2},\hfill \\ \hfill \frac{B_0}{{10}^{12}\mathrm{G}}& =& 5.2{\left(\frac{{\lambda }_0}{{10}^{-3}}\right)}^{1/2}{\left(\frac{{\tau }_{\mathrm{sd}}}{{10}^4\mathrm{yr}}\right)}^{-1}{\left(\frac{L_{\max }}{{10}^{34}{\mathrm{erg}\mathrm{s}}^{-1}}\right)}^{-1/2}.\hfill \end{array}$$

(23)

Moreover, the total flux produced by the considered population in the H.E.S.S. OW is evaluated by using Equation (13) with the total Milky Way luminosity given by Equation (17). The cumulative unresolved emission is finally estimated by using Equation (22) as it is better discussed in Section 3.2.

The above relationships are valid if $P_0$ and $B_0$ dispersions are neglected and, consequently, all the sources in the considered population have approximately the same maximal luminosity and spin-down time. If $P_0$ and $B_0$ dispersions are not negligible, one can still determine the average spin-down time $\tilde{\tau }$ and maximal luminosity $\tilde{L}$ of the PWNe population by fitting the H.E.S.S. observational results. This allows us to calculate the average initial period ${\tilde{P}}_0$ and magnetic field ${\tilde{B}}_0$ by using Equation (23) with the replacements $L_{\max }\to \tilde{L}$ and ${\tau }_{\mathrm{sd}}\to \tilde{\tau }$. The total and unresolved emissions from the considered population are still calculated by using Equations (13) and (22) with the total Milky Way luminosity given by Equation (18).

3.1. The Reference Case

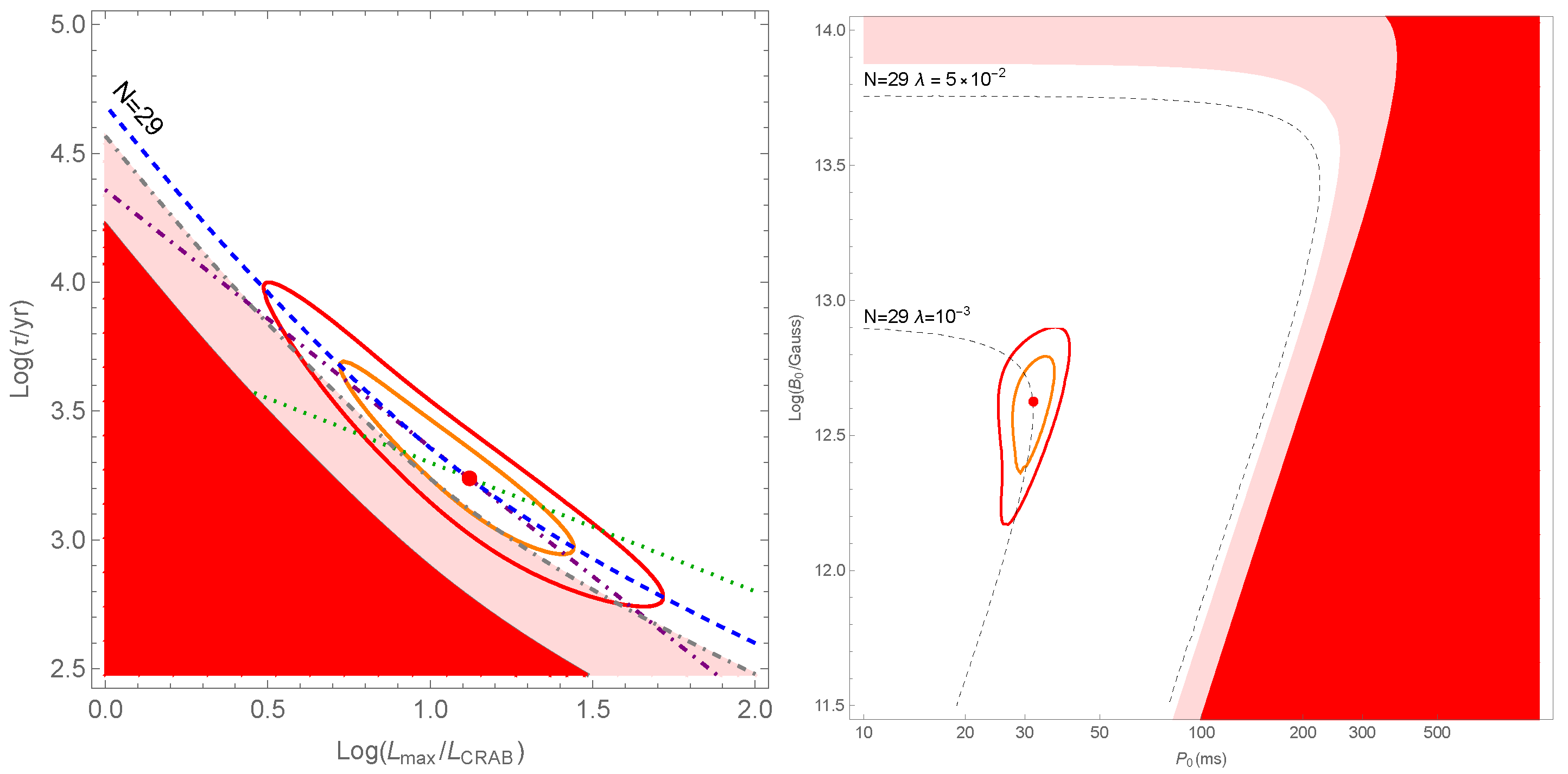
As the first case, indicated as the reference case in the following, we assume that the efficiency parameter $\lambda$ is constant. In this assumption, the power law index of the luminosity distribution is $\alpha =1.5$. By maximising the likelihood function, we find the best-fit values and allowed regions for the maximal luminosity $L_{\max }$ and the spin-down time scale ${\tau }_{\mathrm{sd}}$ displayed in the left panel of Figure 1. These correspond to

$$\begin{array}{ccc}\hfill L_{\max }& =& 4.9_{-2.1}^{+3.0}\times {10}^{35}\mathrm{erg}{\mathrm{s}}^{-1}\hfill \\ \hfill {\tau }_{\mathrm{sd}}& =& 1.8_{-0.6}^{+1.5}\times {10}^3\mathrm{yr},\hfill \end{array}$$

(24)

where the quoted uncertainties correspond to the $1\sigma$ confidence level (CL). By considering that the Crab luminosity (above 1 TeV) is $L_{\mathrm{Crab}}=3.8\times {10}^{34}\mathrm{erg}{\mathrm{s}}^{-1}$, we can express the constraint of the maximal luminosity as $L_{\max }={13}_{-6}^{+8}{L}_{\mathrm{Crab}}$.

One important point to note in the left panel of Figure 1 is that the allowed region, despite being relatively extended along the two directions $L_{\max }$ and ${\tau }_{\mathrm{sd}}$, essentially lies along the purple dash-dotted line that corresponds to the condition ${\mathsf{\Phi }}_{\mathrm{tot}}=\mathrm{const}$ (equivalently ${\mathcal{L}}_{\mathrm{MW}}=\mathrm{const}$). This is due to the fact that this condition basically coincides with the requirement that the number of predicted sources with $\varphi \ge 0.1{\varphi }_{\mathrm{Crab}}$ reproduces the observational value $N_{\mathrm{obs}}=29$ (blue dashed line in left panel of Figure 1), which is automatically implemented by best-fit models with fixed $L_{\max }$ values. At a practical level, this implies that the total flux (or the total luminosity) of the considered population is constrained with a much better relative accuracy than the population parameters $L_{\max }$ and ${\tau }_{\mathrm{sd}}$.

The ability of the data to single out a specific region of the parameter space is connected to the flux distribution of HGPS sources as it graphically explained in Figure 2. In this plot, theoretical predictions for the number $N\left(\varphi \right)$ of sources with a flux larger than $\varphi$ are compared with observational results (grey line). Theoretical calculations are constrained to reproduce the observed number of source above 0.1 ${\varphi }_{\mathrm{Crab}}$, i.e., we restrict to $L_{\max }$ and ${\tau }_{\mathrm{sd}}$ values that lie along the blue dashed line in the left panel Figure 1. The behaviour of the function $N\left(\varphi \right)$ can be analytically calculated in the limiting assumptions $L_{\max }\to 0$ and $L_{\max }\to \infty$ as discussed in [19]. In the first case, only sources relatively close to the position of the Sun are observable, and one obtains $dN/d\varphi \propto {\varphi }^{-5/2}$, predicting $N\left(\varphi \right)\propto {\varphi }^{-3/2}$ independently of the assumed source space and luminosity distribution (magenta dot-dashed line). When $L_{\max }\to \infty$, the entire galaxy is visible, and one obtains that the source flux distribution $dN/d\varphi$ is described by a power law with the same index of the luminosity function, thus predicting $N\left(\varphi \right)\propto {\varphi }^{-\alpha +1}$ (blue dotted line). The observed source flux distribution has an intermediate slope with respect to both cases (see Figure 2) that can be only obtained by assuming a specific $L_{\max }$ value. The black solid line in Figure 2 represents the best-fit value $L_{\max }=13L_{\mathrm{Crab}}$ and reproduces quite well the flux distribution in the range $\varphi \ge 0.1{\varphi }_{\mathrm{Crab}}$, adopted in our analysis. The expected behaviour of $N\left(\varphi \right)$ for $L_{\max }=30L_{\mathrm{Crab}}$ is also shown with the red dashed line for comparison. The HGPS data disfavour this value at the $2\sigma$ level because bright sources are overproduced in comparison to the observational results.

Under the assumption that the observed objects are powered by a pulsar, the above values of $L_{\max }$ and ${\tau }_{\mathrm{sd}}$ can be used to determine through Equation (23) the initial period $P_0$ and magnetic field $B_0$ of the considered population. We obtain the following constraints:

$$\begin{array}{ccc}\hfill P_0& =& 33.5_{-4.3}^{+5.4}\mathrm{ms}\times {\left(\frac{\lambda }{{10}^{-3}}\right)}^{1/2}\hfill \\ \hfill B_0& =& 4.3\left(1\pm 0.45\right){10}^{12}\mathrm{G}\times {\left(\frac{\lambda }{{10}^{-3}}\right)}^{1/2}\hfill \end{array}$$

(25)

that correspond to the orange solid line in the right panel of Figure 1. The small uncertainty associated with the period $P_0$ is obtained because this quantity scales as $P_0\propto {\left(L_{\max }{\tau }_{\mathrm{sd}}\right)}^{-1/2}$. Being that the parameters $L_{\max }$ and ${\tau }_{\mathrm{sd}}$ are anti-correlated, their product $L_{\max }{\tau }_{\mathrm{sd}}$ is relatively well determined from the observational data.

The inferred magnetic field in this work is ${log}_{10}(B_0/1G)\simeq$ 12.65, which is similar to the value obtained by pulsar population studies [36]. On the other hand, the inferred period is consistent with the value $P_0\sim$ 50 ms obtained by [38] studying the gamma-ray pulsar population, while showing a discrepancy with respect to the value $P_0\sim$ 300 ms, obtained from pulsar radio observation [36]. This last value can be recovered only if we assume that a very large fraction ${\lambda }_0\sim$${10}^{-1}$ of the spin-down power is converted to TeV $\gamma$-ray emission.

Throughout this work, we assumed that all the sources in the HGPS catalogue with flux $\varphi \ge 0.1{\varphi }_{\mathrm{Crab}}$ (except those firmly identified as SNRs) are powered by pulsar activity. Among these 29 sources, 10 are firmly identified as PWNe or composite sources. In general, it is possible to obtain a conservative upper bound for the $P_0$ period considering that no fewer than 10 of the 29 sources observed by H.E.S.S. should be PWNe. The lines $N\left(0.1{\varphi }_{\mathrm{Crab}}\right)=\mathrm{const}$ correspond to a fixed number of sources above the threshold $0.1{\varphi }_{\mathrm{Crab}}$ and are represented with grey dashed lines both in planes $(L_{\max },{\tau }_{\mathrm{sd}})$ and $(P_0,B_0)$ and Figure 1. Analytically, $N\left(\varphi \right)$ is

$$N\left(\varphi \right)\propto {\tau }_{\mathrm{sd}}{L}_{\max }^{3/2}\propto B_0{P}_0^{-4}{\lambda }^{3/2}$$

if $L_{\max }\to 0$, while it scales as

$$N\left(\varphi \right)\propto {\tau }_{\mathrm{sd}}{L}_{\max }^{\alpha -1}\propto B_0^{2\alpha -4}{P}_0^{6-4\alpha }{\lambda }^{\alpha -1}$$

for $L_{\max }\to \infty$. For $1<\alpha <2$, the condition $N\left(\varphi \right)=\mathrm{const}$ always defines a maximum allowed period $P_0$ (at the transition between the above regimes), whose specific value depends on the fraction $\lambda$ of the pulsar spin-down energy that can produce the TeV $\gamma$-ray emission. Particularly, the dark red shaded area in Figure 1 can be excluded because it corresponds to $N\left(0.1{\varphi }_{\mathrm{Crab}}\right)\le 10$ and the relatively large value $\lambda =5\times {10}^{-2}$. If we consider that 12 additional sources in the HGPS catalogue are considered candidate PWNe on the basis of new data and/or phenomenological considerations [9,10,14,31], the excluded region enlarges to the light red shaded area that corresponds to $N\left(0.1{\varphi }_{\mathrm{Crab}}\right)\le 22$. This allows us to obtain the bound $P_0\le 260$ ms for $\alpha =1.5$ and $\lambda =5\times {10}^{-2}$ that can be strengthened by adding an upper limit of the magnetic field $B_0\le {10}^{14}\mathrm{G}$.

3.2. The TeV Total and Unresolved Flux Due to PWNe

We compute the total luminosity of the galaxy and the total flux in the energy range $1–100\mathrm{TeV}$ produced by sources in the H.E.S.S. OW. Using Equations (13) and (17), we obtain

$$\begin{array}{ccc}\hfill {\mathcal{L}}_{\mathrm{MW}}& =& 1.7_{-0.4}^{+0.5}\times {10}^{37}\mathrm{erg}{\mathrm{s}}^{-1}\hfill \\ \hfill {\mathsf{\Phi }}_{\mathrm{tot}}& =& 3.8_{-1.0}^{+1.0}\times {10}^{-10}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1},\hfill \end{array}$$

(26)

where ${\mathcal{L}}_{\mathrm{MW}}={445}_{-112}^{+138}{L}_{\mathrm{Crab}}$ and ${\mathsf{\Phi }}_{\mathrm{tot}}=16.8_{-3.5}^{+4.4}{\varphi }_{\mathrm{Crab}}$. The total TeV luminosity is only a factor ∼4 smaller than what is obtained in the energy range $1–100\mathrm{GeV}$ by fitting the Fermi-LAT data in 3FGL [39] and 1FHL [40] catalogs.

We compare the total flux ${\mathsf{\Phi }}_{\mathrm{tot}}$ with the cumulative emission produced by 78 resolved sources in the HGPS catalogue, i.e., ${\mathsf{\Phi }}_{\mathrm{HGPS}}=10.4{\varphi }_{\mathrm{Crab}}$. The fact that ${\mathsf{\Phi }}_{\mathrm{tot}}$ is substantially larger than ${\mathsf{\Phi }}_{\mathrm{HGPS}}$ is not surprising. It is due to unresolved sources that are naturally expected to provide a relevant contribution to the total flux because the observational horizon for H.E.S.S. is limited, while sources are expected to be distributed everywhere in the galaxy4. As expressed by Equation (22), a lower (upper) bound for the unresolved flux is provided by the cumulative emission of faint sources with flux below the H.E.S.S. sensitivity limit $0.01{\varphi }_{\mathrm{Crab}}$ (completeness threshold $0.1{\varphi }_{\mathrm{Crab}}$). By using this approach, we obtain $1.5{\varphi }_{\mathrm{Crab}}\le {\mathsf{\Phi }}_{\mathrm{NR}}\le 5.4{\varphi }_{\mathrm{Crab}}$. A more refined estimate was obtained in [19] by subtraction, i.e., by calculating ${\mathsf{\Phi }}_{\mathrm{NR}}={\mathsf{\Phi }}_{\mathrm{tot}}-{\mathsf{\Phi }}_{\mathrm{HGPS}}$. Here, we propose a conceptually equivalent approach, but we include in the difference only sources with fluxes below $0.1{\varphi }_{\mathrm{Crab}}$, obtaining

$${\mathsf{\Phi }}_{\mathrm{NR}}={\mathsf{\Phi }}_{\mathrm{F}}\left(0.1{\varphi }_{\mathrm{Crab}}\right)-{\mathsf{\Phi }}_{\mathrm{F},\mathrm{HGPS}}=3.9{\varphi }_{\mathrm{Crab}}$$

(27)

where ${\mathsf{\Phi }}_{\mathrm{F}}\left(0.1{\varphi }_{\mathrm{Crab}}\right)=5.3{\varphi }_{\mathrm{Crab}}$ and ${\mathsf{\Phi }}_{\mathrm{F},\mathrm{HGPS}}=1.4{\varphi }_{\mathrm{Crab}}$. As it is discussed in the following, this value is more accurate because it is less sensitive to statistical fluctuations due to the discrete distribution of sources in the galaxy.

The cumulative fluxes are indeed calculated by integrating over the continuous source space and luminosity distribution, and the quoted errors are obtained by propagating uncertainties in the determination of $L_{max}$ and ${\tau }_{\mathrm{sd}}$. The possible role of statistical fluctuations due to the discrete distribution of sources in the galaxy is not included and could be, in principle, very large. In order to discuss the robustness of our results in this respect, we create 1000 random realisations of the TeV PWNe population. Namely, we fix the parameters $L_{\max }$ and ${\tau }_{\mathrm{sd}}$ to their best-fit values and we randomly extract the position and intrinsic luminosity of each source according to the spatial and luminosity distributions described by our model. The total number of sources $N_{\mathrm{tot}}=R{T}_{\mathrm{d}}$ for each realisation is determined by the source formation rate R and the assumed duration of the TeV emission $T_{\mathrm{d}}={10}^5\mathrm{yr}$, and is scaled to the H.E.S.S. OW.

For each realisation, we estimate the total TeV flux due to PWNe, the cumulative emission of bright PWNe with flux above $0.1{\varphi }_{\mathrm{Crab}}$, and that of faint PWNe with flux below $0.1{\varphi }_{\mathrm{Crab}}$. The average values of these quantities and their standard deviations are reported in

Table 2. The total TeV gamma-ray flux inside the H.E.S.S. OW and the contribution due to bright (>$0.1{\varphi }_{\mathrm{Crab}}$) and faint (<$0.1{\varphi }_{\mathrm{Crab}}$) sources obtained by integrating over the continuous source distribution function (first and third line) and from 1000 random realisations of PWNe source population (second and fourth line, labelled as MC). All the quantities are given in units of ${\varphi }_{\mathrm{Crab}}$. The errors quoted in the MC cases are due to statistical fluctuations in MC realisations; the errors quoted in the first and third lines are obtained by propagating uncertainties in $L_{\max }$ and ${\tau }_{\mathrm{sd}}$.

	Total TeV Flux	Bright Sources (>$0.1{\mathit{\varphi }}_{\mathbf{Crab}}$)	Faint Sources (<$0.1{\mathit{\varphi }}_{\mathbf{Crab}}$)
$\alpha =1.5$ (Ref.)	$16.8_{-3.5}^{+4.4}$	$11.3_{-3.4}^{+4.9}$	$5.3_{-1.6}^{+3.5}$
MC	$16.6\pm 8.9$	$11.3\pm 8.4$	$5.3\pm 0.4$
$\alpha =1.8$	$19.3_{-0.4}^{+7.9}$	$11.3_{-3.3}^{+5.7}$	$7.9_{-1.9}^{+2.1}$
MC	$19\pm 5$	$11\pm 4.6$	$7.9\pm 0.5$

, where they are compared with the predictions obtained under the same assumptions by integrating over the continuous source distribution function and neglecting the statistical fluctuations. In particular, the first two lines correspond to the reference case of Table 1 with $\alpha =1.5$. The third and fourth lines correspond to the case $\alpha =1.8$ that will be discussed in Section 3.3; the differences between the values of ${\mathsf{\Phi }}_{\mathrm{tot}}$ reported here and in Table 1 are due to the fact that we consider a finite value for $\mathsf{\Delta }={(1+T_{\mathrm{d}}/{\tau }_{\mathrm{sd}})}^{\gamma }$, whereas the limit $\mathsf{\Delta }\to \infty$ is considered in Table 1.

To estimate the relevance of the statistical fluctuations of the MC realisations, we compare them with the uncertainties in the corresponding quantities due to the $L_{\max }$ and ${\tau }_{\mathrm{sd}}$ parameter estimations by the unbinned likelihood fit of HGPS sources. We see that the MC statistical fluctuations of the total flux are larger (by a factor ∼ 2) than the uncertainties due to parameter estimation. This is due to the fact that there is a non-negligible probability of extracting a source with a very high flux, either due to having a nearby position or very high intrinsic luminosity. To be more precise, the expected behaviour of the source flux distribution $dN/d\varphi$ for $\varphi \to \infty$ implies that the standard deviation of cumulative fluxes that are obtained by integrating/summing over the source population is determined by the high flux integration/summation limit. If we consider ${\mathsf{\Phi }}_{\mathrm{tot}}$, this limit is not defined, i.e., we have to include in the summation very bright sources that can produce large fluctuations of the total flux of the population. For the same reason, the cumulative flux associated with bright sources (with $\varphi >0.1{\varphi }_{\mathrm{Crab}}$) is also characterised by a large uncertainty in the MC simulation. On the other hand, the problem is automatically solved if we consider the cumulative contribution of faint sources (with $\varphi <0.1{\varphi }_{\mathrm{Crab}}$). This quantity is indeed very well-defined and shows an uncertainty in the MC realisations much smaller than the one associated with the likelihood analysis. Based on this fact, we conclude that the estimate of the unresolved flux ${\mathsf{\Phi }}_{\mathrm{NR}}={\mathsf{\Phi }}_{\mathrm{tot}}-{\mathsf{\Phi }}_{\mathrm{HGPS}}$ given in [19] may be affected by large statistical uncertainties. A better procedure is to estimate the unresolved emission by only considering faint sources as it is performed in this paper, with the result given in Equation (27).

3.3. Robustness of the Results

In this section, the robustness of the results with respect to different assumptions considered in our analysis is further discussed following the approach of [19]. We assume different scenarios with respect to ingredients such as the spatial distribution, the disk thickness, the source physical dimension, the power law index of the luminosity distribution, etc., as reported in Table 1. We obtain the best-fit results; the $1\sigma$ allowed regions for the source luminosity function parameters ($L_{\max }$ and ${\tau }_{\mathrm{sd}}$), the corresponding pulsar properties $P_0$ and $B_0$, the total flux produced at Earth ${\mathsf{\Phi }}_{\mathrm{tot}}$, and the level of agreement with the data are expressed in terms of $\mathsf{\Delta }{\chi }^2$ with respect to the reference case.

• Power index of the luminosity function:

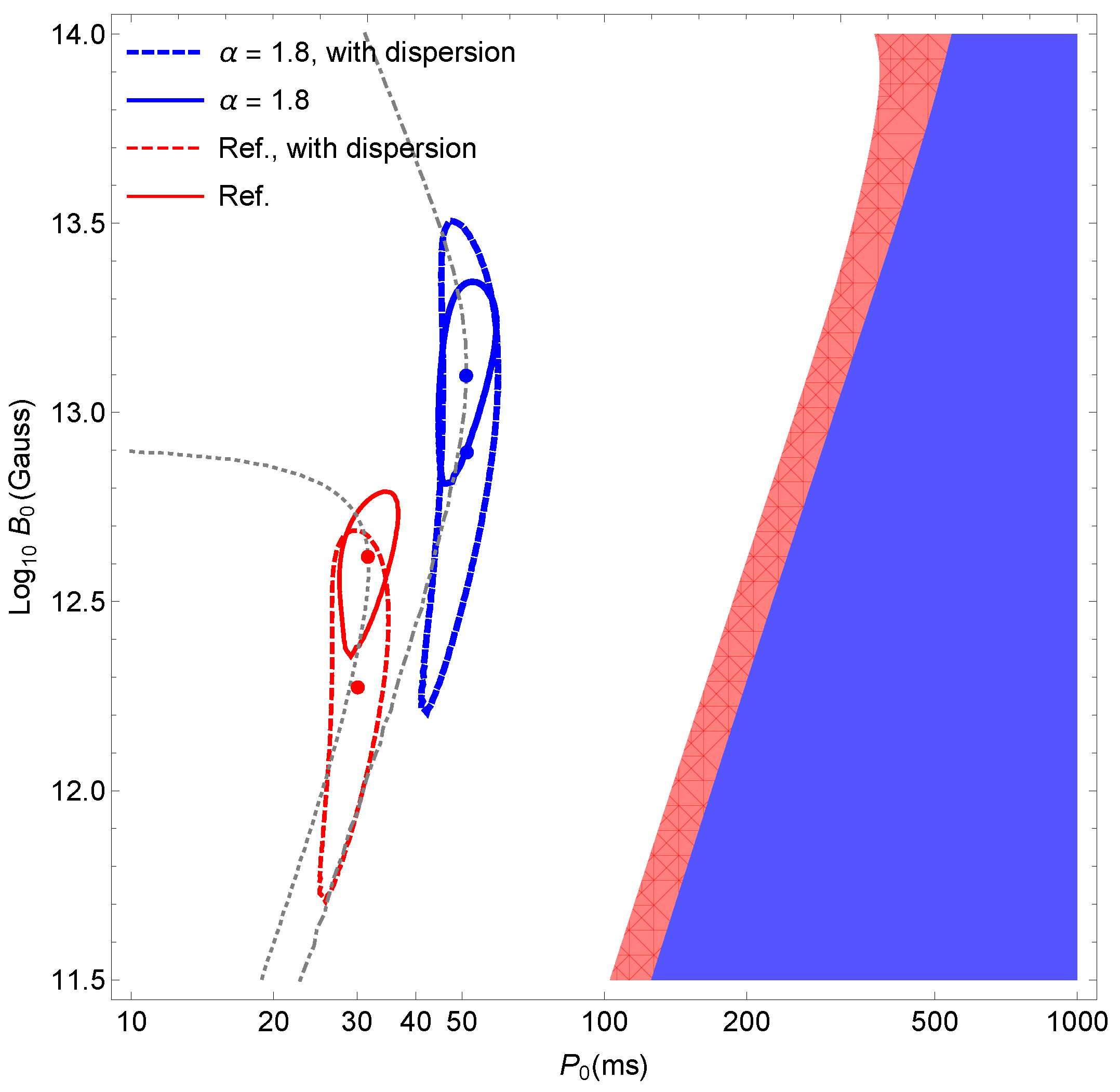
We discuss the effects produced by a variation of the power index $\alpha$ of the luminosity function by considering two additional cases: $\alpha =1.3$ and $\alpha =1.8$. We obtain a ∼10% decrease (∼50% increase) in the TeV Milky Way luminosity and the total flux at Earth for $\alpha =1.3$ ($\alpha =1.8$), with a little preference for the case $\alpha =1.3$. Considering the correlation of $\lambda$ and the spin-down power [9], for $\alpha =1.8$, we obtain a fading time scale ${\tau }_{\mathrm{sd}}=0.5_{-0.2}^{+0.4}\times {10}^3$ yr, while the initial period and magnetic field are given by

$$\begin{array}{ccc}\hfill P_0& =& 51.0_{-6.4}^{+8.1}\mathrm{ms}\times {\left(\frac{{\lambda }_0}{{10}^{-3}}\right)}^{1/2},\hfill \\ \hfill B_0& =& 12.7_{-5.8}^{+9.6}{10}^{12}\mathrm{G}\times {\left(\frac{{\lambda }_0}{{10}^{-3}}\right)}^{1/2}.\hfill \end{array}$$

(28)

The above results are compared with the reference case ($\alpha =1.5$) in Figure 3.

• $P_0$ and $B_0$ dispersion:

We hypothesise that the initial pulsar periods and magnetic fields have log-normal dispersion around preferred values ${\tilde{P}}_0$ and ${\tilde{B}}_0$ with widths ${\sigma }_{logP}={log}_{10}\left(f_p\right)$ and ${\sigma }_{logB}={log}_{10}\left(f_b\right)$. The constraints on ${\tilde{P}}_0$ and ${\tilde{B}}_0$ that are obtained by choosing $f_p=\sqrt{2}$ and $f_b=2$ are displayed by the dashed red and blue lines in Figure 3. We see that the inferred value for ${\tilde{P}}_0$ is basically insensitive to the assumed dispersion, while the preferred magnetic field ${\tilde{B}}_0$ is slightly reduced with respect to the reference case as a consequence of the high-luminosity tail of the luminosity function that is computed by assuming $f_p\ne 0$ and $f_b\ne 0$. In summary, the results displayed in Figure 3 show that the bounds on the initial period and magnetic field do not critically depend on the adopted assumptions, being that $P_0$ is constrained to the narrow range $25–60\mathrm{ms}$ for $\lambda ={10}^{-3}$. The inferred values for $B_0$ and $P_0$ are consistent with the expectations, and this justifies our working assumption that a large fraction of bright sources observed by H.E.S.S. belongs to a population of young pulsars. It also supports the hypothesis formulated by [12,13], i.e., the majority of TeV bright sources in the sky are PWNe and/or TeV halos. On the contrary, the large values of $P_0\sim 300\mathrm{ms}$ can explain the HGPS results if a limited fraction of observed sources belongs to the considered population of PWNe and/or a consistent fraction of the spin-down energy is converted into TeV $\gamma$ rays.

• Source sample:

The sample considered in our analysis is listed in

Table 3. The list of HGPS sources included in this analysis. Column 1 reports the name of the source (the values for sources indicated with an asterisk are taken from external references; see Table 1 of Ref. [30] for details). In columns 2 and 3, we show its galactic coordinates, and in column 4, we report the respective measured flux integrated above 1 TeV. In column 5, we show the class of the source as reported in the HGPS catalogue, while in column 6, we indicate the possible association of each source to a PWN based on the literature subsequent to the HGPS catalogue [10,14,30,41]. Finally, in the last column, we include the estimation of the PWN age performed in [14].

Source Name	GLON	GLAT	$\mathit{\varphi }(>1\mathbf{TeV})$	Class	PWN	Age
	deg	deg	%Crab	HGPS	Association	kyr
HESS $J0835-455$	$263.96$	$-3.05$	$67.7\pm 2.4$	PWN	yes	11.3
HESS $J0852-463{}^{*}$	$266.29$	$-1.24$	$103.2\pm 10.3$	SNR	no
HESS $J1023-575$	$284.19$	$-0.40$	$11.3\pm 0.8$	UNID	yes	4.6
HESS $J1303-631$	$304.24$	$-0.35$	$23.2\pm 1.2$	PWN	yes	11
HESS $J1356-645$	$309.79$	$-2.50$	$24.4\pm 2.3$	PWN	yes	7.3
HESS $J1418-609$	$313.24$	$0.14$	$13.3\pm 1.4$	PWN	yes	10.3
HESS $J1420-607$	$313.58$	$0.27$	$14.5\pm 1.1$	PWN	yes	13
HESS $J1442-624{}^{*}$	$315.43$	$-2.29$	$10.8\pm 3.0$	SNR	no
HESS $J1457-593$	$318.35$	$-0.42$	$11.0\pm 1.8$	UNID	no
HESS $J1458-608$	$317.95$	$-1.70$	$10.8\pm 1.3$	UNID	yes
HESS $J1507-622$	$317.97$	$-3.48$	$13.2\pm 1.4$	UNID	no
HESS $J1514-591$	$320.32$	$-1.19$	$28.4\pm 0.9$	PWN	yes	1.6
HESS $J1614-518{}^{*}$	$331.47$	$-0.60$	$25.9\pm 1.9$	UNID	no
HESS $J1616-508$	$332.48$	$-0.17$	$37.4\pm 1.9$	UNID	yes	8.1
HESS $J1632-478$	$336.39$	$0.26$	$12.9\pm 2.3$	UNID	yes
HESS $J1634-472$	$337.12$	$0.26$	$12.8\pm 1.6$	UNID	no
HESS $J1640-465$	$338.28$	$-0.04$	$14.7\pm 0.8$	Composite	yes
HESS $J1646-458$	$339.33$	$-0.78$	$24.2\pm 2.0$	UNID	no
HESS $J1702-420$	$344.23$	$-0.19$	$17.3\pm 2.9$	UNID	no
HESS $J1708-443$	$343.07$	$-2.32$	$10.1\pm 1.4$	UNID	yes	17.5
HESS $J1713-397{}^{*}$	$347.31$	$-0.46$	$74.4\pm 3.6$	SNR	no
HESS $J1800-240$	$5.96$	$-0.42$	$10.8\pm 1.5$	UNID	no
HESS $J1804-216$	$8.38$	$-0.09$	$25.9\pm 1.2$	UNID	yes	15.8
HESS $J1809-193$	$11.11$	$-0.02$	$23.2\pm 1.3$	UNID	yes	51.3
HESS $J1825-137$	$17.53$	$-0.62$	$81.2\pm 2.5$	PWN	yes	21.4
HESS $J1834-087$	$23.26$	$-0.33$	$14.7\pm 1.1$	Composite	yes	147
HESS $J1837-069$	$25.15$	$-0.09$	$53.1\pm 2.0$	PWN	yes	22.7
HESS $J1841-055$	$26.71$	$-0.23$	$44.8\pm 1.9$	UNID	yes
HESS $J1843-033$	$28.90$	$0.07$	$12.7\pm 1.3$	UNID	yes
HESS $J1857+026$	$36.06$	$-0.06$	$16.6\pm 1.8$	UNID	yes	20.6
HESS $J1908+063$	$40.55$	$-0.84$	$28.8\pm 2.2$	UNID	yes	19.5
HESS $J1912+101{}^{*}$	$44.46$	$-0.13$	$11.0\pm 1.5$	UNID	yes

and consists of 29 bright sources in the HGPS catalogue (i.e., with flux larger than $0.1{\varphi }_{\mathrm{Crab}}$) and does not include three sources firmly identified as SNR.

We verify that the inclusion of the three excluded sources (case denoted as $N_{\mathrm{obs}}$ = 32 in Table 1) does not change our conclusions, marginally affecting the maximal luminosity $L_{\max }$.

• Source spatial distribution:

There are not any noticeable changes in our results if sources follow SNR distribution [26] (case denoted as SNR) instead of the pulsar [25]. However, we find variation in the total flux up to ∼17 % when we decrease the thickness of the galactic disk from our reference case $H=0.2\mathrm{kpc}$ to $H=0.1\mathrm{kpc}$ or $H=0.05\mathrm{kpc}$. Reduction in the disk thickness substantially improves the quality of the fit with respect to our reference choice. This is due to the fact that the latitudinal distribution of the HGPS sources is quite narrow, having an RMS latitude of $0.017$ as expected for a population of young sources connected with the site of past core-collapse supernova explosions. This information can be used especially in favour of a fading sources population, such as young PWNe, not aged enough to drift off the galactic plane [9].

• Source physical dimension:

In order to avoid selection effects, we include in our fit only bright sources with flux above the H.E.S.S. completeness threshold ($0.1{\varphi }_{\mathrm{Crab}}$). This allows us to perform our analysis in full generality without imposing a prescribed physical dimension for the PWNe because the angular extension does not discriminate the possible identification. However, the H.E.S.S. detector is not able to resolve sources with angular extension larger than ∼1${}^{\circ }$ due to the implemented background subtraction procedure. For this reason, sources extremely close and largely extended can escape detection. In order to investigate the importance of this situation, we consider the cases denoted as $d=20\mathrm{pc}$ and $d=40\mathrm{pc}$, i.e., all sources in the galaxy have a fixed physical dimension. We checked that these assumptions do not affect our results.

• Source spectrum:

The assumed source spectrum only affects the average energy $\langle E\rangle$ of emitted photons in the $1–100$ TeV energy range; see Equation (11). It can be shown mathematically that the fit is not modified if the ratio $L_{\max }/\langle E\rangle$ is kept constant. As a consequence, if the average energy $\langle E\rangle$ is changed, only the best-fit value of the maximal luminosity is affected. However, the shift in $L_{\max }$ that is produced by the assumption of a different $\langle E\rangle$ does not alter the predicted value of ${\mathsf{\Phi }}_{\mathrm{tot}}$, see Equation (13), and only affects the total Milky Way luminosity that scales as ${\mathcal{L}}_{\mathrm{MW}}\propto \langle E\rangle$ (see Equation (17)), e.g., when the source spectral index is changed in the range $2.2<\beta <2.4$, the total Milky Way luminosity is varied by ∼10% in comparison to the reference case.

In conclusion, our results are stable with respect to possible modifications of the assumptions adopted in the analysis. The cumulative sources contribution to the Milky Way luminosity in the $1–100\mathrm{TeV}$ range and to the total $\gamma$-ray flux in the H.E.S.S. OW are included in the ranges ${\mathcal{L}}_{\mathrm{MW}}=\left(1.2–2.5\right)\times {10}^{37}\mathrm{erg}{\mathrm{s}}^{-1}$, ${\mathsf{\Phi }}_{\mathrm{tot}}=\left(3.5–5.9\right)\times {10}^{-10}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$, showing that they can be constrained within factors of $2.1$ and $1.7$, respectively, by the present observational data. The unresolved PWNe contribution, evaluated by using Equation (22), is always relatively large, and it is included in the range ${\mathsf{\Phi }}_{\mathrm{NR}}=\left(2.5–6.2\right){\varphi }_{\mathrm{Crab}}$ that corresponds to $25–60\%$ of the cumulative emission of the resolved sources. This estimate should be considered an update of that presented in [19]. Even if it is slightly smaller than our previous result, it represents, however, a confirmation of the relevance of unresolved PWNe in the TeV domain, which is, moreover, based on theoretical and observational quantities that are stable with respect to the statistical fluctuation of the PWNe population. The flux of unresolved PWNe is comparable to expectations for the truly diffuse contribution produced by the interaction of high-energy cosmic rays (CRs) with the gas in the galactic disk. This implies that the unresolved emission is likely to provide a relevant contribution to the diffuse large-scale $\gamma$-ray signal observed by H.E.S.S. and other experiments, and cannot be neglected for the interpretation of observational results in the TeV domain; see, for example, [42] for a recent discussion.

3.4. Implications in the GeV Energy Domain

The sources that we are considering, i.e., PWNe and/or TeV halos, represent a subdominant class in the GeV energy domain, where they are overwhelmed by brighter and more abundant objects, like pulsars and extragalactic objects. Nevertheless, they could have relevant implications also in this energy domain. In particular, the cumulative emission of unresolved PWNe in the GeV domain can provide a relevant contribution to the large-scale diffuse emission observed by Fermi-LAT.

This contribution was evaluated in [21] by taking advantage of the population study performed at TeV energies (where this source class is dominant) and considering a phenomenological model that is based on the average spectral properties of PWNe. We remark that PWNe are naturally expected to produce hard $\gamma$-ray emissions in the GeV energy domain. The observed $\gamma$-ray emission is indeed produced by IC scattering of HE electrons and positrons on background photons (CMB, starlight, and infrared). At GeV energies, this naturally produces a hard spectrum since the scattered photon spectral index in the Thompson regime is $\beta \sim (p+1)/2$, where p is the spectral index of injected electrons/positrons. In the TeV energy domain, a softer emission with a larger spectral index $\beta \sim (p+1)$ is produced either due to the Klein–Nishina regime and/or to electron/positron energy losses; see, for example, [10,43,44].

To take into account both effects, the average source emission spectrum is parameterised with a broken power law with different spectral indexes ${\beta }_{\mathrm{GeV}}$ and $\beta$ in the GeV and TeV energy domains, with transition energy $E_0=\left[0.1–1.0\right]\mathrm{TeV}$ located between the ranges probed by Fermi-LAT and H.E.S.S. At energies ($E\ge E_0$), the source spectral index is allowed to be in the range $\beta =[1.9–2.5]$ measured by H.E.S.S. [30] for identified PWNe. The index ${\beta }_{\mathrm{GeV}}$ is instead determined by requiring realistic values for the parameter $R_{\varphi }$, defined as

$$R_{\varphi }\equiv \frac{{\varphi }_{\mathrm{GeV}}}{\varphi }$$

(29)

between the integrated fluxes ${\varphi }_{\mathrm{GeV}}$ and $\varphi$ emitted by a given source at GeV and TeV energies, respectively. The relationship between the flux ratio $R_{\varphi }$, the energy break $E_0$ and the two spectral indexes ${\beta }_{\mathrm{GeV}}$ and $\beta$ can be analytically calculated, and it is given by

$$R_{\varphi }=\frac{1-\beta }{1-{\beta }_{\mathrm{GeV}}}\frac{\left[{\left({ϵ}_{\mathrm{GeV}}^{\sup }\right)}^{1-{\beta }_{\mathrm{GeV}}}-{\left({ϵ}_{\mathrm{GeV}}^{\inf }\right)}^{1-{\beta }_{\mathrm{GeV}}}\right]}{\left[{\left({ϵ}_{\mathrm{TeV}}^{\sup }\right)}^{1-\beta }-{\left({ϵ}_{\mathrm{TeV}}^{\inf }\right)}^{1-\beta }\right]}$$

(30)

where ${ϵ}_{\mathrm{GeV}}^{\inf }\equiv (1.0\mathrm{GeV}/E_0)$ and ${ϵ}_{\mathrm{GeV}}^{\sup }\equiv (100\mathrm{GeV}/E_0)$ (${ϵ}_{\mathrm{TeV}}^{\inf }\equiv (1.0\mathrm{TeV}/E_0)$ and ${ϵ}_{\mathrm{TeV}}^{\sup }\equiv (100\mathrm{TeV}/E_0)$) are the lower and upper bounds of the GeV (TeV) energy domains. The above equation implies that, once the source spectral properties (i.e., $\beta$ and $E_0$ are fixed) at high energies are known, then the flux ratio $R_{\varphi }$ is an increasing function of ${\beta }_{\mathrm{GeV}}$. Generally, the harder the spectrum at GeV energies, the smaller the integrated flux in the GeV domain.

As it is discussed in [21], a consistent description of the HGPS and the Fermi-LAT Fourth Source Catalogue (4FGL-DR2) is obtained for $R_{\varphi }=\left[250–1500\right]$ that corresponds to ${\beta }_{\mathrm{GeV}}$ inside the global range ${\beta }_{\mathrm{GeV}}=\left[1.06–2.19\right]$. The knowledge of $R_{\varphi }$ allows us to predict the source flux distribution in the GeV domain. One indeed obtains

$$\frac{dN}{d{\varphi }_{\mathrm{GeV}}}=\frac{1}{R_{\varphi }}\frac{dN}{d\varphi }\left({\varphi }_{\mathrm{GeV}}/R_{\varphi }\right),$$

(31)

where $dN/d\varphi$ is the source flux distribution in the TeV domain that is efficiently constrained by HGPS observations as it is explained in the previous sections. With the additional information that the Fermi-LAT detection threshold for objects contained in the galactic plane is ${\varphi }_{\mathrm{GeV},\mathrm{th}}={10}^{-9}{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$, we can estimate the unresolved PWNe emission in a given OW. By considering that the flux distribution scales as $dN/d\varphi \propto {\varphi }^{-\alpha }$ for $\varphi \to 0$ (see Section 3.2), we expect that ${\mathsf{\Phi }}_{\mathrm{NR},\mathrm{GeV}}\propto R_{\varphi }^{\alpha -1}$, i.e., the unresolved emission by PWNe in the GeV domain is a growing function of the flux ratio $R_{\varphi }$.

The PWNe unresolved emission is expected to be particularly relevant at small galactic longitudes because the source density is peaked at a few kpc from the galactic centre. Indeed, we show in [21] that it can account for a fraction included within $4\%$ (for $R_{\varphi }=250$ and $\alpha =1.5$) and $40\%$ (for $R_{\varphi }=1500$ and $\alpha =1.8$) of the total diffuse emission observed by Fermi-LAT from the inner galaxy. An important point to note is that PWNe unresolved emission is either relatively large or has a hard spectrum because the GeV spectral index ${\beta }_{\mathrm{GeV}}$ and the flux ratio $R_{\varphi }$ are correlated. As a result of this, the contribution at ∼100 GeV is almost independent of $R_{\varphi }$. It is due to the fact that the source emission above 1 TeV is fixed by HGPS data.

By using the above approach, we calculated in [21] the cumulative emission by unresolved PWNe as a function of the energy and observation direction, and we discussed its relevance for the correct interpretation of Fermi-LAT observations. 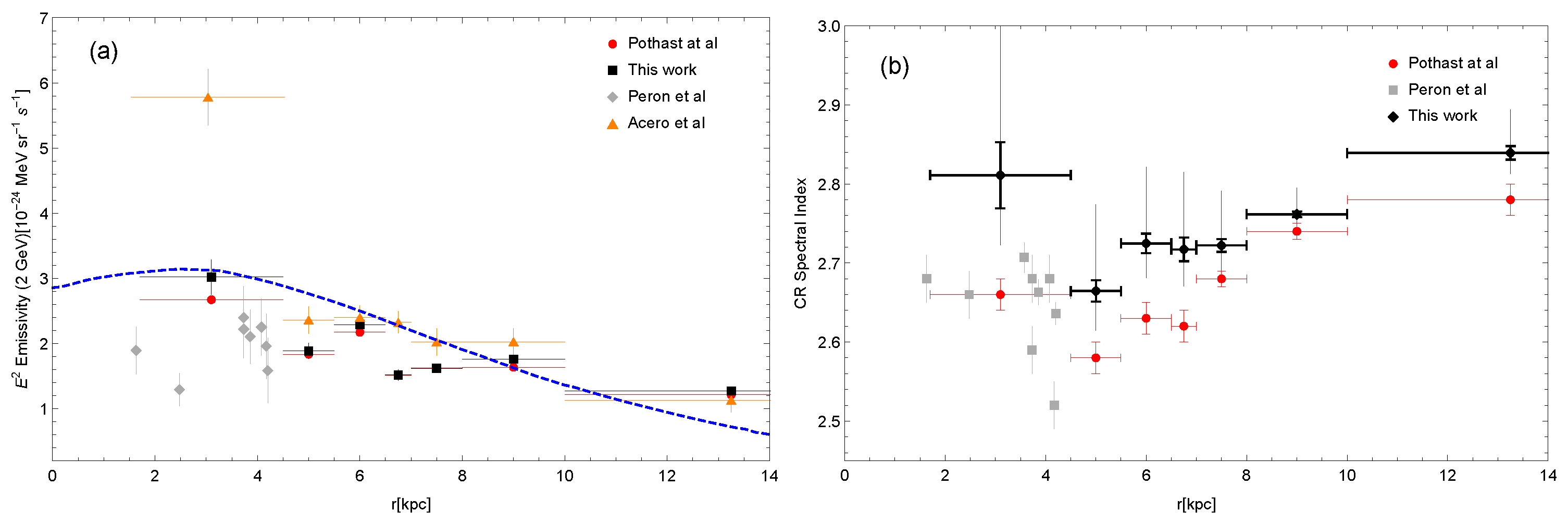This is particularly important because it was recently argued that the spectral index $\mathsf{\Gamma }$ of the extragalactic diffuse $\gamma$-ray flux observed by Fermi-LAT in the $1–100$ GeV energy range depends on the distance from the galactic centre. If this signal is attributed to the diffuse emission produced by CRs interactions with the interstellar gas, then the above feature can be interpreted as evidence of a continuous CR spectral hardening towards the galactic centre. This interpretation challenges, however, the paradigm of a uniform CR diffusion coefficient throughout the galaxy. The results of recent analyses of Fermi-LAT data at different distances from the galactic centres are reported in Figure 4, where we show the $\gamma$-ray emissivity per H atom at 2 GeV (left panel), which is a proxy of the CR spatial distribution in the galaxy, and the CR proton spectral index (right panel), obtained by adding 0.1 to the spectral indexes of the truly diffuse gamma emission [45]. The red and orange data points are obtained in [46,47], where Fermi-LAT data are analysed in rings at different distances from the galactic centre. We also show the $\gamma$-ray emission in the direction of giant molecular clouds obtained by [48].

The above results, however, are only valid if unresolved source contribution is negligible such that the total observed flux is associated with the “truly” diffuse component produced by the CR interaction with the interstellar gas. Unresolved PWNe, having a hard emission spectrum and a spatial distribution peaked at ∼$4\mathrm{kpc}$ from the galactic centre, can potentially account for the spectral index observed variation reported in the right panel of Figure 4. In order to check this possibility, we repeat the analysis performed by [46] by taking unresolved PWNe emission into account. Our results are given in

Table 4. Gamma-ray spectral indexes of the diffuse emission obtained by fitting the Fermi-LAT data with (${\mathsf{\Gamma }}_{\mathrm{BF}}$) and without (${\mathsf{\Gamma }}_1$) TeV PWNe unresolved contribution. The ${\mathsf{\Gamma }}_{\mathrm{BF}}$ values are given for two different assumptions on the luminosity index $\alpha$ of the PWNe population. The first error associated with ${\mathsf{\Gamma }}_{\mathrm{BF}}$ shows the systematic uncertainty, while the second is the statistical one; see text for details. The indexes ${\mathsf{\Gamma }}_1$ are taken from the previous analysis [46].

Ring $\left(\mathbf{kpc}\right)$	${\mathbf{\Gamma }}_1$	${\mathbf{\Gamma }}_{\mathbf{BF}}$ ($\mathit{\alpha }=1.8$)	${\mathbf{\Gamma }}_{\mathbf{BF}}$ ($\mathit{\alpha }=1.5$)
$1.7–4.5$	$2.56\pm 0.02$	$2.{71}_{-0.09}^{+0.19}\pm 0.01$	$2.{60}_{-0.03}^{+0.10}\pm 0.01$
$4.5–5.5$	$2.48\pm 0.02$	$2.{56}_{-0.05}^{+0.11}\pm 0.01$	$2.{50}_{-0.02}^{+0.06}\pm 0.01$
$5.5–6.5$	$2.53\pm 0.02$	$2.{62}_{-0.04}^{+0.10}\pm 0.01$	$2.{57}_{-0.01}^{+0.05}\pm 0.01$
$6.5–7$	$2.52\pm 0.02$	$2.{62}_{-0.05}^{+0.10}\pm 0.01$	$2.{56}_{-0.01}^{+0.05}\pm 0.01$
$7–8$	$2.58\pm 0.01$	$2.{62}_{-0.03}^{+0.07}\pm 0.008$	$2.{58}_{-0.008}^{+0.02}\pm 0.008$
$8–10$	$2.64\pm 0.01$	$2.{66}_{-0.01}^{+0.03}\pm 0.004$	$2.{64}_{-0.004}^{+0.01}\pm 0.004$
$10–16.5$	$2.68\pm 0.02$	$2.{74}_{-0.03}^{+0.05}\pm 0.009$	$2.{70}_{-0.008}^{+0.04}\pm 0.008$
$16.5–50$	$2.73\pm 0.05$	$2.{77}_{-0.04}^{+0.10}\pm 0.04$	$2.{73}_{-0.03}^{+0.08}\pm 0.04$

, where we report the spectral index of the “truly” diffuse component obtained by fitting the Fermi-LAT data with (${\mathsf{\Gamma }}_{\mathrm{BF}}$) and without (${\mathsf{\Gamma }}_1$), including the PWNe unresolved contribution. The indexes ${\mathsf{\Gamma }}_1$ coincide with those obtained by previous analysis [46]. The reported differences between ${\mathsf{\Gamma }}_{\mathrm{BF}}$ and ${\mathsf{\Gamma }}_1$ show that the inclusion of unresolved PWNe affects the CR spectral index, which can be increased up to 0.18 in the central ring (for the case $\alpha =1.8$). The first errors in Table 4 describe systematic uncertainties, and are obtained by simultaneously changing $(R_{\varphi },E_0,\beta )$ in the 3-dim parametric space defined as $R_{\varphi }=\left[250–1500\right]$, $E_0=\left[0.1–1.0\right]\mathrm{TeV}$ and $\beta =\left[1.9–2.5\right]$. The inclusion of systematic effects connected with the assumed source spectrum does not change our conclusion. Note that our estimates for systematic uncertainties are very conservative. The smaller (larger) values for ${\mathsf{\Gamma }}_{\mathrm{BF}}$ are obtained by assuming that all sources in the considered population have $\beta =1.9$ ($\beta =2.5$), $E_0=1.0\mathrm{TeV}$ ($E_0=0.1\mathrm{TeV}$) with marginal dependence on the considered $R_{\varphi }$, which correspond to an extremely unlikely physical situation. In our galaxy, TeV PWNe are expected to have a distribution of spectral properties with compensating effects among extreme assumptions. The central values for ${\mathsf{\Gamma }}_{\mathrm{BF}}$ obtained by integrating over the whole parametric space are shown in Table 4. In particular, a logarithmic uniform distribution is considered for the spectral break position and for the flux ratio, while for $\beta$, we assume a Gaussian distribution centred in $\beta =2.4$ with dispersion $0.15$ as reported in the HGPS catalogue [30].

For the case that produces the most relevant effects (i.e., $\alpha =1.8$), our results are also shown by the black data points in Figure 4. The thin error bars represent the systematic uncertainties conservatively estimated as discussed above. The thick error bars instead only include statistical uncertainties. The emissivity calculated in our work is similar to the one obtained by [46,48]. This is not surprising because the contribution of unresolved sources at 2 GeV is negligible and does not produce any significant effect. The results from three data sets are similar to the theoretical expectations for the CR distribution from GALPROP code [49] (dashed blue line). However, the inclusion of unresolved PWNe affects the CR spectral index that realigns with the locally observed value in the central ring, i.e., ∼2.8. The CR spectrum inferred from the Fermi-LAT observation of the large-scale diffuse emission still shows a residual difference with the local value in the other rings. However, the unresolved PWNe naturally account for a large part of the spectral index variation reported by previous analyses, weakening the evidence for CR spectral hardening in the inner galaxy.

3.5. The Sub-PeV Energy Domain

For the first time, the Tibet AS$\gamma$ collaboration provided evidence that the galactic diffuse $\gamma$-ray emission can be extended up to sub-PeV energies [7]. The origin of this high-energy diffuse emission is critically discussed in many recent works; see, for example, [50,51,52,53]. The Tibet AS$\gamma$ result is obtained as the total source-subtracted diffuse gamma-ray signal in the energy range of 100 TeV-PeV. This signal is expected to be due to the sum of the diffuse emission due to CR interactions with interstellar matter and the cumulative flux produced by sources that are too faint to be included in the TeVCAT catalogue. We argued in [21] that unresolved PWNe may account for a relevant part of it.

Following the previous sections, we can estimate the contribution due to unresolved sources by considering our reference model (first line in Table 1) and by extending the energy spectrum in the TeV energy range to higher energy as a power law with an exponential cut-off, i.e., $\phi \left(E_{\gamma }\right)\propto E_{\gamma }^{-\beta }exp\left(-E_{\gamma }/E_{\mathrm{cut}}\right)$. For definiteness, we select $E_{\mathrm{cut}}=500\mathrm{TeV}$ as the value for the cut-off energy. This quantity is still unconstrained, and our assumption implies that the source spectrum observed by H.E.S.S. in the range 1–100 TeV could be extrapolated in the sub-PeV region with a small suppression. In this respect, recent observations of high-energy sources provided by HAWC [54] and Tibet AS$\gamma$ [55] support the presence of a high-energy cut-off above 100 TeV, also compatible with theoretical expectations from leptonic emission [10]. As we are going to show in the following, the value that we adopted for $E_{\mathrm{cut}}$ moderately affects our flux predictions, particularly for the low-energy data points given by Tibet AS$\gamma$ that are relatively close to the range probed by H.E.S.S.

It is important to note that for energies $E_{\gamma }\ge 1\mathrm{PeV}$, photon absorption in the interstellar radiation field suppresses the flux from distant sources. The main contribution is due to interaction with the cosmic microwave background. We include this effect inside the function $\eta (E_{\gamma },{\varphi }_{\mathrm{th}})$ describing the average survival probability of photons with energy $E_{\gamma }$ emitted by sources; see [21,56] for details.

The cumulative differential emission of unresolved PWNe can be estimated as

$${\phi }_{\mathrm{NR}}\left(E_{\gamma }\right)=\phi \left(E_{\gamma }\right)\eta (E_{\gamma },{\mathsf{\Phi }}_{\mathrm{th}}){\mathsf{\Phi }}_{\mathrm{F}}\left({\varphi }_{\mathrm{th}}\right),$$

(32)

where $\phi \left(E_{\gamma }\right)$ is the average source emission spectrum, and the quantity ${\mathsf{\Phi }}_{\mathrm{F}}\left({\varphi }_{\mathrm{th}}\right)$ is the cumulative flux of faint sources defined in Equation (20) in a given region of the sky. As already discussed, the diffuse $\gamma$-ray flux measured by Tibet AS$\gamma$ in the sub-PeV energy range is obtained by subtracting/masking events within 0.5${}^{\circ }$ from galactic sources listed in the TeVCAT catalogue [31]. This catalogue is based on detection capabilities of TeV gamma-ray detectors. For this reason, we adopted a range for the flux detection threshold based on the performance of the H.E.S.S. detector covering the band ${\varphi }_{\mathrm{th}}=\left[0.01–0.1\right]{\varphi }_{\mathrm{Crab}}$.

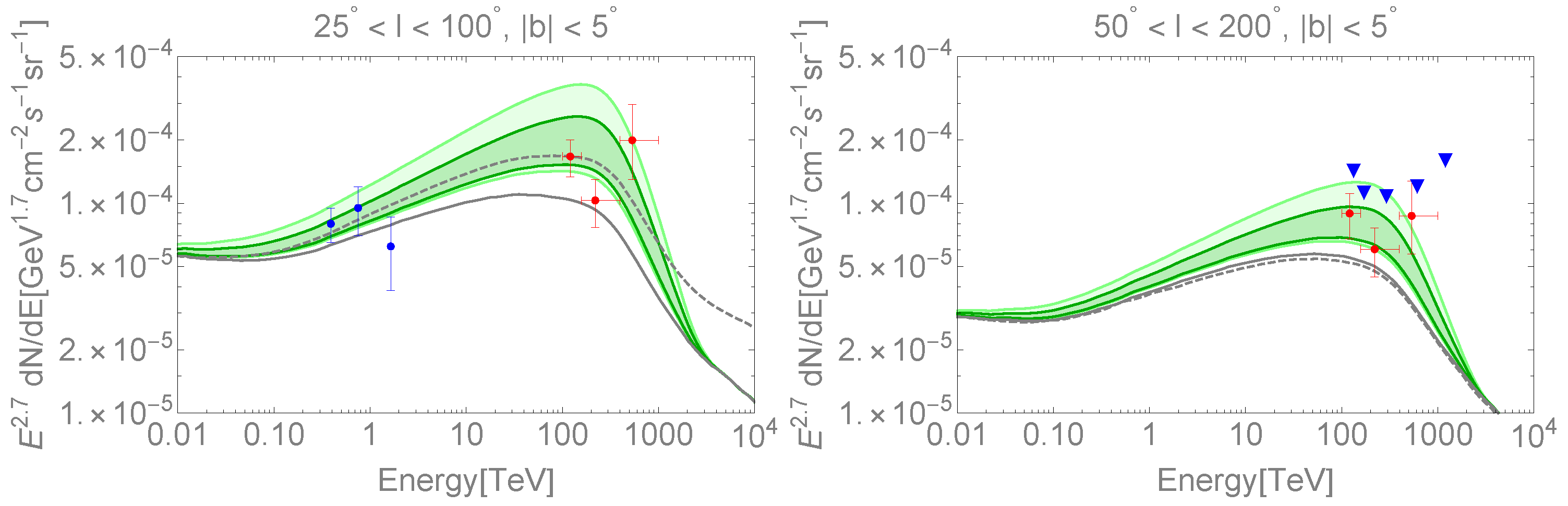
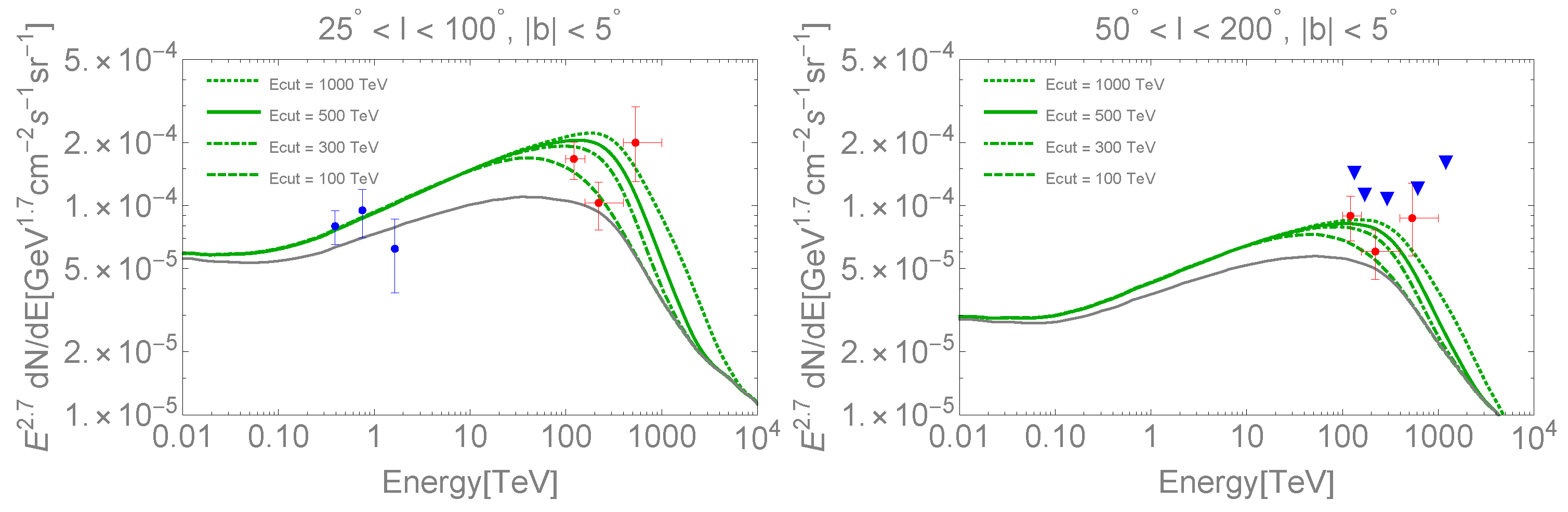
In Figure 5, we show our predictions for the total diffuse $\gamma$-ray flux (green band) as a function of $E_{\gamma }$ in the two sky regions probed by the Tibet AS$\gamma$ experiment [7]. The left panel shows the region ${25}^{\circ }<l<{100}^{\circ }$, while the right panel reports the region ${50}^{\circ }<l<{200}^{\circ }$; both of them correspond to the latitude range $\left|b\right|<5^{\circ }$. The contribution of unresolved sources is obtained as described in the previous paragraph, and the thickness of the darker green band shows the uncertainty due to the adopted flux detection threshold ${\varphi }_{\mathrm{th}}$. In particular, the upper and lower green lines are obtained by assuming ${\varphi }_{\mathrm{th}}=0.1{\varphi }_{\mathrm{Crab}}$ and ${\varphi }_{\mathrm{th}}=0.01{\varphi }_{\mathrm{Crab}}$, respectively. By including also the $1\sigma$ correlated uncertainties of the parameters describing the PWNe population, i.e., $L_{\max }$ and ${\tau }_{\mathrm{sd}}$, the total uncertainty band increases to the light-green one.

The truly diffuse emission, produced by CR interactions with the interstellar gas, is shown by grey solid lines in Figure 5 and corresponds to the “space-independent” model of [58]. Red data points show the diffuse flux measured by Tibet AS$\gamma$ with their 1$\sigma$ statistical errors. Finally, we show with grey dashed lines the truly diffuse flux estimated for the “space-dependent” model of [58]. These expectations are obtained by including the possibility of the hardening of the CR spectrum in the inner galaxy as suggested by Fermi-LAT data [46,47,59] and discussed in the previous section dedicated to the GeV energy range.

The results in Figure 5 show that the contribution due to unresolved sources, already not negligible at $E_{\gamma }\sim$ 1 TeV, becomes progressively more relevant as energy increases. The main reason is that PWNe are expected to have, on average, a harder spectrum (aside from energy cut-off effects) than the CR diffuse emission, in agreement with [12]. The cumulative flux produced by faint PWNe is estimated to be $49–154\%$ ($25–79\%$) of the truly diffuse signal in the region ${25}^{\circ }<l<{100}^{\circ }$ (${50}^{\circ }<l<{200}^{\circ }$) for $E_{\gamma }\simeq 150\mathrm{TeV}$. This conclusion is not changed if we repeat our analysis by only including the subsample of 22 bright HGPS sources presently showing a clear association with PWNe. In this case, the best-fit values of the population parameters change to ${\tau }_{\mathrm{sd}}=1.1\times {10}^3\mathrm{yr}$ and $L_{\max }=6.2\times {10}^{35}\mathrm{erg}{\mathrm{s}}^{-1}$. The contribution due to unresolved sources decreases as expected; however, the prediction for the total diffuse emission is still included within the light-green band in Figure 5.

We also investigate the dependence of our prediction on the adopted value of the cut-off energy. As is evident in Figure 6, the role of unresolved PWNe is always relevant for an energy cut-off in the range from 100 TeV to 1 PeV, in particular for the lowest data point of Tibet AS$\gamma$. In this case, green lines show the total diffuse gamma-ray prediction by assuming the intermediate value of ${\varphi }_{\mathrm{th}}\sim 0.05{\varphi }_{\mathrm{Crab}}$ for the sensitivity threshold. The unresolved source flux at 150 TeV decreases by ∼17% (∼68%) with respect to the reference case $E_{\mathrm{cut}}=500$ TeV if we assume a lower energy cut-off $E_{\mathrm{cut}}=300$ TeV ($E_{\mathrm{cut}}=100$ TeV). Further, we discuss the effect of changing the assumed source spectral index, e.g., for $\beta =2.4$ ($\beta =2.5$), the unresolved source flux at 150 TeV decreases by ∼32% (∼54%) with respect to the reference assumption $\beta =2.3$. In all the considered cases, predictions for the total diffuse $\gamma$-ray emission are still consistent with the first two data points of Tibet AS$\gamma$.

An additional piece of interesting information we can extract from our analysis is the typical age of PWNe mainly contributing to the unresolved flux. We show the relative contribution to unresolved emission as a function of the PWNe age in Figure 7, in which thick lines represents the sky region $\left|b\right|<5^{\circ }$ and ${25}^{\circ }<l<{100}^{\circ }$, while dashed ones correspond to the most lateral region ${50}^{\circ }<l<{200}^{\circ }$. For an optimal sensitivity threshold of ${\varphi }_{\mathrm{th}}=0.01{\varphi }_{\mathrm{Crab}}$ (blue lines), the dominant contribution to the unresolved diffuse flux is due to PWNe with an age of about t ∼ (22–33) kyr, depending on the sky region considered. A young population of unresolved PWNe peak around t ∼ (7–11) kyr is instead dominating the unresolved flux for ${\varphi }_{\mathrm{th}}=0.1{\varphi }_{\mathrm{Crab}}$ (red lines). Nevertheless, the contribution of old sources like TeV halos (with age $>100$ kyr) to the diffuse flux is less than $20\%$.

It is important to note that our calculations naturally reproduce the Tibet AS$\gamma$ results both in the low- and high-longitude OW, supporting the conclusion that the unresolved PWNe can provide a non-negligible contribution in this energy range. Additional observations in the TeV and PeV energy domains will test our models in the future. We expect that CTA should detect ∼280 PWNe in the whole galaxy by assuming a sensitivity threshold as in [13] and considering a typical source size of 10 pc.

As the last remark, by comparing our results with the “space-dependent” model [58] for CR diffuse emission in Figure 6, we see that unresolved PWNe produce in the ${25}^{\circ }\le l\le {100}^{\circ }$ sky region a similar effect to CR spectral hardening in the inner galaxy. However, the above statement is not valid for the longitude range ${50}^{\circ }\le l\le {200}^{\circ }$. In this OW, the CR spectral hardening hypothesis has marginal effects because CR diffuse emission is mainly produced, due to geometrical reasons, from regions at galactic radii larger than $8.5$ kpc, i.e., outside the inner galaxy. On the contrary, unresolved sources, being distributed throughout the galaxy, provide a non-vanishing contribution, even at large longitudes. This point is extremely important because it provides the possibility to distinguish between these two effects in present and future experiments.

4. Summary

In this work, we report our studies on the galactic population of PWNe and we discuss the contribution of faint PWNe to the total diffuse gamma-ray emission observed in the whole energy range from GeV to sub-PeV. Our golden energy region to investigate the properties of PWNe is the TeV energy band, where their contribution becomes statistically dominant compared to other galactic sources. We construct a statistical analysis of the HGPS data, providing fairly stable and robust predictions of the characteristics of the pulsars population powering the observed TeV PWNe. These results agree with previous studies on TeV pulsars [38] while showing some tensions with the properties of the radio pulsars population [36]. This point deserves further investigation in the future.

The knowledge of the PWNe average properties allows us to estimate the total gamma-ray flux in the range of 1–100 TeV produced by these sources. By adding the additional information of a flux energy threshold above which the HGPS source catalogue is complete, we can infer the expected cumulative contribution due to faint PWNe, i.e., the diffuse flux due to unresolved sources. This contribution is not negligible and accounts for ∼40% of the total contribution due to detected sources in the TeV energy domain. This information strengthens the tension already discussed in [42] between the gamma-ray signal measured by H.E.S.S. and the possibility that the CR spectral index decreases toward the galactic centre (hardening hypothesis).

Our results in the GeV and sub-PeV energy ranges point in the same direction. In both cases, we need to extrapolate what we learned in the TeV range relying on suitable assumptions on the PWNe spectrum. In particular, the extension to the GeV energy range is delicate, and we use a phenomenological approach based on energy-integrated quantities of the identified PWNe observed in both GeV and TeV source catalogues. The considered spectrum is consistent with theoretical predictions of PWNe emissions [43,44], and it can be refined in the future by adopting a dynamical model for PWNe gamma-ray emissions, shown, for example, in [37]. Our analysis shows that the inferred cumulative contribution due to unresolved PWNe in the 1–100 GeV energy range is not negligible. The inclusion of this additional gamma-ray component in the analysis of the total diffuse emission measured by Fermi-LAT changes the inferred CR spectral index. Interestingly, when a fraction of the observed Fermi-LAT gamma-ray signal is associated to unresolved PWNe, the cosmic-ray spectral index moves in the direction to flatten its value to the local one as expected for the standard assumption of cosmic-ray diffusion in the galactic plane.

Moving to the sub-PeV energy range, we estimate the contribution due to unresolved PWNe in the two OWs of the Tibet AS$\gamma$ experiment. The prediction in this case only requires to introduce a spectral energy cut-off for the TeV PWNe population. Despite the value of the energy cut-off being uncertain, we show that unresolved PWNe provide a relevant contribution in this energy range unless the spectral energy cut-off moves below 100 TeV (in contrast with recent observations [54]). Moreover, the inclusion of the unresolved PWNe contribution produces a better description of the Tibet AS$\gamma$ data than CR spectral hardening.