Differential Geometry of the Family of Helical Hypersurfaces with a Light-like Axis in Minkowski Spacetime ${\mathbb{L}}^4$

Abstract

We investigate the class of helical hypersurfaces parametrized by $\mathfrak{x}=\mathfrak{x}(u,v,w)$, characterized by a light-like axis in Minkowski spacetime ${\mathbb{L}}^4$. We determine the matrices that represent the fundamental forms, Gauss map, and shape operator of $\mathfrak{x}$. Furthermore, employing the Cayley–Hamilton theorem, we compute the curvatures associated with $\mathfrak{x}$. We explore the conditions under which the curvatures of $\mathfrak{x}$ possess the property of being umbilical. Moreover, we provide the Laplace–Beltrami operator for the family of helical hypersurfaces with a light-like axis in ${\mathbb{L}}^4$.

1. Introduction

Mathematicians, physicists, and other researchers have dedicated significant efforts to the study of hypersurfaces over the years. Let us briefly touch upon some of the studies that have been conducted.

Obata [1] established certain conditions under which a Riemannian manifold can be isometrically equivalent to a sphere. Takahashi [2] demonstrated that a connected Euclidean submanifold is of 1-type if and only if it is either minimal in ${\mathbb{E}}^m$ or minimal in a hypersphere within ${\mathbb{E}}^m$. He focused on minimal surfaces and determined that spheres are the only surfaces satisfying the condition $\Delta x=\lambda x,$ where $\Delta$ describes the Laplace–Beltrami operator, $\lambda \in \mathbb{R}\backslash \left\{0\right\}$, and x realizes a minimal immersion in a sphere, the radius of which is entirely determined by $\lambda$. Chern et al. [3] investigated minimal submanifolds of a sphere with a second fundamental form of constant length. Cheng and Yau [4] explored hypersurfaces with constant scalar curvature, while Lawson [5] delved into the study of minimal submanifolds and provided a comprehensive definition of the Laplace–Beltrami operator.

Chen [6,7,8,9] provided a comprehensive study of finite-type submanifolds that can be immersed into ${\mathbb{E}}^m$ (or ${\mathbb{E}}_{\nu }^m$) using a finite set of eigenfunctions of their Laplacian. The works of [7,10,11] explored certain aspects of 2-type closed submanifolds with spherical geometry. Garay [12] focused on extending Takahashi’s theorem in the context of ${\mathbb{E}}^m$. Additionally, Chen and Piccinni [13] researched submanifolds in ${\mathbb{E}}^m$ that possess a finite-type Gauss map. In the realm of space forms, Chen et al. [14] dedicated four decades to the study of 1-type submanifolds and the 1-type Gauss map. These investigations have contributed significantly to our understanding of the properties and characteristics of these submanifolds.

In the three-dimensional Euclidean space ${\mathbb{E}}^3$, a significant result, known as Bour’s theorem [15], emerges when considering the properties of ruled surfaces, specifically helicoidal or helical surfaces. Do Carmo and Dajczer [16] utilized Bour’s theorem to establish the existence of a two-parameter family of helical surfaces that are isometric to a given helical surface. Ferrandez et al. [17] proved that surfaces satisfying $\Delta H=AH$ are either minimal, open portions of a sphere, or open portions of a right circular cylinder, where H denotes the mean curvature vector field in an $(n+1)$-dimensional real space, $A\in Mat(3,3)$. Choi and Kim [18] carried out a classification of minimal helicoids based on the pointwise 1-type Gauss map of the first kind. Garay [19] studied a specific class of revolution surfaces that exhibit finite-type characteristics. Dillen et al. [20] discovered that the only surfaces satisfying $\Delta r=Ar+B$ (where $A\in Mat(3,3)$ and $B\in Mat(3,1)$) are minimal surfaces, spheres, and circular cylinders. Stamatakis and Zoubi [21] focused on revolution surfaces satisfying ${\Delta }^{\mathbb{III}}x=Ax$. Senoussi and Bekkar [22] investigated finite-type helical surfaces $M^2$ with respect to the fundamental forms $\mathbb{I},\mathbb{II}$, and $\mathbb{III}$, where the position vector field $r(u,v)$ satisfies the condition ${\Delta }^{J}r=Ar$ (with $J=\mathbb{I},\mathbb{II},\mathbb{III}$, and $A\in Mat(3,3)$). Kim et al. [23] introduced the Cheng–Yau operator and studied the Gauss map of revolution surfaces. These various studies have contributed to a deeper understanding of the properties and classifications of surfaces in the three-dimensional Euclidean space.

Within a three-dimensional Minkowski space ${\mathbb{L}}^3:={\mathbb{E}}_1^3$, several researchers have delved into the properties of helical surfaces with various axis types, such as space-like, time-like, and light-like. Beneki et al. [24] explored helical surfaces in the Minkowski space, while Güler and Turgut Vanlı [25] investigated Bour’s theorem within this context.

Mira and Pastor [26] focused on helical maximal surfaces in the three-dimensional Minkowski space, while Kim and Yoon [27,28,29] examined both ruled and rotational surfaces within the pseudo-Euclidean space. It is also worth mentioning references [25,30,31] in this field. These collective studies contribute to our understanding of the properties and characteristics of helical surfaces within the Minkowski geometry framework.

In the realm of the four-dimensional Euclidean space ${\mathbb{E}}^4$, various researchers have explored different aspects of hypersurfaces and surfaces. Moore [32,33] provided a general treatment of rotational surfaces. Hasanis and Vlachos [34] focused on hypersurfaces with a harmonic mean curvature vector field. Cheng and Wan [35] obtained complete hypersurfaces with a constant mean curvature (CMC). Arslan et al. [36] introduced the Vranceanu surface, which exhibits a pointwise 1-type Gauss map. They also introduced generalized rotational surfaces [37]. Magid et al. [38] investigated affine umbilical surfaces within a four-dimensional space. Scharlach [39] studied the affine geometry of surfaces and hypersurfaces in a four-dimensional space.

Arslan et al. [40] delved into the study of Weyl pseudosymmetric hypersurfaces. Arslan et al. [41] focused on meridian surfaces in a four-dimensional space with a pointwise 1-type Gauss map. Yoon [42] explored rotation surfaces with a finite-type Gauss map in a four-dimensional space. Güler et al. [43] investigated helical hypersurfaces, while Güler et al. [44] focused on the Gauss map and the third Laplace–Beltrami operator of rotational hypersurfaces.

Within Minkowski’s four-dimensional space ${\mathbb{L}}^4$, several investigations have contributed to our understanding of different types of surfaces and hypersurfaces. Ganchev and Milousheva [45] explored the analogs of the surfaces discussed in [32,33]. Arvanitoyeorgos et al. [46] identified conditions under which a mean curvature vector field of a three-dimensional hypersurface $M_1^3$ satisfies the equation $\Delta H=\alpha H$ (with $\alpha$ being a constant), resulting in a constant mean curvature (CMC) for $M_1^3$. Arslan and Milousheva [47] focused on meridian surfaces of elliptic and hyperbolic types with a pointwise 1-type Gauss map. Güler [48] introduced helical hypersurfaces within Minkowski’s four-dimensional space.

In a different line of research, Iliadis [49] investigated the fuzzy algebraic modeling of paradoxes in spatiotemporal time series within cosmic-scale kinematics. Leuenberger [50] examined the emergence of Minkowski spacetime through simple deterministic graph rewriting. Güler [51] introduced generalized helical hypersurfaces with a time-like axis in Minkowski spacetime.

In Minkowski space with the metric signature $(+,+,+,-)$, let us consider the behavior of helical hypersurfaces with the specified space-like and time-like axes.

If the axis of a helical hypersurface in Minkowski space has the vector $(1,0,0,0)$, it represents a space-like direction. In this case, the hypersurface will exhibit a rotational behavior around the axis. As we move along the axis, the hypersurface will undergo a rotation, forming a helical shape. The precise mathematical expression of the helical hypersurface having a space-like axis will dictate the specific characteristics of the helix, such as its curvature, spiral rate, and any additional variations or distortions.

If the axis of a helical hypersurface in Minkowski space has the vector $(0,0,0,1)$, it represents a time-like direction. In this case, the hypersurface will exhibit temporal behavior along the axis. As we move along the axis, the hypersurface will undergo temporal changes, potentially resulting in oscillatory or pulsating patterns. The mathematical form of the helical hypersurface having a time-like axis will determine the specific nature of these temporal changes and any associated deformations or twists.

It is important to note that the behaviors of helical hypersurfaces in Minkowski space are influenced by various factors, including the specific mathematical equations defining the hypersurface, the curvature, and any additional constraints or forces acting upon it. The author of references [48,51] provided a comprehensive explanation, which included the relevant equations and mathematical derivations to fully describe the behaviors of helical hypersurfaces with space-like or time-like axes in Minkowski space with metric signature $(+,+,+,-)$.

The aim of this study is to comprehensively investigate a specific class of helical hypersurfaces parametrized by $\mathfrak{x}=\mathfrak{x}(u,v,w)$, possessing a distinctive light-like axis in Minkowski spacetime ${\mathbb{L}}^4$. Our objectives are as follows.

We aim to determine the matrices representing the fundamental forms of the helical hypersurfaces described by $\mathfrak{x}$. By analyzing these forms, we will gain insights into the intrinsic properties and geometric characteristics of hypersurfaces. We will explore the Gauss map associated with the parameterization $\mathfrak{x}$ and calculate the corresponding shape operator. Understanding the Gauss map and shape operator will provide valuable information about the curvature and shape of the helical hypersurfaces. Utilizing the Cayley–Hamilton theorem, we will compute the curvatures associated with the helical hypersurfaces. By investigating these curvatures, we aim to identify any unique features or properties exhibited by the hypersurfaces. Specifically, we will focus on identifying conditions under which the curvatures display the property of being umbilical. We will provide an in-depth analysis of the Laplace–Beltrami operator for the family of helical hypersurfaces with a light-like axis in ${\mathbb{L}}^4$. This operator will allow us to study the behaviors of various differential operators on these hypersurfaces, contributing to a comprehensive understanding of their mathematical properties.

By achieving these objectives, we aim to advance our knowledge of helical hypersurfaces with a light-like axis in Minkowski spacetime, unravel their intrinsic characteristics, and explore their unique geometric and mathematical properties.

Our main focus is on a specific family of helical hypersurfaces denoted by $\mathfrak{x}=\mathfrak{x}\left(u,v,w\right)$, which is formed by rotating the light-like axis $\left(0,0,1,1\right)$ in Minkowski’s four-dimensional space ${\mathbb{L}}^4$.

In Section 2, we delve into the properties of ${\mathbb{L}}^4$, providing formulations for the components of the fundamental forms, Gauss map, and shape operator applicable to any hypersurface.

Section 3 is dedicated to describing the family of helical hypersurfaces within ${\mathbb{L}}^4$. By utilizing the Cayley–Hamilton theorem, we derive the curvatures of these hypersurfaces and compute the curvatures specifically for the helical hypersurfaces with a light-like axis. Additionally, we establish various relationships among the curvatures ${\mathbb{K}}_{j=0,\dots ,3}$ of $\mathfrak{x}$.

Moving on to Section 4, we demonstrate the relationship $\Delta \mathfrak{x}=\mathcal{L}\mathfrak{x}$, where $\mathcal{L}$ represents a $4\times 4$ matrix.

Finally, in Section 5, we present the conclusions drawn from our comprehensive investigation.

2. Preliminaries

In this section, we provide basic facts and definitions and describe notations used in this paper.

Let ${\mathbb{L}}^m$ denote the semi-Euclidean (i.e., Minkowski) m-space with the semi-Euclidean metric tensor given by $\tilde{g}={\langle ,\rangle }_{{\mathbb{L}}^m}={\displaystyle \sum _{i=1}^{m-1}}d{x}_i^2-d{x}_m^2,$ where $(x_1,x_2,\dots ,x_m)$ is an element of length (or Lorentz metric) and $x_i$ are the pseudo-Euclidean coordinates of type $(m-1,1)$. We consider an m-dimensional semi-Riemannian submanifold M of a space ${\mathbb{L}}^m$. We denote the Levi–Civita connections [52] of the manifold $\tilde{M},$ and its submanifold M of ${\mathbb{L}}^m$ by $\tilde{\nabla },$ $\nabla ,$ respectively. We use letters $X,Y,Z,W$ (resp., $\xi ,\eta$) to denote vector fields that are tangent (resp., normal) to M. The Gauss and Weingarten formulas are given, respectively, by

$$\begin{array}{rrr}\hfill {\tilde{\nabla }}_{X}Y& =& {\nabla }_{X}Y+h(X,Y),\hfill \\ \hfill {\tilde{\nabla }}_X\xi & =& -A_{\xi }\left(X\right)+D_X\xi ,\hfill \end{array}$$

where h, D, and A are the second fundamental form, the normal connection, and the shape operator of M, respectively.

For each $\xi \in T_p^{\perp }M$, the shape operator $A_{\xi }$ is a symmetric endomorphism of the tangent space $T_{p}M$ at $p\in M$. The shape operator and the second fundamental form are related by

$$〈h(X,Y),\xi 〉=〈A_{\xi }X,Y〉.$$

The Gauss and Codazzi equations are given, respectively, by

$$\begin{array}{ccc}\hfill \langle R(X,Y,)Z,W\rangle & =& \langle h(Y,Z),h(X,W)\rangle -\langle h(X,Z),h(Y,W)\rangle ,\hfill \\ \hfill \left({\overline{\nabla }}_{X}h\right)(Y,Z)& =& \left({\overline{\nabla }}_{Y}h\right)(X,Z),\hfill \end{array}$$

where $R,R^D$ are the curvature tensors associated with connections ∇ and D, respectively, and $\overline{\nabla }h$ is defined by

$$\left({\overline{\nabla }}_{X}h\right)(Y,Z)=D_{X}h(Y,Z)-h({\nabla }_{X}Y,Z)-h(Y,{\nabla }_{X}Z).$$

Now, let M be an oriented hypersurface in the Minkowski space ${\mathbb{L}}^{n+1}$, $\mathbb{S}$ be the shape operator, and x be a position vector of it. We consider a local orthonormal frame field $\{e_1,e_2,\dots ,e_n\}$, consisting of principal directions of M, corresponding to the principal curvature $k_i$ for $i=1,2,\dots ,n$. Let the dual basis of this frame field be $\{{\theta }_1,{\theta }_2,\dots ,{\theta }_n\}$. Then, the first structural equation of the Cartan is given by

$$d{\theta }_i=\sum _{i=1}^n{\theta }_j\wedge {\omega }_{ij},i,j=1,2,\dots ,n,$$

where ${\omega }_{ij}$ denotes the connection forms corresponding to the chosen frame field. We denote the Levi–Civita connection of M of ${\mathbb{L}}^{n+1}$ by ∇. Then, from the Codazzi equation, we have

$$\begin{array}{ccc}\hfill e_i\left(k_j\right)& =& {\omega }_{ij}\left(e_j\right)(k_i-k_j),\hfill \\ \hfill {\omega }_{ij}\left(e_l\right)(k_i-k_j)& =& {\omega }_{il}\left(e_j\right)(k_i-k_l)\hfill \end{array}$$

for distinct $i,j,l=1,2,\dots ,n$.

We put $s_j={\sigma }_j(k_1,k_2,\dots ,k_n)$, where ${\sigma }_j$ is the j-th elementary symmetric function given by

$${\sigma }_j(a_1,a_2,\dots ,a_n)=\sum _{1\le i_1<i_2<\dots <i_j\le n}{a}_{i_1}{a}_{i_2}\dots a_{i_j}.$$

We use the following notation

$$r_i^j={\sigma }_j(k_1,k_2,\dots ,k_{i-1},k_{i+1},k_{i+2},\dots ,k_n).$$

By the definition, we have $r_i^0=1$ and $s_{n+1}=s_{n+2}=\cdots =0$. We call the function $s_k$ as the k-th mean curvature of M. We would like to note that functions $H=\frac{1}{n}{s}_1$ and $K=s_n$ are called the mean curvature and the Gauss–Kronecker curvature of M, respectively. In particular, M is said to be j-minimal if $s_j\equiv 0$ on M. See also [53,54].

In ${\mathbb{L}}^{n+1},$ to find the curvature formulas ${\mathbb{K}}_i$, where $i=0,1,\dots ,n,$ firstly, we use the characteristic polynomial ${\mathcal{P}}_{\mathbb{S}}\left(\zeta \right)=0$:

$$\sum _{k=0}^n{\left(-1\right)}^k{s}_k{\zeta }^{n-k}=\det (\mathbb{S}-\zeta {\mathcal{I}}_n)=0,$$

where ${\mathcal{I}}_n$ denotes the identity matrix of order $n.$ Then, we obtain the curvature formulas $\left(\genfrac{}{}{0pt}{}{n}{i}\right){\mathbb{K}}_i=s_i$. That is, $\left(\genfrac{}{}{0pt}{}{n}{0}\right){\mathbb{K}}_0=s_0=1$ (by definition), $\left(\genfrac{}{}{0pt}{}{n}{1}\right){\mathbb{K}}_1=s_1,\dots ,\left(\genfrac{}{}{0pt}{}{n}{n}\right){\mathbb{K}}_n=s_n.$

The k-th fundamental form of the manifold M can be described by $\mathbb{I}\left({\mathbb{S}}^{k-1}\left(X\right),Y\right)=〈{\mathbb{S}}^{k-1}\left(X\right),Y〉$. Therefore, we have the following Equation.

$$\sum _{i=0}^n{\left(-1\right)}^i\left(\genfrac{}{}{0pt}{}{n}{i}\right){\mathbb{K}}_i\mathbb{I}\left({\mathbb{S}}^{n-i}\left(X\right),Y\right)=0.$$

For a more in-depth understanding, we recommend referring to Kühnel [54] for additional details and comprehensive information on the subject matter.

Let $\mathfrak{x}=\mathfrak{x}(u,v,w)$ be an immersion from $M\subset {\mathbb{E}}^3$ to ${\mathbb{L}}^4=({\mathbb{R}}_1^4,{〈.,.〉}_{{\mathbb{L}}^4})$. A space-time M is isometric to Minkowski’s four-dimensional space, which is a connected time-oriented four-dimensional Lorentz manifold. See O’Neill’s work [55] for details.

Definition 1.

In ${\mathbb{L}}^4,$ a Lorentzian inner product of two vectors is defined by

$${〈\overrightarrow{\mathfrak{a}},\overrightarrow{\mathfrak{b}}〉}_{{\mathbb{L}}^4}={\mathfrak{a}}_1{\mathfrak{b}}_1+{\mathfrak{a}}_2{\mathfrak{b}}_2+{\mathfrak{a}}_3{\mathfrak{b}}_3-{\mathfrak{a}}_4{\mathfrak{b}}_4,$$

where $\overrightarrow{\mathfrak{a}}=({\mathfrak{a}}_1,{\mathfrak{a}}_2,{\mathfrak{a}}_3,{\mathfrak{a}}_4),\overrightarrow{\mathfrak{b}}=({\mathfrak{b}}_1,{\mathfrak{b}}_2,{\mathfrak{b}}_3,{\mathfrak{b}}_4).$

For the sake of brevity, we will just use $〈.,.〉$ instead of ${〈.,.〉}_{{\mathbb{L}}^4}.$

Definition 2.

In ${\mathbb{L}}^4$, a Lorentzian triple vector product is determined by

$$\overrightarrow{\mathfrak{a}}\times \overrightarrow{\mathfrak{b}}\times \overrightarrow{\mathfrak{c}}=\det \left(\begin{array}{cccc}{e}_1\hfill & e_2\hfill & e_3\hfill & -e_4\hfill \\ {\mathfrak{a}}_1\hfill & {\mathfrak{a}}_2\hfill & {\mathfrak{a}}_3\hfill & {\mathfrak{a}}_4\hfill \\ {\mathfrak{b}}_1\hfill & {\mathfrak{b}}_2\hfill & {\mathfrak{b}}_3\hfill & {\mathfrak{b}}_4\hfill \\ {\mathfrak{c}}_1\hfill & {\mathfrak{c}}_2\hfill & {\mathfrak{c}}_3\hfill & {\mathfrak{c}}_4\hfill \end{array}\right)$$

with the vectors denoted by $\overrightarrow{\mathfrak{a}}=({\mathfrak{a}}_1,{\mathfrak{a}}_2,{\mathfrak{a}}_3,{\mathfrak{a}}_4),\overrightarrow{\mathfrak{b}}=({\mathfrak{b}}_1,{\mathfrak{b}}_2,{\mathfrak{b}}_3,{\mathfrak{b}}_4),\overrightarrow{\mathfrak{c}}=({\mathfrak{c}}_1,{\mathfrak{c}}_2,{\mathfrak{c}}_3,{\mathfrak{c}}_4)$, and $e_{i=1,2,3,4}$ determine the generators of ${\mathbb{E}}^4$, “det” describes the determinant of the matrix.

Definition 3.

For a hypersurface $\mathfrak{x}$ in Minkowski’s four-dimensional space ${\mathbb{L}}^4$, the fundamental forms are described by

$$\mathbb{I}={\left({\mathfrak{g}}_{ij}\right)}_{3\times 3},\mathbb{II}={\left({\mathfrak{h}}_{ij}\right)}_{3\times 3},\mathbb{III}={\left({\mathfrak{t}}_{ij}\right)}_{3\times 3},$$

(1)

where $\left({\mathfrak{g}}_{ij}\right),\left({\mathfrak{h}}_{ij}\right),\left({\mathfrak{t}}_{ij}\right)$ denote the symmetric first, second, and third fundamental form matrices, respectively. Here, the components of the matrices are given by

$$\begin{array}{ccc}{\mathfrak{g}}_{11}=〈{\mathfrak{x}}_u,{\mathfrak{x}}_u〉,\hfill & {\mathfrak{g}}_{12}=〈{\mathfrak{x}}_u,{\mathfrak{x}}_v〉={\mathfrak{g}}_{21},\hfill & {\mathfrak{g}}_{13}=〈{\mathfrak{x}}_u,{\mathfrak{x}}_w〉={\mathfrak{g}}_{31},\hfill \\ \\ {\mathfrak{g}}_{22}=〈{\mathfrak{x}}_v,{\mathfrak{x}}_v〉,\hfill & {\mathfrak{g}}_{23}=〈{\mathfrak{x}}_v,{\mathfrak{x}}_w〉={\mathfrak{g}}_{32},\hfill & {\mathfrak{g}}_{33}=〈{\mathfrak{x}}_w,{\mathfrak{x}}_w〉,\hfill \\ \\ {\mathfrak{h}}_{11}=〈{\mathfrak{x}}_{uu},\mathbb{G}〉,\hfill & {\mathfrak{h}}_{12}=〈{\mathfrak{x}}_{uv},\mathbb{G}〉={\mathfrak{h}}_{21},\hfill & {\mathfrak{h}}_{13}=〈{\mathfrak{x}}_{uw},\mathbb{G}〉={\mathfrak{h}}_{31},\hfill \\ \\ {\mathfrak{h}}_{22}=〈{\mathfrak{x}}_{vv},\mathbb{G}〉,\hfill & {\mathfrak{h}}_{23}=〈{\mathfrak{x}}_{vw},\mathbb{G}〉={\mathfrak{h}}_{32},\hfill & {\mathfrak{h}}_{33}=〈{\mathfrak{x}}_{ww},\mathbb{G}〉,\hfill \\ \\ {\mathfrak{t}}_{11}=〈{\mathbb{G}}_u,{\mathbb{G}}_u〉,\hfill & {\mathfrak{t}}_{12}=〈{\mathbb{G}}_u,{\mathbb{G}}_v〉={\mathfrak{t}}_{21},\hfill & {\mathfrak{t}}_{13}=〈{\mathbb{G}}_u,{\mathbb{G}}_w〉={\mathfrak{t}}_{31},\hfill \\ \\ {\mathfrak{t}}_{22}=〈{\mathbb{G}}_v,{\mathbb{G}}_v〉,\hfill & {\mathfrak{t}}_{23}=〈{\mathbb{G}}_v,{\mathbb{G}}_w〉={\mathfrak{t}}_{32},\hfill & {\mathfrak{t}}_{33}=〈{\mathbb{G}}_w,{\mathbb{G}}_w〉,\hfill \end{array}$$

${\mathfrak{x}}_u=\frac{\partial \mathfrak{x}}{\partial u},$ ${\mathfrak{x}}_{uv}=\frac{{\partial }^2\mathfrak{x}}{\partial u\partial v},$ ${\mathbb{G}}_u=\frac{\partial \mathbb{G}}{\partial u},$ etc., and

$$\mathbb{G}=\frac{{\mathfrak{x}}_u\times {\mathfrak{x}}_v\times {\mathfrak{x}}_w}{∥{\mathfrak{x}}_u\times {\mathfrak{x}}_v\times {\mathfrak{x}}_w∥}$$

(2)

determines the Gauss map of $\mathfrak{x}$.

For a more detailed exploration within the Euclidean framework, we recommend consulting references [43,44].

Definition 4.

In Minkowski spacetime ${\mathbb{L}}^4$, a hypersurface $\mathfrak{x}$ is characterized by the following relations:

$$\begin{array}{c}\mathbb{S}={\mathbb{I}}^{-1}·\mathbb{II}={\mathbb{II}}^{-1}·\mathbb{III}={\mathbb{III}}^{-1}·\mathbb{IV},\hfill \end{array}$$

where $\mathbb{S}$ represents the shape operator, and $\mathbb{I}$, $\mathbb{II}$, $\mathbb{III}$, and $\mathbb{IV}={\left({\mathfrak{f}}_{ij}\right)}_{3\times 3}$ describe the fundamental forms of the hypersurface $\mathfrak{x}$. Thus, the shape operator matrix of the hypersurface $\mathfrak{x}$ is given by

$$\mathbb{S}=\frac{1}{\mathfrak{g}}\left(\begin{array}{ccc}{\mathfrak{s}}_{11}& {\mathfrak{s}}_{12}& {\mathfrak{s}}_{13}\\ {\mathfrak{s}}_{21}& {\mathfrak{s}}_{22}& {\mathfrak{s}}_{23}\\ {\mathfrak{s}}_{31}& {\mathfrak{s}}_{32}& {\mathfrak{s}}_{33}\end{array}\right),$$

(3)

where

$$\begin{array}{ccc}\hfill {\mathfrak{s}}_{11}& =& \left({\mathfrak{g}}_{22}{\mathfrak{g}}_{33}-{\mathfrak{g}}_{23}^2\right){\mathfrak{h}}_{11}+\left({\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}{\mathfrak{g}}_{33}\right){\mathfrak{h}}_{12}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{22}\right){\mathfrak{h}}_{13},\hfill \\ \\ \hfill {\mathfrak{s}}_{12}& =& \left({\mathfrak{g}}_{22}{\mathfrak{g}}_{33}-{\mathfrak{g}}_{23}^2\right){\mathfrak{h}}_{12}+\left({\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}{\mathfrak{g}}_{33}\right){\mathfrak{h}}_{22}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{22}\right){\mathfrak{h}}_{23},\hfill \\ \\ \hfill {\mathfrak{s}}_{13}& =& \left({\mathfrak{g}}_{22}{\mathfrak{g}}_{33}-{\mathfrak{g}}_{23}^2\right){\mathfrak{h}}_{13}+\left({\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}{\mathfrak{g}}_{33}\right){\mathfrak{h}}_{23}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{22}\right){\mathfrak{h}}_{33},\hfill \\ \\ \hfill {\mathfrak{s}}_{21}& =& \left({\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}{\mathfrak{g}}_{33}\right){\mathfrak{h}}_{11}+\left({\mathfrak{g}}_{11}{\mathfrak{g}}_{33}-{\mathfrak{g}}_{13}^2\right){\mathfrak{h}}_{12}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{13}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}\right){\mathfrak{h}}_{13},\hfill \\ \\ \hfill {\mathfrak{s}}_{22}& =& \left({\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}{\mathfrak{g}}_{33}\right){\mathfrak{h}}_{12}+\left({\mathfrak{g}}_{11}{\mathfrak{g}}_{33}-{\mathfrak{g}}_{13}^2\right){\mathfrak{h}}_{22}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{13}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}\right){\mathfrak{h}}_{23},\hfill \\ \\ \hfill {\mathfrak{s}}_{23}& =& \left({\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}{\mathfrak{g}}_{33}\right){\mathfrak{h}}_{13}+\left({\mathfrak{g}}_{11}{\mathfrak{g}}_{33}-{\mathfrak{g}}_{13}^2\right){\mathfrak{h}}_{23}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{13}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}\right){\mathfrak{h}}_{33},\hfill \\ \\ \hfill {\mathfrak{s}}_{31}& =& \left({\mathfrak{g}}_{12}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{22}\right){\mathfrak{h}}_{11}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{13}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}\right){\mathfrak{h}}_{12}+\left({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2\right){\mathfrak{h}}_{13},\hfill \\ \\ \hfill {\mathfrak{s}}_{32}& =& \left({\mathfrak{g}}_{12}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{22}\right){\mathfrak{h}}_{12}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{13}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}\right){\mathfrak{h}}_{22}+\left({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2\right){\mathfrak{h}}_{23},\hfill \\ \\ \hfill {\mathfrak{s}}_{33}& =& \left({\mathfrak{g}}_{12}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{22}\right){\mathfrak{h}}_{13}+\left({\mathfrak{g}}_{12}{\mathfrak{g}}_{13}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}\right){\mathfrak{h}}_{23}+\left({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2\right){\mathfrak{h}}_{33},\hfill \end{array}$$

and

$$\mathfrak{g}=\det \left({\mathfrak{g}}_{ij}\right)=-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}^2+2{\mathfrak{g}}_{12}{\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{12}^2{\mathfrak{g}}_{33}-{\mathfrak{g}}_{13}^2{\mathfrak{g}}_{22}+{\mathfrak{g}}_{11}{\mathfrak{g}}_{22}{\mathfrak{g}}_{33},$$

also the symbol “·” denotes the operation of matrix multiplication.

Definition 5.

In Minkowski’s four-dimensional space ${\mathbb{L}}^4$, the polynomial ${\mathcal{P}}_{\mathbb{S}}\left(\zeta \right)=\det (\mathbb{S}-\zeta {\mathcal{I}}_3)=0$ is used to determine the characteristic polynomial $\mathcal{P}$ of the shape operator $\mathbb{S}$, where ${\mathcal{I}}_3$ denotes the identity matrix. The curvature formulas are given by $\left(\genfrac{}{}{0pt}{}{3}{i}\right){\mathbb{K}}_i=s_i$, where ${\mathbb{K}}_1$ and ${\mathbb{K}}_3$ represent the mean curvature and Gauss–Kronecker curvature, respectively.

Definition 6.

When ${\mathbb{K}}_{j=1,2,3}=0$ on a hypersurface $\mathfrak{x}$, $\mathfrak{x}$ is called j-minimal.

For a comprehensive understanding of the topic, consult references [43,44,54].

Hence, we can derive the following expressions for the curvatures, which depend on the coefficients of the fundamental forms $\left({\mathfrak{g}}_{ij}\right)$ and $\left({\mathfrak{h}}_{ij}\right)$, in Minkowski’s four-dimensional space.

Theorem 1.

The expressions for the curvatures of a hypersurface in ${\mathbb{L}}^4$ are given, respectively, by, ${\mathbb{K}}_0=1$ (by definition),

$$\begin{array}{ccc}\hfill {\mathbb{K}}_1& =& \frac{\left\{\begin{array}{c}({\mathfrak{g}}_{11}{\mathfrak{h}}_{22}+{\mathfrak{g}}_{22}{\mathfrak{h}}_{11}-2{\mathfrak{g}}_{12}{\mathfrak{h}}_{12}){\mathfrak{g}}_{33}+({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2){\mathfrak{h}}_{33}\\ -2({\mathfrak{g}}_{13}{\mathfrak{h}}_{13}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{23}{\mathfrak{h}}_{13}{\mathfrak{g}}_{12}-{\mathfrak{g}}_{13}{\mathfrak{h}}_{23}{\mathfrak{g}}_{12}\\ +{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}{\mathfrak{h}}_{23}-{\mathfrak{g}}_{13}{\mathfrak{g}}_{23}{\mathfrak{h}}_{12})-{\mathfrak{g}}_{23}^2{\mathfrak{h}}_{11}-{\mathfrak{g}}_{13}^2{\mathfrak{h}}_{22}\end{array}\right\}}{3\left[({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2){\mathfrak{g}}_{33}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}^2+2{\mathfrak{g}}_{12}{\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{22}{\mathfrak{g}}_{13}^2\right]},\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\mathbb{K}}_2& =& \frac{\left\{\begin{array}{c}\left({\mathfrak{g}}_{11}{\mathfrak{h}}_{22}+{\mathfrak{g}}_{22}{\mathfrak{h}}_{11}-2{\mathfrak{g}}_{12}{\mathfrak{h}}_{12}\right){\mathfrak{h}}_{33}+\left({\mathfrak{h}}_{11}{\mathfrak{h}}_{22}-{\mathfrak{g}}_{12}^2\right){\mathfrak{g}}_{33}\\ -2({\mathfrak{g}}_{13}{\mathfrak{h}}_{13}{\mathfrak{h}}_{22}-{\mathfrak{g}}_{23}{\mathfrak{h}}_{13}{\mathfrak{h}}_{12}-{\mathfrak{g}}_{13}{\mathfrak{h}}_{23}{\mathfrak{h}}_{12}\\ +{\mathfrak{g}}_{23}{\mathfrak{h}}_{23}{\mathfrak{h}}_{11}-{\mathfrak{h}}_{13}{\mathfrak{h}}_{23}{\mathfrak{g}}_{12})-{\mathfrak{g}}_{11}{\mathfrak{h}}_{23}^2-{\mathfrak{g}}_{22}{\mathfrak{h}}_{13}^2\end{array}\right\}}{3\left[({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2){\mathfrak{g}}_{33}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}^2+2{\mathfrak{g}}_{12}{\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{22}{\mathfrak{g}}_{13}^2\right]},\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\mathbb{K}}_3& =& \frac{\left({\mathfrak{h}}_{11}{\mathfrak{h}}_{22}-{\mathfrak{h}}_{12}^2\right){\mathfrak{h}}_{33}-{\mathfrak{h}}_{11}{\mathfrak{h}}_{23}^2+2{\mathfrak{h}}_{12}{\mathfrak{h}}_{13}{\mathfrak{h}}_{23}-{\mathfrak{h}}_{22}{\mathfrak{h}}_{13}^2}{({\mathfrak{g}}_{11}{\mathfrak{g}}_{22}-{\mathfrak{g}}_{12}^2){\mathfrak{g}}_{33}-{\mathfrak{g}}_{11}{\mathfrak{g}}_{23}^2+2{\mathfrak{g}}_{12}{\mathfrak{g}}_{13}{\mathfrak{g}}_{23}-{\mathfrak{g}}_{22}{\mathfrak{g}}_{13}^2}.\hfill \end{array}$$

(6)

Proof. 

Utilizing Definitions 3–5, and performing direct computations, we can determine the characteristic polynomial. The components of this polynomial yield the curvatures. Additionally, we obtain the following expressions

$$3{\mathbb{K}}_1=tr\left(\mathbb{S}\right)=\sum _{i=1}^3{\mathfrak{s}}_{ii},$$

$${\mathbb{K}}_3=\det \left(\mathbb{S}\right)=\frac{\det \mathbb{II}}{\det \mathbb{I}}=\frac{\det \mathbb{III}}{\det \mathbb{II}}=\frac{\det \mathbb{IV}}{\det \mathbb{III}},$$

where “tr” denotes the trace of the matrix. □

3. Family of Helical Hypersurfaces with a Light-like Axis in ${\mathbb{L}}^{\mathbf{4}}$

For further insights and results on rotational hypersurfaces in Riemannian spaces, readers are encouraged to refer to the work of Do Carmo and Dajczer [56].

Moving forward, we will now introduce the concept of helical hypersurfaces.

Definition 7.

Let I be an open interval in $\mathbb{R}$, and consider a curve $\gamma :I⟶\Pi$ in a plane. Additionally, let ℓ be a line in the same plane. We define a rotational hypersurface as the result of rotating the generating curve γ around the line ℓ. During this rotation, the parallel lines orthogonal to ℓ are simultaneously replaced, with the speed of rotation matching the speed of replacement. The resulting hypersurface, known as the helical hypersurface with axis ℓ, exhibits pitches a and b, where $a,b\in \mathbb{R}\backslash \left\{0\right\}$.

For more detailed information, readers can refer to the work by Kühnel [54].

In the following, we present a description of the family of helical hypersurfaces with a light-like axis in ${\mathbb{L}}^4$.

The rotation matrix $\mathcal{R}=\mathcal{R}(v,w)$ obtained by the light-like rotating axis $\ell =\left(0,0,1,1\right)$ in ${\mathbb{L}}^4$ is described by

$$\mathcal{R}(v,w)=\left(\begin{array}{cccc}1& 0& -v& v\\ 0& 1& -w& w\\ v& w& 1-\frac{1}{2}\left(v^2+w^2\right)& \frac{1}{2}\left(v^2+w^2\right)\\ v& w& -\frac{1}{2}\left(v^2+w^2\right)& 1+\frac{1}{2}\left(v^2+w^2\right)\end{array}\right),$$

where $v,w\in \mathbb{R}$, and $\mathcal{R}$ supplies $\det \mathcal{R}=1, \mathcal{R}$·$\ell =\ell , {\mathcal{R}}^T$·$\epsilon$·$\mathcal{R}=\mathcal{R}$·$\epsilon$·${\mathcal{R}}^T=\epsilon$, $\epsilon =$ diag$(1,1,1,-1)$. The generating curve is determined by

$$\gamma \left(u\right)=\left(0,0,g\left(u\right),f\left(u\right)\right).$$

(7)

Here, $f,g$ denote the differentiable functions. In ${\mathbb{L}}^4$, the helical hypersurface $\mathfrak{x}=\mathfrak{x}(u,v,w)$ determined by ℓ is described by $\mathfrak{x}(u,v,w)=\mathcal{R}(v,w)$·$\gamma {\left(u\right)}^T+(av+bw){\ell }^T,$ where $u\in I,$ $v,w\in [0,2\pi )$ pitches $a,b\in \mathbb{R}\backslash \left\{0\right\}$. The parameterization of the helical hypersurfaces family M with a light-like axis is determined by

$$\mathfrak{x}(u,v,w)=\left(\begin{array}{c}\left(f-g\right)v\\ \left(f-g\right)w\\ g+\frac{1}{2}(v^2+w^2)(f-g)+av+bw\\ f+\frac{1}{2}(v^2+w^2)(f-g)+av+bw\end{array}\right)=\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right),$$

(8)

where $f=f\left(u\right),$ $g=g\left(u\right),$ $u,a,b\in \mathbb{R}\backslash \left\{0\right\}$ and $v,w\in \mathbb{R}.$

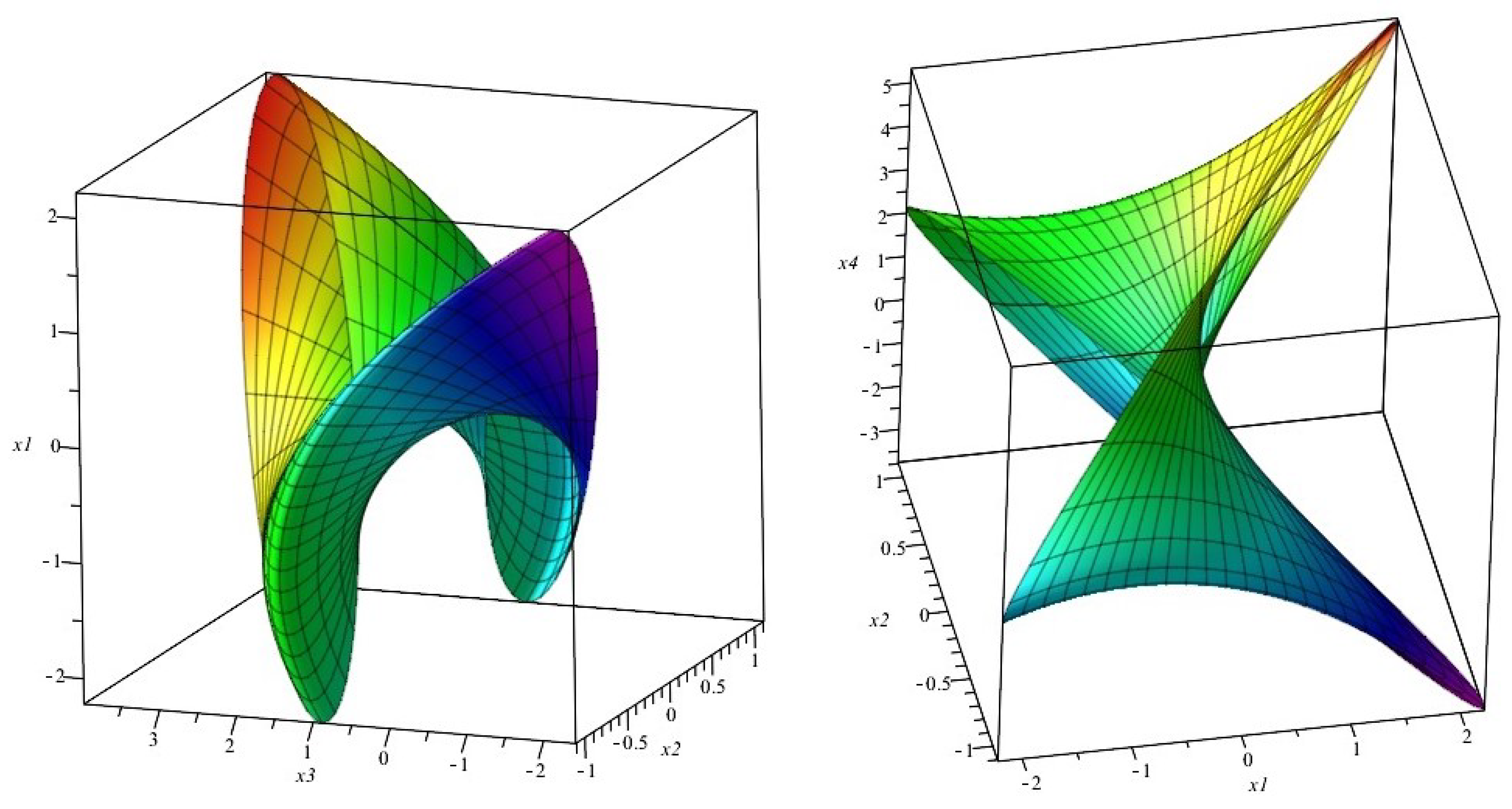
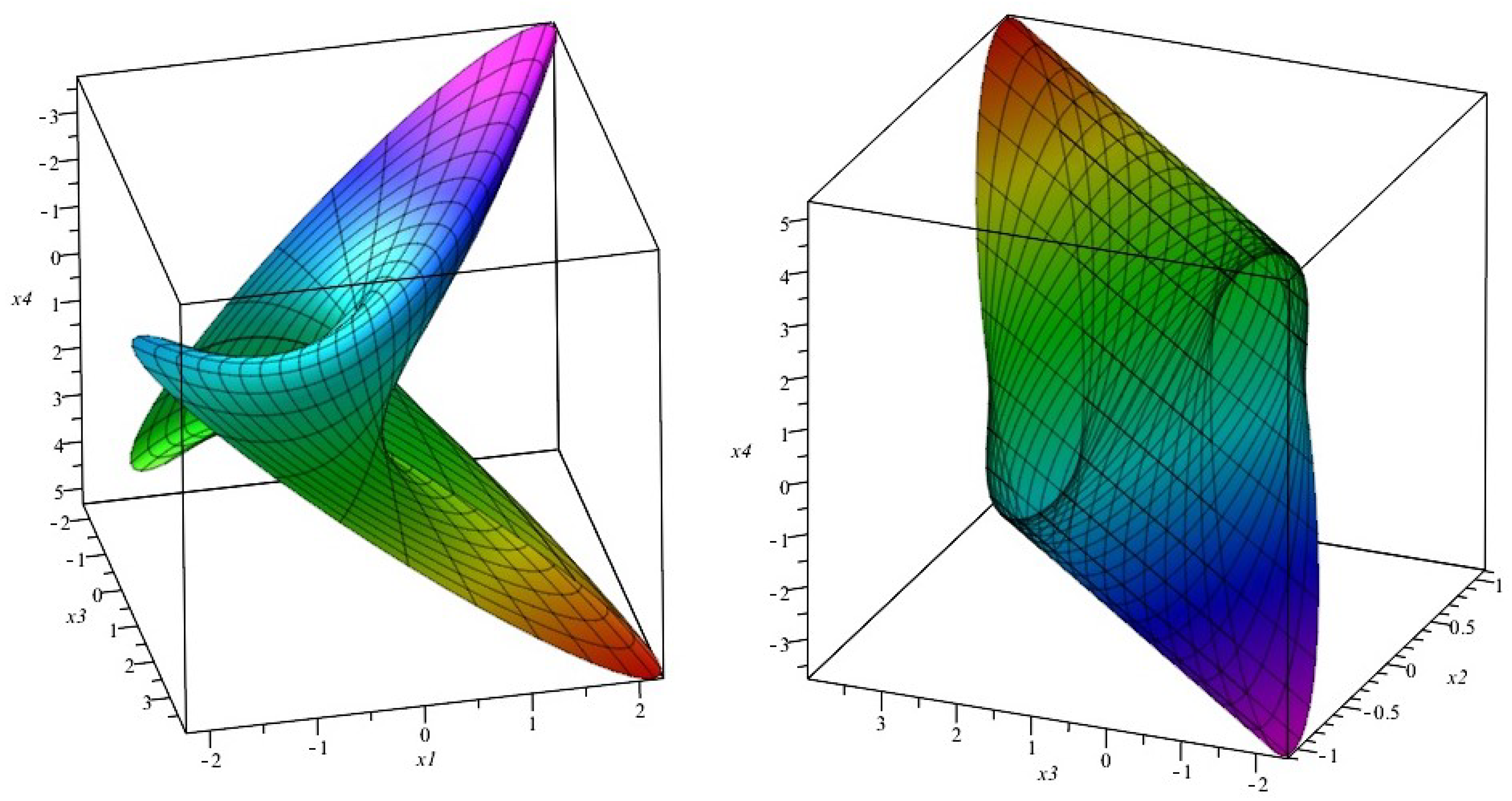
The readers can refer to Figure 1 and Figure 2 for illustrative depictions of the projections of the helical hypersurface family $\mathfrak{x}$ on three-dimensional spaces. It should be noted that these projections were obtained by considering a light-like axis, which is precisely defined by Equation (8).

By differentiating Equation (8) with respect to u, v, and w, we compute the first fundamental form matrix

$$\left({\mathfrak{g}}_{ij}\right)=\left(\begin{array}{ccc}{g^{\prime }}^2-{f^{\prime }}^2& a\left(g^{\prime }-f^{\prime }\right)& b\left(g^{\prime }-f^{\prime }\right)\\ a\left(g^{\prime }-f^{\prime }\right)& {\left(g-f\right)}^2& 0\\ b\left(g^{\prime }-f^{\prime }\right)& 0& {\left(g-f\right)}^2\end{array}\right).$$

(9)

We obtain $\mathfrak{g}=\det \left({\mathfrak{g}}_{ij}\right)={\left(f-g\right)}^2\mathcal{W},$ where $\mathcal{W}={\left(f-g\right)}^2\left({g^{\prime }}^2-{f^{\prime }}^2\right)-c^2{\left(f^{\prime }-g^{\prime }\right)}^2,$ $c^2=a^2+b^2,$ $f^{\prime }=\frac{df}{du},$ $g^{\prime }=\frac{dg}{du}.$

Definition 8.

For any curve $\gamma \left(u\right)$ or hypersurface $\mathfrak{x}=\mathfrak{x}(u,v,w)$ in Minkowski’s four-dimensional space, the following holds, where ${\gamma }^{\prime }=\frac{d\gamma }{du}$,

i. 

When $〈{\gamma }^{\prime },{\gamma }^{\prime }〉>0$ or ${\gamma }^{\prime }=0$ (resp., $\mathfrak{g}>0)$, the curve γ (resp. the hypersurface $\mathfrak{x}$) is called space-like.

ii. 

When $〈{\gamma }^{\prime },{\gamma }^{\prime }〉<0$ (resp., $\mathfrak{g}<0)$, the curve γ (resp., the hypersurface $\mathfrak{x}$) is called time-like.

iii. 

When $〈{\gamma }^{\prime },{\gamma }^{\prime }〉=0$ and ${\gamma }^{\prime }\ne 0$ (resp., $\mathfrak{g}=0)$. the curve γ (resp., the hypersurface $\mathfrak{x}$) is called light-like.

For a comprehensive discussion on the topic, refer to the work by O’Neill [55].

Corollary 1.

Consider the profile curve $\gamma \left(u\right)=(0,0,g(u),f(u\left)\right)$ of the family of helical hypersurfaces with a light-like axis, given by Equation (8). If $\gamma \left(u\right)$ is a unit speed curve, i.e., $\langle {\gamma }^{\prime },{\gamma }^{\prime }\rangle ={g^{\prime }}^2-{f^{\prime }}^2=1$, where prime denotes the derivative with respect to u, then $\gamma \left(u\right)$ is a space-like curve. Moreover, the following relationship holds

$$\mathfrak{g}={\left(f-g\right)}^2\left({\left(f-g\right)}^2-c^2{\left(f^{\prime }-g^{\prime }\right)}^2\right),c^2=a^2+b^2.$$

Corollary 2.

Consider the profile curve $\gamma \left(u\right)=(0,0,g(u),f(u\left)\right)$ of the family of helical hypersurfaces with a light-like axis given by Equation (8). Assume that $\gamma \left(u\right)$ is a unit speed curve, where $f\left(u\right)\ne g\left(u\right)$. Then, the following statements hold

a. 

If ${\left(f-g\right)}^2>c^2{\left(f^{\prime }-g^{\prime }\right)}^2$, then $\mathfrak{g}>0$; therefore, Equation (8) represents a space-like hypersurface.

b. 

If ${\left(f-g\right)}^2<c^2{\left(f^{\prime }-g^{\prime }\right)}^2$, then $\mathfrak{g}<0$; therefore, Equation (8) represents a time-like hypersurface.

c. 

If ${\left(f-g\right)}^2=c^2{\left(f^{\prime }-g^{\prime }\right)}^2$, then $\mathfrak{g}=0$; therefore, Equation (8) represents a light-like hypersurface. In this case, $g\left(u\right)=c_1{e}^{\pm u/c}+f\left(u\right)$, where $c_1\in \mathbb{R}$.

The Gauss map of the hypersurface defined by Equation (8) is characterized by the following expression

$$\mathbb{G}=\frac{1}{{\mathcal{W}}^{1/2}}\left(\begin{array}{c}-\left(Av+a\right)C\\ -\left(Aw+b\right)C\\ A{f}^{\prime }-\left(\frac{1}{2}{c}^{2}A+av+bw\right)C\\ A{g}^{\prime }-\left(\frac{1}{2}{c}^{2}A+av+bw\right)C\end{array}\right),$$

(10)

where $\mathcal{W}=-A^{2}D-c^2{C}^2,$ $A=f-g$, $C=f^{\prime }-g^{\prime },$ $D={f^{\prime }}^2-{g^{\prime }}^2,$ $c^2=a^2+b^2$. By taking the second derivatives with respect to u, v, and w of the hypersurface defined by Equation (8), we calculate the second fundamental form matrix

$$\left({\mathfrak{h}}_{ij}\right)=\frac{1}{{\mathcal{W}}^{1/2}}\left(\begin{array}{ccc}AB& -a{C}^2& -b{C}^2\\ -a{C}^2& A^{2}C& 0\\ -b{C}^2& 0& A^{2}C\end{array}\right),$$

where $B=f^{\prime }{g}^{″}-g^{\prime }{f}^{″}$, $f^{″}=\frac{d^{2}f}{d{u}^2},$ $g^{″}=\frac{d^{2}g}{d{u}^2},$ and $\mathfrak{h}=\det \left({\mathfrak{h}}_{ij}\right)={\mathcal{W}}^{-3/2}{A}^2{C}^2\left(A^{3}B-c^2{C}^3\right).$ Hence, utilizing Equation (3), we can express the shape operator matrix of the hypersurface determined by Equation (8):

$$\mathbb{S}=\frac{1}{{\mathcal{W}}^{3/2}}\left(\begin{array}{ccc}{A}^{3}D-c^2{C}^3& 0& 0\\ aC\left(AB+CD\right)& C\mathcal{W}& 0\\ bC\left(AB+CD\right)& 0& C\mathcal{W}\end{array}\right).$$

Finally, we unveil the curvatures of the family of helical hypersurfaces with a light-like axis determined by Equation (8); we present the following results

Theorem 2.

In ${\mathbb{L}}^4$, the family of helical hypersurfaces with a light-like axis given by Equation (8) has the following curvatures, respectively:

$$\begin{array}{ccc}\hfill {\mathbb{K}}_0& =& 1\mathrm{by}\mathrm{definition},\hfill \\ \hfill 3{\mathbb{K}}_1& =& \frac{{\left(f-g\right)}^3\left(f^{\prime }{g}^{″}-f^{″}{g}^{\prime }\right)+\left(f^{\prime }-g^{\prime }\right)\left(2\mathcal{W}-c^2{\left(f^{\prime }-g^{\prime }\right)}^2\right)}{{\left({\left(f-g\right)}^2\left(g^{\prime 2}-f^{\prime 2}\right)-c^2{\left(f^{\prime }-g^{\prime }\right)}^2\right)}^{3/2}},\hfill \\ \hfill 3{\mathbb{K}}_2& =& \frac{\left(f^{\prime }-g^{\prime }\right)\left[2{\left(f-g\right)}^3\left(f^{\prime }{g}^{″}-f^{″}{g}^{\prime }\right)+\left(f^{\prime }-g^{\prime }\right)\left(\mathcal{W}-2c^2{\left(f^{\prime }-g^{\prime }\right)}^2\right)\right]}{{\left({\left(f-g\right)}^2\left(g^{\prime 2}-f^{\prime 2}\right)-c^2{\left(f^{\prime }-g^{\prime }\right)}^2\right)}^2},\hfill \\ \hfill {\mathbb{K}}_3& =& \frac{{\left(f^{\prime }-g^{\prime }\right)}^2\left[{\left(f-g\right)}^3\left(f^{\prime }{g}^{″}-f^{″}{g}^{\prime }\right)-c^2{\left(f^{\prime }-g^{\prime }\right)}^3\right]}{{\left({\left(f-g\right)}^2\left(g^{\prime 2}-f^{\prime 2}\right)-c^2{\left(f^{\prime }-g^{\prime }\right)}^2\right)}^{5/2}},\hfill \end{array}$$

where $c^2=a^2+b^2.$

Proof. 

Using the Cayley–Hamilton theorem, we determine the characteristic polynomial $P_{\mathbb{S}}\left(\zeta \right)=0$ of the matrix $\mathbb{S}$ associated with the family of helical hypersurfaces with a light-like axis given by Equation (8). The characteristic polynomial can be expressed as

$${\mathbb{K}}_0{\zeta }^3-3{\mathbb{K}}_1{\zeta }^2+3{\mathbb{K}}_2\zeta -{\mathbb{K}}_3=0.$$

□

For the sake of brevity, we denote the variables as follows: $A=f-g$, $B=f^{\prime }{g}^{″}-g^{\prime }{f}^{″}$, $C=f^{\prime }-g^{\prime }$, $D={f^{\prime }}^2-{g^{\prime }}^2$, and $c^2=a^2+b^2$. Using these notations, we simplify the following Equations.

Corollary 3.

The curvatures of the family of helical hypersurfaces with a light-like axis, as defined in Equation (8), are connected by the following relationships

$${\left(\frac{3{\mathbb{K}}_1}{A^{3}B+2A^{2}CD-c^2{C}^3}\right)}^{20}={\left(\frac{3{\mathbb{K}}_2}{2A^{3}CB+A^2{C}^{2}D-3c^2{C}^4}\right)}^{15}={\left(\frac{{\mathbb{K}}_3}{A^3{C}^{2}B-c^2{C}^5}\right)}^{12}.$$

Corollary 4.

The family of helical hypersurfaces given by Equation (8) is considered one-minimal if and only if the following Equation holds

$$A^2(AB-2CD)-3c^2{C}^3=0.$$

(11)

Problem 1.

We find solutions $g=g\left(u\right)$ to the aforementioned differential Equation (11) for the family of helical hypersurfaces with a light-like axis defined by Equation (8).

Corollary 5.

The family of helical hypersurfaces described by Equation (8) is considered two-minimal if and only if the following Equation comes out

$$A^{2}C(2AB-CD)-3c^2{C}^4=0.$$

(12)

Problem 2.

We discovered the solutions $g=g\left(u\right)$ for the differential Equation (12) within the context of the family of helical hypersurfaces characterized by a light-like axis, as described by Equation (8).

Corollary 6.

The family of helical hypersurfaces determined by Equation (8) is three-minimal if and only if the following Equation occurs

$$A^{3}B{C}^2-c^2{C}^5=0.$$

(13)

The solutions $g=g\left(u\right)$ to the differential Equation (13) for the family of helical hypersurfaces with a light-like axis given by Equation (8) are determined by

$$\begin{array}{ccc}\hfill g\left(u\right)& =& \frac{\left(6c^2{d}_1-1\right)f\left(u\right)\pm \sqrt{{\left(f\left(u\right)-d_2\right)}^2-6c^4{d}_1}+d_2}{6c^2{d}_1},\hfill \\ \hfill g\left(u\right)& =& f\left(u\right)+d_3,\hfill \end{array}$$

where $d_1\ne 0,$ $c^2=a^2+b^2,$ $d_i\in \mathbb{R}$.

Corollary 7.

When $g=\eta =const.$ by Theorem 2, we have the following curvatures

$$\begin{array}{ccc}\hfill {\mathbb{K}}_1& =& -\frac{2{\left(f-\eta \right)}^2+3c^2}{3{\left(c^2+{\left(f-\eta \right)}^2\right)}^{3/2}},\hfill \\ \hfill {\mathbb{K}}_2& =& -\frac{{\left(f-\eta \right)}^2+3c^2}{3{\left(c^2+{\left(f-\eta \right)}^2\right)}^2},\hfill \\ \hfill {\mathbb{K}}_3& =& -\frac{c^2}{{\left(c^2+{\left(f-\eta \right)}^2\right)}^{5/2}},\hfill \end{array}$$

where $c^2+{\left(f-\eta \right)}^2\ne 0$. Here,

$$\begin{array}{ccc}\hfill {\mathbb{K}}_1& =& 0\iff f=\eta \pm \frac{1}{2}c\sqrt{-6},\hfill \\ \hfill {\mathbb{K}}_2& =& 0\iff f=\eta \pm c\sqrt{-3},\hfill \\ \hfill {\mathbb{K}}_3& =& 0\iff c=0.\hfill \end{array}$$

Corollary 8.

While $g=\eta =const,$ $a=b=0,$ we find

$$\begin{array}{ccc}\hfill {\mathbb{K}}_1& =& -\frac{2}{3\left(f-\eta \right)},\hfill \\ \hfill {\mathbb{K}}_2& =& -\frac{1}{3{\left(f-\eta \right)}^2},\hfill \\ \hfill {\mathbb{K}}_3& =& 0,\hfill \end{array}$$

where $f\ne \eta ,$ i.e., the family of helical hypersurfaces given by Equation (8) is a 3-minimal rotational hypersurface.

Therefore, we present the following.

Theorem 3.

A hypersurface $\mathfrak{x}=\mathfrak{x}(u,v,w)$ in Minkowski’s four-dimensional space ${\mathbb{L}}^4$ has

$${\mathbb{K}}_0\mathbb{IV}-3{\mathbb{K}}_1\mathbb{III}+3{\mathbb{K}}_2\mathbb{II}-{\mathbb{K}}_3\mathbb{I}={\mathcal{O}}_3,$$

(14)

where $\mathbb{I}$,$\mathbb{II}$,$\mathbb{III}$,$\mathbb{IV}$ describe the fundamental form matrices of $\mathfrak{x}$, and ${\mathcal{O}}_3$ determines the zero matrix with order 3.

Proof. 

By utilizing the Cayley–Hamilton theorem, we are able to establish the Equation ${\mathcal{P}}_{\mathbb{S}}\left(\zeta \right)=0$:

$${\mathbb{K}}_0{\zeta }^3-3{\mathbb{K}}_1{\zeta }^2+3{\mathbb{K}}_2\zeta -{\mathbb{K}}_3=0.$$

Additionally, we calculate the fundamental form matrices of the hypersurface $\mathfrak{x}$ as follows:

$$\mathbb{III}=\frac{1}{{\mathcal{W}}^2}\left(\begin{array}{ccc}\left(A^4{B}^2-c^2{C}^3\left(2AB+CD\right)\right)& -a{C}^3\mathcal{W}& -b{C}^3\mathcal{W}\\ -a{C}^3\mathcal{W}& A^2{C}^2\mathcal{W}& 0\\ -b{C}^3\mathcal{W}& 0& A^2{C}^2\mathcal{W}\end{array}\right)$$

and

$$\mathbb{IV}=\frac{1}{{\mathcal{W}}^{7/2}}\left(\begin{array}{ccc}{A}^7{B}^3+c^4{C}^6\left(3AB+2CD\right)+c^2{A}^2{C}^3\left(-3A^2{B}^2+C^2{D}^2\right)& -a{C}^4{\mathcal{W}}^2& -b{C}^4{\mathcal{W}}^2\\ -a{C}^4{\mathcal{W}}^2& A^2{C}^3{\mathcal{W}}^2& 0\\ -b{C}^4{\mathcal{W}}^2& 0& A^2{C}^3{\mathcal{W}}^2\end{array}\right),$$

where $\mathcal{W}=-A^{2}D-c^2{C}^2,$ $A=f-g,$ $B=f^{\prime }{g}^{″}-g^{\prime }{f}^{″},$ $C=f^{\prime }-g^{\prime },$ $D={f^{\prime }}^2-{g^{\prime }}^2,$ $c^2=a^2+b^2$. Then, we establish the relation stated in the theorem. □

Next, we introduce the concept of an umbilical hypersurface in Minkowski’s four-dimensional space. The relationship between the curvatures and the principal curvatures of any hypersurface in ${\mathbb{L}}^4$ is given by the following equations

$$\begin{array}{ccc}\hfill {\mathbb{K}}_0& =& 1,\hfill \\ \hfill 3{\mathbb{K}}_1& =& k_1+k_2+k_3,\hfill \\ \hfill 3{\mathbb{K}}_2& =& k_1{k}_2+k_1{k}_3+k_2{k}_3,\hfill \\ \hfill {\mathbb{K}}_3& =& k_1{k}_2{k}_3.\hfill \end{array}$$

Therefore, the following relationship holds.

Definition 9.

The hypersurface $M^3$ immersed in ${\mathbb{L}}^4$ is called umbilical if all its points are umbilical, which means that $k_1=k_2=k_3$ or, equivalently, ${\left({\mathbb{K}}_1\right)}^3={\mathbb{K}}_3$ with ${\mathbb{K}}_1{\mathbb{K}}_2={\mathbb{K}}_3,$ ${\left({\mathbb{K}}_1\right)}^2={\mathbb{K}}_2$.

An umbilical point holds great geometric importance and is intricately linked to the concept of the line of curvature. It serves as a singularity or pivotal point where a line of curvature reaches its end. The presence of such umbilical points can be attributed, in part, to the availability of a dependable criterion that applies to smooth hypersurfaces defined by either parametric or implicit formulations.

Consequently, we serve the following problem.

Problem 3.

We find solutions $g=g\left(u\right)$ to the following system of differential Equations for the family of helical hypersurfaces with a light-like axis defined by Equation (8):

$$\begin{array}{ccc}\hfill A^4{\left(AB+CD\right)}^2\left(A^{3}B-8A^{2}CD-9c^2{C}^3\right)& =& 0,\hfill \\ \hfill 9\left(A^{2}D+c^2{C}^2\right)\left(-A^{3}B+c^2{C}^3\right)C^2& =& 0,\hfill \\ \hfill A^4{\left(AB+CD\right)}^2& =& 0,\hfill \end{array}$$

(15)

where $A=f-g,$ $B=f^{\prime }{g}^{″}-g^{\prime }{f}^{″},$ $C=f^{\prime }-g^{\prime },$ $D=f^{\prime 2}-g^{\prime 2},$ $c^2=a^2+b^2.$

In the context of the system of Equations described by $\left(15\right)$, the solutions $g=g\left(u\right)$ correspond to the umbilic points of the hypersurface defined by Equation (8).

4. Family of Helical Hypersurfaces with a Light-like Axis Having $\Delta \mathfrak{x}=\mathcal{L}\mathfrak{x}$

In this section, we present the formulation of the Laplace–Beltrami operator for a smooth function defined on ${\mathbb{L}}^4$; subsequently, we compute this operator specifically for the family of helical hypersurfaces determined by Equation (8).

Definition 10.

The Laplace–Beltrami operator of a smooth function $\varphi =\varphi (x^1,x^2,x^3,x^4)$ defined on a subset $\mathbb{D}\subset {\mathbb{R}}^4$, where ϕ is of class $C^4$, is defined in terms of the first fundamental form, as follows:

$$\Delta \varphi =\frac{1}{\sqrt{\mathfrak{g}}}\sum _{i,j=1}^4\frac{\partial }{\partial x^i}\left(\sqrt{\mathfrak{g}}{\mathfrak{g}}^{ij}\frac{\partial \varphi }{\partial x^j}\right).$$

(16)

Here, $\left({\mathfrak{g}}^{ij}\right)={\left({\mathfrak{g}}_{kl}\right)}^{-1}$ and $\mathfrak{g}=\det \left({\mathfrak{g}}_{ij}\right)$.

The inverse of the matrix given by Equation $\left(9\right)$ is described by

$$\left({\mathfrak{g}}^{ij}\right)=\frac{1}{\mathcal{W}}\left(\begin{array}{ccc}{\left(f-g\right)}^2& a\left(f^{\prime }-g^{\prime }\right)& b\left(f^{\prime }-g^{\prime }\right)\\ a\left(f^{\prime }-g^{\prime }\right)& -\frac{b^2{\left(f^{\prime }-g^{\prime }\right)}^2+{\left(f-g\right)}^2\left(f^{\prime 2}-g^{\prime 2}\right)}{{\left(f-g\right)}^2}& \frac{ab{\left(f^{\prime }-g^{\prime }\right)}^2}{{\left(f-g\right)}^2}\\ b\left(f^{\prime }-g^{\prime }\right)& \frac{ab{\left(f^{\prime }-g^{\prime }\right)}^2}{{\left(f-g\right)}^2}& -\frac{a^2{\left(f^{\prime }-g^{\prime }\right)}^2+{\left(f-g\right)}^2\left(f^{\prime 2}-g^{\prime 2}\right)}{{\left(f-g\right)}^2}\end{array}\right),$$

where $\mathcal{W}={\left(f-g\right)}^2\left({g^{\prime }}^2-{f^{\prime }}^2\right)-c^2{\left(f^{\prime }-g^{\prime }\right)}^2,$ $c^2=a^2+b^2$.

By applying Equation $\left(16\right)$ with the aforementioned matrix $\left({\mathfrak{g}}^{ij}\right)$ obtained from Equation $\left(8\right)$, we derive the following results.

Theorem 4.

The Laplace–Beltrami operator of the family of helical hypersurfaces with a light-like axis determined by Equation (8) is given by

$$\Delta \mathfrak{x}=4{\mathbb{K}}_1\mathbb{G},$$

where ${\mathbb{K}}_1$ represents the mean curvature and $\mathbb{G}$ denotes the Gauss map of $\mathfrak{x}$.

Proof. 

By performing a direct computation of Equation (16), we obtain the expression for $\Delta \mathfrak{x}$. □

Theorem 5.

Consider immersion $\mathfrak{x}$ $M^3\subset {\mathbb{E}}^3$⟶${\mathbb{L}}^4$ given by Equation (8). We have $\Delta \mathfrak{x}=\mathcal{L}\mathfrak{x}$, where $\mathcal{L}$ represents a $4\times 4$ matrix, if and only if $\mathfrak{x}$ has ${\mathbb{K}}_1=0$, i.e., it has zero mean curvature.

Proof. 

We investigate the equation

$$4{\mathbb{K}}_1\mathbb{G}=\mathcal{L}\mathfrak{x},$$

and, subsequently, we deduce the following

$$\begin{array}{c}{\mathfrak{l}}_{11}\left(f-g\right)v+{\mathfrak{l}}_{12}\left(f-g\right)w+{\mathfrak{l}}_{13}\left(g+\frac{c^2}{2}\left(f-g\right)+\left(av+bw\right)\right)+{\mathfrak{l}}_{14}\left(f+\frac{c^2}{2}\left(f-g\right)+av+bw\right)\hfill \\ =\Psi \left(\left(f-g\right)v+a\right)\left(g^{\prime }-f^{\prime }\right),\hfill \\ \\ {\mathfrak{l}}_{21}\left(f-g\right)v+{\mathfrak{l}}_{22}\left(f-g\right)w+{\mathfrak{l}}_{23}\left(g+\frac{c^2}{2}\left(f-g\right)+\left(av+bw\right)\right)+{\mathfrak{l}}_{24}\left(f+\frac{c^2}{2}\left(f-g\right)+av+bw\right)\hfill \\ =\Psi \left(\left(f-g\right)w+b\right)\left(g^{\prime }-f^{\prime }\right),\hfill \\ \\ {\mathfrak{l}}_{31}\left(f-g\right)v+{\mathfrak{l}}_{32}\left(f-g\right)w+{\mathfrak{l}}_{33}\left(g+\frac{c^2}{2}\left(f-g\right)+\left(av+bw\right)\right)+{\mathfrak{l}}_{34}\left(f+\frac{c^2}{2}\left(f-g\right)+av+bw\right)\hfill \\ =\Psi \left[\left(\frac{1}{2}{c}^2\left(f-g\right)+av+bw\right)\left(g^{\prime }-f^{\prime }\right)+\left(f-g\right)f^{\prime }\right],\hfill \\ \\ {\mathfrak{l}}_{41}\left(f-g\right)v+{\mathfrak{l}}_{42}\left(f-g\right)w+{\mathfrak{l}}_{43}\left(g+\frac{c^2}{2}\left(f-g\right)+\left(av+bw\right)\right)+{\mathfrak{l}}_{44}\left(f+\frac{c^2}{2}\left(f-g\right)+av+bw\right)\hfill \\ =\Psi \left[\left(\frac{1}{2}{c}^2\left(f-g\right)+av+bw\right)\left(g^{\prime }-f^{\prime }\right)+\left(f-g\right)g^{\prime }\right],\hfill \end{array}$$

where $\mathcal{L}={\left({\mathfrak{l}}_{ij}\right)}_{4\times 4}$, $\Psi =\Psi \left(u\right)=4{\mathbb{K}}_1{\mathcal{W}}^{-1/2}$. By taking the derivative of the above ordinary differential Equations with respect to v, we find that ${\mathfrak{l}}_{i2}=0$ for $i=1,2,3,4$. Then, we obtain the following expressions:

$$\begin{array}{ccc}{\mathfrak{l}}_{11}\left(f-g\right)+\left({\mathfrak{l}}_{13}+{\mathfrak{l}}_{14}\right)a-\Psi \left(f-g\right)\left(g^{\prime }-f^{\prime }\right)\hfill & =\hfill & 0,\hfill \\ {\mathfrak{l}}_{21}\left(f-g\right)+\left({\mathfrak{l}}_{23}+{\mathfrak{l}}_{24}\right)a\hfill & =\hfill & 0,\hfill \\ {\mathfrak{l}}_{31}\left(f-g\right)+\left({\mathfrak{l}}_{33}+{\mathfrak{l}}_{34}\right)a+a\Psi \left(f^{\prime }-g^{\prime }\right)\hfill & =\hfill & 0,\hfill \\ {\mathfrak{l}}_{41}\left(f-g\right)+\left({\mathfrak{l}}_{43}+{\mathfrak{l}}_{44}\right)a+a\Psi \left(f^{\prime }-g^{\prime }\right)\hfill & =\hfill & 0.\hfill \end{array}$$

Considering that functions f and g are linearly independent with respect to $v,$ f and g are linearly independent with respect to v; and taking the derivatives of the above ordinary differential equations with respect to v, we find that all components of $\mathcal{L}$ are equal to zero.

Consequently, under the condition $\Psi =4{\mathbb{K}}_1{\mathcal{W}}^{-1/2}$, it can be deduced that ${\mathbb{K}}_1=0$. As a result, the entity denoted by $\mathfrak{x}$ signifies a collection of one-minimal helical hypersurfaces characterized by a light-like axis. □

5. Conclusions

Our investigation focused on the analysis of a specific class of helical hypersurfaces parametrized by $\mathfrak{x}=\mathfrak{x}(u,v,w)$, which possess a distinctive property of a light-like axis within Minkowski spacetime ${\mathbb{L}}^4$. Throughout our study, we successfully determined crucial mathematical entities that characterized these helical hypersurfaces, including the matrices representing their fundamental forms, Gauss map, and shape operator. By leveraging the Cayley–Hamilton theorem, we were able to compute the curvatures associated with $\mathfrak{x}$, shedding light on their geometric properties.

In particular, we delved into the conditions that led to the curvatures of $\mathfrak{x}$ exhibiting the desirable umbilical property. Additionally, we provided a comprehensive description of the Laplace–Beltrami operator specifically tailored for the family of helical hypersurfaces with a light-like axis in ${\mathbb{L}}^4$. Our findings contribute to a deeper understanding of these intriguing hypersurfaces and pave the way for further investigations in this field of study.