Abstract
In this article, we apply the formalism of (classical) Extended Irreversible Thermodynamics (EIT) to the dynamics of density fluctuations for a self-gravitating fluid in a static Universe, considering only bulk viscosity. The problem is characterized by gravitational instability, for which the Jeans criterion is shown to hold. However, both the relaxation time in the constitutive equation and the viscosity itself affect the behavior of both stable and unstable modes. In particular, the stable scenario features three modes, two of them corresponding to damped oscillations which decay faster that in the CIT scene. The third mode, inexistent in the CIT, corresponds to a very quickly decaying mode. In the unstable case, growing modes are observed in both EIT and CIT theories, for which the slowest growth is the one predicted by the CIT theory followed by the EIT, while the non-dissipative case corresponds to the fastest one.
1. Introduction
One of the fundamental current open problems in astrophysics and cosmology is structure formation; how do galaxies, galaxy clusters, and other large-scale structures emerge? Sir James Jeans took the first step towards understanding this question in 1902 [1,2], by determining the criterion under which a small perturbation in the density of an initially uniform, static, neutral, self-gravitating cloud occupying a vast region of space1 can grow in time, allowing matter to agglomerate and thus form structure. His research demonstrates that the gas cloud has a critical size, called Jeans’ wavelength , above which the cloud becomes unstable since the density perturbation grows exponentially with time, making a collapse unavoidable if the cloud exceeds such magnitude. Below , the density perturbation oscillates in time and no structure is formed. General relativity had not yet been developed at that time, so Jeans’ treatment was purely Newtonian. This had to wait until 1946 with Lifshitz [4], who extended Jeans’ idea to the relativistic regime. Since then, several authors have attempted to understand structure formation more deeply.
Current theoretical research on gravitational instability follows the work of Bonnor [5], who placed Jeans’ idea into a hydrodynamic framework, a treatment now found in many standard textbooks [3,6]. Bonnor went further, pushing the Jeans’ idea into an expanding Newtonian universe (or Newtonian cosmology)2 comparing his result with those obtained from the relativistic point of view, finding agreement with Lifshitz’s work as far as analogy allows. These first treatments have demonstrated that the Jeans’ criterion is preserved, but not so the perturbation propagation modes, which at the relativistic level grow not exponentially but as a power law. This difference is intuitively understood, since the expansion acts against gravity, slowing the agglomeration process. Despite these contributions, there are pathologies in the Jeans’ mass predictions, and this deficiency has been the impetus for further research.
In the course of these efforts, the problem has become more refined and less ideal. One of these considerations has been assuming that the gas in the cloud is ionized [9]; therefore, besides gravity, magnetic fields are considered—see for example, Ref. [10], and the case of a dusty plasma discuss in Refs. [11,12]. Another approach, given in Ref. [13], is to model the medium as a viscoelastic fluid. A further consideration is that the medium is a non-ideal fluid. This has been the subject of discussion by several authors. For example, Corona-Galindo and Dehnen [14] consider a compressible fluid with (shear and bulk) viscosity and heat flux, and follow the standard approach by linearizing the system of equations and obtaining a dispersion relation, which comes from a constitutive equation for the heat flux (Fourier law) and additionally the Maxwell relation for the thermodynamic quantities. Then, from the numerical analysis, they conclude that shear and heat flux are negligible in a galaxy formation at very high redshifts (z∼1200), while bulk viscosity becomes relevant. Carlevaro and Montani (CM) in Refs. [15,16] investigate how the bulk viscosity can affect the top-down fragmentation mechanism of structure formation and conclude that viscosity dampens the evolution of the density contrast, thereby suppressing the formation of substructures. At the same time, they demonstrate that Jeans’ criterion is not modified for a static or an expanding universe. In Ref. [16], (CM), under the assumption made for the viscosity coefficient, allowed them to treat Jeans’ instability straightforwardly and completely equivalent to the non-viscous case for both the static and the expanding universe. Velten and collaborators in [17] consider cold dark matter (CDM) with bulk viscosity for (i) an expanding Newtonian universe and (ii) a neo-Newtonian expanding universe, a term they use, which means that they take into account pressure effects in the Newtonian description, such as Friedman’s equations for the expanding (Newtonian) cosmology, which hold. The works mentioned above have in common that the viscosity is modeled by classical irreversible thermodynamics within Eckart’s framework3. In [17], Velten et al. compare their result with that of Carlevaro [16] for Newtonian cosmology, and also examine neo-Newtonian and relativistic cosmology cases, concluding that Newtonian cosmology is unreliable for modeling CDM structure growth.
In the astrophysical context, Jeans’ mechanism is also relevant. For example, it is a fundamental tool for addressing the problem of star formation (see, for instance, Refs. [18,19,20] and references therein), where the current view is that stars are formed from collapsed dense molecular cloud cores. It is important to note that the molecular clouds that serve as the seed for star formation are composed of a variety of particle species, mostly hydrogen, and helium in the form of gas, but also heavier elements such as carbon, oxygen, and so on, which form dust. It is this mixture that accounts for the appearance of bulk viscosity. Moreover, works taking into account dark matter modeled as WIMPS are explored (i.e., a mixture of baryonic matter and dark matter). Kremer et al. [21] also study the formation of stellar structures, and compare the Jeans mass for an ideal and non-ideal fluid within the five-field approximation in a static space, neglecting some factors such as radiation pressure and stellar wind, among others. They conclude that the astrophysical configuration, when viscosity is considered, requires a higher Jeans mass for collapse. In his book, Weinberg [3] also discusses the discrepancies between the results for galaxy masses obtained from the Jeans mechanism and those observed.
Another open question in astrophysics is related to the stability of the spiral structure of rotationally supported galaxies, a work that began very early with Ostriker and Peebles [22], who demonstrated that the instability of a self-gravitating rotating disk could be suppressed if the system is embedded in a static (dark) halo potential. However, more recent work has pointed out that instability occurs if a dynamic halo is considered [23]; note that these treatments usually neglect dissipation processes and heavily rely on numerical simulations, which in certain cases goes beyond a Newtonian treatment and the Jeans mechanism which we are interested in here.
In the present paper, we aim to analyze the gravitational instability considering a viscous fluid. We limit ourselves to considering just bulk viscosity; one of the reasons for this limitation is our interest in the relativistic level, where we have in mind (spatially) homogeneous and isotropic spacetimes where the only dissipative effect consistent with the spacetime symmetries is bulk pressure. Our aim in this work is thus to study Jeans instability for a viscous fluid within extended irreversible thermodynamics for a static space. The main motivation for analyzing the results in such a framework are the mathematical advantages that EIT possesses over CIT, i.e., stability and causality. As far as the authors are aware, this problem has been addressed under different considerations. For example, in [24], viscous CDM is considered for an expanding the Newtonian universe using transient thermodynamics to describe the bulk pressure. Moreover, Kremer and collaborators [21] carried out an analysis of the Jeans instability for static and expanding universes using both theories: classical irreversible thermodynamics, and (rational) extended irreversible thermodynamics. In that work, only shear stress and heat flow are considered, neglecting bulk viscosity. The argument for this lies in its approach from the kinetic theory, where the bulk viscosity is not present if one takes into account a small deviation for a non-relativistic ideal gas. From a phenomenological point of view, however, this kind of dissipation is present4. The authors refer to this as five and thirteen field theories, following the language of Müller and Ruggeri [26].
The outline of this article is as follows. In Section 2, we briefly review Jeans’ work, closely following classic references [3,5]. Section 3 serves to briefly recall the differences between classical irreversible thermodynamics (CIT) and extended irreversible thermodynamics (EIT). We are interested in explicitly giving the constitutive equation for the bulk and the shear stresses in both theories, which will be needed later in the work. In Section 4, the linearized system of equations is given together with the dispersion relation, which is analyzed through the Routh–Hurwitz criterion. In Section 5, we analyze the behavior of the roots of the cubic dispersion relation. In Section 6, we summarize and discuss the results obtained and sketch some possibilities for future extension.
2. Jeans’ Gravitational Instability
In this section, we briefly recall Jeans’ work for the sake of completeness and comparison. As we already mentioned in the introduction, a self-gravitating (ideal) fluid in Euclidean 3-dimensional space is considered, for which the Euler–Poisson system of equations in index notation reads
Here, is the Levi–Civita symbol and G denotes Newton’s constant. is the mass density of the fluid, are the Newtonian gravitational force field components, are the local 3-velocity components, and all the indices range as {1,2,3}. The interest lies in the time evolution of a small density fluctuation of the mass density within the cloud. Thus, a linear perturbation of the system of Equations (1)–(3) is considered, under the assumption that the background cloud is static and uniform5, requirements lead to the so-called Jeans–Swindle [6]. Many arguments regarding this hypothesis exist, ranging from magnetic forces, rotations, or other sources being present and adjusting to cancel the contribution of the unperturbed gravitational field. A possible argument to solve the problem is that in an expanding universe with a cosmological constant, there is a term that balances with the background density, so there would be no need for the swindle [27,28]. As for the perturbation analysis, one assumes that only the fluctuations satisfy Poisson’s equation, and write
where a barotropic equation of state with is also considered where is the speed of sound. The linear version of Equations (1)–(3) is given by
Then, an evolution equation for is obtained by taking the divergence of Equation (6) together with Equations (5) and (7), it follows that
A plane wave solution of the form is proposed, with the angular frequency and the wavenumber. By substituting this into Equation (8), the following dispersion relation is obtained
where k is the magnitude of and the solutions are given by:
where
is the so-called Jeans wavenumber. For , the density perturbation oscillates, while for the perturbation grows (or decays) exponentially, i.e., behaves like ∼, where . If instead of using the wavenumber , we use the wavelength, we can write the Jeans wavelength as
which gives us the bound on the size of the system. Moreover, a characteristic dynamical time can be obtained; this can be observed more properly if is rewritten as
This form of allows us to estimate the dynamical time when the cloud is large enough, i.e., when , then the effective frequency goes as ∼. Therefore, the dynamical collapse time is about ∼. Finally, the Jeans mass can be obtained by assuming that the cloud is spherical with radius , given as:
We conclude this section by mentioning that the Jeans instability can be described in terms of the time scale associated with the gravitational collapse and the time during which pressure is applied to the system as , where and . The next section will clarify the path when instead of assuming an ideal fluid, as is conducted here, a non-ideal fluid is considered. Since this problem goes beyond the mechanical treatment, a thermodynamic point of view is needed. Therefore, the next section serves this purpose.
3. Non-Equilibrium Thermodynamics: CIT and EIT
As mentioned above, our interest in this work is to consider non-ideal fluids. In order to treat these media properly, it is necessary to appeal to a non-equilibrium theory. It is therefore important to consider the framework under which we will describe these phenomena, since there is a wide range of theories that attempt to adequately include dissipation; see, for instance, Refs. [29,30] for an overview6. In this article, we consider two theories known in the literature as classical irreversible thermodynamics (CIT) and extended irreversible thermodynamics (EIT). The reasons for this particular choice are: (i) The structure of the theories allows a direct application and (ii) the relativistic extensions are widely employed7.
In CIT, the constitutive equations linearly relate dissipative fluxes and forces and give rise to Navier–Stokes–Fourier type equations. Indeed, the distinction between (CIT) and (EIT) can be observed in the expressions for the dissipative fluxes. In the case at hand, the relevant difference resides in the equations for the quantities and , which appear in the stress tensor , which decomposes as follows8
where p is the hydrostatic pressure, denotes the viscous stress tensor while and denotes the bulk pressure and the shear stress (a spatially symmetric traceless tensor), respectively, with the Euclidean inverse metric with . However, the real difference resides on their foundations, which deserves a closer look. We devote the next two subsections to a brief outline on this regard in a phenomenological sense.
3.1. CIT
The main tenet in this formalism is the local equilibrium postulate, which assumes that at each point, considered as an infinitesimal volume element, the fluid is in thermodynamical equilibrium. Under this assumption, at any point within the media all relations of equilibrium thermodynamics are valid. This allows one to define in a clear manner the concept of entropy, pressure, etc., and make use of the Gibbs relation with one major difference: that the thermodynamical quantities are now space and time-dependent:
Above s denotes the entropy density, is the internal energy per unit mass (specific internal energy), and is the specific volume. The Gibbs relation (16) comes along with an equation for the balance of energy and mass conservation. The behavior of the entropy density along the flow lines is given by:
Above and here on, a dot over a quantity denotes
Moreover, is the entropy flux vector (which can enter or leave the volume element), and denotes the entropy production which, according to the second law of thermodynamics, must satisfy that . The particular form of and comes from two aspects (i) the Gibbs relation (16), and (ii) the balance equation for (which takes into account the Cauchy stress tensor, heat flux, and heat supply). Among the relevance of these lines of thought is that the Fourier–Navier–Stokes laws are proposed in order to comply with the second law. That is, they are not taken as known a priori9 but formulated as:
with
and denoting the shear viscosity and bulk viscosity, also referred to as first and second viscosity, respectively. The expressions (19) and (20) will be used later on in this paper and are the constitutive equations for bulk viscosity and shear stress within CIT theory. As we will observe below, within the extended theory, the constitutive relations given above cease to be purely algebraic relations between the primary variables (, ) and , with the latter becoming dynamic.
3.2. EIT
In extended irreversible thermodynamics, the local equilibrium postulate is discarded. Instead, a drastic and novel perspective is considered. The idea was first put forward by Müller in 1967 [45] and led him and collaborators to formulate the program of rational10 extended irreversible thermodynamics, as well as its extension to the relativistic case known as the theory of Liu, Müller and Ruggeri (or relativistic extended thermodynamics) [34]. It turns out that the work of Müller at the relativistic level served as the basis for a new formulation given a few years later, known as the divergent type theory.
The central point in extended thermodynamics is the assumption that there exists a function called the “generalized entropy”, which depends not only on the equilibrium state variables but now also on the dissipative fluxes11, i.e., . Now, since the entropy density must be maximal at equilibrium and must be a scalar function, the dissipative fluxes appear quadratic in it (see, for instance, Refs. [26,29,30] and references therein).
As in the previous subsection, the behavior of the generalized entropy along the flow lines results in a continuity equation for , and demanding that the second law should be fulfilled leads to the following equation for and
where and are relaxation times. The resulting expressions (22) turn out to be the Maxwell–Cattaneo equations12, first proposed ad hoc in order to remove the infinite speed of propagation but now derived from the first principles. Our aim in this work is to consider Equation (22) to treat Jeans’ instability when bulk viscosity is considered and obtain the CIT counterpart by taking the limit. Following the approach outlined in Section 2, we now consider a non-ideal fluid and close the system of equations with Equation (22).
4. Stability Criterion in the Presence of Bulk Viscous Dissipation
In this section, the dynamics of the fluctuations are analyzed in the linear regime by considering only bulk viscous dissipation, as mentioned above. With the discussion of Section 3 in mind, we propose an analysis based on EIT which reduces mathematically to the CIT case when considering . Thus, the viscous contribution to the stress tensor is given by
with being given by the dynamic Equation (221). Upon considering the hypotheses in Equation (4) and adding an analogous one for , the linearized set of equations for the corresponding fluctuations is given by
where we write again Equation (7) for the gravitational field for completeness. Notice that Equations (24) and (27) only depend on the velocity fluctuations through its divergence. Thus, in order to analyze the modes, we separate the problem by defining and . Such a procedure decouples the so-called transverse mode which, in this particular case where only bulk viscous dissipation is considered, remains constant. Indeed, calculating the curl of Equation (25), one obtains .
On the other hand, the behavior of the longitudinal mode is given by the solution of the following system:
Notice that this procedure not only isolates the components of the velocity which can lead to an instability but also reduces the system of equations significantly. Assuming a plane wave solution (denoting the wave vector as instead of ) as in Section 2, Equations (28) and (29) can be recast as
where the behavior of the solution can be inspected by analyzing the nature of the roots of the dispersion relation, which is given by
Indeed, the solution for density fluctuations will present the following structure
being and the real and imaginary parts of the three roots of Equation (31), respectively. An instability thus occurs if at least one root of the dispersion relation lies on the right half of the complex plane. Notice that, normalizing the norm of the wave vector and time parameter, as follows
allows us to write Equation (31) in a compact form, namely
where , and is the ratio of the relaxation time of the dynamic pressure and a time characterizing the scale corresponding to the gravitational field of the equilibrium state:
Notice that in the limit , one recovers the case of CIT [16], where the dispersion relation is a quadratic polynomial, namely,
Unstable modes can be identified by applying the Routh–Hurwitz criterion to the cubic polynomial given by Equation (33). Indeed, the number of roots with positive real parts is given by the number of sign changes in the following array
Clearly and , while for , one has
which is also positive. This leaves the criterion for instability up to , or , which entails
Thus, the threshold for the system to be unstable is not altered by introducing a dynamic pressure as a dissipation effect within EIT. Indeed, the relaxation time contained in the parameter R does not enter the criterion whatsoever, and the result obtained by considering the dispersion relation given by Equation (33) holds as is the case in the CIT scenario. However, notice that in the present situation, the requirement is not present and the Jeans criterion applies for any magnitude of the bulk viscosity.
The analysis performed above yields a criterion that separates two physical scenarios. For , the density fluctuations decay in time and the system remains stable, returning to its equilibrium state. On the other hand, for the initial fluctuation grows exponentially, which may be traced down to the gravitational field created by it winning over the pressure gradient of the cloud, even in the presence of dissipation. Figure 1 shows the real and imaginary parts of the corresponding modes in both scenarios for the CIT and EIT cases. Notice that for both theories feature a growing mode, corresponding to the gravitational instability. However, there exists a narrow region within this scenario in the EIT case where the unstable mode oscillates with a growing amplitude. This behavior is exclusive of this framework and depends on the magnitude of the corresponding relaxation time .
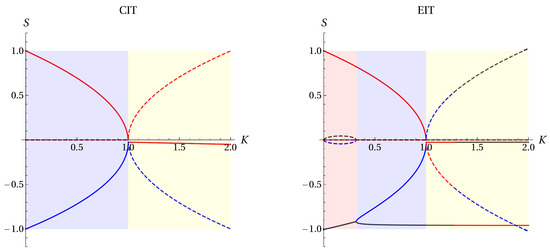
Figure 1.
The real (continuous line) and imaginary (dotted line) parts of the corresponding modes in the CIT (left) and EIT (right) scenarios for , just for schematical purposes. The different roots of the corresponding modes are plotted in different colors (blue, red, and gray) and the background colors separate the behavior of the former. It must be mentioned that the red background region decreases with growing R and disappears when .
5. Dynamics of Fluctuations in the Low-Density Limit
Extended irreversible thermodynamics leaves the magnitude of the relaxation parameter unspecified while assuming that it shall be “small”. Due to this assumption, it seems plausible to consider as a relevant case to study. Moreover, this assumption implies a weak gravitational field in the equilibrium configuration, which is consistent with the classical treatment carried out in this work. Notice that this limit shall contain the result obtained for the dynamics of fluctuations in the CIT case. Indeed, the dispersion relation in such a scenario is given by Equation (34), where one can readily identify the threshold for stable behavior to be also given by . Moreover, the regime which is here considered for the EIT case corresponds to the blue (middle) region of the right-hand side plot of Figure 1, where the three roots of the dispersion relation are real.
5.1. Damped Modes
If , the three roots of Equation (33) lie on the left hand side of the complex plane and thus an exponential decay is expected for density fluctuations. Figure 2 shows the behavior of the roots. Notice that the purely decaying mode is not plotted and the figure only features the damped oscillating ones. In order to simplify the notation and allow for a more direct comparison with previous results, we introduce the following definitions.
which correspond to the characteristic decay time and oscillation frequency respectively in the stable CIT case, namely the two roots of Equation (34) in the case. The modes in the EIT can thus be written in this approximation as
and
The real root corresponds to a very fast decaying mode. To leading order, the characteristic decay time for this component goes as . On the other hand, the conjugate roots imply damped modes whose decay time and frequency can be rewritten in terms of the corresponding quantities in the CIT case, as follows:
with
Figure 3 shows the behavior of the characteristic time and oscillation frequency for these conjugate roots compared with the CIT case (). Here, it is worthwhile to comment that in this stable region, the non-dissipative characteristic time can be thought of as infinite since the modes present a free oscillation. Thus, in this stable scenario, one obtains , where here and in the rest of the analysis we use ND to denote the non-dissipative case quantities. This implies that in the stable case, the decay time for fluctuations in the three theories satisfies:
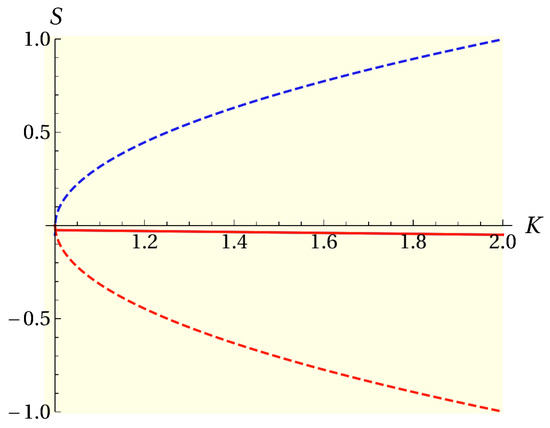
Figure 2.
The behavior of the oscillating modes in the case as functions of K and for the values and . The root corresponding with the decaying mode is not being plotted because it is at least 3 orders of magnitude larger than the others. Again, the continuous lines represent the real parts, and the dotted lines represent the imaginary parts of the roots.
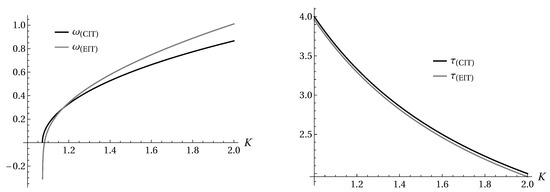
Figure 3.
The oscillation frequency (left) and the decay time (right) of the stable modes for CIT and EIT theories.
5.2. Ustable Mode
Even though the criterion for instability to be present in the system is not modified by bulk viscous dissipation, its effect in the characteristic time for the growth of unstable modes can be addressed in the relevant limit. Considering as before and , the three roots of Equation (33) are real and can be written as
and
where . In particular, one can demonstrate that the exponentially growing behavior for large values of R corresponds to (considering the “+” sign in Equation (43)). In order to compare the growth time with the one obtained in the CIT case, we define the corresponding root in the limit as (and for emphasis we have added a subscript J in the following equations to indicate Jeans’ instability.)
which enables us to write
or, in terms of the characteristic growth time
where
The present result implies a smaller growth time compared to CIT, but still larger than in the non-dissipative case, where . Indeed, one can demonstrate that
which is illustrated in Figure 4. Thus, dissipation clearly delays the onset of the gravitational instability, demonstrating that viscosity works in favor of the pressure gradient. This effect is less sharp in the EIT case compared to the CIT one.
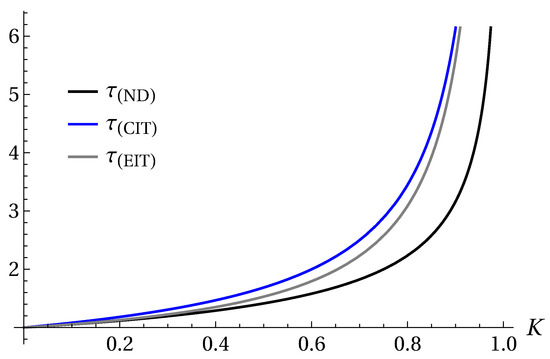
Figure 4.
In the unstable region: the growth times for the non-dissipative, CIT and EIT cases.
6. Discussion and Concluding Remarks
In this work, we have used the classical theory of extended irreversible thermodynamics to study the gravitational instability of a fluid with viscous pressure. To keep the work self-contained, we used the first sections of the paper to recall the Jeans mechanism, i.e., the Euler–Poisson, and Navier–Stokes–Poisson systems of equations. It is worth noting that our treatment is entirely Newtonian, although our interest is in the relativistic regime. This remark is intended to draw attention to the fact that, as we mentioned in the introduction, several works combine two aspects: on the one hand, the fluid is described by the classical Navier–Stokes–Poisson system within Newtonian or neo-Newtonian cosmology, while the bulk viscosity is described by Eckart’s theory and transient thermodynamics, which are completely relativistic. We would like to emphasize that although the basis of first- and second-order non-equilibrium thermodynamics follows the “same principles”, whether relativistic or not, and the structure is quite similar, the relativistic case has its own complications. For example, in the relativistic case, the 4-velocity plays a role in first-order theories, in which it is not uniquely defined. Moreover, Eckart’s theory, which is formulated in the particle frame, leads to unphysical dynamics in the linear regime, and thus one needs to be cautious when applying such theory to physical problems such as gravitational instability. Landau’s energy frame or modifications to Eckart’s formulation have been shown to circumvent this problem in a comoving frame but present pathologies in a boosted one [35,46]. On the other hand, in the second-order theory, there is freedom; any 4-velocity within the cone of pseudo-angle is adequate, and the theory is form-invariant under a change of frame in this case. However, this does not happen in the Newtonian domain where the 3-velocity is unambiguously defined.
As we have demonstrated, the introduction of an extended theory to describe dissipation leads to a cubic dispersion relation for the linearized system, instead of the quadratic relation which appears in the non-dissipative case as well as in the dissipative one when CIT is used. Here, we have carefully analyzed the modes’ propagation and compared them with the case of those obtained in the CIT scenario; the results are summarized in Table 1. The precise dynamics of both damped and growing modes were addressed in the low-density scenario.

Table 1.
A summary of the growth times and oscillation frequencies obtained from the non-dissipative, CIT and EIT theories for the stable () and the unstable () regions.
In the stable region, three modes are identified for the EIT case: two corresponding to damped oscillations and a purely decaying one. The purely damped mode decays in a very short time, while the oscillating ones decay in a time that is shown to be smaller than in the CIT case. Indeed, in the CIT framework, only two damped oscillating modes are obtained whose frequencies can be lower or higher than in the EIT counterpart depending on the value of the viscosity for each wavenumber. This behavior is illustrated in Figure 3 for both cases. In the non-dissipative case, only oscillating modes are obtained, which can be thought of as having an infinite decay time (oscillation amplitude is constant), and thus one can order the characteristic decay time of fluctuations in the stable scenario as specified in Equation (41) and can be observed in Figure 3 and in Table 1.
The unstable case analyzed in this work corresponds to non-oscillating modes in both CIT and EIT. As mentioned above, there is a regime for small values of R, in which the instability in EIT corresponds to a growing amplitude of an oscillating solution. However, in the low-density case here considered, the three formalisms predict real solutions to the dispersion relation, whose inverse corresponds to a characteristic time. In this case, the CIT theory predicts a slower growth than in both EIT and ND cases; thus, the non-dissipative scenario corresponds to the fastest onset. This behavior can be observed in Figure 4.
The previous paragraph’s discussion suggests that bulk viscous dissipation favors the pressure gradient in the case of gravitational instability by delaying the onset of a collapse. Indeed, the non-dissipative case shows a speedy onset, while the time predicted by both non-equilibrium theories is large. Moreover, including a relaxation time in the constitutive equation for the dynamic pressure makes this delay less intense. In the stable case, fluctuations also die off slower in the EIT case. The particulars of this scenario can be more thoroughly explored by studying the properties of the Rayleigh–Brillouin spectrum. Such a discussion will be addressed elsewhere.
The results here obtained, and summarized in the paragraphs above, shed light on how the relaxation time parameter present in the EIT formalism (and absent in CIT) affects the Jeans mechanism for structure formation. As mentioned in the Section 1, the applications range from astrophysical systems (e.g., star formation) to cosmological problems (formation of large-scale structures). As we have demonstrated, this parameter affects the efficiency with which the bulk viscosity delays the decay or growth of density fluctuations. Note, however, that a Newtonian treatment limits the scope and thus the applicability; for example, at the cosmological level we are limited to certain epochs of the Universe, and for astrophysical systems we are limited to only those whose gravitational fields are weak with cold matter. We remark that our work can provide insights into the analysis of the top-down fragmentation process, i.e., the simultaneous comparison of the evolution of two structures: a collapsing cloud with a larger mass than the Jeans limit and an internal cloud with a lower one [16]. It can also be used to compare Jeans’ masses for ideal and non-ideal fluids appealing to the Jeans’ mass-temperature relation () for different astrophysical configurations, for example, diffuse hydrogen clouds where the temperature is approximate to the order of T∼50 K, giant molecular clouds—T∼10 K, cold neutral media—10–100 K, warm neutral media—– K, HII regions, etc., (see Ref. [21] and references therein), with K denoting Kelvin.
An interesting question is how an expanding background might affect the conclusions drawn within the EIT framework. This entails considering that the background is no longer static, but an expanding Newtonian universe. As we noted earlier, this has been discussed in the literature, where cold dark matter (CDM) is modeled as viscous (CDM), i.e., (vCDM), considering the profile for the bulk viscosity as , which is the same one used by Carlevaro. This profile goes unnoticed when CIT is used and a static space is considered. On the contrary, for an expanding (Newtonian) universe, it plays a role, since the first term of the perturbation does not vanish, and this directly affects the dispersion relation. This problem is being currently addressed and will be reported elsewhere.
Author Contributions
Conceptualization, All authors; methodology, All authors; software, A.L.G.-P. and A.R.M.; validation, J.F.S. and A.L.G.-P.; formal analysis, All authors; investigation, J.F.S., A.L.G.-P. and G.C.-A.; resources, All authors; writing—original draft preparation, J.F.S.; writing—review and editing, All authors; visualization, A.L.G.-P. and A.R.M.; supervision, A.L.G.-P.; project administration, A.L.G.-P. All authors have read and agreed to the published version of the manuscript.
Funding
JFS’s research was funded by CONAHCyT through a postdoctoral grant.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Weinberg [3] assumes that the gas cloud is infinite, i.e., the universe is filled with a non-relativistic fluid. This in turn means that the gravitational field strength at any point is not well-defined within the Newtonian theory of gravity. However, the hydrostatic equilibrium equation is not satisfied in the case of finite mass, which, again, is an issue. |
| 2 | By Newtonian cosmology, we refer to the articles of Milne [7], Milne and McCrea [8], and subsequent work |
| 3 | We would like to comment that Eckart and Landau–Lifshitz’s formalisms are relativistic theories for non-perfect fluids, whose structure is similar to the non-relativistic case. Indeed, they can be thought of as the relativistic equivalent to the Navier–Stokes formalism and have been shown to lead to unphysical behavior in some scenarios (see the discussion in Section 3). |
| 4 | More precisely, from the kinetic point of view, a small deviation from the Maxwellian distribution function is considered, i.e., the first (some authors call it second) order approximation and the Chapman–Enskog method is applied; as a result, no bulk viscous term appears in the pressure tensor, only the (thermodynamic) pressure and shear. See the appendix in [21] and chapter 3 of [25]. On the contrary, the bulk viscosity at the macroscopic level is included in the viscous stress tensor. The same happens in the relativistic domain for non-perfect fluids, where an effective pressure is assumed to be , with the dynamic pressure or bulk pressure, and P defined as , indices running as and being the projection tensor. In equilibrium, vanishes, leaving only , but doing this leads to the question of how we distinguish one from the other. |
| 5 | For the sake of clarity, let us note the following: We are considering a static space, i.e., a space that does not evolve in time (it does not expand or contract), while we say that the cloud is static because the medium’s velocity is zero. On the other hand, the cloud is uniform. In other words, the mass density within the cloud is homogeneous or constant (independent of space and time). A point worth noting is that considering a finite cloud requires specific boundary conditions, while an infinite one does not. Moreover, problems with the gravitational field are present in both scenarios, and are already mentioned in the Note 1. |
| 6 | It is worth mentioning that the theories summarized in [29] are entirely phenomenological, regardless of whether they are microscopically supported by statistical mechanics or kinetic theory. Indeed, in this article, we have used classical irreversible thermodynamics and extended irreversible thermodynamics, which have a well-established microscopic basis in both relativistic and non-relativistic scenarios. For instance, CIT is obtained from the Chapman–Enskog expansion of the Boltzmann equation, while EIT is associated with the Grad’s moments method. For a detailed description of these kinetic formalisms, see Refs. [25,31,32]. In addition, it should be mentioned that Jeans’ instability has been studied from a kinetic theory approach in Ref. [33]. |
| 7 | We want to emphasize that our treatment is entirely Newtonian. However, since we keep mentioning non-equilibrium relativistic thermodynamics, we wish to clarify its meaning. First, the relativistic extension of CIT are the so-called first-order theories, namely Eckart, Landau–Lifshitz (LL) and Hiscock–Lindblom (HL), while the relativistic extensions of EIT are the Müller-Israel-Stewart (MIS) [31] and the Liu-Müller-Ruggeri (LMR) [34] theories. In Ref. [35] the authors demonstrate that first-order theories are unstable in a general (non-comoving) frame, i.e., velocity perturbations diverge, while Ref. [36] establishes that (MIS) is a causal and stable theory. This makes (MIS) a consistent theory, adequate for describing non-equilibrium relativistic processes. However, a weakness of (MIS) is whether the equations form a symmetric-hyperbolic system. Several efforts were heading in this direction, for instance, in Liu-Müller-Ruggeri [34], the divergent type theory [37], and more recently in the BDNK theory [38,39]. A feature of these theories is that they all point to a close relationship between (thermodynamic) stability and causality, which is also carefully explored in Refs. [40,41]. However, obtaining a symmetric-hyperbolic system of equations is not unique to the relativistic case. Moreover, the Newtonian approach follows this direction, and in fact, Müller and co-workers have pushed this idea ahead, developing their (rational) extended irreversible thermodynamics [26]. |
| 8 | The notation used here to denote the stress, viscous stress and shear tensors follows Landau–Lifshitz (see Equation (15.2), Chapter II: Viscous fluids, in Ref. [42]), with a different sign convention. The motivation for this choice also comes from Marsden [43], where the (Cauchy) stress tensor is denoted by . This lack of standard notation is a source of confusion even among the community. This is also true in the relativistic case, e.g., Israel in Ref. [44] uses and with to denote the bulk and shear stresses, respectively, while in [31] and are used. On the other hand, Hiscock and Lindblom used and in [36], respectively. |
| 9 | For a full discussion and details, see, for instance, [26,29,30]. |
| 10 | The authors themselves explain the term rational in the preface [26]. |
| 11 | In this article, we omit any discussion of the problems associated with the foundations of the theories used here for analysis. A critical and very readable treatment can be found in the book by Jou and collaborators [29]; see also [26]. |
| 12 | Note that the constitutive equations in EIT are much richer than those shown here (see, e.g., Equations (2.70)–(2.72) in [29] and also Equation (2.13) in [26]), but neglecting the heat flux reduces the system, resulting in constitutive equations for viscous stress and viscous pressure such as in the Maxwell–Cattaneo system. |
References
- Jeans, J.H. The Stability of a Spherical Nebula. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1902, 199, 454–455. [Google Scholar]
- Jeans, J. Astronomy and Cosmogony, 2nd ed.; Cambridge Library Collection—Astronomy, Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons: New York, NY, USA, 1972. [Google Scholar]
- Lifshitz, E. Republication of: On the gravitational stability of the expanding universe. Gen. Relativ. Gravit. 2017, 49, 18. [Google Scholar] [CrossRef]
- Bonnor, W.B. Jeans’ Formula for Gravitational Instability. Mon. Not. R. Astron. Soc. 1957, 117, 104–117. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Milne, E.A. A Newtonian expanding universe. Q. J. Math. 1934, os-5, 64–72. [Google Scholar] [CrossRef]
- McCrea, W.H.; Milne, E.A. Newtonian universes and the curvature of space. Q. J. Math. 1934, os-5, 73–80. [Google Scholar] [CrossRef]
- Shukla, P.; Stenflo, L. Jeans instability in a self-gravitating dusty plasma. Proc. R. Soc. Math. Phys. Eng. Sci. 2006, 462, 403–407. [Google Scholar] [CrossRef]
- Ren, H.; Wu, Z.; Cao, J.; Chu, P.K. Jeans instability in quantum magnetoplasma with resistive effects. Phys. Plasmas 2009, 16, 072101. [Google Scholar] [CrossRef]
- Pandey, B.P.; Avinash, K.; Dwivedi, C.B. Jeans instability of a dusty plasma. Phys. Rev. E 1994, 49, 5599–5606. [Google Scholar] [CrossRef]
- Dolai, B.; Prajapati, R. Effects of dust-charge gradient and polarization forces on the waves and Jeans instability in strongly coupled dusty plasma. Phys. Lett. A 2020, 384, 126462. [Google Scholar] [CrossRef]
- Janaki, M.S.; Chakrabarti, N.; Banerjee, D. Jeans instability in a viscoelastic fluid. Phys. Plasmas 2011, 18, 012901. [Google Scholar] [CrossRef]
- Corona-Galindo, M.G.; Dehnen, H. The jeans instability criterion for a compressible fluid including viscosity and heat conduction. Astrophys. Space Sci. 1989, 153, 87–94. [Google Scholar] [CrossRef]
- Carlevaro, N.; Montani, G. On the gravitational collapse of a gas cloud in the presence of bulk viscosity. Class. Quantum Gravity 2005, 22, 4715. [Google Scholar] [CrossRef]
- Carlevaro, N.; Montani, G. Jeans Instability in the Presence of Viscous Effects. Int. J. Mod. Phys. D 2009, 18, 1257–1272. [Google Scholar] [CrossRef]
- Velten, H.; Schwarz, D.J.; Fabris, J.C.; Zimdahl, W. Viscous dark matter growth in (neo-)Newtonian cosmology. Phys. Rev. D 2013, 88, 103522. [Google Scholar] [CrossRef]
- Shu, F.H.; Adams, F.C.; Lizano, S. Star formation in molecular clouds: Observation and theory. Annu. Rev. Astron. Astrophys. 1987, 25, 23–81. [Google Scholar] [CrossRef]
- Hosseinirad, M.; Naficy, K.; Abbassi, S.; Roshan, M. Gravitational instability of filamentary molecular clouds, including ambipolar diffusion. Mon. Not. R. Astron. Soc. 2016, 465, 1645–1653. [Google Scholar] [CrossRef]
- Tsiklauri, D. Jeans Instability of Interstellar Gas Clouds in the Background of Weakly Interacting Massive Particles. Astrophys. J. 1998, 507, 226. [Google Scholar] [CrossRef]
- Kremer, G.M.; Richarte, M.G.; Teston, F. Jeans instability in a universe with dissipation. Phys. Rev. D 2018, 97, 023515. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E. A Numerical Study of the Stability of Flattened Galaxies: Or, Can Cold Cold Galaxies Survive? Astrophys. J. 1973, 186, 467–480. [Google Scholar] [CrossRef]
- Esquivel, O.; Fuchs, B. Jeans instability of a galactic disk embedded in a live dark halo. Astron. Astrophys. 2007, 468, 803–805. [Google Scholar] [CrossRef]
- Acquaviva, G.; John, A.; Pénin, A. Dark matter perturbations and viscosity: A causal approach. Phys. Rev. D 2016, 94, 043517. [Google Scholar] [CrossRef]
- Kremer, G. An Introduction to the Boltzmann Equation and Transport Processes in Gases; Interaction of Mechanics and Mathematics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Müller, I.; Ruggeri, T. Rational Extended Thermodynamics; Springer Tracts in Natural Philosophy; Springer: New York, NY, USA.
- Falco, M.; Hansen, S.H.; Wojtak, R.; Mamon, G.A. Why does the Jeans Swindle work? Mon. Not. R. Astron. Soc. Lett. 2013, 431, L6–L9. [Google Scholar] [CrossRef]
- Kiessling, M.K.H. The “Jeans swindle”: A true story—Mathematically speaking. Adv. Appl. Math. 2003, 31, 132–149. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vázquez, J.; Lebon, G. Extended Irreversible Thermodynamics; Springer: Dordrecht, The Netherlands, 2010; pp. 1–483. [Google Scholar] [CrossRef]
- Salazar, J.F.; Zannias, T. On extended thermodynamics: From classical to the relativistic regime. Int. J. Mod. Phys. D 2020, 29, 2030010. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Zhdanov, V.M.; Roldugin, V.I. Non-equilibrium thermodynamics and kinetic theory of rarefied gases. Physics-Uspekhi 1998, 41, 349. [Google Scholar] [CrossRef]
- Trigger, S.A.; Ershkovich, A.I.; van Heijst, G.J.F.; Schram, P.P.J.M. Kinetic theory of Jeans instability. Phys. Rev. E 2004, 69, 066403. [Google Scholar] [CrossRef]
- Liu, I.S.; Müller, I.; Ruggeri, T. Relativistic thermodynamics of gases. Ann. Phys. 1986, 169, 191–219. [Google Scholar] [CrossRef]
- Hiscock, W.A.; Lindblom, L. Generic instabilities in first-order dissipative relativistic fluid theories. Phys. Rev. D 1985, 31, 725–733. [Google Scholar] [CrossRef]
- Hiscock, W.A.; Lindblom, L. Stability and causality in dissipative relativistic fluids. Ann. Phys. 1983, 151, 466–496. [Google Scholar] [CrossRef]
- Geroch, R.; Lindblom, L. Dissipative relativistic fluid theories of divergence type. Phys. Rev. D 1990, 41, 1855–1861. [Google Scholar] [CrossRef] [PubMed]
- Bemfica, F.S.; Disconzi, M.M.; Noronha, J. First-Order General-Relativistic Viscous Fluid Dynamics. Phys. Rev. X 2022, 12, 021044. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M. Unified Extended Irreversible Thermodynamics and the Stability of Relativistic Theories for Dissipation. Front. Astron. Space Sci. 2021, 8, 686344. [Google Scholar] [CrossRef]
- Gavassino, L. Can We Make Sense of Dissipation without Causality? Phys. Rev. X 2022, 12, 041001. [Google Scholar] [CrossRef]
- Gavassino, L.; Antonelli, M.; Haskell, B. Thermodynamic Stability Implies Causality. Phys. Rev. Lett. 2022, 128, 010606. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Marsden, J.; Hughes, T. Mathematical Foundations of Elasticity; Dover Civil and Mechanical Engineering Series; Dover: Kent, UK, 1994. [Google Scholar]
- Israel, W. Nonstationary irreversible thermodynamics: A causal relativistic theory. Ann. Phys. 1976, 100, 310–331. [Google Scholar] [CrossRef]
- Müller, I. Zum Paradoxon der Wärmeleitungstheorie. Z. Phys. 1967, 198, 329–344. [Google Scholar] [CrossRef]
- García-Perciante, A.L.; Rubio, M.E.; Reula, O.A. Generic instabilities in the relativistic Chapman–Enskog heat conduction law. J. Stat. Phys. 2020, 181, 246–262. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).