Improved Model of Primordial Black Hole Formation after Starobinsky Inflation
Abstract
1. Introduction
2. The New Model
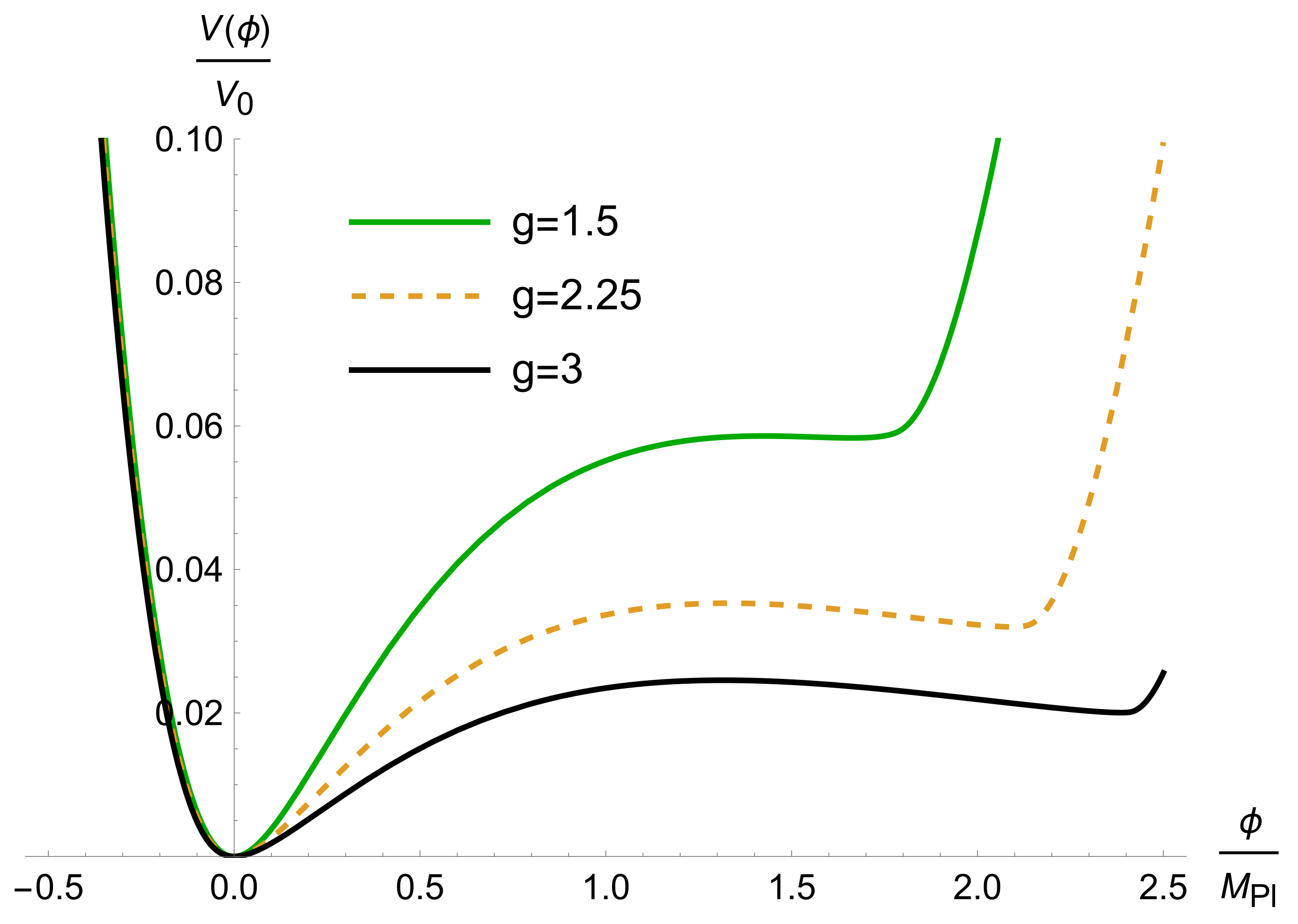
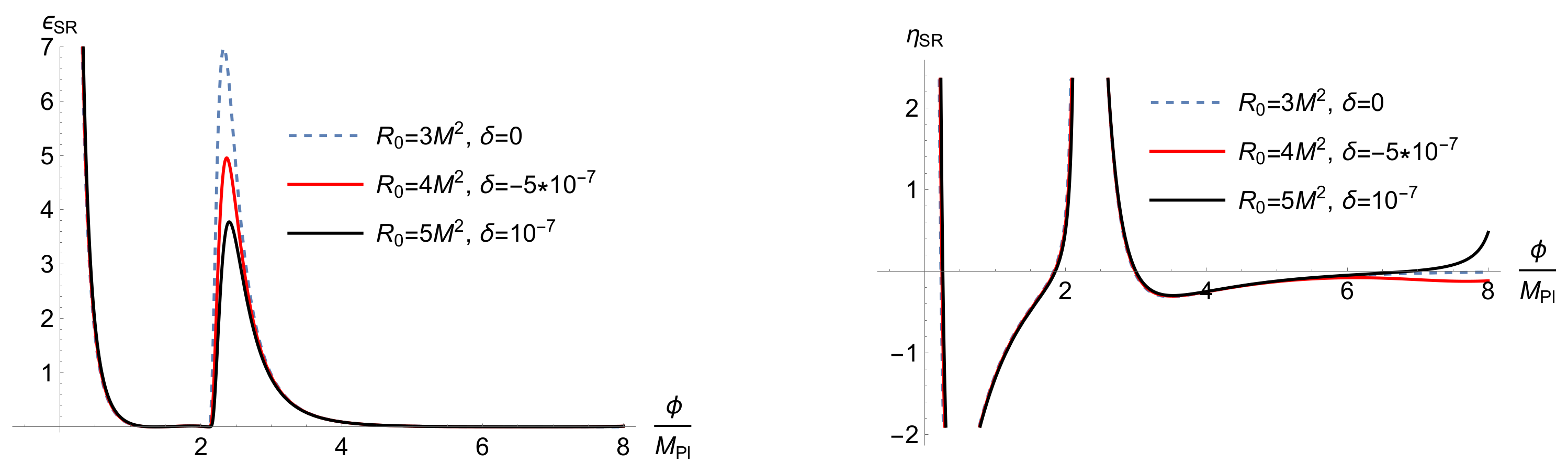
3. Inflaton Potential and Slow-Roll
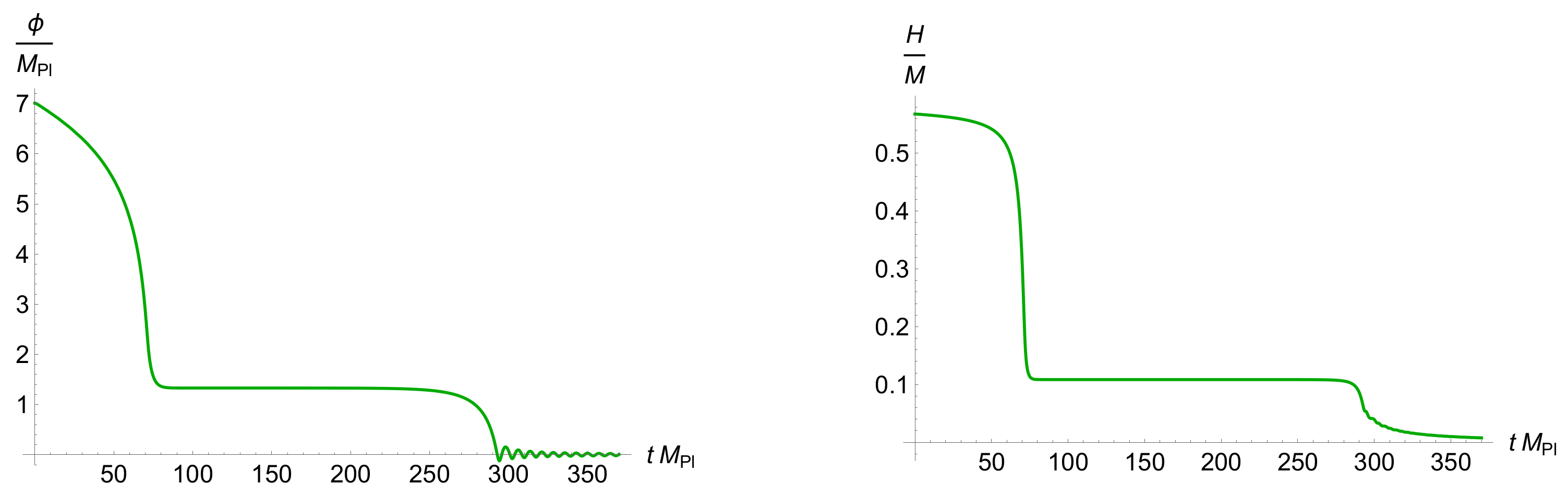
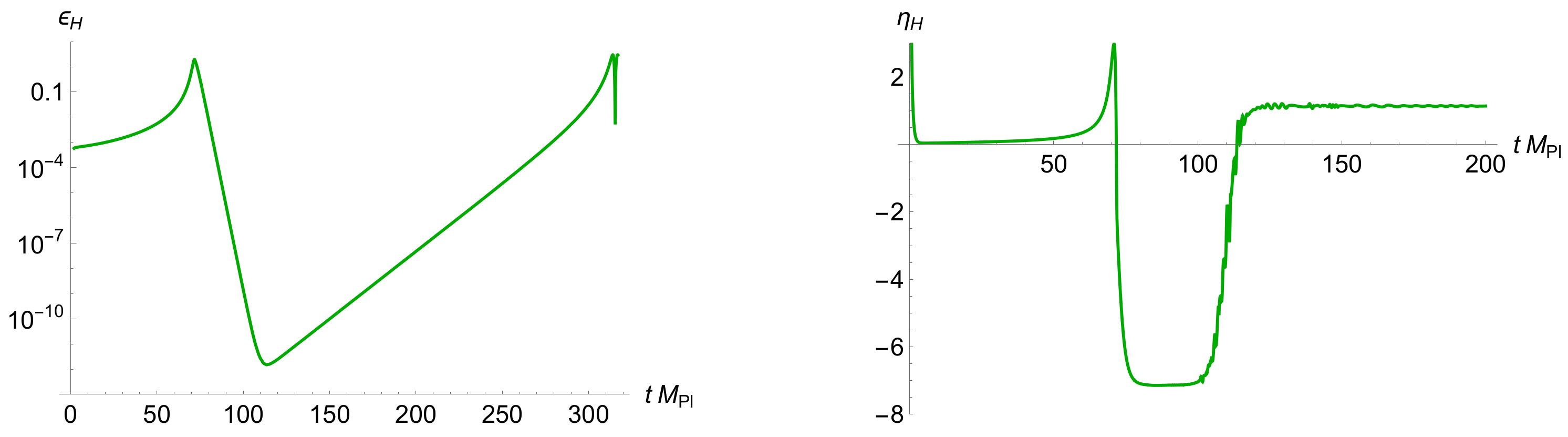
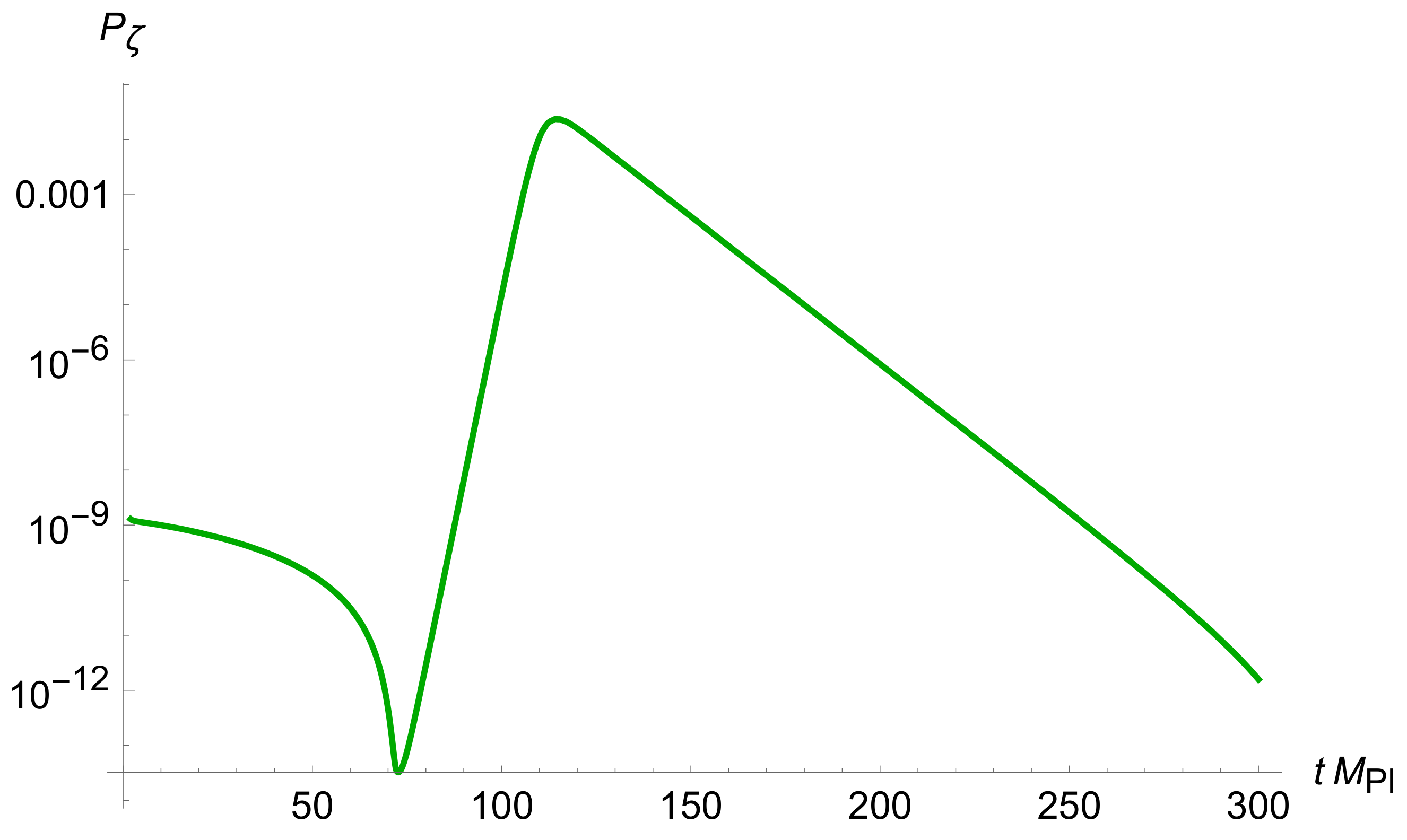
4. Power Spectrum of Scalar Perturbations and PBH Masses
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Accordingly, we changed the notation for the AB-parameter denoted by in Ref. [20] to . |
References
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Akrami, Y. et al. [Planck Collaboration] Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [BICEP, Keck Collaboration] Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef] [PubMed]
- Tristram, M.; Banday, A.J.; Górski, K.M.; Keskitalo, R.; Lawrence, C.R.; Andersen, K.J.; Wehus, I.K. Improved limits on the tensor-to-scalar ratio using BICEP and Planck data. Phys. Rev. D 2022, 105, 83524. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Novikov, I.; Zeldovic, Y. Cosmology. Ann. Rev. Astron. Astrophys. 1967, 5, 627–649. [Google Scholar] [CrossRef]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. R. Astron. Soc. 1971, 152, 75. [Google Scholar] [CrossRef]
- Barrow, J.D.; Copeland, E.J.; Liddle, A.R. The Cosmology of black hole relics. Phys. Rev. D 1992, 46, 645–657. [Google Scholar] [CrossRef]
- Ivanov, P.; Naselsky, P.; Novikov, I. Inflation and primordial black holes as dark matter. Phys. Rev. D 1994, 50, 7173–7178. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on primordial black holes. Rept. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef]
- Escrivà, A.; Kuhnel, F.; Tada, Y. Primordial Black Holes. arXiv 2022, arXiv:2211.05767. [Google Scholar]
- Ketov, S.V.; Starobinsky, A.A. Inflation and non-minimal scalar-curvature coupling in gravity and supergravity. J. Cosmol. Astropart. Phys. 2012, 8, 22. [Google Scholar] [CrossRef]
- Ketov, S.V. Multi-Field versus Single-Field in the Supergravity Models of Inflation and Primordial Black Holes. Universe 2021, 7, 115. [Google Scholar] [CrossRef]
- Ketov, S. On the large-field equivalence between Starobinsky and Higgs inflation in gravity and supergravity. In Proceedings of the 7th Symposium on Prospects in the Physics of Discrete Sources, Bergen, Norway, 29 November–3 December 2021; p. 14. [Google Scholar] [CrossRef]
- Maeda, K.-I. Towards the Einstein–Hilbert Action via Conformal Transformation. Phys. Rev. D 1989, 39, 3159. [Google Scholar] [CrossRef]
- Ivanov, V.R.; Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. Analytic extensions of Starobinsky model of inflation. J. Cosmol. Astropart. Phys. 2022, 3, 58. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Morales, E.R. Primordial black holes from single field models of inflation. Phys. Dark Univ. 2017, 18, 47–54. [Google Scholar] [CrossRef]
- Frolovsky, D.; Ketov, S.V.; Saburov, S. Formation of primordial black holes after Starobinsky inflation. Mod. Phys. Lett. A 2022, 37, 2250135. [Google Scholar] [CrossRef]
- Appleby, S.A.; Battye, R.A.; Starobinsky, A.A. Curing singularities in cosmological evolution of F(R) gravity. J. Cosmol. Astropart. Phys. 2010, 6, 5. [Google Scholar] [CrossRef]
- Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. On the superstring-inspired quantum correction to the Starobinsky model of inflation. J. Cosmol. Astropart. Phys. 2022, 12, 32. [Google Scholar] [CrossRef]
- Ivanov, V.; Ketov, S.; Pozdeeva, E.; Vernov, S. On Extensions of the Starobinsky Model of Inflation. Phys. Sci. Forum 2023, 7, 6. [Google Scholar] [CrossRef]
- Pozdeeva, E.; Ketov, S.; Vernov, S. String-Inspired Correction to R2 Inflation. Phys. Sci. Forum 2023, 7, 2. [Google Scholar]
- Frolovsky, D.; Ketov, S.V. Inflationary E-models revisited. arXiv 2023, arXiv:2304.12558. [Google Scholar]
- Aoki, S.; Ishikawa, R.; Ketov, S.V. Pole inflation and primordial black holes formation in Starobinsky-like supergravity. Class. Quant. Grav. 2023, 40, 65002. [Google Scholar] [CrossRef]
- Germani, C.; Prokopec, T. On primordial black holes from an inflection point. Phys. Dark Univ. 2017, 18, 6–10. [Google Scholar] [CrossRef]
- Dimopoulos, K. Ultra slow-roll inflation demystified. Phys. Lett. B 2017, 775, 262–265. [Google Scholar] [CrossRef]
- Mukhanov, V.F. Gravitational Instability of the Universe Filled with a Scalar Field. JETP Lett. 1985, 41, 493–496. [Google Scholar]
- Sasaki, M. Large Scale Quantum Fluctuations in the Inflationary Universe. Prog. Theor. Phys. 1986, 76, 1036. [Google Scholar] [CrossRef]
- Karam, A.; Koivunen, N.; Tomberg, E.; Vaskonen, V.; Veermäe, H. Anatomy of single-field inflationary models for primordial black holes. J. Cosmol. Astropart. Phys. 2023, 3, 13. [Google Scholar] [CrossRef]
- Pi, S.; Zhang, Y.-L.; Huang, Q.-G.; Sasaki, M. Scalaron from R2-gravity as a heavy field. J. Cosmol. Astropart. Phys. 2018, 5, 42. [Google Scholar] [CrossRef]
- Papanikolaou, T.; Tzerefos, C.; Basilakos, S.; Saridakis, E.N. Scalar induced gravitational waves from primordial black hole Poisson fluctuations in f(R) gravity. J. Cosmol. Astropart. Phys. 2022, 10, 13. [Google Scholar] [CrossRef]
- Cole, P.S.; Gow, A.D.; Byrnes, C.T.; Patil, S.P. Primordial black holes from single-field inflation: A fine-tuning audit. arXiv 2023, arXiv:2304.01997. [Google Scholar]
- Kristiano, J.; Yokoyama, J. Ruling Out Primordial Black Hole Formation From Single-Field Inflation. arXiv 2022, arXiv:2211.03395. [Google Scholar]
- Kristiano, J.; Yokoyama, J. Response to criticism on “Ruling Out Primordial Black Hole Formation From Single-Field Inflation”: A note on bispectrum and one-loop correction in single-field inflation with primordial black hole formation. arXiv 2023, arXiv:2303.00341. [Google Scholar]
- Choudhury, S.; Panda, S.; Sami, M. Quantum loop effects on the power spectrum and constraints on primordial black holes. arXiv 2023, arXiv:2303.06066. [Google Scholar]
- Riotto, A. The Primordial Black Hole Formation from Single-Field Inflation is Not Ruled Out. arXiv 2023, arXiv:2301.00599. [Google Scholar]
- Riotto, A. The Primordial Black Hole Formation from Single-Field Inflation is Still Not Ruled Out. arXiv 2023, arXiv:2303.01727. [Google Scholar]
- Firouzjahi, H.; Riotto, A. Primordial Black Holes and Loops in Single-Field Inflation. arXiv 2023, arXiv:2304.07801. [Google Scholar]
- Franciolini, G.; Iovino, A., Jr.; Taoso, M.; Urbano, A. One loop to rule them all: Perturbativity in the presence of ultra slow-roll dynamics. arXiv 2023, arXiv:2305.0349. [Google Scholar]
- Fumagalli, J. Absence of one-loop effects on large scales from small scales in non-slow-roll dynamics. arXiv 2023, arXiv:2305.19263. [Google Scholar]

| r | , g | ||||||
|---|---|---|---|---|---|---|---|
| 6.36 | 0.964959 | 0.0359 | 26 | 47 | 21 | ||
| 6.70 | 0.964905 | 0.0182 | 34 | 54 | 20 | ||
| 7.01 | 0.964944 | 0.0095 | 43 | 65 | 22 | ||
| 7.07 | 0.964917 | 0.0083 | 45 | 64 | 19 | ||
| 7.12 | 0.964925 | 0.0074 | 47 | 65 | 18 | ||
| 7.15 | 0.964908 | 0.0070 | 49 | 66 | 17 | ||
| 7.20 | 0.964961 | 0.0062 | 51 | 64 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saburov, S.; Ketov, S.V. Improved Model of Primordial Black Hole Formation after Starobinsky Inflation. Universe 2023, 9, 323. https://doi.org/10.3390/universe9070323
Saburov S, Ketov SV. Improved Model of Primordial Black Hole Formation after Starobinsky Inflation. Universe. 2023; 9(7):323. https://doi.org/10.3390/universe9070323
Chicago/Turabian StyleSaburov, Sultan, and Sergei V. Ketov. 2023. "Improved Model of Primordial Black Hole Formation after Starobinsky Inflation" Universe 9, no. 7: 323. https://doi.org/10.3390/universe9070323
APA StyleSaburov, S., & Ketov, S. V. (2023). Improved Model of Primordial Black Hole Formation after Starobinsky Inflation. Universe, 9(7), 323. https://doi.org/10.3390/universe9070323








