The Hawking Radiation in Massive Gravity: Path Integral and the Bogoliubov Method
Abstract
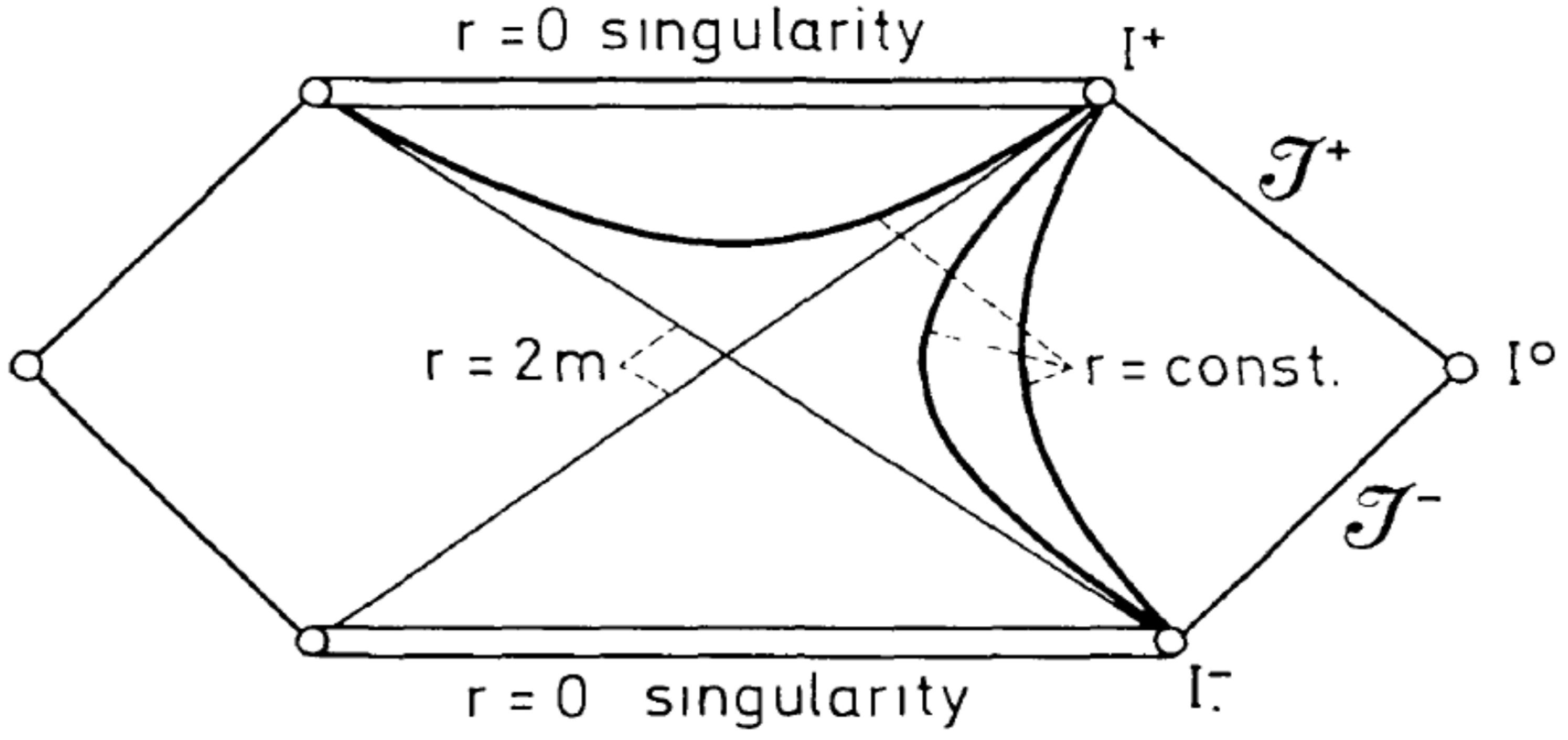
1. Introduction
2. The Black Hole Solution in Massive Gravity
3. The Bogoliubov Transformation Method in Massive Gravity: Hawking Radiation
3.1. The Case of GR: Observers Defining the Time in Agreement with in Massive Gravity
3.2. The Case of Observers Defining the Time Arbitrary
4. The Path Integral Formulation of the Black Hole Radiation in Massive Gravity
Further Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 1974, 9, 3292–3300. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Universal Bound on the Entropy to Energy Ratio for Bounded Systems. Phys. Rev. D 1981, 23, 287–298. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206.. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Path-Integral derivation of black-hole radiance. Phys. Rev. D 1976, 13, 2188–2203. [Google Scholar] [CrossRef]
- Kodama, H.; Arraut, I. Stability of the Schwarzschild-de Sitter black hole in the dRGT Massive Gravity theory. Prog. Theor. Exp. Phys. 2014, 2014, 023E02. [Google Scholar] [CrossRef]
- De Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef] [PubMed]
- De Rham, C.; Gabadadze, G. Generalization of the Fierz-Pauli Action. Phys. Rev. D 2010, 82, 044020. [Google Scholar] [CrossRef]
- Arraut, I. On the apparent loss of predictability inside the de-Rham-Gabadadze-Tolley non-linear formulation of Massive Gravity: The Hawking radiation effect. EPL 2015, 109, 10002. [Google Scholar] [CrossRef]
- Arraut, I. Path-Integral derivation of black-hole radiance inside the de-Rham-Gabadadze-Tolley formulation of Massive Gravity. Eur. Phys. J. C 2017, 77, 501. [Google Scholar] [CrossRef]
- Arraut, I. The Black Hole Radiation in Massive Gravity. Universe 2018, 4, 27. [Google Scholar] [CrossRef]
- Rubakov, V.; Tinyakov, P.G. Infrared-modified gravities and massive gravitons. Phys.-Usp. 2008, 51, 759–792. [Google Scholar] [CrossRef]
- Rubakov, V. Lorentz-violating graviton masses: Getting around ghosts, low strong coupling scale and VDVZ discontinuity. arXiv 2004, 0407104. [Google Scholar]
- Birrell, N.D.; Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I.; Segovia, C.; Rosado, W. The Hawking Radiation in Massive Gravity: Path Integral and the Bogoliubov Method. Universe 2023, 9, 228. https://doi.org/10.3390/universe9050228
Arraut I, Segovia C, Rosado W. The Hawking Radiation in Massive Gravity: Path Integral and the Bogoliubov Method. Universe. 2023; 9(5):228. https://doi.org/10.3390/universe9050228
Chicago/Turabian StyleArraut, Ivan, Carlos Segovia, and Wilson Rosado. 2023. "The Hawking Radiation in Massive Gravity: Path Integral and the Bogoliubov Method" Universe 9, no. 5: 228. https://doi.org/10.3390/universe9050228
APA StyleArraut, I., Segovia, C., & Rosado, W. (2023). The Hawking Radiation in Massive Gravity: Path Integral and the Bogoliubov Method. Universe, 9(5), 228. https://doi.org/10.3390/universe9050228





