Magnetic Activity of Different Types of Variable Stars Observed by TESS Mission
Abstract
1. Introduction
2. Data
2.1. TESS Data
2.2. LAMOST Spectra
3. Flare Detection
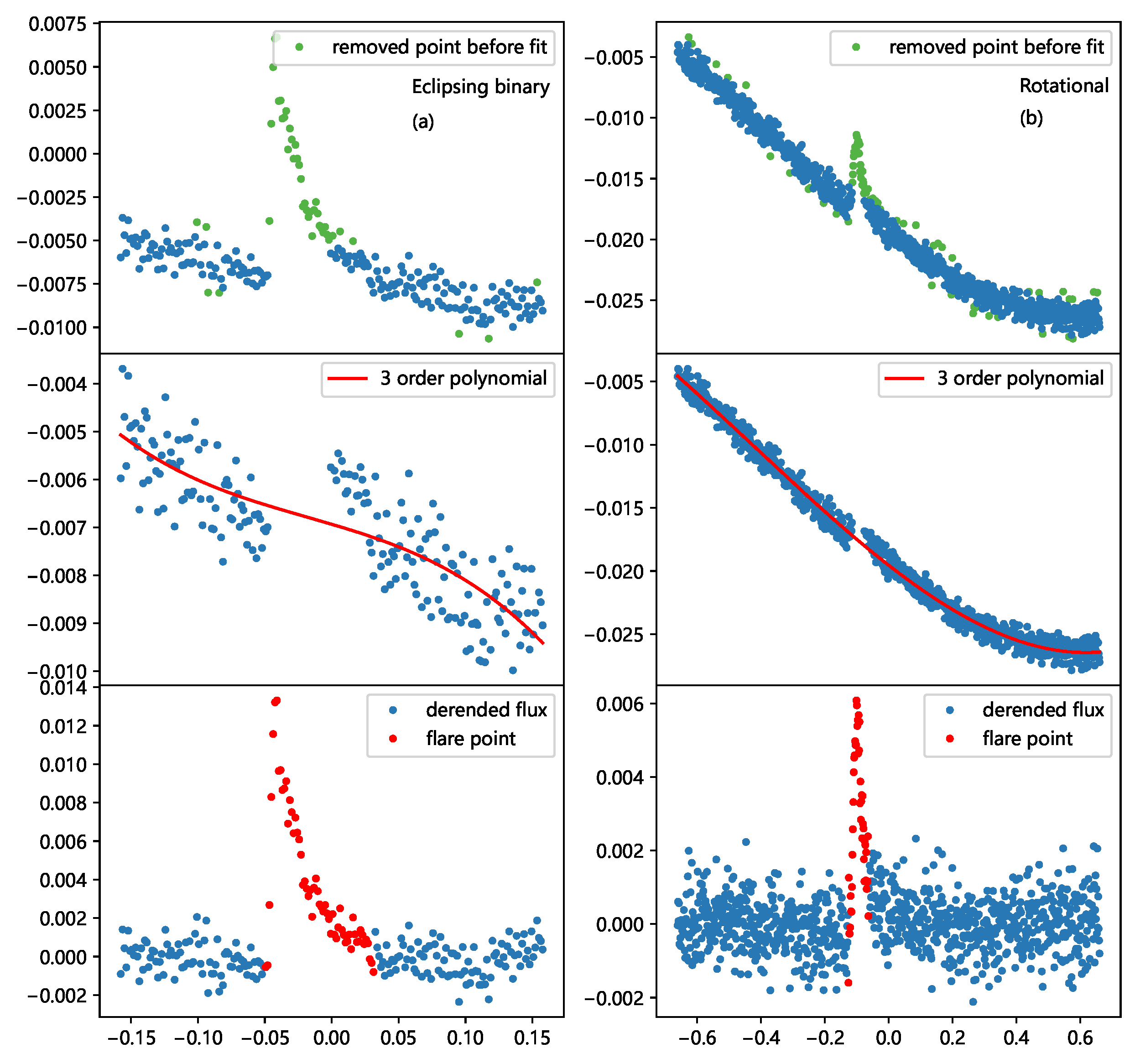
3.1. Searching for TESS Flare
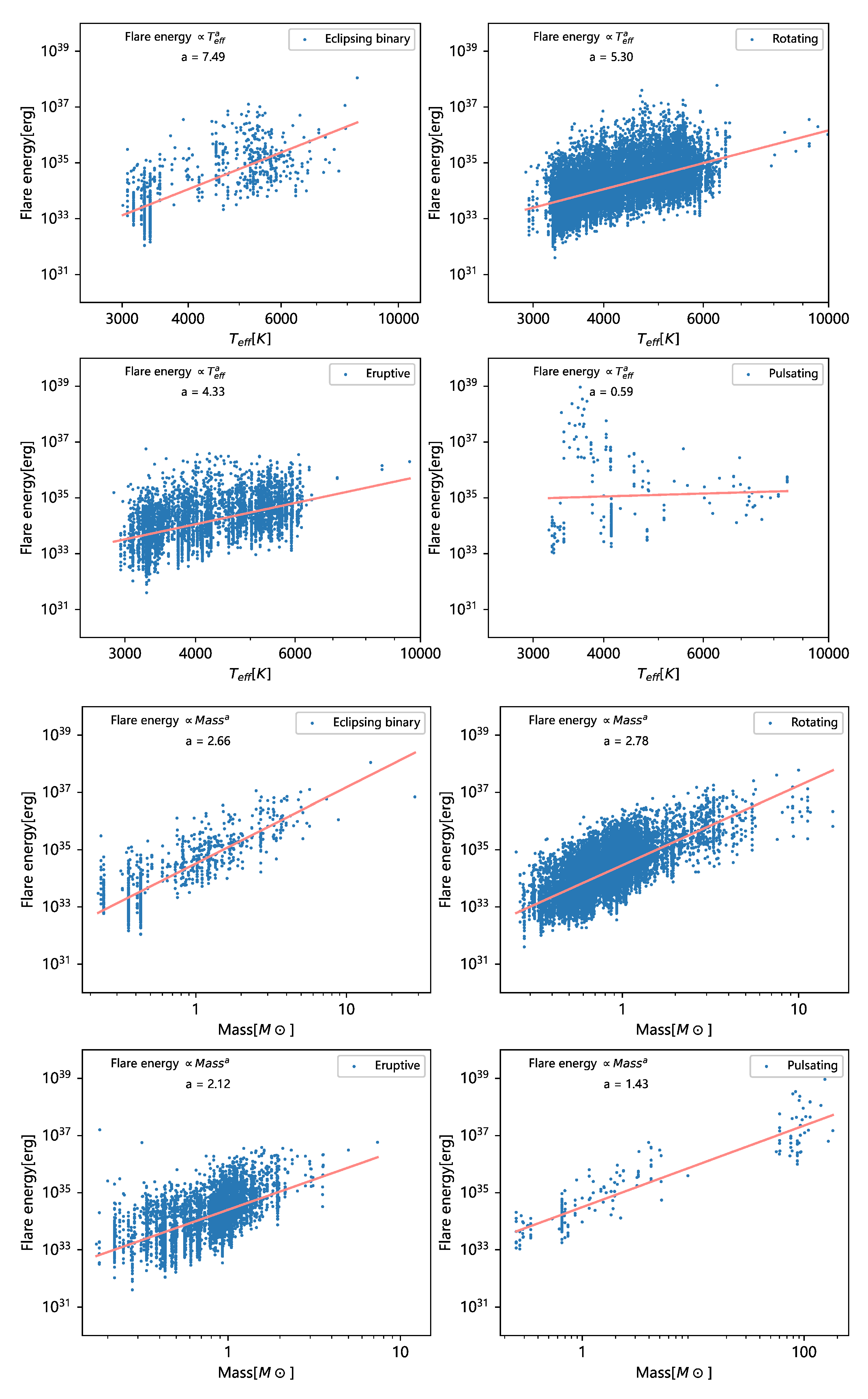
3.2. TESS Flare Energies
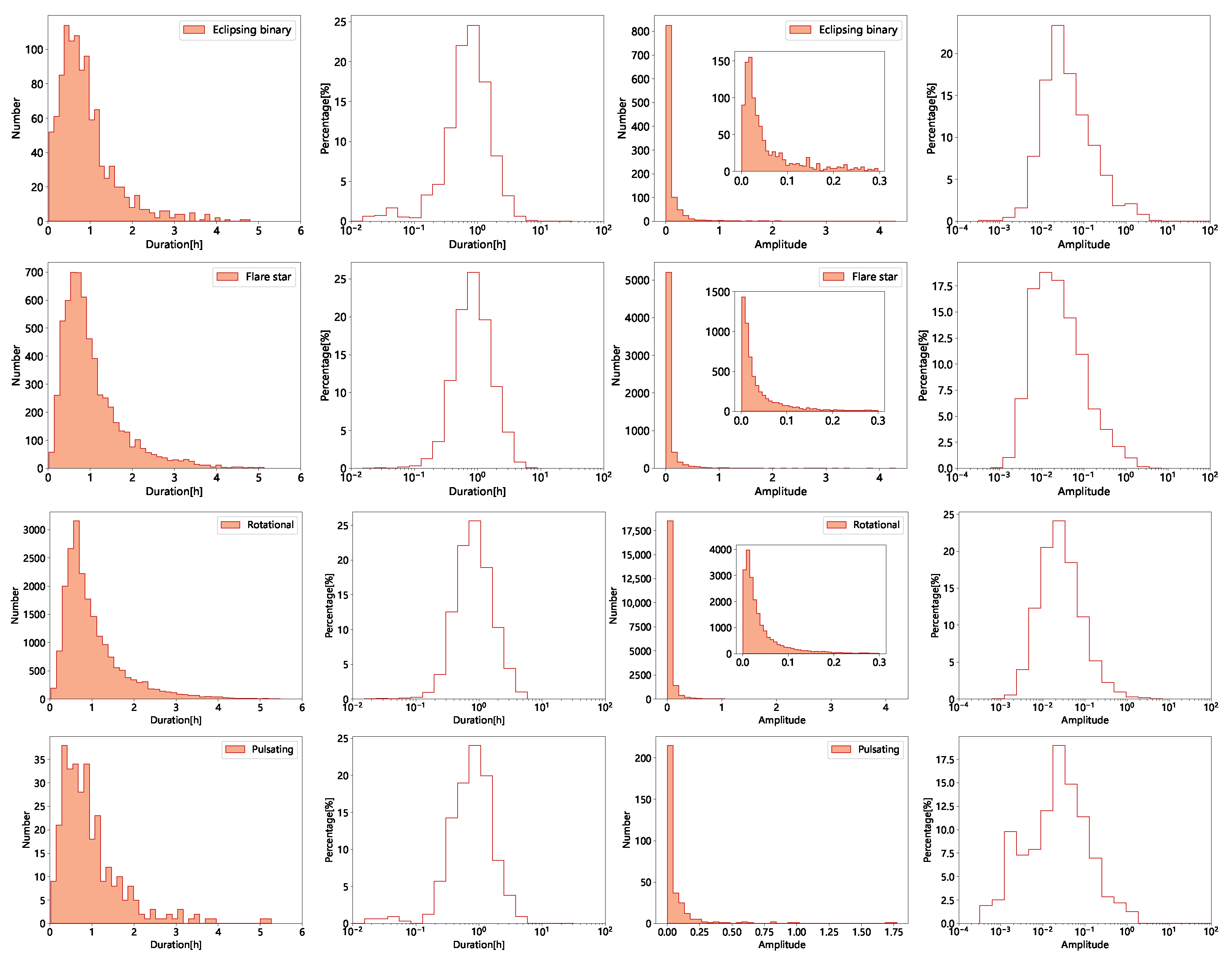
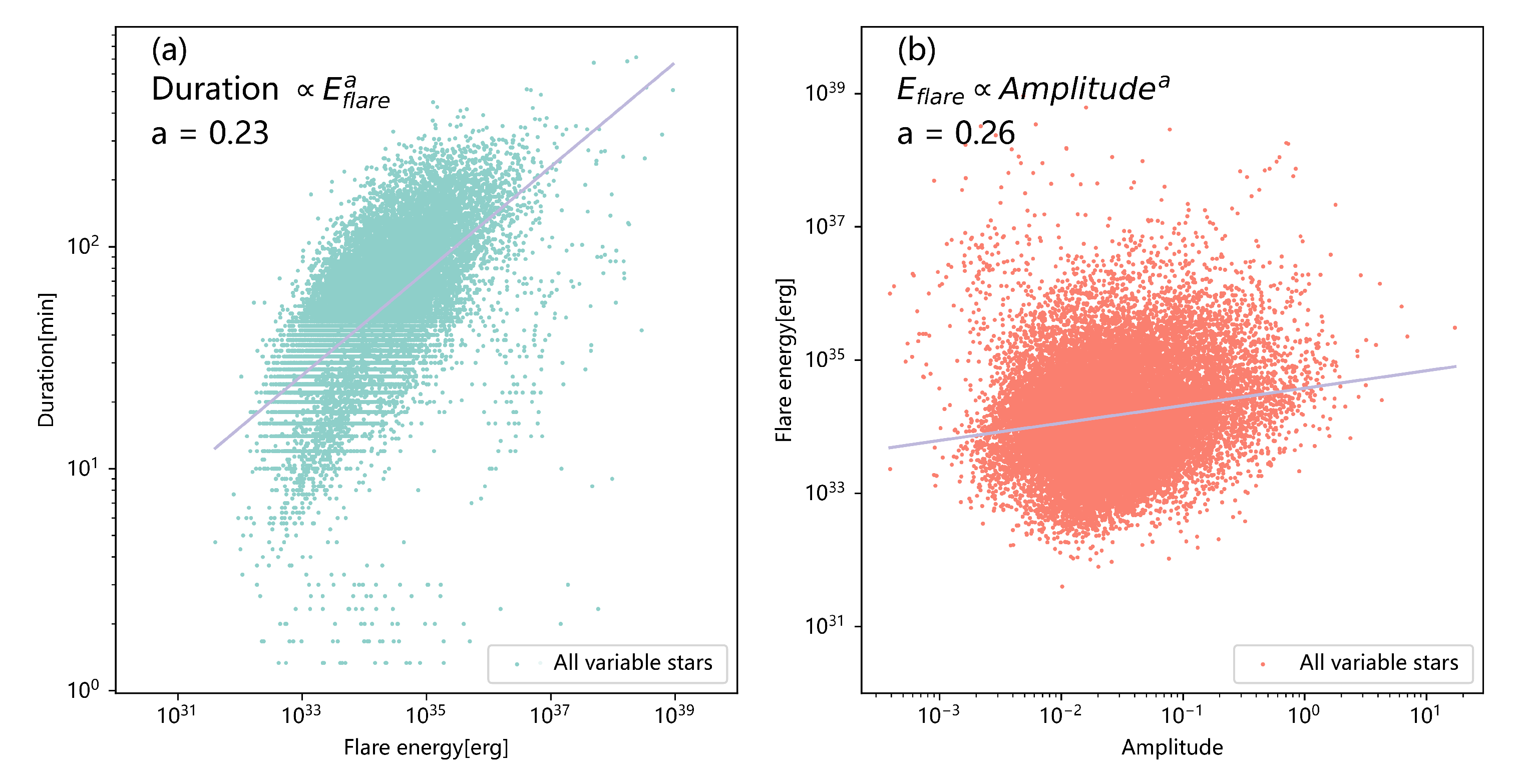
3.3. Flare Duration and Amplitude
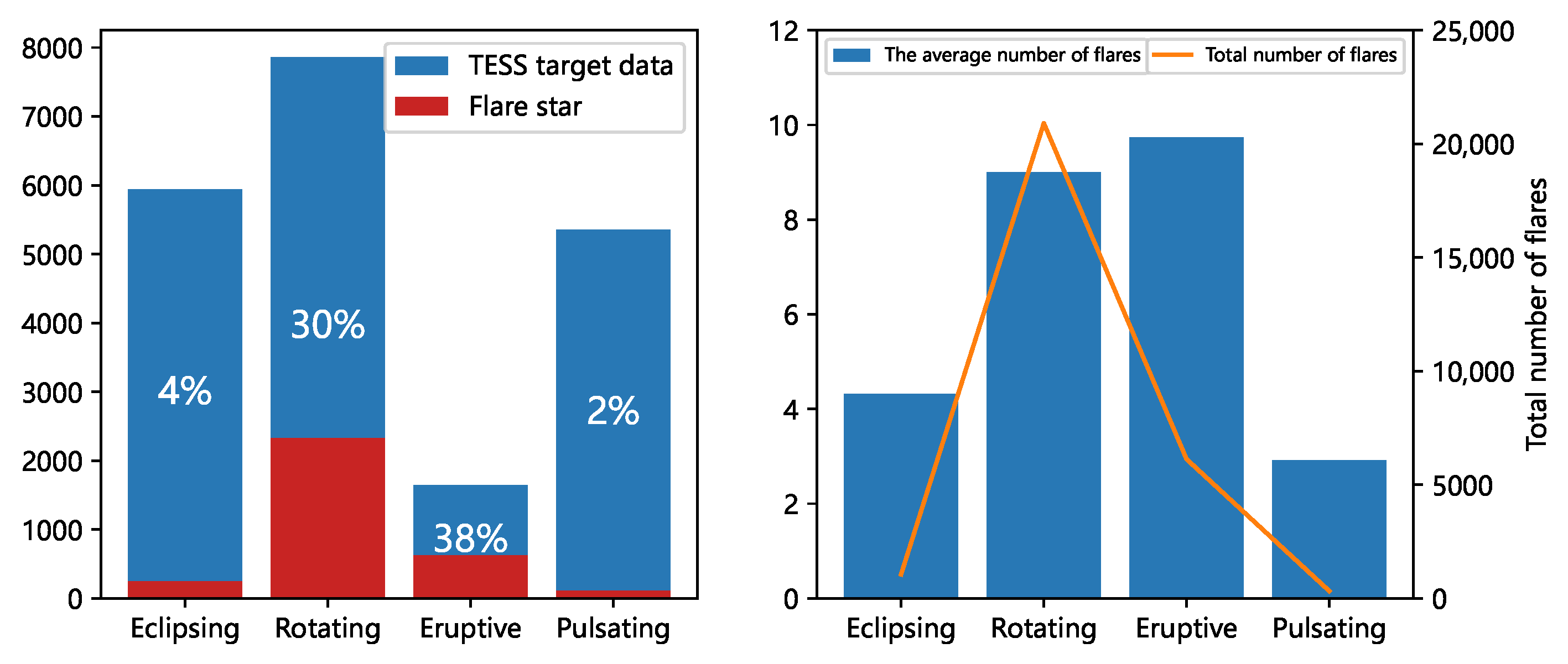
3.4. Flare Occurrence Percentages
3.5. Ratio of Flaring Stars to Total Stars
3.6. Duration, Amplitude, and Energy
3.7. TESS Flare Frequency Distribution
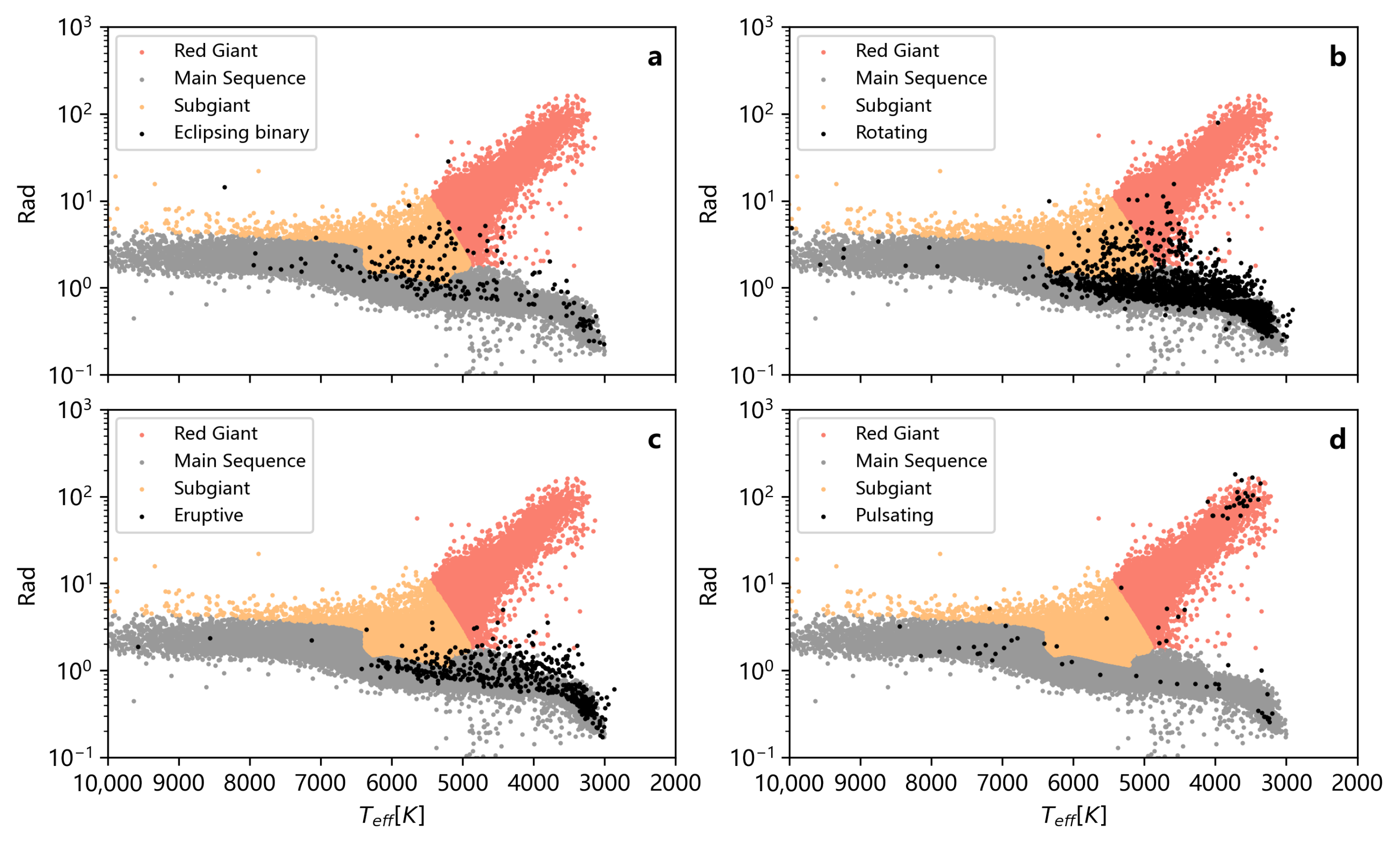
4. Chromospheric Activity
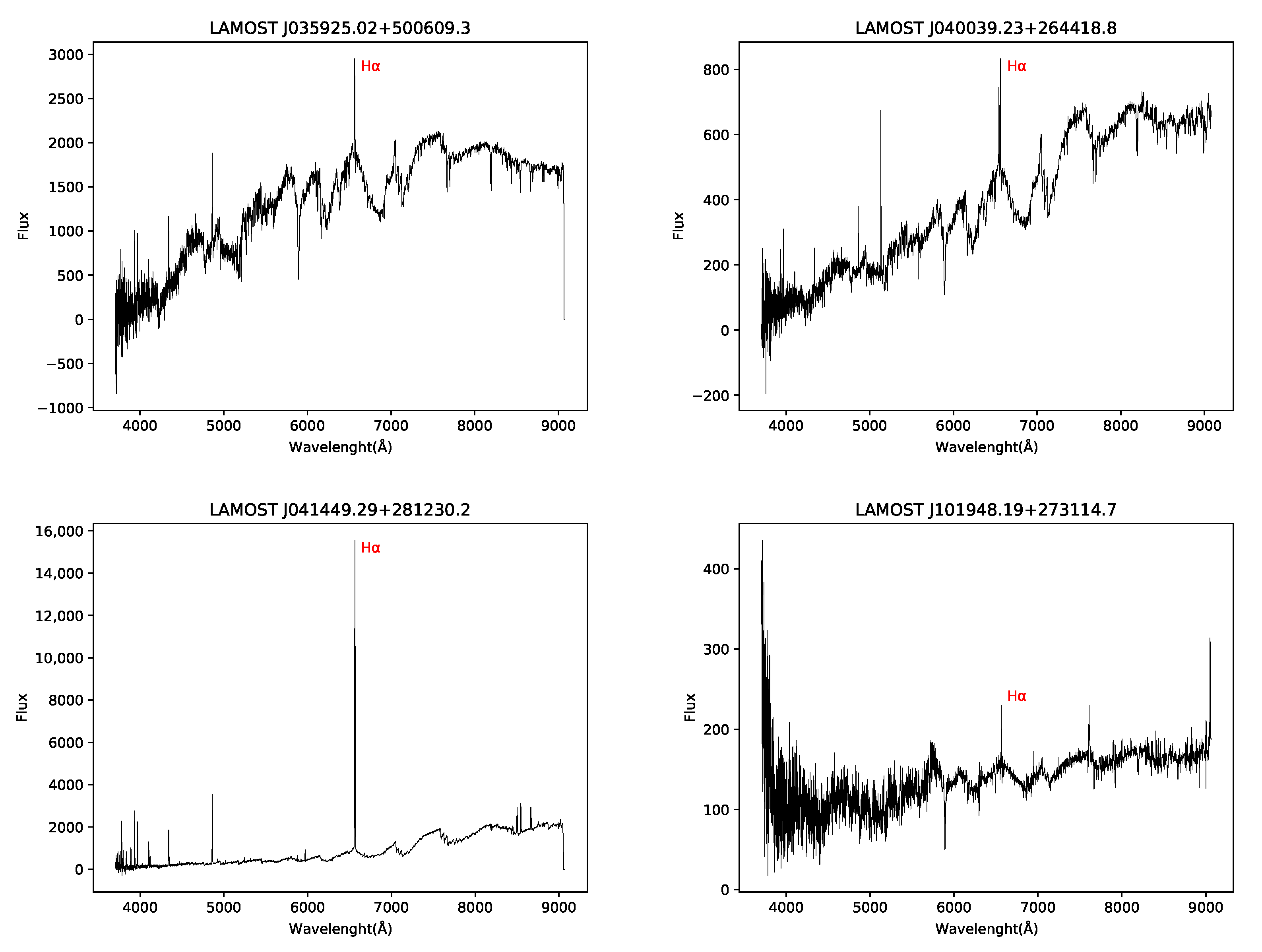
4.1. LAMOST Data
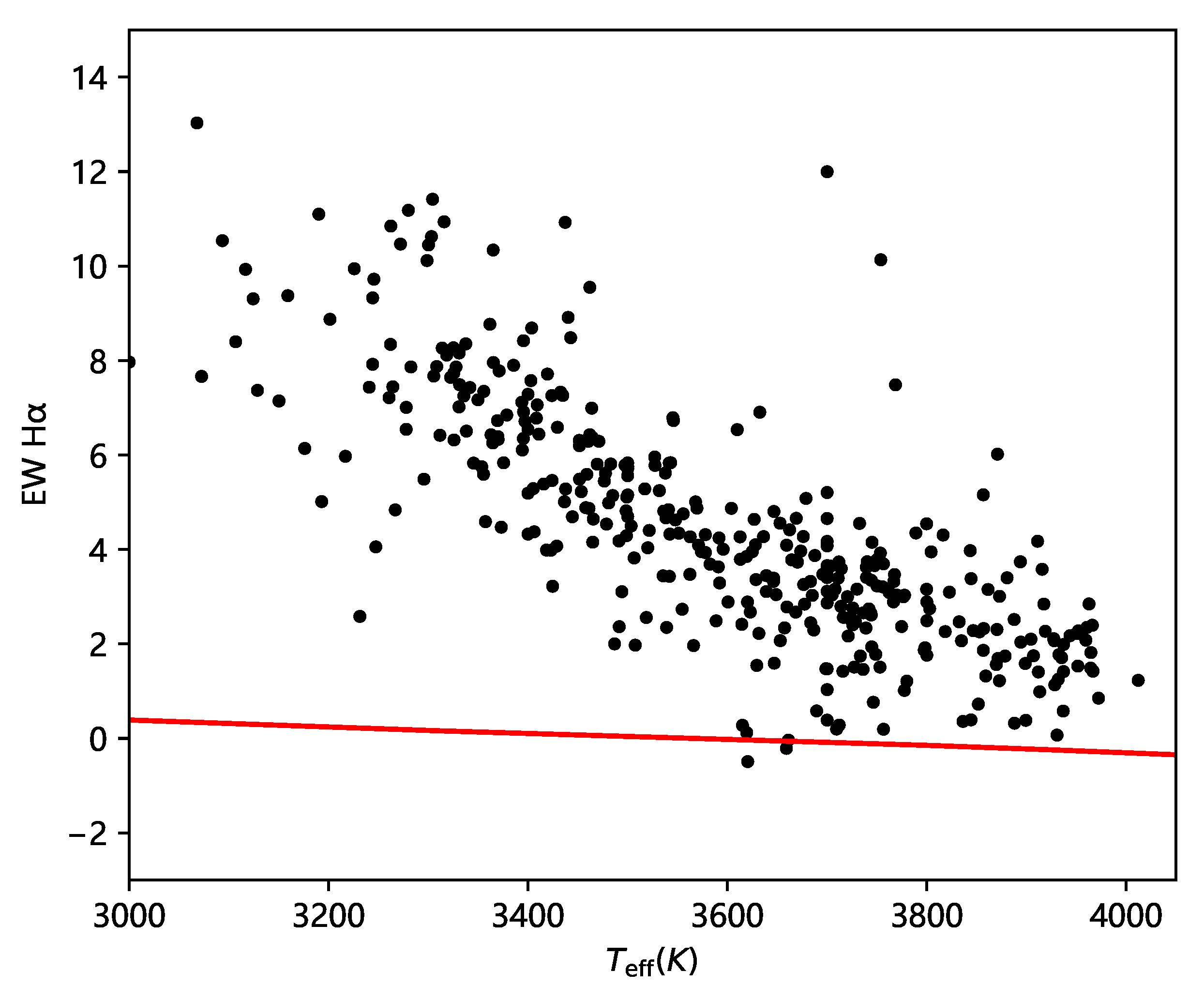
4.2. Chromospheric Activity and Variation
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parker, E.N. The Solar-Flare Phenomenon and the Theory of Reconnection and Annihiliation of Magnetic Fields. Astrophys. J. Suppl. Ser. 1963, 8, 177. [Google Scholar] [CrossRef]
- Masuda, S.; Kosugi, T.; Hara, H.; Tsuneta, S.; Ogawara, Y. A loop-top hard X-ray source in a compact solar flare as evidence for magnetic reconnection. Nature 1994, 371, 495–497. [Google Scholar] [CrossRef]
- Su, Y.; Veronig, A.M.; Holman, G.D.; Dennis, B.R.; Wang, T.; Temmer, M.; Gan, W. Imaging coronal magnetic-field reconnection in a solar flare. Nat. Phys. 2013, 9, 489–493. [Google Scholar] [CrossRef]
- Maehara, H.; Shibayama, T.; Notsu, S.; Notsu, Y.; Nagao, T.; Kusaba, S.; Honda, S.; Nogami, D.; Shibata, K. Superflares on solar-type stars. Nature 2012, 485, 478–481. [Google Scholar] [CrossRef]
- Haisch, B.; Strong, K.T.; Rodono, M. Flares on the Sun and other stars. Annu. Rev. Astron. Astrophys. 1991, 29, 275–324. [Google Scholar] [CrossRef]
- Hawley, S.L.; Pettersen, B.R. The Great Flare of 1985 April 12 on AD Leonis. Astrophys. J. 1991, 378, 725. [Google Scholar] [CrossRef]
- Ambartsumian, V.A.; Mirzoian, L.V. Flare stars in star clusters and associations. In Symposium-International Astronomical Union, Volume 67: Variable Stars and Stellar Evolution; Sherwood, V.E., Plaut, L., Eds.; Reidel: Kufstein, Austria, 1975; pp. 3–14. [Google Scholar]
- Haro, G. The possible connexion between T Tauri stars and UV Ceti stars. In Symposium–International Astronomical Union, Volume 3: Non-Stable Stars; Herbig, G.H., Ed.; Cambridge University Press: Cambridge, UK, 1957; p. 26. [Google Scholar]
- Hilton, E.J. The Galactic M Dwarf Flare Rate. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2011. [Google Scholar]
- Rubenstein, E.P.; Schaefer, B.E. Are Superflares on Solar Analogues Caused by Extrasolar Planets? Astrophys. J. 2000, 529, 1031–1033. [Google Scholar] [CrossRef]
- Parsamyan, E.S. Dependence of the absolute magnitudes (energies) of flares on the age of the cluster in which the flare stars occur. Astrophysics 1976, 12, 145–151. [Google Scholar] [CrossRef]
- Parsamyan, E.S. Determination of the age of stellar aggregates and flare stars of the galactic field. Astrophysics 1995, 38, 206–212. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.; Basri, G.; Batalha, N.; Brown, T.; Caldwell, D.; Caldwell, J.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Kepler Planet-Detection Mission: Introduction and First Results. Science 2010, 327, 977. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.A.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). In Proceedings of the Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, Montreal, QC, Canada, 22–27 June 2014; Oschmann Jacobus, M.J., Clampin, M., Fazio, G.G., MacEwen, H.A., Eds.; Volume 9143, p. 914320. [Google Scholar] [CrossRef]
- Wang, S.G.; Su, D.Q.; Chu, Y.Q.; Cui, X.; Wang, Y.N. Special configuration of a very large Schmidt telescope for extensive astronomical spectroscopic observation. Appl. Opt. 1996, 35, 5155–5161. [Google Scholar] [CrossRef] [PubMed]
- Su, D.Q.; Cui, X.Q. Active Optics in LAMOST. Chin. J. Astron. Astrophys. 2004, 4, 1–9. [Google Scholar] [CrossRef]
- Cui, X.Q.; Zhao, Y.H.; Chu, Y.Q.; Li, G.P.; Li, Q.; Zhang, L.P.; Su, H.J.; Yao, Z.Q.; Wang, Y.N.; Xing, X.Z.; et al. The Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST). Res. Astron. Astrophys. 2012, 12, 1197–1242. [Google Scholar] [CrossRef]
- Koch, D.G.; Borucki, W.J.; Basri, G.; Batalha, N.M.; Brown, T.M.; Caldwell, D.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; Dunham, E.W.; et al. Kepler Mission Design, Realized Photometric Performance, and Early Science. Astrophys. J. 2010, 713, L79–L86. [Google Scholar] [CrossRef]
- Jenkins, J.M. Initial Performance of the TESS Science Pipeline; American Astronomical Society: Washington, DC, USA, 2019. [Google Scholar]
- Walkowicz, L.M.; Basri, G.; Batalha, N.; Gilliland, R.L.; Jenkins, J.; Borucki, W.J.; Koch, D.; Caldwell, D.; Dupree, A.K.; Latham, D.W.; et al. White-light Flares on Cool Stars in the Kepler Quarter 1 Data. Astron. J. 2011, 141, 50. [Google Scholar] [CrossRef]
- Balona, L.A. Kepler observations of flaring in A–F type stars. Mon. Not. R. Astron. Soc. 2012, 423, 3420–3429. [Google Scholar] [CrossRef]
- Davenport, J.R.A.; Hawley, S.L.; Hebb, L.; Wisniewski, J.P.; Kowalski, A.F.; Johnson, E.C.; Malatesta, M.; Peraza, J.; Keil, M.; Silverberg, S.M.; et al. Kepler Flares. II. The Temporal Morphology of White-light Flares on GJ 1243. Astrophys. J. 2014, 797, 122. [Google Scholar] [CrossRef]
- Davenport, J.R.A. The Kepler Catalog of Stellar Flares. Astrophys. J. 2016, 829, 23. [Google Scholar] [CrossRef]
- Gao, Q.; Xin, Y.; Liu, J.F.; Zhang, X.B.; Gao, S. White-light Flares on Close Binaries Observed with Kepler. Astrophys. J. Suppl. Ser. 2016, 224, 37. [Google Scholar] [CrossRef]
- Lin, C.L.; Ip, W.H.; Hou, W.C.; Huang, L.C.; Chang, H.Y. A Comparative Study of the Magnetic Activities of Low-mass Stars from M-type to G-type. Astrophys. J. 2019, 873, 97. [Google Scholar] [CrossRef]
- Günther, M.N.; Zhan, Z.; Seager, S.; Rimmer, P.B.; Ranjan, S.; Stassun, K.G.; Oelkers, R.J.; Daylan, T.; Newton, E.; Kristiansen, M.H.; et al. Stellar Flares from the First TESS Data Release: Exploring a New Sample of M Dwarfs. Astron. J. 2020, 159, 60. [Google Scholar] [CrossRef]
- Ilin, E.; Schmidt, S.J.; Davenport, J.R.A.; Strassmeier, K.G. Flares in open clusters with K2. I. M 45 (Pleiades), M 44 (Praesepe), and M 67. Astron. Astrophys. 2019, 622, A133. [Google Scholar] [CrossRef]
- Feinstein, A.D.; Montet, B.T.; Ansdell, M.; Nord, B.; Bean, J.L.; Günther, M.N.; Gully-Santiago, M.A.; Schlieder, J.E. Flare Statistics for Young Stars from a Convolutional Neural Network Analysis of TESS Data. Astron. J. 2020, 160, 219. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, L.; Meng, G.; Han, X.L.; Misra, P.; Yang, J.; Pi, Q. Properties of flare events based on light curves from the TESS survey. Astron. Astrophys. 2023, 669, A15. [Google Scholar] [CrossRef]
- Parker, E.N. Cosmical Magnetic Fields. In Their Origin and Their Activity; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Reiners, A.; Joshi, N.; Goldman, B. A Catalog of Rotation and Activity in Early-M Stars. Astron. J. 2012, 143, 93. [Google Scholar] [CrossRef]
- Douglas, S.T.; Agüeros, M.A.; Covey, K.R.; Bowsher, E.C.; Bochanski, J.J.; Cargile, P.A.; Kraus, A.; Law, N.M.; Lemonias, J.J.; Arce, H.G.; et al. The Factory and the Beehive. II. Activity and Rotation in Praesepe and the Hyades. Astrophys. J. 2014, 795, 161. [Google Scholar] [CrossRef]
- Fang, X.S.; Zhao, G.; Zhao, J.K.; Bharat Kumar, Y. Stellar activity with LAMOST—II. Chromospheric activity in open clusters. Mon. Not. R. Astron. Soc. 2018, 476, 908–926. [Google Scholar] [CrossRef]
- Yi, Z.; Luo, A.; Song, Y.; Zhao, J.; Shi, Z.; Wei, P.; Ren, J.; Wang, F.; Kong, X.; Li, Y.; et al. M Dwarf Catalog of the LAMOST Pilot Survey. Astron. J. 2014, 147, 33. [Google Scholar] [CrossRef]
- Chang, H.Y.; Song, Y.H.; Luo, A.L.; Huang, L.C.; Ip, W.H.; Fu, J.N.; Zhang, Y.; Hou, Y.H.; Cao, Z.H.; Wang, Y.F. LAMOST Observations of Flaring M Dwarfs in the Kepler Field. Astrophys. J. 2017, 834, 92. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J.; Gao, Q.; Fang, X.; Guo, J.; Zhang, Y.; Hou, Y.; Wang, Y.; Cao, Z. The Flaring Activity of M Dwarfs in the Kepler Field. Astrophys. J. 2017, 849, 36. [Google Scholar] [CrossRef]
- Lu, H.p.; Zhang, L.y.; Shi, J.; Han, X.L.; Fan, D.; Long, L.; Pi, Q. Magnetic Activities of M-type Stars Based on LAMOST DR5 and Kepler and K2 Missions. Astrophys. J. Suppl. Ser. 2019, 243, 28. [Google Scholar] [CrossRef]
- Watson, C.L.; Henden, A.A.; Price, A. The International Variable Star Index (VSX). Soc. Astron. Sci. Annu. Symp. 2006, 25, 47. [Google Scholar]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.A.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Jenkins, J.M. The Impact of Solar-like Variability on the Detectability of Transiting Terrestrial Planets. Astrophys. J. 2002, 575, 493–505. [Google Scholar] [CrossRef]
- Jenkins, J.M.; Chandrasekaran, H.; McCauliff, S.D.; Caldwell, D.A.; Tenenbaum, P.; Li, J.; Klaus, T.C.; Cote, M.T.; Middour, C. Transiting planet search in the Kepler pipeline. In Proceedings of the Software and Cyberinfrastructure for Astronomy, San Diego, CA, USA, 27–30 June 2010; Radziwill, N.M., Bridger, A., Eds.; Volume 7740, p. 77400D. [Google Scholar] [CrossRef]
- Jenkins, J.M.; Twicken, J.D.; McCauliff, S.; Campbell, J.; Sanderfer, D.; Lung, D.; Mansouri-Samani, M.; Girouard, F.; Tenenbaum, P.; Klaus, T.; et al. The TESS science processing operations center. In Proceedings of the Software and Cyberinfrastructure for Astronomy IV, Edinburgh, UK, 26–30 June 2016; Chiozzi, G., Guzman, J.C., Eds.; Volume 9913, p. 99133E. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Agudo, I.; Ajello, M.; Allafort, A.; Aller, H.D.; Aller, M.F.; Antolini, E.; Arkharov, A.A.; Axelsson, M.; et al. Fermi Large Area Telescope and Multi-wavelength Observations of the Flaring Activity of PKS 1510-089 between 2008 September and 2009 June. Astrophys. J. 2010, 721, 1425–1447. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; et al. Multi-wavelength Observations of the Flaring Gamma-ray Blazar 3C 66A in 2008 October. Astrophys. J. 2011, 726, 43. [Google Scholar] [CrossRef]
- Davenport, J.R.A.; Covey, K.R.; Clarke, R.W.; Boeck, A.C.; Cornet, J.; Hawley, S.L. The Evolution of Flare Activity with Stellar Age. Astrophys. J. 2019, 871, 241. [Google Scholar] [CrossRef]
- Wu, C.J.; Ip, W.H.; Huang, L.C. A Study of Variability in the Frequency Distributions of the Superflares of G-type Stars Observed by the Kepler Mission. Astrophys. J. 2015, 798, 92. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Shariati, H.; Debosscher, J. Stellar Flares Observed in Long-cadence Data from the Kepler Mission. Astrophys. J. Suppl. Ser. 2017, 232, 26. [Google Scholar] [CrossRef]
- Huang, L.C.; Ip, W.H.; Lin, C.L.; Zhang, X.L.; Song, Y.H.; Luo, A.L. M-dwarf Eclipsing Binaries with Flare Activity. Astrophys. J. 2020, 892, 58. [Google Scholar] [CrossRef]
- Günther, M.N.; Pozuelos, F.J.; Dittmann, J.A.; Dragomir, D.; Kane, S.R.; Daylan, T.; Feinstein, A.D.; Huang, C.X.; Morton, T.D.; Bonfanti, A.; et al. A super-Earth and two sub-Neptunes transiting the nearby and quiet M dwarf TOI-270. Nat. Astron. 2019, 3, 1099–1108. [Google Scholar] [CrossRef]
- Shporer, A.; Fuller, J.; Isaacson, H.; Hambleton, K.; Thompson, S.E.; Prša, A.; Kurtz, D.W.; Howard, A.W.; O’Leary, R.M. Radial Velocity Monitoring of Kepler Heartbeat Stars. Astrophys. J. 2016, 829, 34. [Google Scholar] [CrossRef]
- Webb, S.; Lochner, M.; Muthukrishna, D.; Cooke, J.; Flynn, C.; Mahabal, A.; Goode, S.; Andreoni, I.; Pritchard, T.; Abbott, T.M.C. Unsupervised machine learning for transient discovery in deeper, wider, faster light curves. Mon. Not. R. Astron. Soc. 2020, 498, 3077–3094. [Google Scholar] [CrossRef]
- Lochner, M.; Bassett, B.A. ASTRONOMALY: Personalised active anomaly detection in astronomical data. Astron. Comput. 2021, 36, 100481. [Google Scholar] [CrossRef]
- Vida, K.; Roettenbacher, R.M. Finding flares in Kepler data using machine-learning tools. Astron. Astrophys. 2018, 616, A163. [Google Scholar] [CrossRef]
- Su, T.; Zhang, L.y.; Long, L.; Han, X.L.; Misra, P.; Meng, G.; Pi, Q.; Yang, Z.; Yang, J. Magnetic Activity and Physical Parameters of Exoplanet Host Stars Based on LAMOST DR7, TESS, Kepler, and K2 Surveys. Astrophys. J. Suppl. Ser. 2022, 261, 26. [Google Scholar] [CrossRef]
- Tu, Z.L.; Yang, M.; Wang, H.F.; Wang, F.Y. Superflares, Chromospheric Activities, and Photometric Variabilities of Solar-type Stars from the Second-year Observation of TESS and Spectra of LAMOST. Astrophys. J. Suppl. Ser. 2021, 253, 35. [Google Scholar] [CrossRef]
- Notsu, Y.; Maehara, H.; Honda, S.; Hawley, S.L.; Davenport, J.R.A.; Namekata, K.; Notsu, S.; Ikuta, K.; Nogami, D.; Shibata, K. Do Kepler Superflare Stars Really Include Slowly Rotating Sun-like Stars?—Results Using APO 3.5 m Telescope Spectroscopic Observations and Gaia-DR2 Data. Astrophys. J. 2019, 876, 58. [Google Scholar] [CrossRef]
- Berger, T.A.; Huber, D.; Gaidos, E.; van Saders, J.L. Revised Radii of Kepler Stars and Planets Using Gaia Data Release 2. Astrophys. J. 2018, 866, 99. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J. The Flare Catalog and the Flare Activity in the Kepler Mission. Astrophys. J. Suppl. Ser. 2019, 241, 29. [Google Scholar] [CrossRef]
- Stassun, K.G.; Oelkers, R.J.; Pepper, J.; Paegert, M.; De Lee, N.; Torres, G.; Latham, D.W.; Charpinet, S.; Dressing, C.D.; Huber, D.; et al. The TESS Input Catalog and Candidate Target List. Astron. J. 2018, 156, 102. [Google Scholar] [CrossRef]
- Huber, D.; Silva Aguirre, V.; Matthews, J.M.; Pinsonneault, M.H.; Gaidos, E.; García, R.A.; Hekker, S.; Mathur, S.; Mosser, B.; Torres, G.; et al. Revised Stellar Properties of Kepler Targets for the Quarter 1–16 Transit Detection Run. Astrophys. J. Suppl. Ser. 2014, 211, 2. [Google Scholar] [CrossRef]
- Skrutskie, M.F.; Cutri, R.M.; Stiening, R.; Weinberg, M.D.; Schneider, S.; Carpenter, J.M.; Beichman, C.; Capps, R.; Chester, T.; Elias, J.; et al. The Two Micron All Sky Survey (2MASS). Astron. J. 2006, 131, 1163–1183. [Google Scholar] [CrossRef]
- Zacharias, N.; Finch, C.T.; Girard, T.M.; Henden, A.; Bartlett, J.L.; Monet, D.G.; Zacharias, M.I. The Fourth US Naval Observatory CCD Astrograph Catalog (UCAC4). Astron. J. 2013, 145, 44. [Google Scholar] [CrossRef]
- Paegert, M.; Stassun, K.G.; De Lee, N.; Pepper, J.; Fleming, S.W.; Sivarani, T.; Mahadevan, S.; Mack Claude, E.I.; Dhital, S.; Hebb, L.; et al. Target Selection for the SDSS-III MARVELS Survey. Astron. J. 2015, 149, 186. [Google Scholar] [CrossRef]
- Wright, E.L.; Eisenhardt, P.R.M.; Mainzer, A.K.; Ressler, M.E.; Cutri, R.M.; Jarrett, T.; Kirkpatrick, J.D.; Padgett, D.; McMillan, R.S.; Skrutskie, M.; et al. The Wide-field Infrared Survey Explorer (WISE): Mission Description and Initial On-orbit Performance. Astron. J. 2010, 140, 1868–1881. [Google Scholar] [CrossRef]
- Samus’, N.N.; Kazarovets, E.V.; Durlevich, O.V.; Kireeva, N.N.; Pastukhova, E.N. General catalogue of variable stars: Version GCVS 5.1. Astron. Rep. 2017, 61, 80–88. [Google Scholar] [CrossRef]
- Tu, Z.L.; Yang, M.; Zhang, Z.J.; Wang, F.Y. Superflares on Solar-type Stars from the First Year Observation of TESS. Astrophys. J. 2020, 890, 46. [Google Scholar] [CrossRef]
- Jackman, J.A.G.; Wheatley, P.J.; Acton, J.S.; Anderson, D.R.; Bayliss, D.; Briegal, J.T.; Burleigh, M.R.; Casewell, S.L.; Gänsicke, B.T.; Gill, S.; et al. Stellar flares detected with the Next Generation Transit Survey. Mon. Not. R. Astron. Soc. 2021, 504, 3246–3264. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Morris, S.A.; Yen, G.G. Problems with fitting to the power-law distribution. Eur. Phys. J. B 2004, 41, 255–258. [Google Scholar] [CrossRef]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Bauke, H. Parameter estimation for power-law distributions by maximum likelihood methods. Eur. Phys. J. B 2007, 58, 167–173. [Google Scholar] [CrossRef]
- Li, Y.P. Fitting Power-law Frequency Distribution with a Modified Maximum Likelihood Estimator. Acta Astron. Sin. 2014, 55, 437–443. [Google Scholar]
- Shibata, K.; Takasao, S. Fractal Reconnection in Solar and Stellar Environments. In Magnetic Reconnection: Concepts and Applications; Gonzalez, W., Parker, E., Eds.; Springer: Cham, Switzerland, 2016; Volume 427, p. 373. [Google Scholar] [CrossRef]
- Shibayama, T.; Maehara, H.; Notsu, S.; Notsu, Y.; Nagao, T.; Honda, S.; Ishii, T.T.; Nogami, D.; Shibata, K. Superflares on Solar-type Stars Observed with Kepler. I. Statistical Properties of Superflares. Astrophys. J. Suppl. Ser. 2013, 209, 5. [Google Scholar] [CrossRef]
- Fang, X.S.; Zhao, G.; Zhao, J.K.; Chen, Y.Q.; Bharat Kumar, Y. Stellar activity with LAMOST—I. Spot configuration in Pleiades. Mon. Not. R. Astron. Soc. 2016, 463, 2494–2512. [Google Scholar] [CrossRef]
- Fang, X.S.; Bidin, C.M.; Zhao, G.; Zhang, L.Y.; Bharat Kumar, Y. Stellar activity with LAMOST. III. Temporal variability pattern in Pleiades, Praesepe, and Hyades. Mon. Not. R. Astron. Soc. 2020, 495, 2949–2965. [Google Scholar] [CrossRef]
- Du, B.; Luo, A.L.; Zuo, F.; Bai, Z.R.; Wang, R.; Song, Y.H.; Hou, W.; Li, Y.B.; Zhang, J.N.; Guo, Y.X.; et al. An Empirical Template Library for FGK and Late-type A Stars Using LAMOST Observed Spectra. Astrophys. J. Suppl. Ser. 2019, 240, 10. [Google Scholar] [CrossRef]
- Kruse, E.A.; Berger, E.; Knapp, G.R.; Laskar, T.; Gunn, J.E.; Loomis, C.P.; Lupton, R.H.; Schlegel, D.J. Chromospheric Variability in Sloan Digital Sky Survey M Dwarfs. II. Short-timescale Hα Variability. Astrophys. J. 2010, 722, 1352–1359. [Google Scholar] [CrossRef]
- Bell, K.J.; Hilton, E.J.; Davenport, J.R.A.; Hawley, S.L.; West, A.A.; Rogel, A.B. Hα Emission Variability in Active M Dwarfs. Publ. Astron. Soc. Pac. 2012, 124, 14. [Google Scholar] [CrossRef]










| TESS ID | Begin | Peak Time | End | Duration | Amplitude | Radius | Type | Period | Flare Energy | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| – | d | d | d | d | – | K | – | Rsun | – | d | erg |
| 8195886 | 1349.067463 | 1349.207736 | 1349.242457 | 0.174993 | 0.006858393 | 5704 | – | 1.123 | ROT | 3.2 | |
| 24695725 | 1328.524342 | 1328.528509 | 1328.541009 | 0.016667 | 2.068877509 | – | 5.0013 | 0.239 | AM + E | 0.078915 | – |
| 24695725 | 1328.913237 | 1328.917404 | 1328.925737 | 0.012500 | 1.775812587 | – | 5.0013 | 0.239 | AM + E | 0.078915 | – |
| 24695725 | 1352.178655 | 1352.199488 | 1352.203655 | 0.025000 | 1.846063035 | – | 5.0013 | 0.239 | AM + E | 0.078915 | – |
| 24695725 | 1352.573098 | 1352.577265 | 1352.581432 | 0.008333 | 1.815789406 | – | 5.0013 | 0.239 | AM + E | 0.078915 | – |
| 25078924 | 1347.117637 | 1347.127359 | 1347.162082 | 0.044444 | 0.032550198 | 5737 | 4.2756 | 1.218 | EB | 1.8088 | |
| 25078924 | 1372.574684 | 1372.577462 | 1372.584406 | 0.009722 | 0.011402875 | 5737 | 4.2756 | 1.218 | EB | 1.8088 | |
| 25118964 | 1430.494737 | 1430.516959 | 1430.57668 | 0.081942 | 0.051189899 | 3323 | 4.7301 | 0.508 | ROT | 1.0182 | |
| 25118964 | 1434.059952 | 1434.064118 | 1434.090507 | 0.030554 | 0.067075056 | 3323 | 4.7301 | 0.508 | ROT | 1.0182 | |
| 25118964 | 1434.797438 | 1434.800215 | 1434.815493 | 0.018055 | 0.031548701 | 3323 | 4.7301 | 0.508 | ROT | 1.0182 | |
| 25118964 | 1435.244651 | 1435.250207 | 1435.311317 | 0.066665 | 0.051271541 | 3323 | 4.7301 | 0.508 | ROT | 1.0182 | |
| 25118964 | 1435.805752 | 1435.808529 | 1435.829362 | 0.023609 | 0.025066236 | 3323 | 4.7301 | 0.508 | ROT | 1.0182 | |
| 25118964 | 1470.789816 | 1470.800927 | 1470.827315 | 0.037499 | 0.058276681 | 3323 | 4.7301 | 0.508 | ROT | 1.0182 | |
| 29830830 | 1563.2767 | 1563.285033 | 1563.321144 | 0.044444 | 0.013305017 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1565.204483 | 1565.212816 | 1565.222539 | 0.018056 | 0.05243868 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1571.828119 | 1571.83923 | 1571.865619 | 0.037499 | 0.016261713 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1577.480932 | 1577.487877 | 1577.548988 | 0.068056 | 0.051243498 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1593.163006 | 1593.165784 | 1593.194951 | 0.031944 | 0.024806023 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1608.404845 | 1608.409012 | 1608.432623 | 0.027777 | 0.050768616 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1609.456246 | 1609.482635 | 1609.588191 | 0.131945 | 0.177984067 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1621.350855 | 1621.367522 | 1621.399467 | 0.048612 | 0.02128801 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 | |
| 29830830 | 1637.813597 | 1637.817764 | 1637.849708 | 0.036110 | 0.048961098 | 3608 | 4.5793 | 0.688 | ROT | 4.2347 |
| LAMOST Name | MJD | SNr | Sp | RV | Fe/H | EW H | E | ||
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
| J053204.58-030529.3 | 56965 | 119.37 | dM1 | – | 3703.59 ± 85.85 | 5.266 ± 0.21 | – | 3.648007 ± 0.0011 | 1 |
| J053204.58-030529.3 | 56965 | 119.37 | dM1 | – | 3703.59 ± 85.85 | 5.266 ± 0.21 | – | 3.648007 ± 0.0011 | 1 |
| J053359.82-022132.3 | 56965 | 173.62 | dM4 | – | 3543.1 ± 92.02 | 5.174 ± 0.24 | – | 5.836873 ± 0.000438 | 1 |
| J053359.82-022132.3 | 56965 | 173.62 | dM4 | – | 3543.1 ± 92.02 | 5.174 ± 0.24 | – | 5.836873 ± 0.000438 | 1 |
| J041658.50+144617.9 | 56680 | 78.67 | dM1 | – | 3683.38 ± 80.85 | 5.417 ± 0.19 | – | 3.323599 ± 0.006691 | 1 |
| J041658.50+144617.9 | 57385 | 37.11 | dM2 | – | 3700.0 ± 91.12 | 5.477 ± 0.21 | – | 3.787314 ± 0.010092 | 1 |
| J041658.50+144617.9 | 56680 | 78.67 | dM1 | – | 3683.38 ± 80.85 | 5.417 ± 0.19 | – | 3.323599 ± 0.006691 | 1 |
| J041658.50+144617.9 | 57385 | 37.11 | dM2 | – | 3700.0 ± 91.12 | 5.477 ± 0.21 | – | 3.787314 ± 0.010092 | 1 |
| J082247.49+075717.2 | 57052 | 58.93 | dM5 | – | 3330.84 ± 84.7 | 5.165 ± 0.21 | – | 7.017833 ± 0.002155 | 1 |
| J082247.49+075717.2 | 57059 | 54.05 | dM5 | – | 3338.73 ± 85.85 | 5.157 ± 0.21 | – | 7.403388 ± 0.003257 | 1 |
| J082247.49+075717.2 | 57100 | 55.46 | dM5 | – | 3351.79 ± 85.08 | 5.133 ± 0.21 | – | 7.031153 ± 0.001737 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, M.; Zhang, L.; Yang, Z.; Su, T. Magnetic Activity of Different Types of Variable Stars Observed by TESS Mission. Universe 2023, 9, 227. https://doi.org/10.3390/universe9050227
Zhong M, Zhang L, Yang Z, Su T. Magnetic Activity of Different Types of Variable Stars Observed by TESS Mission. Universe. 2023; 9(5):227. https://doi.org/10.3390/universe9050227
Chicago/Turabian StyleZhong, Ming, Liyun Zhang, Zilu Yang, and Tianhao Su. 2023. "Magnetic Activity of Different Types of Variable Stars Observed by TESS Mission" Universe 9, no. 5: 227. https://doi.org/10.3390/universe9050227
APA StyleZhong, M., Zhang, L., Yang, Z., & Su, T. (2023). Magnetic Activity of Different Types of Variable Stars Observed by TESS Mission. Universe, 9(5), 227. https://doi.org/10.3390/universe9050227







