Probing the Lorentz Invariance Violation via Gravitational Lensing and Analytical Eigenmodes of Perturbed Slowly Rotating Bumblebee Black Holes
Abstract
1. Introduction
2. RBBH Spacetime
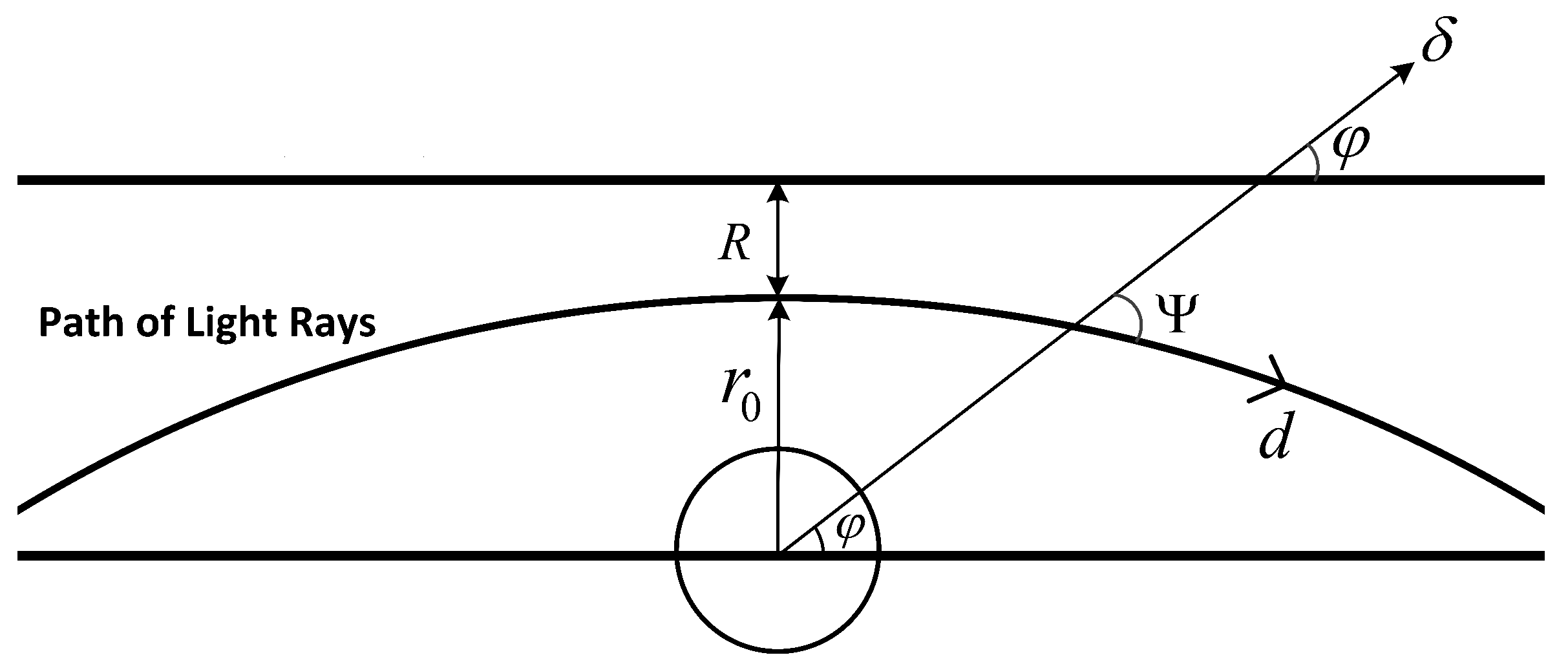
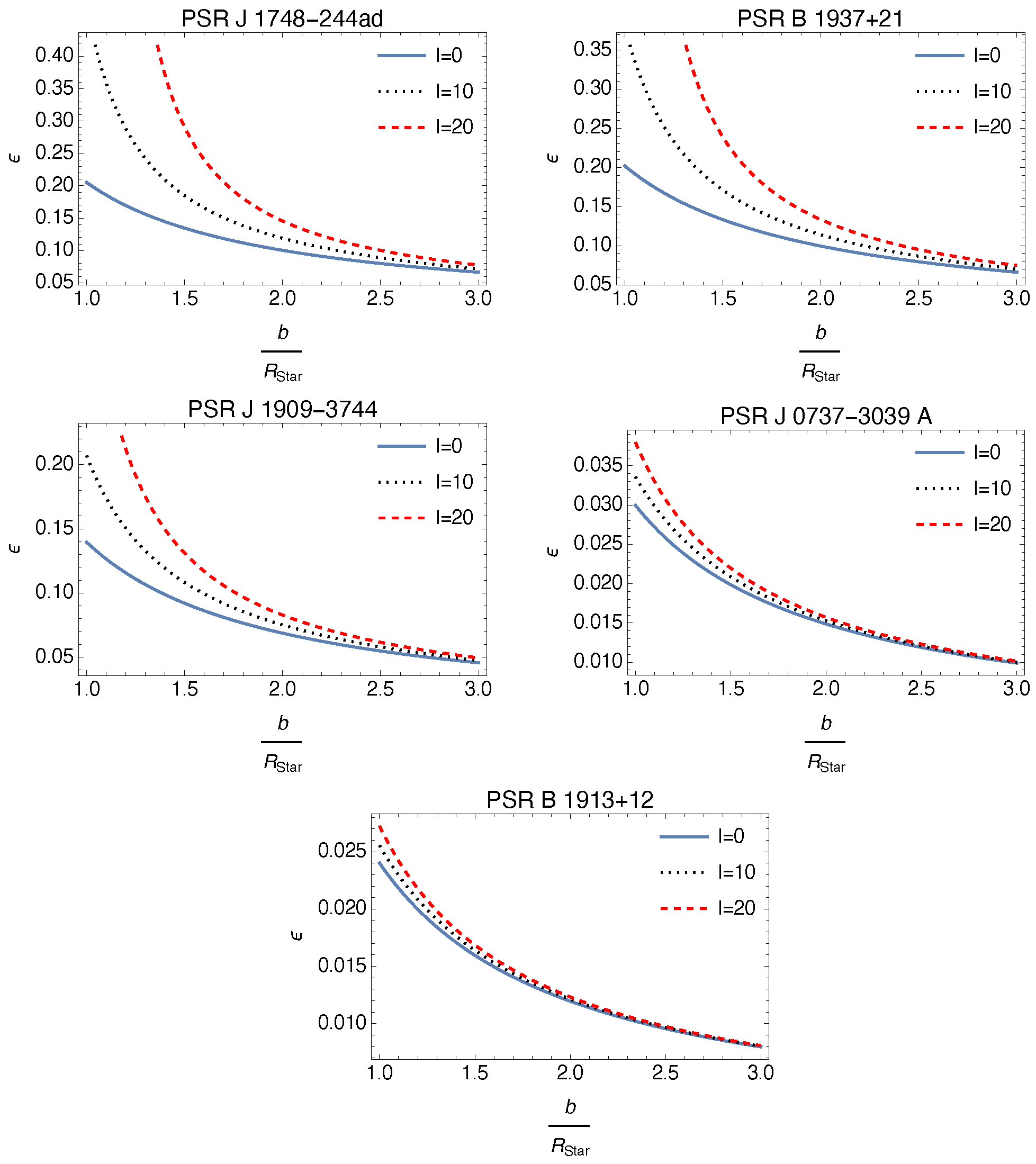
3. Gravitational Lensing of SRBBH via RIM
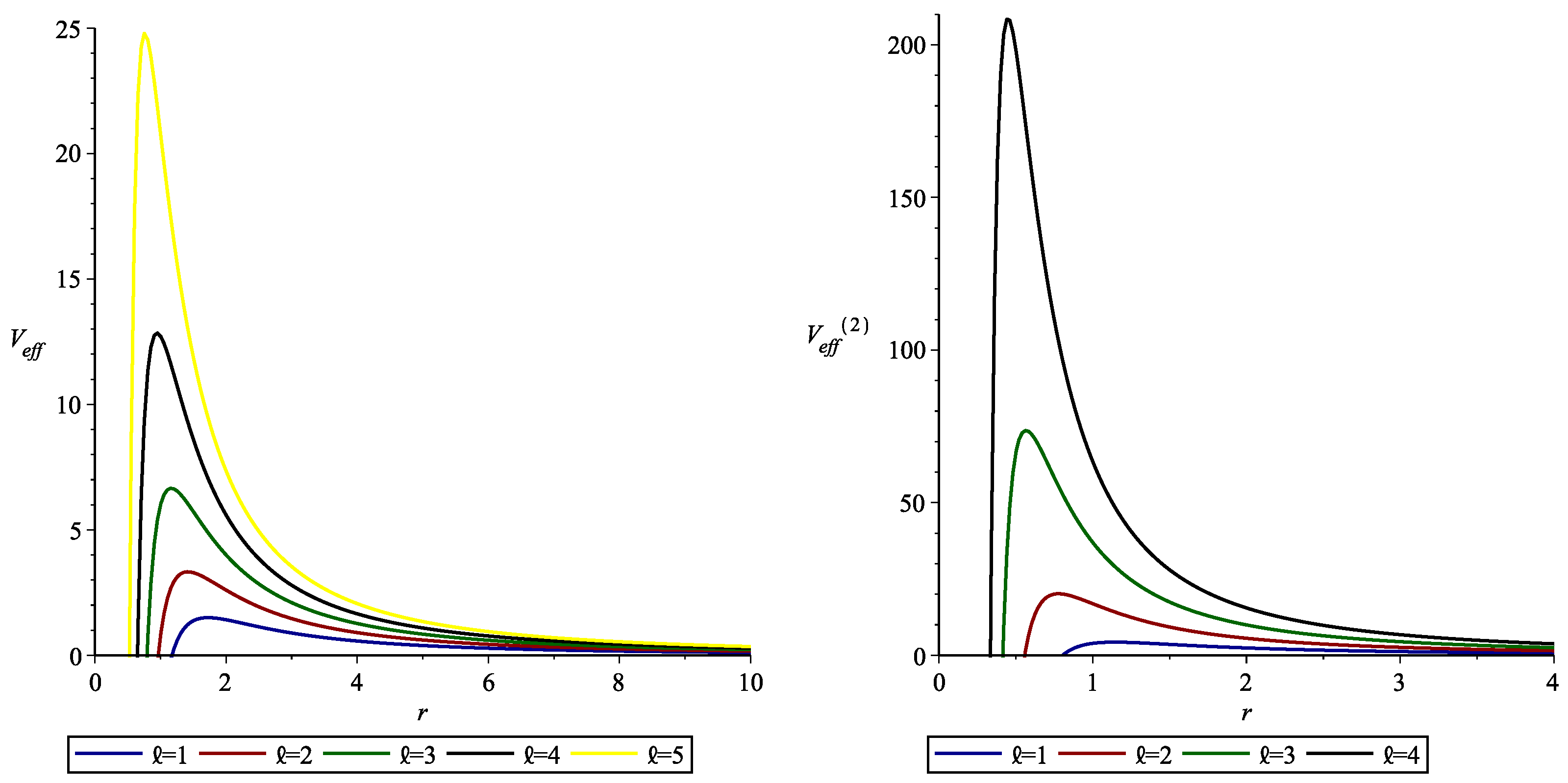
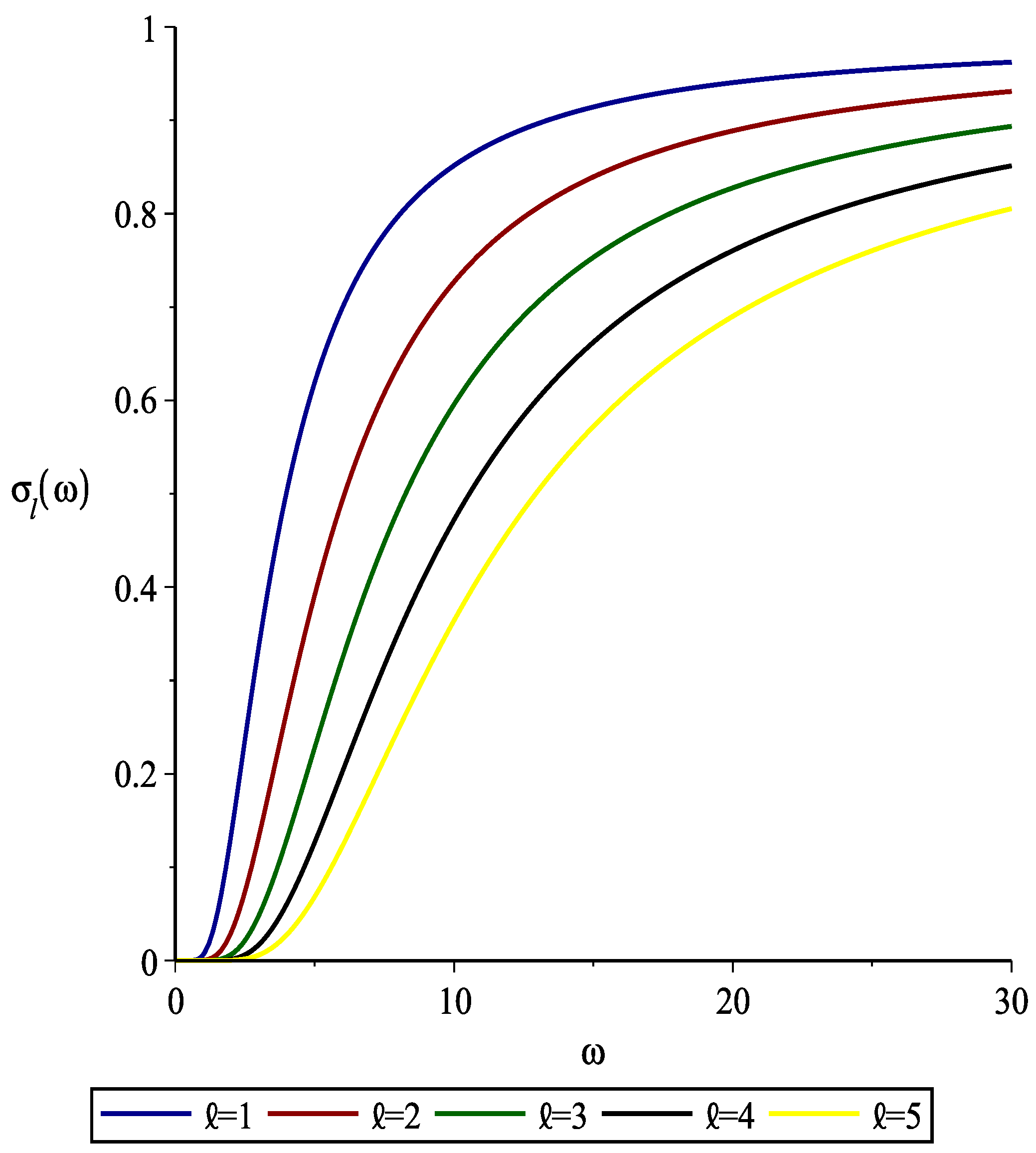
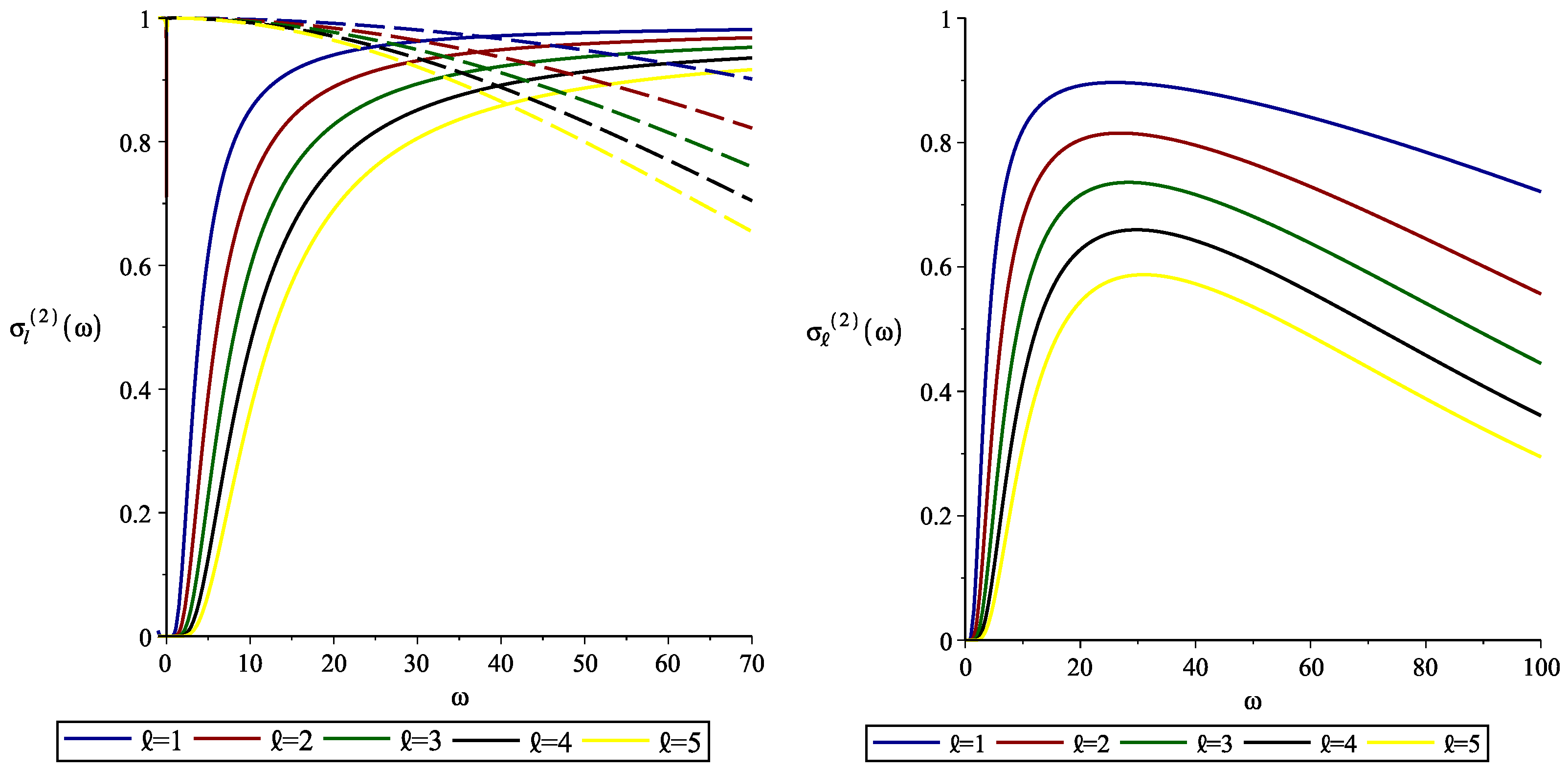
4. GFs of SRBBH Spacetime
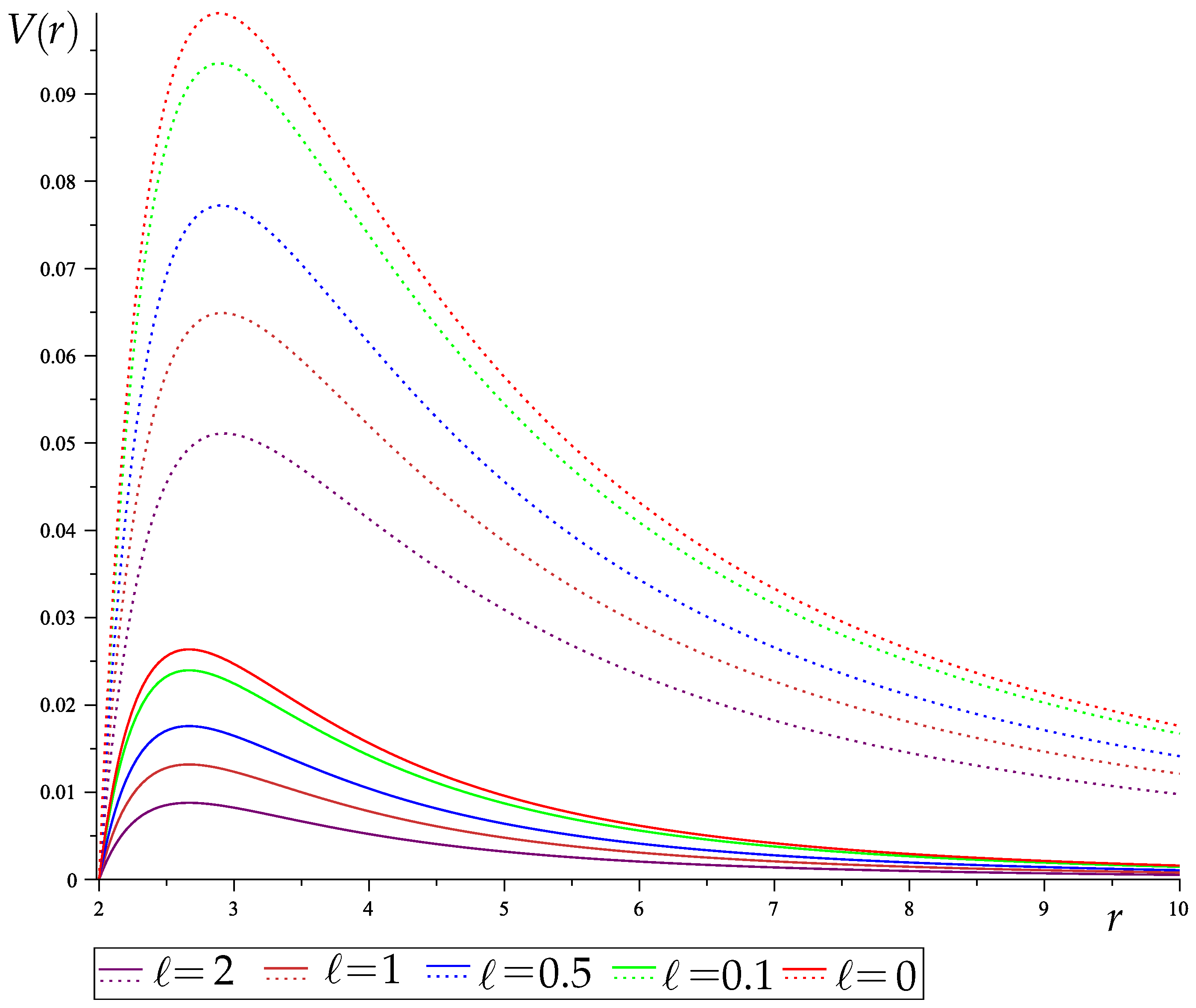
5. QNMs of Extremely Slow Rotating DRBBH via Unstable Circular Null Geodesic Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wiesendanger, C. Local Lorentz invariance and a new theory of gravitation equivalent to General Relativity. Class. Quant. Grav. 2018, 36, 065015. [Google Scholar] [CrossRef]
- Bailey, Q.G.; Kostelecky, V.A. Signals for Lorentz violation in post-Newtonian gravity. Phys. Rev. D 2006, 74, 045001. [Google Scholar] [CrossRef]
- Greenberg, O.W. CPT violation implies violation of Lorentz invariance. Phys. Rev. Lett. 2002, 89, 231602. [Google Scholar] [CrossRef]
- Betschart, G.; Kant, E.; Klinkhamer, F.R. Lorentz violation and black-hole thermodynamics. Nucl. Phys. B 2009, 815, 198–214. [Google Scholar] [CrossRef]
- Khodadi, M. Black Hole Superradiance in the Presence of Lorentz Symmetry Violation. Phys. Rev. D 2021, 103, 064051. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. GUP Modified Hawking Radiation in Bumblebee Gravity. Nucl. Phys. B 2019, 946, 114703. [Google Scholar] [CrossRef]
- Khlebnikov, S. Bulk black hole, escaping photons, and bounds on violations of Lorentz invariance. Phys. Rev. D 2007, 75, 065021. [Google Scholar] [CrossRef]
- Feng, Z.W.; Ding, Q.C.; Yang, S.Z. Modified fermion tunneling from higher-dimensional charged AdS black hole in massive gravity. Eur. Phys. J. C 2019, 79, 445. [Google Scholar] [CrossRef]
- Feng, Z.W.; Li, H.L.; Zu, X.T.; Yang, S.Z. Corrections to the thermodynamics of Schwarzschild-Tangherlini black hole and the generalized uncertainty principle. Eur. Phys. J. C 2016, 76, 212. [Google Scholar] [CrossRef]
- Khodadi, M.; Lambiase, G. Probing Lorentz symmetry violation using the first image of Sagittarius A*: Constraints on standard-model extension coefficients. Phys. Rev. D 2022, 106, 104050. [Google Scholar] [CrossRef]
- Neves, J.C.S. Kasner cosmology in bumblebee gravity. arXiv 2022, arXiv:2209.00589. [Google Scholar] [CrossRef]
- Delhom, A.; Nascimento, J.R.; Olmo, G.J.; Petrov, A.Y.; Porfírio, P.J. Metric-affine bumblebee gravity: Classical aspects. Eur. Phys. J. C 2021, 81, 287. [Google Scholar] [CrossRef]
- Halprin, A.; Kim, H.B. Mapping Lorentz invariance violations into equivalence principle violations. Phys. Lett. B 1999, 469, 78–80. [Google Scholar] [CrossRef]
- Lehnert, R. CPT and Lorentz-invariance violation. Hyperfine Interact. Hyperfine Interact. 2009, 193, 275–281. [Google Scholar] [CrossRef]
- Torri, M.D.C. Neutrino Oscillations and Lorentz Invariance Violation. Universe 2020, 6, 37. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Physics: Particle data groups. J. Phys. G 2006, 33, 1–1232. [Google Scholar]
- Chan, H.M.; Tsou, S.T. A Model Behind the Standard Model. Eur. Phys. J. C 2007, 52, 635–663. [Google Scholar] [CrossRef]
- Kostelecky, A.V.; Tasson, J.D. Matter-gravity couplings and Lorentz violation. Phys. Rev. D 2011, 83, 016013. [Google Scholar] [CrossRef]
- Bluhm, R.; Kostelecky, V.A. Spontaneous Lorentz violation, Nambu-Goldstone modes, and gravity. Phys. Rev. D 2005, 71, 065008. [Google Scholar] [CrossRef]
- Bluhm, R.; Fung, S.H.; Kostelecky, V.A. Spontaneous Lorentz and Diffeomorphism Violation, Massive Modes, and Gravity. Phys. Rev. D 2008, 77, 065020. [Google Scholar] [CrossRef]
- Bertolami, O.; Paramos, J. The Flight of the bumblebee: Vacuum solutions of a gravity model with vector-induced spontaneous Lorentz symmetry breaking. Phys. Rev. D 2005, 72, 044001. [Google Scholar] [CrossRef]
- Casana, R.; Cavalcante, A.; Poulis, F.P.; Santos, E.B. Exact Schwarzschild-like solution in a bumblebee gravity model. Phys. Rev. D 2018, 97, 104001. [Google Scholar] [CrossRef]
- Li, Z.; Övgün, A. Finite-distance gravitational deflection of massive particles by a Kerr-like black hole in the bumblebee gravity model. Phys. Rev. D 2020, 101, 024040. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, G.; Övgün, A. Circular Orbit of a Particle and Weak Gravitational Lensing. Phys. Rev. D 2020, 101, 124058. [Google Scholar] [CrossRef]
- Ding, C.; Liu, C.; Casana, R.; Cavalcante, A. Exact Kerr-like solution and its shadow in a gravity model with spontaneous Lorentz symmetry breaking. Eur. Phys. J. C 2020, 80, 178. [Google Scholar] [CrossRef]
- Maluf, R.V.; Neves, J.C.S. Black holes with a cosmological constant in bumblebee gravity. Phys. Rev. D 2021, 103, 044002. [Google Scholar] [CrossRef]
- Chen, S.; Wang, M.; Jing, J. Polarization effects in Kerr black hole shadow due to the coupling between photon and bumblebee field. JHEP 2020, 7, 54. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model. Eur. Phys. J. C 2021, 81, 501. [Google Scholar] [CrossRef]
- Liu, C.; Ding, C.; Jing, J. Thin accretion disk around a rotating Kerr-like black hole in Einstein–bumblebee gravity model. arXiv 2019, arXiv:1910.13259. [Google Scholar]
- Güllü, İ.; Övgün, A. Schwarzschild-like black hole with a topological defect in bumblebee gravity. Ann. Phys. 2022, 436, 168721. [Google Scholar] [CrossRef]
- Gomes, D.A.; Maluf, R.V.; Almeida, C.A.S. Thermodynamics of Schwarzschild-like black holes in modified gravity models. Ann. Phys. 2020, 418, 168198. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakallı, İ. Reply to “Comment on ‘Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model’”. Eur. Phys. J. C 2022, 82, 93. [Google Scholar] [CrossRef]
- Maluf, R.V.; Muniz, C.R. Comment on “Greybody radiation and quasinormal modes of Kerr-like black hole in Bumblebee gravity model”. Eur. Phys. J. C 2022, 82, 94. [Google Scholar] [CrossRef]
- Jha, S.K.; Aziz, S.; Rahaman, A. Study of Einstein-bumblebee gravity with Kerr-Sen-like solution in the presence of a dispersive medium. Eur. Phys. J. C 2022, 82, 106. [Google Scholar] [CrossRef]
- Ding, C.; Chen, X.; Fu, X. Einstein-Gauss-Bonnet gravity coupled to bumblebee field in four dimensional spacetime. Nucl. Phys. B 2022, 975, 115688. [Google Scholar] [CrossRef]
- Jiang, R.; Lin, R.H.; Zhai, X.H. Superradiant instability of a Kerr-like black hole in Einstein-bumblebee gravity. Phys. Rev. D 2021, 104, 124004. [Google Scholar] [CrossRef]
- Övgün, A.; Jusufi, K.; Sakallı, İ. Exact traversable wormhole solution in bumblebee gravity. Phys. Rev. D 2019, 99, 024042. [Google Scholar] [CrossRef]
- Ovgün, A.; Jusufi, K.; Sakallı, İ. Gravitational lensing under the effect of Weyl and bumblebee gravities: Applications of Gauss–Bonnet theorem. Ann. Phys. 2018, 399, 193–203. [Google Scholar] [CrossRef]
- Xu, R.; Liang, D.; Shao, L. Bumblebee Black Holes in Light of Event Horizon Telescope Observations. Astrophys. J. 2023, 945, 148. [Google Scholar] [CrossRef]
- Xu, R.; Liang, D.; Shao, L. Static spherical vacuum solutions in the bumblebee gravity model. Phys. Rev. D 2023, 107, 024011. [Google Scholar] [CrossRef]
- Ding, C.; Shi, Y.; Chen, J.; Zhou, Y.; Liu, C.; Xiao, Y. Rotating BTZ-like black hole and central charges in Einstein-bumblebee gravity. arXiv 2023, arXiv:2302.01580. [Google Scholar]
- Ding, C.; Chen, X. Slowly rotating Einstein-bumblebee black hole solution and its greybody factor in a Lorentz violation model. Chin. Phys. C 2021, 45, 025106. [Google Scholar] [CrossRef]
- Oliveira, R.; Dantas, D.M.; Almeida, C.A.S. Quasinormal frequencies for a black hole in a bumblebee gravity. EPL 2021, 135, 10003. [Google Scholar] [CrossRef]
- Jha, S.K.; Rahaman, A. Bumblebee gravity with a Kerr-Sen-like solution and its Shadow. Eur. Phys. J. C 2021, 81, 345. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, S.; Jing, J. Constraint on parameters of a rotating black hole in Einstein-bumblebee theory by quasi-periodic oscillations. Eur. Phys. J. C 2022, 82, 528. [Google Scholar] [CrossRef]
- Khodadi, M. Magnetic reconnection and energy extraction from a spinning black hole with broken Lorentz symmetry. Phys. Rev. D 2022, 105, 023025. [Google Scholar] [CrossRef]
- Kuang, X.M.; Övgün, A. Strong gravitational lensing and shadow constraint from M87* of slowly rotating Kerr-like black hole. Ann. Phys. 2022, 447, 169147. [Google Scholar] [CrossRef]
- Jha, S.K.; Rahaman, A. Superradiance scattering off Kerr-like black hole and its shadow in the bumblebee gravity with noncommutative spacetime. Eur. Phys. J. C 2022, 82, 728. [Google Scholar] [CrossRef]
- Liu, W.; Fang, X.; Jing, J.; Wang, J. QNMs of slowly rotating Einstein–Bumblebee black hole. Eur. Phys. J. C 2023, 83, 83. [Google Scholar] [CrossRef]
- Khodadi, M.; Lambiase, G.; Mastrototaro, L. Spontaneous Lorentz symmetry breaking effects on GRBs jets arising from neutrino pair annihilation process near a black hole. arXiv 2023, arXiv:2302.14200. [Google Scholar] [CrossRef]
- Turner, E.L. Gravitational lensing limits on the cosmological constant in a flat universe. Astrophys. J. Lett. 1990, 365, L43. [Google Scholar] [CrossRef]
- Bartelmann, M.; Schneider, P. Weak gravitational lensing. Phys. Rep. 2001, 340, 291–472. [Google Scholar] [CrossRef]
- Sauer, T. A brief history of gravitational lensing. Einstein Online Band 2010, 4, 3–1005. [Google Scholar]
- Bartelmann, M. Gravitational Lensing. Class. Quant. Grav. 2010, 27, 233001. [Google Scholar] [CrossRef]
- Sultana, J.; Kazanas, D. Bending of light in modified gravity at large distances. Phys. Rev. D 2012, 85, 081502. [Google Scholar] [CrossRef]
- Rindler, W.; Ishak, M. Contribution of the cosmological constant to the relativistic bending of light revisited. Phys. Rev. D 2007, 76, 043006. [Google Scholar] [CrossRef]
- Ishak, M.; Rindler, W.; Dossett, J. More on Lensing by a Cosmological Constant. Mon. Not. R. Astron. Soc. 2010, 403, 2152–2156. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Panchenko, A.; Scalia, M.; Cattani, C.; Nandi, K.K. Light bending in the galactic halo by Rindler-Ishak method. JCAP 2010, 9, 4. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Garipova, G.M.; Laserra, E.; Bhadra, A.; Nandi, K.K. The Vacuole Model: New Terms in the Second Order Deflection of Light. JCAP 2011, 2, 28. [Google Scholar] [CrossRef]
- Cattani, C.; Scalia, M.; Laserra, E.; Bochicchio, I.; Nandi, K.K. Correct light deflection in Weyl conformal gravity. Phys. Rev. D 2013, 87, 047503. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Mojahed, S.; Rokni, S.Y. Light bending in Reissner-Nordstrom-de Sitter black hole by Rindler-Ishak method. Astrophys. Space Sci. 2014, 351, 251–253. [Google Scholar] [CrossRef]
- Fernando, S.; Meadows, S.; Reis, K. Null trajectories and bending of light in charged black holes with quintessence. Int. J. Theor. Phys. 2015, 54, 3634–3653. [Google Scholar] [CrossRef]
- Ali, M.S.; Bhattacharya, S. Light bending, static dark energy, and related uniqueness of Schwarzschild–de Sitter spacetime. Phys. Rev. D 2018, 97, 024029. [Google Scholar] [CrossRef]
- Seçuk, M.H.; Delice, Ö. Bending of light from Reissner–Nordström–de Sitter-monopole black hole. Eur. Phys. J. Plus 2020, 135, 610. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Sepangi, H.R. Bending of light in novel 4D Gauss-Bonnet-de Sitter black holes by the Rindler-Ishak method. EPL 2021, 133, 50006. [Google Scholar] [CrossRef]
- Mangut, M.; Gürsel, H.; Sakallı, İ. Gravitational lensing in Kerr–Newman anti de Sitter spacetime. Astropart. Phys. 2023, 144, 102763. [Google Scholar]
- He, G.; Zhou, X.; Feng, Z.; Mu, X.; Wang, H.; Li, W.; Pan, C.; Lin, W. Gravitational deflection of massive particles in Schwarzschild-de Sitter spacetime. Eur. Phys. J. C 2020, 80, 835. [Google Scholar] [CrossRef]
- Maldacena, J.M.; Strominger, A. Black hole grey body factors and d-brane spectroscopy. Phys. Rev. D 1997, 55, 861–870. [Google Scholar] [CrossRef]
- Cvetic, M.; Larsen, F. Grey body factors for rotating black holes in four-dimensions. Nucl. Phys. B 1997, 506, 107–120. [Google Scholar] [CrossRef]
- Harmark, T.; Natario, J.; Schiappa, R. Greybody Factors for d-Dimensional Black Holes. Adv. Theor. Math. Phys. 2010, 14, 727–794. [Google Scholar] [CrossRef]
- Sakalli, İ.; Kanzi, S. Topical Review: Greybody factors and quasinormal modes for black holes in various theories—Fingerprints of invisibles. Turk. J. Phys. 2022, 46, 51–103. [Google Scholar] [CrossRef]
- Sakalli, İ.; Aslan, O.A. Absorption cross-section and decay rate of rotating linear dilaton black holes. Astropart. Phys. 2016, 74, 73–78. [Google Scholar] [CrossRef]
- Sakalli, İ. Analytical solutions in rotating linear dilaton black holes: Resonant frequencies, quantization, greybody factor, and Hawking radiation. Phys. Rev. D 2016, 94, 084040. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The Four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Ngampitipan, T.; Boonserm, P. Bounding the Greybody Factors for Non-rotating Black Holes. Int. J. Mod. Phys. D 2013, 22, 1350058. [Google Scholar] [CrossRef]
- Boonserm, P.; Ngampitipan, T.; Wongjun, P. Greybody factor for black string in dRGT massive gravity. Eur. Phys. J. C 2019, 79, 330. [Google Scholar] [CrossRef]
- Boonserm, P. Rigorous bounds on Transmission, Reflection, and Bogoliubov coefficients. arXiv 2009, arXiv:0907.0045. [Google Scholar]
- Boonserm, P.; Visser, M. Transmission probabilities and the Miller-Good transformation. J. Phys. A 2009, 42, 045301. [Google Scholar] [CrossRef]
- Oshita, N. Thermal Ringdown of a Kerr Black Hole: Overtone Excitation, Fermi-Dirac Statistics and Greybody Factor. arXiv 2022, arXiv:2208.02923. [Google Scholar] [CrossRef]
- Cardoso, V.; Miranda, A.S.; Berti, E.; Witek, H.; Zanchin, V.T. Geodesic stability, Lyapunov exponents and quasinormal modes. Phys. Rev. D 2009, 79, 064016. [Google Scholar] [CrossRef]
- Övgün, A. Black hole with confining electric potential in the scalar-tensor description of regularized 4-dimensional Einstein-Gauss-Bonnet gravity. Phys. Lett. B 2021, 820, 136517. [Google Scholar] [CrossRef]
- Tuleganova, G.Y.; Karimov, R.K.; Izmailov, R.N.; Potapov, A.A.; Bhadra, A.; Nandi, K.K. Gravitational time advancement effect in Bumblebee gravity for Earth bound systems. Eur. Phys. J. Plus 2023, 138, 94. [Google Scholar] [CrossRef]
- Schutz, B.F. A First Course in General Relativity; Cambridge University Press: London, UK, 1985. [Google Scholar]
- Wald, R.M. General Relativity; Chicago University Press: New York, NY, USA, 1984. [Google Scholar]
- Gurtug, O.; Mangut, M.; Halilsoy, M. Gravitational Lensing in Rotating and Twisting Universes. Astropart. Phys. 2021, 128, 102558. [Google Scholar] [CrossRef]
- Fricke, T.T.; Smith-Lefebvre, N.D.; Abbott, R.; Adhikari, R.; Dooley, K.L.; Evans, M.; Fritschel, P.; Frolov, V.V.; Kawabe, K.; Kissel, J.S.; et al. DC readout experiment in Enhanced LIGO. Class. Quant. Grav. 2012, 29, 065005. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef]
- Leung, P.T.; Liu, Y.T.; Suen, W.M.; Tam, C.Y.; Young, K. Perturbative approach to the quasinormal modes of dirty black holes. Phys. Rev. D 1999, 59, 044034. [Google Scholar] [CrossRef]
- Daghigh, R.G.; Green, M.D. Validity of the WKB Approximation in Calculating the Asymptotic Quasinormal Modes of Black Holes. Phys. Rev. D 2012, 85, 127501. [Google Scholar] [CrossRef]
- Decanini, Y.; Folacci, A.; Raffaelli, B. Unstable circular null geodesics of static spherically symmetric black holes, Regge poles, and quasinormal frequencies. Phys. Rev. D 2010, 81, 104039. [Google Scholar] [CrossRef]
- Giri, S.; Nandan, H.; Joshi, L.K.; Maharaj, S.D. Geodesic stability and quasinormal modes of non-commutative Schwarzschild black hole employing Lyapunov exponent. Eur. Phys. J. Plus 2022, 137, 181. [Google Scholar] [CrossRef]
- Bhar, P.; Rej, P. Stable and self-consistent charged gravastar model within the framework of f(R, T) gravity. Eur. Phys. J. C 2021, 81, 763. [Google Scholar] [CrossRef]
| ℓ | l | n | ||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | −0.09622504490 |
| 0 | 0 | 1 | 0 | −0.2886751347 |
| 0 | 0 | 2 | 0 | −0.4811252245 |
| 0 | 1 | 0 | 0.1924500898 | −0.09622504490 |
| 0 | 1 | 1 | 0.1924500898 | −0.2886751347 |
| 0 | 1 | 2 | 0.1924500898 | −0.4811252245 |
| 0 | 2 | 0 | 0.3849001795 | −0.09622504490 |
| 0 | 2 | 1 | 0.3849001795 | −0.2886751347 |
| 0 | 2 | 2 | 0.3849001795 | −0.4811252245 |
| 0.1 | 0 | 0 | 0 | −0.09174698047 |
| 0.1 | 0 | 1 | 0 | −0.2752409415 |
| 0.1 | 0 | 2 | 0 | −0.4587349024 |
| 0.1 | 1 | 0 | 0.1879186773 | −0.09174698047 |
| 0.1 | 1 | 1 | 0.1879186773 | −0.2752409415 |
| 0.1 | 1 | 2 | 0.1879186773 | −0.4587349024 |
| 0.1 | 2 | 0 | 0.3758373544 | −0.09174698047 |
| 0.1 | 2 | 1 | 0.3758373544 | −0.2752409415 |
| 0.1 | 2 | 2 | 0.3758373544 | −0.4587349024 |
| 1 | 0 | 0 | 0 | −0.06804138176 |
| 1 | 0 | 1 | 0 | −0.2041241452 |
| 1 | 0 | 2 | 0 | −0.3402069088 |
| 1 | 1 | 0 | 0.1618305907 | −0.06804138176 |
| 1 | 1 | 1 | 0.1618305907 | −0.2041241452 |
| 1 | 1 | 2 | 0.1618305907 | −0.3402069088 |
| 1 | 2 | 0 | 0.3236611813 | −0.06804138176 |
| 1 | 2 | 1 | 0.3236611813 | −0.2041241452 |
| 1 | 2 | 2 | 0.3236611813 | −0.3402069088 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangut, M.; Gürsel, H.; Kanzi, S.; Sakallı, İ. Probing the Lorentz Invariance Violation via Gravitational Lensing and Analytical Eigenmodes of Perturbed Slowly Rotating Bumblebee Black Holes. Universe 2023, 9, 225. https://doi.org/10.3390/universe9050225
Mangut M, Gürsel H, Kanzi S, Sakallı İ. Probing the Lorentz Invariance Violation via Gravitational Lensing and Analytical Eigenmodes of Perturbed Slowly Rotating Bumblebee Black Holes. Universe. 2023; 9(5):225. https://doi.org/10.3390/universe9050225
Chicago/Turabian StyleMangut, Mert, Huriye Gürsel, Sara Kanzi, and İzzet Sakallı. 2023. "Probing the Lorentz Invariance Violation via Gravitational Lensing and Analytical Eigenmodes of Perturbed Slowly Rotating Bumblebee Black Holes" Universe 9, no. 5: 225. https://doi.org/10.3390/universe9050225
APA StyleMangut, M., Gürsel, H., Kanzi, S., & Sakallı, İ. (2023). Probing the Lorentz Invariance Violation via Gravitational Lensing and Analytical Eigenmodes of Perturbed Slowly Rotating Bumblebee Black Holes. Universe, 9(5), 225. https://doi.org/10.3390/universe9050225






