Particles of Negative and Zero Energy in Black Holes and Cosmological Models

Abstract

Particles with negative energies are considered for three different cases: inside the horizon of a Schwarzschild black hole, Milne’s coordinates in flat Minkowski space–time (Milne’s universe using nonsynchronous coordinates) and in the cosmological Gödel model of the rotating universe. It is shown that, differently from the Gödel model with a nondiagonal term, where it occurs that negative energies are impossible, they are present in all other cases considered in the paper. Particles with zero energy are also possible in the first two cases.

1. Introduction

In 1922, Alexander Friedmann, in Petrograd, Russia, predicted an expansion of the Universe. Today, Friedmann’s model of the Universe is called the Standard Model. Many observations confirm this model to be correct. The new world of galaxies and the stages of the Universe’s evolution were discovered. New phenomena, such as black holes, relict radiation and many others, are actively investigated. Trajectories of particles with negative and zero energy are examples of such new phenomena. The possibility of relativistic particles with negative energy is important because it makes it possible to obtain large energy in interactions or decays of bodies. A simple example of this situation was proposed by R. Penrose in the case of the decays of particles in the ergospheres of rotating black holes [1,2].

It appears that in order to have negative energy of the relativistic particle with nonzero mass, one must have a very strong external field leading to large potential energy, as is the case for rotating black holes. However, it is well known that the value of the energy depends on the choice of the reference frame and the time coordinate or Killing vector in case of conserved energy. It leads to the situation whereby states with negative energies in the relativistic case occur in the case of a rotating coordinate system outside the static limit [3], where an effect analogical to the Penrose effect is found to be observable [4], and in a nonsynchronous coordinate system in cosmology [5,6].

It seems from these examples that negative energies arise in the case of the existence of nondiagonal terms in a metrical tensor (gravymagnetism), but, in this paper, we show that in the Gödel Universe, in spite of the presence of such terms, negative energies are absent. The negative energies are present in cases of the movement inside of the horizon of the Schwarzschild black hole and in Milne’s universe where nondiagonal terms are present in a nonsynchronous coordinate frame.

2. Negative Energy in Nonrotating Black Hole

A nonrotating black hole of mass M in Schwarzschild coordinates is described by the metric

$$d{s}^2=\left(1-\frac{r_g}{r}\right)c^{2}d{t}^2-\frac{d{r}^2}{1-\frac{r_g}{r}}-r^2\left(d{\theta }^2+{sin}^2\theta d{\phi }^2\right),$$

(1)

where $r_g=2GM/c^2$ is the gravitational radius of the black hole, G is the gravitational constant, and c is the light velocity. The geodesic complete space–time of the nonrotating black hole can be described in Kruskal–Szekeres coordinates, $\{u,v\}\in (-\infty ,+\infty )$, which, in region $u>\left|v\right|\ge 0$, are connected with the Schwarzschild coordinate in $r>r_g$ in the following way:

$$u=\sqrt{\frac{r}{r_g}-1}exp\left(\frac{r}{2r_g}\right)cosh\frac{ct}{2r_g},v=\sqrt{\frac{r}{r_g}-1}exp\left(\frac{r}{2r_g}\right)sinh\frac{ct}{2r_g}.$$

(2)

For $r<r_g$ and $v>\left|u\right|\ge 0$, the transformation from the Schwarzschild coordinate into the Kruskal–Szekeres coordinates has the form

$$u=\sqrt{1-\frac{r}{r_g}}exp\left(\frac{r}{2r_g}\right)sinh\frac{ct}{2r_g},v=\sqrt{1-\frac{r}{r_g}}exp\left(\frac{r}{2r_g}\right)cosh\frac{ct}{2r_g}.$$

(3)

Schwarzschild coordinates are singular at $r=r_g$. Regarding their connection with Kruskal–Szekeres coordinates for other $u,v$, see [7], Section 31.5.

Any possible movement of physical bodies and particles must satisfy the condition $d{s}^2>0$ leading to

$$r>r_g\Rightarrow \left|\frac{dr}{dt}\right|\le c\left(1-\frac{r_g}{r}\right),$$

(4)

$$r<r_g\Rightarrow \left|\frac{dr}{dt}\right|\ge c\left(\frac{r_g}{r}-1\right).$$

(5)

For $r<r_g$, the coordinate $ct$ is space and $r/c$ is the time coordinate.

Geodesic equations in Schwarzschild coordinates in the plane $\theta =0$ are [8]

$$\frac{dt}{d\lambda }=\frac{r}{r-r_g}\frac{E}{c^2},\frac{d\phi }{d\lambda }=\frac{J}{r^2},{\left(\frac{dr}{d\lambda }\right)}^2=\frac{E^2}{c^2}+\frac{r_g-r}{r^3}{J}^2+\frac{r_g-r}{r}{m}^2{c}^2,$$

(6)

where E is the energy of a moving particle (measured by the static observer in r, $\theta$, $\varphi$ coordinates), J is the conserved projection of the particle’s angular momentum on the axis orthogonal to the plane of motion, m is the particle mass, and $\lambda$ is an affine parameter on the geodesic. For massive particles, $\lambda =\tau /m$, where $\tau$ is the proper time.

In an external region of the black hole ($r>r_g$) for any physical object, the time coordinate t is always increasing and so the energy E of the particle is positive (see (6). Inside the horizon of the black ($r<r_g$), where t is space-like ($g_{tt}<0$), one has movement as in increasing as in decreasing t. As is seen from the first formula in (6) for a particle moving inside the horizon in the direction of a decrease in the coordinate t, the energy E of the particle will be positive, while, for increasing coordinate t, the energy E is negative. For constant t inside the black hole, $E=0$ due to formula (6).

Surely, t inside of the black hole is space-like and E is proportional to the t-component of the momentum. Inside a black hole, one can use other reference frames and corresponding energies [9]. However, for the observer outside the black hole, the conserved E along all trajectories of the free fall is equal (see formula (88.9) in [10]) to

$$E=m{c}^2\sqrt{\left(1-\frac{r_g}{r}\right)/\left(1-\frac{{\mathbf{v}}^2}{c^2}\right)},$$

(7)

where $\mathbf{v}$ is the velocity measured by the observer at rest in the Schwarzschild coordinates. Thus, we can call E inside the black hole, following [7], the “energy at infinity”. For a discussion of other ways to determine the energy within the horizon and the movement of particles there, see, for example, the articles [9,11,12,13].

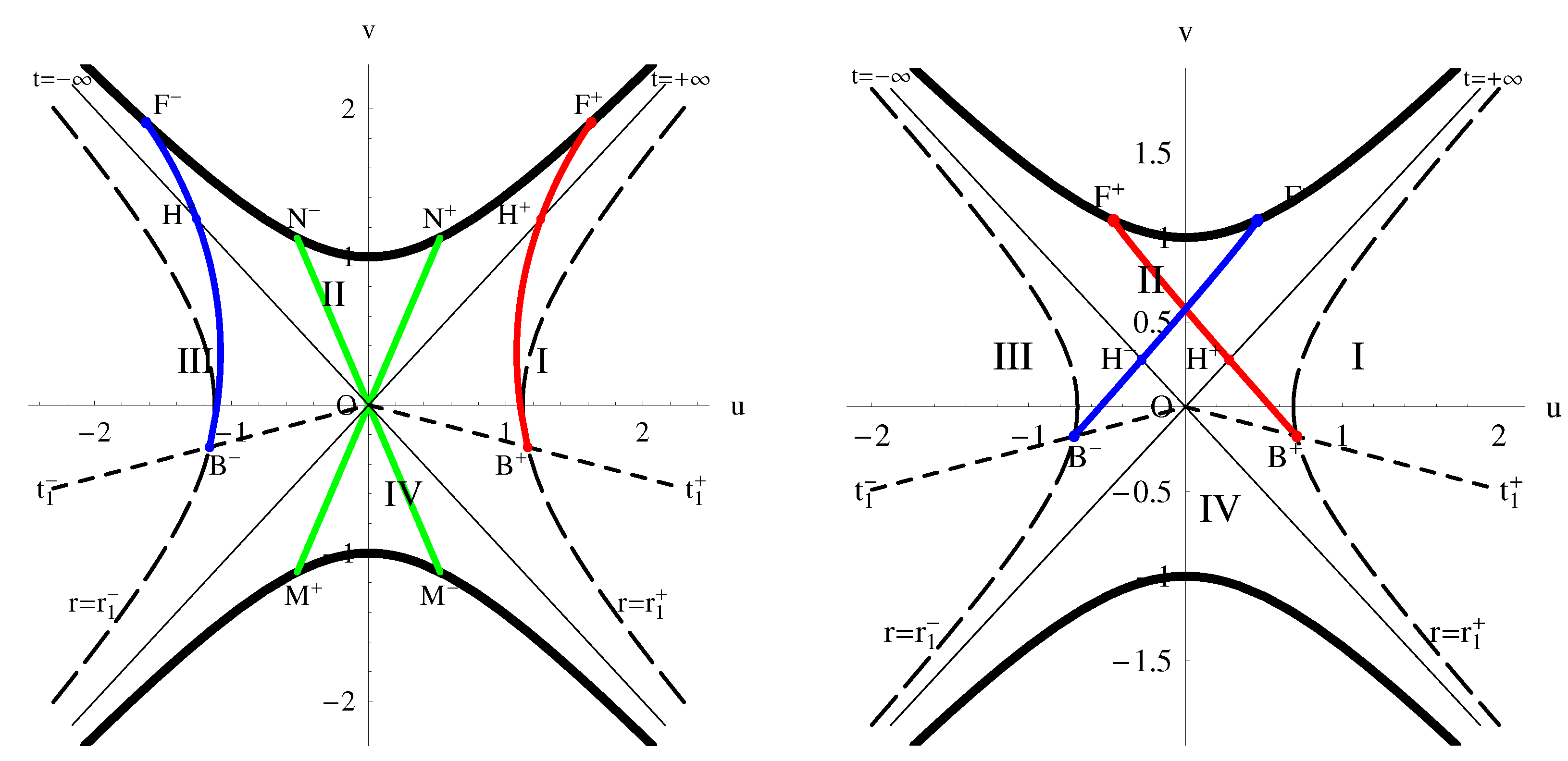
In Figure 1, the trajectories for radial movement with positive, zero and negative energies in Kruskal–Szekeres coordinates are represented by red, green and blue lines.

As one can see from (2) and (3), the coordinate lines of constant t in Kruskal–Szekeres coordinates are straight lines through the origin of the coordinates. In region II, coordinate t decreases when moving from $H^{+}$ to $F^{+}$ (positive E) and increases when moving from $H^{-}$ to $F^{-}$ (negative value of E). Direct lines ($M^{\pm }O{N}^{\pm }$) correspond to constant $t=\pm r_g/c$ and therefore $E=0$.

Let us consider the problem of the back influence of falling particles on the metric of the black hole space–time. For macroscopic bodies with 4-velocity $\left(u^i\right)$, with the energy density $\epsilon$ and pressure p in space–time with metric $g_{ik}$, the energy–momentum density tensor is [10]

$$T_{ik}=(\epsilon +p)u_i{u}_k-p{g}_{ik},$$

(8)

$i,k=0,1,2,3$. The trace of the energy–momentum tensor

$$T_i^i=\epsilon -3p$$

(9)

is invariant and it will be negative for $\epsilon -3p<0$—in particular, for dust-like matter ($p=0$) with negative energy $\epsilon <0$. The back influence of falling particles with negative energy will be determined by the energy–momentum tensor in the right-hand side of the Einstein equations. The notion of the existence of particles with negative energies as it is known was used by S. Hawking to predict the Hawking effect for black holes [14].

For a discussion of other ways to determine the energy within the horizon and the movement of particles there, see, for example, works

3. Negative and Zero Energies in Flat Space–Time

The geodesic line equations can be obtained for space–time with metric $g_{ik}$ from the Lagrangian

$$L=\frac{g_{ik}}{2}\frac{d{x}^i}{d\lambda }\frac{d{x}^k}{d\lambda },$$

(10)

where $\lambda$ is the affine parameter on the geodesic [8]. The energy of the particle E is equal to the zero covariant component of the momentum $\left(p_i\right)$ multiplied on the light velocity

$$p_i=\frac{\partial L}{\partial \left(\frac{d{x}^i}{d\lambda }\right)}=g_{ik}\frac{d{x}^k}{d\lambda },$$

(11)

$$E=c{p}_0=c{g}_{0k}\frac{d{x}^k}{d\lambda }.$$

(12)

Defining the affine parameter for the massive particle as $\lambda =\tau /m$, where $\tau$ is the proper time of the moving particle, one obtains

$$p_i{p}^i=m^2{c}^2$$

(13)

and the energy of the particle is

$$E=mc{g}_{0k}\frac{d{x}^k}{d\tau }.$$

(14)

Using notation $\left({\zeta }^i\right)=(1,0,0,0)$ for the translation in the time coordinate generator, one can write (12) for the energy of the particle as

$$E=c(p,\zeta ).$$

(15)

If the metric components do not depend on the time coordinate $x^0$, then $\zeta$ is the time-like Killing vector and the energy E is conserved on the geodesic. For time-like vector $\zeta$ and a massive particle, one has [15]

$$\sqrt{(\zeta ,\zeta )}\le \frac{E}{m{c}^2}<+\infty$$

(16)

and the energy (15) is positive. For space-like vector $\zeta$, as it takes place in the ergosphere of a rotating black hole, the arbitrary positive and negative values are possible (see [15], p. 325).

Note that in spite of the invariance of the scalar product (15), the value (14) of the energy depends on the choice of the reference frame. This occurs due to the fact that by changing the reference frame in which the physical measurements are made, the observer is changing vector $\zeta$. The analysis of the situation in a rotating coordinate system in flat space–time is provided in [3].

In Minkowski space–time in the Galilean coordinate system or any other coordinate system with $g_{00}=1$, $g_{0\alpha }=0$, ($\alpha =1,2,3$), the energy (12) is

$$E=c^2\frac{dt}{d\lambda }$$

(17)

and it is always positive in movement “forward” in time because in the future light cone, one has $dt/d\lambda >0$.

Consider the coordinate system in which the metric of flat space–time has the form of the metric of the expanding homogeneous isotropic Universe—the Milne universe [16]:

$$d{s}^2=c^{2}d{t}^2-c^2{t}^2\left(d{\chi }^2+{sinh}^2\chi d{\mathsf{\Omega }}^2\right),$$

(18)

where $d{\mathsf{\Omega }}^2=d{\theta }^2+{sin}^2\theta d{\phi }^2$, and coordinate $\chi$ is changing from 0 to $+\infty$. In new coordinates

$$T=tcosh\chi ,r=ctsinh\chi ,cT>r>0$$

(19)

the interval (18) takes the form of a Minkowski interval

$$d{s}^2=c^{2}d{T}^2-d{r}^2-r^{2}d{\mathsf{\Omega }}^2.$$

(20)

This space–time with coordinate $t\ge 0$, $\chi \ge 0$ corresponds to the future cone in coordinates $cT,r$.

The radial distance between points $\chi =0$ and $\chi$ in metric (18) is $D=ct\chi$. Taking D as the radial coordinate [17], one obtains the interval as

$$d{s}^2=\left(1-\frac{D^2}{c^2{t}^2}\right)c^{2}d{t}^2+2\frac{D}{t}dtdD-d{D}^2-c^2{t}^2{sinh}^2\left(\frac{D}{ct}\right)d{\mathsf{\Omega }}^2.$$

(21)

From the condition $d{s}^2\ge 0$, one obtains that if D is larger than $D_s=ct$, no physical object can be at rest in coordinates $t,D,\theta ,\varphi$. The value $D_s$ corresponds to $\chi =1$ and it plays the role of the static limit for the rotating black hole in Boyer–Lindquist [18] coordinates.

The energy of the particle with mass m in coordinates $t,D,\theta ,\varphi$ is

$$E=c{g}_{0k}\frac{d{x}^k}{d\lambda }=m{c}^2\frac{dt}{d\tau }\left(1-\frac{D^2}{c^2{t}^2}+\frac{D}{c^{2}t}\frac{dD}{dt}\right)=m{c}^2\frac{dt}{d\tau }\left(1+\chi t\frac{d\chi }{dt}\right).$$

(22)

From (18), one obtains, for any physical object, the inequality

$$t\left|\frac{d\chi }{dt}\right|\le 1.$$

(23)

Thus, a particle can have negative energy only for $\chi >1$, i.e., out of the static limit, if

$$\frac{d\chi }{dt}<-\frac{1}{\chi t}.$$

(24)

Note that the components of metric (21) depend on time and the energy (22) in general is not conserved on the geodesics. If the energy is zero, then the particle is moving noninertial according to the law

$$\begin{array}{c}\hfill \frac{d\chi }{dt}=-\frac{1}{\chi t}\iff \chi =\sqrt{{\chi }_0^2-2log(t/t_0)},t\in \left[t_0,t_{0}exp(({\chi }_0^2-1)/2)\right].\end{array}$$

(25)

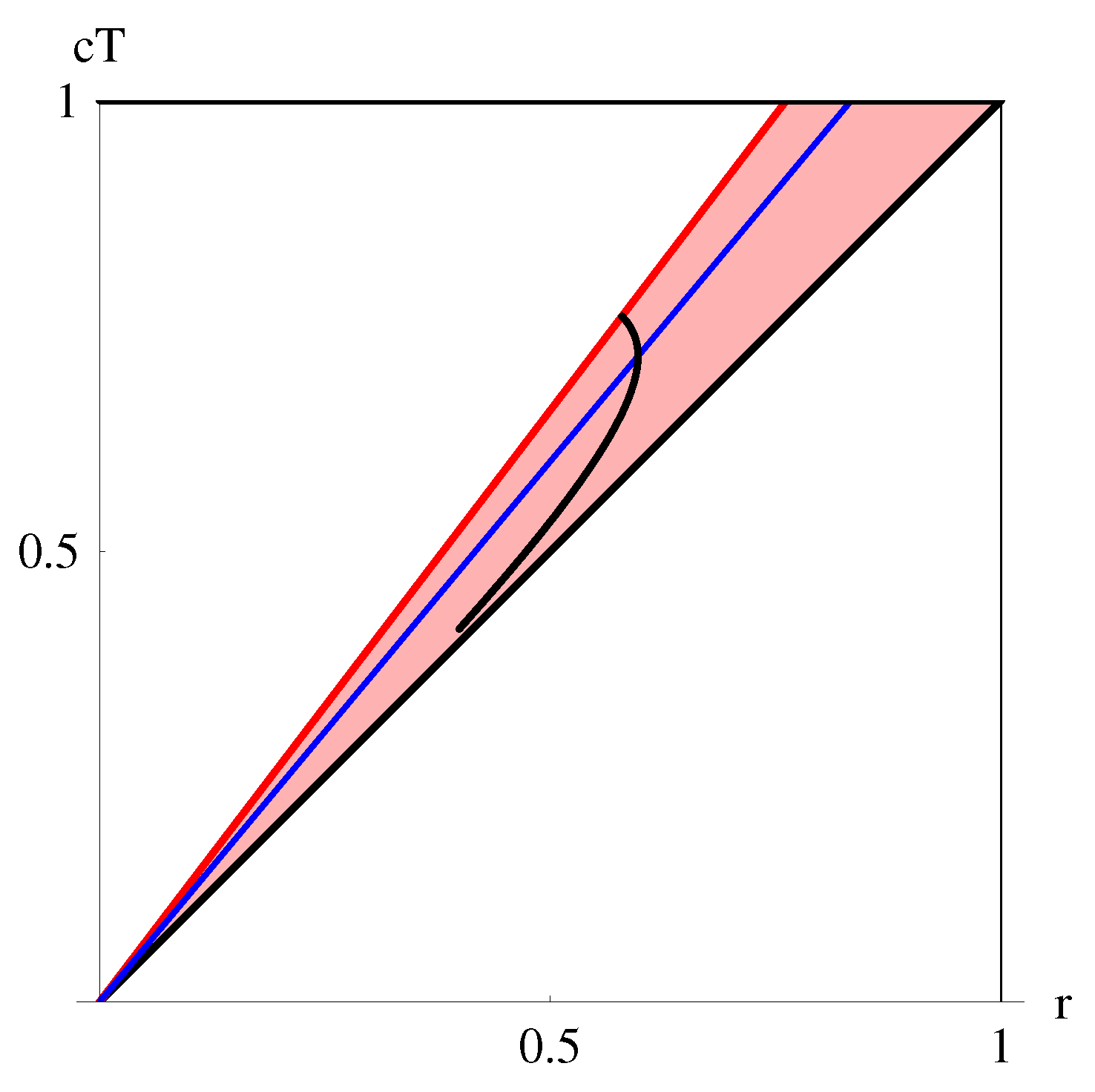
The trajectory of such movement for case ${\chi }_0=2$, $t_0=0.11$ is represented by the curve in Figure 2 in coordinates T, r (see (19)).

In the event that the inertial movement trajectory in these coordinates is a straight line, the possible region of movement of particles with negative and zero energies in the reference frame $t,D$ is defined in the coordinate $T,r$ by conditions $1\le cT/r\le coth1\approx 1.313$.

Velocities of movement in coordinates $T,r$ and $t,\chi$ satisfy condition [19]

$$t\frac{d\chi }{dt}=\frac{{\displaystyle \frac{dr}{dT}-ctanh\chi }}{{\displaystyle c-\frac{dr}{dT}tanh\chi }}.$$

(26)

Thus, for

$$\chi tanh\chi \ge 1$$

(27)

particles at rest in inertial frame $T,r$ will have negative energies in the frame $t,D$. This region can be seen in Figure 2 as the region above the blue line in the red district. Zero energy of the particle at rest in $T,r$ coordinates is possible only if the blue line is defined by the root of equation $\chi tanh\chi =1$, i.e., $\chi \approx 1.1997$.

Thus, one can see that for a specific choice of coordinates, one can obtain negative and zero energies for particles at rest in an inertial frame.

Note that for small distances ($D/\left(ct\right)=\chi \ll 1$), the metric (21) becomes the metric of a comoving spherical coordinate system of Minkowski space–time

$$d{s}^2=c^{2}d{t}^2-d{D}^2-D^{2}d{\mathsf{\Omega }}^2,$$

(28)

and the energy (22) will be equal to the usual energy in the inertial system of flat space–time

$$E_u=m{c}^2\frac{dt}{d\tau }\approx m{c}^2\frac{dT}{d\tau },$$

(29)

because, for $\chi \ll 1$, one has $t\approx T$.

The decay of the body on two bodies, one with negative energy and the other with the positive energy being larger than the energy of the initial decaying one, corresponds to the Penrose process. This process occurs outside the static limit on distance $D>ct$. However, later, these two products of the decay move inside the static limit, and, during flight in the direction of the origin, where the metric is that of Minkowski space, they change their energies in such a manner that the result will be the same as in the inertial frame. In fact, due to (22)

$$\begin{array}{c}\hfill E=E_u+m{c}^2\chi t\frac{d\chi }{d\tau }.\end{array}$$

(30)

Here, $E_u$ is the energy in the reference frame $t,\chi$, such that $g_{0i}=0$, $i\ne 0$, and $g_{00}$ does not depend on time. Thus, $E_u$ is conserved. At the point of decay, both energies E and $E_u$ are conserved. When body 2 with the positive energy arrives at the coordinate origin $\chi =0$, its energy E (30) will be equal to $E_u$ and no growth in the energy will be observed.

Body 1, with the negative energy E due to (22) after decay, will have a negative value of velocity $d\chi /dt$ larger (in absolute value) than that of body 2. This means that it will arrive at the origin before the arrival of body 2. Its energy in the origin of the coordinate frame will be also positive and the full energy of 1 and 2 will be equal to that of the decaying body. Thus, at the origin, one will not observe any effect that makes this situation similar to the situation for Kerr’s black hole.

In fact, for rotating black hole [1], as in the case of rotating coordinate system [4], the energy is conserved. In this case, when body 2 travels out of the ergosphere, far from it, body 1, with negative energy, moves further inside the horizon of the black hole or goes to infinity in case of rotating coordinates in Minkowski space. Thus, the energy of the body with positive energy, due to the conservation of the energy, will be always larger than that of the initial decaying body.

Note that the existence of states with negative energies for Milne’s metric leads to an effect similar to the Hawking effect [14] for the Schwarzschild metric. Particle creation in quantum theory will occur and the detector of particles checks them (see Section 5.3 in [20]). This will be the creation of virtual particles (see Section 9.8 in [21]) so no change in the metric due to them can be observed.

4. Negative Energy in Gödel Universe

The metric of the Gödel cosmological model of the rotating Universe proposed in 1949 (see [22] or [23]) can be written as

$$d{s}^2=c^{2}d{t}^2-d{x}_1^2+\frac{exp\left(2\sqrt{2}\omega x_1/c\right)}{2}d{x}_2^2+2exp\left(\sqrt{2}\omega x_1/c\right)cdtd{x}_2-d{x}_3^2,$$

(31)

where $\omega$ is constant. Such a metric is the exact solution of Einstein’s equation with background matter as an ideal liquid without pressure and negative cosmological constant $\mathrm{\Lambda }$

$$R_{ik}-\frac{1}{2}R{g}_{ik}+\mathrm{\Lambda }{g}_{ik}=-8\pi \frac{G}{c^4}{T}_{ik},$$

(32)

where

$$-\mathrm{\Lambda }={\left(\frac{\omega }{c}\right)}^2=4\pi \frac{G}{c^2}\rho ,T_{ik}=\rho c^2{u}_i{u}_k,$$

(33)

$u^i={\delta }_0^i$. Here, $\omega$ has the sense of the angular velocity of rotation of the vector of fluid of the background matter $u^i$.

Taking, instead of $t,x_1,x_2$, new coordinates $t^{\prime },r,\varphi$,

$$exp\left(\sqrt{2}\omega x_1/c\right)=cosh2r+cos\varphi sinh2r,$$

(34)

$$\omega x_{2}exp\left(\sqrt{2}\omega x_1/c\right)=sin\varphi sinh2r,$$

(35)

$$tan\frac{1}{2}\left(\varphi +\omega t-\sqrt{2}{t}^{\prime }\right)=exp(-2r)tan\frac{\varphi }{2},$$

(36)

one writes the interval (31) in the form [22,24]

$$d{s}^2=2{\left(\frac{c}{\omega }\right)}^2\left(d{t}^{\prime 2}-d{r}^2+({sinh}^{4}r-{sinh}^{2}r)d{\varphi }^2+2\sqrt{2}{sinh}^{2}rd\varphi d{t}^{\prime }\right)-d{x}_3^2,$$

(37)

where $-\infty <t^{\prime }<\infty$, $0\le r<\infty$, $0\le \varphi <2\pi$ and identifying $\varphi =0$ and $\varphi =2\pi$.

Now, consider the general case of space–time $t^{\prime },r,\varphi ,z$ with the interval

$$d{s}^2=a^2\left[{\left(d{t}^{\prime }+\mathrm{\Phi }\left(r\right)d\varphi \right)}^2-d{r}^2-d{z}^2-R^2\left(r\right)d{\varphi }^2\right],$$

(38)

where a is constant, $-\infty <t<\infty$, $0\le r<\infty$, $-\infty <z<\infty$, $0\le \varphi \le 2\pi$, and identifying $\varphi =0$ and $\varphi =2\pi$. Let us say $\mathrm{\Phi }\left(r\right)>0$ and $R\left(r\right)>0$ for $r>0$. For Gödel Universe $a=\sqrt{2}c/\omega$, $z=x_3/a$ and

$$\mathrm{\Phi }\left(r\right)=\sqrt{2}{sinh}^{2}r,R\left(r\right)=sinhrcoshr.$$

(39)

The metrical tensor is

$$\left(g_{ik}\right)=a^2\left(\begin{array}{cccc}1& \mathrm{\Phi }& 0& 0\\ \mathrm{\Phi }& {\mathrm{\Phi }}^2-R^2& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right),$$

(40)

$$\left(g^{ik}\right)=\frac{1}{a^2{R}^2\left(r\right)}\left(\begin{array}{cccc}{R}^2-{\mathrm{\Phi }}^2& \mathrm{\Phi }& 0& 0\\ \mathrm{\Phi }& -1& 0& 0\\ 0& 0& -R^2& 0\\ 0& 0& 0& -R^2\end{array}\right),$$

(41)

where indexes $i,k=0,1,2,3$ correspond to $t^{\prime },\varphi ,r,z$. Note that for any $r>0$, the metrical tensor is not degenerate $\det \left(g_{ik}\right)=-a^8{R}^2\left(r\right)<0$. The degeneration for $r=0$ in the Gödel Universe is coordinate degeneracy. The eigenvalues of the $g_{ik}$ tensor are

$$\begin{array}{ccc}\hfill {\lambda }_{1,2}& =& \frac{a^2}{2}\left({\mathrm{\Phi }}^2-R^2+1\pm \sqrt{{({\mathrm{\Phi }}^2-R^2+1)}^2+4R^2}\right),\hfill \\ \hfill {\lambda }_{3,4}& =& -a^2.\hfill \end{array}$$

(42)

For $r>0$, one has

$${\lambda }_1\ge a^2,0>{\lambda }_2\ge -a^2{R}^2.$$

(43)

Note that although $g_{\varphi \varphi }$ is positive for $\mathrm{\Phi }\left(r\right)>R\left(r\right)$, the signature of $g_{ik}$ for all $r>0$ is the standard $(+,-,-,-)$.

Possible movement of particles is defined by $d{s}^2\ge 0$, so, for the interval (38), one has

$$d{t}^{{}^{\prime }2}+\left({\mathrm{\Phi }}^2\left(r\right)-R^2\left(r\right)\right)d{\varphi }^2+2\mathrm{\Phi }\left(r\right)d\varphi d{t}^{\prime }-d{r}^2-d{z}^2\ge 0.$$

(44)

It is important that for any coordinate system with interval (38), the physical body for any values of $r,\varphi ,z$ can be at rest, i.e., there is no static limit. However, in (38), there is nondiagonal term $d{t}^{\prime }d\varphi$ as in Kerr’s metric. However, differently from the case of rotating coordinate system [3], there is the possibility of a change in the sign before $d{\varphi }^2$.

From (44), one obtains

$${\left(\frac{d{t}^{\prime }}{d\varphi }\right)}^2+2\mathrm{\Phi }\left(r\right)\frac{d{t}^{\prime }}{d\varphi }+{\mathrm{\Phi }}^2\left(r\right)-R^2\left(r\right)\ge 0.$$

(45)

The solution of this inequality is the union of two intervals

$$\frac{d{t}^{\prime }}{d\varphi }\in \left(-\infty ,-\left(\mathrm{\Phi }\right(r)+R(r\left)\right)\right]\cup \left[R\left(r\right)-\mathrm{\Phi }\left(r\right),+\infty \right).$$

(46)

Considering cases of different signs of $d\varphi$, one obtains the following sets of solutions of (45):

$$d\varphi \ge 0\Rightarrow \begin{array}{c}d{t}^{\prime }\ge (R-\mathrm{\Phi })d\varphi \vee d{t}^{\prime }\le -(R+\mathrm{\Phi })d\varphi ,\hfill \end{array}$$

(47)

$$d\varphi \le 0\Rightarrow \begin{array}{c}d{t}^{\prime }\ge -(R+\mathrm{\Phi })d\varphi \vee d{t}^{\prime }\le (R-\mathrm{\Phi })d\varphi .\hfill \end{array}$$

(48)

These sets define light “cones” of the future and past for the metric (38). The form of these cones in cases $\mathrm{\Phi }\ll R$, $\mathrm{\Phi }=R$ and $\mathrm{\Phi }>R$ is shown in Figure 3 for the Gödel Universe with

$$\mathrm{\Phi }\left(r\right)>R\left(r\right)\iff r>r_0=log(1+\sqrt{2}).$$

(49)

Let us find limitations on possible values of the energy of particles moving in such a Universe. The coordinate $t^{\prime }$ is dimensionless, so the “physical energy” of the particle is expressed through the time component of the momentum as

$$E=p_0\frac{c}{a}=g_{0k}\frac{c}{a}\frac{d{x}^k}{d\lambda }.$$

(50)

For the frame with coordinates (38), the covariant $t^{\prime },\varphi ,z$ components are conserved, because the components of the metric depend only on r. Thus, the conserved energy on the geodesic for the interval (38) is

$$E=ca\left(\frac{d{t}^{\prime }}{d\lambda }+\mathrm{\Phi }\left(r\right)\frac{d\varphi }{d\lambda }\right).$$

(51)

From (47) and (48), for the case of movement “forward” in time, i.e., in the future light cone, one obtains

$$d{t}^{\prime }+\mathrm{\Phi }d\varphi \ge R\left|d\varphi \right|,$$

(52)

so

$$E\ge caR\frac{\left|d\varphi \right|}{d\lambda }.$$

(53)

It means that for a particle moving in the future cone in the Gödel Universe, the energy is not negative.

For movement “back in time”, the energy is limited from above by

$$E\le -caR\frac{\left|d\varphi \right|}{d\lambda }$$

(54)

and so it can be less than or equal to zero. However, such movement physically is inconsistent. The “time machine” effect in the Gödel Universe corresponds to continuous movement in the future cone. Thus, for $r>r_0$, where $\mathrm{\Phi }\left(r\right)>R\left(r\right)$ closed loops (they are not geodesic lines) $r=\mathrm{const}$, $z=\mathrm{const}$, called Gödel cycles, from $\varphi =0$ to $\varphi =2\pi$, are closed time-like curves [24]. Particles moving along such a cycle are moving “forward” in time but, due to the identification of values $\varphi$ different on $2\pi$, it occurs in the past after the whole cycle. Its energy is positive due to (53). Such a “time machine” is different from that moving in the past by the sign of the particle energy.

5. Conclusions

Three different cases are investigated concerning the possibility of the existence of particles with negative and zero energies.

• Schwarzschild black hole of the mass M. Trajectories of particles with negative and zero energies exist inside the horizon of the black hole, which can be shown in Kruskal–Szekeres coordinates.
• Flat space–time in Milne’s coordinates. Here, one also has the possibility of the existence of particles with negative and zero energies if a nonsynchronous system of coordinates is used.
• Gödel cosmological model with rotation. Here, we proved that, in this model, in Gödel’s coordinates, particles with negative and zero energies do not exist.

As for observations of the discussed effects, one can say that even the well-established Penrose and Hawking effects are still not observed. However, we hope that in the future development of observational astrophysics, one will see the consequences of the existence of negative and zero energies.