The Casimir Effect between Parallel Plates Separated by Uniaxial Media: The Effects Due to the Orientation of the Optical Axis
Abstract
1. Introduction
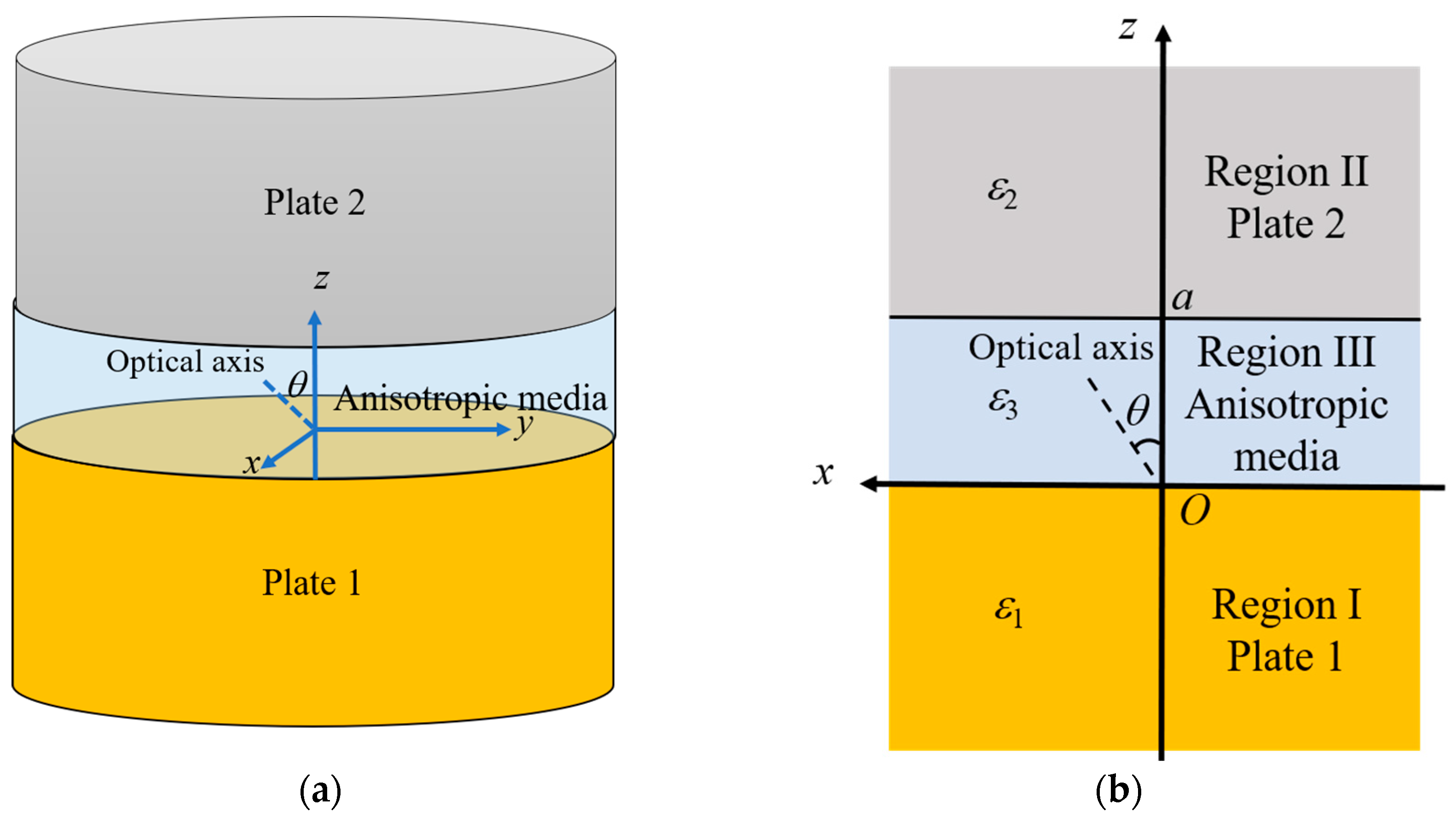
2. Casimir Energy and the Force between Parallel Slabs Separated by Uniaxial Media
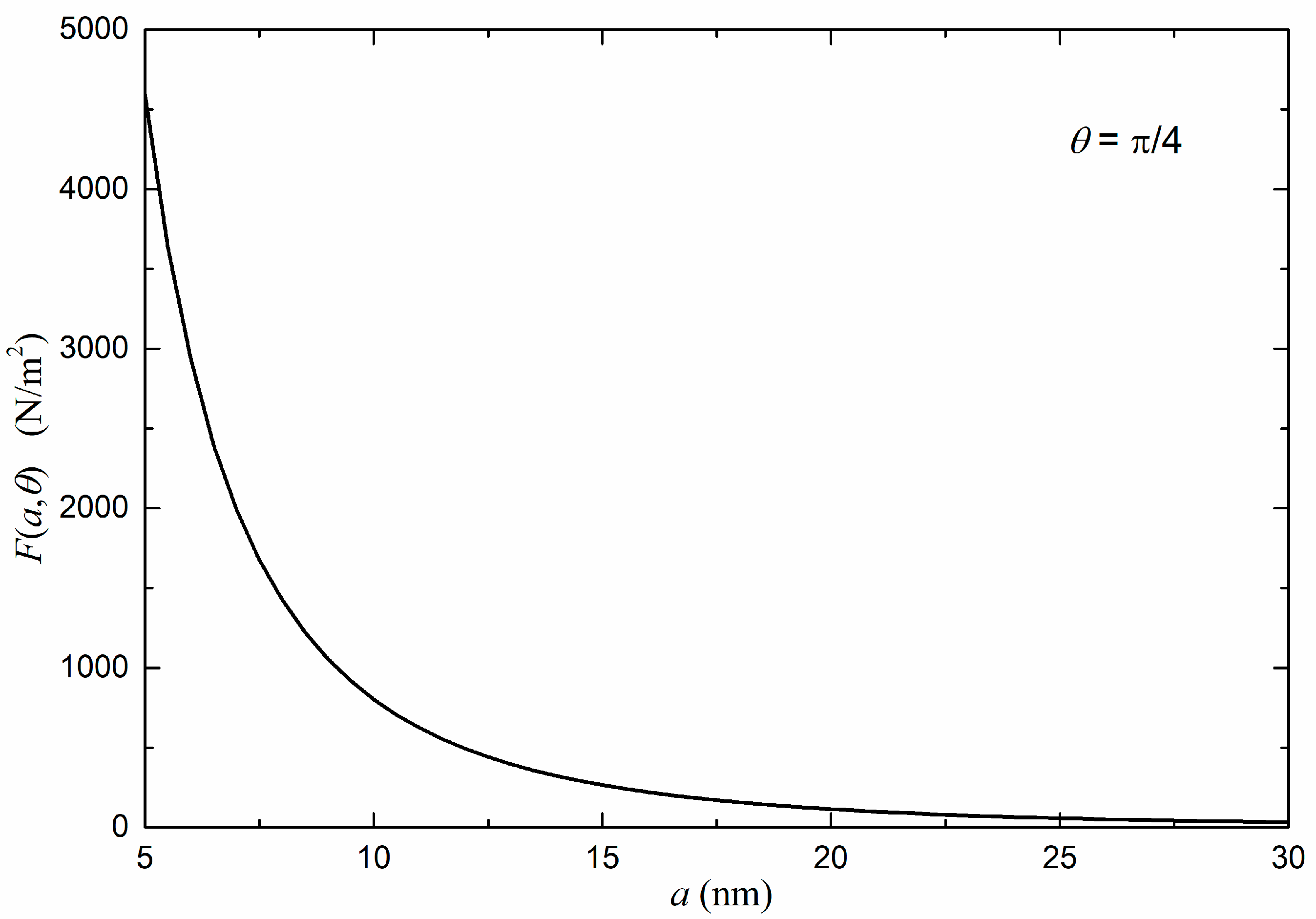
3. The Impact of the Orientation of the Optical Axis of the Intervening Media on the Casimir Force
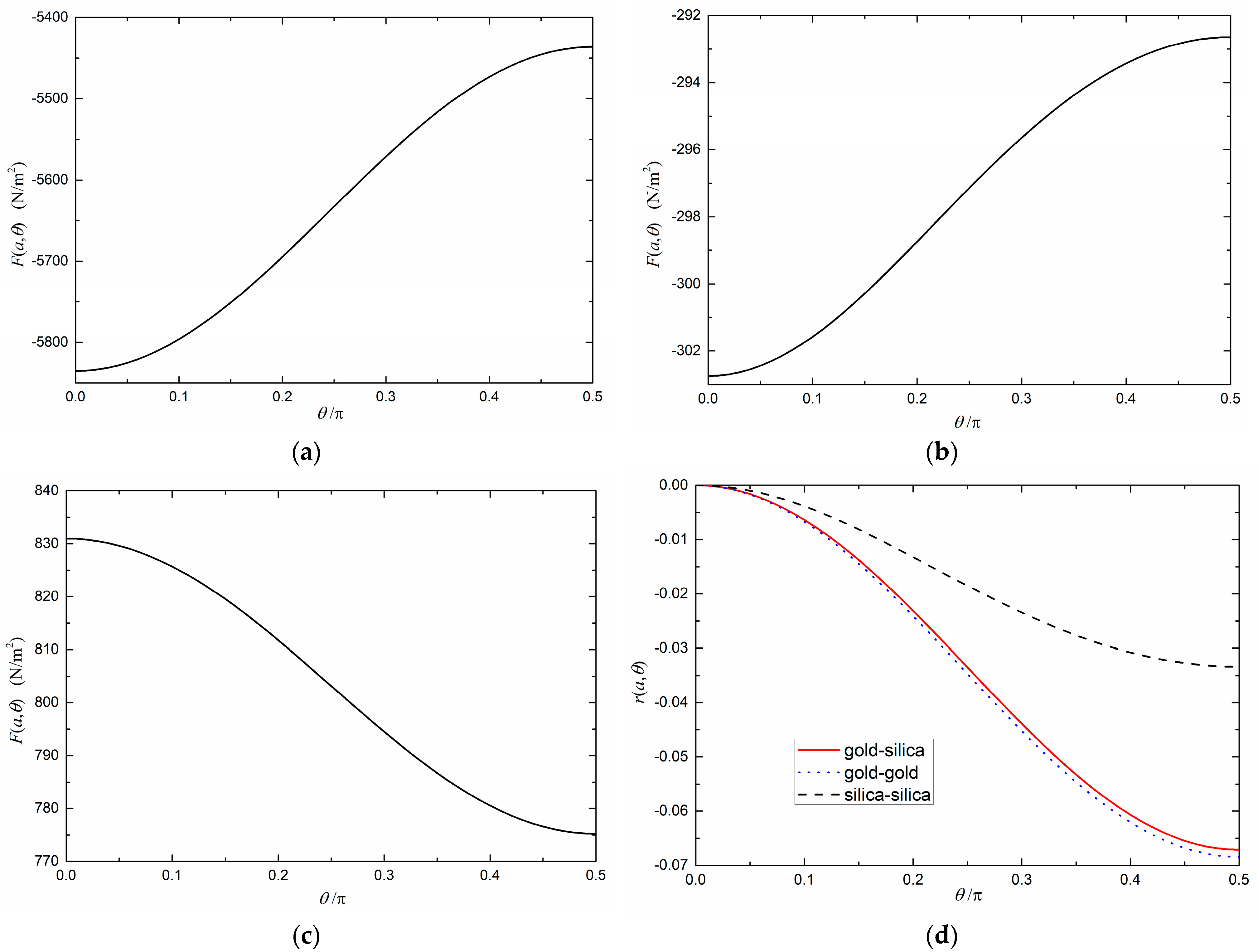
3.1. Positive Uniaxial Intervening Media (ε3|| > ε3⊥)
3.2. Negative Uniaxial Intervening Media (ε3|| < ε3⊥)
3.3. The Infulunce of Non-Zero Temperature
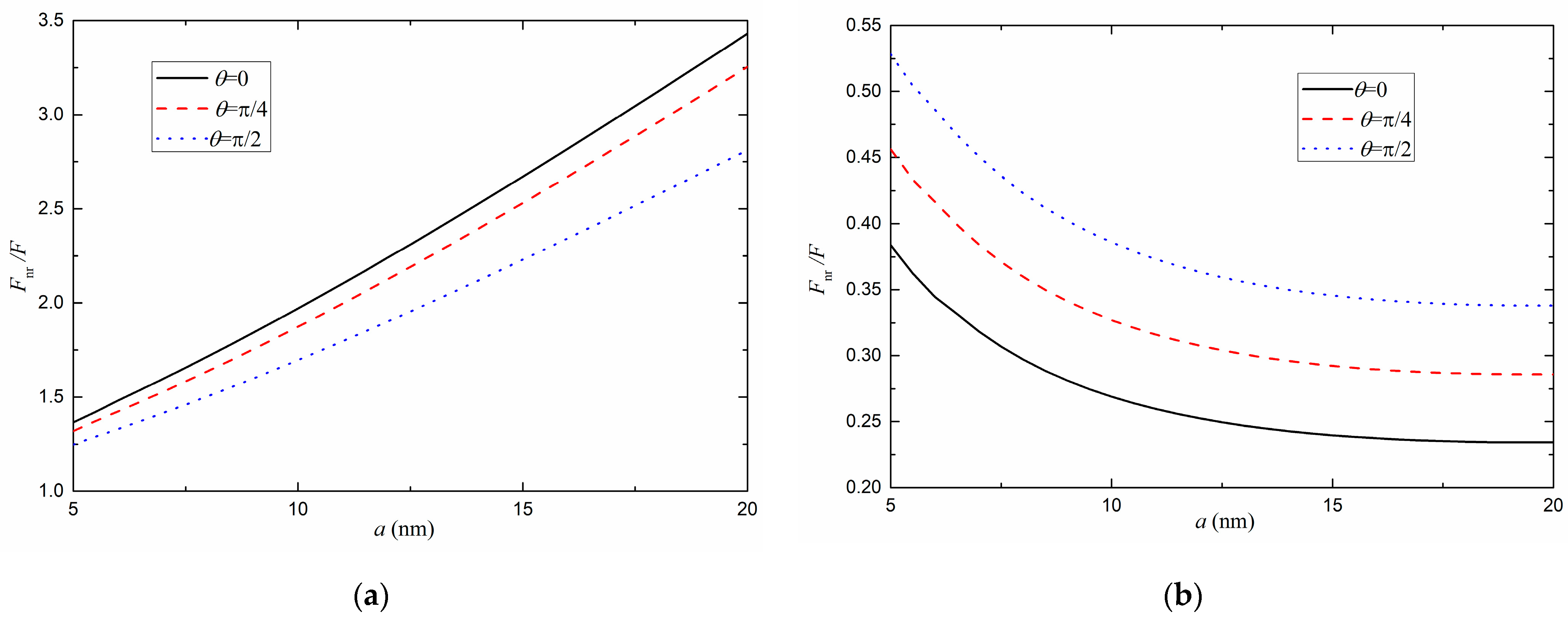
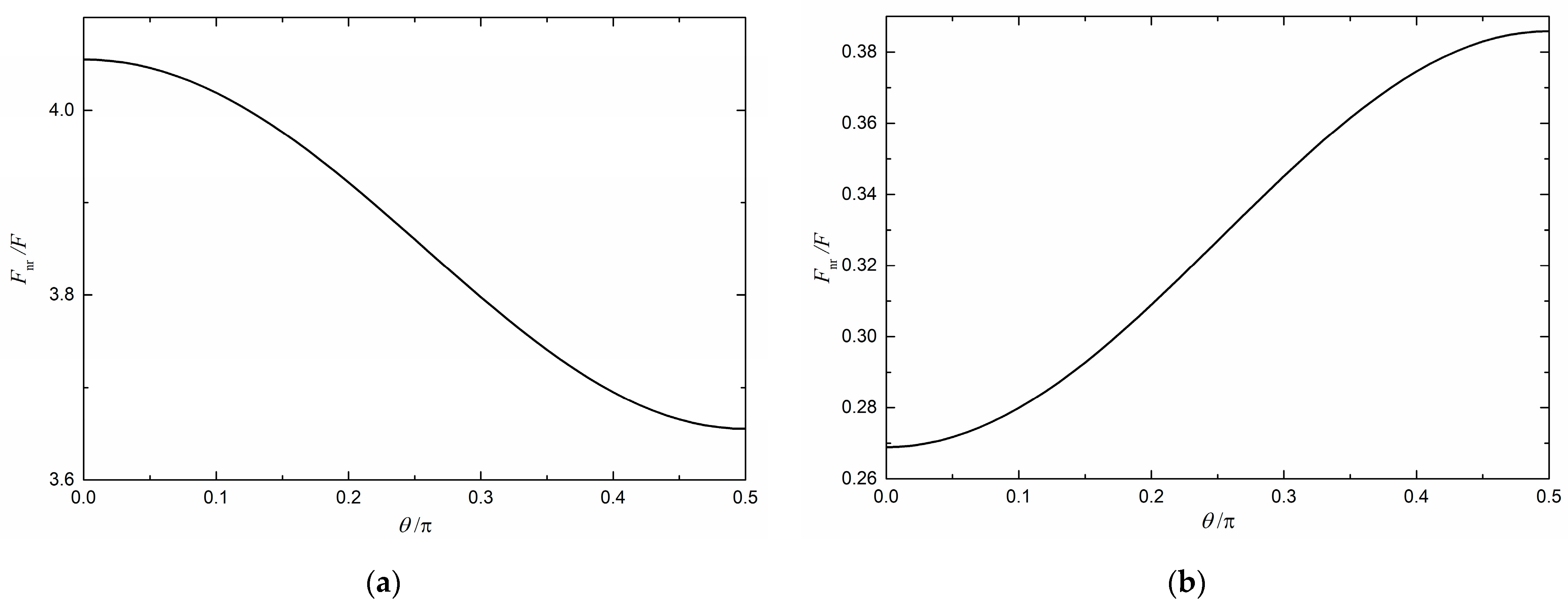
4. A Comparison between Retarded and Nonretarded Results
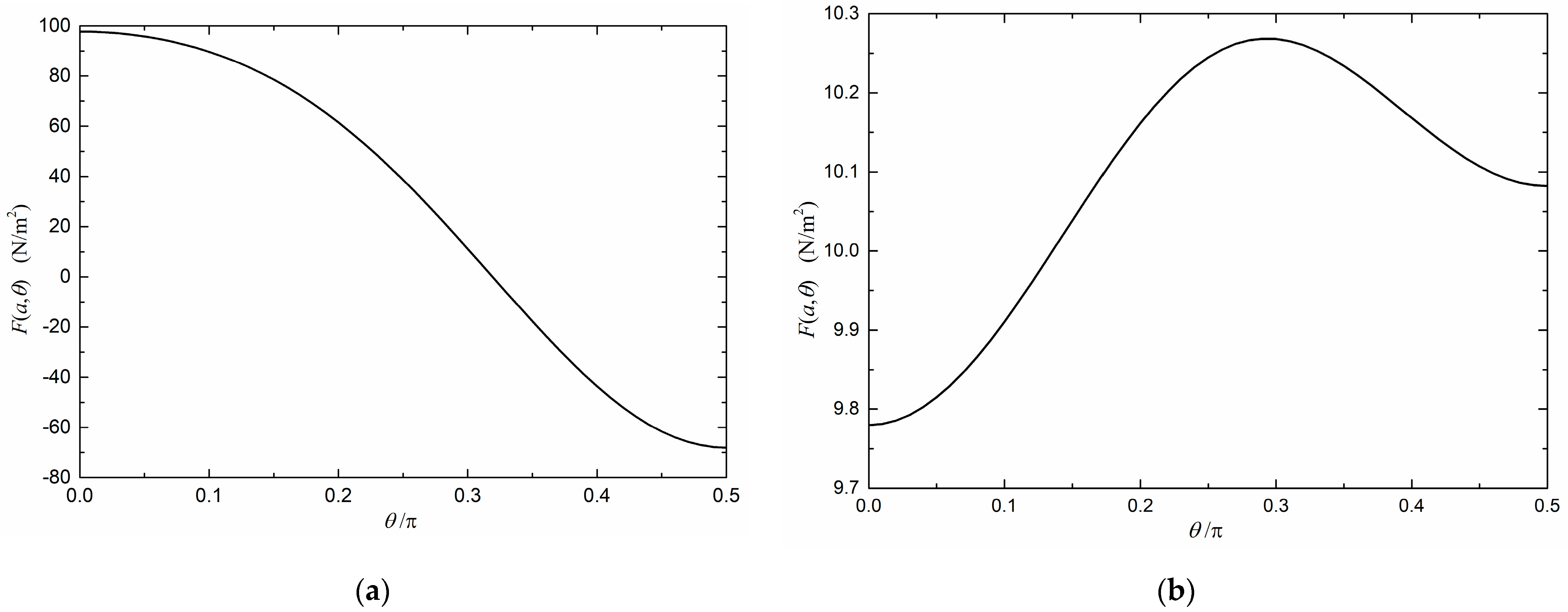
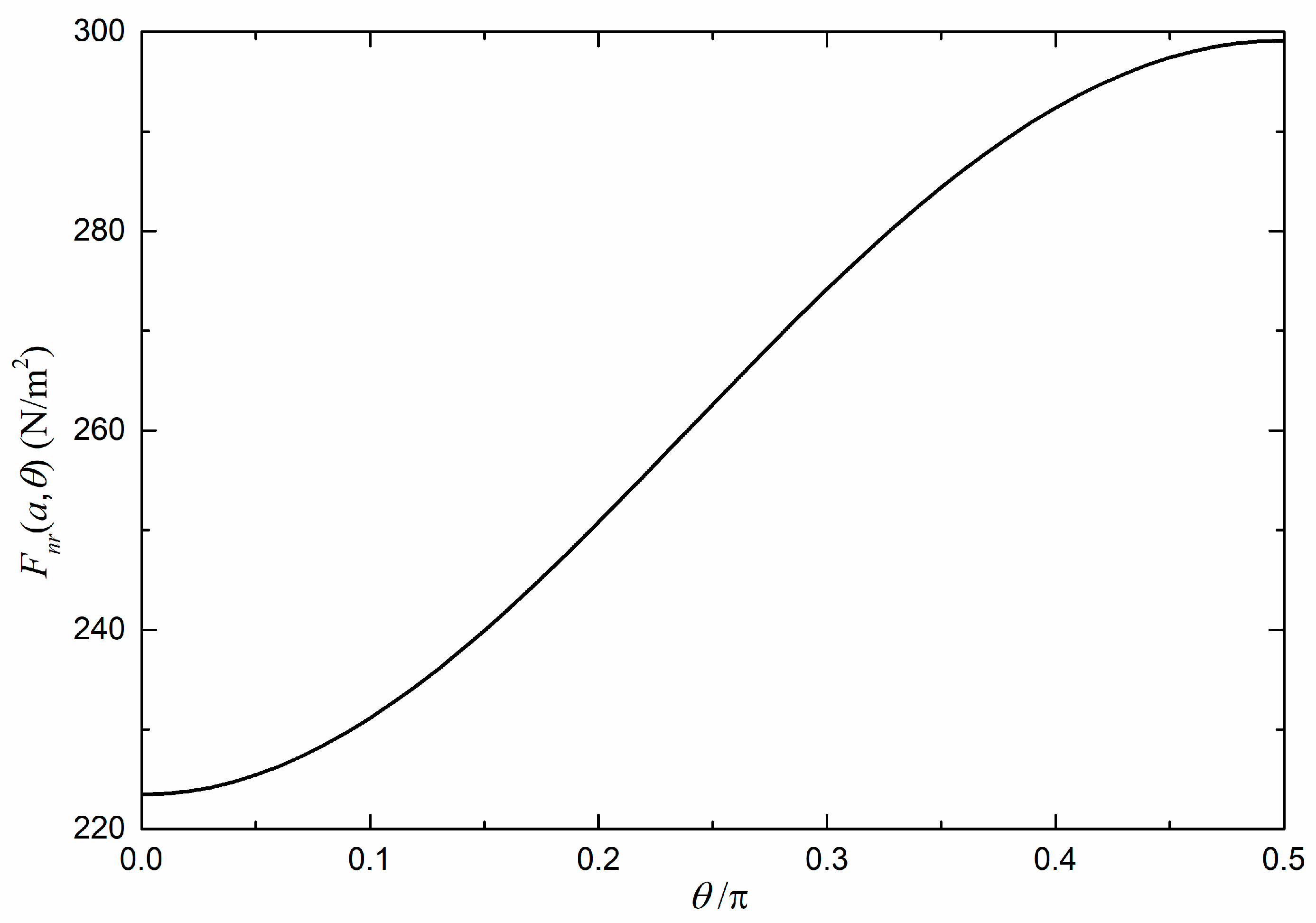
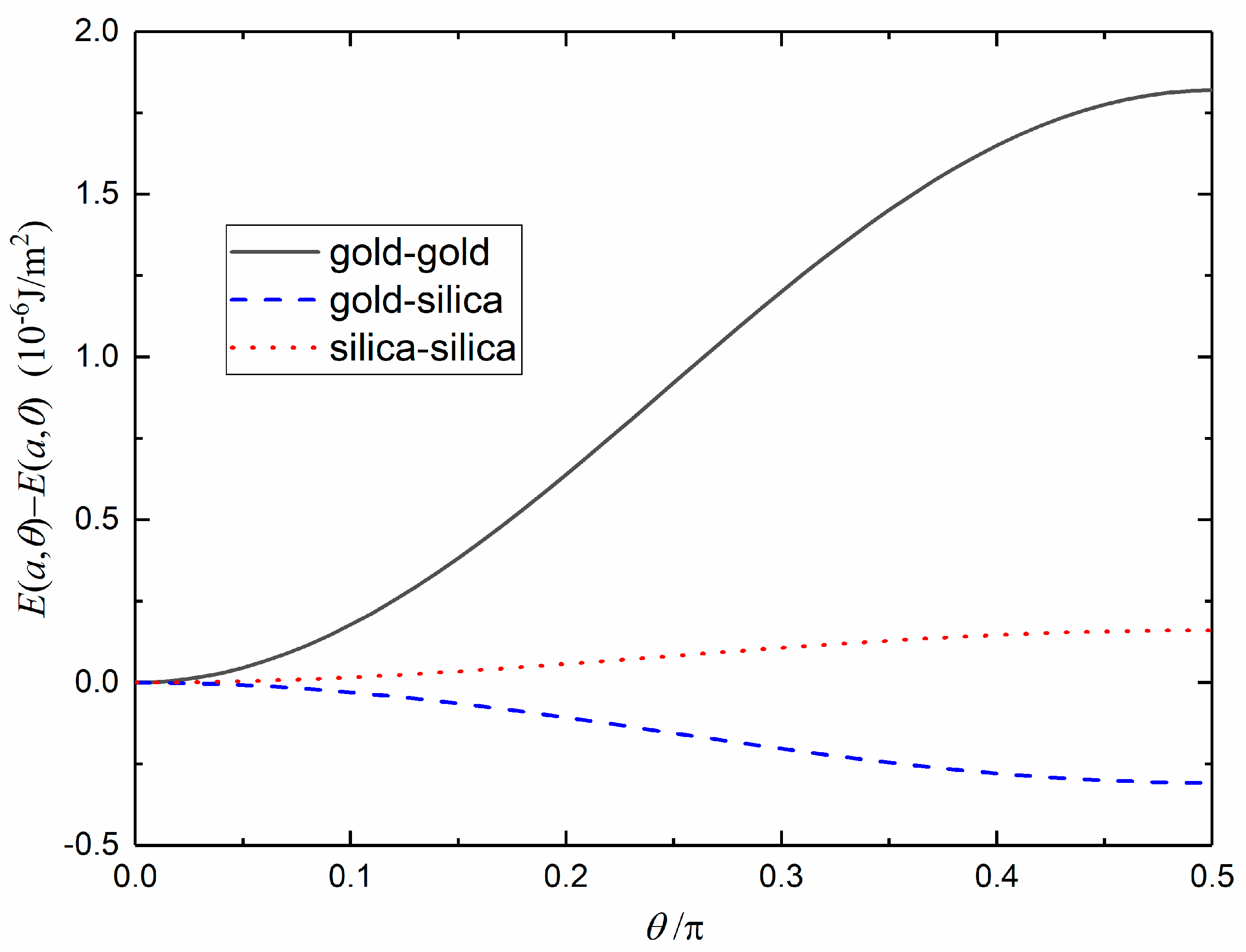
5. The Dependence of the Casimir Energy on the Orientation of the Optical Axis of the Intervening Media
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casimir, H.B.G. On the Attraction Between Two Perfectly Conducting Plates. Proc. Kon. Ned. Akad. Wet. 1948, 51, 793. [Google Scholar]
- Lifshitz, E.M. The Theory of Molecular Attractive Forces Between Solids. Sov. Phys. JETP 1956, 2, 73. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. The General Theory of van der Waals Forces. Adv. Phys. 1961, 10, 165–209. [Google Scholar] [CrossRef]
- Bordag, A.; Mohideen, U.; Mostepanenko, V.M. New developments in the Casimir effect. Phys. Rep. 2001, 353, 1–205. [Google Scholar] [CrossRef]
- Milton, K.A. The Casimir Effect: Physical Manifestations of Zero-Point Energy; World Scientific: Singapore, 2001; ISBN 978-981-02-4397-5. [Google Scholar]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827. [Google Scholar] [CrossRef]
- Parsegian, V.A.; Weiss, G.H. Dielectric Anisotropy and the van der Waals Interaction between Bulk Media. J. Adhes. 1972, 3, 259. [Google Scholar] [CrossRef]
- Barash, Y.S. Moment of van der Waals forces between anisotropic bodies. Radiophys. Quantum Elec. 1978, 21, 1138. [Google Scholar] [CrossRef]
- Munday, J.N.; Iannuzzi, D.; Barash, Y. Torque on birefringent plates induced by quantum fluctuations. Phys. Rev. A 2005, 71, 042102. [Google Scholar] [CrossRef]
- Somers, D.A.T.; Munday, J.N. Casimir-Lifshitz Torque Enhancement by Retardation and Intervening Dielectrics. Phys. Rev. Lett. 2017, 119, 183001. [Google Scholar] [CrossRef]
- Shao, C.G.; Tong, A.H.; Luo, J. Casimir torque between two birefringent plates. Phys. Rev. A 2005, 72, 022102. [Google Scholar] [CrossRef]
- Deng, G.; Liu, Z.Z.; Luo, J. Impact of magnetic properties on the Casimir torque between anisotropic metamaterial plates. Phys. Rev. A 2009, 80, 062104. [Google Scholar] [CrossRef]
- Romanowsky, M.B.; Capasso, F. Orientation-dependent Casimir force arising from highly anisotropic crystals Application to Bi2Sr2CaCu2O8+δ. Phys. Rev. A 2008, 78, 042110. [Google Scholar] [CrossRef]
- Parashar, P.; Milton, K.; Shajeshand, K.V.A.; Schaden, M. Electromagnetic semitransparent δ-function plate: Casimir interaction energy between parallel infinitesimally thin plates. Phys. Rev. D 2012, 86, 085201. [Google Scholar] [CrossRef]
- Shao, C.G.; Zheng, D.L.; Luo, J. Repulsive Casimir effect between anisotropic dielectric and permeable plates. Phys. Rev. A 2006, 74, 012103. [Google Scholar] [CrossRef]
- Deng, G.; Liu, Z.Z.; Luo, J. Attractive-repulsive transition of the Casimir force between anisotropic plates. Phys. Rev. A 2008, 78, 062111. [Google Scholar] [CrossRef]
- Somers, D.A.T.; Munday, J.N. Conditions for repulsive Casimir forces between identical birefringent materials. Phys. Rev. A 2017, 95, 022509. [Google Scholar] [CrossRef]
- Kornilovitch, P.E. Van der Waals interaction in uniaxial anisotropic media. J. Phys. Condens. Matter 2013, 25, 035102. [Google Scholar] [CrossRef]
- Poulin, P.; Stark, H.; Lubensky, T.C.; Weitz, D.A. Novel Colloidal Interactions in Anisotropic Fluids. Science 1997, 275, 1770. [Google Scholar] [CrossRef]
- Akhmetov, A.T.; Valiev, A.A.; Rakhimov, A.A.; Sametov, S.P. Anisotropic Properties of Blood in a Vessel with Stenosis. Dokl. Phys. 2018, 63, 476. [Google Scholar] [CrossRef]
- Nahmad-Rohen, A.; Contreras-Tello, H.; Morales-Luna, G.; García-Valenzuela, A. On the effective refractive index of blood. Phys. Scr. 2016, 91, 015503. [Google Scholar] [CrossRef]
- Gang, D.; Hua, T.B.; Ling, P.; Ni, H.; Rong, Z.J. Casimir force between parallel plates separated by anisotropic media. Phys. Rev. A 2015, 91, 062126. [Google Scholar]
- Deng, G.; Pei, L.; Hu, N.; Liu, Y.; Zhu, J.R. The impact of the anisotropy of the media between parallel plates on Casimir force. Symmetry 2018, 10, 61. [Google Scholar] [CrossRef]
- Deng, G.; Lv, C.Y.; Su, Q.; Pei, L.; Hu, N.; Liu, Y. The Casimir force between parallel plates separated by anisotropic media with in-plane optical axis. Europhys. Lett. 2019, 126, 40002. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Special features of the thermal Casimir effect across a uniaxial anisotropic film. Phys. Rev. A 2015, 92, 012911. [Google Scholar] [CrossRef]
- Bergstrom, L. Hamaker constants of inorganic materials. Adv. Colloid Interface Sci. 1997, 70, 125. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, G.; Xu, Y.; Pei, L.; Hu, N.; Xu, H. The Casimir Effect between Parallel Plates Separated by Uniaxial Media: The Effects Due to the Orientation of the Optical Axis. Universe 2023, 9, 216. https://doi.org/10.3390/universe9050216
Deng G, Xu Y, Pei L, Hu N, Xu H. The Casimir Effect between Parallel Plates Separated by Uniaxial Media: The Effects Due to the Orientation of the Optical Axis. Universe. 2023; 9(5):216. https://doi.org/10.3390/universe9050216
Chicago/Turabian StyleDeng, Gang, Ye Xu, Ling Pei, Ni Hu, and Hongjing Xu. 2023. "The Casimir Effect between Parallel Plates Separated by Uniaxial Media: The Effects Due to the Orientation of the Optical Axis" Universe 9, no. 5: 216. https://doi.org/10.3390/universe9050216
APA StyleDeng, G., Xu, Y., Pei, L., Hu, N., & Xu, H. (2023). The Casimir Effect between Parallel Plates Separated by Uniaxial Media: The Effects Due to the Orientation of the Optical Axis. Universe, 9(5), 216. https://doi.org/10.3390/universe9050216




