The Neutron Mean Life and Big Bang Nucleosynthesis
Abstract
1. Introduction
2. Standard BBN
3. Abundance Sensitivities to
4. BBN ‘Predictions’ of
5. Summary and Outlook
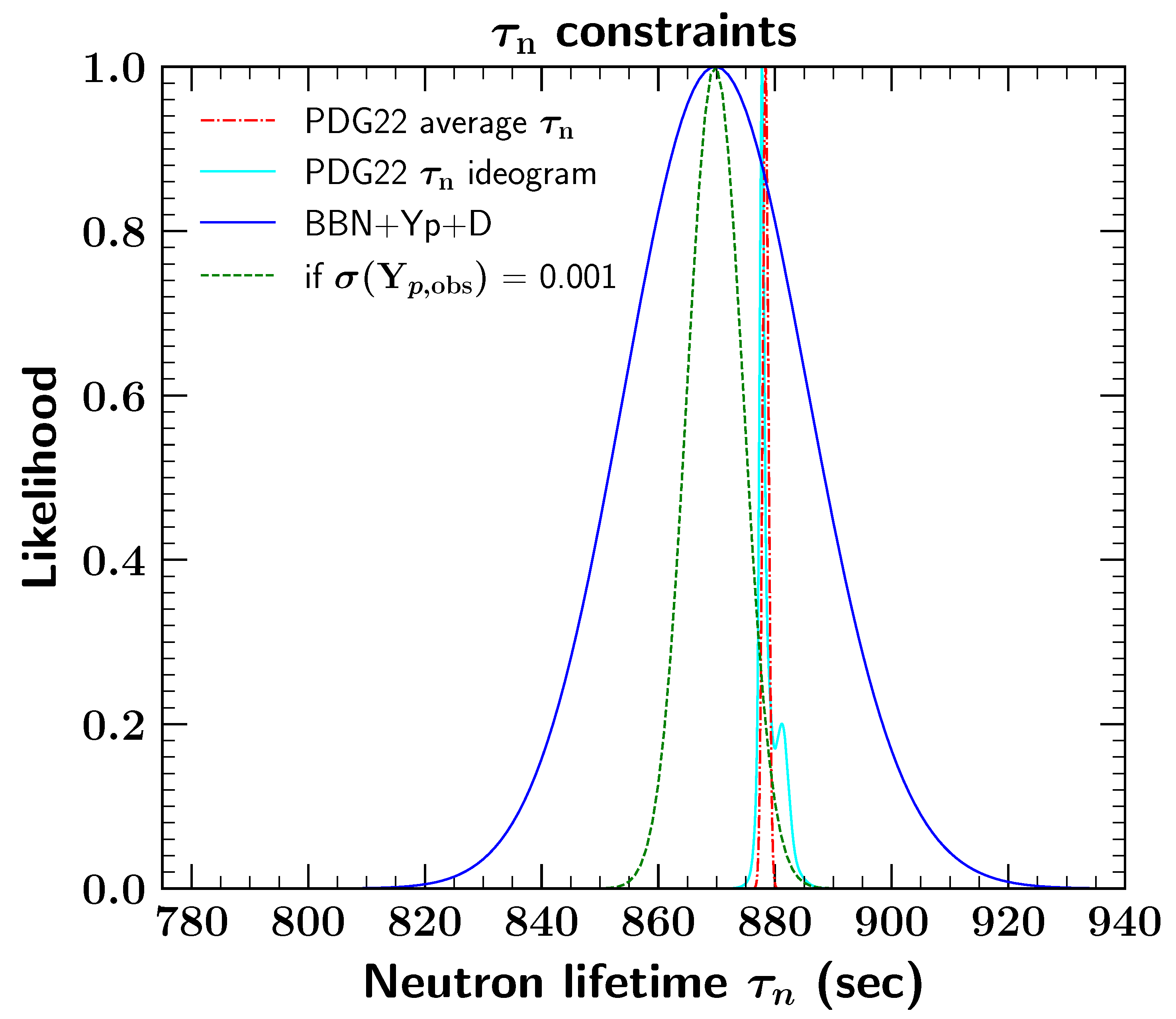
- New neutron lifetime measurements are planned. These include (a) both an upgrade magneto-gravitational trap experiment UCN+, and (b) an upgraded pulsed beam experiment, Beam Lifetime 3 (BL3) [68]. These can shed new light on and perhaps resolve the puzzle.
- The next generation CMB measurements from CMB-S4 will significantly improve both the determination of and from the CMB [66]. Improved measurements will be important for BBN to fully exploit these results, particularly .
- The ongoing effort to improve astronomical determinations continues. As we have discussed here and elsewhere [19], reaching the ambitious goal of would open a new window on new physics generally and in particular, approaching a precision near that of the present experimental discrepancy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
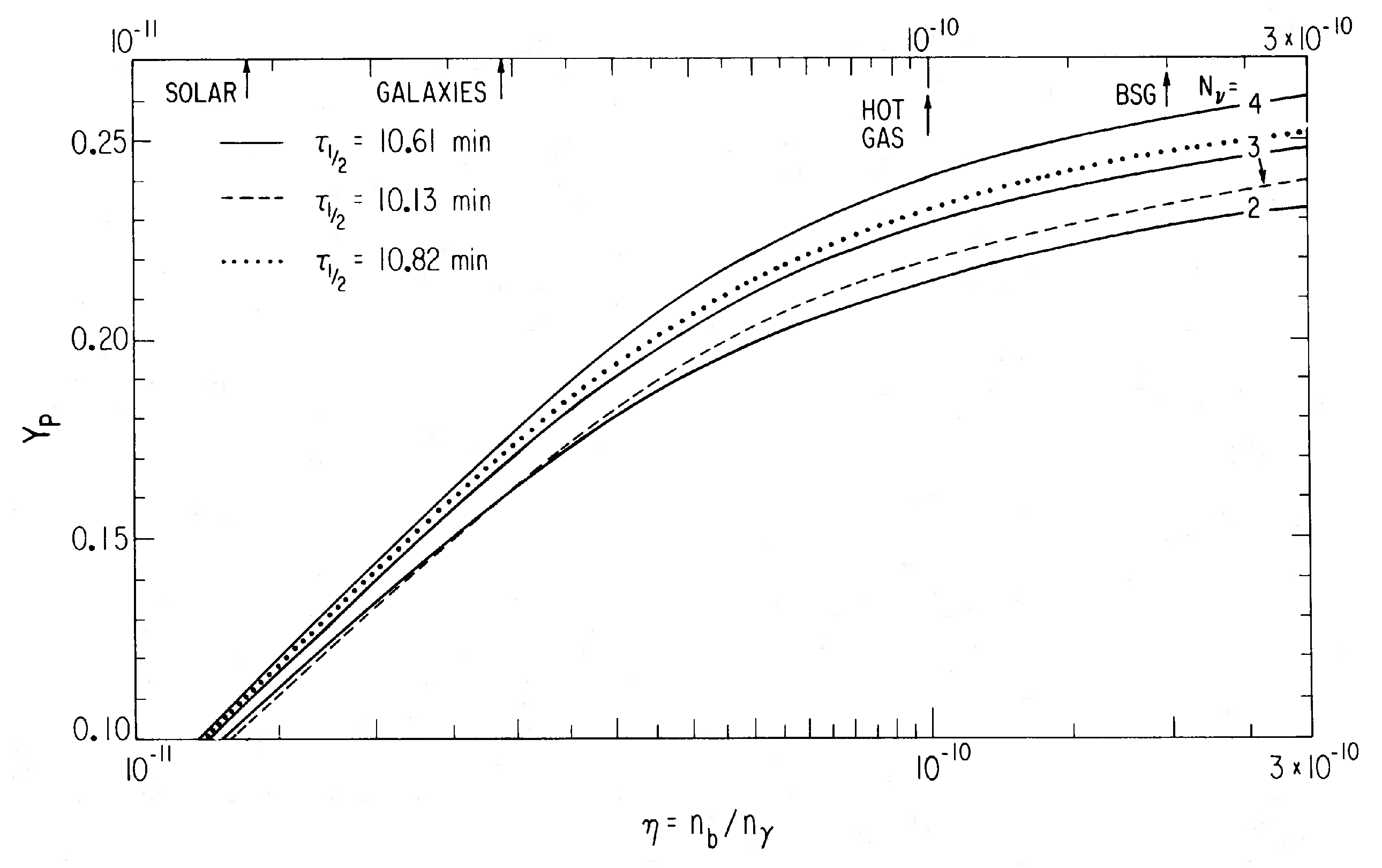
| 1 | The arrows at the top of the figure correspond to typical baryon densities taken from mass-to-light ratios typical of the solar neighborhood, the central parts of galaxies, hot gas, and binaries and small groups of galaxies (BSG). At the time, it was not clear what object was truly representative of the cosmological average. |
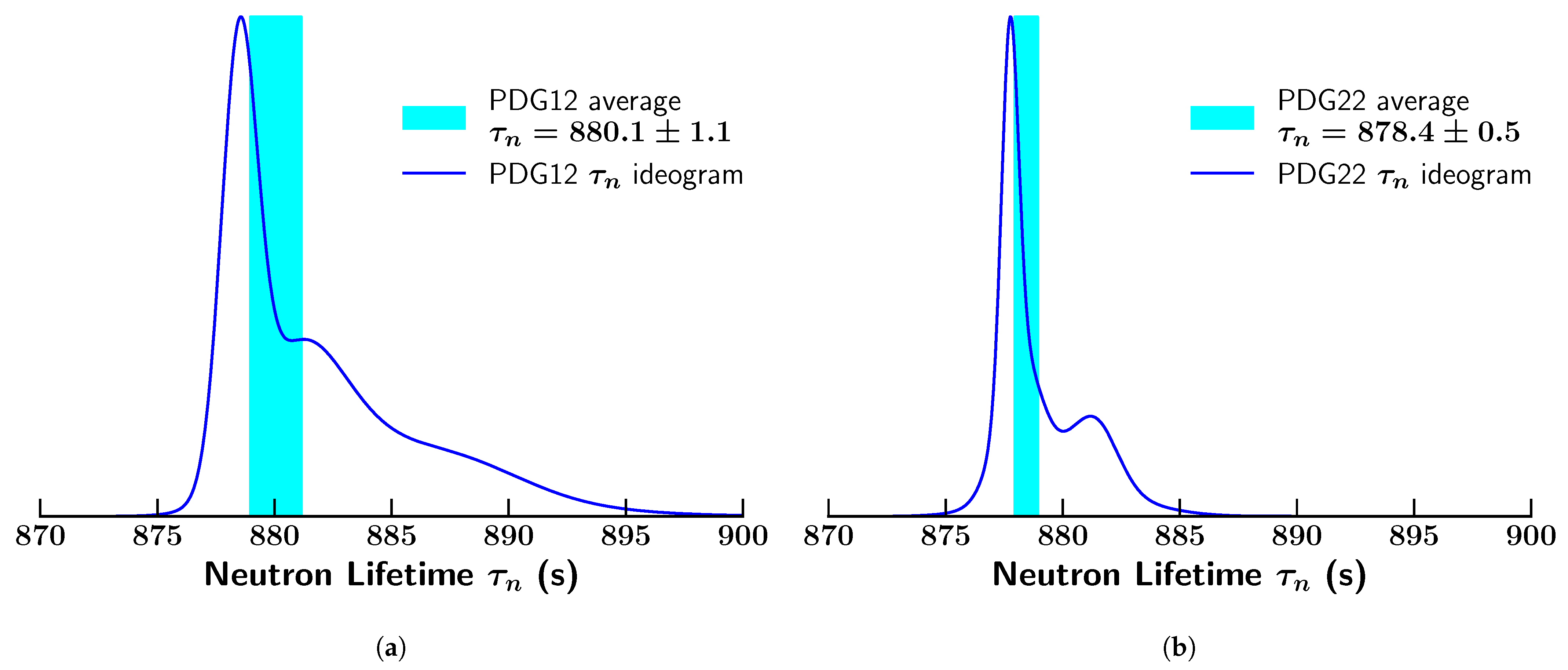
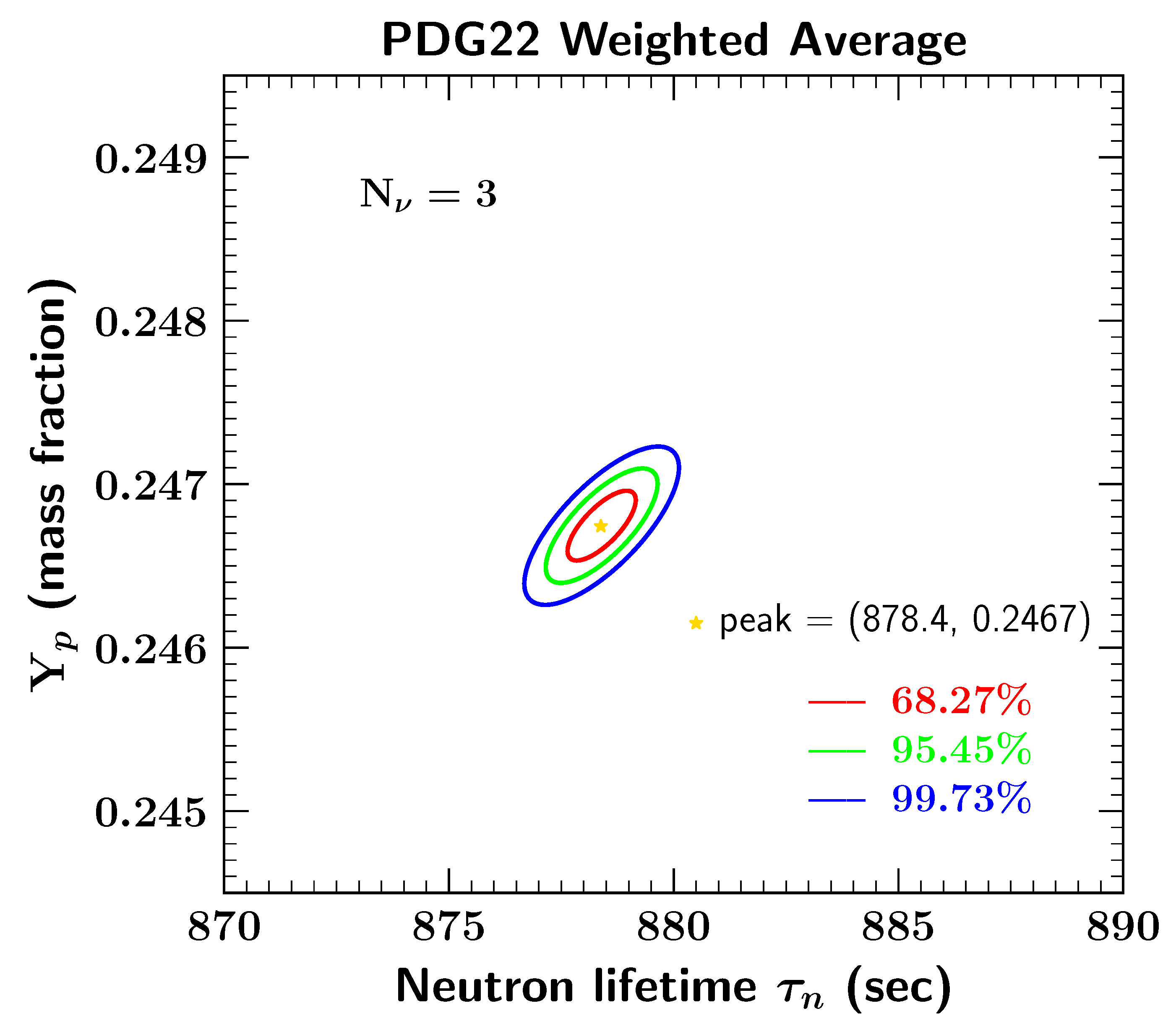
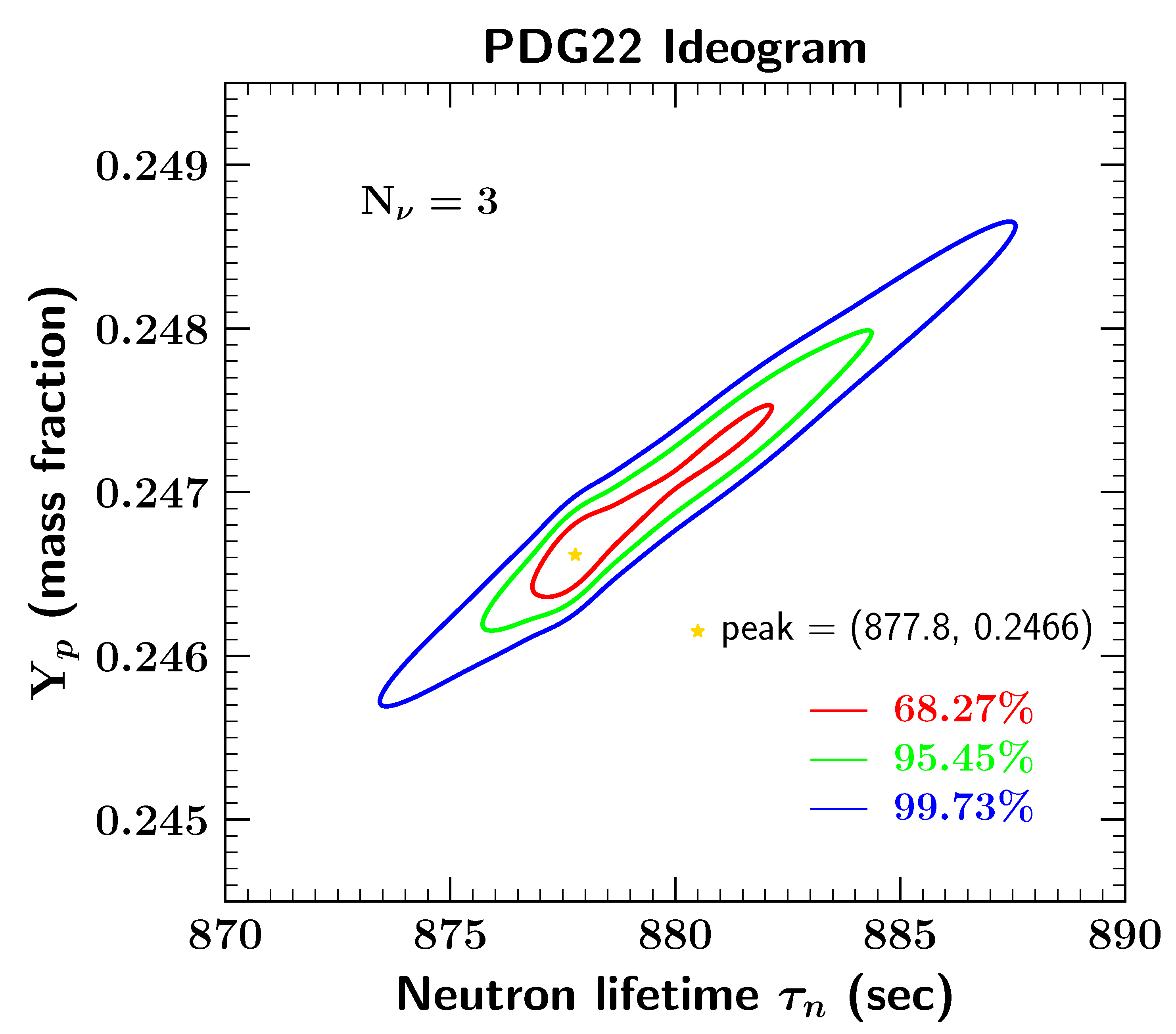
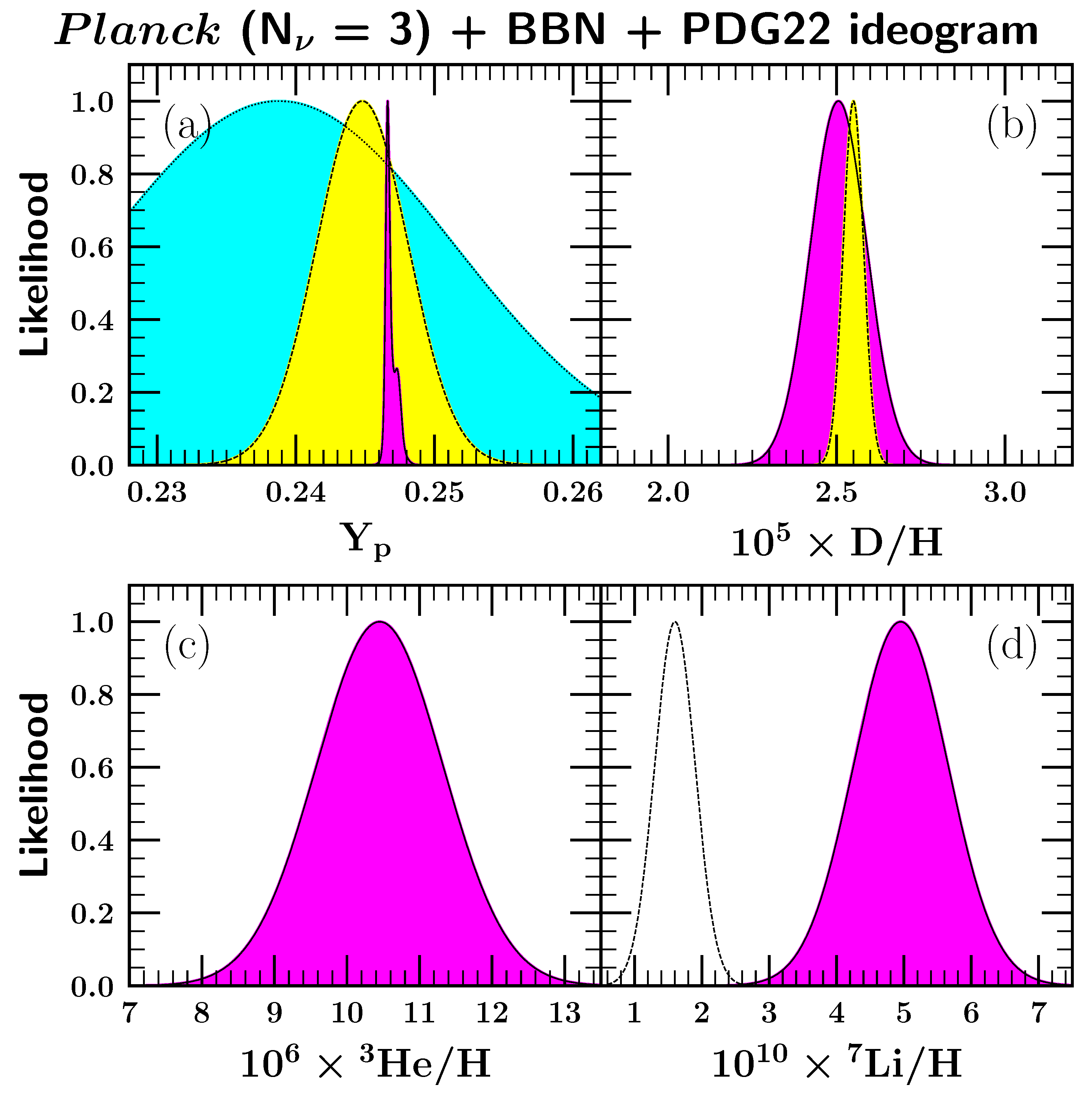
| 2 | For more information about the construction and use of ideograms, see any issue of the Review of Particle Properties or the Review of Particle Physics. |
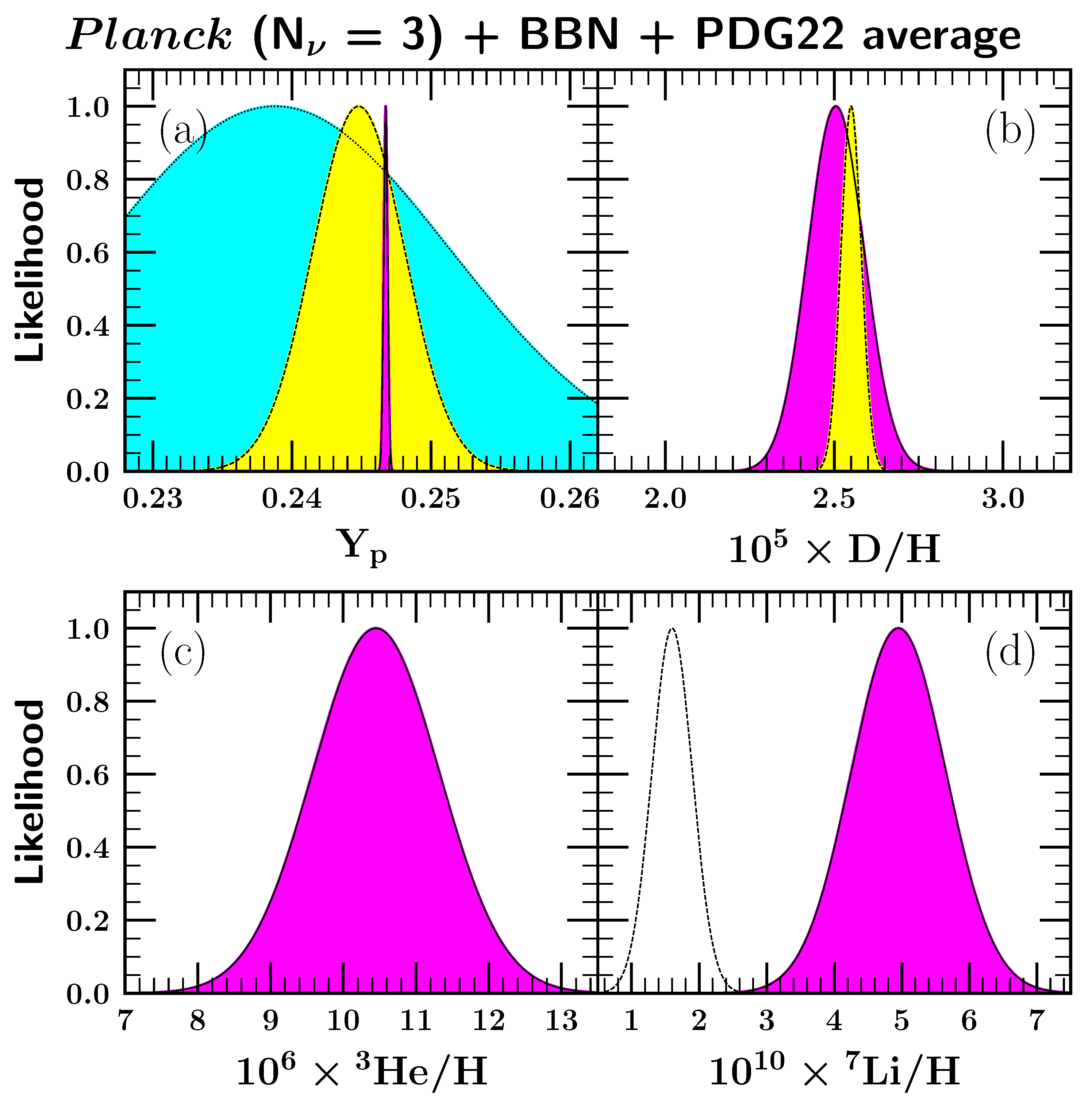
| 3 | In fact, we assume CDM, so that in addition to these Standard Model particles and interactions, there is (1) a nonzero cosmological constant which will be negligible during BBN, and (2) cold dark matter which we take to be so weakly interacting as to have no effect on BBN. These assumptions can be relaxed; see reviews in refs. [45,46,47]. |
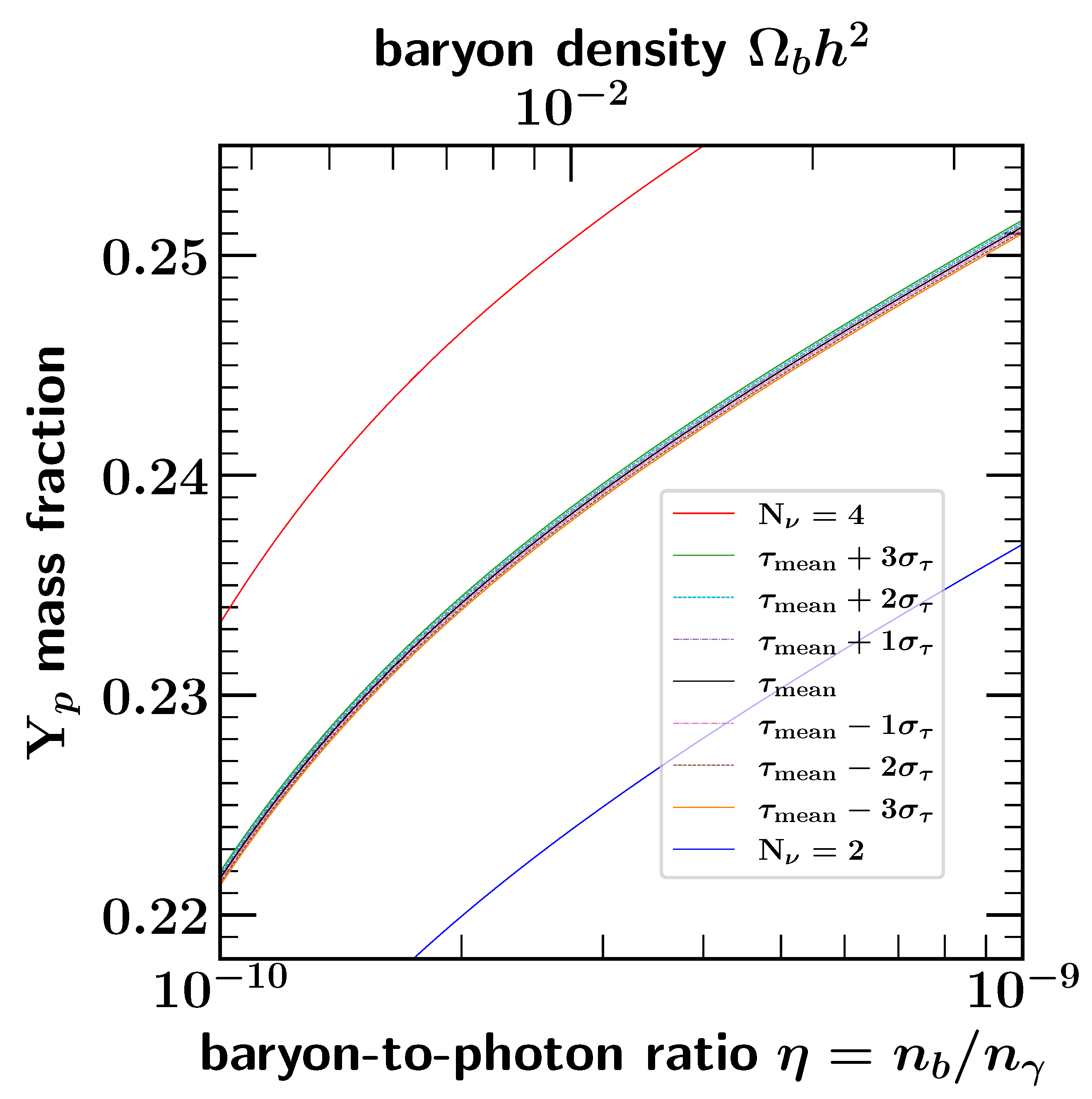
| 4 | Including the in-beam measurement would further increase the dispersion requiring a scale factor of 2.2. |
References
- Walker, T.P.; Steigman, G.; Schramm, D.N.; Olive, K.A.; Kang, H.S. Primordial nucleosynthesis redux. Astrophys. J. 1991, 376, 51–69. [Google Scholar] [CrossRef]
- Olive, K.A.; Steigman, G.; Walker, T.P. Primordial nucleosynthesis: Theory and observations. Phys. Rept. 2000, 333, 389–407. [Google Scholar] [CrossRef]
- Fields, B.D.; Olive, K.A. Big bang nucleosynthesis. Nucl. Phys. 2006, 777, 208–225. [Google Scholar] [CrossRef]
- Fields, B.D.; Molaro, P.; Sarkar, S. Big-Bang Nucleosynthesis. Chin. Phys. C 2014, 38, 339–344. [Google Scholar] [CrossRef]
- Steigman, G. Primordial Nucleosynthesis in the Precision Cosmology Era. Ann. Rev. Nucl. Part. Sci. 2007, 57, 463–491. [Google Scholar] [CrossRef]
- Iocco, F.; Mangano, G.; Miele, G.; Pisanti, O.; Serpico, P.D. Primordial Nucleosynthesis: From precision cosmology to fundamental physics. Phys. Rep. 2009, 472, 1–76. [Google Scholar] [CrossRef]
- Pitrou, C.; Coc, A.; Uzan, J.P.; Vangioni, E. Precision big bang nucleosynthesis with improved Helium-4 predictions. Phys. Rep. 2018, 754, 1–66. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.-H. Big Bang Nucleosynthesis: 2015. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Fields, B.D.; Olive, K.A.; Yeh, T.H.; Young, C. Big-Bang Nucleosynthesis after Planck. J. Cosmol. Astropart. Phys. 2020, 3, 010. [Google Scholar] [CrossRef]
- Particle Data Group; Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Barreiro, R.B.; Bartolo, N.; Basak, S.; Battye, R. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Janot, P.; Jadach, S. Improved Bhabha cross section at LEP and the number of light neutrino species. Phys. Lett. B 2020, 803, 135319. [Google Scholar] [CrossRef]
- Olive, K.A.; Schramm, D.N.; Steigman, G.; Turner, M.S.; Yang, J.M. Big Bang Nucleosynthesis as a Probe of Cosmology and Particle Physics. Astrophys. J. 1981, 246, 557. [Google Scholar] [CrossRef]
- Yang, J.M.; Turner, M.S.; Steigman, G.; Schramm, D.N.; Olive, K.A. Primordial Nucleosynthesis: A Critical Comparison of Theory and Observation. Astrophys. J. 1984, 281, 493–511. [Google Scholar] [CrossRef]
- Ellis, J.R.; Olive, K.A. Constraints on Light Particles From Stellar Evolution. Nucl. Phys. B 1983, 223, 252–268. [Google Scholar] [CrossRef]
- Christensen, C.J.; Nielsen, A.; Bahnsen, A.; Brown, W.K.; Rustad, B.M. Free-Neutron Beta-Decay Half-Life. Phys. Rev. D 1972, 5, 1628–1640. [Google Scholar] [CrossRef]
- Bondarenko, L.N.; Kurguzov, V.V.; Prokofev, Y.A.; Rogov, E.V.; Spivak, P.E. Measurement of the Neutron Half Time. Pisma Zh. Eksp. Teor. Fiz. 1978, 28, 328–333. [Google Scholar]
- Byrne, J.; Morse, J.; Smith, K.F.; Shaikh, F.; Green, K.; Greene, G.L. A New Measurement of the Neutron Lifetime. Phys. Lett. B 1980, 92, 274–278. [Google Scholar] [CrossRef]
- Yeh, T.H.; Shelton, J.; Olive, K.A.; Fields, B.D. Probing physics beyond the standard model: Limits from BBN and the CMB independently and combined. J. Cosmol. Astropart. Phys. 2022, 10, 046. [Google Scholar] [CrossRef]
- Baltrusaitis, R.M.; Becker, J.; Blaylock, G.; Brown, J.S.; Bunnell, K.; Burnett, T.; Cassell, R.; Coffman, D.; Cook, V.; Coward, D.H.; et al. [Particle Data Group]. Decays of the J/ψ into Two Pseudoscalar Mesons. Phys. Lett. B 1982, 111, 1–294. [Google Scholar]
- Kosvintsev, Y.Y.; Kushnir, Y.A.; Morozov, V.I.; Terekhov, G.I. Application of Ultracold Neutrons for Neutron Lifetime Measurement. JETP Lett. 1980, 31, 236. (In Russian) [Google Scholar]
- Wilkinson, D.H. The neutron lifetime. Prog. Part. Nucl. Phys. 1981, 6, 325–332. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of Particle Properties. Particle Data Group. Rev. Mod. Phys. 1984, 56, S1–S304. [Google Scholar]
- Mampe, W.; Ageron, P.; Bates, C.; Pendlebury, J.M.; Steyerl, A. Neutron Lifetime Measured With Stored Ultracold Neutrons. Phys. Rev. Lett. 1989, 63, 593–596. [Google Scholar] [CrossRef]
- Olive, K.A.; Schramm, D.N.; Steigman, G.; Walker, T.P. Big Bang Nucleosynthesis Revisited. Phys. Lett. B 1990, 236, 454–460. [Google Scholar] [CrossRef]
- Yeh, T.H.; Olive, K.A.; Fields, B.D. The impact of new d(p,γ)3 rates on Big Bang Nucleosynthesis. J. Cosmol. Astropart. Phys. 2021, 3, 046. [Google Scholar] [CrossRef]
- Hagiwara, K. Review of Particle Physics. Phys. Rev. D 2002, 66, 010001. [Google Scholar] [CrossRef]
- Arzumanov, S.; Bondarenko, L.; Chernavsky, S.; Fomin, A.; Morozov, V.; Panin, Y.; Drexel, W.; Schreckenbach, K.; Geltenbort, P.; Pendlebury, J. Neutron life time value measured by storing ultracold neutrons with detection of inelastically scattered neutrons. Phys. Lett. B 2000, 483, 15–22. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A. The NACRE Thermonuclear Reaction Compilation and Big Bang Nucleosynthesis. New Astron. 1996, 6, 215. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A. Primordial nucleosynthesis with CMB inputs: Probing the early universe and light element astrophysics. Astropart. Phys. 2002, 17, 87–100. [Google Scholar] [CrossRef]
- Serebrov, A.; Varlamov, V.; Kharitonov, A.; Fomin, A.; Pokotilovski, Y.; Geltenbort, P.; Butterworth, J.; Krasnoschekova, I.; Lasakov, M.; Tal’daev, R.; et al. Measurement of the neutron lifetime using a gravitational trap and a low-temperature Fomblin coating. Phys. Lett. B 2005, 605, 72–78. [Google Scholar] [CrossRef]
- Mathews, G.J.; Kajino, T.; Shima, T. Big Bang nucleosynthesis with a new neutron lifetime. Phys. Rev. D 2005, 71, 021302. [Google Scholar] [CrossRef]
- Beringer, J.; Arguin, J.F.; Barnett, R.M.; Copic, K.; Dahl, O.; Groom, D.E.; Lin, C.J.; Lys, J.; Murayama, H.; Wohl, C.G.; et al. [Particle Data Group]. Review of Particle Physics (RPP). Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
- Wietfeldt, F.E.; Greene, G.L. Colloquium: The neutron lifetime. Rev. Mod. Phys. 2011, 83, 1173–1192. [Google Scholar] [CrossRef]
- Pichlmaier, A.; Varlamov, V.; Schreckenbach, K.; Geltenbort, P. Neutron lifetime measurement with the UCN trap-in-trap MAMBO II. Phys. Lett. B 2010, 693, 221–226. [Google Scholar] [CrossRef]
- Steyerl, A.; Pendlebury, J.M.; Kaufman, C.; Malik, S.S.; Desai, A.M. Quasielastic scattering in the interaction of ultracold neutrons with a liquid wall and application in a reanalysis of the Mambo I neutron-lifetime experiment. Phys. Rev. C 2012, 85, 065503. [Google Scholar] [CrossRef]
- Arzumanov, S.; Bondarenko, L.; Chernyavsky, S.; Geltenbort, P.; Morozov, V.; Nesvizhevsky, V.V.; Panin, Y.; Strepetov, A. A measurement of the neutron lifetime using the method of storage of ultracold neutrons and detection of inelastically up-scattered neutrons. Phys. Lett. B 2015, 745, 79–89. [Google Scholar] [CrossRef]
- Serebrov, A.P.; Kolomensky, E.A.; Fomin, A.K.; Krasnoshchekova, I.A.; Vassiljev, A.V.; Prudnikov, D.M.; Shoka, I.V.; Chechkin, A.V.; Chaikovskiy, M.E.; Varlamov, V.E.; et al. Neutron lifetime measurements with a large gravitational trap for ultracold neutrons. Phys. Rev. C 2018, 97, 055503. [Google Scholar] [CrossRef]
- Pattie, R.W., Jr.; Callahan, N.B.; Cude-Woods, C.; Adamek, E.R.; Broussard, L.J.; Clayton, S.M.; Currie, S.A.; Dees, E.B.; Ding, X.; Engel, E.M.; et al. Measurement of the neutron lifetime using a magneto-gravitational trap and in situ detection. Science 2018, 360, 627–632. [Google Scholar] [CrossRef]
- Ezhov, V.F.; Andreev, A.Z.; Ban, G.; Bazarov, B.A.; Geltenbort, P.; Glushkov, A.G.; Knyazkov, V.A.; Kovrizhnykh, N.A.; Krygin, G.B.; Naviliat-Cuncic, O.; et al. Measurement of the neutron lifetime with ultra-cold neutrons stored in a magneto-gravitational trap. JETP Lett. 2018, 107, 671–675. [Google Scholar] [CrossRef]
- Gonzalez, F.M.; Fries, E.M.; Cude-Woods, C.; Bailey, T.; Blatnik, M.; Broussard, L.J.; Callahan, N.B.; Choi, J.H.; Clayton, S.M.; Currie, S.A.; et al. Improved neutron lifetime measurement with UCNτ. Phys. Rev. Lett. 2021, 127, 162501. [Google Scholar] [CrossRef] [PubMed]
- Yue, A.T.; Dewey, M.S.; Gilliam, D.M.; Greene, G.L.; Laptev, A.B.; Nico, J.S.; Snow, W.M.; Wietfeldt, F.E. Improved Determination of the Neutron Lifetime. Phys. Rev. Lett. 2013, 111, 222501. [Google Scholar] [CrossRef] [PubMed]
- Czarnecki, A.; Marciano, W.J.; Sirlin, A. Neutron Lifetime and Axial Coupling Connection. Phys. Rev. Lett. 2018, 120, 202002. [Google Scholar] [CrossRef] [PubMed]
- Pospelov, M.; Pradler, J. Big Bang Nucleosynthesis as a Probe of New Physics. Ann. Rev. Nucl. Part. Sci. 2010, 60, 539–568. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pospelov, M. Big Bang Nucleosynthesis and Particle Dark Matter. New J. Phys. 2009, 11, 105028. [Google Scholar] [CrossRef]
- Malaney, R.A.; Mathews, G.J. Probing the early universe: A Review of primordial nucleosynthesis beyond the standard Big Bang. Phys. Rept. 1993, 229, 145–219. [Google Scholar] [CrossRef]
- Bernstein, J.; Brown, L.S.; Feinberg, G. Cosmological Helium Production Simplified. Rev. Mod. Phys. 1989, 61, 25. [Google Scholar] [CrossRef]
- Mukhanov, V.F. Nucleosynthesis without a computer. Int. J. Theor. Phys. 2004, 43, 669. [Google Scholar] [CrossRef]
- Froustey, J.; Pitrou, C. Incomplete neutrino decoupling effect on big bang nucleosynthesis. Phys. Rev. D 2020, 101, 043524. [Google Scholar] [CrossRef]
- Aver, E.; Berg, D.A.; Olive, K.A.; Pogge, R.W.; Salzer, J.J.; Skillman, E.D. Improving helium abundance determinations with Leo P as a case study. J. Cosmol. Astropart. Phys. 2021, 3, 027. [Google Scholar] [CrossRef]
- Aver, E.; Berg, D.A.; Hirschauer, A.S.; Olive, K.A.; Pogge, R.W.; Rogers, N.S.J.; Salzer, J.J.; Skillman, E.D. A comprehensive chemical abundance analysis of the extremely metal poor Leoncino Dwarf galaxy (AGC 198691). Mon. Not. R. Astron. Soc. 2021, 510, 373–382. [Google Scholar] [CrossRef]
- Pettini, M.; Cooke, R. A new, precise measurement of the primordial abundance of Deuterium. Mon. Not. R. Astron. Soc. 2012, 425, 2477–2486. [Google Scholar] [CrossRef]
- Cooke, R.; Pettini, M.; Jorgenson, R.A.; Murphy, M.T.; Steidel, C.C. Precision measures of the primordial abundance of deuterium. Astrophys. J. 2014, 781, 31. [Google Scholar] [CrossRef]
- Riemer-Sørensen, S.; Webb, J.K.; Crighton, N.; Dumont, V.; Ali, K.; Kotuš, S.; Bainbridge, M.; Murphy, M.T.; Carswell, R. A robust deuterium abundance; Re-measurement of the z = 3.256 absorption system towards the quasar PKS1937-1009. Mon. Not. R. Astron. Soc. 2015, 447, 2925–2936. [Google Scholar] [CrossRef]
- Balashev, S.A.; Zavarygin, E.O.; Ivanchik, A.V.; Telikova, K.N.; Varshalovich, D.A. The primordial deuterium abundance: SubDLA system at zabs = 2.437 towards the QSO J 1444+2919. Mon. Not. R. Astron. Soc. 2016, 458, 2188–2198. [Google Scholar] [CrossRef]
- Cooke, R.J.; Pettini, M.; Nollett, K.M.; Jorgenson, R. The primordial deuterium abundance of the most metal-poor damped Lyα system. Astrophys. J. 2016, 830, 148. [Google Scholar] [CrossRef]
- Riemer-Sørensen, S.; Kotuš, S.; Webb, J.K.; Ali, K.; Dumont, V.; Murphy, M.T.; Carswell, R.F. A precise deuterium abundance: Remeasurement of the z = 3.572 absorption system towards the quasar PKS1937?101. Mon. Not. R. Astron. Soc. 2017, 468, 3239–3250. [Google Scholar] [CrossRef]
- Zavarygin, E.O.; Webb, J.K.; Dumont, V.; Riemer-Sørensen, S. The primordial deuterium abundance at zabs = 2.504 from a high signal-to-noise spectrum of Q1009 + 2956. Mon. Not. R. Astron. Soc. 2018, 477, 5536–5553. [Google Scholar] [CrossRef]
- Cooke, R.J.; Pettini, M.; Steidel, C.C. One Percent Determination of the Primordial Deuterium Abundance. Astrophys. J. 2018, 855, 102. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A. An Update on the big bang nucleosynthesis prediction for Li-7: The problem worsens. J. Cosmol. Astropart. Phys. 2008, 11, 012. [Google Scholar] [CrossRef]
- Fields, B.D.; Olive, K.A. Implications of the non-observation of 6Li in halo stars for the primordial 7Li problem. J. Cosmol. Astropart. Phys. 2022, 10, 078. [Google Scholar] [CrossRef]
- Ryan, S.G.; Beers, T.C.; Olive, K.A.; Fields, B.D.; Norris, J.E. Primordial Lithium and Big Bang Nucleosynthesis. Astrophys. J. 2000, 530, L57. [Google Scholar] [CrossRef]
- Sbordone, L.; Bonifacio, P.; Caffau, E.; Ludwig, H.-G.; Behara, N.T.; Hernandez, J.I.G.; Steffen, M.; Cayrel, R.; Freytag, B.; Van’t Veer, C. et al. The metal-poor end of the Spite plateau. 1: Stellar parameters, metallicities and lithium abundances. Astron. Astrophys. 2010, 522, A26. [Google Scholar] [CrossRef]
- Salvati, L.; Pagano, L.; Consiglio, R.; Melchiorri, A. Cosmological constraints on the neutron lifetime. J. Cosmol. Astropart. Phys. 2016, 3, 055. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Wilson, J.T.; Lawrence, D.J.; Peplowski, P.N.; Eke, V.R.; Kegerreis, J.A. Measurement of the free neutron lifetime using the neutron spectrometer on NASA’s Lunar Prospector mission. Phys. Rev. C 2021, 104, 045501. [Google Scholar] [CrossRef]
- Wietfeldt, F.E.; Biswas, R.; Caylor, J.; Crawford, B.; Dewey, M.S.; Fomin, N.; Greene, G.L.; Haddock, C.C.; Hoogerheide, S.F.; Mumm, H.P.; et al. Comments on Systematic Effects in the NIST Beam Neutron Lifetime Experiment. arXiv 2022, arXiv:2209.15049. [Google Scholar]


| Year | Year | Year | ||||||
|---|---|---|---|---|---|---|---|---|
| 1959 | 1013 | ±26 | 1967 | 935 | ±14 | 1972 | 918 | ±14 |
| 1980 | 937 | ±18 | 1982 | 925 | ±11 | 1984 | 898 | ±16 |
| 1988 | 896 | ±10 | 1990 | 888.6 | ±3.5 | 1992 | 889.1 | ±2.1 |
| 1994 | 887.0 | ±2.0 | 1998 | 886.7 | ±1.9 | 2002 | 885.7 | ±0.8 |
| 2012 | 880.1 | ±1.1 | 2014 | 880.3 | ±1.1 | 2016 | 880.2 | ±1.0 |
| 2020 | 879.4 | ±0.6 | 2022 | 878.4 | ±0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, T.-H.; Olive, K.A.; Fields, B.D. The Neutron Mean Life and Big Bang Nucleosynthesis. Universe 2023, 9, 183. https://doi.org/10.3390/universe9040183
Yeh T-H, Olive KA, Fields BD. The Neutron Mean Life and Big Bang Nucleosynthesis. Universe. 2023; 9(4):183. https://doi.org/10.3390/universe9040183
Chicago/Turabian StyleYeh, Tsung-Han, Keith A. Olive, and Brian D. Fields. 2023. "The Neutron Mean Life and Big Bang Nucleosynthesis" Universe 9, no. 4: 183. https://doi.org/10.3390/universe9040183
APA StyleYeh, T.-H., Olive, K. A., & Fields, B. D. (2023). The Neutron Mean Life and Big Bang Nucleosynthesis. Universe, 9(4), 183. https://doi.org/10.3390/universe9040183






