Abstract
The thermodynamical quantities and response functions are useful to describe the particle production in heavy-ion collisions as they reveal crucial information about the produced system. While the study of isothermal compressibility provides an inference about the viscosity of the medium, speed of sound helps in understanding the equation of state. With an aim towards understanding the system produced in the heavy-ion collision, we have made an attempt to study isothermal compressibility and speed of sound as function of charged particle multiplicity in heavy-ion collisions at = TeV, TeV, and TeV using unified formalism.
1. Introduction
Among the main aim of heavy-ion collision program at present collider experiments such as Relativistic Heavy Ion Collider (RHIC) and Large Hadron Collider (LHC) is to mimic the state that was created few microseconds after the Big Bang. This state of matter, created at extremely high temperature and energy density, is called the Quark-Gluon Plasma (QGP) and is also believed to be present at the core of massive neutron stars. Interaction between quark and gluon, which leads to the formation of QGP, is governed by the Quantum Chromo-dynamics (QCD). Asymptotic freedom, which is an important pillar of QCD, suggests a confinement deconfinement phase transition, during which the hadronic degree of freedom changes to partonic degree of freedom. Whether the phase transition is first-order, second-order or a simple cross-over and the search for the critical point are some of the important questions that are of immediate interest in the particle physics community.
Since the formation of QGP occurs at a very short time scale, it is not possible to directly probe in the experiment using current technologies. Therefore, we rely on the information carried by the final state particles to the detectors to gain insight into the medium created in the heavy-ion collision. Although we only measure the kinematic quantities such as the pseudorapidity , transverse momentum , energy E etc. of the final state particles in the experiment, a breadth of information about the medium can be extracted by studying these kinematic observables.
Another set of quantities that are not directly observable, however, play an important role in understanding the nature of the medium and the equation of state are the thermodynamical response functions. This includes quantities that express how a system responds to change in some external parameters such as pressure, temperature etc. Isothermal compressibility (), and speed of sound () are some of the response function that are of interest in high-energy physics [1,2,3]. The isothermal compressibility, , which exhibits the important property of the medium, tells us how much the volume of the medium changes on the change in pressure at a fixed temperature. This quantity can be used to study how close a medium is to be called perfect fluid. Perfect fluids are ideal fluids that do not possess shear stress, viscosity and also do not conduct heat. The of perfect fluid is zero and the zero value signifies that the fluid is incompressible. Although the incompressible fluids do not exist in nature, the recent findings of the value of , as in Ref. [4], are almost close to zero which suggests that the medium created is almost a perfect fluid. Estimation of will tell us about how close the medium to be a perfect fluid which will lead us an approximation about the viscosity as viscosity describes a fluid’s resistance to flow, hence perfect fluid has zero viscosity. Isothermal compressibility and viscosity of a liquid is related to the low-shear viscosity of a liquid dispersion of solid particles [5]. Perfect fluid can also be characterized by the ratio of shear viscosity to entropy density (/s). Calculation based on correspondence has put up a universal lower bound of for strongly interacting quantum field theories [6]. On the other hand, the value of /s has been found to be close to the lower bound based on the flow harmonics calculation of the experimental data, indicating the near-perfect behaviour of medium created in heavy-ion collision [7,8].
As explained in Ref. [9], the speed of sound can quantify the nature of the same as it connects and explains the hydrodynamical evolution of the produced matter in the heavy-ion collisions. Fundamentally the speed of sound also gives the information about the equation of state, which relates pressure and the energy density . For a non-interacting massless ideal gas, the value of the squared speed of sound is expected to be times speed of light squared [10]. Hence, the comparison with the massless ideal gas will give crucial information about the system dynamics and reveals the nature of the medium [11]. Different studies suggested that for the system created in heavy-ion collision the value of is close to the ideal value [1,3,11,12,13,14,15,16,17].
As already discussed, these quantities are not directly observable in the experiment and we extract them by utilizing the distribution of kinematic observables such as the transverse momentum -spectra, rapidity, angle of emission etc. The -spectra carries sufficient information to study such quantities as it is directly related to the energy of the system. Understanding the distribution of is in itself a tedious task because in the low- region, the QCD coupling strength is very high and hence we cannot apply the perturbative QCD theories to explain the spectra. Several phenomenological models have been developed to tackle this issue, and the most widely accepted are the statistical thermal models. We can utilize the statistical thermal models to extract the thermodynamical quantities such as temperature, number density, energy density etc.
If we assume the purely thermal origin of final state particles, the most natural choice to explain the energy distribution of particles is Boltzmann-Gibbs (BG) statistics [18,19,20]. However, it has been discussed in many works [21,22] that the BG distribution function deviates significantly from the experimental data because the spectra are more like a power-law rather than the simple exponential. Also, the BG statistics fails to explain the strongly correlated systems [23] in which the long-range correlations are present, and entropy becomes non-additive and non-extensive [24]. The existence of long-range interaction in high-energy heavy-ion collisions is discussed in Ref. [25] motivating to explore beyond the extensive BG regime to study the spectra. In 1988, C. Tsallis proposed a statistics [26,27,28], introducing an additional parameter q, which takes care of the non-extensivity in the system. It is a thermodynamically consistent [29,30], generalized version of Boltzmann distribution [31]. The power-law behavior of Tsallis distribution makes it a good choice to study the -spectra and it is shown to nicely fit the spectra, particularly in the low- region. Although Tsallis statistics nicely explain the data in the low- region, however, it starts to deviate from the experimental data as we move toward the high- part of the spectra.
Particle spectra in heavy-ion collisions can be divided into two distinct regions, low- regime corresponds to the particle produced in soft processes whereas the hard processes dominate particle production in the high- region. The limitation of Tsallis statistics in explaining the particle produced in hard processes demands a framework that can consider the effect of both soft and hard processes in the particle spectra. Some modification in Tsallis statistics [32,33,34,35] has been proposed to explain the high- part of spectra in the heavy-ion collision, however, more work is required in this direction to get the full benefit from the spectra. To explain both the hard and soft part of particle spectra in a consistent manner, a unified theory using Pearson distribution is introduced in Ref. [21]. It is a generalized form of the Tsallis distribution and is shown to be thermodynamically consistent and backward compatible to the Tsallis statistics within some limit on its parameters [22].
In this work, we have calculated the isothermal compressibility and speed of sound for charged hadrons produced in heavy-ion collisions using the unified statistical framework. For this analysis, we have taken the experimental data of transverse momentum spectra for charged hadrons produced in collision at = TeV [36], TeV [37], and collision at TeV [38] measured by the ALICE experiment.
2. Methodology
The basic thermodynamic quantities that are of interest to formulate the isothermal compressibility and speed of sound include energy density , number density n and pressure P. From the standard thermodynamics, the number of particles N in a system and its total energy E can be calculated as:
where is the energy of state and is the corresponding distribution function. The standard replacement while going from summation to integration for small energy intervals is given as [29]:
Here, V is the volume and p represent the momentum. So, using the above transformation, the number density n will be of the form:
and the corresponding energy density will be given as:
Since the momentum distribution of the final state particles are fixed at kinetic freeze-out [12], the pressure of the system could be estimated from the moments of energy distribution. The pressure P is given as:
Among all the quantities discussed above, one common factor is the energy distribution of the particles (). Energy is related to the transverse mass and pseudorapadity y as and the transverse mass is defined in term of transverse momentum and mass of particle m as . So, the distribution of transverse momenta acts as a proxy for the energy distribution. Hence, the proper parameterization of transverse momentum spectra is crucial to understand the thermodynamics of the system created in high-energy collisions. In the present work, we have used the unified statistical framework to explain the -spectra and extract the thermodynamical quantities such as temperature T, non-extensive parameter q.
In the seminal work [39], Karl Pearson discussed a family of the curve, based on the first four moments (mean, variance, skewness, and kurtosis), called Pearson distribution. Before the introduction of Pearson formalism in 1895, all probability distribution was only constructed based on mean and variance and did not take care of skewness and kurtosis. Pearson introduced a new probability distribution function where skewness and kurtosis can also be adjusted along with the mean and variance of a distribution. An important characteristic of this distribution is that depending on the limit on its parameters, it reduces to different distribution function such as Gaussian, normal, Student’s T, Gamma distribution etc. The differential form of a Pearson distribution function, , for a variable x is expressed as [40]:
where a, , , and are related to first four moments of the distribution. By integrating this differential equation, one can get,
Solving above equation we get the general solution of the form:
upto some normalization constant . Here, are the parameters of the equation and can be related to the physical parameters such as temperature T, non-extensivity parameter q etc.
Distribution function, in case of unified statistical framework, obtained from the above Pearson distribution, is given as [22]:
where
and
In the above equation, and n are the free parameters with parameter n is related to the second order flow coefficient [21]. This formalism reduces to Tsallis statistics within the limit and . Therefore, it can be considered as a generalized version of the Tsallis function and explains both soft and hard process contributions to -spectra. The equation for the average number of particles and energy, in the case of unified formalism, remains the same as Tsallis [22]:
and, the energy of the system will be:
Here, the additional power of q comes from the thermodynamic consistency. In case of the unified formalism, the transverse momentum spectra is defined as:
where , T is temperature and q is non-extensive parameter. Here we considered the chemical potential to be zero because at LHC energy, the net-baryonic number is extremely small at the central rapidity region. Thermodynamic parameters such as T, q and the other quantities can be obtained by fitting the measured transverse momentum spectra with the unified distribution using the Equation (17). These quantities extracted from the spectra can be used to calculate the response function as discussed below.
2.1. Isothermal Compressibility
In the high-energy collider experiment, we only consider a part of phase space because of the limited acceptance of the detectors. The overall number of particles in the collision is conserved, but number of particles and energy in a particular phase space window may vary. Hence, the system can be considered as a grand canonical ensemble for the estimation of isothermal compressibility. Therefore, the variance of number of particles N, can be written as [41]:
And, the isothermal compressibility, , can be written as:
Using the expression of variance of N and [41,42], we can write:
Equation (20) requires an event-by-event information of N to estimation . On contrary, we can compare Equations (18) and (20) to derive a fluctuation independent formula for isothermal compressibility as:
As per Equation (21), the estimation of does not depend on the fluctuation of N and it makes the estimation possible without having event-by-event information of particle number.
Number density, n, in case of unified formalism, is of the form:
and,
By using the above equations, we have estimated the values of for heavy-ion collisions at different energies.
2.2. Speed of Sound
For a thermodynamic system at temperature T and volume V, the squared speed of sound is given by,
where P is pressure and is energy density of the system. As discussed in Ref. [43], the propagation of sound wave in a medium is an adiabatic process and entropy is constant in such process, hence the squared speed of sound is estimated at constant entropy density (s). Above equation can be further reduced to:
where
and,
By using the above equations, the squared speed of sound reduces to
We have used the Equation (28) to estimate the squared speed of sound in the medium created in heavy-ion collision at three different energies.
3. Results and Discussion
This study presents a formalism to calculate and using the non-extensive unified statistical framework discussed in Ref. [22]. We have estimated the and in the medium formed of charged hadrons as a function of charged particle multiplicity for different collision systems. The data for charged particle multiplicity corresponding to a particular centrality is taken from the experimental results Refs. [44,45,46].
For this analysis, we have considered the transverse momentum spectra of charged hadrons produced in collision at [36] and TeV [37] and collision at TeV [38]. The range is restricted to GeV/c since we are trying to study bulk properties and the majority of high particles are produced from hard processes. The experimental data for the -spectra for all the energies used in the paper belongs to the pseudorapidity range . The unified function fit to the -spectra at , and TeV is provided in the Refs. [21,47,48]. The numerical value of T, q and the other fitting parameters are calculated by fitting the measured transverse momentum spectra with the unified formalism as in Equation (17) and the best fit value of the parameters are provided in Table 1.

Table 1.
Numerical values of the fit parameters T (GeV), q, (GeV/c) and n obtained by fitting the experimental data of -spectra fitted with the unified formalism Equation (17).
In Figure 1, we have plotted the isothermal compressibility over volume calculated using the Equations (21)–(23). It is observed that there is a decline in the values of with an increase in the multiplicity. At higher charged-particle multiplicity, becomes the lowest, which suggests that the system move toward near-ideal behaviour with the increase in multiplicity. This trend is in line with the expectation as higher multiplicity class contains a larger number of particles and hence a higher pressure is required to attain a small change in volume. Similar values of for different collision systems show an indication of similar dynamics of the produced medium. It is worth mentioning here that the ideal fluid is incompressible, hence , implying that the volume cannot be changed by applying pressure. For water, the corresponding value is several order of magnitude higher than what is obtained in case of heavy-ion collision. The values for obtained in the case of heavy-ion collision using the unified formalism is in the range from to .
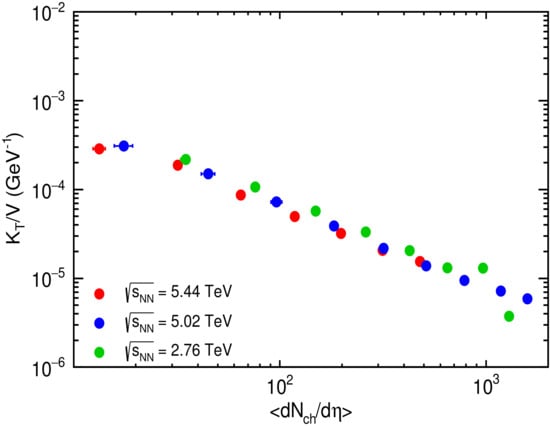
Figure 1.
(Color online) Variation of isothermal compressibility over volume with the average charged particle multiplicity for collision at = TeV, collision at = TeV and collision at = TeV using Unified formalism Equations (21)–(23).
A proper estimation of volume is required to extract the value of . Different techniques have been developed and tested on diverse datasets to extract the volume parameter [32,49,50,51,52,53,54,55]. Although the numerical values vary greatly in different models, all of them are in the order of and hence utilizing the value of volume from these models will give us the value of in the order of . This range of the value of matches well with the values obtained by other techniques in the Refs. [4,56]. The obtained value of is very low as compared to the water and other materials, indicating that the compressibility of the system created in the heavy-ion collision is very close to an ideal fluid. Proper estimation of volume is still an undergoing field of research, hence, we did not select a particular model and instead, we presented the value in terms of .
We have also attempted to study the speed of sound for different collision systems in order to explore the properties of matter. The speed of sound in a medium reveals the properties of the medium via the equation of state. In Figure 2, we have plotted the squared speed of sound with charged-particle multiplicity for three different energies estimated using the Equation (28). It is observed that the value of the squared speed of sound is very close to times the speed of light squared, and there is an increase in the value with increasing , suggesting that the system becomes more ideal at larger multiplicity. This observation complements the near-ideal behaviour already indicated from the measurement of isothermal compressibility.
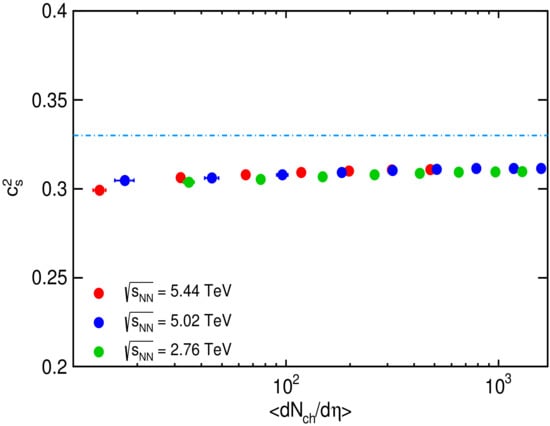
Figure 2.
(Color online) Variation of squared speed of sound as a function of for collision at = TeV, collision at = TeV and collision at = TeV using Unified formalism as Equation (28). The dotted line represents the theoretical value for ideal gas system.
4. Conclusions
With an aim towards understanding the system produced in the heavy-ion collision, we have made an attempt to study some thermodynamic response functions such as isothermal compressibility and speed of sound. Since transverse momentum spectra carries information about the system, we have analyzed spectra of charged hadrons at three different LHC energies using the unified formalism and used the extracted value of thermodynamical parameters to study the isothermal compressibility and speed of sound. The -spectra of charged hadrons produced in collision at TeV, TeV and collision at 5.44 TeV are taken with range upto 5 . We have estimated the value of and and studied their variation as a function of charged particle multiplicity. We observed that while the value of decreases with respect to increase in multiplicity, the values of approaches to 1/3.
These estimations of and using unified formalism represent that the medium tends to move toward a near-ideal behavior with an increase in charged particle multiplicity. In conclusion, we have presented the theoretical formalism to study some of the thermodynamical response functions within the unified statistical framework discussed in the Ref. [22]. The extracted values point toward the creation of a near-ideal medium in high-energy collision and the system approach the ideal behavior as we move from peripheral to the central collision.
Author Contributions
Methodology, S.J. (Shubhangi Jain), R.G.; investigation, S.J. (Shubhangi Jain); data curation, R.G. and S.J. (Satyajit Jena); writing—original draft preparation, R.G. and S.J. (Satyajit Jena); writing—review and editing, S.J. (Shubhangi Jain), R.G. and S.J. (Satyajit Jena). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used for this analysis are already published and are cited at relevant places within the text as references.
Conflicts of Interest
The authors do not have any conflict of interest.
References
- Sahu, D.; Tripathy, S.; Sahoo, R.; Dash, A.R. Multiplicity dependence of shear viscosity, isothermal compressibility and speed of sound in pp collisions at = 7 TeV. Eur. Phys. J. A 2020, 56, 187. [Google Scholar] [CrossRef]
- Basu, S.; Chatterjee, S.; Chatterjee, R.; Nayak, T.K.; Nandi, B.K. Specific Heat of Matter Formed in Relativistic Nuclear Collisions. Phys. Rev. C 2016, 94, 044901. [Google Scholar] [CrossRef]
- Khuntia, A.; Sahoo, P.; Garg, P.; Sahoo, R.; Cleymans, J. Speed of sound in hadronic matter using non-extensive Tsallis statistics. Eur. Phys. J. A 2016, 52, 292. [Google Scholar] [CrossRef]
- Sahu, D.; Tripathy, S.; Sahoo, R.; Tiwari, S.K. Possible formation of a Perfect Fluid in pp, p-Pb, Xe-Xe and Pb-Pb Collisions at the Large Hadron Collider Energies: A color string percolation approach. Eur. Phys. J. 2022, 58, 78. [Google Scholar] [CrossRef]
- Mezzasalma, S.A. An Equation for Viscosity and Isothermal Compressibility of Simple Liquids from a Closed-Form Expression for the Effective Viscosity of a Dispersed System. Phys. Chem. Liq. 2002, 100, 135–142. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; et al. Higher harmonic anisotropic flow measurements of charged particles in Pb-Pb collisions at =2.76 TeV. Phys. Rev. Lett. 2011, 107, 032301. [Google Scholar] [CrossRef]
- Luzum, M.; Romatschke, P. Conformal Relativistic Viscous Hydrodynamics: Applications to RHIC results at s(NN)**(1/2) = 200-GeV. Phys. Rev. C 2008, 78, 034915. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly Relativistic Nucleus-Nucleus Collisions: The Central Rapidity Region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Hallman, T.J.; Kharzeev, D.E.; Mitchell, T.J.; Ullrich, T.S. Quark matter 2001. In Proceedings of the 15th International Conference on Ultrarelativistic Nucleus Nucleus Collisions, QM 2001, Stony Brook, New York, NY, USA, 15–20 January 2001; Volume 698. [Google Scholar]
- Deb, S.; Sarwar, G.; Sahoo, R.; Alam, J.E. Study of QCD dynamics using small systems. Eur. Phys. J. A 2021, 57, 195. [Google Scholar] [CrossRef]
- Deb, S.; Tripathy, S.; Sarwar, G.; Sahoo, R.; Alam, J.E. Deciphering QCD dynamics in small collision systems using event shape and final state multiplicity at the Large Hadron Collider. Eur. Phys. J. A 2020, 56, 252. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Tripathy, S.; Sahoo, R.; Kakati, N. Dissipative Properties and Isothermal Compressibility of Hot and Dense Hadron Gas using Non-extensive Statistics. Eur. Phys. J. C 2018, 78, 938. [Google Scholar] [CrossRef]
- Castorina, P.; Cleymans, J.; Miller, D.E.; Satz, H. The Speed of Sound in Hadronic Matter. Eur. Phys. J. C 2010, 66, 207–213. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Magdy, H. Hadronic Equation of State and Speed of Sound in Thermal and Dense Medium. Int. J. Mod. Phys. A 2014, 29, 1450152. [Google Scholar] [CrossRef]
- Deppman, A. Properties of hadronic systems according to the nonextensive self-consistent thermodynamics. J. Phys. G 2014, 41, 055108. [Google Scholar] [CrossRef]
- Gardim, F.G.; Giacalone, G.; Luzum, M.; Ollitrault, J.Y. Thermodynamics of hot strong-interaction matter from ultrarelativistic nuclear collisions. Nat. Phys. 2020, 16, 615–619. [Google Scholar] [CrossRef]
- Schnedermann, E.; Sollfrank, J.; Heinz, U.W. Thermal phenomenology of hadrons from 200-A/GeV S+S collisions. Phys. Rev. C 1993, 48, 2462–2475. [Google Scholar] [CrossRef]
- Stodolsky, L. Temperature fluctuations in multiparticle production. Phys. Rev. Lett. 1995, 75, 1044–1045. [Google Scholar] [CrossRef]
- Sharma, N.; Cleymans, J.; Hippolyte, B.; Paradza, M. A Comparison of p-p, p-Pb, Pb-Pb Collisions in the Thermal Model: Multiplicity Dependence of Thermal Parameters. Phys. Rev. C 2019, 99, 044914. [Google Scholar] [CrossRef]
- Jena, S.; Gupta, R. A unified formalism to study transverse momentum spectra in heavy-ion collision. Phys. Lett. B 2020, 807, 135551. [Google Scholar] [CrossRef]
- Gupta, R.; Menon, A.; Jain, S.; Jena, S. The Theoretical Description of the Transverse Momentum Spectra: A Unified Model. Universe 2023, 9, 111. [Google Scholar] [CrossRef]
- Tsallis, C. Some comments on Boltzmann-Gibbs statistical mechanics. Chaos Solitons Fractals 1995, 6, 539–559. [Google Scholar] [CrossRef]
- Lemanska, M. Non-additive entropy: Reason and conclusions. arXiv 2012, arXiv:1207.2172. [Google Scholar]
- Alberico, W.M.; Lavagno, A.; Quarati, P. Nonextensive statistics, fluctuations and correlations in high-energy nuclear collisions. Eur. Phys. J. C 2000, 12, 499–506. [Google Scholar] [CrossRef]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Statist. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Bíró, G.; Barnaföldi, G.G.; Biró, T.S. Tsallis-thermometer: A QGP indicator for large and small collisional systems. J. Phys. G 2020, 47, 105002. [Google Scholar] [CrossRef]
- Parvan, A.S. Self-consistent thermodynamics for the Tsallis statistics in the grand canonical ensemble: Nonrelativistic hadron gas. Eur. Phys. J. A 2015, 51, 108. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. The Tsallis Distribution in Proton-Proton Collisions at = 0.9 TeV at the LHC. J. Phys. G 2012, 39, 025006. [Google Scholar] [CrossRef]
- Conroy, J.M.; Miller, H.G.; Plastino, A.R. Thermodynamic Consistency of the q-Deformed Fermi-Dirac Distribution in Nonextensive Thermostatics. Phys. Lett. A 2010, 374, 4581–4584. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The Role of constraints within generalized nonextensive statistics. Phys. A 1998, 261, 534. [Google Scholar] [CrossRef]
- Azmi, M.D.; Cleymans, J. The Tsallis Distribution at Large Transverse Momenta. Eur. Phys. J. C 2015, 75, 430. [Google Scholar] [CrossRef]
- Cirto, L.J.L.; Tsallis, C.; Wong, C.Y.; Wilk, G. The transverse-momenta distributions in high-energy pp collisions—A statistical-mechanical approach. arXiv 2014, arXiv:1409.3278. [Google Scholar]
- Wong, C.Y.; Wilk, G. Tsallis fits to pT spectra and multiple hard scattering in pp collisions at the LHC. Phys. Rev. D 2013, 87, 114007. [Google Scholar] [CrossRef]
- Wong, C.Y.; Wilk, G.; Cirto, L.J.L.; Tsallis, C. Possible Implication of a Single Nonextensive pT Distribution for Hadron Production in High-Energy pp Collisions. EPJ Web Conf. 2015, 90, 04002. [Google Scholar] [CrossRef]
- ALICE Collaboration; Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Agostinelli, A.; Salazar, S.A.; et al. Centrality Dependence of Charged Particle Production at Large Transverse Momentum in Pb–Pb Collisions at =2.76 TeV. Phys. Lett. B 2013, 720, 52–62. [Google Scholar] [CrossRef]
- The ALICE Collaboration; Acharya, S.; Acosta, S.; Adamová, F.T.D.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Transverse momentum spectra and nuclear modification factors of charged particles in pp, p-Pb and Pb-Pb collisions at the LHC. JHEP 2018, 11, 13. [Google Scholar] [CrossRef]
- The ALICE Collaboration; Acharya, S.; Acosta, F.T.; Adamová, D.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Transverse momentum spectra and nuclear modification factors of charged particles in Xe-Xe collisions at = 5.44 TeV. Phys. Lett. B 2019, 788, 166–179. [Google Scholar] [CrossRef]
- Pearson, K. Philosophical Transactions of the Royal Society of London A: Mathematical. Phys. Eng. Sci. 1895, 186, 343. [Google Scholar]
- Pollard, J.H. A Handbook of Numerical and Statistical Techniques: With Examples Mainly from the Life Sciences; Cambridge University Press: Cambridge, UK, 1977. [Google Scholar]
- Kardar, M. Statistical Physics of Particles; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Mrowczynski, S. Hadronic matter compressibility from event by event analysis of heavy ion collisions. Phys. Lett. B 1998, 430, 9–14. [Google Scholar] [CrossRef]
- Landau, L.; Lifshitz, E. Chapter VIII—Sound. In Fluid Mechanics, 2nd ed.; Springer: Berling, Germany, 1987; Volume 6, pp. 251–312. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Centrality dependence of π, K, p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adhya, S.P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Production of charged pions, kaons, and (anti-)protons in Pb-Pb and inelastic pp collisions at = 5.02 TeV. Phys. Rev. C 2020, 101, 044907. [Google Scholar] [CrossRef]
- Acharya, S.; Torales-Acosta, F.; Adamová, D.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.U.; et al. Centrality and pseudorapidity dependence of the charged-particle multiplicity density in Xe–Xe collisions at =5.44TeV. Phys. Lett. B 2019, 790, 35–48. [Google Scholar] [CrossRef]
- Gupta, R.; Jena, S. Model Comparison of the Transverse Momentum Spectra of Charged Hadrons Produced in PbPb Collision at =5.02 TeV. Adv. High Energy Phys. 2022, 2022, 5482034. [Google Scholar] [CrossRef]
- Gupta, R.; Katariya, A.S.; Jena, S. A unified formalism to study the pseudorapidity spectra in heavy-ion collision. Eur. Phys. J. A 2021, 57, 224. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Kalweit, A.; Redlich, K.; Stachel, J. Confronting fluctuations of conserved charges in central nuclear collisions at the LHC with predictions from Lattice QCD. Phys. Lett. B 2015, 747, 292–298. [Google Scholar] [CrossRef]
- Cleymans, J.; Worku, D. Relativistic Thermodynamics: Transverse Momentum Distributions in High-Energy Physics. Eur. Phys. J. A 2012, 48, 160. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Aggarwal, M.M.; Agnello, M.; Agostinelli, A.; Agrawal, N.; Ahammed, Z.; Ahmad, N.; Ahmed, I.; et al. Freeze-out radii extracted from three-pion cumulants in pp, p–Pb and Pb–Pb collisions at the LHC. Phys. Lett. B 2014, 739, 139–151. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Yassin, H.; Elyazeed, E.R.A. Extensive/nonextensive statistics for pT distributions of various charged particles produced in p+p and A+A collisions in a wide range of energies. arXiv 2019, arXiv:1905.12756. [Google Scholar]
- Gardim, F.G.; Giacalone, G.; Luzum, M.; Ollitrault, J.Y. Effects of initial state fluctuations on the mean transverse momentum. Nucl. Phys. A 2021, 1005, 121999. [Google Scholar] [CrossRef]
- Chatterjee, S.; Das, S.; Kumar, L.; Mishra, D.; Mohanty, B.; Sahoo, R.; Sharma, N. Freeze-Out Parameters in Heavy-Ion Collisions at AGS, SPS, RHIC, and LHC Energies. Adv. High Energy Phys. 2015, 2015, 349013. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J.; Wetterich, C. Chemical freezeout and the QCD phase transition temperature. Phys. Lett. B 2004, 596, 61–69. [Google Scholar] [CrossRef]
- Khuntia, A.; Tiwari, S.K.; Sharma, P.; Sahoo, R.; Nayak, T.K. Effect of Hagedorn States on Isothermal Compressibility of Hadronic Matter formed in Heavy-Ion Collisions: From NICA to LHC Energies. Phys. Rev. C 2019, 100, 014910. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).