Abstract
It is shown that the non-unitary Newtonian gravity (NNG) model admits a simple interpretation in terms of the Feynman path integral, in which the sum over all possible histories is replaced by a summation over pairs of paths. Correlations between different paths are allowed by a fundamental decoherence mechanism of gravitational origin and can be interpreted as a kind of communication between different branches of the wave function. The ensuing formulation could be used in turn as a motivation to introduce non-unitary gravity itself.
1. Introduction
At present, there is a growing interest in the topic of intrinsic decoherence [1] as a phenomenon which, on one hand, is analogous to the well-known environmental decoherence [2,3] in destroying phase coherence, but on the other hand, is very different because it is not the result of averaging over an environment. As such, it is intrinsic to nature and may also arise, in principle, in isolated systems. However, it is also expected to lead to an entropy growth as a consequence of the entanglement between the system and something which plays the role of an environment. Of course, this irreversible process is in sharp contrast with the deterministic unitary evolution of quantum mechanics (QM) governed by the Schrödinger equation, which means that intrinsic decoherence is involved in the so-called measurement problem in QM, as well as in the related issue of the emergence of classicality from the quantum world.
Many different proposals of modification of QM have been put forward in the last 50 years, ranging from the inclusion of nonlinear terms [4,5] or a random noise source [6,7,8,9,10] in the Schrödinger equation, to the suggestion of a possible role of gravity in the collapse of the wave function [11,12,13,14,15,16,17,18]. Some of these models include free parameters as new constants of nature, while some others have been recently falsified by accurate experiments [19]. In particular, the so-called Diosi–Penrose gravity-induced collapse model, that has no free parameters, predicts a certain degree of energy non-conservation via spontaneous emission of X-rays, a feature that has not been observed. The idea of a gravitational decoherence [20,21] in particular is attractive, since gravity is ubiquitous in nature and gravitational effects depend on the size of objects. As put forward by R. Penrose [17,18], a conflict emerges when a balanced superposition of two separate wave packets representing two different positions of a massive object is considered, signaling a possible inconsistency between the general covariance of general relativity and the quantum mechanical superposition principle. On the other hand, the discovery by Hawking that black holes radiate, leading to a highly mixed state of the radiation field after complete evaporation, appears to be a strong indication towards non-unitary time evolution of state vectors within a future quantum theory of gravitation [22,23]. This adds further evidence to the intrinsic character of gravitational decoherence as well.
More recent proposals assume as sources of decoherence fluctuations deriving from gravitational waves, gravitons, or metric fluctuations, which obey Einstein equations and can be identified with transverse traceless perturbations [24,25]. These differ from models of gravitational decoherence in which the perturbations of the metric do not satisfy linearized Einstein equations, but are described by a stochastic process [26,27]. An alternative route to decoherence proposes that it descends from time dilation in an external macroscopic gravitational field like the Earth’s and doesn’t require modifications of quantum mechanics [28,29]. In fact, it has been shown how time dilation is effective in producing a universal coupling between internal degrees of freedom and the center of mass of a composite particle, whose result is decoherence of the particle’s position, even in the absence of an external environment. Finally, it is worthy to mention gravitationally induced decoherence models based on specific quantum gravity models. Here, the starting point is the specific classical model, which is quantized, and then, within the quantum model, a master equation is derived in order to describe system’s dynamics in the presence of gravitational decoherence. See for instance the model in Ref. [30], inspired by loop quantum gravity and constructed in terms of Ashtekar variables.
On the experimental side, huge advances in technology have been carried out in the last decade in order to test the predictions of models of gravitational decoherence. Viable platforms for large-mass experiments include non-interferometric opto- and magneto-mechanical systems [31,32], and matter wave interferometers with molecules and nanoparticles [33]. Meanwhile, ground-to-space optical links, such as the entangled photon pairs of the Space QUEST mission [34] and the long-baseline quantum links proposed in the context of the DSQL mission [35], are currently pursued because of the peculiar experimental conditions with respect to the ground (see for a detailed account Ref. [36] and references therein). Finally, a novel underground experiment in operation at the Italian Gran Sasso National Laboratory [19] is very promising as well, thanks to a reduced exposition to cosmic radiation.
To address the quest for a viable model of gravitational decoherence that is based on expected general features and doesn’t rely on the presence of external gravitational fields or on specific theories of quantum gravity, a consistent proposal was put forward by De Filippo twenty years ago and then further developed [37,38,39]. At variance with other attempted non-unitary modifications of QM, De Filippo’s one; namely, non-unitary Newtonian gravity (NNG), is non-Markovian and guarantees energy conservation. It was obtained as the non-relativistic limit of a non-unitary variant of higher derivative gravity, which makes the theory classically stable while providing a mechanism to tame singularities [37]. Its non-unitary dynamics results from a unitary meta-system that is built of the physical system plus a replica of it; these two subsystems interacting with each other only via gravity. The model treats mutual and self-interactions on an equal footing, which, according to some authors, are believed to produce wave function localization and/or reduction [11,12,13,14,15,16,17]. In particular, for ordinary condensed matter densities, it exhibits a localization threshold at about proton masses, above which self-localized centers of mass wave functions exist. This means that initially pure states evolve in time into an ensemble of localized states, consistent with the expectation that, even for an isolated system, an entropy growth takes place due to the entanglement between observable and hidden degrees of freedom via gravitational interaction [40,41,42,43]. In particular, the energy pumping into the system, necessary to get localization, is only due to quantum fluctuations and the natural conversion of gravitational potential energy into kinetic energy.
Another interesting feature of De Filippo’s model is its field-theoretical formulation, obtained by a Hubbard–Stratonovich transformation of the gravitational interaction [37], which obtains the well-known nonlinear Newton–Schrödinger equation [18,44] by gravitationally coupling N exact copies of the physical system and then taking the limit [45]. It has also been shown that for any finite value of N, the same model is completely free from the usual causality violation problems that plagued the Newton–Schrödinger model [46]; this happens thanks to the intrinsic mechanism of spontaneous state reduction of the model, absent in the Newton-Schrödinger limit. Furthermore, since within NNG the density matrix plays a fundamental role, amounting to the most complete characterization of a physical system’s state, the Everett many-world interpretation appears to be the most natural conceptual framework for that theory. Here, in agreement with some other nonlinear modifications of QM [47], the possibility of constructing an Everett phone connecting different branches of the wave function has been shown, though its basic mechanism appears to be strongly inhibited. In fact, the theory gets rid of the huge number of branches continuously forming by turning the macroscopic states superposition each time into ensembles of localized states through gravitational self-interaction.
In this work, our aim is to give a novel interpretation of the above-mentioned Everett phone by introducing a path integral formulation of De Filippo’s model [48]. As a peculiar feature, we find that the sum over all possible histories gets replaced by a summation over pairs of paths, talking together via correlations, which are induced by a fundamental decoherence mechanism of gravitational origin. Such correlations can be interpreted as a kind of communication between different branches of the wave function, in agreement with our previous findings [46].
The plan of the present work is as follows. In Section 2, we give a brief survey of the relevant features of De Filippo’s model, while Section 3 contains its path integral formulation for a simple system made of a homogeneous spherical particle with radius R. As a concrete example, the case of microscopic-to-mesoscopic systems is explicitly worked out, showing that in such a range the contribution of non-unitary gravity amounts to a correction with respect to ordinary QM. In Section 4, an evaluation of this correction is carried out in the framework of a COW-like experiment [49]. Finally some perspectives of this work are outlined.
2. Nonunitary Newtonian Gravity Model: A Brief Survey
In this section, a brief introduction to the NNG model and its relevant features is given by resorting to a second quantization formalism that allows for a general formulation [37,38,39].
The general idea underlying the NNG model is to start from a gravity-free system and to make it to interact with a copy of itself (which plays the role of a bath) via gravitational interaction. Then, upon tracing out unobservable (i.e., bath) degrees of freedom, a non-unitary dynamics is obtained, which includes both the usual aspects of classical gravitational interactions and a kind of fundamental decoherence, which is expected to play a role in the emergence of classicality for macroscopic bodies. In this way, the evolution of an initial pure state of the system into a mixture of localized states takes place, accompanied by a fundamental entropy growth [40,41,42,43].
Here we present the general formulation in which a system is put in interaction with hidden copies of itself. To this end, let denote the second quantized non-relativistic Hamiltonian of a finite number of particle species, such as electrons, nuclei, ions, atoms and/or molecules, according to the energy scale. For notational simplicity, denotes the whole set of creation-annihilation operators, i.e., one couple per particle species and spin component. This Hamiltonian includes the usual electromagnetic interaction accounted for in atomic and molecular physics. Gravitational interactions as well as self-interactions are incorporated by introducing a color quantum number , in such a way that each couple is replaced by N couples of creation-annihilation operators.
The resulting overall Hamiltonian, including gravitational interactions and acting on the tensor product of the Fock space of the operators, is given by
where here and henceforth Greek indices denote color indices, and denotes the mass of the i-th particle species, while G is the gravitational constant. While the operators obey the same statistics as the original operators , we take advantage of the arbitrariness pertaining to distinct operators and, for simplicity, we choose them commuting with one another: .
The meta-particle state space S is identified with the subspace of , including the meta-state obtained from the vacuum , applying operators built in terms of the product and symmetrical with respect to arbitrary permutations of the color indices, which, as a consequence for each particle species, have the same number of meta-particles of each color. This is a consistent definition, since the time evolution generated by the overall Hamiltonian is a group of (unitary) endomorphism of S. If we prepare a pure n-particle state, represented in the original setting, excluding gravitational interactions, by
its representative in S is given by the meta-state
As for the physical algebra, it is identified with the operator algebra of, for instance, the meta-world. In view of this, expectation values can be evaluated by previously tracing out the unobservable operators; namely, with , and then taking the average of an operator belonging to the physical algebra. Clearly, this should not be viewed as an ad hoc restriction of the observable algebra. Indeed, once the constraint restricting to S is taken into account, in order to get an effective gravitational interaction between particles of one and the same color, the resulting state space does not contain states that can distinguish between operators of different colors. Restricting the algebra to that of operators is the only way to accommodate a faithful representation of the physical algebra within the meta-state space. Furthermore, the resulting constrained theory is, by construction, a fully consistent QM theory.
The general formulation of NNG introduced above allows one to recover the Newton-Schrödinger model in the limiting case [44] as a result of a well-defined procedure [39,45]. This limit has been shown to completely suppress quantum fluctuations while preserving mean field features. On the other hand, a simple thermodynamic argument suggests taking [43], thus giving a free-parameter model.
3. Path Integral Formulation of NNG Model in a Simple Case
Let us consider, within the NNG model, a system composed (for simplicity) by a single body of mass m and study its dynamics by resorting to a path integral formulation [48]. We show that the evolution of the system cannot be expressed by a summation over a single path history, but instead needs to be written as a summation over pairs of histories.
The (meta-)amplitude for the particle to go from a position at time to a position at time , while its hidden counterpart is going from to at the same time, is given by:
Here, is the action for the particle, which includes the kinetic energy and an external potential added, in the general case, to the halved Newtonian gravitational potential. Instead, contains the non-unitary gravitational interaction and takes the form
where is the halved gravitational potential between the body and its hidden counterpart, which for a homogeneous spherical particle of mass m and radius R is [41]:
and denotes the Heaviside function.
Starting from Equation (2), the density matrix of the particle can be calculated integrating over the space coordinates :
where
It follows immediately that, because of the coupling term , the expression of , containing all the information that can be experimentally accessible, cannot be reduced to a path integral over a single history. Indeed, inter-path correlations between different branches of the propagator arise, so that the whole transition amplitude is obtained by summing both over the different paths and over correlations between them, or in other words, by summing over pairs of paths. Here, such correlations are induced by a fundamental decoherence mechanism of gravitational origin, which is built in the NNG model, and can be interpreted as a kind of communication between different branches of the wave function.1 These conclusions are consistent with previous findings, pointing out the appearance of communications among Everett branches of the wave function as a consequence of the introduction of nonlinearities in some modified theories of quantum mechanics [46,47]. Furthermore, our results are in agreement with existing treatments of intrinsic decoherence mechanisms [1,50]. Generalization to the case with n particles is straightforward.
It is important to note that even if it has been shown that the non-unitary Newtonian gravity model has neat observational signatures (able, in principle, to distinguish it from the other proposed models), its observational implications are far from being obvious [51]. In fact, they concern mainly measurements of coherences in the basis of positions, rather than some probability of occurrence. As an example, let us write down explicitly the probability of finding the particle at point at time :
For microscopic systems, gravity is irrelevant, and the term can be neglected. Then the meta-amplitude factorizes, and due to the normalization
the probability above obviously reduces to a single history expression, according to ordinary QM.
Instead, for microscopic-to-mesoscopic systems, typically is comparable to or greater than ℏ, but we have still . Then, it is possible to calculate the contribution of non-unitary gravity as a small correction with respect to ordinary QM. To be specific, we can write the probability above as
the last term in square parenthesis representing the expected correction.
4. Analysis of a COW-like Experiment
In this section, we deal with the explicit calculation of the correction term provided in Equation (4) in a specific context. The aim is to estimate the contribution of NNG to the quantum dynamics.
To this end, let us consider an experiment similar to the famous 1975 experiment by Colella, Overhauser and Werner [49] using a neutron interferometer to detect the Earth’s gravitational field effect, as depicted in Figure 1.
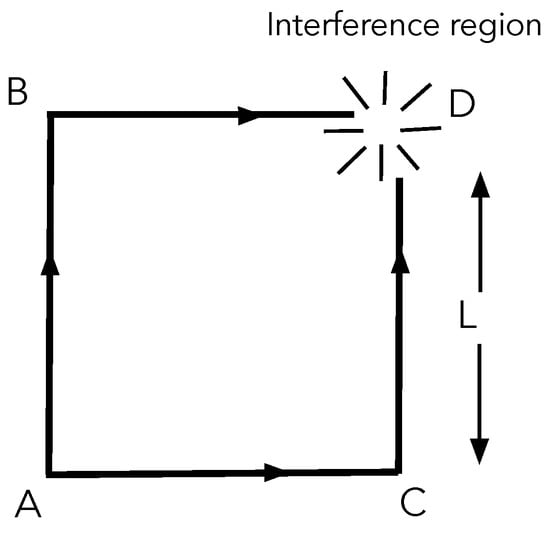
Figure 1.
Scheme of the matter interferometry apparatus. A superposition of two wave packets is sent in point A towards B and C, respectively, where they are reflected, and then recombine in D.
A nearly mono-energetic beam of particles with velocity v, that may be thermal neutrons or almost-spherical macromolecules, such as fullerene , is split into two parts at a point A. The resulting beams travel towards the mirrors B and C where they are reflected and then are brought together in D at time , as shown in Figure 1. Because the size of the wave packets can be assumed to be much smaller than the macroscopic dimension of the square loop (that in a neutron interferometer is of the order of 10 cm), it is possible to consider the trajectories as classic. Let us make the assumption that the two alternative paths ABD and ACD are subject to different external potentials (for example, the Earth’s gravitational potential, or an electric potential). Under these conditions, the term in (4), corresponding to ordinary QM amplitudes’ summation, is given by
where is the overall phase difference in D induced by the paths’ different potentials. Instead the correction term , corresponding to the pairs of histories’ summation, is given by developing explicitly the double path summation of Equation (4) on the interferometer arms as
where
Since the expression in Equation (5) is purely imaginary, no contribution at all comes from the correction term! This happens in spite of the asymmetry between the two different paths brought by the external potential.
Then, the lesson to be drawn from the above analysis is that it is almost impossible to distinguish between ordinary QM and its pairs of histories modification due to NNG, as far as micro/mesoscopic systems and not-very-tailored experiments are considered. An example of a possible experimental test of NNG, involving mesoscopic masses and currently still beyond our technological reach, can be found in Ref. [51].
5. Concluding Remarks
In this work, we give a simple path integral formulation of NNG model in which the sum over all possible histories gets replaced by a sum over pairs of paths, thanks to the occurrence of inter-path correlations induced by a fundamental decoherence mechanism built in the model.
Our results add further motivation to introduce non-unitary Newtonian gravity itself. In fact, in the search for a viable low-energy theory incorporating in a consistent way (quantum) self-gravitational effects, several indications [9,10,14,15,16,17,18,52] point to fundamental decoherence as a general characteristic of the theory. Then, according to the analysis performed in Ref. [1], a natural way to guess the form of such a modification of QM is to write the Feynman propagator by a sum over pairs of histories rather than over single histories. This is inspired by the theory of open quantum systems (i.e., of environmental decoherence), in which the central quantity to compute is the Feynman–Vernon influence functional [48], amounting to a double path integral. In our case, the fundamental view of an interaction between the different branches of the particle itself is considered. On the other hand, the interaction between Everett branches has to be taken into account when dealing with the measurement problem, since a complete independence of the Everett worlds cannot account for amechanism of objective reduction of the quantum state by means of a (macroscopic) measuring apparatus (see Ref. [46] for a more detailed discussion on this point).
The ensuing picture of a soft version of the Everett many-world theory avoids the continuous macroscopic splitting of ourselves, while leaving room for a real quantum parallelism in the mesoscopic domain.
It is worth stressing that other decoherence mechanisms of gravitational origin, such as the one due to time dilation in the Earth’s gravitational field, are also certainly present and contribute to the general environmental decoherence. Nevertheless, the present approach is meant to include in the picture self-gravity produced by the quantum matter itself.
A further remark is in order concerning the possible experimental detection of fundamental decoherence signatures within the NNG model. As shown by our analysis of a COW-like experiment, the choice of the system, as well as the design of the apparatus, are very challenging. Nevertheless, a successful experimental protocol could also provide the means to discriminate intrinsic decoherence against ordinary environmental decoherence. Huge technological efforts in this direction, aiming to push further the limits of experimental accessibility towards meso- to macroscopic domain, are currently under way.
Author Contributions
Conceptualization, all authors; Data curation, all authors; Formal analysis, all authors; Investigation, all authors; Methodology, all authors; Project administration, all authors; Supervision, all authors; Writing: original draft, all authors; Writing: review and editing, all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the anonymous referees for critical comments which allowed them to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | In a different view, instead of a communication between Everett branches, the whole mechanism can be interpreted, in general, in terms of interactions between the “environments" formed by the bodies’ copies and the bodies themselves. |
References
- Stamp, P.C.E. Environmental decoherence versus intrinsic decoherence. Phil. Trans. R. Soc. A 2012, 370, 4429–4453. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–785. [Google Scholar] [CrossRef]
- Joos, E.; Zeh, D.H.; Kiefer, C.; Giulini, D.; Kupsch, K.; Stamatescu, I.O. Decoherence and the Appearance of a Classical World in Quantum Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Weinberg, S. Precision Tests of Quantum Mechanics. Phys. Rev. Lett. 1989, 62, 485–488. [Google Scholar] [CrossRef]
- Weinberg, S. Testing quantum mechanics. Ann. Phys. 1989, 194, 336–386. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar] [CrossRef]
- Pearle, P. Ways to describe dynamical state-vector reduction. Phys. Rev. A 1993, 48, 913–923. [Google Scholar] [CrossRef]
- Bassi, A.; Ghirardi, G.C. Dynamical reduction models. Phys. Rep. 2003, 379, 257–426. [Google Scholar] [CrossRef]
- Pearle, P. Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 1989, 39, 2277–2289. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Pearle, P.; Rimini, A. Markov processes in Hilbert space and continuous spontaneous localization of systems of identical particles. Phys. Rev. A 1990, 42, 78–89. [Google Scholar] [CrossRef]
- Károlyházy, F. Gravitation and quantum mechanics of macroscopic objects. Il Nuovo Cimento A 1966, 42, 390–402. [Google Scholar] [CrossRef]
- Frenkel, A. Spontaneous localizations of the wave function and classical behavior. Found. Phys. 1990, 20, 159–188. [Google Scholar] [CrossRef]
- Frenkel, A. A Tentative Expression of the Károlyházy Uncertainty of the Space-Time Structure Through Vacuum Spreads in Quantum Gravity. Found. Phys. 2002, 32, 751–771. [Google Scholar] [CrossRef]
- Diosi, L. Gravitation and quantum mechanical localization of macroobjects. Phys. Lett. A 1984, 105, 199–202. [Google Scholar] [CrossRef]
- Diosi, L. Models for universal reduction of macroscopic quantum fluctuations. Phys. Rev. A 1989, 40, 1165–1174. [Google Scholar] [CrossRef]
- Diosi, L. Notes on certain Newton gravity mechanisms of wavefunction localization and decoherence. J. Phys. A Math. Gen. 2007, 40, 2989–2995. [Google Scholar] [CrossRef]
- Penrose, R. Gravity and state-vector reduction. In Quantum Concepts in Space and Time; Penrose, R., Isham, C.J., Eds.; Clarendon Press: Oxford, UK, 1986; pp. 129–146. [Google Scholar]
- Penrose, R. On gravity’s role in quantum state reduction. Gen. Rel. Grav. 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Napolitano, F.; Addazi, A.; Bassi, A.; Bazzi, M.; Bragadireanu, M.; Cargnelli, M.; Clozza, A.; De Paolis, L.; Del Grande, R.; Derakhshani, M.; et al. Underground Tests of Quantum Mechanics by the VIP Collaboration at Gran Sasso. Symmetry 2023, 15, 480. [Google Scholar] [CrossRef]
- Bassi, A.; Großardt, A.; Ulbricht, H. Gravitational decoherence. Class. Quant. Grav. 2017, 34, 193002. [Google Scholar] [CrossRef]
- Anastopoulos, C.; Hu, B.L. Gravitational Decoherence: A Thematic Overview. AVS Quantum Sci. 2022, 4, 015602. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Comm. Math. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Anastopoulos, C.; Hu, B.L. A Master Equation for Gravitational Decoherence: Probing the Textures of Spacetime. Class. Quant. Grav. 2013, 30, 165007. [Google Scholar] [CrossRef]
- Blencowe, M. Effective Field Theory Approach to Gravitationally Induced Decoherence. Phys. Rev. Lett. 2013, 111, 021302. [Google Scholar] [CrossRef] [PubMed]
- Kok, P.; Yurtsever, U. Gravitational Decoherence. Phys. Rev. D 2003, 68, 085006. [Google Scholar] [CrossRef]
- Asprea, L.; Gasbarri, G.; Ulbricht, H.; Bassi, A. On the decoherence effect of a stochastic gravitational perturbation on scalar matter and the possibility of its interferometric detection. Phys. Rev. Lett. 2021, 126, 200403. [Google Scholar] [CrossRef] [PubMed]
- Pikowski, I.; Zych, M.; Costa, F.; Brukner, C. Universal decoherence due to gravitational time dilation. Nat. Phys. 2015, 11, 668–672. [Google Scholar] [CrossRef]
- Pikowski, I.; Zych, M.; Costa, F.; Brukner, C. Time dilation in quantum systems and decoherence. New J. Phys. 2017, 19, 025011. [Google Scholar] [CrossRef]
- Fahn, M.J.; Giesel, K.; Kobler, M. A gravitationally induced decoherence model using Ashtekar variables. arXiv 2022, arXiv:2206.06397. [Google Scholar]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Ulbricht, H. Testing Fundamental Physics by Using Levitated Mechanical Systems. In Molecular Beams in Physics and Chemistry; Friedrich, B., Schmidt-Bocking, H., Eds.; Springer: Cham, Switzerland, 2021; pp. 303–332. [Google Scholar]
- Fein, Y.Y.; Geyer, P.; Zwick, P.; Kialka, F.; Pedalino, S.; Mayor, M.; Gerlich, S.; Arndt, M. Quantum superposition of molecules beyond 25 kDa. Nat. Phys. 2019, 15, 1242–1245. [Google Scholar] [CrossRef]
- Joshi, S.K.; Pienaar, J.; Ralph, T.C.; Cacciapuoti, L.; McCutcheon, W.; Rarity, J.; Giggenbach, D.; Lim, J.G.; Makarov, V.; Fuentes, I.; et al. Space quest mission proposal: Experimentally testing decoherence due to gravity. New J. Phys. 2018, 20, 063016. [Google Scholar] [CrossRef]
- Mohageg, M.; Mazzarella, L.; Anastopoulos, C.; Gallicchio, J.; Hu, B.-L.; Jennewein, T.; Johnson, S.; Lin, S.-Y.; Ling, A.; Marquardt, C.; et al. The Deep Space Quantum Link: Prospective fundamental physics experiments using long-baseline quantum optics. EPJ Quantum Technol. 2022, 9, 25. [Google Scholar] [CrossRef] [PubMed]
- Bassi, A.; Cacciapuoti, L.; Capozziello, S.; Dell’Agnello, S.; Diamanti, E.; Giulini, D.; Iess, L.; Jetzer, P.; Joshi, S.K.; Landragin, A.; et al. A way forward for fundamental physics in space. npj Microgravity 2022, 8, 49. [Google Scholar] [CrossRef] [PubMed]
- De Filippo, S.; Maimone, F. Nonunitary higher derivative gravity classically equivalent to Einstein gravity and its Newtonian limit. Phys. Rev. D 2002, 66, 044018. [Google Scholar] [CrossRef]
- De Filippo, S.; Maimone, F. Nonunitary Classically Stable HD Gravity. AIP Conf. Proc. 2002, 643, 373–378. [Google Scholar]
- De Filippo, S.; Naddeo, A. Microscopic foundation of thermodynamics, transition to classicality and regularization of gravitational collapse singularities within non-unitary fourth-derivative gravity and its Newtonian limit. Eur. Phys. J. Plus 2022, 137, 467. [Google Scholar] [CrossRef]
- De Filippo, S.; Maimone, F. Entropic localization in non-unitary Newtonian gravity. Entropy 2004, 6, 153–157. [Google Scholar] [CrossRef]
- De Filippo, S.; Maimone, F.; Robustelli, A.L. Numerical simulation of non-unitary gravity-induced localization. Physica A 2003, 330, 459–468. [Google Scholar] [CrossRef]
- Scelza, G.; Maimone, F.; Naddeo, A. A two-particle simulation of nonunitary Newtonian gravity. J. Phys. Comm. 2018, 2, 015014. [Google Scholar] [CrossRef]
- De Filippo, S.; Maimone, F.; Naddeo, A.; Scelza, G. Microscopic foundation of the second law of thermodynamics within nonunitary Newtonian gravity. Int. J. Quant. Inf. 2019, 17, 1941006. [Google Scholar] [CrossRef]
- Bahrami, M.; Großardt, A.; Donadi, S.; Bassi, A. The Schrödinger-Newton equation and its foundations. New J. Phys. 2014, 16, 115007. [Google Scholar] [CrossRef]
- De Filippo, S. The Schrödinger-Newton model as N→∞ limit of a N color model. arXiv 2001, arXiv:gr-qc/0106057. [Google Scholar]
- Maimone, F.; Scelza, G.; Naddeo, A. A natural cure for causality violations in Newton–Schrödinger equation. Phys. Scr. 2019, 94, 075001. [Google Scholar] [CrossRef]
- Polchinski, J. Weinberg’s nonlinear quantum mechanics and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 1991, 66, 397–400. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Colella, R.; Overhauser, A.W.; Werner, S.A. Observation of Gravitationally Induced Quantum Interference. Phys. Rev. Lett. 1975, 34, 1472–1474. [Google Scholar] [CrossRef]
- Stamp, P.C.E. Rationale for a correlated worldline theory of quantum gravity. New J. Phys. 2015, 17, 065017. [Google Scholar] [CrossRef]
- Maimone, F.; Scelza, G.; Naddeo, A.; Pelino, V. Quantum superpositions of a mirror for experimental tests for nonunitary Newtonian gravity. Phys. Rev. A 2011, 83, 062124. [Google Scholar] [CrossRef]
- Milburn, G.J. Lorentz invariant intrinsic decoherence. New J. Phys. 2006, 8, 96. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).