Inertial Frame Dragging and Relative Rotation of ZAMOs in Axistationary Asymptotically Flat Spacetimes

Abstract

In axistationary, asymptotically flat spacetimes, zero angular momentum observers (ZAMOs) define an absolute standard of non-rotation locally, as can be verified by the absence of any Sagnac effect for these observers. Nevertheless, we argue that on a global scale the only physically meaningful concept is that of relative rotation. The argument is substantiated by solving Einstein’s equations for an approximate thin shell model, where we maintain a degree of freedom, by relaxing the natural assumption of vanishing rotation at asymptotic infinity, at the outset of the analysis. The solution reveals that Einstein’s equations only determine differences in the rotation rate of ZAMOs, thereby establishing the concept of relative rotation globally. The interpretation of rotation as relative in a global context is inherently linked to the freedom to transform between coordinate systems rotating relative to each other, implying that an arbitrary ZAMO located at any radius may claim to be the one that is non-rotating on a global scale, and that the notion of an asymptotic Lorentz frame relative to which one may measure absolute rotation is devoid of any meaning. The concept of rotation in Kerr spacetime is then briefly discussed in the context of this interpretation.

1. Introduction

The dragging of inertial frames, often called the Lense–Thirring effect, is now a well-established prediction of Einstein’s general theory of relativity, whereby rotating matter, due to its angular momentum, drags test particles or observers with zero angular momentum (ZAMOs) [1] in a co-rotating direction, and causes the spin axes of gyroscopes to precess. The effect of frame dragging of orbits was first predicted by H. Thirring [2] (1917) and by J. Lense and H. Thirring [3] (1918), while the closely related effect of (Schiff) frame dragging of gyroscope axes around the Earth was calculated by L. I. Schiff [4] in 1960, and much more recently confirmed experimentally by Gravity Probe B [5].

With the continuing advancement of experimental precision and sensitivity, the effects of frame dragging may constitute increasingly important aspects of experimental tests of general relativity, and of other, alternative theories of gravity in a wide range of gravitating systems. Indeed, the feasibility of detecting frame dragging and other gravitomagnetic effects in relation to systems such as, e.g., the planets in our solar system, the sun, supermassive black holes and even on the laboratory scale, has been investigated in several fairly recent reports [6,7,8,9,10,11,12,13,14]. Moreover, a test for the Lense–Thirring effect was recently conducted even in the strong-field regime of double pulsars [15]. For an historical account of the Lense–Thirring effect, see, e.g., [16]. For frequent misconceptions related to gravitomagnetic effects, see [17].

The seminal predictions by Thirring, Lense and Schiff were, however, based on approximations of slowly rotating and weak gravitational sources of matter. D.R. Brill and J.M. Cohen [18] later considered an idealized model of a slowly rotating, infinitely thin shell of matter, and obtained a strong-field solution to the dragging rate of inertial frames, by treating the geometry due to the rotating shell as a first order perturbation in the shell’s angular velocity ${\omega }_{\mathrm{S}}$ of the static Schwarzschild geometry. When evaluated to first order in ${\omega }_{\mathrm{S}}$, the thin shell was spherically symmetric, and spacetime in the interior of the shell was that of the flat Minkowski spacetime. Thus, Brill and Cohen found that the angular dragging velocity $\mathsf{\Omega }$ of the inertial frames in the exterior of the shell steadily increased as one approached the shell radius, until it reached a maximal value equal to a constant angular dragging velocity in the interior of the shell. In particular, the constant angular dragging velocity in the interior of the shell approached the angular velocity of the shell itself, as the shell mass increased and the Schwarzschild radius approached the shell radius. Hence, they concluded that, within this limit, the inertial properties of space in the interior of the shell did not depend on the inertial frames infinitely far away from the shell, but were completely determined by the shell itself. This effect is often called perfect or exact dragging of inertial frames. If one considers, as Brill and Cohen did, the shell of matter as an idealized model of the distant matter in our universe, then one may establish a connection between the notion of perfect inertial dragging and the origin of inertia and Mach’s principle. Expressed in Brill’s and Cohen’s own words: “In this sense our result explains why the “fixed stars” are indeed fixed in our inertial frame, and in this sense the result is consistent with Mach’s principle”.

Mach’s principle—essentially the idea that notions of acceleration and rotation relative to an empirically unverifiable absolute space or element are meaningless, and that these quantities can be meaningfully defined only with respect to the average motion of the total matter of the universe—and its connection with frame dragging has been discussed in great detail by several authors (see, e.g., [1,19,20,21,22,23,24,25,26,27] and references therein. For a somewhat different viewpoint on incorporating Mach’s principle in general relativity, see also [28]).

In a homogeneous and isotropic spacetime governed by general relativity, there is perfect inertial dragging relative to the cosmic matter [27]. More generally, using cosmological perturbation theory, C. Schmid [23,24] convincingly demonstrated perfect dragging and the validity of Mach’s principle within cosmological general relativity.

However, even if Mach’s principle is demonstrably valid in a general-relativistic cosmological context, many important solutions to Einstein’s equations evidently do not share this property. In particular, this is true for the asymptotically empty and flat solutions, such as the Schwarzschild and Kerr solutions or Brill’s and Cohen’s approximate shell model, which all approach flat Minkowski spacetime in regions far away from the localized mass distribution. These solutions are completely devoid of any cosmic matter at great distances from the localized mass. In the far-away regions, the physical mechanism of frame dragging induced by the total matter present in these spacetimes is certainly far too weak to account for the perfect dragging required for the inertial frames to be fully determined by the motion of the present matter. Invoking fictitious cosmic matter not included in Einstein’s equations as external causes outside of the theory, as an explanation for the origin of inertia, would render general relativity as a gravitational theory of spacetime and matter incomplete. (This should not, however, be confused with the seemingly remarkable fact that the general-relativistic predictions of frame dragging in asymptotically flat solutions do match the experimental measurements made relative to the fixed stars, which could be explained by somehow merging the metric of an asymptotically flat solution with the metric determined by the cosmic matter far away).

Asymptotic Minkowski spacetimes thus pose a challenge with regard to the interpretation of the origin of inertia in general relativity. This rather intricate difficulty was already recognized by Einstein as early as 1917 [29], stating “From what has now been said it will be seen that I have not succeeded in formulating boundary conditions for spatial infinity. Nevertheless, there is still a possible way out, without resigning. For if it were possible to regard the universe as a continuum which is finite (closed) with respect to its spatial dimensions, we should have no need at all of any such boundary conditions.” The argument of incorporating Mach’s principle into general relativity through imposing restrictions on the topology of spacetime seems to have been maintained by Einstein also in his later expositions of general relativity [30], and was expanded on in [20], Chapter 5, and in [21].

It is, nevertheless, quite clear that somehow the local inertial frames are partially determined through the imposed boundary conditions at infinity in asymptotically flat spacetimes; therefore, it might be natural at first to assume that this influence of the boundary conditions can be traced directly to the unique properties of the globally empty and nondynamical Minkowski spacetime, for which there is a well-defined absolute state of non-rotation. One might further infer that this nondynamical property, unaffected by the matter content of spacetime, rather seamlessly will be transferred to the asymptotic Minkowski spacetimes, as boundary conditions “at infinity”. In other words, one might draw the conclusion that ZAMOs located “at infinity” and “at rest” in asymptotic Minkowski spacetimes correspondingly define an absolute standard of non-rotation, even globally, relative to which the orbital angular velocity of all other ZAMOs in the spacetime is measured.

However, we note here that even if a spacetime asymptotically approaches Minkowski spacetime, nowhere is it exactly flat and, in a global analysis of rotational motion, this renders the above line of reasoning questionable. Indeed, in contrast to the conclusion drawn above, our analysis presented below indicates that only differences in angular velocities between ZAMOs have physical significance. This implies that we are completely free to choose any convenient numerical reference value for the angular velocity of a ZAMO at an arbitrarily chosen radius. Only angular velocities relative to this arbitrary reference value are physically meaningful. As a consequence, the absolute numerical value of the angular velocity of ZAMOs located at infinity is irrelevant, and the notion of an absolutely non-rotating asymptotic Lorentz frame is devoid of any meaning.

Undoubtedly, in most circumstances the most practical choice for the reference value in asymptotically flat spacetimes will be that of vanishing rotation as one approaches infinity, but fundamentally this only means that rotation of ZAMOs is measured relative to a conveniently chosen zero point infinitely far away (as will be clarified below). Similarly, the importance of accounting for relative rotation implicitly appears in connection with the first law of thermodynamics applied to Kerr–anti-de Sitter spacetimes [31,32]. In Boyer–Lindquist-type coordinates for these spacetimes, ZAMOs rotate with an angular velocity equal to the angular velocity of the black hole at the horizon, but they also turn out to rotate with a non-zero angular velocity at asymptotic infinity, in contrast to the asymptotically flat case. In order for the first law of black hole thermodynamics to be satisfied in this case, one must use the angular velocity of the black hole measured relative to a frame that is “non-rotating” at infinity, i.e., it is the relative rotation between infinity and the black hole that enters the first law. Leaving quantum effects aside, however, the concepts of relative and absolute rotation can be discussed within general relativity independently of the laws of black hole thermodynamics, which will be the topic of interest in this work.

2. Inertial Frame Dragging in Brill’s and Cohen’s Slowly Rotating Shell Model

Our purpose now is to derive an expression for the angular velocity of ZAMOs in Brill’s and Cohen’s rotating shell model [18], but where our choice of reference point for the angular velocity is completely arbitrary and not necessarily equal to the asymptotic boundary condition chosen at the outset in Brill’s and Cohen’s original work.

In their investigation of inertial frame dragging, Brill and Cohen considered an infinitely thin shell rotating sufficiently slowly that, to first order in the shell’s angular velocity ${\omega }_s$, the shell might be considered spherically symmetric in shape [33]. The resulting spacetime might then be treated as a small perturbation of the spherically symmetric Schwarzschild spacetime. In isotropic coordinates, the line element for the spacetime outside and inside the shell could then be written as

$$d{s}^2=V^{2}d{t}^2-{\psi }^4\left(d{r}^2+r^2\left(d{\vartheta }^2+{sin}^2\vartheta {\left(d\varphi -\mathsf{\Omega }\left(r\right)dt\right)}^2\right)\right),$$

(1)

where

$$V\left(r\right)=\left\{\begin{array}{c}\left(r-r_S\right)/\left(r+r_S\right)\mathrm{for}r>R\\ V_0\mathrm{for}r<R\end{array},\right.$$

(2)

and

$$\psi \left(r\right)=\left\{\begin{array}{c}1+r_S/r\mathrm{for}r>R\\ {\psi }_0\mathrm{for}r<R\end{array}\right..$$

(3)

Here, $\mathsf{\Omega }\left(r\right)$ is the angular velocity of ZAMOs, R denotes the radius of the shell, $r_S$ denotes the shell’s Schwarzschild radius, and $V_0\equiv \left(R-r_S\right)/\left(R+r_S\right)$ and ${\psi }_0\equiv 1+r_S/R$ are constants that make the components of the metric tensor continuous across the shell. Clearly, spacetime in the interior of the shell is then manifestly flat Minkowski spacetime, expressed in conveniently scaled coordinates.

If, as Brill and Cohen did in their original work, we now impose the asymptotic boundary condition ${\displaystyle \underset{r\to \infty }{lim}\mathsf{\Omega }\left(r\right)=0}$ at the outset, then the line element above approaches that of Minkowski spacetime in standard “non-rotating” spherical coordinates. However, in so doing, one might, in the final result, end up with the wrong impression that the inertial frames at infinity somehow, without any choice of freedom, single out a global standard of non-rotation. For this reason, we shall not impose any boundary conditions on $\mathsf{\Omega }\left(r\right)$ at this stage in the derivation, but instead keep this degree of freedom temporarily until the boundary condition is naturally to be determined at a later stage.

We may now use Einstein’s equations, in combination with the line element given above, in order to find the explicit expression for $\mathsf{\Omega }\left(r\right)$. A detailed step-by-step rederivation of Brill’s and Cohen’s original result, with the restriction ${\displaystyle \underset{r\to \infty }{lim}\mathsf{\Omega }\left(r\right)=0}$ at the outset, has already been given in [27]. The derivation for the more general case, with no such restriction on $\mathsf{\Omega }\left(r\right)$ at the outset, is essentially identical to the one presented in [27]. Hence, we shall not repeat the derivation in full detail here, but only give an outline of that derivation, while we keep track of where the modifications to Einstein’s equations, ${\displaystyle G_{\alpha \beta }=8\pi G{T}_{\alpha \beta }}$, occur, once underway.

For the present purpose, Einstein’s equations are most easily solved by using Cartan formalism [34]. In this context, a useful set of orthonormal basis one-forms are given by

$${\omega }^0=Vdt,{\omega }^1={\psi }^{2}dr,{\omega }^2=r{\psi }^{2}d\vartheta ,{\omega }^3=r{\psi }^{2}sin\vartheta \left(d\varphi -\mathsf{\Omega }dt\right).$$

(4)

From Cartan’s structural equations, we then find that, for the non-zero components of the Einstein tensor,

$$G^{00}=\frac{4r_S}{r^2{\psi }^5}\delta \left(r-R\right),$$

(5)

$$G^{22}=G^{33}=\frac{r_S}{2r\psi V}{G}^{00},$$

(6)

$$G^{03}=-\frac{sin\vartheta }{2r^3{\psi }^8}{\left(\frac{r^4{\psi }^6{\mathsf{\Omega }}^{\prime }}{V}\right)}^{\prime }.$$

(7)

Here, $\delta \left(r\right)$ is the Dirac delta function, and V and $\psi$ are given in Equations (2) and (3), respectively. For the diagonal components of the stress–energy tensor $T^{\mu \nu }$, Einstein’s field equations now immediately yield

$$\rho \equiv T^{00}=\frac{G^{00}}{8\pi }=\frac{r_S{r}^3}{2\pi {\left(r+r_S\right)}^5}\delta \left(r-R\right),$$

(8)

$$T^{33}=T^{22}=\frac{G^{22}}{8\pi }=\frac{r_S}{2\left(r-r_S\right)}\rho .$$

(9)

Here, $\rho$ denotes the mass density of the shell in the rest frame of an element of the shell.

To proceed, we next consider the Einstein equation containing the nondiagonal components, ${\displaystyle G^{03}=8\pi G{T}^{03}}$. Because spacetime is empty both in the interior ($r<R$) and exterior ($r>R$) of the shell, we have $T^{03}=0$, and this equation reduces to

$${\left(\frac{r^4{\psi }^6{\mathsf{\Omega }}^{\prime }}{V}\right)}^{\prime }=0r\ne R.$$

(10)

Thus, we find

$${\mathsf{\Omega }}_{\pm }^{\prime }=\frac{K_{\pm }V}{r^4{\psi }^6}.$$

(11)

In this expression, $K_{-}$ and $K_{+}$ are constants of integration in the two regions $r<R$ and $r>R$, respectively. For $r<R$, we have $\psi ={\psi }_0$ and $V=V_0$. Hence, we obtain

$${\mathsf{\Omega }}_{-}=-\frac{K_{-}{V}_0}{3r^3{\psi }_0^6}+{\mathsf{\Omega }}_B,$$

(12)

where ${\mathsf{\Omega }}_B$ is another constant of integration yet to be determined. In the shell’s interior, spacetime is assumed to be flat. We therefore require a regular solution as $r\to 0$, from which it follows that $K_{-}=0$ and ${\mathsf{\Omega }}_{-}={\mathsf{\Omega }}_B$. For $r>R$, we may integrate Equation (11), to give

$${\mathsf{\Omega }}_{+}\left(r\right)-{\mathsf{\Omega }}_{+}\left(r_Q\right)=K_{+}{\int }_{r_Q}^r\frac{r-r_S}{r^5\psi {\left(r\right)}^7}dr=-\frac{K_{+}}{3}\left[\frac{1}{r^3\psi {\left(r\right)}^6}-\frac{1}{r_Q^3\psi {\left(r_Q\right)}^6}\right].$$

(13)

Here, $r_Q$ is an arbitrarily chosen reference radius. It is important to note here that Einstein’s equation determines only the difference, ${\mathsf{\Omega }}_{+}\left(r\right)-{\mathsf{\Omega }}_{+}\left(r_Q\right)$, in angular velocity between ZAMOs located at two different radii. Moreover, this difference is completely independent of the numerical value of ${\mathsf{\Omega }}_{+}\left(r_Q\right)$. Thus, we are free to choose any convenient reference value ${\mathsf{\Omega }}_Q\equiv {\mathsf{\Omega }}_{+}\left(r_Q\right)$ at the reference point $r_Q$. In essence, the choice of the reference point and reference value for the angular velocity here is analogous to the arbitrary choice of a reference point for potential energy in classical mechanics, or to the arbitrary choice of a specific inertial frame for measuring velocities. In practice, this always allows us to conveniently define a new angular velocity function, ${\mathsf{\Omega }}_{\mathrm{rel}}\left(r\right)\equiv {\mathsf{\Omega }}_{+}\left(r\right)-{\mathsf{\Omega }}_Q$, which then describes the local rotation of inertial frames relative to the arbitrarily chosen local rotation ${\mathsf{\Omega }}_Q$ of inertial frames located at the arbitrarily chosen reference radius $r_Q$. Equivalently, one may instead simply declare the angular velocity ${\mathsf{\Omega }}_Q$ of the ZAMOs located at the radius $r_Q$ to be zero. The angular velocity ${\mathsf{\Omega }}_{+}\left(r\right)$ then describes the rotation rate of the ZAMOs relative to the arbitrarily chosen zero rotation rate of the ZAMOs located at $r_Q$. Finally, this analysis makes it clear that the angular velocities of ZAMOs located at asymptotic infinity play no particular role in determining a reference value for the angular velocity in this spacetime.

The constant $K_{+}$ may now be determined by requiring the metric to be continuous across the shell, ${\mathsf{\Omega }}_{-}\left(R\right)={\mathsf{\Omega }}_B={\mathsf{\Omega }}_{+}\left(R\right)$, giving

$$K_{+}=-\frac{3\left({\mathsf{\Omega }}_B-{\mathsf{\Omega }}_Q\right)}{\frac{1}{r^3\psi {\left(r\right)}^6}-\frac{1}{r_Q^3\psi {\left(r_Q\right)}^6}}.$$

(14)

Thus, the angular velocity in the two regions can be expressed as

$$\mathsf{\Omega }\left(r\right)=\left\{\begin{array}{c}{\mathsf{\Omega }}_Q+\frac{\left[\frac{1}{r^3\psi {\left(r\right)}^6}-\frac{1}{r_Q^3\psi {\left(r_Q\right)}^6}\right]\left({\mathsf{\Omega }}_B-{\mathsf{\Omega }}_Q\right)}{\frac{1}{R^3{\psi }_0^6}-\frac{1}{r_Q^3\psi {\left(r_Q\right)}^6}}\mathrm{for}r>R\\ {\mathsf{\Omega }}_B\mathrm{for}r<R\end{array}.\right.$$

(15)

Combining this expression with Equation (7), the nondiagonal component of the Einstein tensor can be written as

$$G^{03}=\frac{3\left({\mathsf{\Omega }}_B-{\mathsf{\Omega }}_Q\right){\left(R{\psi }_0^2\right)}^{3}sin\upsilon }{1-{\left(\frac{r_Q{\left(R+r_S\right)}^2}{R{\left(r_Q+r_S\right)}^2}\right)}^3}\delta \left(r-R\right).$$

(16)

Our next task is to determine the constant ${\mathsf{\Omega }}_B$ entering the expression above. This we may accomplish by once again integrating Einstein’s equation, ${\displaystyle G^{03}=8\pi G{T}^{03}}$, but this time over a region crossing the shell radius R. Accordingly, we must first consider the stress–energy tensor of the shell. From the requirement that the momentum densities $T^{i0}$ must vanish in the rest frames of the matter comprising the shell, Brill and Cohen [18] deduced that this stress–energy tensor should have the form

$$T^{\mu \nu }=\rho u^{\mu }{u}^{\nu }+\sum _{i,j=1}^3{t}^{ij}{v}_{\left(i\right)}^{\mu }{v}_j^{\nu },$$

(17)

where, as before, $\rho$ denotes the mass density in the rest frame of the shell, $u^{\mu }$ are the components of the four-velocity of a given element of the shell, and $v_{\left(i\right)}^{\mu }$ are the components of the three spatial orthonormal vectors spanning the hypersurface orthogonal to $u^{\mu }$. We shall here also assume that this form of the stress–energy tensor is adequate to first order in angular velocities.

We now proceed to find the components $T^{\mu \nu }$ of the shell. Let each element of the shell rotate with a given angular velocity $d\varphi /dt={\omega }_s$ in the isotropic coordinates. Using that $dr=d\vartheta =0$ for the element in the line element (1), the components of the four-velocity in the coordinate basis are calculated as

$${\tilde{u}}^0=\frac{dt}{d\tau }=\frac{1}{V_0}{\left(1-{\sigma }^2\right)}^{-1/2},$$

(18)

$${\tilde{u}}^1={\tilde{u}}^2=0,$$

(19)

$${\tilde{u}}^3={\omega }_s{\tilde{u}}^0,$$

(20)

where we have introduced the quantity

$$\sigma =\frac{R{\psi }_0^{2}sin\vartheta \left({\omega }_s-{\mathsf{\Omega }}_B\right)}{V_0}.$$

(21)

From the relations (4) between the orthonormal basis and the coordinate basis, the components of the four-velocity in the orthonormal basis are obtained as

$$u^0={\left(1-{\sigma }^2\right)}^{-1/2},$$

(22)

$$u^1=u^2=0,$$

(23)

$$u^3=\sigma {\left(1-{\sigma }^2\right)}^{-1/2}.$$

(24)

By choosing the components of the three spatial vectors in the orthonormal basis as

$$v_{\left(1\right)}^{\mu }=\left(0,1,0,0\right),$$

(25)

$$v_{\left(2\right)}^{\mu }=\left(0,0,1,0\right),$$

(26)

$$v_{\left(3\right)}^{\mu }=\left(\sigma ,0,0,1\right){\left(1-{\sigma }^2\right)}^{-1/2},$$

(27)

we ensure that they have unit lengths and are orthogonal to each other, as well as being orthogonal to the four-velocity. Using these expressions for $u^{\mu }$ and $v_{\left(i\right)}^{\mu }$ in Equation (17), in combination with the results already obtained in (8) and (9), the components $T^{\mu \nu }$ are, to first order in ${\omega }_s-{\mathsf{\Omega }}_B$, calculated to be

$$T^{00}=\rho ,$$

(28)

$$T^{22}=\frac{\rho r_S}{2\left(R-r_S\right)}=t^{22},$$

(29)

$$T^{33}=T^{22}=t^{33},$$

(30)

$$T^{03}=\left(\rho +t^{33}\right)\sigma =\frac{\rho \sigma \left(2R-r_S\right)}{2\left(R-r_S\right)}.$$

(31)

If we now integrate Einstein’s field equation, $G^{03}=8\pi T^{03}$, across the shell’s radius, R, we obtain the equation

$$\frac{3\left({\mathsf{\Omega }}_B-{\mathsf{\Omega }}_Q\right)R^{2}sin\vartheta }{2{\left(R+r_S\right)}^2\left[1-{\left(\frac{r_Q{\left(R+r_S\right)}^2}{R{\left(r_Q+r_S\right)}^2}\right)}^3\right]}=\frac{2r_{S}sin\vartheta \left(2R-r_S\right)R^2\left({\omega }_s-{\mathsf{\Omega }}_B\right)}{{\left(R+r_S\right)}^2{\left(R-r_S\right)}^2},$$

(32)

which may be readily solved to give

$${\mathsf{\Omega }}_B={\displaystyle \frac{{\omega }_s+{\displaystyle \frac{3{\left(R-r_S\right)}^2}{4r_S\left(2R-r_S\right)\left[1-{\left(\frac{r_Q{\left(R+r_S\right)}^2}{R{\left(r_Q+r_S\right)}^2}\right)}^3\right]}}{\mathsf{\Omega }}_Q}{1+{\displaystyle \frac{3{\left(R-r_S\right)}^2}{4r_S\left(2R-r_S\right)\left[1-{\left(\frac{r_Q{\left(R+r_S\right)}^2}{R{\left(r_Q+r_S\right)}^2}\right)}^3\right]}}}}.$$

(33)

We now substitute this result for ${\mathsf{\Omega }}_B$ in Equation (15), to obtain our final result for the angular velocity of the inertial frames:

$$\mathsf{\Omega }\left(r\right)=\left\{\begin{array}{c}{\mathsf{\Omega }}_Q+{\displaystyle \frac{g\left(r,r_Q\right)\left({\omega }_s-{\mathsf{\Omega }}_Q\right)}{g\left(R,r_Q\right)\left(1+{\displaystyle \frac{3{\left(R-r_S\right)}^2}{4r_S\left(2R-r_S\right)h\left(R,r_Q\right)}}\right)}}\mathrm{for}r>R\hfill \\ \\ {\mathsf{\Omega }}_Q+{\displaystyle \frac{{\omega }_s-{\mathsf{\Omega }}_Q}{1+{\displaystyle \frac{3{\left(R-r_S\right)}^2}{4r_S\left(2R-r_S\right)h\left(R,r_Q\right)}}}}\mathrm{for}r<R\hfill \end{array},\right.$$

(34)

where

$$g\left(r,r_Q\right)={\left({\displaystyle \frac{r}{{\left(r+r_S\right)}^2}}\right)}^3-{\left({\displaystyle \frac{r_Q}{{\left(r_Q+r_S\right)}^2}}\right)}^3,$$

(35)

$$h\left(R,r_Q\right)=1-{\left(\frac{r_Q{\left(R+r_S\right)}^2}{R{\left(r_Q+r_S\right)}^2}\right)}^3.$$

(36)

We note here that $\mathsf{\Omega }\left(r\right)$ depends only on the difference ${\omega }_s-{\mathsf{\Omega }}_Q$, i.e., only on the angular velocity of the shell relative to the arbitrary reference angular velocity of the inertial frames located at $r_Q$, and not on the numerical value of ${\omega }_s$ alone. Accordingly, if the difference ${\omega }_s-{\mathsf{\Omega }}_Q$ is kept fixed, any difference $\mathsf{\Omega }\left(r_2\right)-\mathsf{\Omega }\left(r_1\right)$ in the angular velocity of the inertial frames at different radii is independent of the arbitrary reference value ${\mathsf{\Omega }}_Q$. This reflects the fact that the numerical value of $\mathsf{\Omega }\left(r\right)$ is insignificant; only relative angular velocities have real physical significance. The difference in angular velocities of inertial frames may of course vanish, as in the interior of the shell, in which case the concepts of relative and absolute rotation become indistinguishable.

The explicit appearance of the term ${\mathsf{\Omega }}_Q$ in (34) can be understood as follows. If the angular velocity of the shell approaches the reference value, i.e., ${\omega }_s\to {\mathsf{\Omega }}_Q$, the angular velocity $\mathsf{\Omega }\left(r\right)$ of the ZAMOs approaches the constant reference value ${\mathsf{\Omega }}_Q$, both in the interior and exterior regions of the shell. This limit therefore describes a gradual transition from a situation in which the ZAMOs in the exterior region rotate relative to each other to a situation where all the ZAMOs eventually end up perfectly co-rotating with an angular velocity ${\mathsf{\Omega }}_Q$ relative to the coordinate system everywhere throughout spacetime. The resulting spacetime is accordingly that of Minkowski and Schwarzchild spacetime in the interior and exterior of the shell, respectively, as described in a coordinate system rotating relative to the collection of co-rotating ZAMOs. Thus, since the relative angular velocities of the ZAMOs completely vanish in this limit, we evidently recover a spacetime with the “apparent” property of absolute rotation everywhere analogous to that of global Minkowski spacetime. We emphasize that the transition occurring here is completely independent of any reference to non-rotating ZAMOs at infinity or non-rotating asymptotic Lorentz frame.

To gain some further insight, consider now, for simplicity, the case ${\omega }_s={\mathsf{\Omega }}_Q$ in the interior region $r<R$ of the shell. Then again $\mathsf{\Omega }\left(r\right)={\mathsf{\Omega }}_Q$, and the line element in (1) simplifies to that of

$$d{s}^2=\left(1-{r^{\prime }}^2{sin}^2\vartheta {{\mathsf{\Omega }}_Q^{\prime }}^2\right)d{t^{\prime }}^2-d{r^{\prime }}^2-{r^{\prime }}^{2}d{\vartheta }^2-{r^{\prime }}^2{sin}^2\vartheta d{\varphi }^2+2{r^{\prime }}^2{sin}^2\vartheta {\mathsf{\Omega }}_Q^{\prime }d{t^{\prime }}^{2}d{\varphi }^2,$$

(37)

where we have introduced the conveniently rescaled coordinates $r^{\prime }={\psi }_0^{2}r$, $t^{\prime }=V_{0}t$, and ${\mathsf{\Omega }}_Q^{\prime }=d\varphi /d{t}^{\prime }={\mathsf{\Omega }}_Q/V_0$. We recognize the line element above as that of Minkowski spacetime described in a spherical coordinate system rotating with constant angular velocity $-{\mathsf{\Omega }}_Q^{\prime }$ relative to a standard inertial reference frame in which the ZAMOs do not rotate. Unless ${\mathsf{\Omega }}_Q^{\prime }=0$, it is clear that inertial effects will appear in the interior of the shell in this rotating coordinate system. More generally, when ${\omega }_s\ne {\mathsf{\Omega }}_Q$, these inertial effects will increase if ${\omega }_s>{\mathsf{\Omega }}_Q$, due to the second term in Equation (34) for $r<R$, which accounts for additional rotational effects caused by increased rotation of the shell relative to ZAMOs located at the reference radius $r_Q$, implying also an increased rotation rate of the shell relative to the coordinate system. Alternatively, keeping the parameters ${\omega }_s$ and ${\mathsf{\Omega }}_Q$ fixed, this second term also implies that these inertial effects depend upon the choice of the reference point $r_Q$. For instance, as $r_Q\to \infty$ the function $h\left(R,r_Q\right)\to 1$, yielding a rotation rate greater than ${\mathsf{\Omega }}_Q$. On the other hand, for $r_Q\to R$, $h\left(R,r_Q\right)\to 0$, such that the second term vanishes, and hence the rotation rate approaches ${\mathsf{\Omega }}_Q$. This dependence on $r_Q$ may at first seem suspect, but is effectively caused by changes in the relative rotation between ZAMOs in the exterior region of the shell, which impact the rotation rate in the interior.

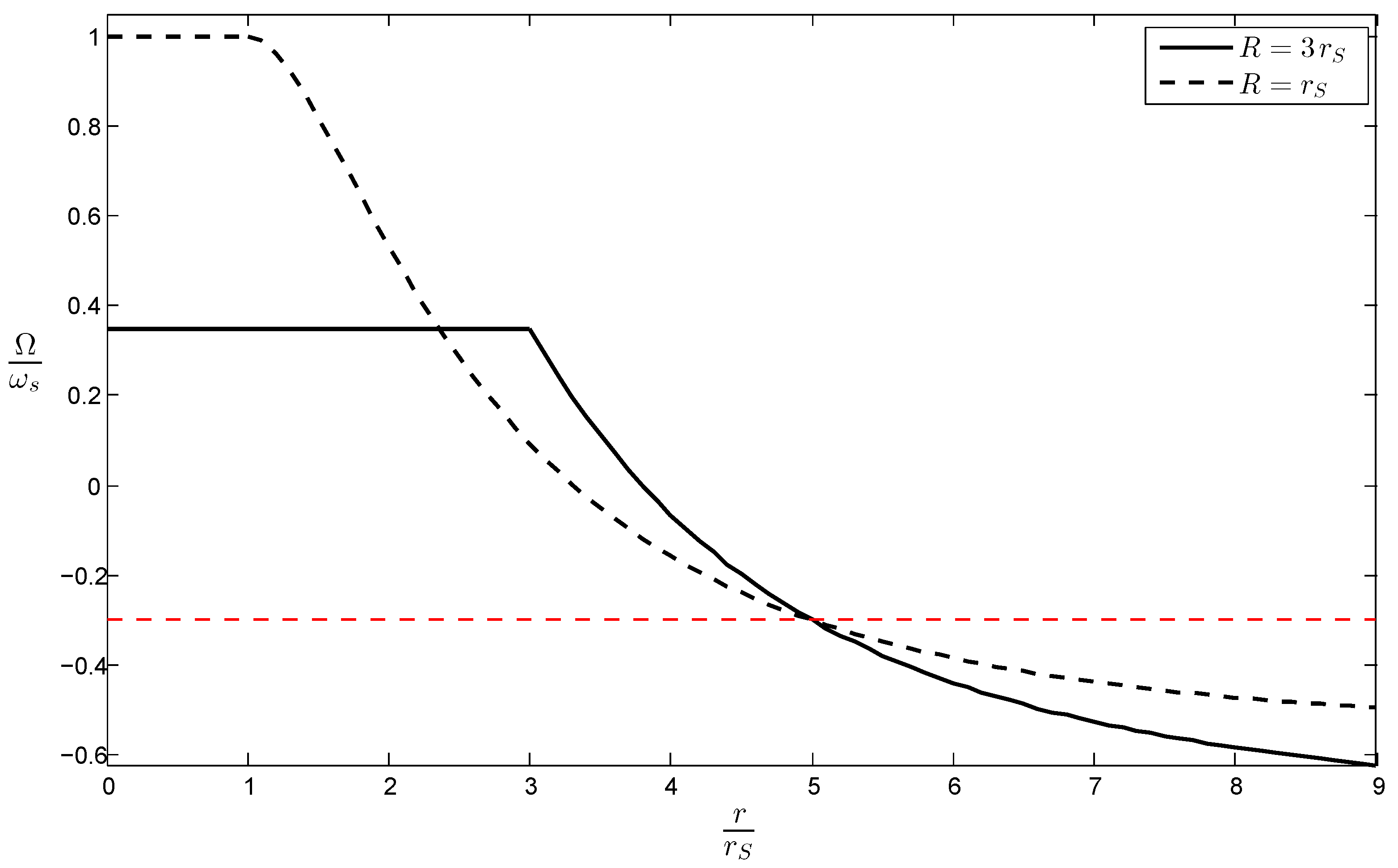
Figure 1 illustrates two examples of the angular velocity $\mathsf{\Omega }\left(r\right)$ in (34) for fixed parameter values ${\mathsf{\Omega }}_Q=-0.3{\omega }_s$ and $r_Q=5r_S$, and for two different choices, $R=3r_S$ and $R=r_S$, for the shell radius.

As can be seen, when the shell radius is larger than the Schwarzschild radius, the inertial frames are only partially dragged around with the shell’s rotation. As the shell radius approaches its Schwarzschild radius, however, the inertial frames in the interior of the shell rotate with the same angular velocity ${\omega }_s$ as the shell, independently of the angular velocity of the inertial frames located “at asymptotic infinity”. This is the phenomenon of “perfect inertial dragging”, first discovered by Brill and Cohen [18]. Yet, in Brill and Cohen’s original calculation of $\mathsf{\Omega }\left(r\right)$, the inertial frames located “at infinity” were non-rotating. In contrast, with our choice above for the reference value ${\mathsf{\Omega }}_Q$, the inertial frames located “at infinity” in our case rotate with a negative angular velocity: in other words, they are not at rest.

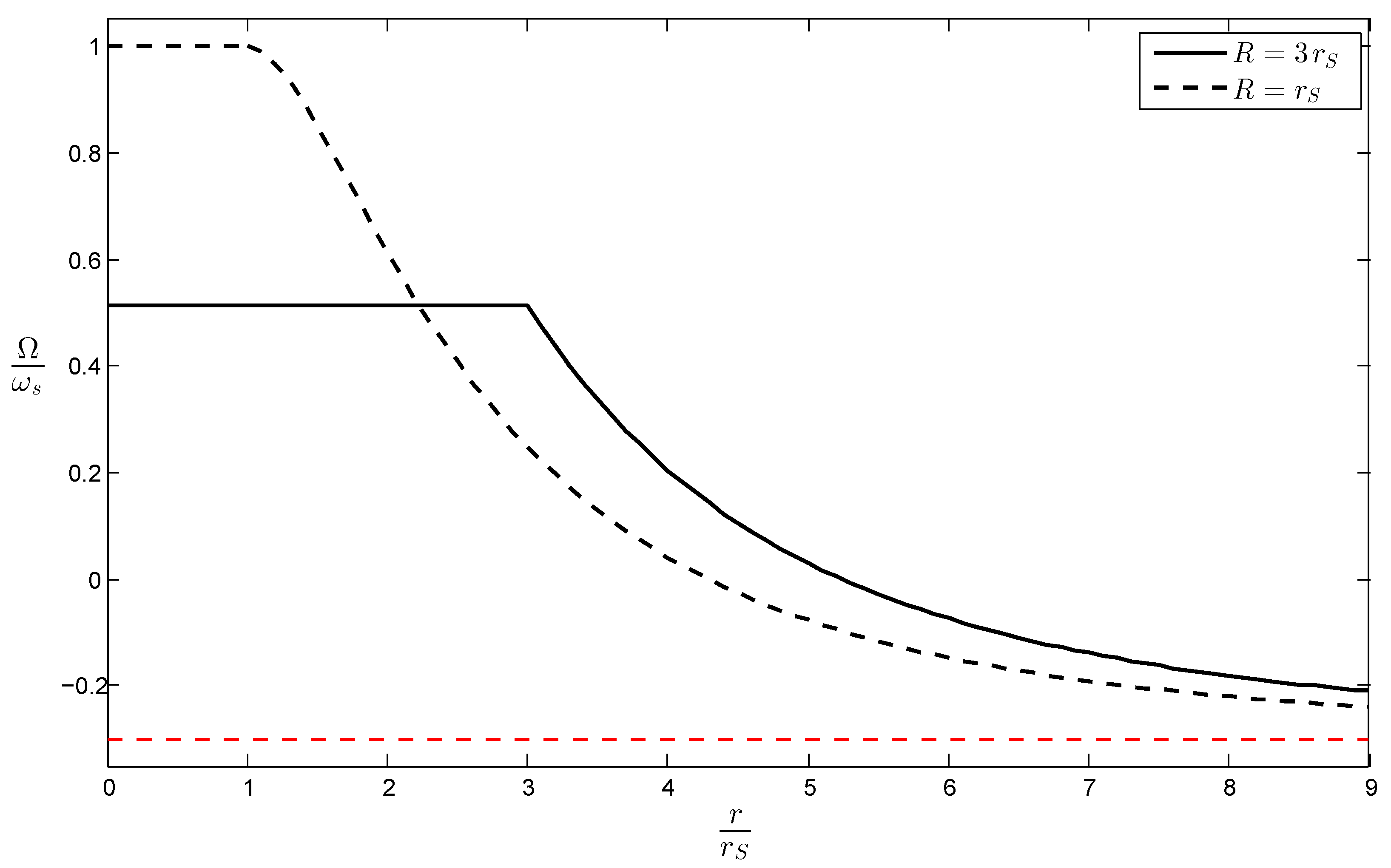
To further compare our result to the original result of Brill and Cohen, it is instructive to consider the case for which $r_Q\to \infty$, as shown in Figure 2.

Then, the ZAMOs located at asymptotic infinity rotate with the angular velocity ${\mathsf{\Omega }}_Q$. The original result of Brill and Cohen is now recovered by making the convenient, but very special choice ${\mathsf{\Omega }}_Q=0$, for which Equation (34) simplifies to

$$\mathsf{\Omega }\left(r\right)=\left\{\begin{array}{c}{\displaystyle \frac{{\left({\displaystyle \frac{r{\left(R+r_S\right)}^2}{R{\left(r+r_S\right)}^2}}\right)}^3{\omega }_s}{1+{\displaystyle \frac{3{\left(R-r_S\right)}^2}{4r_S\left(2R-r_S\right)}}}}\mathrm{for}r>R\hfill \\ \\ {\displaystyle \frac{{\omega }_s}{1+{\displaystyle \frac{3{\left(R-r_S\right)}^2}{4r_S\left(2R-r_S\right)}}}}\mathrm{for}r<R\hfill \end{array}.\right.$$

(38)

Note that Equation (34) can be obtained from Equation (38) by transforming to a coordinate system $\left(\tilde{t},\tilde{r},\tilde{\vartheta },\tilde{\phi }\right)$, rotating relative to the first one with an angular velocity $\omega =\mathsf{\Omega }\left(r_Q\right)-\tilde{\mathsf{\Omega }}\left(r_Q\right)$:

$$\tilde{t}=t,\tilde{r}=r,\tilde{\vartheta }=\vartheta ,\tilde{\phi }=\phi -\left(\mathsf{\Omega }\left(r_Q\right)-{\tilde{\mathsf{\Omega }}}_Q\right)t,$$

(39)

where ${\tilde{\mathsf{\Omega }}}_Q\equiv \tilde{\mathsf{\Omega }}\left(r_Q\right)$ is the arbitrarily chosen reference value for the angular velocity of the ZAMOs located at the reference radius $r_Q$ in the rotating coordinate system. The angular velocity of the rotating shell in the rotating coordinate system is then ${\tilde{\omega }}_s={\omega }_s+{\tilde{\mathsf{\Omega }}}_Q-\mathsf{\Omega }\left(r_Q\right)$. Noting that $\mathsf{\Omega }\left(r_Q\right)$ is also a function of ${\omega }_s$, we may invert this relation to obtain ${\omega }_s$ as a function of ${\tilde{\omega }}_s$. A straightforward substitution for ${\omega }_s$ in terms of ${\tilde{\omega }}_s$ in Equation (38) then yields Equation (34).

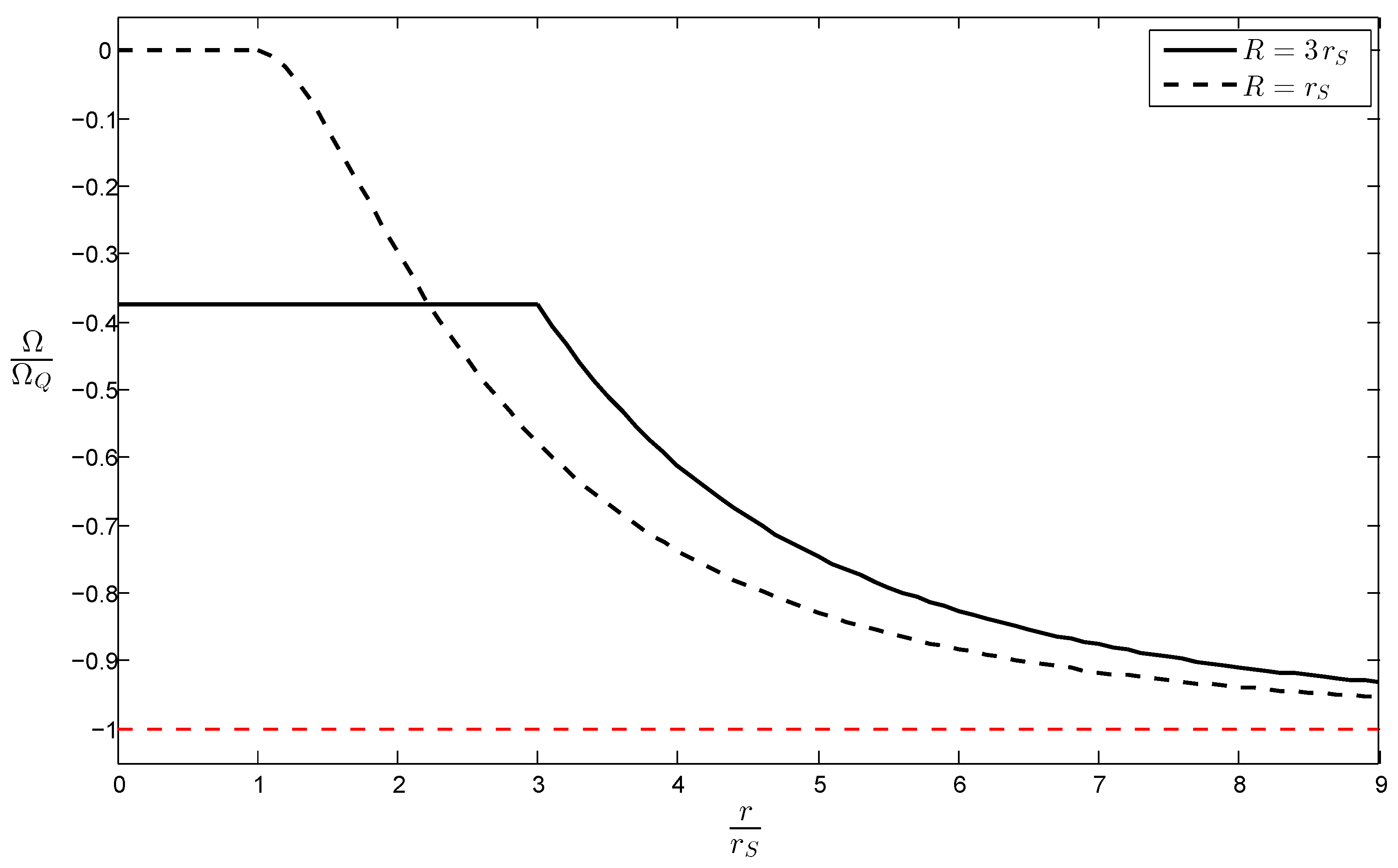
Finally, as a rather vivid illustration of the arbitrariness of the numerical value of $\mathsf{\Omega }\left(r\right)$, we may now consider the case, shown in Figure 3, for which there is perfect dragging, ($R=r_S$), the angular velocity of the shell vanishes, ${\omega }_s=0$, and we keep $r_Q\to \infty$ as above (but let ${\mathsf{\Omega }}_Q$ be arbitrary).

Now, both the shell and the inertial frames in the interior of the shell are non-rotating, but the ZAMOs located at asymptotic infinity rotate with the angular velocity ${\mathsf{\Omega }}_Q$. In this picture, it appears as if the massive shell and space in its interior are at rest, while it is the rest of the universe exterior to the shell that rotates around it.

3. Rotation in Kerr Spacetime

In the previous section, we discussed the rotation of ZAMOs in Brill and Cohen’s approximate spacetime model of a slowly rotating thin shell. In this section, we briefly consider the angular velocity of ZAMOs in Kerr spacetime representing an exact axistationary and asymptotically flat solution to Einstein’s field equations.

In Boyer–Lindquist coordinates $\left(t,r,\vartheta ,\phi \right)$, the angular velocity of ZAMOs due to inertial dragging in the equatorial plane of Kerr spacetime is given by [1]:

$$\mathsf{\Omega }\left(r\right)=\frac{2Ma}{r^3+r{a}^2+2M{a}^2},$$

(40)

where $a=J/M$, J is the angular momentum, and M is the mass characterizing the Kerr geometry. In the asymptotic limit, $r\to \infty$, $\mathsf{\Omega }\left(r\right)$ vanishes. However, this does not imply that ZAMOs located at asymptotic infinity define an absolute state of non-rotation. Indeed, using the same transformations as in Equation (39), we may once again transform to a coordinate system $\left(\tilde{t},\tilde{r},\tilde{\vartheta },\tilde{\phi }\right)$ rotating relative to the Boyer–Lindquist coordinates, to obtain the angular velocity of the ZAMOs in the rotating system as

$$\tilde{\mathsf{\Omega }}\left(r\right)={\tilde{\mathsf{\Omega }}}_Q+\mathsf{\Omega }\left(r\right)-\mathsf{\Omega }\left(r_Q\right).$$

(41)

The ZAMOs are now seen to rotate at asymptotic infinity with, in general, a non-zero angular velocity ${\tilde{\mathsf{\Omega }}}_Q-\mathsf{\Omega }\left(r_Q\right)$, even though their angular momentum is zero. If, in addition, we let the arbitrary reference radius $r_Q\to \infty$, then their rotation rate at infinity equals the arbitrary reference value ${\tilde{\mathsf{\Omega }}}_Q$.

This observation may at first appear completely trivial, as it follows directly from a simple transformation to a rotating coordinate system. However, as was discussed below Equations (34) and (38), this particular freedom of choice of coordinate system is inherently linked to the observation that Einstein’s equations determine only differences in angular velocities of ZAMOs, implying that only relative angular velocities are meaningful concepts. The angular velocity (40) obtained in the Boyer–Lindquist coordinates appears to be a consequence of imposing the asymptotic boundary condition ${\displaystyle \underset{r\to \infty }{lim}\mathsf{\Omega }\left(r\right)=0}$ at the outset of the derivation [35], potentially leading to the misconception that the inertial frames at asymptotic infinity single out a global standard of non-rotation. The coordinate independent boundary condition of asymptotic flatness is independent of the asymptotic boundary condition imposed on the numerical value of the ZAMO angular velocity. This indicates that rotation of ZAMOs located at different radii is best interpreted as a relative concept in Kerr spacetime too.

4. Summary and Conclusions

The effect of inertial frame dragging on the rotation rate of ZAMOs has been analyzed within the framework of the simple thin shell model seminally introduced by Brill and Cohen. By relaxing the quite natural assumption of zero rotation infinitely far away from the massive shell early on in the derivation, the obtained expression for the rotation rate, Equation (34), makes it clear that Einstein’s equations only determine relative angular velocities of ZAMOs. The particular value of the rotation rate of a ZAMO is physically irrelevant unless one also specifies an arbitrarily chosen zero point in space, relative to which this rotation rate is measured. Notably, this applies as well to the rotation rate of ZAMOs located at asymptotic infinity.

Within the simple thin shell model, it was further clarified that the same expression for the rotation rate can be obtained simply by a transformation from the coordinate system in which the ZAMOs at asymptotic infinity are non-rotating, to a coordinate system rotating relative to the first one. Utilizing this connection, we then argued that “global” rotation of ZAMOs in Kerr spacetime should be interpreted as a relative concept, in the same sense as for the thin shell model.

Thus, if there is still some hope that general relativity can be considered a complete (classical) theory of gravitation capable of describing isolated gravitating systems without requiring particular topologies or external causes such as “fixed stars” and absolutely non-rotating Lorentz frames at infinity, then it seems that relative rotation in the sense presented here not only is a valid concept, but perhaps even a necessary one in the interpretation of some solutions to Einstein’s equations; more specifically, in the axistationary, asymptotically flat spacetimes of general relativity.

The question of whether rotational motion can be interpreted as relative according to general relativity was discussed in a relatively recent paper by Ø. Grøn [25]. The arguments presented above provide some support for this possibility. It seems feasible that both the absolute and relational viewpoints can be treated as complementary aspects within the theory of general relativity [36,37].