Tolman VI Fluid Sphere in f(R,T) Gravity

Abstract

We analyze the behavior of relativistic spherical objects within the context of modified $f(R,T)$ gravity considering Tolman VI spacetime, where the gravitational Lagrangian is a function of the Ricci scalar (R) and trace of energy momentum tensor (T), i.e, $f(R,T)$ = R + 2βT, for some arbitrary constant β. For developing our model, we have chosen £_m = −p, where £_m represents the matter Lagrangian. For this investigation, we have chosen three compact stars, namely PSR J1614-2230 (Mass = (1.97 ± 0.4)M_⊙; Radius = ${9.69}_{+0.02}^{-0.02}$ km), Vela X-1 (Mass = (1.77 ± 0.08)M_⊙; Radius = ${9.560}_{+0.08}^{-0.08}$ km) and 4U 1538-52 (Mass = (9.69)M_⊙; Radius = 1.97 km). In this theory, the equation of pressure isotropy is identical to the standard Einstein’s theory. So, all known metric potential solving Einstein’s equations are also valid here. In this paper, we have investigated the effort of a coupling parameter (β) on the local matter distribution. The sound of speed and adiabatic index are higher with grater values of β, while on the contrary, the mass function and gravitational redshift are lower with higher values of β. For supporting the theoretical results, graphical representations are also employed to analyze the physical viability of the compact stars.

1. Introduction

The analysis of the interior of the stars is fascinating to astrophysicists, mainly due to the general theory of relativity (GR), because of the fact that, around the late phase of stellar evolution, general relativistic effects are much more important. In this direction, one incredible work was that of the Tolman [1] solution (1939). Tolman extensively deliberated on the stellar interior and gave us an explicit solution for the static, spherically symmetric equilibrium fluid distribution [2]. It has been tested in different dimensions, which include cosmology, gravitational waves, astrophysics and thermodynamics [3] of the stellar system, and it has presented important contributions to the different astrophysics and cosmological issues. Many of them present the collapsing of wormhole solution with static spherically symmetric geometry [4] and a non-static spherically symmetric object with anisotropic fluid profile. Moraes and his co-authors [5] studied a modified Tolman–Oppenheimer–Volkoff (TOV) equation in which they illustrate the equilibrium conditions of the compact structures.

The modifying form of gravitational action asks for many fundamental challenges. These models can show ghost-like behavior and instabilities, while on the other side, it has to match with experiments and observations in the low energy limit. Additionally, in the framework of $f(R,T)$ gravity, some interesting results have been found at solar system [6], galactic and cosmological scales.

Several models exist that attempt to explain the early acceleration of the universe. The most accepted models contain a slowly varying potential and a scalar field. There is another class of models where the gravity is modified under the general relativity. One of the procedures of the modifications depending upon phenomenological considerations is provided by the $f(R,T)$ theory of gravity. Indeed, $f(R,T)$ theories are conformally identical to Einstein’s theory plus a scalar degree of freedom classified the scalar in which the potential is uniquely established from a Ricci scalar. There are various models, in the literature, where the authors [7] considered Einstein equations with corrections. The consistent theory of gravity, modified or classified, should be equally suitable to the strong gravity regime.

Here, $f(R,T)$ is an analytic (general) function of R (Ricci scalar). As an example, cosmological solutions give the accelerated expansion of the universe at late times. Additionally, it has been found that many stability conditions may lead to avoiding tachyon and ghost solutions. In addition, there exist viable $f(R,T)$ models satisfying both stability conditions [8] and background cosmological constraints, and results have been obtained to place constants on the $f(R,T)$ cosmological model by the cosmic microwave background radiation (CMBR) galaxy and anisotropic power spectrum [9,10]. To consider $f(R,T)$ gravity in a low energy limit, it is viable to obtain accurate gravitational potentials capable of describing the flat rotational curves of the dynamics of galaxy or spiral galaxies clusters without considering large amounts of dark matter [11].

Numerous investigations [12,13,14,15,16] have used different methods to examine the stability as well as consistency of $f\left(R\right)$ gravity theory. There are definite forms of the $f\left(R\right)$ algebraic function which eliminated the existence of the stable astrophysical form and were reported as unrealistic. In recent years, more research has been performed on the steadiness, dynamical unsteadiness, and existence of a celestial stellar system of this theory [17,18,19]. Harko et. al [20] proposed the concept of matter and curvature couplings to represent a new version of an altered theory of gravity, namely $f(R,T)$ gravity. They also represented the relating field equation with the help of the gravitational potential mechanism and showed the importance of alternative gravity theory. Additionally, the same authors have initiated various models for $f(R,T)$ algebraic functional for detachable compose viz. $f(R,T)$ = $f_1\left(R\right)$ + $f_2\left(T\right)$. Houndjo [21] investigated the matter instructed age of accelerating cosmic by $f(R,T)$ gravity. Additionally, Baffou and his teammates [22] examined spatially uniform cosmic in the field of $f(R,T)$ gravity.

Modified and extended models are always popular due to the potential of representation of the gravitational field nature near curvature singularities accurately and as well to overcome the cosmological constant problems. Convincing confirmation for the extension of the universe has been provided by the many independent observations; some of these are supernovas Ia data [23,24,25,26,27,28], cosmic microwave background radiation [29] and baryon acoustic oscillation [30] according to the study by the WMAP. For addressing this phenomenon, several assumptions have been suggested, from the dark energy model to modified theories of gravity. Currently, the dark energy model has no sufficient observational support. In particular, the dark energy idea requires an equation of state (EoS) $\omega =\frac{p}{\rho }$, where $p,q$ represents spatially homogeneous pressure and energy density, respectively, and the value of the parameter $\omega$ is $-1$. Several results have been found for interior exact solutions of the Einstein field equation, and Schwarzschild found the first interior solution. Tolman proposed inventive methods for the treatment of the Einstein field equation, which are known as Tolman I, II, III, IV, V, VI, VII and VIII [31].

In this paper, we consider the Tolman VI model [32] in the class of modified gravity in which the gravitational action carries a general function $f(R,T)$. For this model, the study of the background cosmological evolution can be simplified by performing a transformation on the metric. This type of transformation maps from a frame where the resulting field equations and gravitational action are modified from general relativity (GR), called the Jordan frame, to a frame where the gravitational action for the newly obtained metric is the Einstein–Hilbert one, called the Einstein frame. The $f(R,T)$ gravity theory has been related to stellar astrophysics [33] and cosmology [34], among other areas, giving testable and interesting results.

The present article deals with isotropic Tolman VI in modified $f(R,T)$ gravity. The physical characteristics of our obtained model are studied for three compact stars, namely PSR J1614-2230, Vela X-1 and 4U 1538-52. The paper is organized in the following order of sections. Section 2, we explain about the general formalism of $f(R,T)$ gravity and in Section 3, the proposed model is obtained for different values of coupling parameter $\beta$. At the boundary, we matched our interior space-time to the exterior space-time in Section 4. Section 5 explains the physical properties between Einstein theory and $f(R,T)$ gravity. Finally, in Section 6, we discuss and conclude the whole work by pointing out major findings.

2. Mathematics behind $f(R,T)$ Gravity

In this section, we show how the f(R,T) was introduced. The Ricci scalar is integrated over a four dimensional volume element $d^{4}x$ when Einstein’s field equation is derived from Einstein–Hilbert action as

$$\begin{array}{c}\hfill S_{EH}=\frac{1}{16\pi }\int R\sqrt{-g}{d}^{4}x\end{array}$$

(1)

If we replace the Ricci scalar R with f (R,T), we can obtain the f(R,T) field equations. Therefore, the complete action in f (R,T) formalism is

$$\begin{array}{c}\hfill S=\int {\pounds }_m\sqrt{-g}{d}^{4}x+\frac{1}{16\pi }\int f(R,T)\sqrt{-g}{d}^{4}x\end{array}$$

(2)

where, T is the trace of the energy momentum tensor $T_{\mu \nu }$. Additionally, ${\pounds }_m$ represents the Lagrangian matter density and $g=det\left(g_{\mu \nu }\right)$.

The energy momentum tensor is defined as

$$\begin{array}{c}\hfill T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\partial \left(\sqrt{-g}{\pounds }_m\right)}{\partial g^{\mu \nu }}\end{array}$$

(3)

along with the trace $T=g^{\mu \nu }{T}_{\mu \nu }$. Additionally, the Lagrangian density ${\pounds }_m$ depends on only the metric tensor component $g_{\mu \nu }$, not its derivatives. Here, we have

$$\begin{array}{c}\hfill T_{\mu \nu }=g_{\mu \nu }{\pounds }_m-2\frac{\partial {\pounds }_m}{\partial g^{\mu \nu }}\end{array}$$

(4)

By the variation principle with respect to $g_{\mu \nu }$, Equation (2) gives the field equation

$$\begin{array}{c}\hfill (R_{\mu \nu }-{\nabla }_{\mu }{\nabla }_{\nu })f_R(R,T)+g^{\mu \nu }(\sum _{\mu }{\mathcal{D}}^{\mu }{\mathcal{D}}_{\mu })f_R(R,T)-\frac{1}{2}f(R,T)g_{\mu \nu }\\ \hfill =8\pi T_{\mu \nu }-T_{\mu \nu }{f}_T(R,T)-{\Theta }_{\mu \nu }{f}_T(R,T)\end{array}$$

(5)

where, $f_R(R,T)=\frac{\partial f(R,T)}{\partial R}$ and $f_T(R,T)=\frac{\partial f(R,T)}{\partial T}.$ Here, covariant derivative ${\nabla }_{\mu }$ is associated with the Levi–Civita connection of the metric tensor $g_{\mu \nu }$ and the box operation ${\sum }_{\mu }{\mathcal{D}}^{\mu }{\mathcal{D}}_{\mu }$ is defined as ${\sum }_{\mu }{\mathcal{D}}^{\mu }{\mathcal{D}}_{\mu }\equiv \frac{1}{\sqrt{-g}}\frac{\partial }{\partial x^{\mu }}\left(\sqrt{-g}{g}^{\mu \nu }\frac{\partial }{\partial x^{\nu }}\right)$ with ${\Theta }_{\mu \nu }=g^{\alpha \beta }\frac{\delta T_{\alpha \beta }}{\delta g^{\mu \nu }}$

The covariant derivative of Equation (5) gives

$$\begin{array}{c}\hfill {\nabla }^{\mu }{T}_{\mu \nu }=\frac{f_T(R,T)}{8\pi -f_T(R,T)}\left[(T_{\mu \nu }+{\Theta }_{\mu \nu }){\nabla }^{\mu }ln{f}_T(R,T)+{\nabla }^{\mu }{T}_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }{\nabla }^{\mu }T\right]\end{array}$$

(6)

In $f(R,T)$ gravity, the stress–energy tensor of the matter field does not obey the conservation low due to interaction between the curvature and matter as in general relativity. With the help of Equation (3), we obtain the tensor ${\Theta }_{\mu \nu }$ as follows:

$$\begin{array}{c}\hfill {\Theta }_{\mu \nu }=g_{\mu \nu }{\nabla }^{\mu }-2T_{\mu \nu }-2g^{\alpha \beta }\frac{{\partial }^2{\pounds }_m}{\partial g^{\mu \nu }\partial g^{\alpha \beta }}\end{array}$$

(7)

for the field equation, we assume the energy–momentum tensor as

$$\begin{array}{c}\hfill T_{\mu \nu }=(\rho +p)u_{\mu }{u}_{\nu }-p{g}_{\mu \nu },\end{array}$$

(8)

provided, the ${\mu }^{\mu }$ four velocity, such that ${\mu }_{\mu }{\mu }^{\mu }=1$ and ${\mu }_{\mu }{\nabla }^{\mu }{\mu }_{\mu }=0$ with $\rho ,p_r$ and $p_t$ are matter density, radial pressure and transverse pressure, respectively. If we specify pressure as $-\mathcal{P}={\pounds }_m$, the Equation (7) reduces to

$$\begin{array}{c}\hfill {\Theta }_{\mu \nu }=-\mathcal{P}{g}_{\mu \nu }-2T_{\mu \nu }\end{array}$$

(9)

3. Interior Space-Time and the Realistic Viable $f(R,T)$ Gravity Models

We will represent the model with the help of a realistic $f(R,T)$ gravity model. Here, we consider a separable functional form of $f(R,T)$ given by,

$$\begin{array}{c}\hfill f(R,T)=f_1\left(R\right)+f_2\left(T\right)\end{array}$$

(10)

in the relativistic structures to study the coupling effects of matter and curvature components in $f(R,T)$ gravity, where $f_1\left(R\right)$ and $f_2\left(T\right)$ represent arbitrary functions of R and T, respectively. Several viable models in $f(R,T)$ gravity can be generated in linear combining of different forms of $f_1\left(R\right)$ and $f_2\left(T\right)$. In the present model, we assume $f_1\left(R\right)=R$ and $f_2\left(T\right)=2\beta T$. Then, the expression for $f(R,T)$ becomes

$$\begin{array}{c}\hfill f(R,T)=R+2\beta T\end{array}$$

(11)

where, $\beta$ is an arbitrary constant to be evaluated depending on many physical requirements. In curvature coordinates, we consider the static and spherically symmetric line element describing a wormhole region by the following metric:

$$\begin{array}{c}\hfill d{s}^2=-e^{\nu }d{t}^2+e^{\lambda }d{r}^2+r^{2}d{\Omega }^2,\end{array}$$

(12)

where, both $\nu ,\lambda$ depends on r, i.e., both are purely radial and $d{\Omega }^2={sin}^2\theta d{\varphi }^2+d{\theta }^2$. In modified gravity, the field equation along the line element (12) can be written as

$$\begin{array}{ccc}\hfill 8\pi \rho +\beta (3\rho -p)& =& \frac{1-e^{-\lambda }}{r^2}+\frac{e^{-\lambda }{\lambda }^{\prime }}{r},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill 8\pi p-\beta (\rho -3p)& =& \frac{e^{-\lambda }-1}{r^2}+\frac{e^{-\lambda }{\nu }^{\prime }}{r},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill 8\pi p-\beta (\rho -3p)& =& e^{-\lambda }\left[\frac{{\nu }^{″}}{2}+\frac{{\nu \prime }^2}{4}-\frac{{\nu }^{\prime }{\lambda }^{\prime }}{4}+\frac{{\nu }^{\prime }-{\lambda }^{\prime }}{2r}\right].\hfill \end{array}$$

(15)

where a prime (${}^{\prime }$) denotes differentiation with respect to the radial coordinates “r”.

We denote ${\rho }_E$ and $p_E$ by,

$$\begin{array}{ccc}\hfill {\rho }_E& =& \rho +\frac{\beta }{8\pi }(3\rho -p),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill p_E& =& p-\frac{\beta }{8\pi }(\rho -3p).\hfill \end{array}$$

(17)

where, ${\rho }_E$ represents the density and $p_E$ represents the pressure in Einstein gravity. To solve Equations (13)–(15), we use the metric potential by Tolman [1] in which the expression

$$\begin{array}{ccc}\hfill e^{\lambda }& =& 2-n^2,\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill e^{\nu }& =& {(A{r}^{1-n}-B{r}^{1+n})}^2.\hfill \end{array}$$

(19)

where, A and B are arbitrary constant. The restriction of $\lambda$ is $0<\lambda <\sqrt{2}$, but this is not the most general choice. Using the expression of Equations (18) and (13), we obtain the Einstein density as

$$\begin{array}{c}\hfill {\rho }_E=\frac{1-n^2}{8\pi r^2(2-n^2)}\end{array}$$

(20)

Similarly, using the expression of Equations (18) and (19), and Equation (14), we obtain the Einstein pressure as follows:

$$\begin{array}{c}\hfill p_E=\frac{A{(n-1)}^2-B{(n+1)}^2{r}^{2n}}{8\pi r^2(2-n^2)(A-B{r}^{2n})}.\end{array}$$

(21)

If we eliminate radius r from Equations (20) and (21), we obtain the relation between Einstein density and pressure. Additionally, the positivity of the density profile demands the ranges for n are $n<-\sqrt{2}$, $n>\sqrt{2}$ or $-1<n<1$. So, the interval of validity is $0<n<1$. Now, using the expression ${\rho }_E$ and $p_E$ from Equations (16) and (21), we obtain the expression for matter density $\left(\rho \right)$ and pressure $\left(p\right)$ in modified $f(R,T)$ gravity as follows:

$$\begin{array}{ccc}\hfill \rho & =& \frac{A(n-1){\chi }_1-B(n+1){\chi }_2{r}^{2n}}{4r^2(n^2-2)(2\pi +\beta )(4\pi +\beta )(A-B{r}^{2n})},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill p& =& \frac{-A(n-1){\chi }_2+B(n+1){\chi }_1{r}^{2n}}{4r^2(n^2-2)(2\pi +\beta )(4\pi +\beta )(A-B{r}^{2n})},\hfill \end{array}$$

(23)

where,

$$\begin{array}{ccc}\hfill {\chi }_1& =& 4(n+1)\pi +(n+2)\beta ,\hfill \\ \hfill {\chi }_2& =& 4(n-1)\pi +(n-2)\beta .\hfill \end{array}$$

(24)

The square of the sound velocity for Einstein and our present model are obtained as follows:

$$\begin{array}{ccc}\hfill V_E^2& =& {\left(\frac{dp}{d\rho }\right)}_E=-\frac{{(A(n-1)+B(n+1)r^{2n})}^2}{(n^2-1){(A-B{r}^{2n})}^2},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill V^2& =& \frac{dp}{d\rho }=-\frac{A^2(n-1){\chi }_2+4AB(n^2-1)(2\pi +\beta )r^{2n}+B^2(n+1){\chi }_1{r}^{4n}}{A^2(n-1){\chi }_1-4AB(n^2-1)(2\pi +\beta )r^{2n}+B^2(n+1){\chi }_2{r}^{4n}}\hfill \end{array}$$

(26)

A negative sign in the sound speed index can be removed in the interval $0<n<1$. The profiles of density and pressure are shown in Figure 1 and Figure 2, respectively (using the values given in

Table 1. Numerical values of constants for three well-known celestial compact stars.

Compact Star	${\mathit{M}}_{\mathbf{obs}}/{\mathit{M}}_{\odot }$	${\mathit{R}}_{\mathbf{obs}}$ (km)	M (${\mathit{M}}_{\odot }$)	R (km)	$\mathit{n}=\sqrt{\frac{\mathit{R}-4\mathit{M}}{\mathit{R}-2\mathit{M}}}$
PSR J1614-2230	1.97± 0.4	9.69± 0.02	1.97	9.69	0.56
Vela X-1	1.77± 0.08	9.56± 0.08	1.77	9.56	0.64
4U 1538-52	9.69	1.97	1.97	9.69	0.85

and

Table 2. Numerical values of constants for three well-known celestial compact stars.

$\mathit{n}=0.56$
Compact Star	$\mathbf{\beta }$	$\mathit{A}$	$\mathit{B}$	${\mathbf{\rho }}_{\mathit{s}}$ (g/cm${}^3$)	${\mathit{z}}_{\mathit{s}}$	$\Gamma$(r = 0)	${\mathcal{U}}_{\mathit{s}}$
PSR J1614-2230	2	0.31368	0.00236	1.88338 $\times {10}^{14}$	0.22404	1.80526	0.33257
	4	0.31746	0.00266	1.57940 $\times {10}^{14}$	0.18006	3.42727	0.28188
	6	0.32019	0.00288	1.35301 $\times {10}^{14}$	0.15082	5.59965	0.24493
	8	0.32225	0.00304	1.19365 $\times {10}^{14}$	0.12990	8.32942	0.21671
	10	0.32386	0.00316	1.06375 $\times {10}^{14}$	0.11415	11.6206	0.19441
$\mathit{n}=0.64$
Compact Star	$\mathbf{\beta }$	$\mathit{A}$	$\mathit{B}$	${\mathbf{\rho }}_{\mathit{s}}$ (g/cm${}^3$)	${\mathit{z}}_{\mathit{s}}$	$\Gamma$(r = 0)	${\mathcal{U}}_{\mathit{s}}$
Vela X-1	2	0.37509	0.00128	1.76517 $\times {10}^{14}$	0.19764	1.22451	0.30282
	4	0.37862	0.00148	1.47994 $\times {10}^{14}$	0.15965	2.43408	0.25640
	6	0.38117	0.00162	1.27408 $\times {10}^{14}$	0.13419	4.08345	0.22263
	8	0.38309	0.00173	1.11849 $\times {10}^{14}$	0.11585	6.17906	0.19687
	10	0.38460	0.00181	0.99677 $\times {10}^{14}$	0.10200	8.72458	0.17655
$\mathbf{n}=\mathbf{0}.\mathbf{85}$
Compact Star	$\mathbf{\beta }$	$\mathit{A}$	$\mathit{B}$	${\mathbf{\rho }}_{\mathit{s}}$ (g/cm${}^3$)	${\mathit{z}}_{\mathit{s}}$	$\Gamma$(r = 0)	${\mathcal{U}}_{\mathit{s}}$
4U 1538-52	2	0.65534	0.00230	1.52410$\times {10}^{14}$	0.10190	0.19370	0.17640
	4	0.65764	0.00299	1.27783 $\times {10}^{14}$	0.83973	0.48583	0.14893
	6	0.65930	0.00349	1.10008 $\times {10}^{14}$	0.07154	0.91913	0.12907
	8	0.66055	0.00387	0.96574 $\times {10}^{14}$	0.06237	1.49672	0.11398
	10	0.66153	0.00416	0.860641 $\times {10}^{14}$	0.05532	2.22038	0.10211

). One can see that the density and pressure are both positive definite, but at the stellar center both are infinite. Additionally, from Figure 2, we can see that Einstein pressure are gradually decreasing with increasing value of “n”, i.e., Einstein pressure at the point $n=0.56>$, Einstein pressure at the point $n=0.64>$, and Einstein pressure at the point $n=0.85.$

In the literature, it is well-known that the mass distributions must obey all the energy conditions in its interiors. These energy conditions are named as null, strong, week and dominant energy conditions and symbolized by NEC, SEC, WEC and DEC. All the energy conditions are satisfied for our present model if the following inequalities hold.

NEC: $\rho +p\ge 0$, SEC: $\rho +p\ge 0$, $\rho +3p\ge 0$, WEC: $\rho +p\ge 0$, $p\ge 0$, and DEC: $\rho -p\ge 0$, $p\ge 0$.

$$\begin{array}{ccc}\hfill {(\rho +p)}_E& =& \frac{A(n-1)+B(n+1)r^{2n}}{4\pi r^2(n^2-2)(A-B{r}^{2n})},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill \rho +p& =& \frac{A(n-1)+B(n+1)r^{2n}}{r^2(n^2-2)(4\pi +\beta )(A-B{r}^{2n})},\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {(\rho +3p)}_E& =& \frac{-A(n-1)(n-2)+B(n+1)(n+2)r^{2n}}{4r^2\beta (n^2-2))(A-B{r}^{2n})},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill \rho +3p& =& \frac{A(n-1)(t-2(2\pi +\beta ))B(n+1)r^{2n}(S+2(2\pi +\beta ))}{2r^2(n^2-2)(2\pi +\beta )(4\pi +\beta )(A-B{r}^{2n})},\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {(\rho -p)}_E& =& \frac{n(A(n-1)+B(n+1)r^{2n})}{4\pi r^2(n^2-2)(A-B{r}^{2n})},\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill \rho -p& =& \frac{n(A(n-1)-B(n+1)r^{2n})}{4r^2\beta (n^2-2))(A-B{r}^{2n})},\hfill \end{array}$$

(32)

It is clear from Figure 3 that $\rho +p\ge 0$, in Figure 4, $\rho +3p\ge 0$ and $\rho -p\ge 0$ is non-negative shown in Figure 5. So, all the necessary energy conditions have been fulfilled for our $f(R,T)$ gravity model (see also in Figure 6 and Figure 7).

4. Exterior Space-Time and Boundary Condition

Now, we have matched our interior space-time to the exterior Schwarzschild line element at the $r=R$. The exterior line element is

$$\begin{array}{c}\hfill d{s}_{+}^2=-\left(1-\frac{2M}{r}\right)d{t}^2+{\left(1-\frac{2M}{r}\right)}^{-1}d{r}^2+r^2({sin}^2\theta d{\varphi }^2+d{\theta }^2).\end{array}$$

(33)

and the interior line element is

$$\begin{array}{c}\hfill d{s}_{-}^2=-{(A{r}^{1-n}-B{r}^{1+n})}^{2}d{t}^2+(2-n^2)d{r}^2+r^2({sin}^2\theta d{\varphi }^2+d{\theta }^2).\end{array}$$

(34)

The continuity of the metric

$$\begin{array}{ccc}\hfill {\left(1-\frac{2M}{R}\right)}^{-1}& =& (2-n^2),\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill \left(1-\frac{2M}{R}\right)& =& {(A{R}^{1-n}-B{R}^{1+n})}^2.\hfill \end{array}$$

(36)

The pressure vanishes at the boundary $r=R$, i.e., $p(r=R)=0$, which gives the following equation in modified gravity as follows

$$\begin{array}{c}\hfill \frac{-A(n-1){\chi }_2-B(n+1){\chi }_2{R}^{2n}}{4R^2(n^2-2)(2\pi +\beta )(4\pi +\beta )(A-B{R}^{2n})}=0\end{array}$$

(37)

• Determination of n and the constants A and B: Solving the Equations (35)–(37), we obtain the expression for n and the constants A and B as follows:

$$\begin{array}{ccc}\hfill n& =& \pm \sqrt{\frac{R-4M}{R-2M}},\hfill \\ \hfill A& =& -\frac{(n+1){\chi }_2{R}^{n-2}\sqrt{R(R-2M)}}{2n\beta },\hfill \\ \hfill B& =& \frac{(1-n){\chi }_1{R}^{n-2}\sqrt{R(R-2M)}}{2n\beta }.\hfill \end{array}$$

For numeric values of the constants A and B, we chose Mass M, and radius R accordingly for different compact stars. Additionally, for a well-behaved solution, we use different values of the parameter $\beta$.

5. Physical Properties of the Present Model

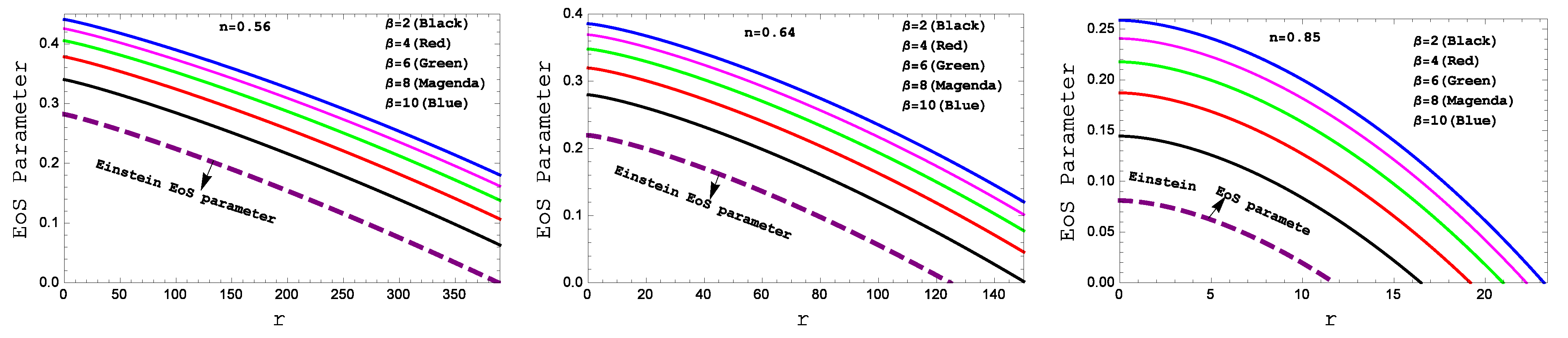
• Nature of equation of state: It is very important to describe a relationship between the energy density and the pressure, which is called the equation of state (EoS). The relation between the pressure and matter density can be found out by the dimensionless quantity, which is known as the equation of state parameter.

  $$\begin{array}{c}\hfill p=\omega \times \rho .\end{array}$$

  (38)
  Hence, the equation of state parameter (w) for Einstein and our model is obtained as follows:

  $$\begin{array}{ccc}\hfill {\omega }_E& =& \frac{p_E}{{\rho }_E}=\frac{A{(n-1)}^2-B{(n+1)}^2{r}^{2n}}{(1-n^2)(A-B{r}^{2n})},\hfill \end{array}$$

  (39)

  $$\begin{array}{ccc}\hfill \omega & =& \frac{p}{\rho }=\frac{-A(n-1){\chi }_2+B(n+1){\chi }_1{r}^{2n}}{A(n-1){\chi }_1-B(n+1){\chi }_2{r}^{2n}}\hfill \end{array}$$

  (40)
  The behavior of equation of state parameter is shown in Figure 8. We can see that the equation of state parameter is a monotonic decreasing function of radius r.
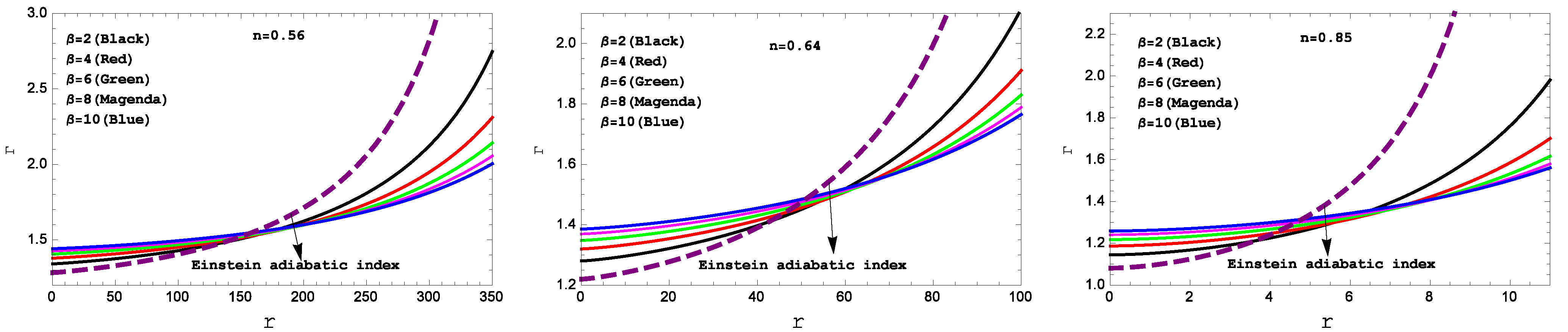
• Relativistic adiabatic index: For a compact star, stability is one of the most crucial requirements. For this reason, we have discussed stability along with the variation of adiabatic index $(\Gamma )$ inside the compact star. The adiabatic index can be displays the stability for both non-relativistic and relativistic compact stars. The stability condition for a Newtonian sphere is $\Gamma >\frac{4}{3}$ and $\Gamma =\frac{4}{3}$ is the condition for a neutral equilibrium according to [35]. The expression relativistic adiabatic index for Einstein and our present model is

  $$\begin{array}{ccc}\hfill {\Gamma }_E& =& {\left(\frac{\rho +p}{p}\frac{dp}{d\rho }\right)}_E=\frac{2(A(n-1)+B(n+1)r^{2n})}{B{(n+1)}^2{r}^{2n}-A{(n-1)}^2}{V}^2\hfill \end{array}$$

  (41)

  $$\begin{array}{ccc}\hfill \Gamma & =& \frac{4(A(n-1)+B(n+1)r^{2n})(2\pi +\beta )}{A(n-1){\chi }_2-B{(n+1)}^2{\chi }_2{r}^{2n}}{V}^2\hfill \end{array}$$

  (42)
• TOV Equation: The hydrostatic equilibrium $\left(F_h\right)$ equation is an important feature of the physical realistic compact objects. The fluid sphere remains at equilibrium under three forces, namely, gravitational force $\left(F_g\right)$, hydrostatic force $\left(F_h\right)$ and the additional force due to modified gravity $\left(F_m\right)$, and this situation is represented by an equation, which is known as the Tolman–Oppenheimer–Volkov (TOV) equation. With the help of a generalized TOV equation, we can analyze the equilibrium equation for our three compact stars. The generalized TOV equation for the isotropic fluid [36] distribution in $f(R,T)$ modified gravity can be written as

  $$\begin{array}{c}\hfill -\frac{{\nu }^{\prime }}{2}(\rho +p)-\frac{dp}{d\rho }-\frac{\beta }{2(4\pi +\beta )}(p^{\prime }-{\rho }^{\prime })=0\end{array}$$

  (43)
  Equation (43) can be written as follows:

  $$\begin{array}{c}\hfill F_g+F_h+F_m=0,\end{array}$$

  (44)

  where,

  $$\begin{array}{ccc}\hfill F_g& =& \frac{{(A(n-1)+B(n+1)r^{2n})}^2}{r^3(n^2-2)(4\pi +\beta ){(A-B{r}^{2n})}^2},\hfill \end{array}$$

  (45)

  $$\begin{array}{ccc}\hfill F_h& =& \frac{A^2(n-1){\chi }_2+4AB(n^2-1)(2\pi +\beta )r^{2n}+B^2(n+1){\chi }_1{r}^{4n}}{2r^3(2-n^2)(2\pi +\beta )(4\pi +\beta ){(A-B{r}^{2n})}^2},\hfill \end{array}$$

  (46)

  $$\begin{array}{ccc}\hfill F_m& =& \frac{n\beta (A^2(n-1)+B^2(n+1)r^{4n})}{2r^3(2-n^2)(2\pi +\beta )(4\pi +\beta ){(A-B{r}^{2n})}^2}.\hfill \end{array}$$

  (47)
  Since $\beta =0$ corresponds to GR. Hence, $F_m=0$, the TOV equation for Einstein reduces to

  $$\begin{array}{c}\hfill -\frac{{\nu }^{\prime }}{2}{(\rho +p)}_E-{\left(\frac{dp}{d\rho }\right)}_E=0\end{array}$$

  (48)
  Equation (48) can be written as follows:

  $$\begin{array}{c}\hfill {\left(F_g\right)}_E+{\left(F_h\right)}_E=0,\end{array}$$

  (49)

  where,

  $$\begin{array}{ccc}\hfill {\left(F_g\right)}_E& =& \frac{{(A(n-1)+B(n+1)r^{2n})}^2}{4\pi r^3(n^2-2){(A-B{r}^{2n})}^2},\hfill \end{array}$$

  (50)

  $$\begin{array}{ccc}\hfill {\left(F_h\right)}_E& =& \frac{{(A(n-1)+B(n+1)r^{2n})}^2}{4\pi r^3(2-n^2){(A-B{r}^{2n})}^2}.\hfill \end{array}$$

  (51)
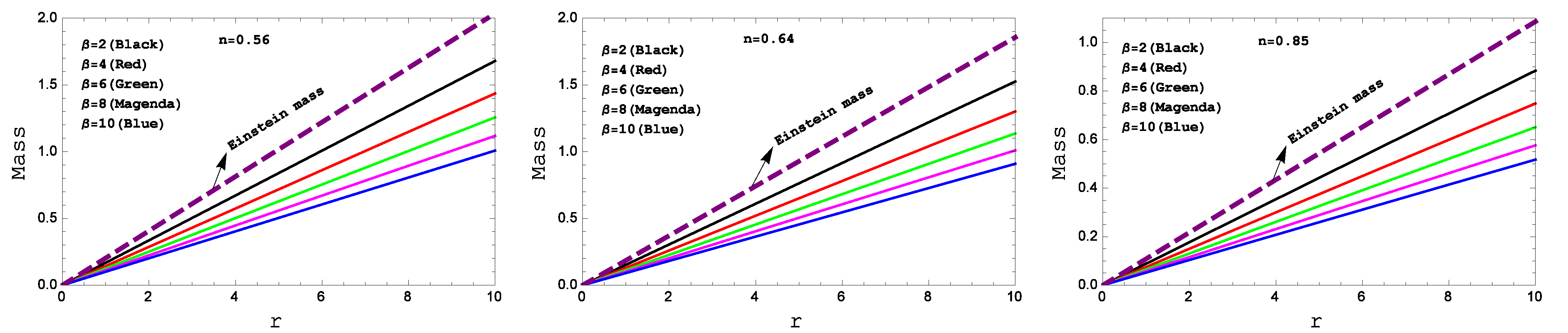
• Mass radius relationship and compactness parameter: let $\mathcal{U}$ be the compactification factor and M be the mass function (see Figure 9 for mass profile). Then, we can obtain the following relation between them:

  $$\begin{array}{ccc}\hfill {\mathcal{U}}_E& =& \frac{{\mathcal{M}}_E}{R}=\frac{(1-n^2)}{2(2-n^2)},\hfill \end{array}$$

  (52)

  $$\begin{array}{ccc}\hfill \mathcal{U}& =& \frac{\mathcal{M}}{R}=\frac{\pi \left((n+1){\chi }_2\right)+2n{\beta }_2{F}_1(1,\frac{1}{2n},1+\frac{1}{2n},\frac{B{R}^{2n}}{A})}{(2\pi +\beta )(4\pi +\beta )(A-B{R}^{2n})}\hfill \end{array}$$

  (53)

  where, $\mathcal{M}=m{\left(r\right)}_{r=R}.$ and ${}_2{F}_1$ represents the hypergeometric function. The expression for mass function for Einstein and our present model are

  $$\begin{array}{ccc}\hfill m_E& =4\pi {\int }_0^r{\rho }_E{r}^{2}dr& =\frac{(1-n^2)r}{2(2-n^2)},\hfill \end{array}$$

  (54)

  $$\begin{array}{ccc}\hfill m& =4\pi {\int }_0^r\rho r^{2}dr& =\frac{\pi r\left((n+1){\chi }_2\right)+2n{\beta }_2{F}_1(1,\frac{1}{2n},1+\frac{1}{2n},\frac{B{r}^{2n}}{A})}{(2\pi +\beta )(4\pi +\beta )(A-B{r}^{2n})}\hfill \end{array}$$

  (55)
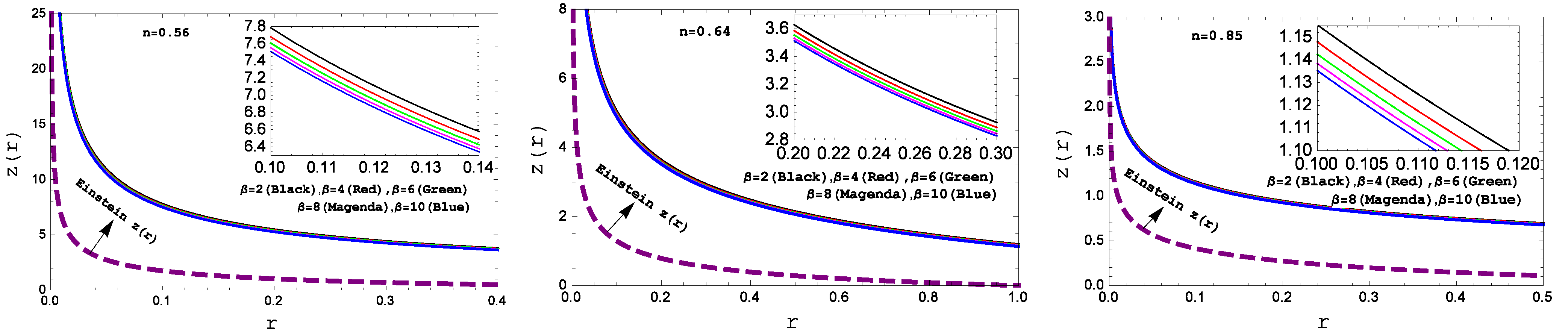
• Gravitational red-shift ($z\left(r\right)$) function and surface red-shift ($z_s$): The gravitational redshift can be determined by the formula

  $$\begin{array}{c}\hfill z\left(r\right)=e^{-\nu /2}-1=\frac{1}{(A{r}^{1-n}-B{r}^{1+n})}-1\end{array}$$

  (56)
  Furthermore, the following formula can be used to calculate the surface redshift $\left(z_s\right)$ for Einstein and our present model:

  $$\begin{array}{ccc}\hfill {\left(z_s\right)}_E& =& \frac{1}{\sqrt{1-2{\mathcal{U}}_E}}-1=\sqrt{2-n^2}-1\hfill \end{array}$$

  (57)

  $$\begin{array}{ccc}\hfill z_s& =& \frac{1}{\sqrt{1-2\mathcal{U}}}-1\hfill \end{array}$$

  (58)

  $$\begin{array}{ccc}& =& \frac{1}{\sqrt{1-\frac{2\pi \left((n+1){\chi }_2\right)+2n{\beta }_2{F}_1(1,\frac{1}{2n},1+\frac{1}{2n},\frac{B{R}^{2n}}{A})}{(2\pi +\beta )(4\pi +\beta )(A-B{R}^{2n})}}}-1\hfill \end{array}$$

  (59)
  Figure 10 shows the nature of the redshift function with respect to the radial coordinate function r. For our model, $z\left(r\right)$ is a monotonically decreasing function. The values of the surface redshift $\left(z_s\right)$ for three compact stars are shown in Table 2. One can see from the table that the value of redshift $\left(z_s\right)$ lies within the range $z_s<1$.

6. Discussion and Concluding Remarks

In this present work, we have investigated the behavior of Tolman VI spacetime in modified gravity. We endeavored to solve the modified field equations and investigated the physical viability according to the standard theory. We contrasted the behavior of the matter energy density, isotropic pressure, the sound speed energy, the all energy conditions (namely, weak, strong and dominated energy condition), EoS parameter, mass profile as well as gravitational redshift between the modified $f(R,T)$ theory and standard Einstein theory.

For the arbitrary constant $\beta =2,4,6,8$ and 10, the graphical pictures have been presented in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 for the compact stars $PSRJ1614-2230$, $VelaX-1$ and $4U1538-52$, while $\beta =0$ gives the general relativity case.

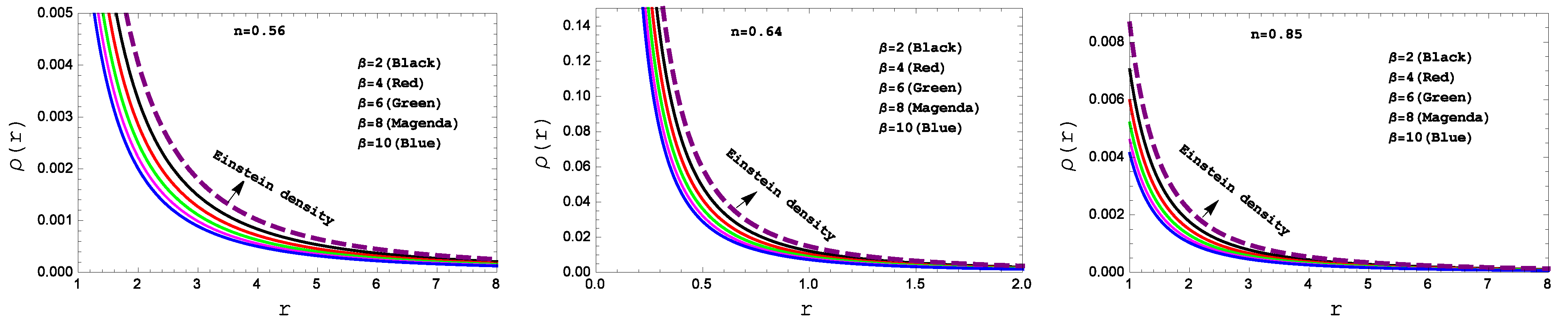
• A clear picture of energy progression has been obtained in Figure 1. The figure shows declining the nature of the surface and promises the real origination of the stellar body with positive behavior at the stellar interior.
• We have plotted pressure p versus radius r in Figure 2 for the three compact stars PSR J1614-2230 (left panel), Vela X-1 (middle panel) and 4U 1538-52 (right panel) for various values of $\beta$. One can see that $p>0$, i.e., positive, continuous and monotonically decreasing. Additionally, at some radial value, the pressure does vanish for both of the cases.
• Square of the sound speed and relativistic adiabatic index have been plotted in Figure 3 and Figure 4, respectively. From Figure 3, one can see that the square of the sound speed lies in the predicted range, i.e., $0<V^2<1$ throughout the fluid sphere. The Figure 4 confirms the stability of under the adiabatic index $\Gamma >\frac{4}{3}$ for our present model.
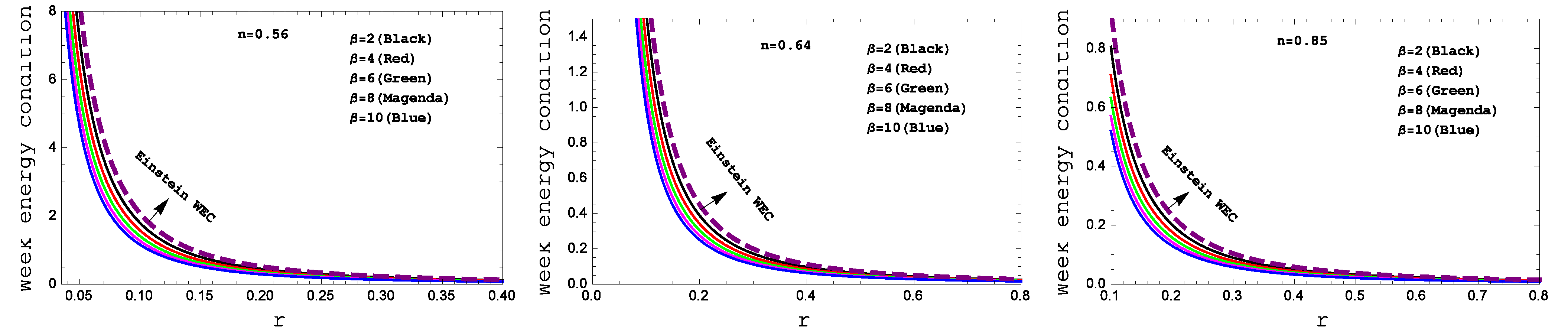
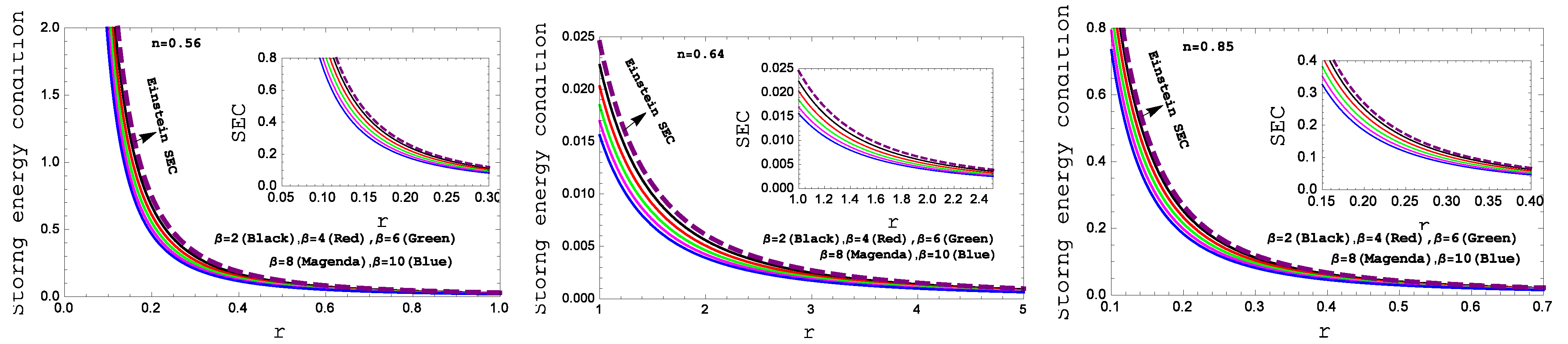
• In our $f(R,T)$ gravity model, the weak energy condition (WEC) in Figure 5, the strong energy condition (SEC) in Figure 6 and dominant energy condition (DEC) in Figure 7 are also met. For the complication in the expressions of density and pressure we have shown a graphical presentation the certifies the well-behaved nature of the energy conditions.
• We have plotted an equation of state parameter profile $\omega$ in Figure 8 for different values of $\beta$. It is clear from the figure that, at the center of the star, these parameter take maximum values, while it decreases towards the boundary. Moreover, $\omega$ lies between 0 and 1, i.e., $0<\omega <1$, which indicates the non-exotic behavior of matter distribution. Additionally, we can see that there are linear relations between the isotropic pressure (p) and matter density ($\rho$).
• The mass function is plotted against the radius in Figure 9. This figure shows that the mass function is a monotonically increasing function of the radius and has no central singularity. The mass functional values are in agreement with the required physical conditions as one can investigate from the figure. In our model, one can see that the maximum mass is less than $2.0M_{\odot }$. Thus, it is less than the critical maximum mass of neutron stars, so we cannot say our studied stars’ cores contain nucleons only, such as neutron star cores, where realistic nuclear forces are used.
• We have plotted the gravitational redshift in Figure 10 for different values of $\beta$. One can see that the gravitational redshift is a monotonically decreasing function of the radius. Additionally, the gravitational redshift is lower with higher values of coupling parameter $\beta$.

From all the graphical illustrations and obtained results, we can conclude that our present model is regular and potentially stable. Additionally, detailed numerical features can be found from Table 1 and Table 2. The numerical values of A and B increase with increasing values of $\beta$. When the coupling parameter $\beta$ is increased, the surface density ${\rho }_s$ and the surface red-shift $z_s$ both decrease. Moreover, the central values of adiabatic index ($\Gamma$ at $r=0$) increase with increasing values of $\beta$, which concludes that, for higher values of $\beta$, our model becomes more stable. Through analytical, numerical and graphical analysis, all the features of our present model are well-described. Finally, we summarize our discussion that we are convinced by the calculated outcomes, which shows that the system is physically reasonable and viably stable. Additionally, our outcomes could be usable in modeling relativistic compact objects as real astrophysical phenomena. In the future, we will study a perceptible magnetic pressure influence [32] to the equilibrium of forces for the core of the highly compact stars as the magnetic effects calculation can give some idea of the dynamical distortion in nuclear impacts.