Abstract
In this paper, we investigate the thermal stability and thermodynamic geometries of non-rotating/rotating charged black holes. For these black holes, we apply barrow entropy to determine the physical quantities such as mass and temperature of the system and find their stability through first and second phase transitions of the heat capacity. We analyze the effects of scalar charge Q and hair parameter on black holes properties by taking both positive and negative values of these parameters. It is noted that heat capacity provide the stable, unstable regions and phase transition points for both black holes. To investigate the thermodynamic geometry of these black holes, various techniques such as Ruppeiner, Weinhold, Quevedo, and HPEM metrics are considered. It is observed that Weinhold, Quevedo, and HPEM give attractive/repulsive behavior of particles in stable/unstable regions of black holes.
1. Introduction
Black holes (BHs) are the most fundamental and important objects in the universe [1,2]. Einstein proposed the theory of general relativity (GR) in 1915 and demonstrated how gravity can impact light beams and consequently light trajectory [3,4]. In 1916, Schwarzschild discovered the first simplest spherically symmetric metric that indicates an uncharged black hole (BH), known as Schwarzschild BH [5]. Droste [6], after the Schwarzschild solution, independently identified the same solution, which gives more details regarding BHs. In 1918, Reissner and Nordström developed an electrically charged vacuum BH solution called the Reissner-Nordström (R-N) BH [7]. In 1963, Kerr discovered a more general and accurate solution for a rotating BH [8]. Later in 1963, Kerr proposed the rotating BH solution with mass and angular momentum and named it Kerr BH, which contributes to the discovery of many spinning BH solutions [9]. The existence of singularity in BH was a major issue in GR and this was the common problem in most of the solutions of the Einstein field equations.
Despite the efforts of Khalatnikov, Lifshitz, and Belinsky [10,11] to establish that singularities would not exist in any general solution, Penrose [12] and Hawking [13] demonstrated that singularities may appear in any generic solution [14]. Taking the Kerr–Newman (K-N) metric as the most generic static BH, an inequality between three microstates such as mass, angular momentum and electric charge can be obtained as . Extremal BHs are those with the minimum mass that satisfy this inequality. However a solution for Einstein equations exist for a structure that violates this inequality, and the cosmic censorship hypothesis will be disproved by such a solution [15], implying that there is no event horizon encircling the postulated BH, which is known as naked singularity [16].
Let us examine the thermal properties of BHs, which lead to the well-known BH thermodynamics four laws [17,18]. The inverse of BH mass and heat capacity determines the Hawking temperature [19]. Heat capacity is negative in the Schwarzschild case, which implies the instability of the BH solution [20,21]. For the K-N and R-N BHs, the heat capacity might be positive in certain intervals while it can be negative in other regions and, interestingly, it can diverge in the middle area. This phenomenon is known as second-order phase transition, which is proposed by Paul and Davies for the first time after receiving Sciama’s suggestion [20]. After the introduction of the anti-de Sitter/conformal field theory (AdS/CFT) correspondence analysis of the thermal aspects of BHs, the thermodynamics of BHs have attracted a lot of attention [22,23]. Witten [24] demonstrated that the thermodynamics of AdS space may be described by means of the dual CFT that exists on the AdS space’s boundary. R-N metric in the AdS space [25], the Hawking phase transition [26], and other thermodynamical features of phase transitions have been studied in the literature for various scenarios.
The use of thermodynamical geometry to study the phase transition of BH has attracted a lot of interest. In fact, Weinhold was the first to introduce the geometrical approach for thermodynamics [27,28]. Weinhold proposed a metric for the space of equilibrium states based on the second derivatives of internal energy with respect to entropy and other significant variables. The inverse second derivatives of entropy with respect to internal energy and other extended quantities were developed by Ruppeiner [29,30]. Ruppeiner’s metric was conformal to Weinhold’s metric with the inverse of the temperature as the conformal factor [31]. According to the phase space and metric structures however, Weinhold’s and Ruppeiner’s metrics are not consistent under Legendre transformations [32,33]. After that, Quevedo [34] developed a new formalism that integrates the geometric features of the phase space with the space of equilibrium states. In addition, a new metric, Hendi- Panahiyan-Eslam Panah-Momennia (HPEM), was developed to construct a geometrical phase space using thermodynamical quantities [35]. In terms of basic thermodynamic equilibrium, a connection between thermodynamic system and differential geometry characteristics has been proposed and in the latter metric due to the large number of thermodynamic quantities, a geometrical phase space was effectively developed. Khuzani et al., Mansoori et al., and Mustapha discussed the thermodynamic geometry of different BHs [36,37,38,39].
In recent years, different authors have worked on the characterization of Einstein Maxwell (EM) dilation BH solutions. Zhang et al. [40] investigated the methodology of entirely nonlinear dynamical scalarization in the EM dilation theory, beginning with a charged BH flat spacetime. Haroldo et al. [41] studied the topological charge, lensing, and shadows of EM dilation BHs in strong magnetic fields. Richarte et al. [42] studied focused absorption and scattering of charged BH in the EM dilation theory. In order to determine the deflection angle and the differential scattering bend in terms of electric charge, dilatonic charge, and mass, they studied the classical analysis. Rogatko [43] classified the non rotating BHs in different gravities such as anti-Maxwell, Einstein phantom, and EM dilation gravity systems. In addition, several authors have worked on BHs with self-interacting, massive scalar, and expansion of charged dilatonic BHs showing the Joule–Thomson effect [44,45,46].
According to the classical relativistic model, if BHs genuinely had no entropy, then every time an item went into BH, its entropy would be essentially destroyed, decreasing the entropy of the universe and breaking the second law of thermodynamics. Bekenstein proposed that BHs should contain entropy to solve this problem [47]. Hawking proved that this hypothesis was valid using a semi-classical technique, finding that BHs radiate energy and as a result, an external observer would link a temperature with the BH horizon [48]. The horizon temperature is related to the surface gravity by the rules of thermodynamics. Then, the BH entropy, also known as the Bekenstein–Hawking entropy, is given by , where is the entropy and A is the BHs surface area (in units where ). Recently, Barrow proposed that quantum-gravitational forces create a fractal pattern on the BH horizon, which gains a spatial dimension more than two but less than three, as measured by the parameter [49]. Hence, such a complicated structure leads to a modification of the BH entropy. This idea may have interesting consequences in cosmological and holographic applications [50,51]. Recently, Soroushfar et al. [52] discussed the thermodynamic stability as well as thermodynamic geometries (using Ruppeiner, Weinhold, Quevedo and HPEM formalisms) for conformal massive gravity (CMG) corrected static and rotating BHs and found interesting results.
The above intriguing topics encouraged us to use a geothermodynamic technique to examine so-called CMG of BHs through Barrow entropy. In this approach, both static (non-rotating) and rotating BHs, the second phase transition and its features help us to understand the physics of singularities. Interestingly, this method can also be used to better understand the behavior of temperature, heat capacity, and other thermodynamic parameters. We also discuss the thermodynamic geometry of the static and rotating BH with Barrow entropy. The paper is organized as follows. In Section 2, we provide the basic scenario of static regular BH in CMG setup along with Barrow entropy. In Section 3, we explore the thermodynamic properties of above BH such as mass, temperature, and specific heat with respect to various set of values of model constants. Section 4 is devoted to discuss the thermodynamic geometry of static regular BH in CMG with Barrow entropy by taking Ruppeiner, Weinhold, Quevedo, and HPEM metrics. Ins Section 5, we provide details of rotating regular BH with CMG and Barrow entropy setups. Section 6 and Section 7 provide the thermodynamic properties and thermodynamic geometry discussions for rotating regular BH. The last section provides detailed results for both BHs.
2. Non-Rotating Regular Black Hole in Conformal Massive Gravity
In this section, we give an overview of the metric of a static regular BH under CMG. Fierz and Pauli were the first to examine the concept of MG and created a singularity-free spherically symmetric BH solution [36]. By rescaling the metric with a scale factor, a new method is presented for discovering regular BH solutions [53,54]. The resultant metric becomes the solution of a theory having conformal symmetry and is regular everywhere. The basic notion behind conformal gravity (CG) is that the space time singularities that arise in gravity theories are simply display artifacts in CG that may be erased by a proper gauge transformation. The behavior of the MG theory is explained by the following action
where
and R stands for Ricci scalar. In Equation (1), the value of which is the order of mass whereas m and are the graviton mass and Planck mass. We consider the function , which depends on two specific combinations of four Goldstone fields, and , and are minimally related to gravity through derivative coupling. At the action level, this model is generally covariant and can satisfy the Lorentz symmetry condition [43]. For instance, in Ref. [43], various analytical solutions are introduced for the function and among them, one is given by
where is a constant and , or another example, as follows
where , and . In order to investigate the repercussions of symmetry violation, one can use a background solution with the energy momentum tensor being zero, such as
for some constants and by taking for this model of MG. Jusufi et al. [55] discussed a static spherically symmetric BH along with CMG correction by applying a conformal transformation with the help of Equation (3) as [43]
Here, L stands for the CMG parameter, which was added for dimensional reasons and , which stands for the hair parameter and the scalar charge, respectively. In the next sections, we analyze the geothermodynamics of a metric derived from CMG and thermodynamic essential factors such as mass, temperature, and heat capacity.
Barrow Entropy
According to Barrow, quantum-gravitational forces create a fractal structure on the BH horizon, which gains a spatial dimension of more than two but less than three, as measured by the parameter [56]. As a result of this complicated structure, the BH entropy is altered. In cosmological and holographic applications, this concept could have fascinating implications [57,58]. However, it modifies the BH temperature and has interesting consequences for its properties [59,60]. Barrow [56] proposed that quantum gravitational effects could cause a complex fractal pattern on the BHs surface and modify its actual horizon area. As a result, a new BH entropy relationship takes the form
where A is the ordinary event horizon area, is the Planck area, and is the new exponent. The aforementioned deformed entropy differs from the standard “quantum-corrected” one with logarithmic corrections [61,62], yet it resembles Tsallis non extensive entropy [63,64], despite the fundamentally different physical principles. The new exponent specifies the quantum gravitational distortion, which is limited to the range with corresponding to the conventional Bekenstein–Hawking entropy and to the maximum deformation of the horizon structure. Here, we consider the Planck area as and where G is the gravitational constant (we take ) and after replacing these values in Equation (5), we get
3. Thermodynamic Quantities
Here, we will discuss mass, temperature, and heat capacity of non-rotating regular BH in CMG in the presence of Barrow entropy.
3.1. Mass
We can write the mass of non-rotating BH in terms of Barrow entropy by replacing Equation (6) in as
After solving, we get
In Figure 1, we plot the above equation for various cases of a set of values of model parameters such as and to discuss the behavior of mass function for static BH through CMG corrections. Plots (i) and (ii) show the behavior of mass for the fix value of , with and , respectively. For plot (i), the trajectory for represents the positive behavior, which indicates the Schwarzschild BH solution. The remaining curves express the negative behavior initially, which transit to positive behavior with increasing values of and decreasing values of Q. Thus the trajectories of mass function for R-N BH solutions represent negative to positive behavior. In plot (ii), we observe that all the trajectories show the positively increasing behavior of mass function with respect to all values of horizon radius. This indicates that the Schwarzschild BH solution for and R-N BH solutions give positive behavior. Plots (iii) and (iv) represent the evaluation of mass for specific amount of , with and , respectively. In plot (iii), the curve related to shows positive behavior for all the values of while the remaining curves represent negative behavior initially as we increase the value of . However, with the increasing values of , these curves become positive. In plot (iv), we examine that all the curves indicate positive behavior initially, which transit to negative behavior for and to positive behavior for with respect to the increasing horizon radius. Another notable behavior of the mass function that appears in these plots is converging to a specific amount of M at .
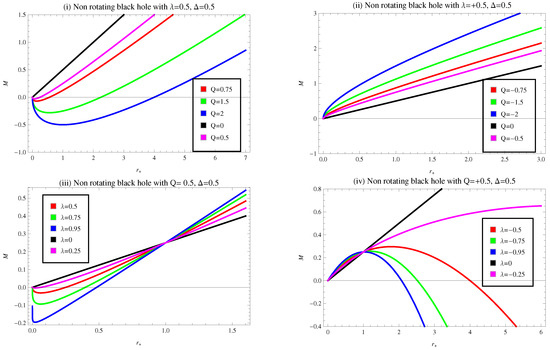
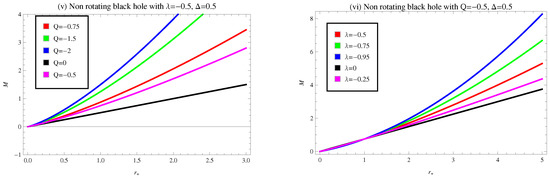
Figure 1.
Plot of mass M versus horizon radius for non-rotating BH for various choices of and Q.
Plots (v) and (vi) indicate the behavior of mass function for the fix value of , with and the fix value along with . The behavior of mass for these plots demonstrate the overall positive values similar to the case of plot (ii). Additionally, plot (vi) inherits the converging point for mass M at . It is noted that the plots (i) and (iii) for smaller values of horizon radius and plot (iv) for higher values of horizon radius depict the negative behavior of mass function for a chosen set of values. The possibility of a negative mass is one of the scenarios that has been thoroughly investigated in Refs. [65,66]. The concept of a negative mass from a gravitational perspective is widely examined in Ref. [65]. Although it is difficult to establish this argument in our everyday lives, it may be essential to explain some key physics events such as Hawking radiation. A claim was also done previously in Ref. [67] that a negative mass can act as both dark matter and dark energy at the same time. According to Ref. [68], the negative mass could be a potential candidate for dark matter, since it does not mix due to gravity and the structures do not naturally form by preventing nuclear fusion and as a result, electromagnetic radiation.
3.2. Temperature
The first law of BH thermodynamics is as follows
where is a scalar potential that is similar to the electrostatic potential and T stands for temperature [69]. Taking the derivative of Equation (7) with respect to entropy S, we get
In Figure 2, we draw the aforementioned equation for different cases of model parameters such as and to examine the behavior of temperature for static BH with CMG corrections. Plot (i) shows the behavior of temperature for fixed values of with . In plot (i), the temperature first is in the negative regions for a specific range of , representing the non-physical BH solution, then approaches to zero. After that, the temperature goes up to the positive region and increases to reach a maximum point, then it falls positively with respect to increasing , showing the physical BH solution. Plots (ii) and (iii) specify the behavior of temperature for a particular value of , , with and , respectively. For plot (ii), the curve for demonstrates the positive behavior that is a Schwarzschild-like physical BH solution through CMG corrections. While for , all the remaining trajectories show the same behavior as of plot (i) ( for smaller values of and for higher values of ). In plot (iii), we note that all curves show the positively decreasing behavior by increasing the values of and decreasing the values of Q, which indicate that physical BH solutions are possible for a chosen set of values of constants.
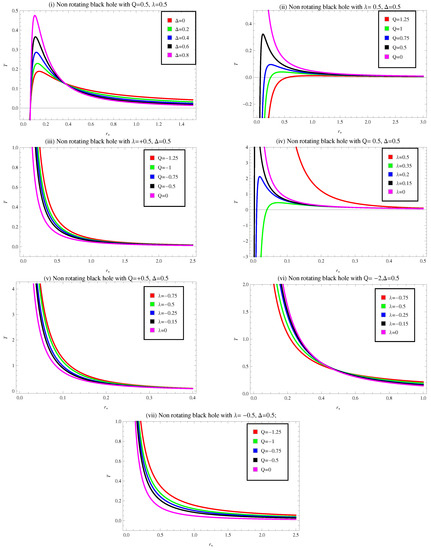
Figure 2.
Plot of temperature T versus horizon radius for non-rotating BH for various choices of and Q.
Plots (iv) and (v) reveal the nature of temperature for a fix value of , with and , respectively. From plot (iv), the curves for represent the decreasing positive behavior, which is a physically acceptable solution while all the remaining trajectories show the same behavior as in plot (ii). In plot (v), the temperature function shows the same behavior as in plot (iii). Plots (vi) and (vii) illustrate the behavior of temperature for specific values of , with and with , respectively. We can see that from these plots all curves represent identical behavior, as we discussed in plots (iii) and (v). With respect to all chosen sets of parameters, the hair parameter may be used as a charge parameter to analyze the evolution of the temperature of BHs at some instances. In addition, it is interesting to mention here that the curves of the temperature approaches zero with respect to the increasing values of horizon radius, and the BH becomes cooler due to the lower temperature.
3.3. Heat Capacity
In BH thermodynamics, the quantity of heat required to alter a BH’s temperature is called thermal capacity or heat capacity. Heat capacities are classified into two types: one type counts the amount of heat transferred to the system while keeping the pressure and the other type examines the specific heat when heat is introduced to the system while preserving the volume constant . We determine the heat capacity at a fixed volume. The heat capacity is defined by the ratio of temperature with its second derivative , i.e., . These parameters individually represent the following outcomes [65]
These equations can be used to impose some limitations on the model in order to differentiate between physical and non-physical outcomes. In other words, they state that the root of heat capacity, i.e., , denotes a physical and non-physical BH boundary, which is referred to as a physical limiting point. Because of this fact, one may normally predict a change in the sign of the heat capacity in the thermodynamic system. Divergence of the heat capacity is also well-known to signify a BH phase transition critical point. Taking into account Equation (9) and its derivative with respect to S and use in heat capacity formula, we obtain
In Figure 3(i)–(vi), we interpret the performance of heat capacity of no-rotating BH through Barrow entropy for various values of . The heat capacity has root points and divergence points , which are related to the physical limitation and phase transition critical points, respectively. Plot (i) and its close-up image (ii) reveal some entrusting physical features of heat capacity for specific values of . This plot indicates the variation of heat capacity between the first and second phase transitions. It is also observed that heat capacity gets negative values in the ranges , which leads to an unstable region of BH. For , it enters the positive region, which implies the stable state of BH solution. The physical limitation points, and phase transition critical point of the BH appears at . Plot (iii) represents the behavior of heat capacity for fixed values of , with . In this plot, the curve for represents negative behavior, which implies that the system is totally unstable, which is a Schwarzschild BH solution. While for R-N BH, the remaining trajectories show the same behavior as plots (i) and (ii).
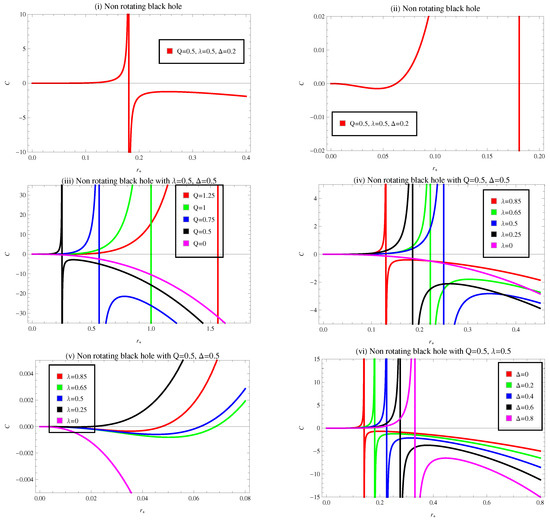
Figure 3.
Plot of heat capacity versus horizon radius for static regular BH in the presence of CMG corrections.
Plots (iv) and (v) evaluate the nature of heat capacity for specific amounts of and with . The system is totally unstable when , while for remaining values of , the heat capacity show the identical behavior as plots (i) and (ii). It is also observed that the variation in phase transition points with respect to the horizon radius occur for increasing Q, which is similar behavior as seen in plot (iii) while for plots (iv) and (v) by decreasing the values of , we get the same behavior as discussed in plot (iii). Plot (vi) illustrates the behavior of heat capacity for constant values of and with . We have found the same behavior as we discussed above. In Figure 4, we investigate the behavior of heat capacity for the different values of model parameters . From plots (i)–(iv) heat capacity represents the negative behavior and also does not display any phase transition for a CMG corrected non-rotating regular BH. It means that the system is totally unstable for negative values of parameters Q and .
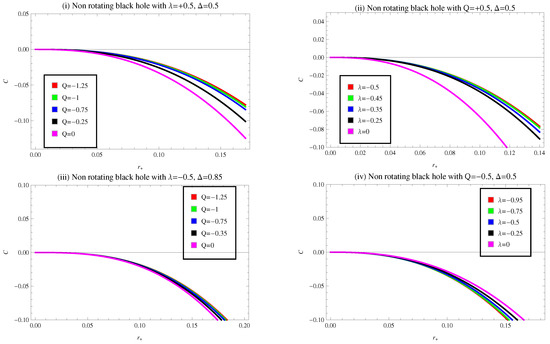
Figure 4.
Plot of heat capacity versus horizon radius for non-rotating BH for various choices of and Q.
4. Thermodynamic Geometries
In this part, we discuss the thermodynamic geometries such as Weinhold, Quevedo, Ruppeiner, and HPEM for a CMG corrected regular BH. Weinhold proposed a new geometric technique in 1975 [27] in which a metric is defined in the space of equilibrium states of thermodynamic system. From Riemannian space to thermodynamic space, Weinhold applied the concept of conformal mapping. The Weinhold geometry and its line element are respectively expressed by [28]
and
where and . The corresponding metric tensor is given by
We cannot characterize the phase transition of this thermodynamic system because of the vanishing curvature scalar in the Weinhold formalism. There is no point that becomes unique for this metric and therefore this system lacks interacting thermodynamics. There are a few solutions to this problem, which we shall go over one by one. In 1979, Ruppeiner [29] proposed a new metric, which is conformally connected to Weinhold’s metric as follows [30,70,71]
Dividing Equation (14) by (9), we obtain the appropriate matrix for Ruppeiner metric as
and by using Equation (16), the Ruppeiner metric’s curvature scalar (which is also called Ricci scalar) becomes
The corresponding curvature scalar plotted against the horizon radius by taking appropriate values of constant parameters are shown in Figure 5(i)–(iv). It can be seen that the divergence of the Ruppeiner metric’s curvature scalar overlaps with the zero points (physical limitation point) of heat capacity. It is observed that the upper branch of the curvature scalar crosses the heat capacity diagram in the stable regions of BH. It is also mentioned here that curvature () show singularity, positive, and negative in certain ranges of the horizon radius. It means that exhibits the attractive as well as repulsive behavior of BH.
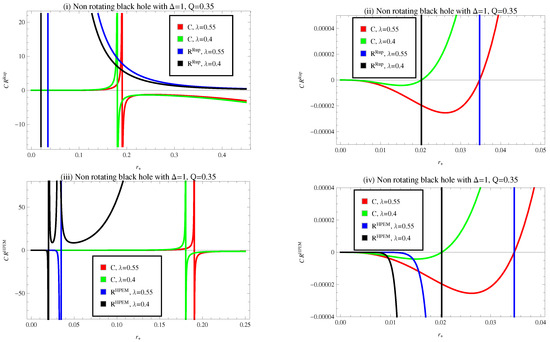
Figure 5.
Plots of heat capacity , curvature scalar of HPEM and Ruppeiner metrics versus horizon radius for CMG corrected non-rotating regular BH.
Let us now turn our focus to other geothermodynamic experiments that have yielded more promising physical results. In this step, we describe the thermodynamic properties of a CMG corrected non-rotating regular BH using the Quevedo and HPEM formalism. In Quevedo formalism, the metric takes the following generic form [34]
in which
where the extensive and intensive thermodynamic variables are and , respectively, while the thermodynamic potential is . In addition to the aforementioned, the HPEM metric with n extensive variables is [35,72,73]
where and are the extensive parameters. The Wienhold and the Ruppeiner thermogeometric metrics mentioned previously are not Legendre-invariant. Furthermore, results obtained using the Ruppeiner and Weinhold metrics may dispute one another. Moreover, Quevedo et al. asserted that the reasons for these discrepancies are caused by the fact that these metrics are not really Legendre-invariant, leading them to develop a Legendre invariant metric framework [34,74,75,76]. Following, we will go through two different kinds of Legendre invariant thermogeometrical metrics. These are Quevedo I and II. The concept that we use was first created by Hermann and Mrugala [77,78,79], and frequently used by Quevedo after that. Therefore, these two metrics can be written as [35,72,73]
and their curvature scalar’s denominator is found in the following form [72,73]
In Figure 5, we plot the above equations for different values of parameters such as and Q. Examining these equations reveals that the Quevedo formalism’s curvature scalar provides no physical information about the system. However, as shown in plots (iii)–(iv), the HPEM metric’s curvature scalar divergence points are in alignment with zero point (physical limitation point) and divergence point (phase transition point) of heat capacity. It is also mentioned here that curvature () shows singularity, positive, and negative in certain ranges of the horizon radius. As, we can seen from Figure 5, the curvature scalar of the Ruppeiner metric is in the positive and negative region, which indicates that exhibits the attractive as well as repulsive behavior of BH. We conclude that the positive behavior of BH reveals the stability of BH.
5. Rotating Regular Black Hole in Conformal Massive Gravity
In this section, we study the singularity-free rotating BHs in the presence of CMG corrections. Azreg [80] found the solutions of rotating BH without complexification, in particular, by rescaling the Kerr–Newman metric, the singularity-free BH solutions have been obtained. Such a metric can be expressed as [55]
where
In this metric, , J stands for angular momentum and parameters L and occur because of CMG corrections. In this case, the entropy-horizon radius relation takes the form and after substituting this value along with the Planck area in Equation (5), we get the Barrow entropy for rotating BH as
6. Thermodynamic Properties
In this section, we examine the thermodynamics properties of rotating charged regular BH such as mass, temperature, and heat capacity in the presence of CMG corrections through Barrow entropy.
6.1. Mass
We obtain the mass function by considering the condition in terms of entropy S to determine the mass function. Using Equation (25) to find the event horizon radius relationship, one gets
In Figure 6, we plot the aforementioned equation for various cases of model parameters such as and a to discuss the behavior of mass function for rotating BH in the presence of CMG corrections. Plots (i) and (ii) demonstrate the behavior of mass function for fix values of with and , respectively. For plot (i), the trajectories for show an initially positively decreasing behavior for small values of , after that it becomes an increasing behavior by increasing . The remaining curves represent an initially positively decreasing behavior, then enter the negative region, and after that show a positively increasing behavior. Furthermore, in plot (i), when , it is a Kerr BH solution. In plot (ii), the curves show a positively decreasing behavior first then a positively increasing behavior by increasing . In both plots by increasing the values of Q, minimum points decrease by increasing . Plots (iii) and (iv) represent the nature of mass for constant values of with and , respectively.
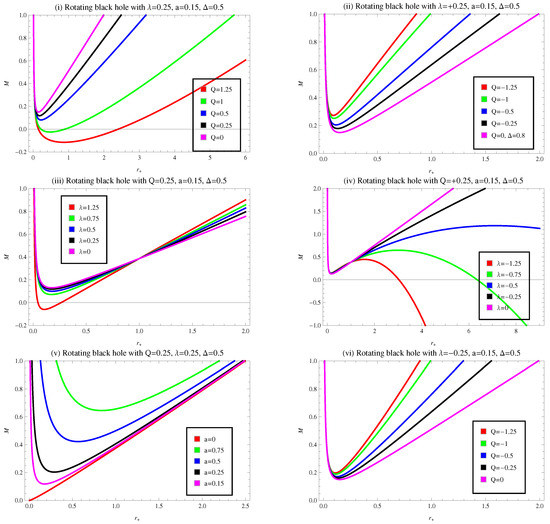
Figure 6.
Plot of mass M versus horizon radius for rotating regular BH in the presence of CMG corrections.
For plot (iii), the curve for describes the initially positively decreasing behavior, while for smaller values of , it shows negative behavior. After that, it enters the positive region by indicating positively increasing behavior. The remaining trajectories display the same behavior as in plots (i) and (iii). In plot (iv), the curves for initially describe a positive behavior, which go to the negative region by increasing the values of . Plot (v) describes the evaluation of mass function for specific values of with . For , the curve represents positively increasing behavior, while the remaining trajectories show the same nature as plot (i). Plot (vi) demonstrates the behavior of mass for fix values of with . This plot shows the same behavior as plot (ii). Another notable behavior of the mass function that appears in plots (iii) and (iv) is converging to a specific amount of M at .
6.2. Temperature
In Figure 7, we plot the equation of temperature for different cases of model parameters such as and a for rotating BH in the presence of CMG corrections. Plots (i) and (ii) describe the behavior of temperature for fix values of with and , respectively. In plot (i), the temperature first is in the negative region for a particular range of , representing the non-physical BH solution, then approaches to zero. After that, the temperature goes up to the positive region and increases to reach a maximum point, then it falls positively with respect to increasing showing physical BH solution, while all the curves in plot (ii) behave like plot (i). Plots (iii) and (iv) describe the nature of temperature for constant values of with and , respectively. In plot (iii), we note that all the trajectories show the same behavior as in plots (i) and (ii).
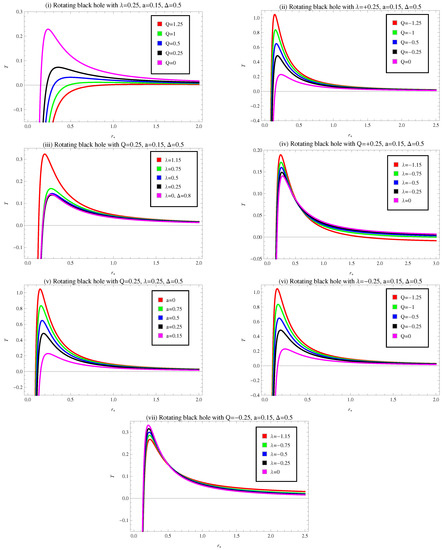
Figure 7.
Plot of temperature T versus horizon radius for CMG corrected rotating regular BH.
In plot (iv), when , the temperature shows initially negative behavior for smaller values of , then gradually increasing. After that, the temperature represents decreasing behavior by increasing . Meanwhile, all the remaining curves show identical behavior to plots (i)–(iii). Plot (v) evaluates the nature of temperature for fix values of with . We can see that temperature function shows the same behavior as plots (i)–(iii). Furthermore, when , which corresponds to non rotating R-N BH solution. Plots (vi) and (vii) demonstrate the behavior of temperature for constant values of with and for fix with , respectively. In these plots all the trajectories represent the same behavior as of plots (i)–(iii).
6.3. Heat Capacity
Now by replacing the values of T and in the expressions , we get the heat capacity as
where
We have plotted the heat capacity for various values of parameters like , , Q, and a in Figure 8(i)–(vii). Plot (i) and its close-up image (ii) represents the behavior of heat capacity for specific amount of , , , and indicates how and where heat capacity moves between the first and second phases transitions. For , heat capacity gets negative values and it specifies that BH will be in an unstable region. For , it enters to the positive region which implies the stable state of BH solution. The physical limitation points, , and phase transition critical point of the BH identifies at . In plots (iii) and (iv) heat capacity shows the same behavior as of plots (i) and (ii). Plots (v) and (vi) indicate the behavior of heat capacity for specific values of , , with , we can see the trajectories represent the same behavior as of plots (i)–(iv). Plot (vii) show the behavior of heat capacity for fix values of with . The curve for shows negative behavior, its mean the system is totally unstable. While all the remaining trajectories express the same behavior as of plots (i)–(vi).
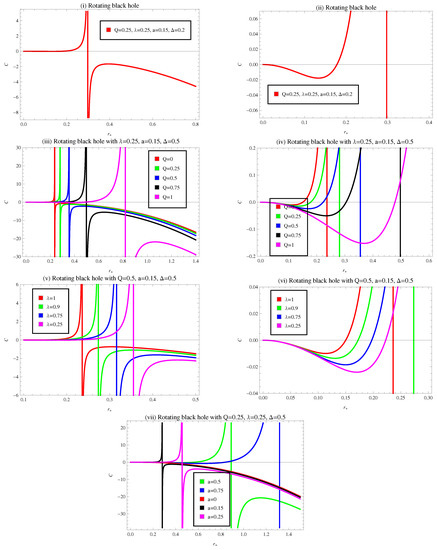
Figure 8.
Plot of heat capacity versus horizon radius for rotating regular BH in the presence of CMG corrections.
The plot of heat capacity versus horizon radius for different appropriate choices of and is shown in Figure 9(i)–(vi) in the presence of Barrow entropy. This exhibits positive behavior, however negative as well as phase transitions at certain values of horizon radius. This behavior points out the stable as well as unstable regions of the rotating BH in the presence of Barrow entropy.
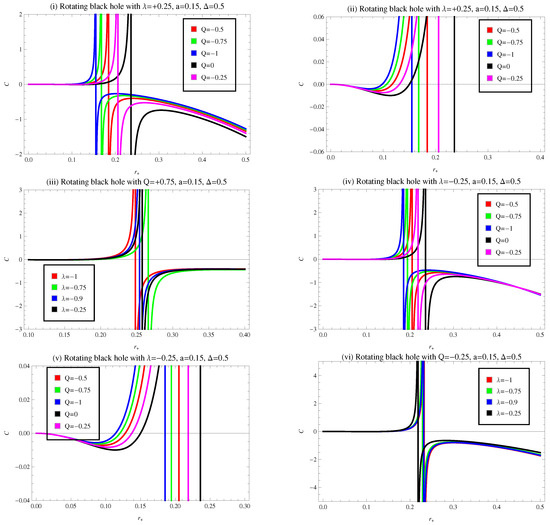
Figure 9.
Plot of heat capacity versus horizon radius for CMG corrected rotating regular BH.
7. Thermodynamic Geometries for Rotating Black Hole
For rotating BH, Ruppeiner, Weinhold, Quevedo, and HPEM metrics turn out to be [30,35,72,73,81,82]
For their curvature scalars, these metrics have the following denominator [30,35,72,73,81,82]
In the above equations, Quevedo formalism does not give any specific physical information about the system because the second derivative of mass function with respect to Q is zero, this means that the curvature scalar of Quevedo is also zero. The obtained curvature scalars for the remaining formalisms are shown in terms of horizon radius in order to analyze the thermodynamic phase transition seen in Figure 10. In plot (i), we can see that the singular point of the Weinhold curvature scalar does not overlap with the heat capacity divergence points for fixed values of with and . We can see that in plots (ii)–(v), the Ruppeiner and HPEM curvature scalar divergence points align with the heat capacity zeros and divergence point, which is the physical limitation points and phase transition point.
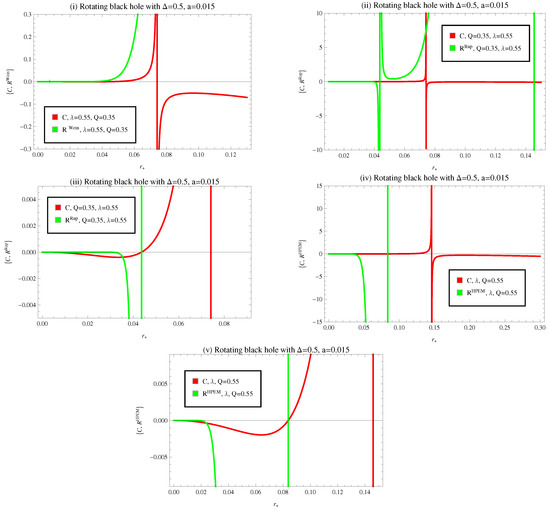
Figure 10.
Combine plots of heat capacity and Ricci scalar R of Ruppeiner, Weinhold, and HPEM metric versus event horizon radius .
8. Concluding Remarks
In this paper, we have investigated the Barrow entropy effects on mass, temperature, and heat capacity for CMG corrected non-rotating/rotating BHs. In addition, thermodynamic geometries such as Ruppiner, Weinhold, Quevedo, and HPEM curvature scalars have also been discussed for these BHs. Firstly, we have analyzed the behavior of thermodynamic properties such as , and of non-rotating BH with CMG corrections in the presence of Barrow entropy. We have figured out that for and , the mass function shows only positive behavior, which is a Schwarzschild BH solution, while for , and , mass function represents the initially negative behavior for smaller values of . After that it goes to a positive region by increasing . When , the mass function demonstrated the positive behavior as well. For negative values of , the mass function shows positive behavior but in some cases gets negative values. We have also investigated the behavior of temperature for different values of model parameters and . For , the curve of temperature represented positively decreasing behavior with increasing , which is a Schwarzschild non-physical BH solution. We have also noted that the trajectories for and indicated the same behavior as of when . For R-N BH, as the curves for , and , the temperature initially in the negative region for a particular range of is represented by a non-physical BH solution, and then approaches zero. After that, the temperature goes up to the positive region and increases to reach a peak point, then it falls positively with respect to the increasing physical BH solution. The hair parameter may be used as a charge parameter to analyze the evolution of the temperature of BHs at some instances. For negative values of all the trajectories expressed positively decreasing behavior.
We have also found that the curves of temperature approach zero with respect to the increasing values of horizon radius, and the BH gets cooler due to the low temperature. We have also discussed the stability of a BH, and we have observed that for , heat capacity gets negative values and it specifies that BH will be in an unstable region. For , it enters the positive region, which implies the stable state of the BH solution. The physical limitation points, and phase transition critical point of the BH appears at . For and the curves of heat capacity indicated negative behavior, which means that the system is totally unstable. The divergence points of heat capacity shifted along the horizon radius by increasing the values of Q and decreasing the values of . For negative values of , heat capacity showed only negative behavior, so the system is in an unstable state in this case.
In case of rotating BH with CMG corrections with Barrow entropy, we have observed that the trajectories for initially represented a positively decreasing behavior for a smaller range of , after it showed negative behavior for a small interval of horizon radius. It then entered the positive region and described the positively increasing behavior. Meanwhile, for all remaining values of Q, mass function indicated positive behavior. Here, expressed the same behavior as , while all other values of mass function always demonstrated positive behavior. The trajectories for the variation of rotation parameter a mass function indicated overall positive behavior. For negative values of , showed the same behavior as we discussed above but in some cases represented negative behavior by increasing . Another entrusting behavior of the mass function converges to a specific amount of M at .
Next we discussed the behavior of temperature. All the curves for , and of the temperature are first in the negative region for a small range of represented non-physical BH solution, then approaches zero. After that, the temperature goes up to the positive region and increases to reach a maximum point, then it falls positively with respect to the increasing , showing the physical BH solution. For negative values of and , the temperature indicated the same behavior as we already discussed, while for , the curve showed negative to positive then positive to negative behavior. We also observed that by increasing the size of BH, the temperature of BH decreased, meaning that the BH becomes cooler. To investigate the stability of a rotating BH one can consider heat capacity as one of the important thermodynamic parameters. We have figured out that the BH is in an unstable phase in this interval , while for , which implies the stable state of BH solution. The physical limitation points, and the phase transition critical point of the BH is identified at . For all other values of , and a, the same behavior as we discussed was shown and the phase transition points shifted along the . The negative values of with demonstrated the same behavior as we discussed above.
Moreover, thermodynamic geometries have shown attractive and repulsive behavior in stable and unstable regions of non-rotating and rotating BH.
Author Contributions
Conceptualization, A.J. and S.R.; methodology, A.J. and M.H.; software, M.H. and A.J.; validation, A.J. and M.H.; Mathematical investigation, M.H. and A.J.; writing original draft preparation, S.R. and M.H.; Review and editing, A.J., S.R. and M.H.; supervision, A.J. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
There is no associate data regarding this manuscript.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Barish, B.C.; Weiss, R. LIGO and the detection of gravitational waves. Phys. Today 1999, 52, 44. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D. First M87 event horizon telescope results. VI. The shadow and mass of the central black hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar]
- Einstein, A. Die Feldgleichungen der Gravitation, Sitzung der Physikalische-Mathematischen Klasse; Scientific Research: Atlanta, GA, USA, 1915; Volume 25, pp. 844–847. [Google Scholar]
- Einstein, A. Die Grundlage der Allgemeinen Relativitätstheorie; Wiley Online library: Hoboken, NJ, USA, 1916; Volume 49, pp. 769–822. [Google Scholar]
- Bel, L. Über das gravitationsfeld eines massenpunktes nach der Einsteinschen theorie. arXiv 2007, arXiv:0709.2257. [Google Scholar]
- Droste, J. The Field of a Single Centre in Einstein’s Theory of Gravitation, and the Motion of a Particle in That Field, Koninklijke Nederlandsche Akademie van Wetenschappen; KNAW: Amsterdam, The Netherlands, 1917; Volume 19, pp. 197–215. [Google Scholar]
- Reissner, H. Über die Eigengravitation des Elektrischen Feldes Nach der Einstein’schen Theorie, Annalen der Physik; Wiley Online library: Hoboken, NJ, USA, 1916; Volume 50, pp. 106–120. [Google Scholar]
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 111, 237–238. [Google Scholar] [CrossRef]
- Newman, E.T.; Couch, R.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a rotating, charged mass. J. Math. Phys 1965, 6, 918–919. [Google Scholar] [CrossRef]
- Belinskii, V.A.; Khalatnikov, I.M. On the nature of the singularities in the general solution of the gravitational equations. Soviet JETP 1969, 29, 911. [Google Scholar]
- Belinsky, V.A.; Khalatnikov, I.M.; Lifshitz, E.M. Oscillatory approach to a singular point in the relativistic cosmology. Adv. Phys. 1970, 19, 525–573. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse and space-time singularities. Phys. Rev. Lett. 1965, 14, 57–59. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Ford, L.H. The classical singularity theorems and their quantum loop holes. Int. J. Theor. Phys. 2003, 42, 1219–1227. [Google Scholar] [CrossRef]
- Hawking, S.W.; Penrose, R. The singularities of gravitational collapse and cosmology. Proc. R. Soc. Lond. A 1970, 314, 529–548. [Google Scholar]
- Penrose, R. Golden Oldie: Gravitational collapse: The role of general relativity. Gen. Relativ. Gravit. 2002, 34, 1141–1165. [Google Scholar] [CrossRef]
- Christodoulou, D. The instability of naked singularities in the gravitational collapse of a scalar field. Ann. Math. 1999, 149, 183–217. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and the second law. Lett. Nuovo C 1972, 4, 737–740. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The four laws of black hole mechanics. Comm. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Davies, P.C.W. Thermodynamics of black holes. Rep. Prog. Phys. 1978, 41, 1313–1355. [Google Scholar] [CrossRef]
- Cai, R.G. Effective spatial dimension of extremal nondilatonic black p-branes and the description of entropy on the world volume. Phys. Rev. Lett. 1997, 78, 2531–2534. [Google Scholar] [CrossRef]
- Maldacena, J.M. The large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1133. [Google Scholar] [CrossRef]
- Shen, J.Y.; Cai, R.G.; Wang, B.; Su, R.K. Thermodynamic geometry and critical behavior of black holes. Inter. J. Mod. Phys. A 2007, 22, 11–27. [Google Scholar] [CrossRef]
- Hawking, S.W.; Page, D.N. Thermodynamics of black holes in anti-de Sitter space. Comm. Math. Phys. 1983, 87, 577. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys 1998, 2, 505–532. [Google Scholar] [CrossRef]
- Weinhold, F. Metric geometry of equilibrium thermodynamics. J. Chem. Phys. 1975, 63, 2479. [Google Scholar] [CrossRef]
- Weinhold, F. Thermodynamics and geometry. Phys. Today 1976, 29, 23. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1979, 20, 1608. [Google Scholar] [CrossRef]
- Ruppeiner, G. Riemannian geometry in thermodynamic fluctuation theory. Rev. Mod. Phys. 1995, 67, 605. [Google Scholar] [CrossRef]
- Salamon, P.; Nulton, J.D.; Ihrig, E. On the relation between entropy and energy versions of thermodynamic length. J. Chem. Phys. 1984, 80, 436. [Google Scholar] [CrossRef]
- Salamon, P.; Ihrig, E.; Berry, R.S. A group of coordinate transformations which preserve the metric of weinhold. J. Math. Phys. 1983, 24, 2515. [Google Scholar] [CrossRef]
- Mrugala, R.; Nulton, J.D.; Schön, J.C.; Salomon, P. Contact structure in thermodynamic theory. Rep. Math. Phys. 1991, 29, 109. [Google Scholar] [CrossRef]
- Quevedo, H. Geometrothermodynamics. J. Math. Phys. 2007, 48, 013506. [Google Scholar] [CrossRef]
- Hendi, S.H.; Panahiyan, S.; Panah, B.E.; Momennia, M. A new approach toward geometrical concept of black hole thermodynamics. Eur. Phys. J. C 2015, 75, 1–12. [Google Scholar] [CrossRef]
- Mansoori, S.A.H.; Mirza, B. Correspondence of phase transition points and singularities of thermodynamic geometry of black holes. Eur. Phys. J. C 2014, 74, 2681. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M. Geometrothermodynamics: Comments, criticisms, and support. Eur. Phys. J. C 2014, 74, 2930. [Google Scholar] [CrossRef]
- Mansoori, S.A.H.; Mirza, B. Geometrothermodynamics as a singular conformal thermodynamic geometry. Phys. Lett. B 2019, 799, 135040. [Google Scholar] [CrossRef]
- Ebrahimi, K.M.; Mirza, B.; Kachi, M.T. Thermodynamic geometry of pure Lovelock black holes. Int. J. Mod. Phys. D 2022, 13, 2250097. [Google Scholar]
- Zhang, C.Y.; Liu, P.; Liu, Y.; Niu, C.; Wang, B. Dynamical scalarization in Einstein-Maxwell-dilaton theory. Phys. Rev. D 2022, 105, 024073. [Google Scholar] [CrossRef]
- Junior, H.C.D.L.; Yang, J.Z.; Crispino, L.C.B.; Cunha, P.V.P.; Herdeiro, C.A.R. Einstein-Maxwell-dilaton neutral black holes in strong magnetic fields: Topological charge, shadows, and lensing. Phys. Rev. D 2022, 105, 064070. [Google Scholar] [CrossRef]
- Richarte, M.G.; Martins, É.L.; Fabris, J.C. Scattering and absorption of a scalar field impinging on a charged black hole in the Einstein-Maxwell-dilaton theory. Phys. Rev. D 2022, 105, 064043. [Google Scholar] [CrossRef]
- Rogatko, M. Classification of static black holes in Einstein phantom-dilaton Maxwell–anti-Maxwell gravity systems. Phys. Rev. D 2022, 105, 104021. [Google Scholar] [CrossRef]
- Karakasis, T.; Papantonopoulos, E.; Tang, Z.Y.; Wang, B. Rotating (2+1)-dimensional Black Holes in Einstein-Maxwell-Dilaton Theory. arXiv 2022, arXiv:2210.15704. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Chen, H.; Hassanabadi, H.; Long, Z.W.; Yang, H. Joule-Thomson expansion of charged dilatonic black holes. Chin. Phys. C 2022. [Google Scholar] [CrossRef]
- Fernandes, P.G.S. Einstein—Maxwell-scalar black holes with massive and self-interacting scalar hair. Phys. Dark Universe 2020, 30, 100716. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Barrow, J.D. The area of a rough black hole. Phys. Lett. B 2020, 808, 135643. [Google Scholar] [CrossRef]
- Mamon, A.A.; Paliathanasis, A.; Saha, S. Dynamics of an interacting Barrow holographic dark energy model and its thermodynamic implications. Eur. Phys. J. Plus 2021, 136, 134. [Google Scholar] [CrossRef]
- Adhikary, P.; Das, S.; Basilakos, S.; Saridakis, E.N. Barrow holographic dark energy in a nonflat universe. Phys. Rev. D 2021, 104, 123519. [Google Scholar] [CrossRef]
- Soroushfar, S.; Saffari, R.; Abebe, A.; Sheikhahmadi, H. Thermodynamic geometry of static and rotating regular black holes in conformal massive gravity. Eur. Phys. J. Plus 2021, 136, 1223. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L.; Rachwal, L. Spacetime completeness of non-singular black holes in conformal gravity. JCAP 2017, 2017, 3. [Google Scholar] [CrossRef]
- Chakrabarty, H.; Benavides-Gallego, C.A.; Bambi, C.; Modesto, L. Unattainable extended spacetime regions in conformal gravity. J. High Energy Phys. 2018, 2018, 13. [Google Scholar] [CrossRef]
- Jusufi, K.; Jamil, M.; Chakrabarty, H.; Wu, Q.; Bambi, C.; Wang, A. Rotating regular black holes in conformal massive gravity. Phys. Rev. D 2020, 101, 044035. [Google Scholar] [CrossRef]
- Jusufi, K.; Anou, M.A.; Jamil, M.; Saridakis, E.N. Constraints on Barrow entropy from M87* and S2 star observations. Universe 2022, 8, 102. [Google Scholar] [CrossRef]
- Saridakis, E.N. Barrow holographic dark energy. Phys. Rev. D 2020, 102, 123525. [Google Scholar] [CrossRef]
- Saridakis, E.N. Modified cosmology through spacetime thermodynamics and Barrow horizon entropy. JCAP 2020, 2020, 31. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A. Barrow black hole corrected-entropy model and Tsallis nonextensivity. Phys. Lett. B 2020, 810, 135805. [Google Scholar] [CrossRef]
- Abreu, E.M.C.; Neto, J.A.; Barboza, E.M. Barrow’s black hole entropy and the equipartition theorem. Europhys. Lett. 2020, 130, 40005. [Google Scholar] [CrossRef]
- Kaul, R.K.; Majumdar, P. Logarithmic correction to the Bekenstein-Hawking entropy. Phys. Rev. Lett. 2000, 84, 5255. [Google Scholar] [CrossRef] [PubMed]
- Carlip, S. Logarithmic corrections to black hole entropy, from the Cardy formula. Class. Quantum Gravity 2000, 17, 4175. [Google Scholar] [CrossRef]
- Tsallis, C. Generalized entropy-based criterion for consistent testing. Phys. Rev. E 1988, 58, 1442. [Google Scholar] [CrossRef]
- Tsallis, C.; Cirto, L.J.L. Black hole thermodynamical entropy. Eur. Phys. J. C 2013, 73, 2487. [Google Scholar] [CrossRef]
- Bondi, H. Negative mass in general relativity. Rev. Mod. Phys. 1957, 29, 423. [Google Scholar] [CrossRef]
- Castelvecchi, D. Artificial black hole creates its own version of Hawking radiation. Nature 2016, 536, 7616. [Google Scholar] [CrossRef] [PubMed]
- Khamehchi, M.A.; Hossain, K.; Mossman, M.E.; Zhang, Y.; Busch, T.; Forbes, M.M.; Engels, P. Negative-mass hydrodynamics in a spin-orbit-coupled Bose-Einstein condensate. Phys. Rev. Lett. 2017, 118, 155301. [Google Scholar] [CrossRef] [PubMed]
- Farnes, V. A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. Astron. Astrophys. 2018, 620, A92. [Google Scholar] [CrossRef]
- Pacilio, C. Scalar charge of black holes in Einstein-Maxwell-dilaton theory. Phys. Rev. D 2018, 98, 064055. [Google Scholar] [CrossRef]
- Salamon, P.; Nulton, J.D.; Ihrig, E. Thermodynamic lengths and intrinsic time scales in molecular relaxation. J. Chem. Phys. 1984, 80, 436. [Google Scholar] [CrossRef]
- Mrugala, R. On equivalence of two metrics in classical thermodynamics. Phys. A Stat. Mech. App. 1984, 125, 631. [Google Scholar] [CrossRef]
- Hendi, S.H.; Sheykhi, A.; Panahiyan, S.; Panah, B.E. Phase transition and thermodynamic geometry of Einstein-Maxwell-dilaton black holes. Phys. Rev. D 2015, 92, 064028. [Google Scholar] [CrossRef]
- Soroushfar, S.; Saffari, R.; Upadhyay, S. Thermodynamic geometry of a black hole surrounded by perfect fluid in Rastall theory. Gen. Relativ. Gravit. 2019, 51, 130. [Google Scholar] [CrossRef]
- Quevedo, H. Geometrothermodynamics of black holes. Gen. Relativ. Gravit. 2008, 40, 971. [Google Scholar] [CrossRef]
- Quevedo, H.; Sanchez, A. Geometric description of BTZ black holes thermodynamics. Phys. Rev. D 2009, 79, 024012. [Google Scholar] [CrossRef]
- Quevedo, H.; Quevedo, M.N.; Sanchez, A. Geometrothermodynamics of phantom AdS black holes. Eur. Phys. J. C 2016, 76, 110. [Google Scholar] [CrossRef]
- Hermann, R. Geometry, Physics and Systems; Marcel Dekker: New York, NY, USA, 1973. [Google Scholar]
- Mrugala, R. Geometrical formulation of equilibrium phenomenological thermodynamics. Rep. Math. Phys. 1978, 14, 419. [Google Scholar] [CrossRef]
- Mrugala, R. Submanifolds in the thermodynamic phase space. Rep. Math. Phys. 1985, 21, 197. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M. Generating rotating regular black hole solutions without complexification. Phys. Rev. D 2014, 90, 064041. [Google Scholar] [CrossRef]
- Soroushfar, S.; Upadhyay, S. Phase transition of a charged AdS black hole with a global monopole through geometrical thermodynamics. Phys. Lett. B 2020, 804, 135360. [Google Scholar] [CrossRef]
- Pourhassan, B.; Wani, S.S.; Soroushfar, S.; Faizal, M. Quantum work and information geometry of a quantum Myers-Perry black hole. J. High Energy Phys. 2021, 2021, 1–27. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).