On Warm Natural Inflation and Planck 2018 Constraints
Abstract
1. Introduction
2. Warm Inflation Setup
2.1. Arena
2.2. Power Spectrum
- Strong Limit :Here, using Equation (27), one can show thatWe have via Equation (34):Thus, , and one gets:Thus, we getThe first term will give, after lengthy calculations look at [5]:whereas we get for the second term:where we have used the identity:Thus, we get:Note that involves the temperature T through the expression of . Additionally, T plays a role in determining the “end of inflation” field, being the argument of the slow-roll parameter () when it equals , whichever among the three meets the equality first. Determining allows one to compute the e-folding number by:The initial time when the inflation started is taken to correspond to the horizon crossing when the dominant quantum fluctuations freeze, transforming into classical perturbations with observed power spectrum.As for the tensor-to-scalar ratio, we get
- Weak LimitUsing Equation (27), one can show thatFrom Equation (34), we haveThus, , and one gets:Thus, we getThe first term will give, after lengthy calculations look at [5]:which gives, under the condition:the answerAs to the second term, we get using Equation (47)Thus, we get:As for the tensor-to-scalar ratio, we get, using , the following:
3. Natural Inflation
- Quadratic NMC:which is considered a leading order of terms allowed in the action generated by loops in the interacting theory. is the free parameter coupling constant characterizing the strength of the NMC to gravity.
- Periodic NMCwhich is similar in form to the original potential, allowing it to be justified in some microscopic models.
4. Comparison to Data: Strong Case
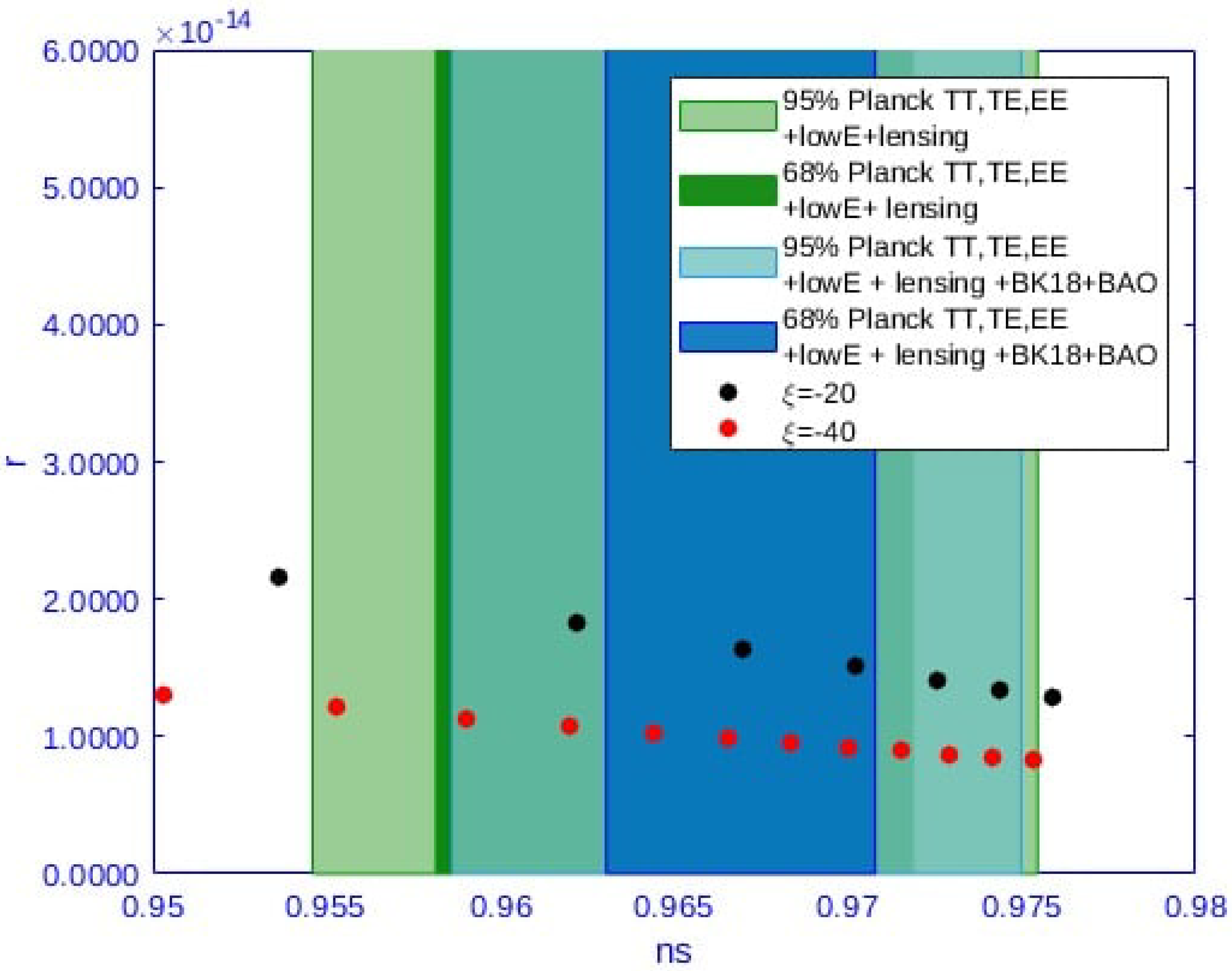
- Quadratic NMCFigure 1 shows the results of scanning the parameters space in the case of strong-limit warm NI with quadratic NMC to gravity. One could accommodate () but with too little . In the figures, the two colors dots correspond to two choices of the coupling .Looking to meet the e-folds constraint, we imposed () with (), and fixed the values of () as before, while scanning over . We found the “bench mark”: () giving the required e-folds with and Q in the order of . However, the scalar spectral index was large () outside the acceptable contours.
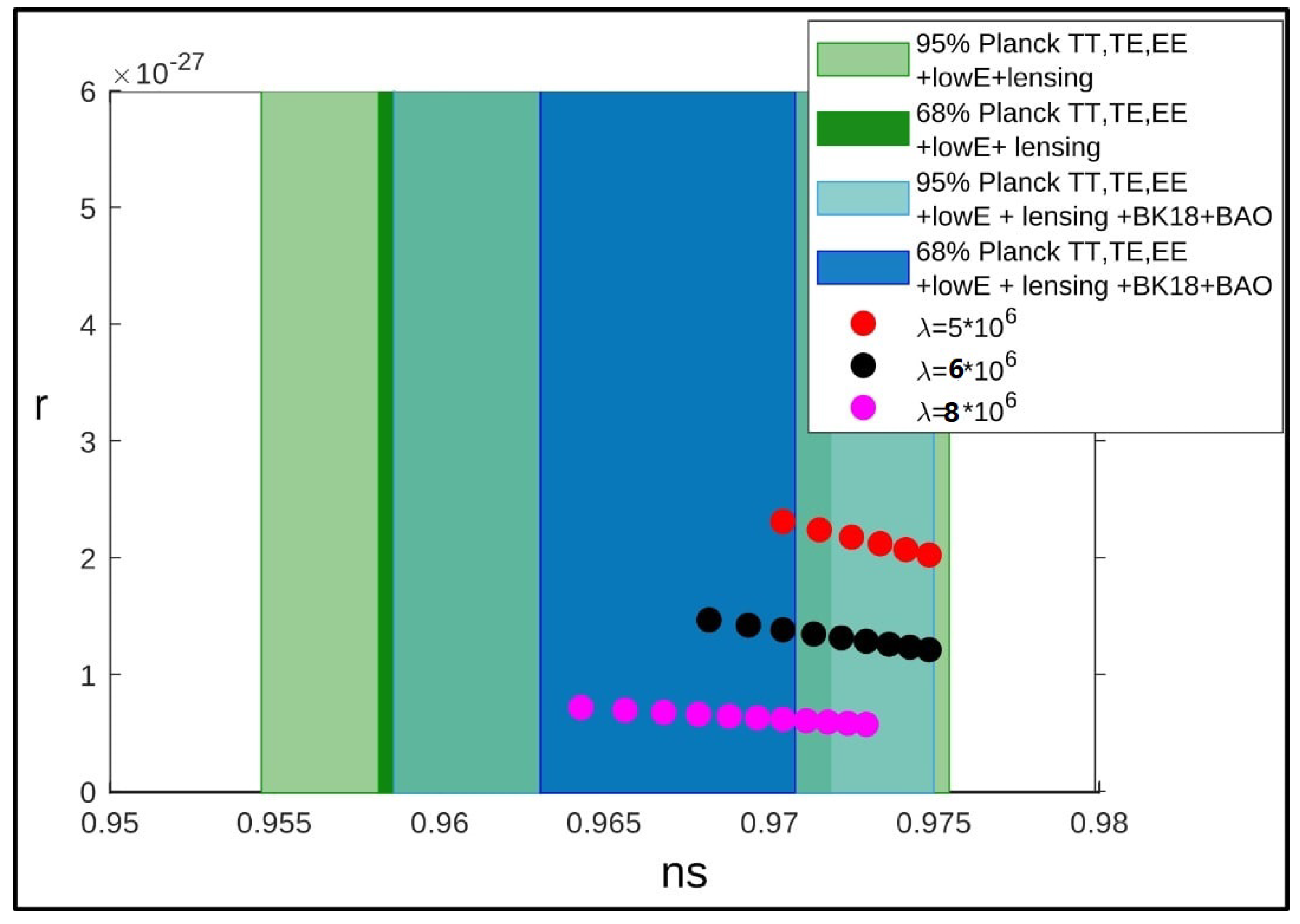
- Periodic NMCFigure 2 shows the results of scanning the parameters space in the case of strong-limit warm NI with periodic NMC to gravity. As in the case of quadratic NMC, one could accommodate () but with too little . In the figures, the three colors dots correspond to three choices of the coupling .Again, one could meet the acceptable value () with () and the values of () as before, through scanning over , and finding a “bench mark”: () giving the required e-folds () with and Q in the order of . However, the scalar spectral index was again large () outside the acceptable contours.
5. Comparison to Data: Weak Case
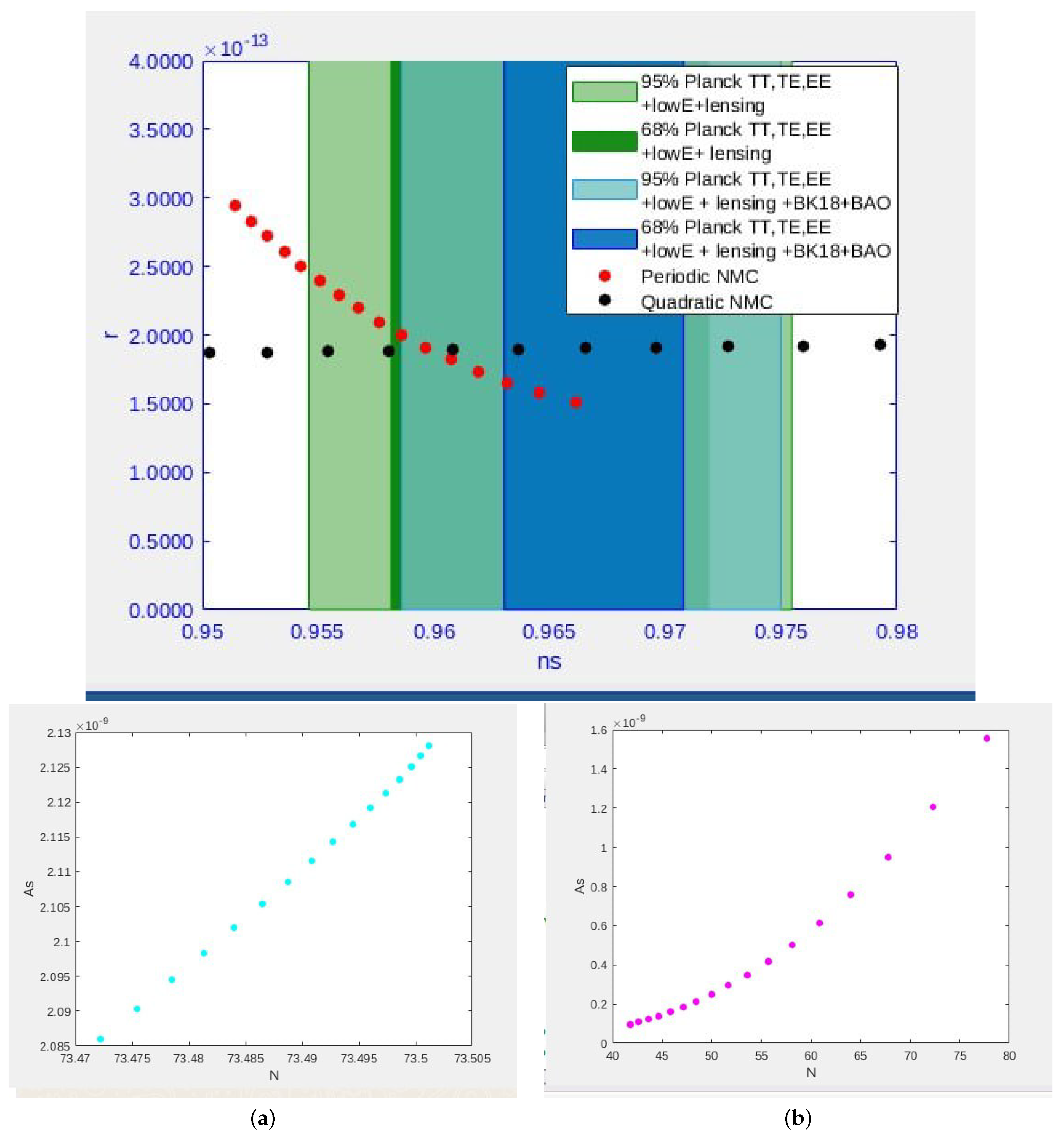
6. Cubic Dissipative Term
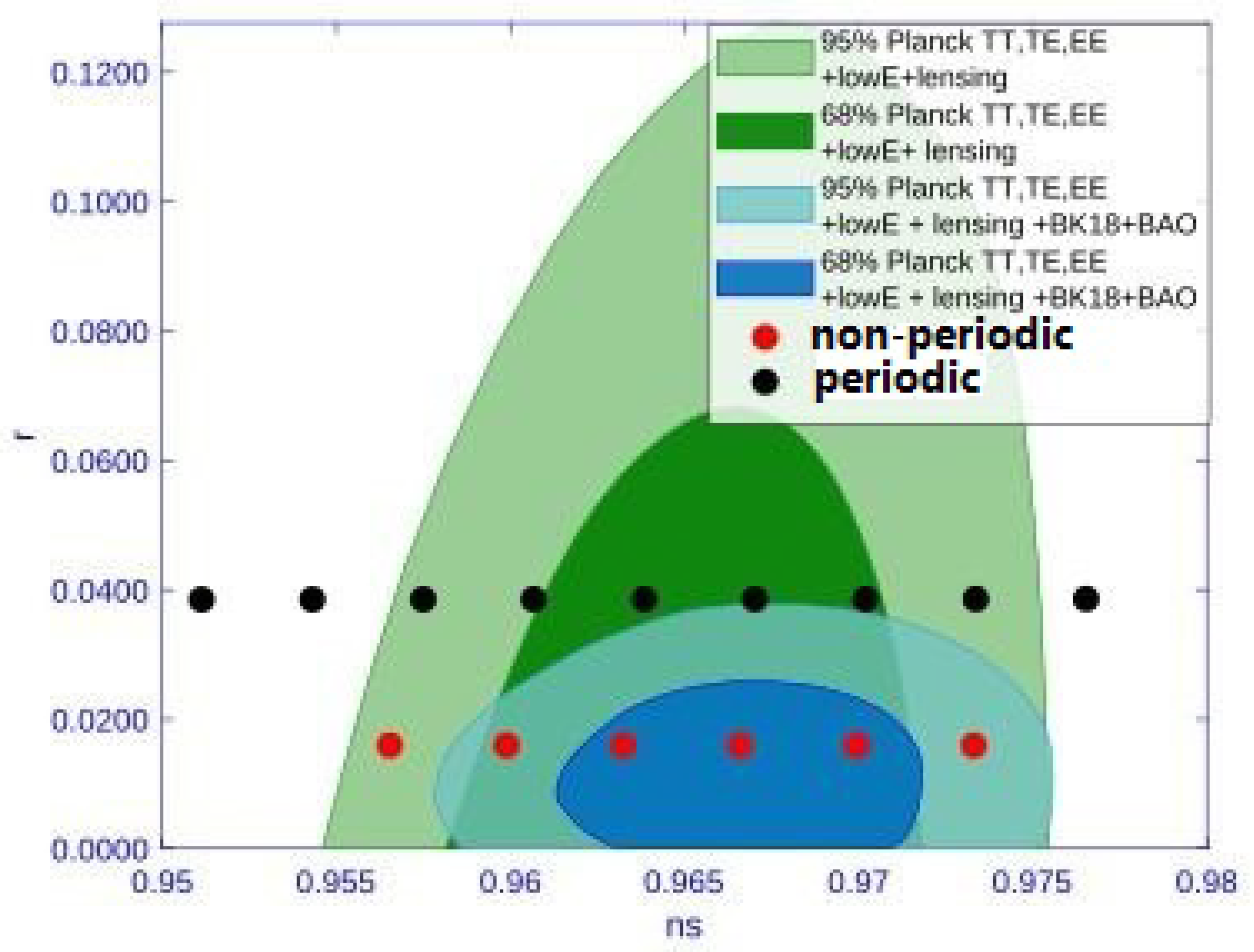
- Non-periodic NMC:Scanning over () withwe found acceptable points with the following ranges:with () increasing (decreasing) with .
- Periodic NMC: Scanning over () withwe found acceptable points with the following ranges:with () increasing (decreasing) with .
7. Summary and Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
| 1 | Note however, that the “measurable” Hubble parameter in the Einstein frame will be the one corresponding to dropping the inhomogeneous term [34]. |
References
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Berera, A.; Fang, L.Z. Thermally induced density perturbations in the inflation era. Phys. Rev. Lett. 1995, 74, 1912–1915. [Google Scholar] [CrossRef] [PubMed]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef] [PubMed]
- Visinelli, L. Observational Constraints on Monomial Warm INflation. J. Cosmol. Astropart. Phys. 2016, 2016, 54. [Google Scholar] [CrossRef]
- Kamali, V. Non-minimal Higgs inflation in the context of warm scenario in the light of Planck data. Eur. Phys. J. C 2018, 78, 975. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Bhattachary, S.; Duttab, K.; Gangopadhyayb, M.R. Constraining Warm Inflation with CMB data. J. Cosmol. Astropart. Phys. 2018, 2018, 54. [Google Scholar] [CrossRef]
- AlHallak, M.; AlRakik, A.; Chamoun, N.; Eldaher, M.S. Palatini f(R) Gravity and Variants of k-/Constant Roll/Warm Inflation within Variation of Strong Coupling Scenario. Universe 2022, 8, 126. [Google Scholar] [CrossRef]
- Amaek, W.; Payaka, A.; Channuie, P. Warm inflation in general scalar-tensor theory of gravity. Phys. Rev. D 2022, 105, 083501. [Google Scholar] [CrossRef]
- Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation with pseudo Nambu-Goldstone bosons. Phys. Rev. Lett. 1990, 65, 3233–3236. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Stein, N.K.; Kinney, W.H. Natural Inflation After Planck 2018. J. Cosmol. Astropart. Phys. 2022, 2022, 22. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Ahmed, Z.; Amiri, M.; Barkats, D.; Thakur, R.B.; Bischoff, C.A.; Beck, D.; Bock, J.J.; Boenish, H.; Bullock, E.; et al. BICEPKeck XIII: Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef]
- Antoniadis, I.; Karam, A.; Lykkas, A.; Pappas, T.; Tamvakisc, K. Rescuing Quartic and Natural Infation in the Palatini Formalism. J. Cosmol. Astropart. Phys. 2019, 2019, 5. [Google Scholar] [CrossRef]
- AlHallak, M.; Chamoun, N.; Eldahera, M.S. Natural Inflation with non minimal coupling to gravity in R2 gravity under the Palatini formalism. arXiv 2022, arXiv:2202.01002. [Google Scholar]
- Visinelli, L. Natural Warm Inflation. J. Cosmol. Astropart. Phys. 2011, 2011, 13. [Google Scholar] [CrossRef]
- Mishraa, H.; Mohantya, S.; Nautiyalb, A. Warm Natural Inflation. Phys. Let. B 2012, 710, 245. [Google Scholar] [CrossRef]
- Reyimuaji, Y.; Zhang, X. Warm-assisted natural infation. J. Cosmol. Astropart. Phys. 2021, 2021, 77. [Google Scholar] [CrossRef]
- Correa, M.; Gangopadhyay, M.R.; Jaman, N.; Mathews, G.J. Primordial Black-Hole Dark Matter via Warm Natural Inflation. Phys. Lett. B 2022, 835, 137510. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Diaz-Blanco, M.S. Gravity Waves and Primordial Black Holes in Scalar Warm Little Inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 52. [Google Scholar] [CrossRef]
- Arya, R. Formation of Primordial Black Holes from Warm Inflation. J. Cosmol. Astropart. Phys. 2020, 2020, 42. [Google Scholar] [CrossRef]
- Basak, S.; Bhattacharya, S.; Gangopadhyay, M.R.; Jaman, N.; Rangarajan, R.; Sami, M. The paradigm of warm quintessential inflation and spontaneous baryogenesis. J. Cosmol. Astropart. Phys. 2022, 2022, 63. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Myrzakul, S.; Sami, M.; Sharma, M.K. A paradigm of warm quintessential inflation and production of relic gravity waves. Phys. Rev. D 2021, 103, 043505. [Google Scholar] [CrossRef]
- Freedman, D.Z.; Muzinich, I.J.; Weinberg, E.J. On the Energy-Momentum Tensor in Gauge Field Theories. Ann. Phys. 1974, 87, 95. [Google Scholar] [CrossRef]
- Salvio, A. Natural-scalaron inflation. J. Cosmol. Astropart. Phys. 2021, 2021, 11. [Google Scholar] [CrossRef]
- Benetti, M.; Ramos, R.O. Warm inflation dissipative effects: Predictions and constraints from the Planck data. Phys. Rev. D 2017, 95, 023517. [Google Scholar] [CrossRef]
- Berera, A.; Ramos, R.O. Construction of a robust warm inflation mechanism. Phys. Lett. B 2003, 567, 294. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Berera, A.; Ramos, R.O.; Rosa, J.G. Warm Little Inflaton. Phys. Rev. Lett. 2016, 117, 151301. [Google Scholar] [CrossRef]
- Bartrum, S.; Bastero-Gil, M.; Berera, A.; Cerezo, R.; Ramos, R.O.; Rosa, J.G. The importance of being warm (during inflation). Phys. Lett. B 2014, 732, 116–121. [Google Scholar] [CrossRef]
- Zhang, Y. Warm inflation with a general form of the dissipative coefficient. J. Cosmol. Astropart. Phys. 2009, 2009, 23. [Google Scholar] [CrossRef]
- Belfiglio, A.; Luongo, O.; Mancini, S. Geometric corrections to cosmological entanglement. Phys. Rev. D 2022, 105, 123523. [Google Scholar] [CrossRef]
- Ford, L.H. Cosmological Particle Production: A Review. Rep. Prog. Phys. 2021, 84, 116901. [Google Scholar] [CrossRef] [PubMed]
- Fujii, Y. Conformal transformation in the scalar-tensor theory applied to the accelerating universe. Prog. Theor. Phys. 2007, 118, 983. [Google Scholar] [CrossRef]
- Chiba, T.; Yamaguchi, M. Conformal-Frame (In)dependence of Cosmological Observations in Scalar-Tensor Theory. J. Cosmol. Astropart. Phys. 2013, 2013, 40. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; AAtrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Bennett, C.L.; Larson, D.; Weil, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. Astrophys. J. Suppl. Ser. 2013, 208, 20. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, T.; Sun, S.; Wang, Y. Echoes of inflationary first-order phase transitions in the CMB. Phys. Lett. B 2017, 765, 339. [Google Scholar] [CrossRef]
- Liddle, A.R.; Leach, S.M. How long before the end of inflation were observable perturbations produced? Phys. Rev. D 2003, 68, 103503. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AlHallak, M.; Al-Said, K.K.; Chamoun, N.; El-Daher, M.S. On Warm Natural Inflation and Planck 2018 Constraints. Universe 2023, 9, 80. https://doi.org/10.3390/universe9020080
AlHallak M, Al-Said KK, Chamoun N, El-Daher MS. On Warm Natural Inflation and Planck 2018 Constraints. Universe. 2023; 9(2):80. https://doi.org/10.3390/universe9020080
Chicago/Turabian StyleAlHallak, Mahmoud, Khalil Kalid Al-Said, Nidal Chamoun, and Moustafa Sayem El-Daher. 2023. "On Warm Natural Inflation and Planck 2018 Constraints" Universe 9, no. 2: 80. https://doi.org/10.3390/universe9020080
APA StyleAlHallak, M., Al-Said, K. K., Chamoun, N., & El-Daher, M. S. (2023). On Warm Natural Inflation and Planck 2018 Constraints. Universe, 9(2), 80. https://doi.org/10.3390/universe9020080






