Cosmic Evolution of the Logarithmic f(R) Model and the dS Swampland Conjecture
Abstract
1. Introduction
2. Gravity and Constant-Roll Evolution
3. Logarithmic Gravity
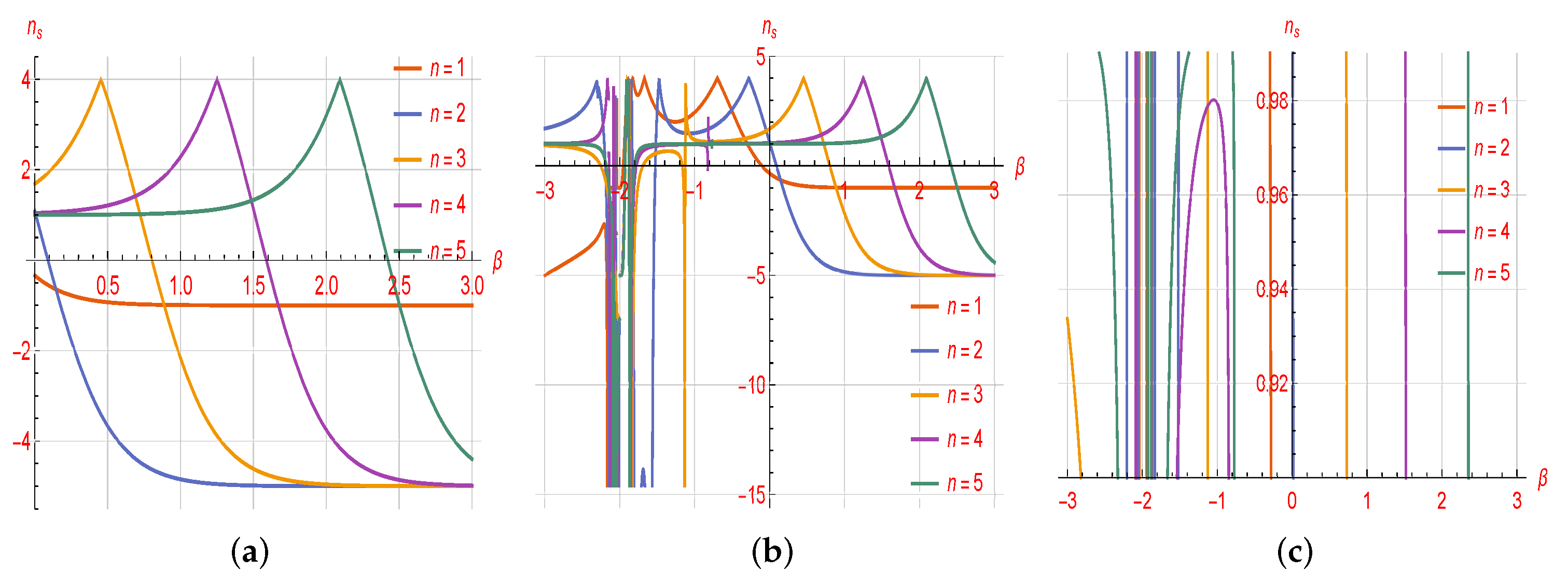
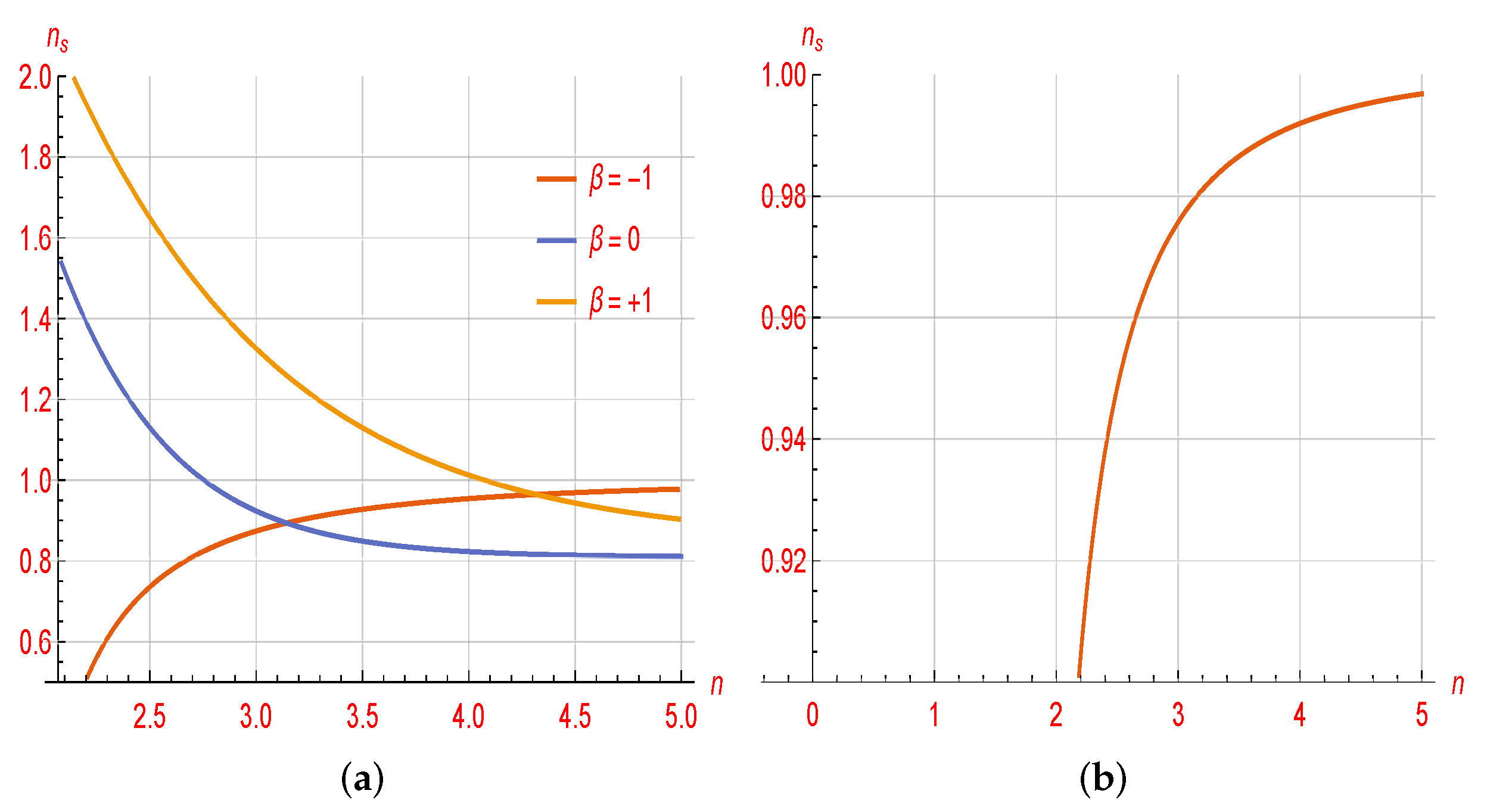
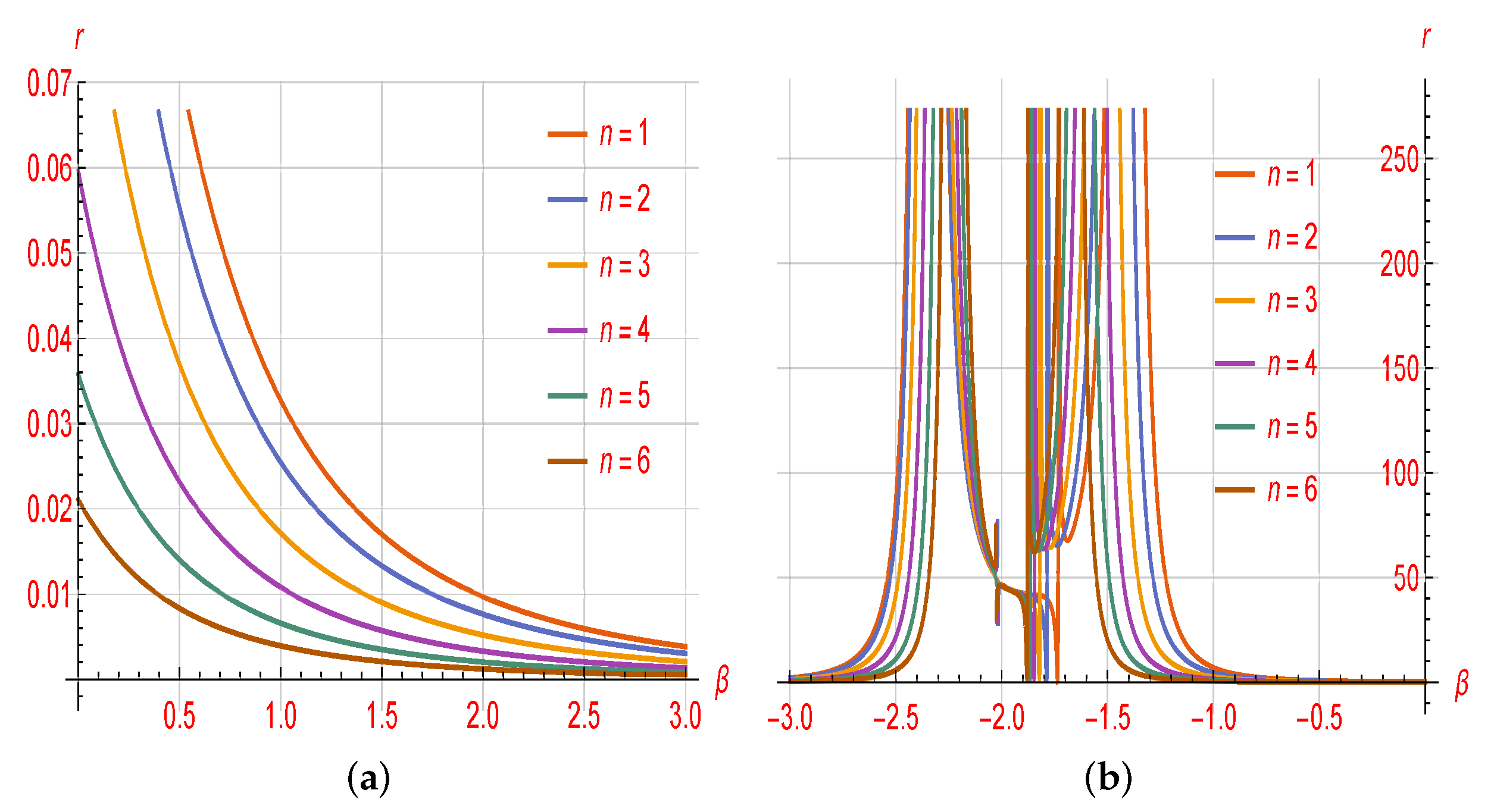
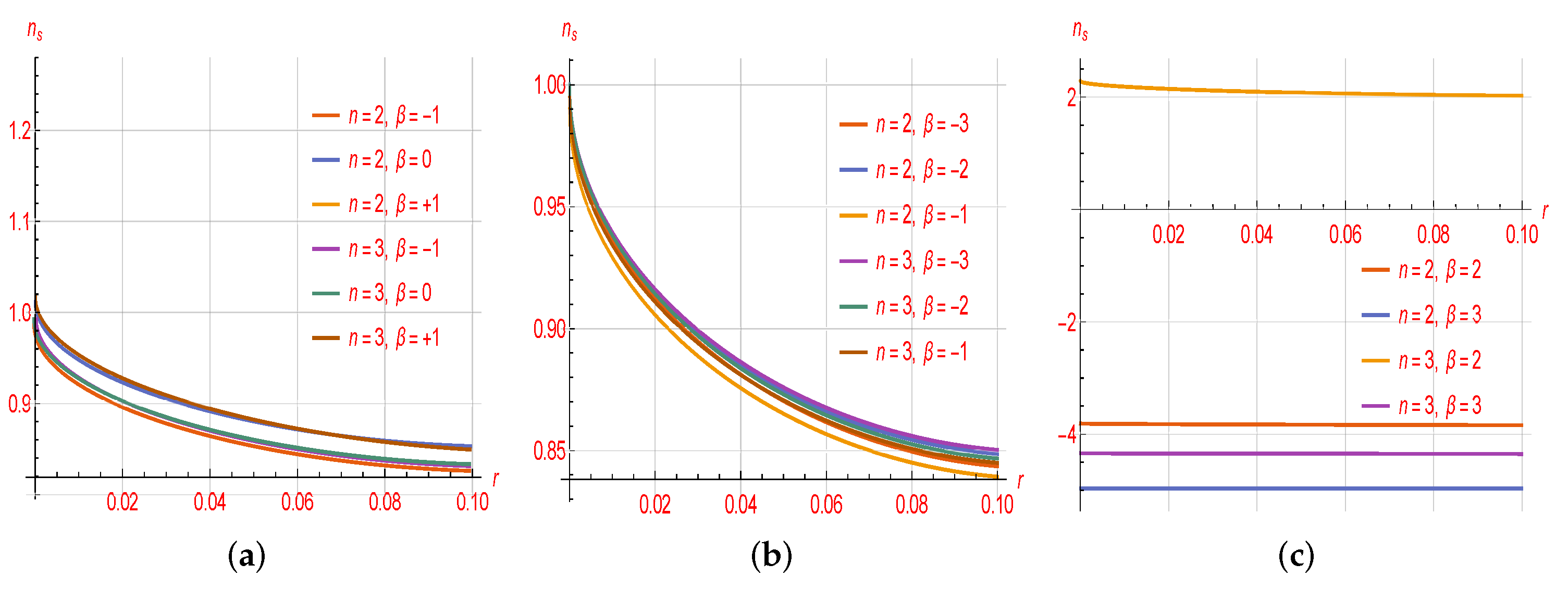
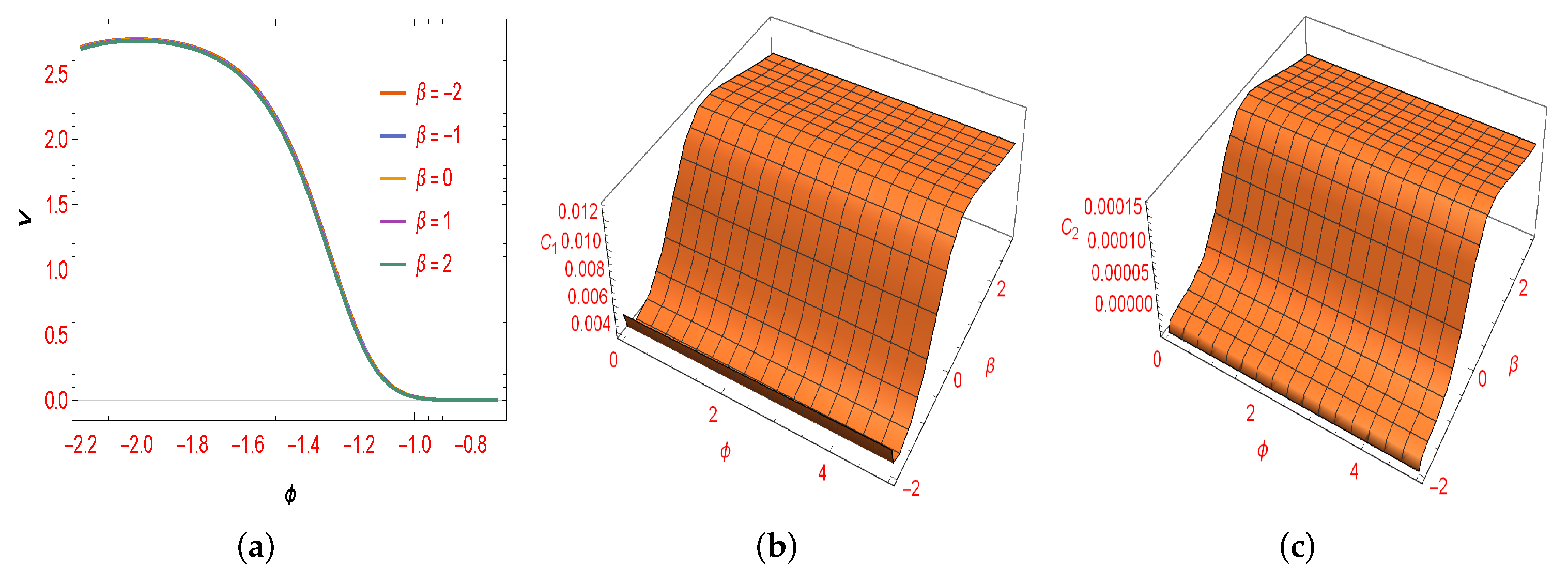
4. RSC in Logarithmic Constant-Roll Inflation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jerome, M.; Christophe, R.; Vincent, V. Encyclopdia Inflationaris. Phys. Dark Universe 2014, 5–6, 75–235. [Google Scholar]
- Akrami Cheghasiahi, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S. Planck 2018 results-X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Ade, P.A.; Ahmed, Z.; Amiri, M.; Barkats, D.; Thakur, R.B.; Bischoff, C.A.; Beck, D.; Bock, J.J.; Boenish, H.; Bullock, E.; et al. BICEP, Keck Collaboration, Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef] [PubMed]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. Extended theories of gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sebastiani, L.; Zerbini, S. Some aspects of generalized modified gravity models. Int. J. Mod. Phys. D 2013, 22, 1330017. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of curvature: Unification of inflation and cosmic acceleration. Phys. Rev. D 2003, 68, 123512. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Nonsingular exponential gravity: A simple theory for early-and late-time accelerated expansion. Phys. Rev. D 2011, 83, 086006. [Google Scholar] [CrossRef]
- Martin, J.; Motohashi, H.; Suyama, T. Ultra slow-roll inflation and the non-Gaussianity consistency relation. Phys. Rev. D 2013, 87, 023514. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A.; Yokoyama, J. Inflation with a constant rate of roll. J. Cosmol. Astropart. Phys. 2015, 1509, 018. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. Constant-roll inflation: Confrontation with recent observational data. Europhys. Lett. 2017, 117, 39001. [Google Scholar] [CrossRef]
- Rashidi, M.N.; Heidarzadeh, M.; Nozari, K. Constant-roll inflation with hilltop potential. Eur. Phys. J. Plus 2022, 137, 514. [Google Scholar] [CrossRef]
- Shokri, M.; Sadeghi, J.; Gashti, S.N. Quintessential constant-roll inflation. Phys. Dark Universe 2022, 35, 100923. [Google Scholar] [CrossRef]
- Namjoo, M.H.; Firouzjahi, H.; Sasaki, M. Violation of non-Gaussianity consistency relation in a single-field inflationary model. Europhys. Lett. 2013, 101, 39001. [Google Scholar] [CrossRef]
- Antoniadis, I.; Lykkas, A.; Tamvakis, K. Constant-roll in the Palatini-R2 models. J. Cosmol. Astropart. Phys. 2020, 4, 033. [Google Scholar] [CrossRef]
- Orellana, M.; Garcia, F.; Pannia, F.T.; Romero, G. Structure of neutron stars in R-squared gravity. Gen. Relativ. Gravit. 2013, 45, 771–783. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D.; Odintsov, S.D.; Stabile, A. Hydrostatic equilibrium and stellar structure in gravity. Phys. Rev. D 2011, 83, 064004. [Google Scholar] [CrossRef]
- Capozziello, S.; Faizal, M.; Hameeda, M.; Pourhassan, B.; Salzano, V.; Upadhyay, S. Clustering of galaxies with f(R) gravity. Mon. Not. Roy. Astron. Soc. 2018, 474, 2430–2443. [Google Scholar] [CrossRef]
- Arapoglu, A.; Deliduman, C.; Eksi, K.Y. Constraints on perturbative f(R) gravity via neutron stars. J. Cosmol. Astropart. Phys. 2011, 1107, 020. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended gravity cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Rational approximations of f(R) cosmography through Pad’e polynomials. J. Cosmol. Astropart. Phys. 2018, 1805, 008. [Google Scholar] [CrossRef]
- Khurshudyan, M.; Pasqua, A.; Pourhassan, B. Higher derivative corrections of f(R) gravity with varying equation of state in the case of variable G and Λ. Can. J. Phys. 2015, 1107, 449–455. [Google Scholar] [CrossRef]
- Channuie, P. Deformed Starobinsky model in gravity’s rainbow. Eur. Phys. J. C 2019, 79, 508. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Kinematic model-independent reconstruction of Palatini f(R) cosmology. Gen. Relativ. Gravit. 2019, 51, 2. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sebastian, L.; Vagnozzi, S. Inflation in f(R,ϕ)-theories and mimetic gravity scenario. Eur. Phys. J. C 2015, 75, 444. [Google Scholar] [CrossRef]
- Sadeghi, J.; Pourhassan, B.; Kubeka, A.S.; Rostami, M. Logarithmic corrected polynomial f(R) inflation mimicking a cosmological constant. Int. J. Mod. Phys. D 2015, 25, 1650077. [Google Scholar] [CrossRef]
- Huang, Q.G. A polynomial f(R) inflation model. J. Cosmol. Astropart. Phys. 2014, 2, 035. [Google Scholar] [CrossRef]
- da-Silva, G.R.; Bezerra-Sobrinho, J.; Medeiros, L. Higher-order extension of Starobinsky inflation: Initial conditions, slow-roll regime, and reheating phase. Phys. Rev. D 2022, 105, 063504. [Google Scholar] [CrossRef]
- Ivanov, V.R.; Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. Analytic extensions of Starobinsky model of inflation. J. Cosmol. Astropart. Phys. 2022, 3, 058. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with lnR terms and cosmic acceleration. Gen. Relativ. Gravit. 2004, 36, 1765. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Sebastiani, L. Unification of constant-roll inflation and dark energy with logarithmic R2-corrected and exponential F(R) gravity. Nucl. Phys. B 2017, 923, 608. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Sebastiani, L.; Myrzakulov, R. Beyond-one-loop quantum gravity action yielding both inflation and late-time acceleration. Nucl. Phys. B 2017, 921, 411. [Google Scholar] [CrossRef]
- Cook, J.L.; Krauss, L.M. Large slow roll parameters in single field inflation. J. Cosmol. Astropart. Phys. 2016, 3, 1603. [Google Scholar] [CrossRef]
- Kumar, K.S.; Marto, J.; Moniz, P.V.; Das, S. Non-slow-roll dynamics in α-attractors. J. Cosmol. Astropart. Phys. 2016, 4, 1604. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflationary dynamics with a smooth slow-roll to constant-roll era transition. J. Cosmol. Astropart. Phys. 2017, 4, 1704. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Inflation with a smooth constant-roll to constant-roll era transition. Phys. Rev. D 2017, 96, 024029. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, Y.; Fei, Q. Constant-roll tachyon inflation and observational constraints. J. Cosmol. Astropart. Phys. 2018, 5, 005. [Google Scholar] [CrossRef]
- Gao, Q.; Gong, Y. Reconstruction of extended inflationary potentials for attractors. Eur. Phys. J. Plus 2018, 133, 491. [Google Scholar] [CrossRef]
- Gao, Q. Reconstruction of constant slow-roll inflation. Sci. China Phys. Mech. Astron. 60 2017, 9, 090411. [Google Scholar] [CrossRef]
- Fei, Q.; Gong, Y.; Lin, J.; Yi, Z. The reconstruction of tachyon inflationary potentials. J. Cosmol. Astropart. Phys. 2017, 8, 018. [Google Scholar] [CrossRef]
- Noori Gashti, S. Two-field inflationary model and swampland de Sitter conjecture. J. Hologr. Appl. Phys. 2022, 2, 13–24. [Google Scholar] [CrossRef]
- Maity, S.; Rudra, P. Inflation driven by Barrow holographic dark energy. J. Hologr. Appl. Phys. 2022, 2, 1–12. [Google Scholar]
- Sadeghi, J.; Mezerji, E.N.; Gashti, S.N. Study of some cosmological parameters in logarithmic corrected gravitational model with swampland conjectures. Mod. Phys. Lett. A 2020, 36, 2150027. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N. Anisotropic constant-roll inflation with noncommutative model and swampland conjectures. Eur. Phys. J. C 2021, 81, 301. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N.; Mezerji, E.N. The investigation of universal relation between corrections to entropy and extremality bounds with verification WGC. Phys. Dark Universe 2020, 30, 100626. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on slow roll and the de Sitter swampland. J. High Energ. Phys. 2019, 2019, 75. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Rescaled Einstein-Hilbert gravity from gravity: Inflation, dark energy, and the swampland criteria. Phys. Rev. D 2021, 103, 124028. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N.; Darabi, F. Swampland conjectures in hybrid metric-Palatini gravity. Phys. Dark Universe 2022, 37, 101090. [Google Scholar] [CrossRef]
- Castellano, A.; Herráez, A.; Ibáñez, L.E. IR/UV mixing, towers of species and swampland conjectures. J. High Energy Phys. 2022, 2022, 217. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J. Refined swampland conjecture in warm vector hybrid inflationary scenario. Eur. Phys. J. Plus 2022, 137, 731. [Google Scholar] [CrossRef]
- Yuennan, J.; Channuie, P. Composite Inflation and further refining dS swampland conjecture. arXiv 2022, arXiv:2208.09842. [Google Scholar]
- Alvarez-Garcia, R.; Blumenhagen, R.; Kneil, C. Swampland conjectures for an almost topological gravity theory. Phys. Lett. B 2022, 825, 136861. [Google Scholar] [CrossRef]
- FSantos, B.M.d.; Silva, R.; da Costa, S.S.; Benetti, M.; Alcaniz, J.S. Warm β -exponential inflation and the Swampland Conjectures. arXiv 2022, arXiv:2209.06153. [Google Scholar]
- Gashti, S.N.; Sadeghi, J.; Pourhassan, B. Pleasant behavior of swampland conjectures in the face of specific inflationary models. Astropart. Phys. 2022, 139, 102703. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J. Constraints on cosmological parameters in light of the scalar-tensor theory of gravity and swampland conjectures. Mod. Phys. Lett. A 2022, 37, 2250110. [Google Scholar] [CrossRef]
- Gonzalo, E.; Ibnaez, L.E.; Valenzuela, I. Swampland constraints on neutrino masses. J. High Energy Phys. 2022, 2022, 88. [Google Scholar] [CrossRef]
- Bertolami, O.; Sa, P.M. Multi-field cold and warm inflation and the de Sitter swampland conjectures. J. Cosmol. Astropart. Phys. 2022, 9, 001. [Google Scholar] [CrossRef]
- Mishra, R.K. Confinement in de Sitter Space and the Swampland. arXiv 2022, arXiv:2207.12364. [Google Scholar]
- Mohammadi, A.; Golanbari, T.; Nasri, S.; Saaidi, K. Brane inflation: Swampland criteria, TCC, and reheating predictions. Astropart. Phys. 2022, 142, 102734. [Google Scholar] [CrossRef]
- Andriot, D.; Horer, L. (Quasi-) de Sitter solutions across dimensions and the TCC bound. arXiv 2022, arXiv:2208.14462. [Google Scholar]
- Sadeghi, J.; Alipour, M.R.; Gashti, S.N. Scalar Weak Gravity Conjecture in Super Yang-Mills Inflationary Model. arXiv 2022, arXiv:2208.13093. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Constant-roll inflation in F(R) gravity. Class. Quantum Gravity 2017, 34, 245012. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. f(R) constant-roll inflation. Eur. Phys. J. C 2017, 77, 538. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Reheating in Constant-roll F(R) Gravity. Mod. Phys. Lett. A 2017, 33, 1750172. [Google Scholar] [CrossRef]
- Guerrero, M.; Rubiera-Garcia, D.; Saez-Chillon Gomez, D. Constant roll inflation in multifield models. Phys. Rev. D 2020, 102, 123528. [Google Scholar] [CrossRef]
- Saidov, T.; Zhuk, A. Bouncing inflation in nonlinear R2+R4 gravitational model. Phys. Rev. D 2010, 81, 124002. [Google Scholar] [CrossRef]
- Sadeghi, J.; Farahani, H. Logarithmic corrected F(R) gravity in the light of Planck 2015. Phys. Lett. B 2015, 751, 89–95. [Google Scholar] [CrossRef]
- Sadeghi, J.; Gashti, S.N. Investigating the logarithmic form of f(R) gravity model from brane perspective and swampland criteria. Pramana 2021, 95, 198. [Google Scholar] [CrossRef]
- Sadeghi, J.; Shokri, M.; Gashti, S.N.; Pourhassan, B.; Rudra, P. Traversable wormhole in logarithmic gravity by various shape and redshift functions. Int. J. Mod. Phys. D 2022, 31, 2250019. [Google Scholar] [CrossRef]
- Noh, H.; Hwang, J. Inflationary spectra in generalized gravity: Unified forms. Phys. Lett. B 2001, 515, 231–237. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H.R. Gauge-ready formulation of the cosmological kinetic theory in generalized gravity theories. Phys. Rev. D 2002, 65, 023512. [Google Scholar] [CrossRef]
- Hwang, J.C.; Noh, H. f(R) gravity theory and CMBR constraints. Phys. Lett. B 2001, 506, 13–19. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Viable mimetic completion of unified inflation-dark energy evolution in modified gravity. Phys. Rev. D 2016, 94, 104050. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Singular F(R) cosmology unifying early-and late-time acceleration with matter and radiation domination era. Class. Quant. Grav. 2016, 33, 125029. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Singular inflationary universe from gravity. Phys. Rev. D 2015, 92, 124024. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef]
- Elizalde, E.; Odintsov, S.D.; Oikonomou, V.K.; Paul, T. Logarithmic-corrected R2 Gravity Inflation in the Presence of Kalb-Ramond Fields. J. Cosmol. Astropart. Phys. 2019, 2, 017. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Gomez, D.S.-C.; Sharov, G.S. Testing logarithmic corrections on R2-exponential gravity by observational data. Phys. Rev. D 2019, 99, 024003. [Google Scholar] [CrossRef]
- Mukhanov, V. Quantum cosmological perturbations: Predictions and observations. Eur. Phys. J. C 2013, 73, 2486. [Google Scholar] [CrossRef]
- Mukhanov, V. Inflation without selfreproduction. Fortsch. Phys. 2015, 63, 36. [Google Scholar] [CrossRef]
- Codello, A.; Joergensen, J.; Sannino, F.; Svendsen, O. Marginally deformed Starobinsky gravity. J. High Energy Phys. 2015, 2, 050. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Bessa, P.; Campista, M.; Bernui, A. Observational constraints on Starobinsky f(R) cosmology from cosmic expansion and structure growth data. Eur. Phys. J. C 2022, 82, 506. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D.; Farinelli, R.; Odintsov, S.D. Mass-radius relation for neutron stars in f(R) gravity. Phys. Rev. D 2016, 93, 023501. [Google Scholar] [CrossRef]
- Bamba, K.; Makarenko, A.N.; Myagky, A.N.; Nojiri, S.I.; Odintsov, S.D. Bounce cosmology from F(R) gravity and F(R) bigravity. J. Cosmol. Astropart. Phys. 2014, 1, 008. [Google Scholar] [CrossRef]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Stellar structure models in modified theories of gravity: Lessons and challenges. Phys. Rep. 2020, 876, 1–75. [Google Scholar] [CrossRef]
- Capozziello, S.; Filippis, E.D.; Salzano, V. Modelling clusters of galaxies by f(R) gravity. Mon. Not. R. Astron. Soc. 2009, 394, 947–959. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hsu, Y.T.; Lu, J.R. Cosmological Constraints on Nonflat Exponential f(R) Gravity. Astrophys. J. 2022, 926, 74. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Pre-inflationary bounce effects on primordial gravitational waves of f(R) gravity. Phys. Lett. B 2022, 824, 136817. [Google Scholar] [CrossRef]
- Channuie, P. Refined Swampland conjecture in deformed Starobinsky gravity. Int. J. Mod. Phys. D 2022, 31, 2250074. [Google Scholar] [CrossRef]
- Leyva, Y.; Otalora, G. Revisiting gravity’s rainbow: Inflation and primordial fluctuations. arXiv 2022, arXiv:2206.09000. [Google Scholar]
- Oikonomou, V.K. Kinetic axion F(R) gravity inflation. Phys. Rev. D 2022, 106, 044041. [Google Scholar] [CrossRef]
- Gashti, S.N.; Sadeghi, J.; Upadhyay, S.; Alipour, M.R. Swampland dS conjecture in mimetic f(R,T) gravity. Commun. Theor. Phys. 2022, 74, 085402. [Google Scholar] [CrossRef]
- Koussour, M.; Shekh, S.H.; Hanin, A.; Sakhi, Z.; Bhoyer, S.R.; Bennai, M. Flat FLRW Universe in logarithmic symmetric teleparallel gravity with observational constraints. arXiv 2022, arXiv:2203.00413v2. [Google Scholar] [CrossRef]
- Jaybhaye, L.V.; Mandal, S.; Sahoo, P.K. Constraints on energy conditions in f(R,Lm) gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250050. [Google Scholar] [CrossRef]
- Sharma, A.K.; Verma, M.M. Power-law Inflation in the f(R) Gravity. Astrophys. J. 2022, 926, 29. [Google Scholar] [CrossRef]
- Inoue, S.; Yokoyama, J. Curvature perturbation at the local extremum of the inflaton potential. Phys. Lett. B 2002, 524, 15. [Google Scholar]
- Gao, T.J. Gauss-Bonnet inflation with a constant rate of roll. Eur. Phys. J. C 2020, 80, 1013. [Google Scholar] [CrossRef]
- Karam, A.; Marzola, L.; Pappas, T.; Racioppi, A.; Tamvakis, K. Constant-roll (quasi-)linear inflation. J. Cosmol. Astropart. Phys. 2018, 5, 011. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadeghi, J.; Pourhassan, B.; Noori Gashti, S.; Naghd Mezerji, E.; Pasqua, A. Cosmic Evolution of the Logarithmic f(R) Model and the dS Swampland Conjecture. Universe 2022, 8, 623. https://doi.org/10.3390/universe8120623
Sadeghi J, Pourhassan B, Noori Gashti S, Naghd Mezerji E, Pasqua A. Cosmic Evolution of the Logarithmic f(R) Model and the dS Swampland Conjecture. Universe. 2022; 8(12):623. https://doi.org/10.3390/universe8120623
Chicago/Turabian StyleSadeghi, Jafar, Behnam Pourhassan, Saeed Noori Gashti, Elaheh Naghd Mezerji, and Antonio Pasqua. 2022. "Cosmic Evolution of the Logarithmic f(R) Model and the dS Swampland Conjecture" Universe 8, no. 12: 623. https://doi.org/10.3390/universe8120623
APA StyleSadeghi, J., Pourhassan, B., Noori Gashti, S., Naghd Mezerji, E., & Pasqua, A. (2022). Cosmic Evolution of the Logarithmic f(R) Model and the dS Swampland Conjecture. Universe, 8(12), 623. https://doi.org/10.3390/universe8120623








