Abstract
In this article, we try to determine the conditions when a ghost field, in conjunction with a barotropic fluid, produces a stable accelerating expansion phase of the universe. It is seen that, in many cases, the ghost field produces a condensate and drives the fluid energy density to zero in the final accelerating phase, but there can be other possibilities. We have shown that a pure kinetic k-essence field (which is not a ghost field) interacting with a fluid can also form an interaction-induced condensate and produce a stable accelerating phase of the universe. In the latter case, the fluid energy density does not vanish in the stable phase.
1. Introduction
Our present universe is going through an epoch of accelerated expansion. During the last fifteen years, several observational evidences established this fact. Estimation of luminosity distance and redshift of type Ia supernovas [1,2,3] are the key ingredients among the several observational ventures. Cosmic microwave background radiation [4], baryon acoustic oscillations [5,6] and the Hubble constant [7] also play significant roles in the accelerated expansion phase. The literature related to the accelerated expansion of the universe [1,2,3] suggests that dark energy is solely responsible for this late-time cosmic acceleration. The large negative pressure of dark energy prevents gravitational collapse and produces late-time cosmic acceleration.
Despite countless theoretical approaches, the physical theory of dark energy is still not established. The earliest theory to probe the nature of dark energy is the CDM model, which consists of both cosmological constant and cold dark matter. This model was favored by the particle physics community. Unfortunately, the CDM model suffers from two drawbacks. The first difficulty of this model is related to the cosmological constant problem [8], and the other one is the cosmic coincidence problem [9]. These two basic problems motivate us to study alternative dark energy models. One such model is the field-theoretic dark energy model, in which the scalar field plays a major role in producing negative pressure resulting in late-time cosmic acceleration. Based on the form of the Lagrangian, mainly two kinds of scalar field models exist so far: one is the ‘quintessence’ model [9,10,11,12,13,14,15,16,17,18,19,20] and the other is the ‘k-essence’ model [21,22,23,24,25,26,27,28,29]. Despite the presence of scalar field models, other kinds of dark energy models are also present in cosmology, such as the theory of gravity [30,31], scalar–tensor theoretical models [32] and brane-world models [33]. In this present work, we will only concentrate on some aspects of the k-essence scalar field dark energy model. One must note that non-canonical scalar fields (a k-essence type of scalar fields) are not only used to study the nature of dark energy, but they are also regularly used to characterize inflation [21,22], dark matter [29] and unified dark sector models [27]. Out of the several theoretical ventures to study the k-essence sector, one fascinating method is investigating the interacting field–fluid framework. Several interlinking field–fluid scenarios have already been investigated in the literature [34,35,36,37,38,39]. In most of the cases, the field part is composed of a quintessence scalar field. In some literature, k-essence [40] has taken the lead role in driving the cosmological dynamics. Algebraic [35] and derivative [36] types of coupling have been used to study this interlinked dark sector. Dynamic stability analysis plays an important role in the study of dark energy. Various applications of dynamical systems are applied in studying the evolution of various field–fluid scenarios. We have extracted the essence of the dynamic stability technique from various literature [36,41,42,43,44,45,46,47,48,49] and implemented it in our study of the dark sector.
Constant potential k-sector defines purely kinetic k-essence models. Purely kinetic k-essence models can unify both dark energy and dark matter [27] sectors. In various dark sector models involving a scalar field and a fluid, it is assumed that the constituents interact gravitationally. Apart from gravity, there may exist some other phenomenological types of interaction that connect these two sectors. In [40,50], non-minimal interaction between the field and the fluid sectors, where k-essence potential plays a vital role, has been discussed thoroughly. Some recent works show that the equation of the state of the field–fluid sector of the universe can cross the phantom barrier [51,52,53]. Other recent works discuss the issue of Hubble tension. One of the possible ways to address these issues is related to the introduction of the non-minimal interaction between field and fluid systems studied in [54,55,56]. In this paper, we will investigate the field–fluid interaction between a purely kinetic k-essence field sector and the relativistic fluid sector. This study is important, as the behavior of the purely kinetic k-essence sector is very different from the standard k-essence sector, where the field potential plays an important role. The purely kinetic k-essence sector includes the ghost field sector in cosmology. Ghost field cosmology was elegantly introduced in [57]. All ghost fields are certain forms of purely kinetic k-essence fields, but all kinetic k-essence fields may not be ghost fields. In this paper, we discuss the role of ghost fields in cosmology where they are accompanied by a barotropic fluid.
In this article, we have presented the conditions required for producing a stable accelerated phase of expansion of the universe in the presence of a ghost field and a barotropic fluid. Most of the time, it is seen that the ghost field forms a ghost condensate in the far future when the fluid energy density becomes vanishingly small. This happens in interactions that vanish when the fluid energy density vanishes. We have also shown a case where the stable accelerating expansion phase is not produced by a ghost condensate. In such a case, due to a novel effect induced by field–fluid coupling, a pure kinetic k-essence field (which is not a ghost field) forms a condensate and stabilizes the accelerating expansion phase. In the last case, the fluid density in the stable phase does not vanish but remains subdominant. In this article, we show that a ghost field is not always needed to produce a stable accelerating expansion of the universe.
The material presented in the article is organized as follows. In Section 2, we will discuss purely kinetic k-essence theory in a detailed manner and present the connection between kinetic k-essence fields and ghost fields. In Section 3, we present the main formal results relating to the interaction between a ghost field and a barotropic fluid. In Section 4, we will introduce a perfect fluid where the fluid and the scalar field do not exchange energy-momentum between them. In Section 5, we will introduce non-minimal coupling and study the field–fluid theory. Finally, we will conclude in Section 6.
2. Purely Kinetic k-Essence Fields and the Ghost Connection
The basic idea of k-essence theory was first introduced by Armendariz-Picon et al. [21,23] to explain the inflationary scenario of the early universe; later, this theory was applied to study the late-time phase of cosmic evolution. The k-essence theory is specified by a scalar field potential1, , and a non-canonical function of the kinetic term . The action of a pure k-essence field, minimally coupled to gravity, is given as:
Here, . The first term in the square bracket characterizes the Einstein–Hilbert action, and the second term represents the k-essence Lagrangian. We consider a homogeneous and isotropic background given by the Friedmann–Lemaître–Robertson–Walker (FLRW) metric, whose line element is given through:
where a is the scale factor in the FLRW metric. Variation of the action with respect to produces the energy-momentum tensor:
Hence, the energy-momentum tensor of the k-essence scalar field is
The energy density and pressure of the k-essence field are,
The pressure of the k-essence field configuration can be shown as . In such a case, the energy density will become
where . We assume that at . This implies that . We expect that when . For this condition to prevail, we require that, at , one must have . Throughout our work we assume .
Unlike the canonical scalar field, the k-essence scalar field has a negative mass dimension. This makes the kinetic term X dimensionless. The mass dimension of the k-essence Lagrangian (density), , solely comes from the potential term . The energy momentum tensor of the field is conserved, , yielding
where the time derivative of any function is expressed as a dot over that function. Here, the Hubble parameter is . The equation of state (EoS) and sound speed in the k-essence field sector are given by and . In the present case, these quantities are:
where . For a constant potential (), varying the k-essence action with respect to , in the background of the FLRW spacetime, produces the scalar field equation:
In the present case, the Friedmann equations are
From the Friedmann equations and the purely kinetic k-essence scalar field equation, it is seen that the scalar field equation has non-trivial critical points (for non-zero values of X) when . The non-trivial solutions have to be non-zero, positive, real numbers. In general, is also a critical point for the pure kinetic k-essence field equation. From the Friedmann equations, it is seen that, at , both H and become zero, showing an unstable phase2. The trivial critical point is never reached. The non-trivial fixed point solutions are stable when is near the solutions. Near the fixed points, for the pure kinetic k-essence field equation, one must have so that . Near the fixed points, we should also have and . If the fixed points are stable, we get accelerating universe solutions in the presence of the field .
The purely kinetic k-essence field has a very close relationship with the ghost fields discussed in [57]. In this reference, the authors have elaborately specified the properties of ghost condensates. According to [57], a ghost field Lagrangian density is given using where
where is a function of X. The function is such that there exists one (or possibly more) real solution(s) of . The ghost condensate is formed when where is a particular solution of . From what has been discussed, it becomes clear that all ghost condensate fields are essentially purely kinetic k-essence fields, but all purely kinetic k-essence fields may not form ghost condensate. There can be kinetic k-essence fields for which is not of the form given in Equation (12). There may be theories where is never satisfied. In our paradigm, these kinds of theories are purely kinetic k-essence theories, which do not have any ghost field correspondence. In [57], the authors have shown that ghost fields can successfully produce a stable accelerating expansion phase of the universe. Our primary attention in this paper is on a stable accelerating phase of the universe in the presence of a kinetic k-essence field and a barotropic fluid. We will see that ghost fields in the presence of a barotropic fluid can produce an accelerating phase of the universe. It will also be pointed out that sometimes a pure kinetic k-essence field, which is not a ghost field, can produce the accelerating phase in the presence of a barotropic fluid. In [57], the authors worked out the theory of ghost condensates and their interaction with standard model fields in cosmology.
In the context of purely kinetic k-essence, Scherrer has shown [27] that both of the dark sectors can be unified. In this unification, it is seen that, near the stable critical point, the energy density of the k-essence scalar field is composed of a constant energy density and another energy density resembling a non-relativistic matter contribution as:
Here, is the constant energy density representing the cosmological constant and is the coefficient of the matter energy density near the critical point. In reality, what Scherrer had shown was also shown by the authors of [57]3. Scherrer actually worked out the theory of ghost condensates in cosmology.
In this present paper, we will try to formulate the cosmology of kinetic k-essence fields in the presence of a perfect fluid which can interact non-minimally with the field. We think this approach is useful and new and can lead to interesting research in this sector. Before we proceed, we want to present some general features of kinetic k-essence fields and ghost condensates in the presence of a perfect fluid.
3. A General Outline of the Paper
In this section, we will give a general outline of the work presented in this paper. It contains the main theoretical input of this paper. The rest of the sections will illustrate the validity of the general results. In the present work, we will be dealing with the cosmological development of a kinetic k-essence field in the presence of a barotropic fluid. We will be especially interested in non-minimal coupling between the field and fluid sectors. The coupling term, introduced in the action4, is naturally given by a function of X and the fluid energy density . This coupling gives rise to interaction pressure and interaction energy density 5. We assume that:
- When and are non-zero, they are functions of and X. The functions are such that none of them can be written as a sum of a function of X and a function of at any time. The factors of and X cannot be separated in and . This assumption is natural because if one can write ( are some functions) at any instant of cosmic evolution, then there appears an ambiguity about the interpretation of the functions 6. Should one interpret as a pure kinetic k-essence pressure or as pressure due to interaction? To avoid such ambiguous situations, the interaction terms are assumed to be made up of functions in which X and remain additively inseparable.
- If , then both and may tend to zero or infinity but cannot take any other values. This assumption is also natural, as we do not expect the field and fluid to interact smoothly with each other when the fluid does not exist in the system at all. For those kinds of interactions where the interaction terms diverge as , one never reaches a stable phase where the fluid energy density vanishes. If an equilibrium is reached, the fluid energy density always remains finite in that phase.
- As the interaction terms do not arise from any particular matter sector, we assume can take all possible values. It can be positive, negative or zero. The total energy density of the system is where individually and . We can sometimes choose the parameters of the theory and the form of the interaction in such a way that throughout the cosmic evolution.
We have specified that if the field is a ghost field, then it can produce a stable accelerating phase of the universe in the far future. The ghost condensate is formed when is satisfied for a particular value of . On the other hand, one can also obtain a stable accelerating solution in the presence of a pure kinetic k-essence field, which is not a ghost field in the presence of a barotropic fluid. Before we proceed, we would like to present some formal discussion on the field–fluid system where the scalar field is a ghost field.
First, we propose a formal statement about the field–fluid system. The statement is as follows: If a pure kinetic k-essence field, with the Lagrangian density , in the presence of a barotropic fluid with a positive semidefinite EoS forms a ghost condensate in a stable, accelerating, spatially flat FLRW spacetime with , then the fluid energy density tends to zero in the far future (when the scale-factor a has increased appreciably from its initial value).
Before we prove the statement, we want to clarify certain points. The ghost condensate is formed when as stated earlier. The condensate value is given by , where is a constant. In our case, the ghost field has an EoS, the fluid has an EoS, , and the field–fluid system has an EoS, .
When the field and fluid do not have any coupling, except gravitational coupling, the field and fluid systems evolve separately. In this case, in the far future, the ghost field will form a condensate when . Here, the subscript c specifies the values of the variables when the stable condensate has formed. Suppose this state is a stable accelerating solution of the field–fluid system. In that case
From this equation we get
or . This shows that must vanish in the stable accelerating phase when the condensate has formed.
If the fluid and the field are non-minimally coupled, there arises interaction energy density and , where both of these variables are functions of X and in general. If, in the asymptotic future, a stable ghost condensate forms, then in this case also we must have . In the present case:
This equation gives . From this equation, we get
From our general assumptions about the interaction terms, we know that the addition of and must be a function of and . In the present case, it is seen that is independent of ; this fact violates our assumption about field–fluid interaction. As a consequence, the above equation can only hold true when . This implies that in the stable phase, the field–fluid interaction vanishes, and consequently both and vanish. The two fluids become uncoupled, and the general statement is satisfied. This ends the proof.
One may also state the reverse: If the barotropic fluid energy density tends to zero in the far future in a stable cosmological phase with accelerated expansion, then a pure kinetic k-essence field with the Lagrangian density in the presence of barotropic fluid with a positive semidefinite EoS, forms a ghost condensate in a spatially flat FLRW spacetime with .
The proof of this statement is as follows. As , we cannot have in the stable phase of acceleration. Thus, when the fluids are decoupled, the fluid sector energy density can only reduce. As a consequence, the final state of zero fluid density can in principle always be reached. When the fluids are not coupled and in the final stable accelerating state the fluid density goes to zero, then the only agent responsible for the accelerating phase must be the ghost condensate.
Next, we discuss what happens when there is non-minimal coupling in the field–fluid system. In this case, we have in the asymptotic stable future. Here, the subscripts specify stable phase state variables. From our assumptions on field–fluid coupling specified at the beginning of this section, we know that the interaction terms and can either be zero or diverge in this phase. If diverges, the total energy density diverges, and the final state does not remain stable; a spacetime singularity emerges in this case. Consequently, if the final phase has to be stable, one must have . As a consequence, in the stable accelerating phase we have only the ghost field, and it can produce stable acceleration only when ghost condensate is formed. In such a case, in the final phase we can replace all the subscripts s with c, because the final stable phase also happens to be the phase where the ghost condensate has formed. The proof of the reverse statement ends here.
From the above statements, we can deduce some general results, as follows:
- In the absence of non-minimal coupling, a stable accelerating phase of the universe will always be formed when the barotropic fluid density (with a positive semidefinite equation of state) tends to zero and the condensate forms in the far future.
- When a stable ghost condensate is formed in the accelerating phase of the universe in the presence of field–fluid non-minimal coupling, the non-minimal coupling term vanishes in the far future and the system becomes decoupled into two non-interacting phases. The fluid density tends to zero in the far future.
It is seen from the above discussion that if the ghost condensate forms, then it reduces the energy density of the fluid to zero. If a dark matter sector is modeled by a fluid in the stable phase when the condensate has formed, there will be no remnants of dark matter. On the other hand, pure ghost condensates (in the absence of any fluid) tend to produce a ‘matter-like’ effect near the stable point, as shown in Equation (13). This matter-like part drops out when the stable condensate is formed [57]. If the dark sector is really composed of a ghost field, one natural question arises: has the condensate formed? If the ghost field alone is responsible for the dark sector, then the answer must be in the negative, as the dark matter density is not zero now. On the other hand, if one claims we have reached the stable phase, then the pure ghost condensate model cannot be the correct model for the dark sector. The quantity which can unravel the nature of the dark sector is the ratio of the dark matter energy density to the dark energy density. If this ratio evolves towards zero as the system stabilizes, then a ghost sector alone can take care of the dark sector. On the other hand, if this ratio tends towards a constant, then the ghost field does not remain a viable option.
In this paper, we will show that both of the options regarding the ratio are achievable. The ratio tends to zero when a ghost field is accompanied by a fluid and their interaction vanishes in the far future. On the other hand, in the presence of non-minimal interaction which resists the extreme dilution of the fluid energy density, one can actually get a simple, pure kinetic k-essence configuration which forms a fluid-induced condensate. In this case, also one obtains a stable accelerating phase where is a constant in the presence of a constant fluid energy density. The condensate is not the standard ghost condensate but a fluid-induced pure kinetic k-essence condensate, which we will specify as the k-condensate.
4. Cosmological Dynamics in the Presence of a Purely Kinetic k-Essence Field and a Relativistic Fluid
In this section, we will study cosmological dynamics in the presence of a kinetic k-essence scalar field and a perfect pressureless fluid. In the present case, the fluid and the field do not exchange energy momentum; consequently they do not interact directly. Although the two matter sectors do not interact directly, they affect each other gravitationally. In the next section, we will deal with the non-minimally coupled field–fluid case. The action for a purely kinetic k-essence scalar field and a relativistic [34] fluid can be written as:
In the above action, the new term designates the action of a relativistic fluid. The commas in the subscripts specify covariant derivatives; they become partial derivatives for scalar functions. In the fluid action, denotes the energy density of the fluid, which depends on particle number density (n) and the entropy density per particle (s). Variables such as , and are all Lagrange multipliers. The Greek indices run from 0 to 3, and is a Lagrangian coordinate of the fluid, where A runs from 1 to 3. The current density is defined as,
Here, is the 4-velocity of the perfect fluid. Variation of the action with respect to gives rise to constraint equations. In this article, we will not require those constraint equations. The only constraint which is worth mentioning is about the constancy of specific entropy density in the cosmological dynamics of the dark sector. Variation of with respect to yields the energy-momentum tensor for the relativistic fluid as
which gives us the energy density of the fluid and pressure . In this case, the energy-momentum tensor of the field and fluid part is separately conserved, i.e., and . For the purely kinetic case, the variation of the action with respect to gives rise to the field equation as given in Equation (9). In the FLRW background, the Friedmann equations can be written as,
In the next subsection, we will explore the dynamics of this field–fluid system using the dynamical stability technique.
Dynamical Analysis in the Case Where the Pure Kinetic k-Essence Field and the Hydrodynamic Fluid Interact Gravitationally
To study the dynamical stability of this system, we chose some dimensionless variables such as:
where is related to the fluid energy density and corresponds to k-essence energy density. In defining z, we have used the parameter . Here is the Hubble parameter at any instant of cosmological time. It is seen that all of the five variables defined above are not independent of each other. Knowing the dynamics of x and z, one can evaluate the values of and . Using Equation (18), the constrained equation can be expressed as
where the fluid energy density is . Here
which is a dimensionless constant. The constraint equation shows that the phase space dynamics are actually two dimensional. We only need to investigate the dynamics of x and z. From the constraint equation, we can then infer the value of .
The second Friedmann equation can be expressed as:
where is equation of the state of the fluid. The energy density and pressure of the scalar field can be written in terms of dynamical variable x using the chosen form of . Until now, we have not chosen any particular form of . All of the statements made until now, and in most parts of the next section, are in general true for any form of .
In the present case, the set of autonomous equations in the two-dimensional phase space is given by
From the definition of and , the total (or effective) EoS and adiabatic sound speed in the k-essence sector are written as:
where and . In the case of fluid, the square of the sound speed is equal to its equation of state .
From the autonomous equations, it is seen that the stability of the x variable is not directly dependent on z. We have when for a non-trivial critical point. Here, one can notice that and are always critical points which are not physical, as demands an extremely high value of the Hubble parameter. In the late phase of the universe, one can safely neglect this critical point. When , one can have only when . This can be verified if one uses the constraint relation, Equation (21), in the autonomous equation for z. The solution is stable if . If the last condition is fulfilled, we see that, in the presence of a barotropic fluid, the only stable fixed point of the system corresponds to a ghost condensate. In the asymptotic future, the fluid energy density vanishes and the universe settles down to an accelerating phase with and . The result is in agreement with the general statements made in the previous section.
From the above discussion, it is clear that near the stable critical point, the effect of the fluid is minimal, and the system settles down in an accelerated expansion phase purely dictated by the ghost-field dynamics. The only effect of the fluid is in the initial transient phase. In the present case, the field configuration and the fluid part do not exchange energy momentum, and the stability of the system is solely guided by the ghost-field sector. This case is a simple application of our general understanding of cosmological dynamics produced by ghost fields in the presence of a barotropic fluid. In the next section, we will present two cases of field–fluid interactions where the cosmological dynamics are relatively more complex.
5. Cosmological Dynamics in the Presence of a Purely Kinetic k-Essence Scalar Field Non-Minimally Interacting with a Relativistic Fluid
The field–fluid action in the present case corresponds to the action for non-minimal coupling of k-essence field and a relativistic fluid [40], given by:
The last term of the action involves the non-minimal coupling term, which is . The functional form of f depends on the type of interaction. Due to the proposed interaction, some of the fluid equations of motion are now generalized. The non-minimal coupling follows the general properties discussed in Section 3.
Varying the total action with respect to gives the energy-momentum tensor as
Comparing the above equation with the perfect fluid’s energy-momentum tensor yields the energy density and pressure of the interaction, which are expressed as
Due to the introduction of non-minimal interaction, the energy-momentum tensor of each component of the field–fluid system is not conserved separately; rather, the total energy-momentum tensor is conserved. For more details, one can refer to [40].
We can rewrite the energy-momentum tensors for both sectors as and . Hence, the Einstein field equation becomes,
The covariant derivative of the field energy momentum tensor is
Here, is a 4-vector that defines energy exchange between the systems. Similarly, we can write a conservation equation for fluid as,
showing that the total energy-momentum tensor is . Varying the action with respect to yields
Friedmann equations can be written for this case in the context of the FLRW background as,
In the next subsection, we will elaborately describe the dynamical technique required to investigate the dynamics of this proposed non-minimally coupled sector.
5.1. Dynamical Analysis of a Non-Minimally Coupled Field–Fluid Scenario
To analyze the behavior of this non-minimally coupled system, we use the dimensionless variables introduced in the last section. The forms of the variables x, and z are given in Equation (20). To tackle non-minimal field–fluid coupling, we introduce some more dimensionless variables:
We have introduced C and D, as using them we can compactly write the autonomous equations. The constrained equation can be found from the Friedmann Equation (33), and it is:
where was defined in the previous section. The other Friedmann equation, as given in Equation (34), written in terms of the dynamical variables becomes
Here, we have used the EoS for the hydrodynamic fluid as . The total equation of the state of the system is:
and the sound speed in the k-essence sector is:
The above sound speed is a suitable generalization of the sound speed in the pure kinetic k-essence sector. In order to have a stable theory, the sound speed must be positive and satisfy the condition of . Next, we explicitly write some of the cosmological variables which appear in the constraint equation:
where is the energy density of k-essence field and is the interaction energy density.
Non-minimal interactions make the cosmological system more complex. The first hint of this complexity arises from the form of the interaction energy term . For matter components, we can always use the standard constraints as and , respectively. On the other hand, does not arise from any matter sector, and consequently one may have negative values of the interaction energy term. The fact that is not positive semidefinite makes the constrained Equation (36) less predictive, as now both and can have values greater than one. In the present paper, we will try to maintain the conventional bounds on the scalar field-energy density, matter-energy density and interaction-energy density and work out the cosmological dynamics when , and , respectively. It must be pointed out here that having , when neither or X is zero, does not imply that non-minimal coupling has vanished; in such cases, will not be zero. From the results specified in Section 3, we know that in the absence of any spacetime singularity, both and are zero when .
The autonomous equations for the present system are:
This 2-D autonomous system encapsulates the behavior of the system. The variables x and z are sufficient to describe the entire behavior of the system. To proceed further, we will choose some form of the interaction term , where is purely a function of the fluid energy density and is a function of the kinetic term X. As we are dealing with a purely kinetic k-essence field, we assume the interaction term also to be a function of and X. In the whole analysis, the field does not appear explicitly in the action. We work with a simple and fairly general form of non-minimal field–fluid interaction; more complicated interaction terms are not ruled out, but their analysis will be complicated. To unravel the nature of field–fluid coupling, we will study two cases which will adequately show the rich mathematical structure of these theories. We have made a list of the model parameters in Table 1. In this table, M is a parameter with the dimension of mass and .

Table 1.
Model variables where and .
The form of the interaction term listed above has where g is a dimensionless coupling constant. Here, and q are real numbers. The factor M with a mass dimension is present for dimensional reasons. If one chooses , then the interaction term becomes . The factor is a dimensionless, positive real constant which can easily be absorbed inside the coupling constant. In such a case, the interaction simply becomes , where we have represented the new, scaled coupling constant by the old symbol g. We will use this kind of interaction to see whether a ghost condensate can actually produce a stable accelerating phase. Later on, we will discuss a model where .
Before we start analyzing the various cases of non-minimal field–fluid interaction, let us spend some time explaining an important difference between these models and the case we dealt with previously in an earlier section. Unlike the pure gravitational coupling case, in the present case the field and fluid sectors directly exchange energy and momentum with each other and consequently can create or destroy each other. The scalar field sector can pump energy and momentum to the fluid sector and can create the fluid or increase or decrease the energy density of the pre-existing fluid. In the present case, both and can become zero momentarily. In our previous discussion with non-interacting fluids, none of the energy densities could become momentarily zero. There, in the accelerated expansion phase, the fluid energy density consistently remained zero. In the present case, non-minimal coupling may annihilate one sector momentarily, but that sector again can be created due to the same interaction.
5.2. Cosmological Dynamics in Case I:
In the present case, we have , as a result of which the interaction term is , where g is the dimensionless coupling constant. Depending on the dynamics of the system, g can take any real value. This kind of an interaction term becomes exactly zero when . In Table 1, some model variables are evaluated that depend on and . We can specify some of those variables in the present case as , and . Using these variables and their derivatives with respect to X, one can predict the cosmological dynamics in this case.
Before we specify the critical points in this model, let us briefly discuss some of the subtle properties of this non-minimal interaction model. In Model I, the interaction energy term is given by:
Using the above expression, one can write the constraint equation, Equation (36), as
where is a function of x and z. From the above equation, one can see that if there is a real X for which , then the constraint equation becomes useless at that value (or values) of X, as becomes indeterminate at that point (or points). As in the present case, the dynamical system used to predict the behavior of the universe is a differential–algebraic system; at those values of X, the algebraic component fails, resulting in a singularity. The root of the equation giving rise to singularities is:
From the above expression one can see that, in general, one can always get real values for X, and as a consequence, the resulting theory is singular. One can avoid such singularities only when
- and , or
- and .
The above choice of parameters shows that the present non-minimal field–fluid coupling term is constrained. If the parameters g and do not follow the constraints, then the cosmological dynamics become indeterminate. Henceforth, we will assume that the above constraints are satisfied.
A general discussion of the critical points of the autonomous system of equations given in Equation (41) reveals interesting features. Due to the presence of non-minimal coupling with a barotropic fluid, the number of critical points in the present case has increased. We will see shortly that most of the critical points are physically uninteresting. For any arbitrary, positive, semidefinite , it is seen from Equation (41) that there exists a class of critical points of the system for zero fluid energy density. In this case, (), the critical points correspond to the critical points in a field–fluid system where the direct coupling vanishes. The critical points are stable if around the solutions of . Can we have more physically relevant stable critical points, where the fluid density does not vanish? If the EoS of the fluid , one cannot prove conclusively that such critical points do not exist. This lack of precise understanding of the system does not affect cosmological dynamics in the dark sector, as we are mainly interested in the field–fluid coupling where the barotropic fluid resembles dark matter with an EoS . When , one can conclusively say that the only stable fixed points of the system correspond to the solutions of . In this case, both C and vanish, as they are proportional to .
Except the physically relevant stable critical points of Equation (41), in the present case we can have more critical points due to field–fluid non-minimal coupling. From Equation (41), one can easily see that, for , the system admits a line of critical points at . The critical points lie on the line specified by the points , where one can use any real value of x. These set of critical points are physically irrelevant, as at these points the Hubble parameter diverges. If the fluid energy density diverges, then the denominator of the first autonomous equation in Equation (41) diverges (as in the present case), giving rise to . This fact gives rise to another non-trivial critical point when . This critical point also turns out to be physically irrelevant, as we do not expect the fluid energy density to blow up in an expanding universe in the far future. Both of the critical points discussed in this paragraph are purely mathematical possibilities, and it turns out that both of these critical points are unstable. Only one class of stable, physically relevant critical points exists in the present case, for , and near it the fluid energy density vanishes. For these classes of critical points, one can always choose the general form of as given in Equation (12), and consequently the critical points correspond to some form of ghost condensates. This fact was predicted by the general discussion in Section 3.
Until now, we have worked with a general form of . If one wants to predict the dynamical evolution of the system, then one must choose some form of and a specific barotropic fluid. As we are interested in the dark sector, we choose the fluid to represent dark matter, and consequently we assume . In this paper, we choose the form of as:
where A and B are non-zero real constants. This form of satisfies all the properties requires, as discussed in Section 2. If both A and B are of the same sign, then the field is not a ghost field, it is a pure kinetic k-essence field. On the other hand, if A is negative and B is positive, then turns out to be a ghost field (it is still a pure kinetic k-essence field). In the present case, we see that if we want a stable accelerating phase, then must form a ghost condensate; consequently, we choose and . With this choice, our coincides with the form as predicted in Equation (12), where . With the above choice of , one can easily find out the physically relevant critical point of the autonomous equations in Equation (41). The coordinates of the critical point are and . The dynamical solutions in our case are symmetric with respect to the sign of x, and consequently, we only use the positive value of . As we are dealing with an expanding universe, we will only consider the case . For and , we see that at this critical point , and consequently, this critical point is a stable critical point.
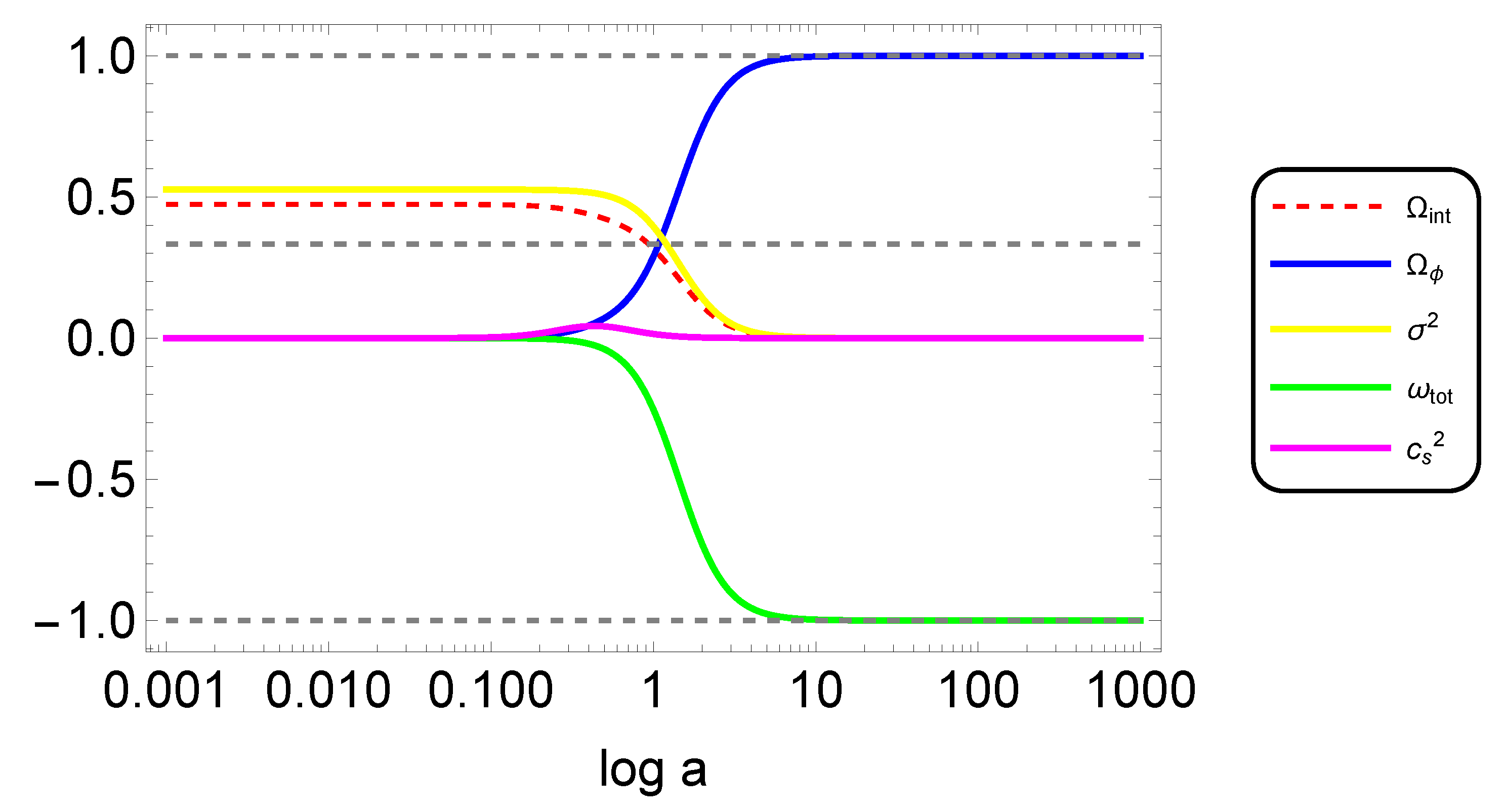
The evolution of the system variables is shown in Figure 1. Here, the barotropic fluid sector has an EoS of . From the figure, we see that starts from a non-zero value and smoothly becomes zero when the ghost condensate forms. Initially, is small but non-zero (a fact that is not that clear from the curve because of scaling) and remains constant for a while. When starts to dip, the ghost field energy-density parameter, smoothly goes up and saturates. The dark-matter fluid energy-density parameter, , remains constant as long as remains constant, and it starts to dip when the ghost condensate starts to form. In the initial phase, remains a positive constant whose magnitude is greater than one. During this phase, the effective system evolves as in a matter-dominated phase. This resembles some form of scaling behavior, which is generally observed in quintessence models of dark energy. In the late phase, fluid energy density tends to zero. The effective fluid EoS, , initially remains zero, and ultimately it settles down to its desired value of , showing a transition from an effective matter-dominated phase to an accelerated expansion phase of the universe. The sound speed almost always remains close to zero.
Figure 1.
Evolution of various Model I variables for and .
The discussion presented in this section serves as a model for the dark energy-dominated universe. It is seen that in the stable accelerating phase, when the ghost condensate is formed, the fluid energy density tends to zero. The interaction terms vanish in the final phase. The result turns out to be similar for all non-minimal field–fluid couplings where . For non-zero EoS, the ghost condensate-dominated stable point is always present. Can there be models where the dark-matter energy density does not vanish in the stable accelerating phase? From our general understanding of ghost fields, we can say that if the non-minimal interaction is such that it resists the fluid density to vanish in the future, then one may obtain a stable accelerating phase with non-zero fluid energy density. In such a case, the scalar field does not have a ghost-like character; it becomes a purely kinetic k-essence condensate, which by itself (in the absence of any fluid) is unstable but can form a kinetic k-essence condensate only in the presence of a barotropic fluid. In the next section, we will present a case that deals with a pure kinetic k-essence condensate.
5.3. Cosmological Dynamics in Case II: , with
Here, we consider the form of interaction given by . We will specifically deal with the case of . The model parameters have been evaluated in Table 1. For a general q, the interaction energy term is given by:
Using the above expression, one can write the constraint equation as,
The theory becomes physically tractable when the field energy density and fluid density satisfy the conventional constraints , . We have worked with parameters which make positive semidefinite. For , we have . The field component parameter is not zero in the late-time phases of the universe, but we have seen from our previous discussions that in general a ghost condensate in the final phase tries to diminish the dark-matter energy density down to zero. When the field and fluid have no direct coupling or when the field–fluid coupling vanishes in the low-matter density regime, formation of ghost condensate in the final phase is a certainty. We know from the general results presented in Section 3 that the interaction terms , and in the limit can either tend to zero or tend to infinity. In the previous case, both , and tended to zero as . In the present, case we see that both of these variables become unbounded from above in the same limit. This fact shows that if we have a stable phase of accelerated expansion, then in that phase the dark-matter energy density cannot go to zero. The interaction resists the dark-matter energy density going below a certain threshold, and it will be seen that the interaction term also resists ghost condensation.
In the dark matter-dominated phase, when the fluid energy density dominates, the interaction has less influence; however, in the final phase, when the fluid energy density becomes subdominant, interaction becomes stronger between the field and the fluid. In the present case, the constraint equation given in Equation (43) becomes a fourth order algebraic equation in whose relevant solution for is given by:
where . As in the previous case, in this case also there are some physically irrelevant critical points. For and for any , it is seen that all the points on the line are critical points. These are unstable points. Other than these, there may be more critical points which lie outside the region of our interest. The choice of model parameters has been made in such a way that the physically relevant critical points remain real in the region of phase space constrained by the relations , and . This constrained region of the phase space defines our region of interest. In the present case, we assume the barotropic fluid to resemble dark matter, and consequently we have . The form of was specified in Equation (45). It is seen that there is only one physically relevant critical point corresponding to this model in our region of interest, and its properties are tabulated in Table 2. The critical point is obtained for a specific set of the model parameters. Changing the model parameters will alter the critical point, and for some values of the parameters, there may be no critical points. In the present case, it is seen that the relevant, stable fixed point is obtained when both and . As a result, in this particular case, it is seen that the stable accelerating phase is obtained only when the scalar field is not a ghost field.

Table 2.
The physically relevant critical point and its nature corresponding to the parameters and .
Choosing and , we have obtained the relevant critical point of the coupled system numerically. Numerically, one can verify that the fixed point specified in the table is stable. One must note that in the present case, both A and B are positive, and consequently cannot be satisfied by any real X. This shows that in the present case, we are actually dealing with a pure kinetic k-essence field which is not a ghost field.
The point P is a stable fixed point specifying accelerated expansion of the universe. Near this point, we have dark energy-like behavior, since the k-essence field energy density dominates at this point.
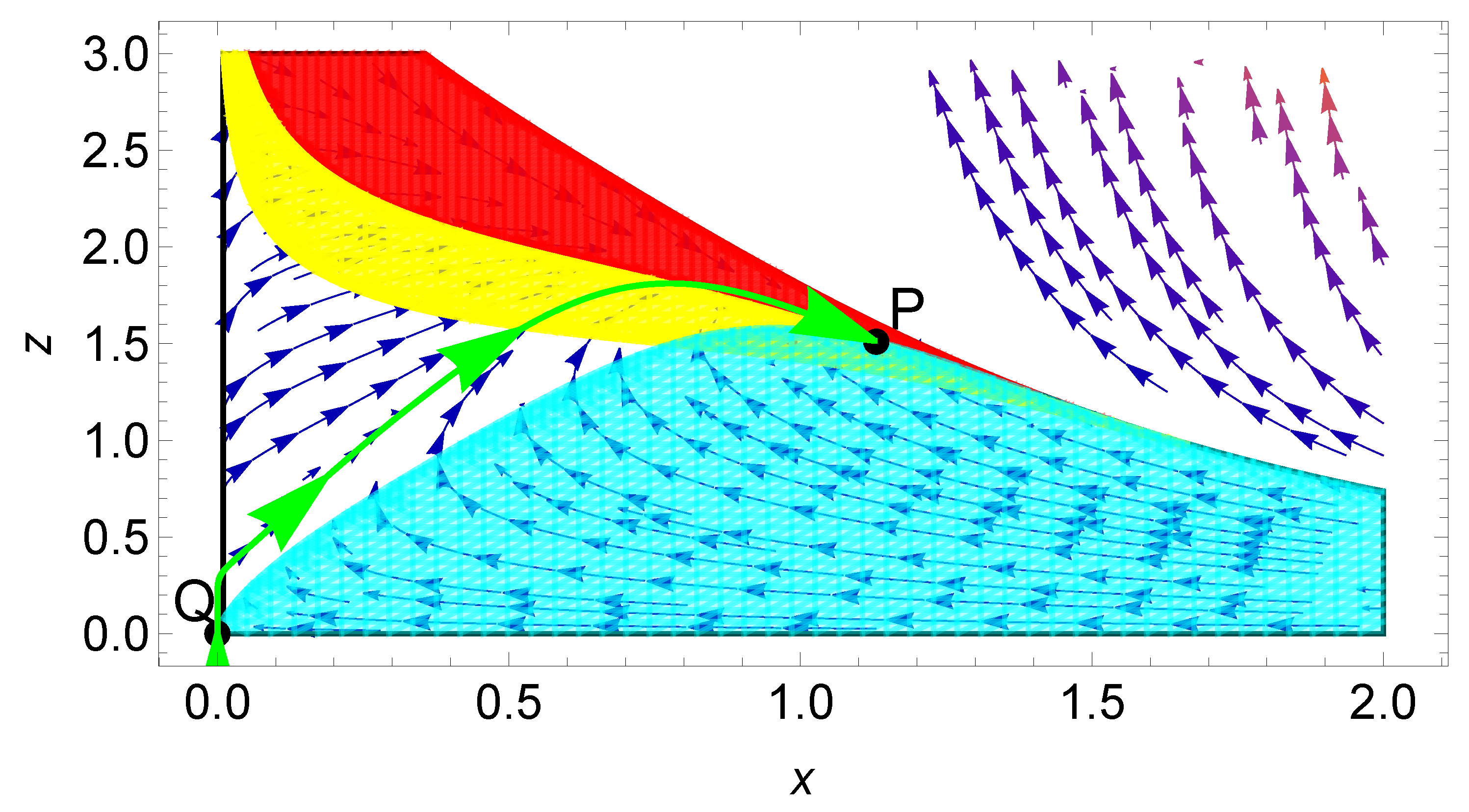
The dynamics near the fixed point can be understood from the phase space plot in Figure 2. The physically relevant portion of the phase space is colored, and the shape of this region is dictated by the constraints on the various parameters , and . For a better understanding of the flow in the phase space, we have marked another reference fixed point Q with coordinates . A trajectory evolves from Q and directly goes towards the accelerating point P through the non-accelerating region, shown in green. In the phase portrait, the red region specifies that part of phase space where the system evolves in an effective phantom-matter-dominated phase, the yellow region signifies the accelerated expansion phase and the blue region shows the sound speed in the scalar-field sector to be positive; for all the points there, the sound speed is between 0 and 1. Apart from these, there is a white region where none of these conditions hold. The arrows that lie outside the constrained region are not relevant for the present case; they simply show that there can be some flows in the unconstrained part of the phase space. We remind the reader that there can be other interesting regions in the complete and unconstrained phase space of the system. Due to the mathematical complexity of the situation, it is very difficult to probe the properties of the whole unconstrained phase space.
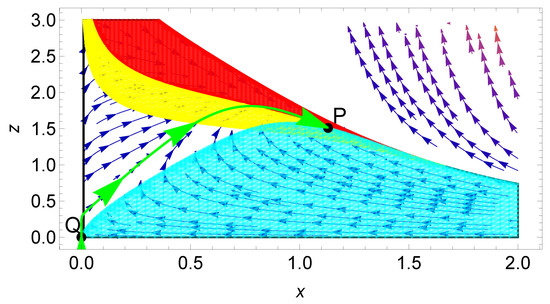
Figure 2.
Phase space of non-minimal coupling of k-essence with matter fluid for , and .
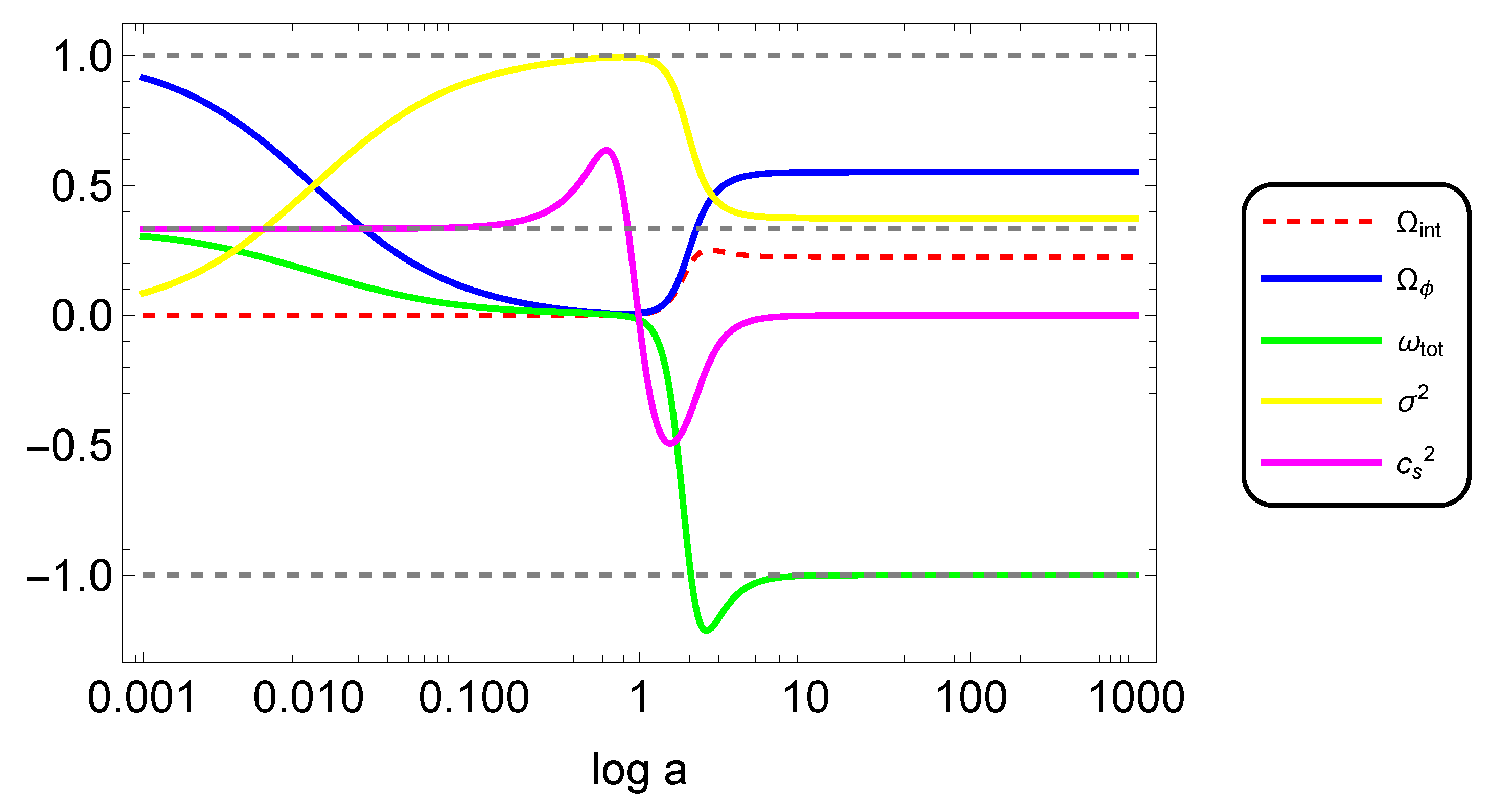
We plotted the evolution of various quantities of interest against in Figure 3. In the very early phase, we see that fluid density is less, and pure kinetic k-essence energy density is dominating. In this case, the total equation of state is , yielding an effective radiation domination, although there is no radiation fluid in the system. This demonstrates that the purely kinetic k-essence sector plays an important role as far as the effective EoS of the system is concerned. Over time, the fluid energy density grows and eventually overwhelms the field energy density, ushering in the matter era as the cosmos develops. The EoS is zero (or very nearly zero) for some period, and the speed of sound is seen to be decreasing in this phase. As the universe further evolves, the kinetic k-essence sector energy density increases, and so does the interaction energy density. The fluid density becomes a non-zero constant in the stable accelerating phase, unlike the previous ghost condensate-dominated phases. Finally, the EoS saturates to , and the speed of sound approaches zero, symbolizing the presence of dark energy.
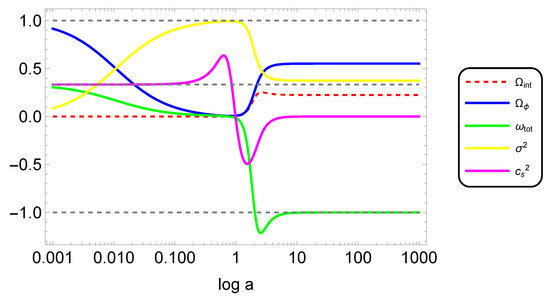
Figure 3.
The evolution plot of various cosmological variables corresponding to , and .
In the present case, we see that the purely kinetic k-essence sector does not correspond to a ghost sector. The purely kinetic k-essence sector, in the absence of dust, lacks stability. Only in the presence of non-minimal coupling with dust does X get a time-independent expectation value . As this expectation value is obtained due to non-minimal coupling with a fluid, we can call it an induced, kinetic k-condensate. This example shows how the system resists ghost condensate formation in the presence of a non-minimal field–fluid coupling which diverges when the fluid density goes to zero. An interesting property of this phase is that the dust energy density does not diminish as the universe expands. This happens due to the non-zero field–fluid coupling. This case convincingly shows that we may have a stable accelerating phase of the universe even without a ghost condensate.
Before we end this section, we would briefly like to specify how these calculations can be connected to real cosmological observations. Primarily, our interest was to produce some toy models which specify the cosmological effects of non-minimal coupling between a pure kinetic k-essence field and a perfect fluid, which constitute the dark sector in our case. The models involve various parameters such as and , and also the model predictions depend upon the initial conditions we imposed upon the autonomous system of equations. This shows that we can actually fit cosmological data by tuning this parameter space. In this paper, we have not tried to explain the exact observational predictions; our aim was to show the qualitative effects of non-minimal field–fluid coupling in cosmology. Nonetheless, our work can always be connected to observational cosmology. Here, we present briefly some directions in which this can be done. In the future, we want to publish a more observation-oriented work based on field–fluid coupling.
We can link our work with late-time cosmic observation through two parameters, viz. (i) the coincidence parameter , and (ii) the deceleration parameter . Details about these two parameters are discussed below.
- Coincidence parameter: The coincidence parameter is defined to be the ratio of dark-matter energy density to dark energy density [58], and it can be written as,We can check the coincidence ratio for both of our cases and investigate the evolutionary dynamics. From an SNe Ia + BAO + OHD observation, we can see that is always a decreasing function at late times. From Case I, we initially get to be approximately a constant, and in Case II, initially increases, while in both models decreases at late times. These features can be useful to rule out some of the present models. We know from the measurement of satellite-borne experiments, WMAP [59] and Planck [60], that, at the present epoch, 96% of total energy density of the universe is due to dark matter and dark energy, with respective dark matter and dark energy contributions amounting to 27% and 69% of total energy density. This implies that, at the present epoch, the coincidence ratio is almost . It is seen that the value of the coincidence ratio at late-time tends to zero for Case I, whereas for Case II, the value has the same order of magnitude as that of the observed value. In Case II, the ratio we have is more than the observed value by a factor of two, but this increase can always be tuned by tuning the parameters of our model.
- Deceleration parameter: The deceleration parameter [58] can be expressed in terms of Hubble’s parameter as,In the late-time accelerating cosmological scenarios, the value of q is always negative at different values of redshift. If in the future an attempt is made to match the results of our calculations with actual observational data, then one can compute the evolution of q from the early to the late-time phase. As time evolves, q changes its sign from positive to negative according to an SNe Ia observation. One can, in principle, figure out the nature of the evolution of the deceleration parameter for both these models and check our result with the recent observational work [61]. Near the critical point, the value of the deceleration parameter (q) always tends to -1 for both the cases we studied.
6. Conclusions
In this paper, we have shown the link between pure kinetic k-essence fields and ghost fields in cosmology. The linkage is not new. All ghost fields are pure kinetic k-essence fields, whereas all pure kinetic k-essence fields may not be ghost fields. The present paper probes a particular feature about the fate of the universe in the presence of a ghost field and a barotropic fluid. It is seen that in isolation, a ghost field in cosmology will in general always lead to a stable accelerating phase of the universe. Does it do so even in the presence of a barotropic fluid, even when a non-minimal coupling is present between the field and the fluid?
We tried to answer the above question formally, and our result showed that a ghost field in the presence of dark matter, modeled as a fluid with , will in general form a ghost condensate at late times and lead to a stable accelerating phase. The ghost sector can answer most of the questions related to the dark sector, but one question remains. It is seen that in the stable phase, when the condensate has formed, there will be no trace of matter. If one claims that the stable phase has already been attained, as is approximately near today (or is assumed to be near it as various observations predict its value near ), then one faces a difficulty. The dark-matter energy density today is not zero. On the other hand, if one claims that we have yet not reached the stable point, then the effective EoS should not be near . Our general results predict that if there are interactions which forbid the fluid energy density to vanish in the future, then the ghost condensate will not form and a stable accelerated expansion phase can be achieved where the fluid energy density remains a subdominant constant. Consequently, if the universe has entered the stable phase, then our model shows that it can retain a subdominant matter energy density. The unique signature of this kind of non-minimal interaction is that the matter energy density remains a constant and does not scale with the factor.
Our work verified the general results in various cases using a particular form of kinetic k-essence Lagrangian density. When the field and fluid are not directly interacting, a ghost condensate always forms in the future when the fluid density vanishes. In the presence of non-minimal interaction between the scalar field and the fluid, with an arbitrary positive semidefinite EoS, the formation of ghost condensate is always a possibility in the stable accelerated expansion phase when the interaction term is such that it vanishes when the fluid energy density vanishes. In particular, when the fluid corresponds to dark matter whose EoS is , the formation of ghost condensate in the accelerated expansion phase is a certainty when the interaction term satisfies the above-mentioned property.
We have shown there can be field–fluid interactions which forbid ghost condensate in the stable phase even when the fluid corresponds to the dark-matter sector with . Such interactions tend to diverge when the fluid energy density tends to zero. Although we have verified the general predictions made in this paper using a particular form of pure kinetic k-essence Lagrangian density and some typical forms of field–fluid interactions, the general predictions hold for all complicated kinds of and all complex forms of field–fluid interactions which satisfy certain basic properties.
We want to emphasize that we have found a novel phase of pure kinetic k-essence condensate which only forms in the presence of a barotropic fluid when the field and fluid sectors are interacting non-minimally. We have shown that there can be a pure kinetic k-essence sector which has no stability in isolation but attains stability only when this sector interacts with a barotropic fluid. One can think of the stable value of X attained in this phase as a condensate, but it is an interaction-induced condensate.
In conclusion, we want to state that, most of the time, ghost fields and a barotropic fluid can produce a stable accelerating phase when the ghost condensate is formed, but not always. There can be cases where pure kinetic k-essence fields, which are not ghost fields, can also produce a stable accelerating expansion phase of the universe where matter energy density remains subdominant.
Author Contributions
All authors contributed equally in this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No external data wa used in this paper.
Acknowledgments
A.C would like to thank the Indian Institute of Technology, Kanpur for supporting this work by means of an Institute Post-Doctoral Fellowship (Ref.No.DF/PDF197/2020-IITK/970).
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | Although we call it a potential, , in reality, it does not play the role of a potential function in the conventional sense. |
| 2 | This conclusion gets modified when a barotropic fluid is also present. |
| 3 | Both the papers were published near the same time. |
| 4 | |
| 5 | The forms of these functions will become explicit when we discuss specific models of field–fluid interaction later in Section 5. |
| 6 | The function does not contain any term which is purely a function of X or . |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gillil, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.G.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. New Hubble Space Telescope Discoveries of Type Ia Supernovae at z≥1: Narrowing Constraints on the Early Behavior of Dark Energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef]
- Gawiser, E.; Silk, J. The Cosmic microwave background radiation. Phys. Rept. 2000, 333, 245–267. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Zehavi, I.; Hogg, D.W.; Scoccimarro, R.; Blanton, M.R.; Nichol, R.C.; Scranton, R.; Seo, H.J.; Tegmark, M.; Zheng, Z.; et al. Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies. Astrophys. J. 2005, 633, 560–574. [Google Scholar] [CrossRef]
- Percival, W.J.; Nichol, R.C.; Eisenstein, D.J.; Weinberg, D.H.; Fukugita, M.; Pope, A.C.; Schneider, D.P.; Szalay, A.S.; Vogeley, M.S.; Zehavi, I.; et al. Measuring the matter density using baryon oscillations in the SDSS. Astrophys. J. 2007, 657, 51–55. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Sosey, M.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R.; et al. A Redetermination of the Hubble Constant with the Hubble Space Telescope from a Differential Distance Ladder. Astrophys. J. 2009, 699, 539. [Google Scholar] [CrossRef]
- Martin, J. Everything You Always Wanted To Know About The Cosmological Constant Problem (But Were Afraid To Ask). C. R. Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.M.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Peccei, R.D.; Sola, J.; Wetterich, C. Adjusting the Cosmological Constant Dynamically: Cosmons and a New Force Weaker Than Gravity. Phys. Lett. B 1987, 195, 183–190. [Google Scholar] [CrossRef]
- Ford, L.H. Cosmological constant damping by unstable scalar fields. Phys. Rev. D 1987, 35, 2339. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Nishioka, T.; Fujii, Y. Inflation and the decaying cosmological constant. Phys. Rev. D 1992, 45, 2140–2143. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Joyce, M. Structure formation with a selftuning scalar field. Phys. Rev. Lett. 1997, 79, 4740–4743. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Joyce, M. Cosmology with a primordial scaling field. Phys. Rev. D 1998, 58, 023503. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Carroll, S.M. Quintessence and the rest of the world. Phys. Rev. Lett. 1998, 81, 3067–3070. [Google Scholar] [CrossRef]
- Copeland, E.J.; Liddle, A.R.; Wands, D. Exponential potentials and cosmological scaling solutions. Phys. Rev. D 1998, 57, 4686–4690. [Google Scholar] [CrossRef]
- Hebecker, A.; Wetterich, C. Quintessential adjustment of the cosmological constant. Phys. Rev. Lett. 2000, 85, 3339–3342. [Google Scholar] [CrossRef]
- Hebecker, A.; Wetterich, C. Natural quintessence? Phys. Lett. B 2001, 497, 281–288. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. B 1999, 458, 219–225. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. A Dynamical solution to the problem of a small cosmological constant and late time cosmic acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef]
- Chimento, L.P.; Feinstein, A. Power-law expansion in k-essence cosmology. Mod. Phys. Lett. A 2004, 19, 761–768. [Google Scholar] [CrossRef]
- Chimento, L.P. Extended tachyon field, Chaplygin gas and solvable k-essence cosmologies. Phys. Rev. D 2004, 69, 123517. [Google Scholar] [CrossRef]
- Scherrer, R.J. Purely kinetic k-essence as unified dark matter. Phys. Rev. Lett. 2004, 93, 011301. [Google Scholar] [CrossRef]
- Chiba, T.; Okabe, T.; Yamaguchi, M. Kinetically driven quintessence. Phys. Rev. D 2000, 62, 023511. [Google Scholar] [CrossRef]
- Bose, N.; Majumdar, A.S. A k-essence Model Of Inflation, Dark Matter and Dark Energy. Phys. Rev. D 2009, 79, 103517. [Google Scholar] [CrossRef]
- Capozziello, S. Curvature Quintessence. Int. J. Mod. Phys. D 2002, 11, 483–492. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Carloni, S.; Troisi, A. Curvature quintessence matched with observational data. Int. J. Mod. Phys. D 2003, 12, 1969–1982. [Google Scholar] [CrossRef]
- Amendola, L. Scaling solutions in general nonminimal coupling theories. Phys. Rev. D 1999, 60, 043501. [Google Scholar] [CrossRef]
- Sahni, V.; Shtanov, Y. Brane world models of dark energy. JCAP 2003, 11, 014. [Google Scholar] [CrossRef]
- Brown, J.D. Action functionals for relativistic perfect fluids. Class. Quant. Grav. 1993, 10, 1579–1606. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Tamanini, N.; Wright, M. Interacting quintessence from a variational approach Part I: Algebraic couplings. Phys. Rev. D 2015, 91, 123002. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Tamanini, N.; Wright, M. Interacting quintessence from a variational approach Part II: Derivative couplings. Phys. Rev. D 2015, 91, 123003. [Google Scholar] [CrossRef]
- Shahalam, M.; Pathak, S.D.; Li, S.; Myrzakulov, R.; Wang, A. Dynamics of coupled phantom and tachyon fields. Eur. Phys. J. C 2017, 77, 686. [Google Scholar] [CrossRef]
- Barros, B.J. Kinetically coupled dark energy. Phys. Rev. D 2019, 99, 064051. [Google Scholar] [CrossRef]
- Kerachian, M.; Acquaviva, G.; Lukes-Gerakopoulos, G. Classes of nonminimally coupled scalar fields in spatially curved FRW spacetimes. Phys. Rev. D 2019, 99, 123516. [Google Scholar] [CrossRef]
- Chatterjee, A.; Hussain, S.; Bhattacharya, K. Dynamical stability of the k-essence field interacting nonminimally with a perfect fluid. Phys. Rev. D 2021, 104, 2021. [Google Scholar] [CrossRef]
- Chakraborty, A.; Ghosh, A.; Banerjee, N. Dynamical systems analysis of a k-essence model. Phys. Rev. D 2019, 99, 103513. [Google Scholar] [CrossRef]
- Roy, N.; Bhadra, N. Dynamical systems analysis of phantom dark energy models. JCAP 2018, 6, 002. [Google Scholar] [CrossRef]
- De-Santiago, J.; Cervantes-Cota, J.L.; Wands, D. Cosmological phase space analysis of the F(X) - V(ϕ) scalar field and bouncing solutions. Phys. Rev. D 2013, 87, 023502. [Google Scholar] [CrossRef]
- Dutta, J.; Khyllep, W.; Tamanini, N. Cosmological dynamics of scalar fields with kinetic corrections: Beyond the exponential potential. Phys. Rev. D 2016, 93, 063004. [Google Scholar] [CrossRef]
- Ng, S.C.C.; Nunes, N.J.; Rosati, F. Applications of scalar attractor solutions to cosmology. Phys. Rev. D 2001, 64, 083510. [Google Scholar] [CrossRef]
- Koivisto, T.S.; Nunes, N.J. Inflation and dark energy from three-forms. Phys. Rev. D 2009, 80, 103509. [Google Scholar] [CrossRef]
- Bahamonde, S.; Böhmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rept. 2018, 775–777, 1–122. [Google Scholar] [CrossRef]
- Tamanini, N. Dynamics of cosmological scalar fields. Phys. Rev. D 2014, 89, 083521. [Google Scholar] [CrossRef]
- Dutta, J.; Khyllep, W.; Tamanini, N. Dark energy with a gradient coupling to the dark matter fluid: Cosmological dynamics and structure formation. JCAP 2018, 1, 038. [Google Scholar] [CrossRef]
- Bhattacharya, K.; Chatterjee, A.; Hussain, S. Dynamical Stability in presence of non-minimal derivative dependent coupling of k-essence field with a relativistic fluid. arXiv 2022, arXiv:2206.12398. [Google Scholar]
- Novosyadlyj, B.; Sergijenko, O.; Durrer, R.; Pelykh, V. Do the cosmological observational data prefer phantom dark energy? Phys. Rev. D 2012, 86, 083008. [Google Scholar] [CrossRef]
- Teng, Y.P.; Lee, W.; Ng, K.W. Constraining the dark-energy equation of state with cosmological data. Phys. Rev. D 2021, 104, 083519. [Google Scholar] [CrossRef]
- Valentino, E.D.; Mukherjee, A.; Sen, A.A. Dark Energy with Phantom Crossing and the H0 Tension. Entropy 2021, 23, 404. [Google Scholar] [CrossRef]
- Pan, S.; Sharov, G.S.; Yang, W. Field theoretic interpretations of interacting dark energy scenarios and recent observations. Phys. Rev. D 2020, 101, 103533. [Google Scholar] [CrossRef]
- Pourtsidou, A.; Skordis, C.; Copeland, E.J. Models of dark matter coupled to dark energy. Phys. Rev. D 2013, 88, 083505. [Google Scholar] [CrossRef]
- Sharov, G.S.; Bhattacharya, S.; Pan, S.; Nunes, R.C.; Chakraborty, S. A new interacting two fluid model and its consequences. Mon. Not. R. Astron. Soc. 2017, 466, 3497–3506. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Cheng, H.C.; Luty, M.A.; Mukohyama, S. Ghost condensation and a consistent infrared modification of gravity. JHEP 2004, 5, 074. [Google Scholar] [CrossRef]
- Rabiei, S.W.; Sheikhahmadi, H.; Saaidi, K.; Aghamohammadi, A. Interacting scalar tensor cosmology in light of SNeIa, CMB, BAO and OHD observational data sets. Eur. Phys. J. C 2016, 76, 66. [Google Scholar] [CrossRef]
- Hinshaw, G.; Weiland, J.L.; Hill, R.S.; Odegard, N.; Larson, D.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Jarosik, N.; et al. Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results. Astrophys. J. Suppl. 2009, 180, 225–245. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).