Abstract
Closed timelike curves (CTCs) are non-intuitive theoretical solutions of general relativity field equations. The main paradox associated with the physical existence of CTCs, the so-called grandfather paradox, can be satisfactorily solved by a quantum model named Deutsch-CTC. An outstanding theoretical result that has been demonstrated in the Deutsch-CTC model is the computational equivalence of a classical and a quantum computer in the presence of a CTC. In this article, in order to explore the possible implications for the foundations of quantum mechanics of that equivalence, a fundamental particle is modelled as a classical-like system supplemented with an information space in which a randomizer and a classical Turing machine are stored. The particle could then generate quantum behavior in real time in case it was controlled by a classical algorithm coding the rules of quantum mechanics and, in addition, a logical circuit simulating a CTC was present on its information space. The conditions that, through the action of evolution under natural selection, might produce a population of such particles with both elements on their information spaces from initial sheer random behavior are analyzed.
1. Introduction
Time is one of the deepest-rooted experiences in adult human beings. As such, it has been a fundamental object of study in philosophy and physics from the antiquity to the present. Naively, we can try to define1 time in a minimalist way as a concept that enables an observer to describe and measure the perceived physical fact that “the world changes”. However, in this definition there is an echo of circularity as for most, if not all, definitions of time.
In Newtonian physics, time is an absolute, primary concept. However, relativity theory demolished the notions of absolute time and absolute simultaneity, and, as a consequence, the flow of time, which shapes the first-person experience of an observer, appeared as an illusion. This paved the way to explore the possibility that time itself were not a primordial concept, but a derived one, and contributed to the impulse of mathematizing and constructing physics [4,5,6,7,8] in terms of more abstract primary concepts2.
Quantum mechanics went beyond relativity concerning the difficulties in grasping the observer-independent reality of nature. The Copenhagen interpretation of quantum mechanics highlighted the absence of meaning in describing a system without referring to the results of a measuring apparatus. Thus, the reality of a system, i.e., the definite value of the intrinsic properties that characterized such a system, could be affirmed only in connection with the actually performed observations by a classical meter.
Quantum mechanics also raised doubts about the validity of the classical principle of causality, i.e., that every event has an antecedent determined cause, and pointed at a possible intrinsic randomness as a fundamental feature of nature [10].
In addition, there was a central tension between quantum mechanics and relativity about the principle of locality3, i.e., the existence of a limiting velocity (the speed of light) for the propagation of an interaction through space, as was especially manifest in the experimental observations of non-classical correlations between entangled particles or Bell inequality violations [15].
Time seems to play a crucial role for the coexistence of both theories. For instance, backward in time causation [16,17,18] could explain Bell inequality violations preserving locality (see also Refs. [19,20]). Even in certain circumstances, quantum mechanics can alleviate some of the problems that the theory of relativity brings about regarding the nature of time. One of these cases is the solution to the difficulties and mysteries in the concept of time supplied by assuming the many-worlds interpretation (MWI) of quantum mechanics [21] as analyzed by Deutsch [22]. Another example is the resolution in the framework of quantum mechanics of the so-called grandfather paradox that appears in general relativity in those regions of spacetime for which closed timelike curves (CTCs) are possible mathematical solutions. The grandfather paradox reflects the logical inconsistency of those closed trajectories in which a time traveler could kill his own grandfather, therefore making impossible his own existence. The resolution of the paradox in a classical framework [23] is generally considered unsatisfactory [24,25] because it essentially requires suppressing by fiat the initial conditions of trajectories driving to the inconsistent solutions (enunciating a global principle of consistency that would prohibit the particular local solutions leading to inconsistency). However, a quantum model devised by Deutsch in order to analyze the closed timelike curves (D-CTCs) in terms of quantum information flows guarantees the existence of a consistent solution for all initial conditions.
The interest of studying CTCs in the framework of quantum mechanics resides not only in the solution of paradoxical results in this specific milieu, but also in the analysis of the interplay between relativity theory and quantum mechanics, and the deep implications on the nature, foundations, and coexistence of both theories.
The real, physical existence of CTCs is still a central, open question. However, simulations of CTCs, and also open timelike curves (OTCs), on photonic circuits have already been performed on the laboratory [26,27].
A set of theoretical studies have also been developed on the special properties that quantum mechanical systems would present near a D-CTC4. One of the most astounding results, obtained by Aaronson and Watrous [30], is the computational equivalence of a classical and a quantum computer in the presence of a CTC. This result highlights the adequacy of the CTC scenario as testing ground to study the relationship between quantumness and classicality.
Mirroring the successful scheme in relativity, a traditional area of study in the foundations of quantum mechanics is the search of fundamental principles from which quantum mechanics might be derived. Different inspiring approaches have been considered, e.g., that of Zeilinger [31] in which information plays a central role. In spite of the tremendous efforts of leading experts in quantum foundations, complete, satisfactory derivation of quantum mechanics has not been achieved yet. Therefore, it remains an open question in the foundations of quantum mechanics. What will be the final solution of this problem (if it can be found at all)? For the moment, it is difficult to forecast. Therefore, a variety of approaches should be tested. We proceed within the information framework unifying a batch of models (see, e.g., [32,33,34,35,36]).
In the present article, the possibility of simulating D-CTCs in the framework of an information-theoretic, Darwinian approach to quantum mechanics (DAQM) [37,38,39,40,41,42] and its implication for the progress in the understanding of the foundations of quantum mechanics are analyzed. There are two specific concepts in this approach that play a central role in the theory. First, time is assumed to be, all the way down, a real fundamental magnitude in nature, in the sense that accepting the reality of time in its deepest meaning implies the possible change of the physical laws of nature, as extensively analyzed by Unger and Smolin [9].
The second specific, crucial concept in DAQM is anticipation. If the previous anticipation by an agent of a future event or algorithm outcome actually coincides with such event or outcome in the future, then from the point of view of information, this situation might be operationally equated to backward in time causation. Anticipation is built on the capacity of a system to process information. This capacity is assumed in DAQM as a fundamental property of matter. If information is central to physics, then it is natural to explore the possibility that matter possesses the capacity of processing information. Supplementing every physical system with an information space in which a methodological probabilistic classical Turing machine processes the information that arrives at the system turns physical systems into information-theoretic Darwinian systems, susceptible of variation, selection, and retention [43], on which natural selection might act as a metalaw, driving the evolution of natural laws or regularities—the algorithms stored on the information space of every physical system that govern their behavior—and plausibly, as will be analyzed within the article, generating quantum mechanical behavior as result of an optimized information strategy that might determine the direction of evolution in the long term.
Darwinism has been successfully applied to a long list of disciplines by several overarching schemes as universal Darwinism [44] or generalized Darwinism [43]. Darwinian processes have also been identified in physics, describing adequately intricate problems ranging from cosmology [45] to the emergence of classical states from quantum interactions [46]. This ubiquity of the Darwinian mechanisms is a reason in favor of examining the implications of DAQM.
The aim of this article is to explore the possibility of inducing quantum behavior for a physical system endowed with a probabilistic classical Turing machine through the simulation of a D-CTC on its information space, exploiting the theoretical equivalence between a classical and a quantum computer both with access to a D-CTC that has been demonstrated by Aaronson and Watrous [30]. In Section 2, a brief description of the D-CTC model is outlined. The characterization of a fundamental physical system in DAQM is analyzed in Section 3. The simulation of a D-CTC on the information space of a physical system in the framework of DAQM is studied in Section 4. The plausible emergence of quantum mechanical behavior from a sketchy mathematization of the dynamics of fundamental physical systems modelled as information-theoretic Darwinian systems in the framework of DAQM is discussed in Section 5. The conclusions are drawn in Section 6.
Finally, notice that, in the present study, the existence of real CTCs in the physical spacetime is not discussed, but only the implications of the possible simulation of a CTC in the information space of a DAQM particle.
2. Deutsch Quantum Model for a CTC
The conventional studies of CTCs are framed in the geometrical analysis of these solutions of Einstein’s field equations of general relativity for classical systems traveling along the spacetime [47]. Deutsch [24], adopting a different perspective, disregards the dynamics of the motion in the spacetime, assuming that the trajectories are classical and given, and considers traveling systems endowed with internal quantum mechanical degrees of freedom. Then, the physics of CTCs is analyzed in terms of the information flows within a physically equivalent quantum computational circuit that models the interaction process. It is assumed that the interactions between systems are localized in the quantum gates. Therefore, the states of the systems stay unchanged between gates.
One of the meaningful elements suggesting the exploration of a quantum mechanical description as a possibility to solve CTCs paradoxes is that, by considering quantum mechanical systems, the space of states of the traveling systems is enhanced, including linear superpositions and mixtures [48]. Deutsch [24] then proceeds to demonstrate (Deutsch’s fixed point theorem) that in quantum mechanics is always possible to find a consistent solution for any possible initial condition in the presence of a CTC. In this way, the D-CTC model overcomes the unsatisfactory limitation imposed by the classical resolutions (e.g., see Lewis [23] and Novikov [49]) of the grandfather paradox in which the way out from the paradox basically consists in claiming a philosophical global consistency criterion that impedes by fiat the initial conditions that, although allowed by local physical laws, would conduct to physical contradictions.
The quantum circuit that represents in the model of Deutsch for a CTC the process for a particle that approaches the CTC is drawn in Figure 1. Let us assume that the particle is a qubit. The particle that enters the CTC (see Figure 1a) in the quantum state ρ(1) interacts in the quantum gate U with an older version of itself that has come out of the past mouth of the wormhole in the state ρ(3). After the interaction, the younger version of the particle is in the state ρ(2) and enters the future mouth of the wormhole as the older version of the particle in the state ρ(4) leaves the CTC region traveling towards the unambiguous future. The process can be described in a “pseudo-time” narrative5 [25] from the intrinsic perspective of the particle following the timelike curve for which the proper time of the particle is increasing [47], with the number between parentheses for every state indicating the proper time order along the line. The model requires as consistent condition that the state of the younger system leaving the gate, ρ(2), be the same as the state of the older system entering the gate, ρ(3). That is to say, ρ(2) = ρ(3).
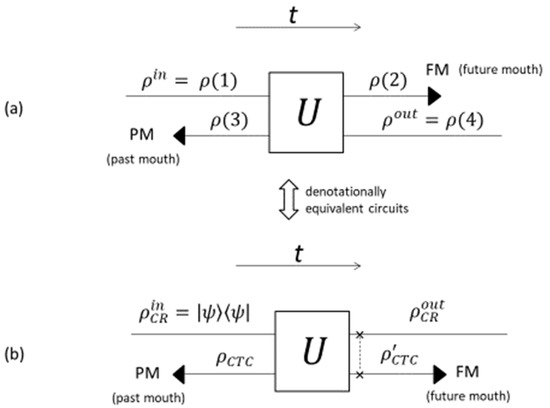
Figure 1.
(a) Quantum circuit representing the model of Deutsch for a CTC. (b) Denotationally equivalent circuit. The description of circuits and the meaning of symbols are given within the text.
The circuit represented in the Figure 1a can be conveniently transformed into a simpler denotationally equivalent circuit [24], as shown Figure 1b, for which the outputs of the transformed circuit are the same function of the inputs as in the original circuit, as defined by Deutsch [24], by including a gate after the original gate , so that the interaction in the transformed circuit is given by . In this way the one-particle circuit is replaced with an equivalent two-particle circuit [26,50] constituted by a chronology-respecting particle (CR) that interacts with another particle confined in a closed timelike curve (CTC). Now, the consistent condition in this equivalent circuit, shown in Figure 1b, is obtained by requiring that the quantum state () of the chronology-violating particle that emerges from the past mouth of the wormhole in the closed timelike curve be the same as the state that enters the future mouth ():
where it has been considered that the chronology-respecting particle enters the gate in the pure state (i.e., ) and the partial trace is over the Hilbert space of the chronology-respecting (CR) particle. Deutsch [24] showed (fixed-point theorem) that in the framework of quantum mechanics for a general interaction there is always at least a solution of Equation (1) for any initial state . This solves the grandfather paradox. An intriguing question of the model is the way in which nature has to manage in order to find the solution to Equation (1). This problem is usually named the knowledge paradox, since the solution to Equation (1) must be known at the same time as the state enters the gate, i.e., before the interaction occurs. Deutsch [24] gives an answer to the knowledge paradox6 in the framework of the many-worlds interpretation (MWI) of quantum mechanics. In our model, in the framework of DAQM, the knowledge paradox would be solved through the action of Darwinian evolution. This point is discussed in Section 5.
On the other hand, the state of the chronology-respecting particle that abandons the CTC region is given by the following expression:
where the partial trace now refers to the Hilbert space of the particle trapped in the closed timelike curve.
The dependence of the output state on the input state is non-unitary, since mixed states can occur on the CTC as solutions () of Equation (1), and nonlinear. This nonlinearity induced by the self-consistent condition (Equation (1)) is the source [30] of the stunning computational efficiency that enables a classical computer in the presence of a CTC to reach the same computational performance as a quantum computer with access to a CTC.
3. Information-Theoretic Model for a Particle in DAQM
The aim of this article is to analyze the relationship between classicality and quantumness in the light of the result of Aaronson and Watrous [30] in the unconventional scenario of a D-CTC. The model of Deutsch, as briefly described in the previous section, is based on the analysis of information flows in the equivalent quantum circuit that encodes the physical process for a quantum particle that traverses a CTC. Information is therefore a key ingredient and for that reason it seems justified to consider an information-theoretic model for physical particles in which information also plays a central role.
Not only is information a crucial concept in the D-CTC model, but also in the modern theory of quantum information and computation [51], and in recent perspectives in physics [52]. However, as Bell pointed out [53,54], prior to introducing the concept of information in the description of physical systems, it seems necessary to specify two points: “About what information?” and “Whose information?”. A basic answer to these two questions might be, namely, information is about the properties of physical systems and information is for physical systems. Therefore, if the emitters and receivers of information are physical systems, particularly elementary physical systems, then it seems reasonable to explore a scenario in which a particle is not a mere passive object that blindly transports information, but an active agent that receives, processes and generates information.
Bearing this in mind, we characterize in DAQM [37,38,39,40,41,42] a fundamental physical system as a particle of mass and position in physical space (see Figure 2). Every particle is methodologically supplemented with a classical Turing machine defined on an information space where a program , which includes an anticipation module or subroutine , and a random number generator7 are also stored. At every run of the program, a carrier of energy () and momentum () is emitted by the particle according to the output calculated by the algorithm . Particles interact absorbing and emitting these carriers that also transport information () about the emitter to the absorber. This information consists in positions of systems. In this framework, the wave function can be considered as a book-keeping tool that appropriately codes the data about the surrounding systems so that the program may calculate efficiently the self-interaction, i.e., the corresponding parameters of the carrier to be emitted. In physical space, particles follow continuous trajectories and comply with the conservation of energy and momentum.
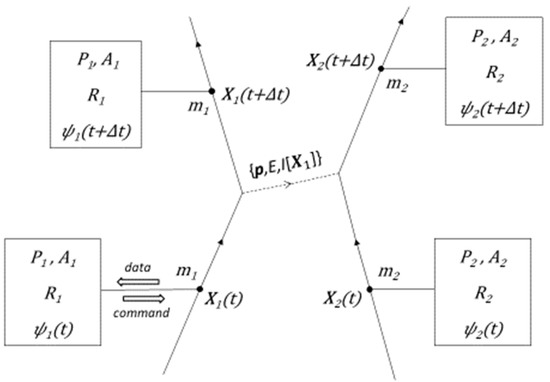
Figure 2.
Representation of an interaction between two fundamental particles in DAQM. See the text for a detailed description and definitions of symbols.
There are a set of parameters of the information processing model to be established that will be crucial for developing experimental tests of the theory. These fundamental parameters are: the minimum response time or minimum time between the emission of two consecutive carriers, the processing speed or number of processed instructions per second, and the processor memory or storage capacity.
It is assumed8 that the program that governs the dynamics of each particle simulates quantum behavior. The question arises whether this simulation, which is carried out on a probabilistic classical Turing machine, may be performed efficiently in order to be properly accomplished in real time. In the next section, it will be analyzed how the presence of the anticipation module in the information space of the particle enables the processor to simulate a CTC that would render the classical Turing machine computationally equivalent to a quantum one, therefore supplying the required efficiency to simulate quantum behavior.
4. Simulation of a CTC on the Information Space of a Particle in DAQM
Let us consider the information space of a particle in DAQM. According to the model, the new, refreshed information about the surrounding systems that has arrived at the particle transported by the information carriers, which also convey momentum and energy, has been coded by the algorithm into a probability distribution function9 on the surrounding particles phase space. This function reflects the epistemic state of the particle about the locations occupied by the surrounding systems and their dynamics at time . The wave function10 of the particle can be constructed from the probability distribution function by the algorithm . That probability distribution function enters the classical network , which is schematically represented in Figure 3, interacting with the second input that has come out from the anticipation module of the particle. After the interaction, the output of the first channel is , the anticipated probability distribution function of the surrounding systems at time , and the output of the second channel is which must equal11 the input .
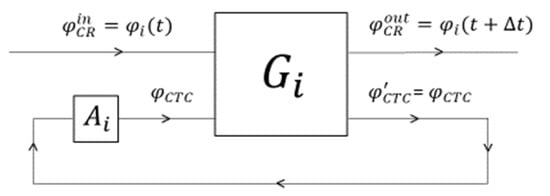
Figure 3.
Classical circuit on the information space of a DAQM particle simulating a CTC. The definitions of symbols and the analysis of the circuit are contained in the text.
Note that is in general a statistical mixture. Therefore, the interaction with , the input in the first channel of the circuit , may cause modifications in different components of the mixture, provided that the modifications statistically compensate each other so that the mixture itself comes out unchanged from the second channel of the circuit.
As will be discussed in the next section, the anticipation module is a particular contextual solution that only works properly at the concrete system in which it has been developed and in the specific environment in which the system is immersed.
The program , the anticipation module and the network are all of them classical elements that perform their task on a classical Turing machine as initially assumed. This means that, first, the program contains and applies the principles of quantum mechanics but on a classical processor, second, the classical anticipation module is able to find out the function that stays stationary after coming out from the second channel of the classical network (i.e., it is able to find out the fixed point for the second channel of the network) and, finally, this circuit correctly calculates as output of the first channel the function that allows the program to compute (on other module) the wave function of the system at time .
Notice that all the elements and functions in the circuit of Figure 3 are classical. Therefore, it seems that this classical circuit would not be able to simulate a D-CTC as represented in Figure 2, given that a quantum circuit with quantum states is apparently required. However, as shown by Tolksdorf and Verch [58] (see also Aaronson and Watrous [30]), the D-CTC model can be implemented on a classical network acting on classical statistical mixtures, since in order to ensure the existence of a fixed point for a map (the core of the model), the key mathematical properties are of statistical nature. In particular, the state space must be convex and complete [58]. In consequence, exclusive quantum properties are not necessary to carry out a D-CTC circuit.
Therefore, the classical circuit shown in Figure 3 could simulate a D-CTC on the information space of particle , provided that a procedure to obtain the objects , and , whose characteristics have been defined in this section, be specified. However, if the classical Turing machine has access to a D-CTC, then according to the result shown by Aaronson and Watrous [30], this classical information processor would be computationally equivalent to a quantum computer and might induce in real time quantum behavior on the particle.
5. Generation of the Anticipation Module and the Program in the Information Space of a Particle in DAQM
The characterization of a fundamental particle in DAQM [37,38,39,40,41,42] potentially endows these particles with the defining properties of information-theoretic Darwinian systems whose populations are then susceptible of evolution under natural selection12. It is assumed that at time there is a distribution of particles that are exclusively governed by their respective randomizers. As time goes on, algorithms that progressively take control of the particles’ behavior are randomly developed as a consequence of the arrival of information at every particle. Different procedures13 on the information space of particles mimicking those encountered in biological genetic systems might enable the variation of the control algorithms and their posterior selection and retention or inheritance through the populations dynamics of DAQM particles in physical space.
The main mechanism of variation is associated with the random errors in the write/read operations in the Turing machine. Then, those populations of particles with variations that induce better adapted traits have more chances to prevail by the action of natural selection. The variations are stored in the memory of the Turing machine.
DAQM particles could disappear through two basic processes satisfying the conservation of energy: emitting all their energy or being absorbed by another particle. These processes would be extremely frequent when the algorithms controlling the particles were still simple and prequantum. Relics of this prequantum world might still exist in certain regions of the universe. The detection of these relics would be a possible experimental test of DAQM.
Unequivocally, fitness is the central magnitude in evolution. However, an open question in the Darwinian evolutionary theory is whether there is a direction for evolution, i.e., whether evolution is predictable in the long run. The successive mathematizations of evolution (Fisher’s synthesis [59], Price equation [60], evolutionary game theory [61], Chaitin’s algorithmic information theory applied to evolution [62], citing some of the main landmarks) have proven crucial to progress in the understanding of the concepts and processes of the theory.
In addition, different hypotheses (maximum entropy production principle [63], free energy principle [64], increasing complexity [65], etc.) have been proposed in order to gain insight into the main mechanisms that would characterize Darwinian evolution in the long run (and also into the processes that would drive to the emergence of life [66]).
In a broad sense, complexity seems to occupy a strategic place in the toolkit of long-term evolution. However, there is no general consensus [65,67] on the definition of complexity14 in evolution. The challenge, therefore, is to find out a characterization of complexity that captures the essence of the underlying mechanisms of evolution in the long term. In addition, this concept should be general enough to encompass all systems in all environments, but at the same time specific enough to have predictive potentiality. Therefore, measures of the detailed structural and functional complexity of a system should better be discarded, since these characteristics of a system are deeply connected to the properties of the niche or environment in which the system is immersed and to the particular role played by the system in such environment.
Information seems to play a central part in the appearance of life. Perhaps the informational aspect of life is the key property [68]. Walker and Davies [68] describe the emergence of life as a kind of physical phase transition in which algorithmic information would gain context-dependent causal efficacy over the matter in which the information was stored [68]. According to Walker and Davies [68], the crucial magnitude would not just be the amount of information, as measured for example by Shannon’s information, but a quantity measuring that type of contextual causal efficacy possessed by biological information [68].
Among the multiple variations in the representation of complexity in biology, there is a contextual definition of “physical complexity”, as it is named by Adami et al. [67], that characterizes the genomic complexity of a biological system in terms of the information about the environment that is stored in the system for a fixed environment. It is then demonstrated [67] that, assuming this definition, according to the performed simulations, complexity must always increase.
In the present article another contextual definition, which is named “survival information complexity”, is introduced. One of the most characteristic features of complex systems is the difficulty in predicting [69] their future behavior. The idea of the new definition is to assign a high degree of complexity to a system that both is able to compute reliably the future behavior of its surrounding systems and, in turn, its outflow of information is minimized (this second characteristic implies that, for the surrounding systems, it would be difficult to predict the behavior of the system). The essentials of the definition are then summarized in that informationally the optimal strategy of any system at any environment would be maximizing the anticipation capacities of the system and minimizing the information sent outside by the system. Thus, survival information complexity measures the capability of a system for optimizing its information flows against survival. This optimization of the information flows for survival would plausibly be a common satisfactory strategy for all systems independently of their specific structures, functions, characteristics or environments. Therefore, if this definition of complexity admits quantification, then it seems an interesting candidate to explore the predictability of evolution in the long run.
Survival information complexity defined in this way does not automatically ensure a higher fitness in the short term. Other specific structural and functional traits or particular strategies may turn out more advantageous for survival in a concrete environment. However, in the long run, assuming an evolving environment, those populations that are informationally more complex, in the sense of the definition we have adopted, would have, in the end, a higher probability of adapting to the changing environment, therefore increasing their survival expectations, and, consequently, suggesting to identify the increase of “survival information complexity” as one of the main properties that would determine the direction of evolution in the long run.
Therefore, a system with information processing capabilities is then considered to be informationally more complex when, on the one side, it is able to anticipate the positions of its surrounding systems with greater precision, and, on the other side, it is also able to minimize the outflow of information.
Let us then define mathematically the survival information complexity of a DAQM system whose location is at time by introducing two terms:
The first one, , measuring the capacity at time of system for anticipating the behaviour of the surrounding systems at a future time is:
where is the number of systems that surround system ; () are the positions that will really be occupied at time by the surrounding systems of system ; is the position that will be occupied at time by the surrounding system of system as calculated by system at time on the Turing machine of its information space; and, finally, is the squared distance between the positions that will be actually occupied by system and system at time (see Figure 4 for a visualization of an example for the definitions of real and calculated systems locations).
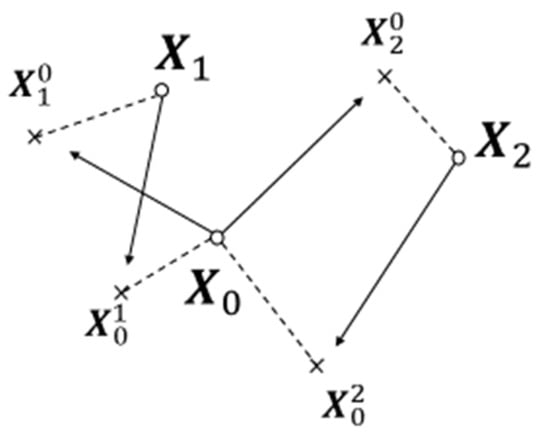
Figure 4.
Actual positions occupied by three DAQM particles at time t + ∆t are marked by small circles. The crosses represent the position at time t + ∆t of the particles indicated by the subscript as calculated at time t in the information space of the particle indicated by the superscript. Dashed lines are drawn between the actual position of a particle and calculated positions. Arrows relate the actual position of every particle to the calculated locations on its information space of its surrounding particles that are relevant for computing the complexity of particle i = 0. See the text for a detailed explanation.
Notice that in DAQM the location of a system is the physical property that is defined at any time, given that the trajectory is continuous.
In the definition of survival information complexity , the second term, , evaluates the degree of optimization of the system’s information outflow by measuring the capacity of stealth of the system , i.e., the lack of precision of the anticipation of its position by its surrounding systems at time in a certain environment:
where , as for the first term, is the number of systems that surround system , with being the position that will be occupied by system at time ; is again the squared distance between the positions that will be actually occupied by system and system at time ; and, finally, is the position that will be occupied at time by system as calculated by system at time on the Turing machine of the information space of system .
More sophisticated definitions of may be envisioned (e.g., including the integration over a meaningful interval of time or introducing a kind of anticipation depth or considering the response time of the information processor of the system) and certain technicalities should be further discussed (e.g., avoiding singularities by defining a minimum value for denominators; discussing the inaccessibility of certain magnitudes for system at time , what implies a delayed calculation of the quantity; the inherent difficulty of calculating the survival information complexity, except for models), but the given definition captures the central elements of the concept.
This mathematical characterization of survival information complexity measures the capability of a system for anticipating the behavior of its environment and for dynamically minimizing the options of its surrounding systems to foresee its location. This magnitude then takes higher values for those systems that predict more accurately the dynamics of their surrounding systems and whose own behavior, on the contrary, is more difficult to be predicted by their surrounding systems.
Therefore, this magnitude might plausibly describe the information processing complexity of biological systems correctly, independently of the structure or ecological niche of the considered biological system, including higher forms of organisms. For example, a higher value of seems to identify a better adapted organism for survival in the long run for both a prey and a predator. Thus, it seems a reasonable candidate to explore its adequacy as a quantity that could identify the trends of evolution in the long term. Is this magnitude also suitable to describe the evolution in the long run of information-theoretic DAQM physical particles?
To answer this question, let us schematically examine the way in which Darwinian evolution would imply the generation of the anticipation module and the program , which codes the mathematical quantum formalism, on the information space of a DAQM particle , assuming that the increase of the survival information complexity would determine the direction of evolution in the long term.
The maximization of the first term would directly induce the selection of those populations of particles that developed an anticipation module on the information space of the particles. Increasing values of would imply more reliable anticipations of the configuration of the surrounding systems, and therefore increasing fitness of the system to its environment in the long term. By developing an anticipation module, the information about the surroundings that had been captured by the system would have an added value for survival.
As mentioned in Section 4, the anticipation module , as a consequence of Darwinian evolution under natural selection, would be a contextual algorithm adapted to the specific evolutionary history of every population of particles. Is nature able to construct such a program? Let us discuss this question.
First, there are some results that point to the capability of Darwinian evolution to find out the paths to transform certain exponential time problems into polynomial time ones [70,71,72]. This is a characteristic feature of quantum computation and the kind of improvement that the presence of an anticipation module could imply in computation problems. In the study of Chatterjee et al. [70,71], there is no connection with an anticipatory procedure. However, in some theoretical scenarios in which the expected time of evolution is exponential with the sequence length that undergoes adaptation in the model [70,71], a mechanism is proposed that is able to beat the exponential barrier and allows evolution to work in polynomial time, as demonstrated in computer simulations [70,71].
Second, a central element in biological complex systems is the brain. The results of neural network studies foster the perspective of defining and characterizing the brain as a predictive machine [73,74] that learns to conjecture the causes of incoming sensory information. Therefore, Darwinian evolution acting on biological systems supports the idea that anticipation elements are generated by natural selection in biological systems with information processing capabilities.
It is meaningful to remark on the different orders of magnitude in the time scale of evolution for biological systems on Earth (at least 3.5 billion years [75]) and for physical systems in the universe, on which Darwinian evolution would be acting (as hypothesized by DAQM) from the Big Bang (around 13.8 billion years [76]). This difference must be taken into account when establishing parallelisms between both realms.
Let us now consider the problem of generating in the information space of a particle the classical algorithm that codes the quantum mechanical rules. Increasing values of the term would imply the generation of the Hilbert space structure for the state space of the systems, since it has been analyzed [77,78,79,80,81] that the Hilbert space structure optimizes the information retrieval and inference capabilities of an information system, therefore leading to the improvement of the response time of the system that would induce an increase in fitness in the long run.
On the other hand, as mentioned above, the optimal dynamics for a system, from a general informational point of view, would be the one that minimizes the information outflow of the system, therefore the one that minimizes the accuracy of the predictions that its surrounding systems calculate about the behavior of the system. Thus, the maximization of the second term, , as implied by the minimization of the outflow of information from the particle, plausibly brings about [37,38,39,40,41,42] the dynamical postulates of quantum mechanics, i.e., the Schrödinger equation and, as in Bohm-like theories, the guiding equation for calculating the velocity of the particle from the wave function. In particular, the Schrödinger equation can be directly derived, following Frieden [82], by applying the principle of minimum Fisher information on the probability distribution function for the position of a particle [82,83].
Notice that although DAQM can be considered a kind of generalization of Bohmian mechanics, DAQM is local, as discussed in Ref. [42], in which Bell inequality violations in the framework of DAQM are analyzed using a natural model for characterizing entanglement in this theory.
Further work has to be done in order to give a detailed account of the mechanisms underlying the deduction15 of the quantum mechanical postulates in DAQM. In particular, the role played by entanglement shaping the interaction between particles.
Finally, let us briefly discuss the role and characteristics of the randomizer that is stored in the information space of every particle as an intrinsic property. At time , the randomizer would completely control the self-interaction of the system. As time goes by, its weight in the dynamics of the successive particle populations would progressively diminish as the program evolved. However, assuming that the evolution of the information-theoretic particles of DAQM could be adequately modelled by a zero-sum elementary game, then, according to game theory [84], Darwinian evolution would plausibly preserve a complementary role in the control of the particle for , since randomness seems to be an essential element to optimize the survival expectations of a system, given that it would protect the system against the risk of completely deciphering its strategy by an adversary.
An open question of the model is the intrinsic nature of the randomizer. Is randomness an authentic fundamental, non-derivable property of matter? Or is it only pseudo-randomness, a kind of classical algorithm that yields an appearance of randomness? The difference is crucial for the model, since while true randomness, in principle, cannot be cracked, on the contrary, algorithmic pseudo-randomness, however intricate might it be, could be theoretically decrypted using enough resources and adequate observational and computational methods, as modern machine learning procedures show [85]. An intermediate road might be to construct the randomizer, although still classical, [39] following the mathematical prescription of the “free will function” defined by Hossenfelder [86] or including a computationally irreducible algorithm as defined by Wolfram [87], which would guarantee its unpredictability even for its own system. Depending on the intrinsic nature of randomness in matter, it could act as a screening wall for the anticipation depth.
The plausible development of the modules and in the information space of DAQM fundamental particles subject to evolution under the main action of natural selection has been analyzed. The emergence of quantum behavior in such particles would be the result of Darwinian evolution acting on matter, “the survival of the fittest” in a universe of information-theoretic fundamental particles.
DAQM helps to explore the relationship between classicality and quantumness from another point of view, namely, the central role that information seems to play in the quantum theory. However, this point of view is common to most modern reconstructions of quantum mechanics [88]. In many of these reconstructions [88], quantum systems are fundamentally characterized as carriers and processors of information. If this is an adequate representation of the world, and Darwinian natural selection might operate, then the appearance of the capability of projecting possible future configurations of the environment, the appearance of anticipation, would just be a question of time.
The second central characteristic of DAQM systems is that their properties are calculated in-flight on their information spaces in response to the interactions with other systems or to measurements in experiments. However, this reflects Bohr’s complementarity [11,12,13,14], from another perspective, the concept of objective indefiniteness [89], or in the saying of Peres [90] ‘unperformed experiments have no results’.
Therefore, in-flight calculated properties and anticipation, the two main elements associated with possessing information processing capabilities, constitute, in addition to the intrinsic randomness supplied by the randomizer on the information space of every particle, the backbone of DAQM for explaining quantum behavior in a natural way.
DAQM also explains in a remarkably natural manner the special adaptation and high-performance level of quantum computation for solving optimization problems and efficiently simulating quantum systems. As it has been analyzed in this article, a fundamental particle in DAQM would be a classical-like system supplemented with information processing capabilities that would simulate quantum mechanical behavior in real time by optimizing its information flows through the action of Darwinian natural selection.
6. Conclusions
A mechanism has been described for the simulation of a CTC on the information space of a fundamental particle endowed with intrinsic information processing capabilities in the framework of DAQM. Assuming a new definition for information complexity, named “survival information complexity”, and that the increase of this magnitude points to the direction in which matter evolves in the long run, then the action of Darwinian evolution under natural selection on the populations of these DAQM fundamental particles would plausibly induce the emergence of both an anticipation module, enabling the particle to drastically enhance its computational performance through the simulation of a CTC to which the information processor of the particle would thus have access, and an algorithm, coding the quantum mechanical rules, that would jointly induce quantum mechanical behavior in real time in the particle. Thus, fundamental particles, which do not possess direct intrinsic quantum features from first principles in this information-theoretic Darwinian approach, could however generate quantum emergent behavior in real time as a consequence of Darwinian evolution acting on information-theoretic physical systems.
In this article, the assumption that matter has information processing capabilities is the central starting point from which quantum mechanics might be deduced (if several important steps in the derivation are completed in future work). Once this assumption is modelled in a basic way (every physical particle is supplemented with an information space in which a classical Turing machine and a randomizer are stored), then fundamental particles become information-theoretic Darwinian systems, since they are susceptible to variation (it is assumed that random mutations in the algorithm are caused by errors in the write/read operation of the Turing machine), selection (those systems with the fittest variations prevail by the action of natural selection), and retention (the variations are stored in the memory of the Turing machine). These are the three defining properties of Darwinian evolutionary systems. The general principle that drives towards quantum mechanics appears naturally: the algorithms that control the behavior of particles evolve under Darwinian natural selection. However, what is the direction of Darwinian evolution in the long run? Is Darwinian evolution predictable? A tentative second general principle is introduced: the direction of Darwinian evolution in the long run is determined by the increase of survival information complexity, a magnitude that measures the degree of optimization of the information flows for survival. From this principle, the deduction of the postulates of quantum mechanics has been discussed. The emergence of quantum behavior in a universe of information-theoretic fundamental particles would be the result of Darwinian evolution acting on matter.
Author Contributions
Conceptualization, C.B. and A.K.; methodology, C.B. and A.K.; investigation, C.B. and A.K.; writing—original draft, C.B. and A.K.; visualization, C.B. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
Research of Andrei Khrennikov was partially supported by the EU-project: CA21169—Information, Coding, and Biological Function: the Dynamics of Life (DYNALIFE). The article processing charges (APC) were in part funded by Universidad de Valladolid.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Notes
| 1 | See Refs. [1,2,3] (and references therein) for a general and deep discussion of the problem of time. |
| 2 | In fact, there was a previous loophole in Newtonian mechanics that pointed to the possible unreality of time in the time symmetry (reversibility) of the equations [3,9]. |
| 3 | See Khrennikov [11,12,13,14] for a modern resolution of the conundrum by getting rid of nonlocality from conventional quantum theory (considered as an observational theory, much like Bohr’s point of view) through reinterpreting Bell inequalities violations as purely showing the incompatibility of observables for a single quantum system. |
| 4 | There are other quantum mechanical models different to that of Deutsch for the study of CTCs, e.g., see Lloyd et al. [28,29], but in this article only the model of Deutsch will be considered. |
| 5 | This kind of account must be taken with care since it can be subject to interpretation [25]. |
| 6 | See Dunlap [25,48] for a discussion on Deutsch’s interpretation of the knowledge paradox. |
| 7 | The question whether in this DAQM model this intrinsic randomness is irreducible and fundamental and, therefore, genuine and unpredictable or it is the result of a pseudo-random classical algorithm, different for every particle, whose code might in principle be deciphered by repeated and massive observation makes a crucial difference that will be briefly discussed in Section 5. |
| 8 | A procedure by which these programs might be developed in nature for the defined information-theoretic model of fundamental physical systems is analyzed in Section 5. |
| 9 | Note that in general this probability distribution function is a classical statistical mixture defined on the classical phase space of the surrounding particles. |
| 10 | As in some interpretations of Bohmian mechanics [55,56,57], the wave function in DAQM is considered to conveniently code the information about the surrounding systems. |
| 11 | If for certain time the output of the second channel didn’t equal the input , then the anticipation module should recalculate the new input for the next temporal cycle in order to restore by successive approximation the adequate functioning of the circuit as a CTC. |
| 12 | For an introduction to universal Darwinism and generalized Darwinism, see Refs. [43,44]. |
| 13 | Errors in the read/write operations in the Turing machine (the analogue of mutation in the genetic biological systems), transference or recombination of algorithms between particles, etc. |
| 14 | Similar difficulties have been found in the definition of fitness [65] in Darwinian evolution. |
| 15 | See Refs. [37,38,39,40,41,42] for discussions on the deduction of the quantum mechanical postulates in DAQM. |
References
- Markosian, N. Time. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Fall 2016 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2016. [Google Scholar]
- Glattfelder, J.B. Information—Consciousness—Reality: How a New Understanding of the Universe Can Help Answer Age-Old Questions of Existence; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Arthur, R. The Reality of Time Flow; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Page, D.N.; Wootters, W.K. Evolution without evolution: Dynamics de-scribed by stationary observables. Phys. Rev. D 1983, 27, 2885. [Google Scholar] [CrossRef]
- Adlam, E. Watching the clocks: Interpreting the Page-Wootters formalism and the internal quantum reference frame programme. arXiv 2022, arXiv:2203.06755. [Google Scholar] [CrossRef]
- Barbour, J. The End of Time: The Next Revolution in Physics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Tegmark, M. The mathematical universe. Found. Phys. 2008, 38, 101–150. [Google Scholar] [CrossRef]
- Rovelli, C. Reality Is Not What It Seems: The Journey to Quantum Gravity; Penguin: London, UK, 2018. [Google Scholar]
- Unger, R.M.; Smolin, L. The Singular Universe and the Reality of Time; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Khrennikov, A. Get rid of nonlocality from quantum physics. Entropy 2019, 21, 806. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum versus classical entanglement: Eliminating the issue of quantum nonlocality. Found. Phys. 2020, 50, 1762–1780. [Google Scholar] [CrossRef]
- Khrennikov, A. Two faced Janus of quantum nonlocality. Entropy 2020, 22, 303. [Google Scholar] [CrossRef]
- Khrennikov, A. Is the Devil in h? Entropy 2021, 23, 632. [Google Scholar] [CrossRef]
- Shimony, A. Bell’s Theorem. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Fall 2017 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2017. [Google Scholar]
- Costa de Beauregard, O. Méchanique quantique. C. R. Acad. Sci. 1953, 236, 1632. [Google Scholar]
- Aharonov, Y.; Popescu, S.; Tollaksen, J. A time-symmetric formulation of quantum mechanics. Phys. Today 2010, 63, 27–32. [Google Scholar] [CrossRef]
- Faye, J. Backward Causation. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Spring 2021 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2021. [Google Scholar]
- Elitzur, A.C.; Cohen, E. Quantum oblivion: A master key for many quantum riddles. Int. J. Quantum Inf. 2015, 12, 1560024. [Google Scholar] [CrossRef]
- Aharonov, Y.; Cohen, E.; Elitzur, A.C. Can a future choice affect a past measurement’s outcome? Ann. Phys. 2015, 355, 258–268. [Google Scholar] [CrossRef]
- Vaidman, L. Many-Worlds Interpretation of Quantum Mechanics. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Fall 2021 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2021. [Google Scholar]
- Deutsch, D. The Fabric of Reality; Penguin: London, UK, 1998. [Google Scholar]
- Lewis, D. The paradoxes of time travel. Am. Philos. Q. 1976, 13, 145–152. [Google Scholar]
- Deutsch, D. Quantum mechanics near closed timelike lines. Phys. Rev. D 1991, 44, 3197–3217. [Google Scholar] [CrossRef] [PubMed]
- Dunlap, L. The metaphysics of D-CTCs: On the underlying assumptions of Deutsch’s quantum solution to the paradoxes of time travel. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2016, 56, 39–47. [Google Scholar] [CrossRef]
- Ringbauer, M.; Broome, M.A.; Myers, C.R.; White, A.G.; Ralph, T.C. Experimental simulation of closed timelike curves. Nat. Commun. 2014, 5, 4145. [Google Scholar] [CrossRef] [PubMed]
- Marletto, C.; Vedral, V.; Virzì, S.; Rebufello, E.; Avella, A.; Piacentini, F.; Gramegna, M.; Degiovanni, I.P.; Genovese, M. Theoretical description and experimental simulation of quantum entanglement near open time-like curves via pseudo-density operators. Nat. Commun. 2019, 10, 182. [Google Scholar] [CrossRef]
- Lloyd, S.; Maccone, L.; Giovannetti, R.V.; Shikano, Y. Quantum mechanics of time travel through post-selected teleportation. Phys. Rev. D 2011, 84, 025007. [Google Scholar] [CrossRef]
- Lloyd, S.; Maccone, L.; Garcia-Patron, R.; Giovannetti, V.; Shikano, Y.; Pirandola, S.; Rozema, L.A.; Darabi, A.; Soudagar, Y.; Shalm, L.K.; et al. Closed timelike curves via postselection: Theory and experimental test of consistency. Phys. Rev. Lett. 2011, 106, 040403. [Google Scholar] [CrossRef]
- Aaronson, S.; Watrous, J. Closed timelike curves make quantum and classical computing equivalent. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 631–647. [Google Scholar] [CrossRef]
- Zeilinger, A. A foundational principle for quantum mechanics. Found. Phys. 1999, 29, 631–643. [Google Scholar] [CrossRef]
- Brukner, Č.; Zeilinger, A. Information invariance and quantum probabilities. Found. Phys. 2009, 39, 677–689. [Google Scholar] [CrossRef]
- Hardy, L. Quantum Theory from Intuitively Reasonable Axioms. In Quantum Theory: Reconsideration of Foundations; Khrennikov, A., Ed.; Växjö University Press: Växjö, Sweden, 2002; Volume 2, pp. 117–130. [Google Scholar]
- Chiribella, G.; D’ Ariano, G.M.; Perinotti, P. Informational axioms for quantum theory. In Foundations of Probability and Physics-6; D’ Ariano, M., Fei, S.M., Haven, E., Hiesmayr, B., Jaeger, G., Khrennikov, A., Larsson, J.A., Eds.; AIP: Melville, NY, USA, 2012; pp. 270–279. [Google Scholar]
- D’ Ariano, G.M. Operational axioms for quantum mechanics. In Foundations of Probability and Physics-4; Adenier, G., Fuchs, C., Khrennikov, A., Eds.; AIP: Melville, NY, USA, 2007; pp. 79–105. [Google Scholar]
- Fuchs, C.A.; Mermin, N.D.; Schack, R. An introduction to QBism with an application to the locality of quantum mechanics. Am. J. Phys. 2014, 82, 749–754. [Google Scholar] [CrossRef]
- Baladrón, C. In search of the adaptive foundations of quantum mechanics. Phys. E Low-Dimens. Syst. Nanostructures 2010, 42, 335–338. [Google Scholar] [CrossRef]
- Baladrón, C.; Khrennikov, A. Quantum formalism as an optimisation procedure of information flows for physical and biological systems. BioSystems 2016, 150, 13–21. [Google Scholar] [CrossRef]
- Baladrón, C. Physical microscopic free-choice model in the framework of a Darwinian approach to quantum mechanics. Fortschr. Phys. 2017, 65, 1600052. [Google Scholar] [CrossRef]
- Baladrón, C.; Khrennikov, A. Outline of a unified Darwinian evolutionary theory for physical and biological systems. Prog. Biophys. Mol. Biol. 2017, 130, 80–87. [Google Scholar] [CrossRef]
- Baladrón, C.; Khrennikov, A. At the Crossroads of Three Seemingly Divergent Approaches to Quantum Mechanics. In Quantum Foundations, Probability and Information; Springer: Cham, Switzerland, 2018; pp. 13–21. [Google Scholar]
- Baladrón, C.; Khrennikov, A. Bell inequality violation in the framework of a Darwinian approach to quantum mechanics. Eur. Phys. J. Spec. Top. 2019, 227, 2119–2132. [Google Scholar] [CrossRef]
- Aldrich, H.E.; Hodgson, G.M.; Hull, D.L.; Knudsen, T.; Mokyr, J.; Vanberg, V.J. In defence of generalized Darwinism. J. Evol. Econ. 2008, 18, 577–596. [Google Scholar] [CrossRef]
- Dawkins, R. Universal Darwinism. In Evolution from Molecules to Men; Bendall, D.S., Ed.; Cambridge University Press: Cambridge, UK, 1983; pp. 403–425. [Google Scholar]
- Smolin, L. The status of cosmological natural selection. arXiv 2006, arXiv:hep-th/0612185. [Google Scholar]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Arntzenius, F.; Maudlin, T. Time Travel and Modern Physics. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Winter 2013 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2013. [Google Scholar]
- Dunlap, L. Shakespeare’s Free Lunch: A Critique of the D-CTC Solution to the Knowledge Paradox. 2016. Available online: http://philsci-archive.pitt.edu/12811/1/SFL.pdf (accessed on 17 January 2023).
- Novikov, I. Can we change the past. In The Future of Spacetime; Norton: New York, NY, USA, 2002; pp. 57–86. [Google Scholar]
- Ralph, T.C.; Myers, C.R. Information flow of quantum states interacting with closed timelike curves. Phys. Rev. A 2010, 82, 062330. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computing and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Landauer, R. Information is physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Ghirardi, G. Collapse theories. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Winter 2011 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2011. [Google Scholar]
- Bell, J.S. Against ‘measurement’. In Sixty-Two Years of Uncertainty; Miller, A., Ed.; Plenum: New York, NY, USA, 1990; pp. 17–30. [Google Scholar]
- Bohm, D.; Hiley, B.J. The Undivided Universe. An Ontological Interpretation of Quantum Theory; Routledge: London, UK, 1993. [Google Scholar]
- Hiley, B.J. From the Heisenberg picture to Bohm: A new perspective on active information and its relation to Shannon information. In Quantum Theory: Reconsideration of Foundations; Khrennikov, A., Ed.; Växjö University Press: Växjö, Sweden, 2002; pp. 141–162. [Google Scholar]
- Gernert, D. Pragmatic information: Historical development and general overview. Mind Matter 2006, 4, 141–167. [Google Scholar]
- Tolksdorf, J.; Verch, R. The D-CTC condition is generically fulfilled in classical (non-quantum) statistical systems. arXiv 2019, arXiv:1912.02301. [Google Scholar] [CrossRef]
- Edwards, A.W.F. Mathematizing Darwin. Behav. Ecol. Sociobiol. 2011, 65, 421–430. [Google Scholar] [CrossRef]
- Frank, S.A. Natural selection. IV. The Price equation. J. Evol. Biol. 2012, 25, 1002–1019. [Google Scholar] [CrossRef]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Chaitin, G. Life as Evolving Software. In A Computable Universe: Understanding and Exploring Nature as Computation; Zenil, H., Ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Friston, K. A free energy principle for a particular physics. arXiv 2019, arXiv:1906.10184. [Google Scholar]
- Saunders, P.T.; Ho, M.W. On the increase in complexity in evolution. J. Theor. Biol. 1976, 63, 375–384. [Google Scholar] [CrossRef]
- Pross, A.; Pascal, R. The origin of life: What we know, what we can know and what we will never know. Open Biol. 2013, 3, 120190. [Google Scholar] [CrossRef]
- Adami, C.; Ofria, C.; Collier, T.C. Evolution of biological complexity. Proc. Natl. Acad. Sci. USA 2000, 97, 4463–4468. [Google Scholar] [CrossRef]
- Walker, S.I.; Davies, P.C. The algorithmic origins of life. J. R. Soc. Interface 2013, 10, 20120869. [Google Scholar] [CrossRef] [PubMed]
- Kravtsov, Y.A.; Kadtke, J.B. (Eds.) Predictability of Complex Dynamical Systems; Springer Science & Business Media: Berlin, Germany, 2012; Volume 69. [Google Scholar]
- Chatterjee, K.; Pavlogiannis, A.; Adlam, B.; Nowak, M.A. The Time Scale of Evolutionary Trajectories. Hal Science Ouverte, 2013. Available online: https://hal.science/hal-00907940/document (accessed on 17 January 2023).
- Chatterjee, K.; Pavlogiannis, A.; Adlam, B.; Nowak, M.A. The time scale of evolutionary innovation. PLoS Comput. Biol. 2014, 10, e1003818. [Google Scholar] [CrossRef] [PubMed]
- Kaznatcheev, A. Evolution is exponentially more powerful with frequency-dependent selection. bioRxiv 2021. [Google Scholar] [CrossRef]
- Seth, A. Preface: The brain as a prediction machine. In The Philosophy and Science of Predictive Processing; Bloomsbury Academic: London, UK, 2020. [Google Scholar]
- Ananthaswamy, A. To be energy-efficient, brains predict their perceptions. Quanta Magazine. 15 November 2021. Available online: https://www.quantamagazine.org/to-be-energy-efficient-brains-predict-their-perceptions-20211115/#:~:text=Results%20from%20neural%20networks%20support,that%20way%20to%20conserve%20energy.&text=When%20we%20are%20presented%20with,can%20depend%20on%20the%20context (accessed on 17 January 2023).
- Allwood, A.C.; Grotzinger, J.P.; Knoll, A.H.; Burch, I.W.; Anderson, M.S.; Coleman, M.L.; Kanik, I. Controls on development and diversity of Early Archean stromatolites. Proc. Natl. Acad. Sci. USA 2009, 106, 9548–9555. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results-VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Summhammer, J. Maximum predictive power and the superposition principle. Int. J. Theor. Phys. 1994, 33, 171–178. [Google Scholar] [CrossRef]
- Summhammer, J. Quantum theory as efficient representation of probabilistic information. arXiv 2007, arXiv:quant-ph/0701181. [Google Scholar]
- Aerts, S. An operational characterization for optimal observation of potential properties in quantum theory and signal analysis. Int. J. Theor. Phys. 2008, 47, 2–14. [Google Scholar] [CrossRef]
- De Raedt, H.; Katsnelson, M.I.; Michielsen, K. Quantum theory as the most robust description of reproducible experiments: Application to a rigid linear rotator. In The Nature of Light: What are Photons? International Society for Optics and Photonics: San Francisco, CA, USA, 2013; Volume 8832, p. 883212. [Google Scholar]
- De Raedt, H.; Katsnelson, M.I.; Donker, H.C.; Michielsen, K. Quantum theory as a description of robust experiments: Derivation of the Pauli equation. Ann. Phys. 2015, 359, 166–186. [Google Scholar] [CrossRef]
- Frieden, B.R. Fisher information as the basis for the Schrödinger wave equation. Am. J. Phys. 1989, 57, 1004–1008. [Google Scholar] [CrossRef]
- Frieden, B.R.; Soffer, B.H. Lagrangians of physics and the game of Fisher information transfer. Phys. Rev. E 1995, 52, 2274–2286. [Google Scholar] [CrossRef] [PubMed]
- Ross, D. Game theory. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Spring 2006 Edition; The Metaphysics Research Lab: Stanford, CA, USA, 2006. [Google Scholar]
- Wen, Y.; Yu, W. Machine learning-resistant pseudo-random number generator. Electron. Lett. 2019, 55, 515–517. [Google Scholar] [CrossRef]
- Hossenfelder, S. The free will function. arXiv 2012, arXiv:1202.0720. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2012. [Google Scholar]
- Ball, P. Quantum theory rebuilt from simple physical principles. Quanta Magazine. 30 August 2017. Available online: https://www.quantamagazine.org/quantum-theory-rebuilt-from-simple-physical-principles-20170830/ (accessed on 17 January 2023).
- Jaeger, G. Quantum Objects; Springer: Berlin, Germany, 2015. [Google Scholar]
- Peres, A. Unperformed experiments have no results. Am. J. Phys. 1978, 46, 745–747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).