Abstract
In this work, we interpret the newly observed resonance with exotic quantum numbers in the sector, reported by the BESIII Collaboration, as a dynamically generated state from the interaction between the lightest pseudoscalar mesons and axial-vector mesons. The interaction is derived from the lowest order chiral Lagrangian from which the Weinberg–Tomozawa term is obtained, describing the transition amplitudes among the relevant channels, which are then unitarized using the Bethe–Salpeter equation, according to the chiral unitary approach. We evaluate the decays into the and channels and find that the latter has a larger branching fraction. We also investigate its SU(3) partners, and according to our findings, the and structures may correspond to dynamically generated states, with the former one coupled mostly to the component and the latter one coupled to the channel. In particular, our result for the ratio is consistent with the measured value, which supports our interpretation for the higher state. We also report two poles with a mass about 1.7 GeV in the sector, which may be responsible for the . We suggest searching for two additional exotic mesons with masses around 1.4 and 1.7 GeV. In particular, the predicted is expected to have a width around 0.1 GeV and can decay easily into .
1. Introduction
Over the last two decades, the experimental observation of many new hadronic states is challenging our current understanding of hadrons as conventional mesons and baryons with valence contents of quark–antiquark and three quarks, respectively, since most of them do not fit in the well-known quark model. This difficulty brought back a long-standing discussion on the exotic hadronic structures, i.e., multiquark configurations that might have quantum numbers beyond those assigned to the conventional mesons and baryons [1,2].
Exotic quark configurations, such as tetraquarks [3,4], hadron–hadron molecules [5], glueballs, and hybrids [6,7], among others, have been suggested to describe suitably most of the properties of these new states, such as the quantum numbers, mass, and decay width, especially for those lying in the charmonium and bottomonium spectra.
On the other hand, distinguishing the exotic states from the conventional hadrons is a more complicated task in the light quark sector. Many states have their masses close to each other, and the possibility of mixing brings additional difficulty to the problem. The situation improves as the quantum numbers do not fall into those allowed by the conventional quark model. It seems to be the case of the newly discovered state, dubbed , by the BESIII Collaboration [8,9], observed in the invariant mass distribution of the meson pair in the decay channel with a significance of . Its mass and width reported by BESIII are MeV and MeV, respectively, with likely quantum numbers, which cannot be formed by a pair of quark and antiquark. The is not the only state experimentally found with that set of quantum numbers. As of today, three other hadronic structures, called , , and , with , were observed by several collaborations [7,10].
From the theoretical point of view, the hybrid model has been used to investigate these exotic meson states, in particular the ones. Lattice quantum chromodynamics (QCD) calculations have pointed out hybrid supermultiplets with exotic quantum numbers, including the one [11,12,13,14,15,16]. In this picture, however, the mass of the lightest state and decay modes are inconsistent with the corresponding experimental results, while the and structures can fit into the nonets predicted by lattice QCD [7].
The newly observed state has also been the focus of some studies. In particular, the authors in Ref. [17] proposed two hybrid nonet schemes in which the resonance can be either the lower or higher mass state with isospin . In Ref. [18], an effective Lagrangian respecting flavor, parity, and charge conjugation symmetries is used to study the hybrid nonet decays into two-body meson states. The authors have fixed the couplings to those two-body meson states by performing a combined fit to the experimental and lattice results available. As a result, the decay width value estimated for the isoscalar member of the hybrid nonet agrees with the one observed for state. Additionally, addressing the same picture, Ref. [19] applied the approach of QCD sum rules to describe the mass. By contrast, within the same approach, the resonance is described as a tetraquark state in Ref. [20].
The resonance also supports a meson–meson molecule interpretation due to its proximity to the threshold, as put forward by Refs. [21,22]. In particular, the authors in Ref. [21] have investigated the interaction through the one-boson exchange model. According to their findings, the system binds for cut-off values above 2 GeV with a monopole form factor. In addition, the comparison between their result for the branching fraction to the experimental one led them to conclude that the molecule can explain the structure.
An important point to be addressed is the meson–meson interaction around the threshold for the quantum numbers. In this sector, many meson–meson pairs may contribute to that interaction, so a coupled-channel treatment seems appropriate to take these contributions into account. In particular, hadron–hadron interactions in coupled channels have been studied in many works to describe the properties of the new hadronic systems experimentally observed. In those cases, these hadronic structures are called dynamically generated states.
Following this approach, in this work, we aim to explore the , , and hadronic systems as dynamically generated states from pseudoscalar-axial vector meson interactions in coupled channels. Specifically, the low-energy interactions are given by the Weinberg–Tomozawa (WT) term from chiral Lagrangians at the leading order of the chiral expansion by treating the axial vector mesons as matter fields and the pseudoscalar mesons as the pseudo-Nambu–Goldstone bosons of the spontaneous breaking of chiral symmetry. Such Lagrangians have been used to study many hadron structures stemming from meson–meson and meson–baryon interactions in coupled channels in light and heavy sectors, see, e.g., Refs. [23,24,25,26,27]. In our case, the amplitudes obtained from the WT term are unitarized via the Bethe–Salpeter equation from which bound states/resonances manifest as poles in the physical/unphysical Riemann sheets of the scattering matrices. The existence of a whole family of kaonic bound states has been pointed out in Ref. [28] based on unitarizing the WT term for the scattering of the kaon off isospin-1/2 matter fields taking heavy mesons and doubly-charmed baryons as examples. As we shall show in this work, the newly observed structure may correspond to a dynamically generated state from the pseudoscalar-axial vector interaction in the isospin sector coupling strongly to the channel. Moreover, the and , may be assigned as the SU(3) partners which are also dynamically generated from the pseudoscalar-axial vector meson interactions in the sector. The former resonance couples mainly to the channel, and the latter has the as its main coupled channel.
In addition, we have also found two poles around 1.7 GeV in the sector. These poles are particularly interesting as they could be the origin of the structure observed experimentally [10], which is the main component of the contribution to the mass distribution in the decays recently measured by LHCb [29].
This paper is organized as follows. In Section 2, we discuss the relevant channels contributing to the pseudoscalar-axial vector meson interactions and the use of the chiral unitary approach (ChUA) for the evaluation of the transition amplitudes among those channels. In Section 3 and Section 4, we investigate the dynamical generation of poles stemming from those interactions in the and sectors and discuss their possible decay channels. Finally, in Section 5, we also explore the dynamical generation of poles for and their connection to the vector structure observed experimentally. Section 6 gives a summary.
2. Coupled Channel Scattering in Chiral Unitary Approach
We investigate the interactions between axial and pseudoscalar mesons in coupled channels in the MeV energy range. First, we need to determine the space of states contributing to the interaction in this energy range.
In Table 1, Table 2, Table 3 and Table 4, we list all the relevant channels for the problem under consideration along with their corresponding mass thresholds. The channels are organized from the lower to higher mass values and by the isospin, 0, 1, and , respectively.

Table 1.
meson-meson channels with . The threshold masses are in the units of MeV.

Table 2.
meson–meson channels with . The threshold masses are in the units of MeV.

Table 3.
meson–meson channels with . The threshold masses are in the units of MeV. Here the flavor-neutral axial vector mesons have .

Table 4.
meson–meson channels with . The threshold masses are in the units of MeV. Here, the flavor-neutral axial vector mesons have .
In what follows, we shall discuss the relevant scattering amplitudes among all those channels above for each isospin sector. These transitions can be written in the form of the WT term which then is unitarized. Notice that the channels displayed in Table 3 and Table 4, in principle, should be grouped in the same space of states since they share identical isospin and quantum numbers. However, the relevant transitions among them arise only at the next-to-leading order in the chiral expansion; see the discussion around Equation (17) below. Thus, such transitions are of higher order than that of the WT term and will be neglected here.
2.1. The Weinberg–Tomozawa Term
In order to study the interactions among all the channels listed in the previous tables, we have to evaluate the interactions between the pseudoscalar and axial-vector mesons. The latter are organized in two SU(3) octets according to their quantum numbers.
is the octet of resonances of axial-vector states with for the flavor-neutral mesons, and
describes the octet of axial-vector resonances with . The singlet and octet flavor eigenstates are not mass eigenstates; that is, the pairs of , (also known as ) and , mesons are mixtures of the singlet and octet mesons, such that
and
Furthermore, the and members of the multiplets in Equations (1) and (2) are the strange partners of the and , and their mixture contributes to the physical and mesons, that is
The corresponding values for the mixing angles in Equations (3)–(5) are listed in Table 5, where they are grouped into two sets, denoted by A and B. Although set B is preferred in Ref. [30], we will use both sets to have an estimate of the uncertainties caused by such an angle.

Table 5.
Two sets of values of the axial-vector meson mixing angles taken from Ref. [30]. Set B is preferred in Ref. [30]. The - mixing angle is taken from Ref. [31]. For more discussions about these mixing angles, we refer to the review of Quark Model in the Review of Particle Physics [10].
In order to determine the WT term we start with the Lagrangian (see, e.g., Ref. [32])
where takes trace in the SU(3) flavor space,
while is the chirally covariant derivative, which when acting on SU(3) octet matter fields reads as
with the usual commutator. In addition, stands for the chiral connection, given by
with
where MeV is the pion decay constant [10], and is the pseudoscalar SU(3) octet, that is
In addition, the physical and mesons are the mixtures of and
where becomes the ninth pseudo-Goldstone boson in large QCD [33,34,35,36]. The Goldstone boson nonet is written as
which leads to a relation in the commutator
Therefore, only the scattering of the octet Goldstone bosons off the axial-vector mesons in Weinberg–Tomozawa term contributes to spectrum.
The covariant derivative by means of the connection encodes the leading order interaction between the pseudoscalar mesons and the vector field [32,37,38]. Therefore, by replacing the field to the axial-vector field corresponding to either the or multiplet, the chiral transition between (pseudoscalar) and (axial-vector) is described by the following interaction Lagrangian
which accounts for the WT interaction term for the process, with P and A corresponding to the pseudoscalar and axial-vector mesons, respectively. From this Lagrangian we obtain the S-wave transition amplitude among the channels listed in Table 1, Table 2, Table 3 and Table 4, that is
where stands for the polarization four-vector of the incoming (outgoing) axial-vector meson [25,39]. The masses correspond to the initial (final) axial-vector mesons and initial (final) pseudoscalar mesons, respectively. The indices i and j represent the initial and final states, respectively. The coefficients are given in Table 6, Table 7, Table 8 and Table 9.

Table 6.
coefficients in Equation (16) for axial and pseudoscalar pairs coupled to in S-wave and .

Table 7.
coefficients in Equation (16) for axial and pseudoscalar pairs coupled to in S-wave and .

Table 8.
coefficients in Equation (16) for axial and pseudoscalar pairs coupled to in S-wave and . Here the flavor-neutral axial mesons have .

Table 9.
coefficients in Equation (16) for axial and pseudoscalar pairs coupled to in S-wave and . Here the flavor-neutral axial mesons have .
Before proceeding, let us discuss the transitions, with and the two SU(3) octets of axial-vector mesons and the octet of the pseudo-Nambu–Goldstone bosons. Let and denote the fields for the and axial-vector meson multiplets, respectively. Under parity transformation, we have and ; under charge conjugation, we have and . Then the transitions can only arise at with p the momentum scale in the chiral power counting. They are given by operators, such as
with
Such terms are one order higher in the chiral power counting than the WT terms describing the and transitions, and thus will be neglected.
2.2. Unitarization Procedure
The unitarization procedure we adopt follows ChUA in which the scattering amplitudes in Equation (16) are the elements of a matrix, denoted by V, such that it enters as an input to solve the Bethe–Salpeter equation, which in its on-shell factorization form, reads [23]
The V matrix describes the transition between the channels listed in Table 1, Table 2, Table 3 and Table 4. In addition, G is the diagonal loop function matrix whose diagonal matrix elements are given by
with and the masses of the pseudoscalar and axial-vector mesons, respectively, involved in the loop in the channel l, and P the total four-momentum of those mesons (). After the integration over the temporal component , Equation (20) becomes
with and , and can be regularized by means of a cut-off in the three-momentum . On the other hand, the function can also be regularized using a subtraction constant as [40]
where is the three-momentum of the mesons in the center-of-mass (c.m.) frame
while is an arbitrary scale of the regularization. Any changes in the scale can be absorbed by the subtraction constant such that the result is independent of the scale. We may determine the subtraction constant for each intermediate state of the scattering problem by comparing Equations (21), regularized using , and (22) at the threshold. The equivalence between the two prescriptions for the loop-function is discussed in, e.g., Refs. [41,42,43]. In this work, we follow Ref. [44] and set GeV and , which is obtained by matching to hard cut-off regularization with GeV in the channel. This set of parameters are used for all channels, and a variation of the cut-off within GeV, and correspondingly , will be used to show the dependence of the results on this parameter.
2.3. Searching for Poles
We move on to the complex energy plane to search for poles in the T-matrix. Specifically, for a single-channel problem, there are two Riemann sheets for the complex energy plane. Bound states show up as poles, below the threshold, in the transition matrix on the real energy axis on the first Riemann sheet, while virtual states manifest themselves below the threshold on the real axis on the second Riemann sheet, and resonances correspond to poles off the real axis on the second Riemann sheet. The Riemann sheets come about because the G loop function has a cut extending from the threshold to infinity which is usually chosen to be along the positive real axis. For n coupled channels, there are n cuts and thus Riemann sheets. From unitarity and the Schwarz reflection principle, the discontinuity of the function can be read off from its imaginary part,
which we can use to perform an analytic continuation to the entire complex plane. In this case, the loop function on the “second” Riemann sheet with respect to the lth channel reads
the lower half plane of this Riemann sheet is directly connected to the physical region when the lth channel is open, i.e., . We will label the Riemann sheets according to the sign of the imaginary part of the corresponding c.m. momentum for each channel (see the next section).
Furthermore, it is also possible to determine the pole couplings to the lth channel. Note that close to the pole singularity the T-matrix elements admit a Laurent expansion,
where is the pole location on the complex energy plane, with and standing for the pole mass and width, respectively. Therefore, the product of couplings is the residue at the pole in which takes values on the Riemann sheet where the pole is located. In this way, the couplings can be evaluated straightforwardly. For instance, for a diagonal transition it is given by
where with r the radius of contour for the integral, and the two lines give two equivalent ways of computing residues.
3. and Its Decays
3.1. Dynamical Generation of the
Following the unitarization procedure described previously, we seek dynamically generated states stemming from the S-wave interactions between pseudoscalar and axial-vector mesons. For the case, the transition amplitudes among the channels listed in Table 1 are determined using Equation (16) with the coefficients given in Table 6. In Table 10, we show the isoscalar poles with exotic quantum numbers obtained by solving Equation (19) using those coefficients as well as each set of mixing angles listed in Table 5. We also show the couplings of these poles to the channels spanning the space of states in Table 1.

Table 10.
The poles (in GeV) and their corresponding couplings (in GeV) to the channels contributing to the interaction with and exotic quantum numbers . The corresponding Riemann sheet for each pole is listed below the pole position. The dominantly coupled channel is emphasized in boldface for each pole. The errors of the poles are from varying the subtraction constant within , and only the central values of the couplings are given. For each pole, we also give the central values of the peak mass and width as , after considering the axial-vector meson widths, in the last row of the corresponding panel.
Furthermore, in Table 10 we also highlight the Riemann sheets, the first and the second one for each channel, denoted by the + and − signs, respectively. We obtain three poles such that their locations are barely affected by the change of the mixing angles from set A to set B listed in Table 5. The lower pole is at GeV with a width of about GeV, which is above the threshold. In particular, this channel is open for decay, and the fact that it is this channel the one for which the pole couples mostly, as pointed out in Table 10, explains why that pole has such a value for its width. By contrast, although the channel is also open for decay, the pole at GeV has a much smaller width because its coupling to this channel is small compared to the one for , which is the dominant channel for that pole. Similarly, the highest pole, located at GeV, couples mostly to the channel, and has a small imaginary part. In addition, we can also understand why the highest pole couples more to the than to the . The latter channel is closer to the pole than the former, but from Table 6, the diagonal transition is not allowed since its WT term is zero. Nevertheless, the pole couples to through the non-diagonal – transition, which leads to a small coupling.
3.2. Effects of the Widths of the Axial-Vector Mesons
So far we have neglected the nonzero widths of the axial-vector mesons. In order to investigate their effects on the results, we use complex masses for the intermediate resonances, that is, . However, by doing that, the analytic properties are lost such that the poles of the T matrix do not correspond to the masses and widths of the obtained resonances any more. On the other hand, we can see the impact of such non-zero widths on the lineshapes of the transition matrix elements.
In Figure 1, we show a comparison between the lineshape for the T-matrix element corresponding to the elastic transition with and without including the widths for the intermediate particles. This channel has the strongest coupling to the pole at GeV; therefore, we expect that any non-trivial structure should manifest most in its associated T-matrix element. The dashed and solid lines are the with zero and non-zero width, respectively, for both sets A and B of mixing angles in Table 1. Notice that, for the case of zero width approximation, the lineshape has narrow peaks around 1845 MeV, right at the range of energy where we expect the manifests in our model. The inclusion of finite widths for the axial-vector mesons changes the sharp peak to a broad bump with a width of about 0.2 GeV, which is around the width of the [10]. Notice that the width matches nicely that of the measured by BESIII, [8]. One can obtain a peak mass and a peak width , defined as the width at the half maximum of the line shape of the diagonal T-matrix element modulus squared for the dominant channel. In Table 10, we also list the values of and for each pole. The values for the highest pole in the table agree remarkably well with those of the . These values may be compared with the resonance parameters extracted using the Breit–Wigner form in experimental analyses.
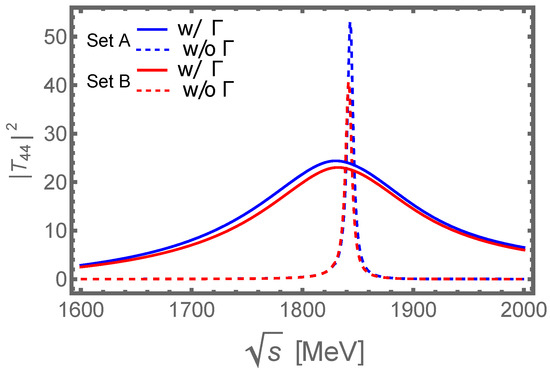
Figure 1.
The blue dashed and solid lines are, respectively, the modulus squared of the T-matrix element, corresponding to the diagonal transition, evaluated with and without the inclusion of the widths associated with the axial-vector mesons taking part in the loop function (Equation (20)).
The results presented may be improved by considering one additional possible contribution due to the axial-meson decays, shown in Figure 2. Since the intermediate vector and pseudoscalar mesons in the triangle diagrams can go on shell, such contributions could further increase the widths of the dynamically generated states. In the following, we will continue to present predictions neglecting the width effects of the axial-vector mesons.
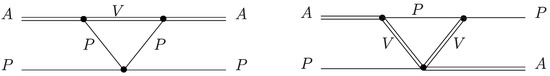
Figure 2.
Possible triangle diagram contributions to the scattering between an axial vector meson and a pseudoscalar meson.
Let us briefly discuss the other two predicted isoscalar exotic mesons in Table 10. The one with a mass of about 1.39 GeV, denoted as , is expected to be rather broad due to the large width of the as it couples most strongly to the channel. It can be searched for in final states, such as and . The one with a mass around 1.7 GeV, denoted as , couples most strongly to the and is expected to have a width similar to that of the , i.e., around 0.1 GeV. It can also be searched for in final states of .
3.3. The and Decays
Let us first discuss the decay, whose Feynman diagram is shown in Figure 3. Within our approach the structure decays via its component, with the corresponding coupling constant listed in Table 10. We also need to evaluate the transition, for which we use the resonance chiral theory (RT) operators given in Ref. [45].
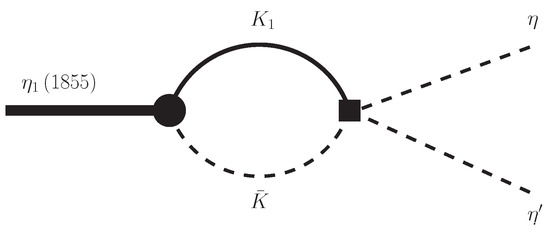
Figure 3.
Diagram corresponding to the decay through the loop.
The RT operators can be divided regarding the intrinsic-parity sector to which they contribute. Due to its nature, the odd-intrinsic parity sector will contain a Levi–Civita tensor [46,47,48]; for the decay one cannot saturate the Lorentz indices in such tensor to obtain a non-zero contribution. Thus, only the even-intrinsic parity operators must give a non-vanishing contribution. Since the chiral Lagrangian does not contribute to such processes [49], we will use the Lagrangian given in Ref. [45]. From these operators, only three will contribute to this decay. To obtain the largest possible contribution from such operators, we use the upper bounds imposed from chiral counting as performed in Ref. [50]. This amounts to making equal the three coupling constants and setting them to , which gives a Lagrangian
where has been given in Equation (18), is the symmetrized covariant derivative of and the spin-1 resonance field is given in the antisymmetric tensor formalism [37]. However, since the transition is given in terms of Proca fields, we need to express the as a Proca field. Following Ref. [49], the antisymmetric tensor field can be expressed in terms of the Proca one as follows,
where is the mass of the resonance. Using the Lagrangian of Equation (28) and expressing the axial resonance in the Proca representation, we obtain the decay amplitude
where is the pion decay constant, is the coupling constant of the pole to the channel, is the loop function for the and mesons, is the vector polarization, and is the momentum of the . Here, and are given in terms of the - mixing angle
Although one might try to rely in a much simpler way to describe the direct coupling of one axial-vector and three pseudoscalar fields by means of the hidden local symmetry (HLS) Lagrangian [51,52,53], it is worth to notice that nonetheless, the total amplitude for this process given by the HLS Lagrangian vanishes, which coincides with Equation (30) in the chiral limit.
The decay of state into is given by
with the amplitude in Equation (30), while J stands for the spin. In addition to that, q reads
with , , and the masses for the , , and mesons, respectively, where is the Källén triangle function. Therefore, we obtain the following results for the decay width in this channel
where the error is from choosing subtraction constant to be in the range , corresponding to the hard cut-off as discussed at the end of Section 2.2. For set A, our result agrees with that of Ref. [21], where the was assumed to be a molecule and the same mixing angle was used for accounting for the and mixture contributing to the physical and states.
As for the three-body decay, Figure 4 shows the Feynman diagrams contributing to this process. In particular, the decays through its molecular components, that in our approach are the and . In this case, the contribution from the component can be ignored for the following reasons: (1) from Table 10, we see that the relative coupling strength for the channel is much smaller than that for the one; (2) the branching ratio is only , while of the decays is dominated by the . Therefore, from Figure 4 the amplitude is written as
where is the coupling of the pole associated with the state to the channel, is the coupling extracted from the reaction in the Review of Particle Physics (RPP) [10], and and are the polarization vectors of the and mesons, respectively.
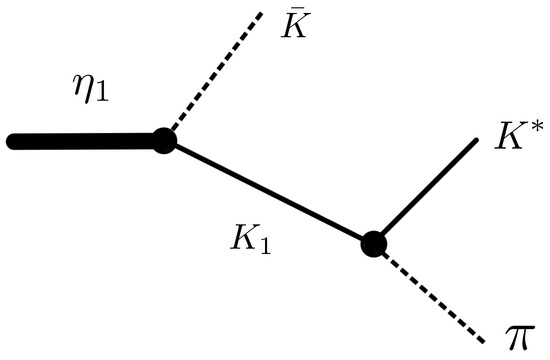
Figure 4.
Feynman diagram associated with the three-body decay of the pole through its main component .
The differential decay width for the process is given by
where
and
with , , being the masses of the , and mesons.
From Equation (36) we obtain the following results for the decay width
where the uncertainties come from the subtraction constant (cut-off) used to regularize the loops in Equation (22) (Equation (21)). As can be seen from Equation (39), we obtain similar results whether we use the sets A or B. For the sake of comparison to other works, we evaluate the ratio , and obtain
which is consistent to the results in Ref. [21], where the is also assumed to be a molecular state. On the other hand, adopting the same multiquark configuration than the present work and Ref. [21], the authors of Ref. [22] have found a different result for the ratio, . Nevertheless, in all the cases the results point out that the three-body channel is more likely than the one.
4. The Dynamical Generation
The WT amplitudes for the pseudoscalar-axial vector meson interactions with are given by Equation (16), with the corresponding coefficients listed in Table 7. In this case, from Equation (19), we obtain two poles shown in Table 11.

Table 11.
Poles and their corresponding couplings to the channels contributing to the interaction with and . The dominantly coupled channel is emphasized in boldface for each pole. The errors of the poles are from varying the subtraction constant within , and only the central values of the couplings are given. The last row of each panel gives the central values of the peak mass and width for the corresponding pole after considering the axial-vector meson widths.
Similar to the previous section, we also provide the couplings of these dynamically generated states to the channels listed in Table 2. Table 11 shows a broad pole at GeV, and a width of about GeV.1 This state is above the and thresholds. Its large width stems from the large coupling to the and the fact that this channel is open for decaying. The channel is also open. However, according to Table 7, the corresponding WT term in Equation (16) is zero for the diagonal transition. On the other hand, the next pole in Table 11 has a sizeable dependence on the mixing angles. Using set A, we find that pole at GeV. It couples most strongly to the channel, which is closed for decaying. Nonetheless, the state can decay into and , albeit their corresponding couplings are small compared to the one, but still large enough to provide a sizeable width for the pole. In contrast, when set B is adopted, the higher pole is now located at GeV, above the threshold, which is now open. One might think that the width should increase since now three channels are open for decaying. However, although the coupling to the has increased in this case, at the same time the couplings to the other open channels have decreased. Hence, the overall effect leads to a smaller width compared to the previous case.
The lower pole mass is slightly higher than the mass of the state listed in RPP, MeV [10]. Notice that we use the same subtraction constant for all channels. In principle, it can take different values and lead to a shift of the poles. In addition, we did not include in the loops the width, that is relatively large and whose effects could influence the pole position. However, it is expected to affect more the imaginary part of the pole than the real one (see Figure 5a below). We can obtain a rough estimate of this change by adding the width to the previous result for , with the lower pole, i.e.,
which is close to the width reported in RPP, MeV [10]. From these results, we are led to claim that the lower pole may explain the resonance; in other words, the is suitably described in our approach as a dynamically generated state with the as its main component.
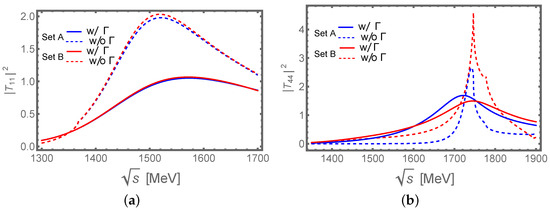
Figure 5.
The dashed and solid lines correspond to zero and full widths of the axial-vector mesons in . (a) Modulus square of elastic scattering; (b) Modulus square of elastic scattering.
Alternatively, following the prescription used in Section 3, we can also study the changes in the results caused by the inclusion of the finite widths for the axial-vector mesons by looking at the line shape for the relevant T-matrix elements. In Figure 5a, we show the line shapes for the T-matrix element corresponding to the elastic transition, which is the one we would expect the lower pole in Table 11 manifests most due to its large coupling to the channel. It becomes clear that the bumps become broader when the widths of axial-vector mesons are taken into account. A similar behavior can be seen in Figure 5b for the T-matrix element associated with the scattering of , which is the channel to which the higher pole couples most strongly. The peak mass and width extracted from the line shape of the diagonal T-matrix element for the dominantly coupled channel are also listed in Table 11 when the axial-vector meson widths are considered.
The higher pole, denoted now by , has a mass consistent with that of the , whose pole mass has been reported to be MeV in Ref. [54] and MeV in Ref. [55]. It can decay into the and channels. The corresponding diagrams for both amplitudes are illustrated in Figure 6, from which we have
and
with and the polarization vectors of the and mesons. Here, , , and are the effective coupling of the pole to the corresponding couplings, and and are the loops involving the and mesons, respectively. Notice that the effective couplings are computed from the residues of the T matrix elements; thus they contain contributions from all coupled channels.
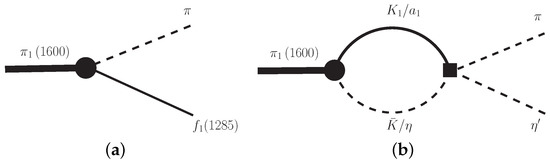
Figure 6.
(a) Diagram corresponding to the reaction, and (b) the decay also via the loop. The filled circles represent the effective couplings of the to the meson pairs calculated from the residues. The rectangles are the transition amplitudes at tree level.
In order to compare our findings with the experimental information, we evaluate the ratio
where q and are the momentum in the c.m. frame of the and pairs, respectively. Numerically, Equation (44) gives
The ratio is slightly bigger for the mixing angles in the set A. Nevertheless, the result in Equation (45) is consistent to the corresponding ratio reported by the E852 Collaboration [56]. This good agreement with the experimental data supports the molecular picture for the state.
5. Dynamical Generation in Sector
In the sector, the corresponding WT amplitudes are given by Equation (16) with the coefficients given in Table 8 and Table 9. For each case, we have found two poles for parameter sets A and B, as shown in Table 12 and Table 13.

Table 12.
Poles and their corresponding couplings to the channels contributing to the interaction with . Here the flavor-neutral axial mesons have . The dominantly coupled channel is emphasized in boldface for each pole. The errors of the poles are from varying the subtraction constant within , and only the central values of the couplings are given. The last row of each panel gives the central values of the peak mass and width for the corresponding pole after considering the axial-vector meson widths.

Table 13.
Poles and their corresponding couplings to the channels contributing to the interaction with . Here the flavor-neutral axial mesons have . The dominantly coupled channel is emphasized in boldface for each pole. The errors of the poles are from varying the subtraction constant within , and only the central values of the couplings are given. The last row of each panel gives the central values of the peak mass and width for the corresponding pole after considering the axial-vector meson widths.
Similarly to the previous cases, the poles are located on the same Riemann sheets in both sets of mixing angles. The interactions in the and channels are strong to generate a bound state in each of them. The existence of a lower channel below the threshold moves the pole in Table 13 to Riemann sheet . It has a non-zero imaginary part of a few MeV, which is not shown in the table due to precision.
As discussed before, the poles in Table 12 and Table 13 will receive sizeable widths once the width effects of the axial-vector mesons are taken into account, and it is expected that the widths are of the order of a few hundred MeV, like those of the and mesons. The peak mass and width for each pole are also listed in the tables when the axial-vector meson widths are considered. Although we neglected the transitions between the and sectors as discussed around Equation (17) in Section 2, strange mesons are not C-parity eigenstates and the two dynamically generated states will inevitably mix. The two mixed states together could correspond to the structure [10].
6. Conclusions
We have studied the interactions between the pseudoscalar and axial-vector mesons in coupled channels with quantum numbers for the isospin 0, 1, and sectors. Using the chiral unitary approach, we describe the interaction with the Weinberg–Tomozawa term derived from chiral Lagrangians. The transition amplitudes among all the relevant channels are unitarized using the Bethe–Salpeter equation from which resonances (bound states) manifest themselves as poles on the (un)physical Riemann sheets of the complex energy plane.
We consider the physical isoscalar axial-vector states as mixtures of the corresponding SU(3) singlets and octets. In addition, the and physical states are also mixtures of the and mesons, which are the strange partners of the and resonances, respectively. We group into two sets, called A and B, the mixing angles accounting for such mechanisms and investigate their influence on the pole positions.
According to our findings, we obtain poles with quantum numbers in the energy range from to GeV, in each isospin sector studied (). The quantum numbers are exotic in the sense that they cannot be formed from a pair of quark and antiquark. In particular, we have found an isoscalar state that may correspond to the state, newly observed by the BESIII Collaboration [8]. In addition, we have also found two dynamically generated isovector states that we assign to be the and resonances. Hence, within our formalism, they are dynamically generated through the pseudoscalar-axial vector meson interactions, with the state coupling mostly to channel, while the couples strongly to the , and structure couples most strongly to the . We also find two states with a mass around 1.7 GeV. They combined together could be responsible to the observed structure.
In addition, we also evaluate the decays of the and the . We find that the three-body decay channel has a significantly larger branching fraction than the , which is the channel where the observation of the was made. The obtained ratio between the and decays, given by Equation (45), is consistent with the corresponding experimental value.
We suggest searching for two additional exotic mesons with masses of about 1.4 and 1.7 GeV, respectively. In particular, the latter should be relatively narrow with a width around 0.1 GeV and one of its main decay channels is .
Author Contributions
Methodology: M.-J.Y.; writing—original draft preparation: J.M.D. and A.G.; writing—review and editing: F.-K.G.; supervision: F.-K.G. and B.-S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This project is supported in part by the National Natural Science Foundation of China (NSFC) under Grants No. 12125507, No. 11835015, and No. 12047503; by the China Postdoctoral Science Foundation under Grant No. 2022M713229; by the NSFC and the Deutsche Forschungsgemeinschaft (DFG) through the funds provided to the Sino-German Collaborative Research Center TRR110 "Symmetries and the Emergence of Structure in QCD" (NSFC Grant No. 12070131001, DFG Project-ID 196253076); and by the Chinese Academy of Sciences under Grant No. XDB34030000.
Data Availability Statement
Data available in a publicly accessible repository.
Acknowledgments
M.-J.Y. is grateful to Shuang-Shi Fang and M.P. Valderrama for valuable discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | As discussed in Section 3.2, the widths of the dynamically generated poles will be significantly increased once the width effects of the axial-vector mesons are taken into account, see also the discussions below. |
References
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. A New Extended Model of Hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef]
- Jaffe, R.L. Multi-Quark Hadrons. 1. The Phenomenology of (2 Quark 2 anti-Quark) Mesons. Phys. Rev. D 1977, 15, 267. [Google Scholar] [CrossRef]
- Maiani, L.; Piccinini, F.; Polosa, A.D.; Riquer, V. Diquark-antidiquarks with hidden or open charm and the nature of X(3872). Phys. Rev. D 2005, 71, 014028. [Google Scholar] [CrossRef]
- Esposito, A.; Pilloni, A.; Polosa, A.D. Multiquark Resonances. Phys. Rept. 2017, 668, 1–97. [Google Scholar] [CrossRef]
- Guo, F.K.; Hanhart, C.; Meißner, U.G.; Wang, Q.; Zhao, Q.; Zou, B.S. Hadronic molecules. Rev. Mod. Phys. 2018, 90, 015004, Erratum in Rev. Mod. Phys. 2022, 94, 029901. [Google Scholar] [CrossRef]
- Luo, X.Q.; Liu, Y. Gluonic excitation of non-exotic hybrid charmonium from lattice QCD. Phys. Rev. D 2006, 74, 034502, Erratum in Phys. Rev. D 2006, 74, 039902. [Google Scholar] [CrossRef]
- Meyer, C.A.; Swanson, E.S. Hybrid Mesons. Prog. Part. Nucl. Phys. 2015, 82, 21–58. [Google Scholar] [CrossRef]
- Ablikim, M.; et al.; [BESIII Collaboration] Observation of an Isoscalar Resonance with Exotic JPC=1-+ Quantum Numbers in J/ψ→γηη’. Phys. Rev. Lett. 2022, 129, 192002. [Google Scholar] [CrossRef]
- Ablikim,, M.; et al.; [BESIII Collaboration] Partial wave analysis of J/ψ→γη′η′. Phys. Rev. D 2022, 105, 072002. [Google Scholar] [CrossRef]
- Workman, R.L.; et al.; [Particle Data Group Collaboration] Review of Particle Physics. PTEP 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Lacock, P.; Michael, C.; Boyle, P.; Rowland, P. Orbitally excited and hybrid mesons from the lattice. Phys. Rev. D 1996, 54, 6997–7009. [Google Scholar] [CrossRef]
- Lacock, P.; Michael, C.; Boyle, P.; Rowland, P. Hybrid mesons from quenched QCD. Phys. Lett. B 1997, 401, 308–312. [Google Scholar] [CrossRef]
- Bernard, C.; Hetrick, J.E.; DeGrand, T.A.; Wingate, M.; DeTar, C.; McNeile, C.; Gottlieb, S.; Heller, U.M.; Rummukainen, K.; Sugar, B.; et al. Exotic mesons in quenched lattice QCD. Phys. Rev. D 1997, 56, 7039–7051. [Google Scholar] [CrossRef]
- McNeile, C.; Michael, C. Decay width of light quark hybrid meson from the lattice. Phys. Rev. D 2006, 73, 074506. [Google Scholar] [CrossRef]
- Dudek, J.J.; Edwards, R.G.; Peardon, M.J.; Richards, D.G.; Thomas, C.E. Toward the excited meson spectrum of dynamical QCD. Phys. Rev. D 2010, 82, 034508. [Google Scholar] [CrossRef]
- Dudek, J.J. The lightest hybrid meson supermultiplet in QCD. Phys. Rev. D 2011, 84, 074023. [Google Scholar] [CrossRef]
- Qiu, L.; Zhao, Q. Towards the establishment of the light JP(C)=1-(+) hybrid nonet *. Chin. Phys. C 2022, 46, 051001. [Google Scholar] [CrossRef]
- Shastry, V.; Fischer, C.S.; Giacosa, F. The phenomenology of the exotic hybrid nonet with π1(1600) and η1(1855). arXiv 2022, arXiv:hep-ph/2203.04327. [Google Scholar] [CrossRef]
- Chen, H.X.; Su, N.; Zhu, S.L. QCD Axial Anomaly Enhances the ηη’ Decay of the Hybrid Candidate η1(1855). Chin. Phys. Lett. 2022, 39, 051201. [Google Scholar] [CrossRef]
- Wan, B.D.; Zhang, S.Q.; Qiao, C.F. A possible structure of newly found exotic state η1(1855). arXiv 2022, arXiv:hep-ph/2203.14014. [Google Scholar] [CrossRef]
- Dong, X.K.; Lin, Y.H.; Zou, B.S. Interpretation of the η1 (1855) as a KK¯1(1400) + c.c. molecule. Sci. China Phys. Mech. Astron. 2022, 65, 261011. [Google Scholar] [CrossRef]
- Yang, F.; Zhu, H.Q.; Huang, Y. Analysis of the η1 (1855) as a KK¯1(1400)molecular state. Nucl. Phys. A 2023, 1030, 122571. [Google Scholar] [CrossRef]
- Oller, J.A.; Oset, E.; Ramos, A. Chiral unitary approach to meson meson and meson - baryon interactions and nuclear applications. Prog. Part. Nucl. Phys. 2000, 45, 157–242. [Google Scholar] [CrossRef]
- Hofmann, J.; Lutz, M.F.M. Open charm meson resonances with negative strangeness. Nucl. Phys. A 2004, 733, 142–152. [Google Scholar] [CrossRef]
- Roca, L.; Oset, E.; Singh, J. Low lying axial-vector mesons as dynamically generated resonances. Phys. Rev. D 2005, 72, 014002. [Google Scholar] [CrossRef]
- Guo, F.K.; Shen, P.N.; Chiang, H.C.; Ping, R.G.; Zou, B.S. Dynamically generated 0+ heavy mesons in a heavy chiral unitary approach. Phys. Lett. B 2006, 641, 278–285. [Google Scholar] [CrossRef]
- Dias, J.M.; Debastiani, V.R.; Xie, J.J.; Oset, E. Doubly charmed Ξcc molecular states from meson-baryon interaction. Phys. Rev. D 2018, 98, 094017. [Google Scholar] [CrossRef]
- Guo, F.K.; Meißner, U.G. More kaonic bound states and a comprehensive interpretation of the DsJ states. Phys. Rev. D 2011, 84, 014013. [Google Scholar] [CrossRef]
- Aaij, R.; Beteta, C.A.; Ackernley, T.; Adeva, B.; Adinolfi, M.; Afsharnia, H.; Aidala, C.A.; Aiola, S.; Ajaltouni, Z.; Akar, S.; et al. Observation of New Resonances Decaying to J/ψK+ and J/ψϕ. Phys. Rev. Lett. 2021, 127, 082001. [Google Scholar] [CrossRef]
- Cheng, H.Y. Revisiting Axial-Vector Meson Mixing. Phys. Lett. B 2012, 707, 116–120. [Google Scholar] [CrossRef]
- Amsler, C.; Close, F.E. Is f0(1500) a scalar glueball? Phys. Rev. D 1996, 53, 295–311. [Google Scholar] [CrossRef]
- Meißner, U.G. Low-Energy Hadron Physics from Effective Chiral Lagrangians with Vector Mesons. Phys. Rept. 1988, 161, 213. [Google Scholar] [CrossRef]
- ’t Hooft, G. A Planar Diagram Theory for Strong Interactions. Nucl. Phys. B 1974, 72, 461. [Google Scholar] [CrossRef]
- Witten, E. Current Algebra Theorems for the U(1) Goldstone Boson. Nucl. Phys. B 1979, 156, 269–283. [Google Scholar] [CrossRef]
- Veneziano, G. Goldstone Mechanism From Gluon Dynamics. Phys. Lett. B 1980, 95, 90–92. [Google Scholar] [CrossRef]
- Guo, Z.H.; Oller, J.A. Resonances from meson-meson scattering in U(3) CHPT. Phys. Rev. D 2011, 84, 034005. [Google Scholar] [CrossRef]
- Ecker, G.; Gasser, J.; Leutwyler, H.; Pich, A.; de Rafael, E. Chiral Lagrangians for Massive Spin 1 Fields. Phys. Lett. B 1989, 223, 425–432. [Google Scholar] [CrossRef]
- Birse, M.C. Effective chiral Lagrangians for spin 1 mesons. Z. Phys. A 1996, 355, 231–246. [Google Scholar] [CrossRef]
- Borasoy, B.; Meißner, U.G. Chiral Lagrangians for baryons coupled to massive spin 1 fields. Int. J. Mod. Phys. A 1996, 11, 5183–5202. [Google Scholar] [CrossRef]
- Oller, J.A.; Oset, E. N/D description of two meson amplitudes and chiral symmetry. Phys. Rev. D 1999, 60, 074023. [Google Scholar] [CrossRef]
- Oller, J.A.; Oset, E.; Pelaez, J.R. Meson meson interaction in a nonperturbative chiral approach. Phys. Rev. D 1999, 59, 074001, Erratum in Phys. Rev. D 1999, 60, 099906; Phys. Rev. D 2007, 75, 099903. [Google Scholar] [CrossRef]
- Oller, J.A.; Meißner, U.G. Chiral dynamics in the presence of bound states: Kaon nucleon interactions revisited. Phys. Lett. B 2001, 500, 263–272. [Google Scholar] [CrossRef]
- Fu, H.L.; Grießhammer, H.W.; Guo, F.K.; Hanhart, C.; Meißner, U.G. Update on strong and radiative decays of the Ds0*(2317) and Ds1(2460) and their bottom cousins. Eur. Phys. J. A 2022, 58, 70. [Google Scholar] [CrossRef]
- Geng, L.S.; Oset, E. Vector meson-vector meson interaction in a hidden gauge unitary approach. Phys. Rev. D 2009, 79, 074009. [Google Scholar] [CrossRef]
- Cirigliano, V.; Ecker, G.; Eidemuller, M.; Kaiser, R.; Pich, A.; Portoles, J. Towards a consistent estimate of the chiral low-energy constants. Nucl. Phys. B 2006, 753, 139–177. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. Consequences of anomalous Ward identities. Phys. Lett. B 1971, 37, 95–97. [Google Scholar] [CrossRef]
- Witten, E. Global Aspects of Current Algebra. Nucl. Phys. B 1983, 223, 422–432. [Google Scholar] [CrossRef]
- Kampf, K.; Novotny, J. Resonance saturation in the odd-intrinsic parity sector of low-energy QCD. Phys. Rev. D 2011, 84, 014036. [Google Scholar] [CrossRef]
- Ecker, G.; Gasser, J.; Pich, A.; de Rafael, E. The Role of Resonances in Chiral Perturbation Theory. Nucl. Phys. B 1989, 321, 311–342. [Google Scholar] [CrossRef]
- Miranda, J.A.; Roig, P. New τ-based evaluation of the hadronic contribution to the vacuum polarization piece of the muon anomalous magnetic moment. Phys. Rev. D 2020, 102, 114017. [Google Scholar] [CrossRef]
- Bando, M.; Fujiwara, T.; Yamawaki, K. Generalized Hidden Local Symmetry and the A1 Meson. Prog. Theor. Phys. 1988, 79, 1140. [Google Scholar] [CrossRef]
- Bando, M.; Kugo, T.; Yamawaki, K. Nonlinear Realization and Hidden Local Symmetries. Phys. Rept. 1988, 164, 217–314. [Google Scholar] [CrossRef]
- Kaiser, N.; Meißner, U.G. Generalized hidden symmetry for low-energy hadron physics. Nucl. Phys. A 1990, 519, 671–696. [Google Scholar] [CrossRef]
- Kopf, B.; Albrecht, M.; Koch, H.; Küßner, M.; Pychy, J.; Qin, X.; Wiedner, U. Investigation of the lightest hybrid meson candidate with a coupled-channel analysis of p¯p-, π−p- and ππ-Data. Eur. Phys. J. C 2021, 81, 1056. [Google Scholar] [CrossRef]
- Rodas, A.; Pilloni, A.; Albaladejo, M.; Fernández-Ramírez, C.; Jackura, A.; Mathieu, V.; Mikhasenko, M.; Nys, J.; Pauk, V.; Ketzer, B.; et al. Determination of the pole position of the lightest hybrid meson candidate. Phys. Rev. Lett. 2019, 122, 042002. [Google Scholar] [CrossRef]
- Kuhn, J.; et al.; [E852 Collaboration] Exotic meson production in the f1(1285)π− system observed in the reaction π−p→ηπ+π−π−p at 18GeV/c. Phys. Lett. B 2004, 595, 109–117. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).