Fermionic Greybody Factors in Schwarzschild Acoustic Black Holes
Abstract
1. Introduction
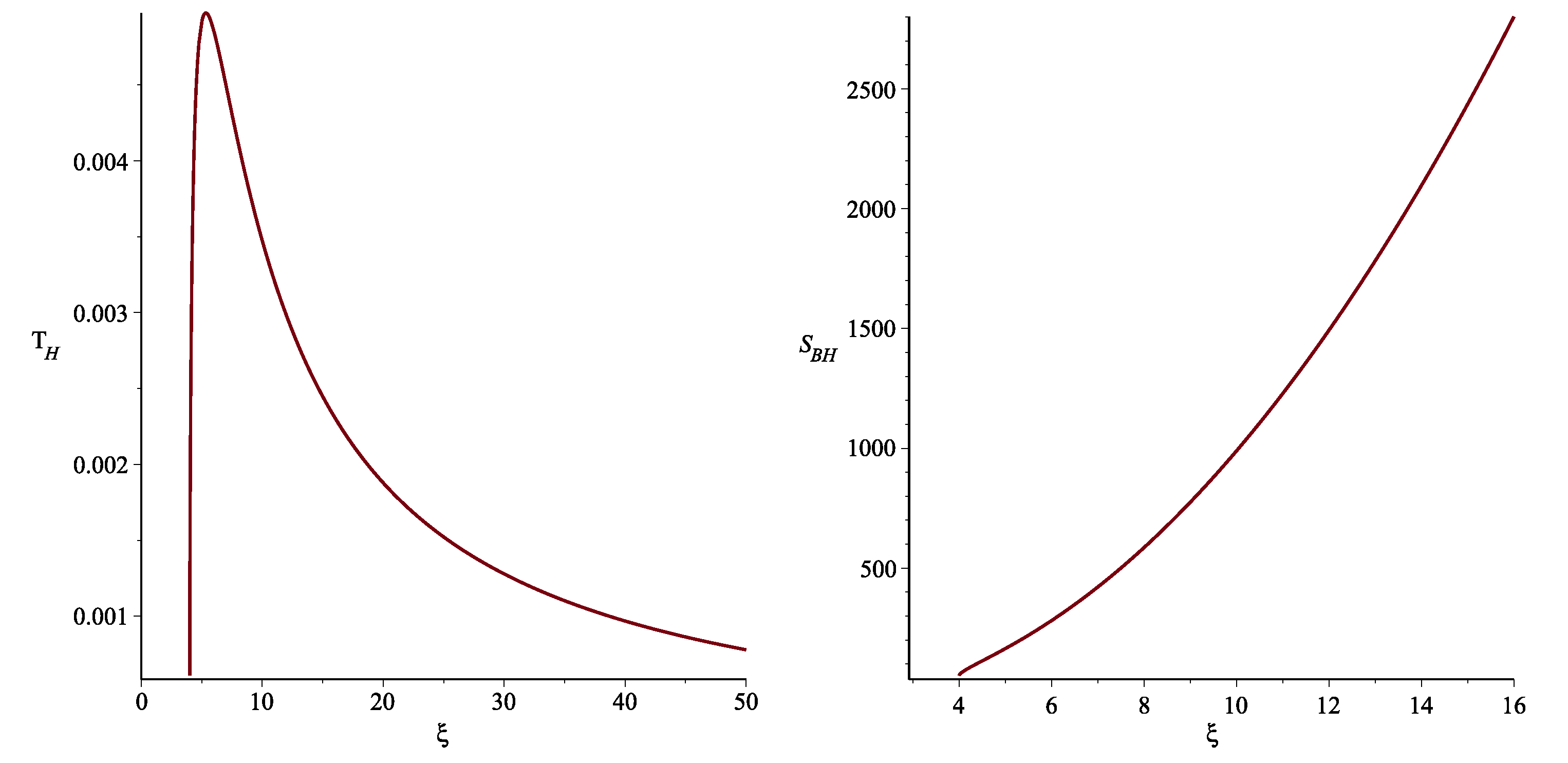
2. SABH Spacetime
3. Dirac Equation
4. Rarita–Schwinger Equation
5. GFs of SABH via Fermion Emission
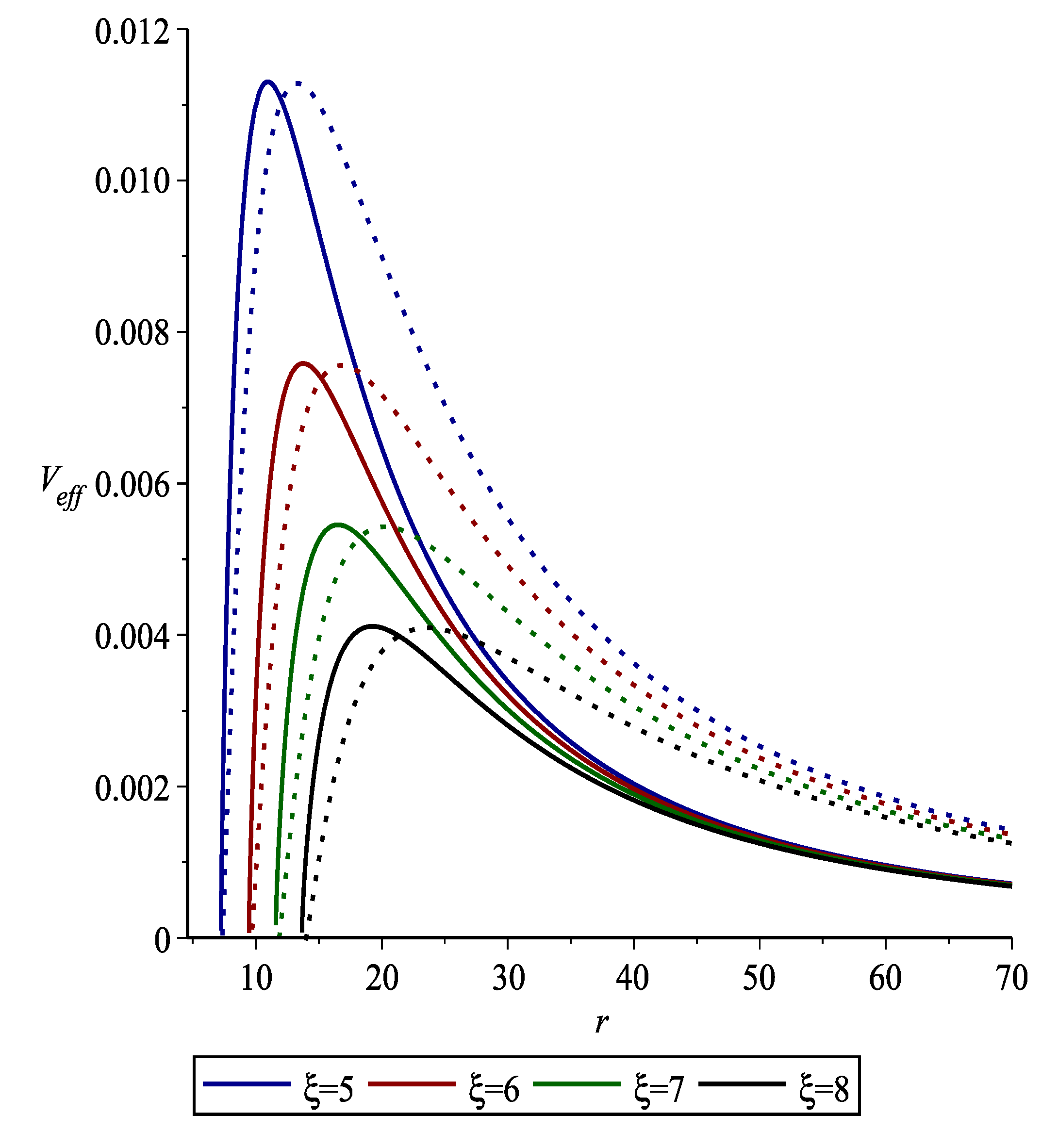
5.1. Spin- Fermions
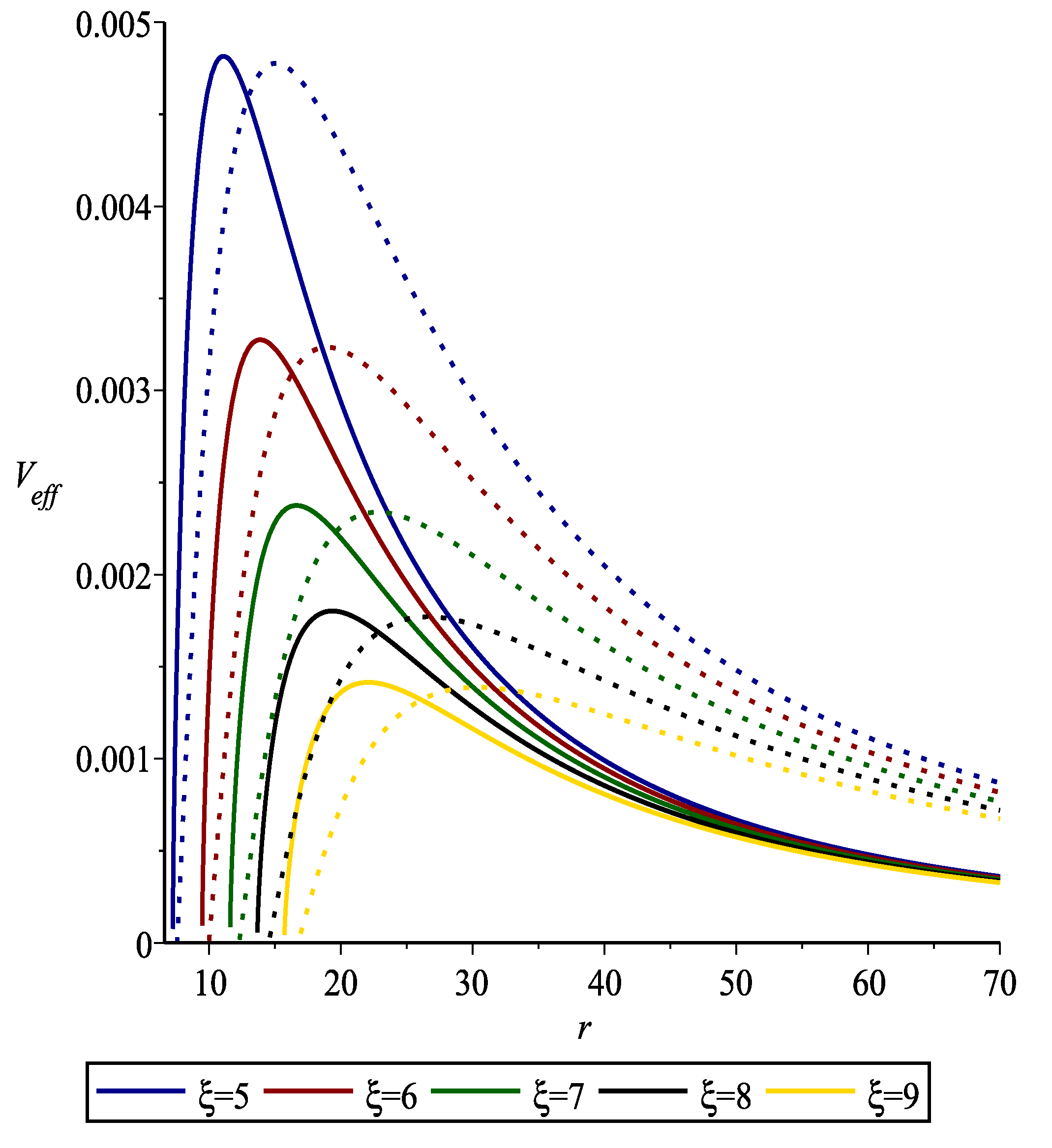
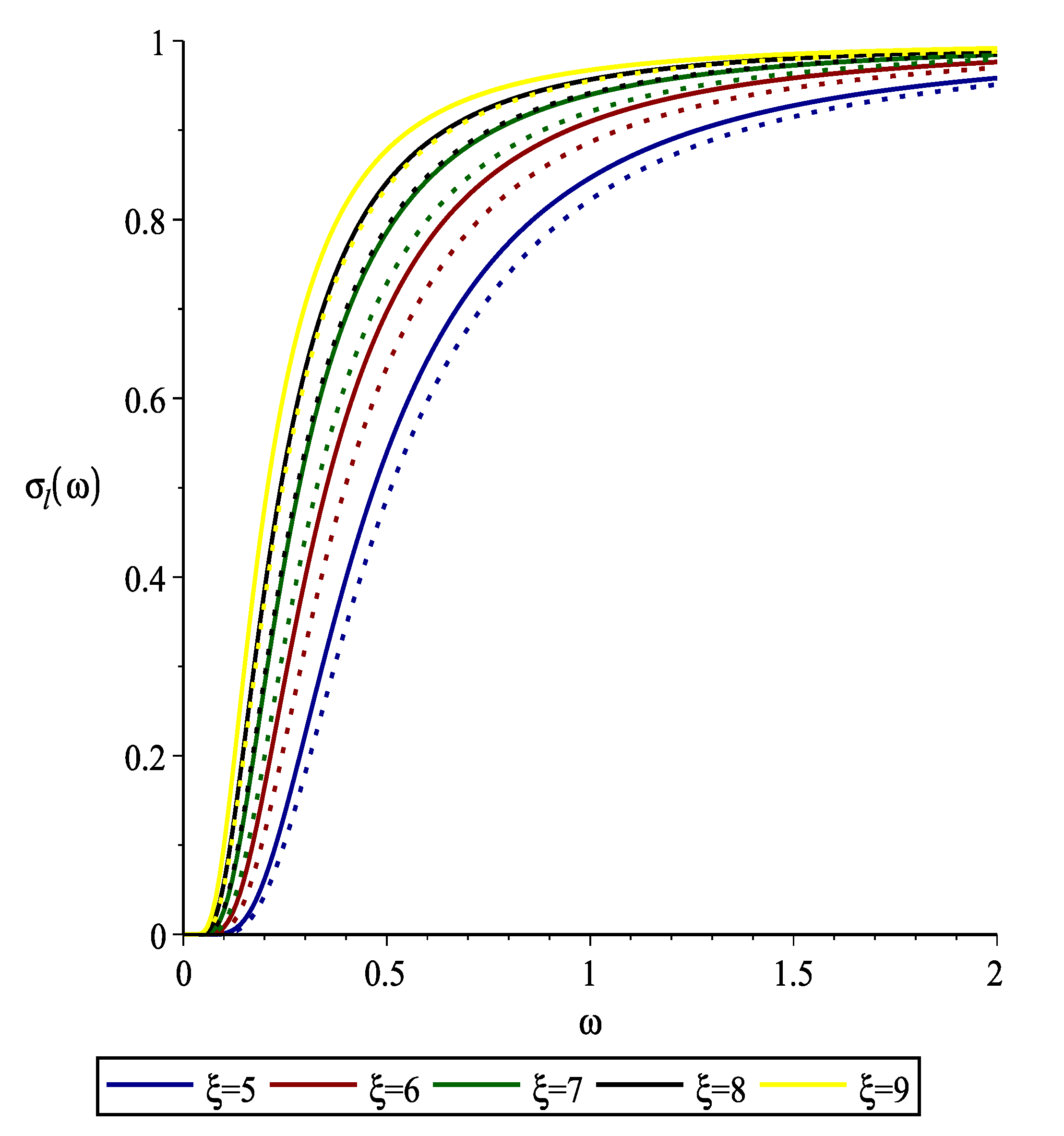
5.2. Spin- Fermions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Unruh, W.G. Experimental Black-Hole Evaporation? Phys. Rev. Lett. 1981, 46, 1351. [Google Scholar] [CrossRef]
- Visser, M. Acoustic black holes. arXiv 1999, arXiv:gr-qc/9901047. [Google Scholar]
- Guo, H.; Liu, H.; Kuang, X.M.; Wang, B. Acoustic black hole in Schwarzschild spacetime: Quasi-normal modes, analogous Hawking radiation and shadows. Phys. Rev. D 2020, 102, 124019. [Google Scholar] [CrossRef]
- Vieira, H.S.; Kokkotas, K.D. Quasibound states of Schwarzschild acoustic black holes. Phys. Rev. D 2021, 104, 024035. [Google Scholar] [CrossRef]
- Qiao, C.K.; Zhou, M. The Gravitational Bending of Acoustic Schwarzschild Black Hole. arXiv 2021, arXiv:2109.05828. [Google Scholar]
- Cardoso, V.; Lemos, J.P.S.; Yoshida, S. Quasinormal modes and stability of the rotating acoustic black hole: Numerical analysis. Phys. Rev. D 2004, 70, 124032. [Google Scholar] [CrossRef]
- Anacleto, M.A.; Brito, F.A.; Passos, E. Hawking radiation and stability of the canonical acoustic black holes. arXiv 2022, arXiv:2212.13850. [Google Scholar]
- Furuhashi, H.; Nambu, Y.; Saida, H. Simulation of acoustic black hole in a Laval nozzle. Class. Quant. Grav. 2006, 23, 5417–5438. [Google Scholar] [CrossRef]
- Fu, W.; Lai, D. Simulations of Overstable Inertial-acoustic Modes in Black-Hole Accretion Discs. Mon. Not. Ro. Astron. Soc. 2013, 431, 3697. [Google Scholar] [CrossRef]
- Ge, X.H.; Sun, J.R.; Tian, Y.; Wu, X.N.; Zhang, Y.L. Holographic Interpretation of Acoustic Black Holes. Phys. Rev. D 2015, 92, 084052. [Google Scholar] [CrossRef]
- Mannarelli, M.; Grasso, D.; Trabucco, S.; Chiofalo, M.L. Phonon emission by acoustic black holes. arXiv 2021, arXiv:2109.11831. [Google Scholar]
- Balbinot, R.; Fagnocchi, S.; Fabbri, A.; Procopio, G.P. Backreaction in acoustic black holes. Phys. Rev. Lett. 2005, 94, 161302. [Google Scholar] [CrossRef]
- Sakalli, İ.; Kanzi, S. Topical Review: Greybody factors and quasinormal modes for black holes in various theories—Fingerprints of invisibles. Turk. J. Phys. 2022, 46, 51–103. [Google Scholar] [CrossRef]
- Holzhey, C.F.E.; Wilczek, F. Black holes as elementary particles. Nucl. Phys. B 1992, 380, 447. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Koga, J.; Maeda, K. Evaporation and fate of dilatonic black holes. Phys. Rev. D 1995, 52, 7066. [Google Scholar] [CrossRef]
- Gibbons, G.W. Vacuum Polarization and the Spontaneous Loss of Charge by Black Holes. Commun. Math. Phys. 1975, 44, 245. [Google Scholar] [CrossRef]
- Page, D.N. Particle Emission Rates from a Black Hole. 3. Charged Leptons from a Nonrotating Hole. Phys. Rev. D 1977, 16, 2402. [Google Scholar]
- Cvetic, M.; Larsen, F. Greybody factors for black holes in four-dimensions: Particles with spin. Phys. Rev. D 1998, 57, 6297. [Google Scholar] [CrossRef]
- Kanti, P.; March-Russell, J. Calculable corrections to brane black hole decay. 2. Greybody factors for spin 1/2 and 1. Phys. Rev. D 2003, 67, 104019. [Google Scholar] [CrossRef]
- Creek, S.; Efthimiou, O.; Kanti, P.; Tamvakis, K. Greybody factors in a rotating black-hole background. II. Fermions and gauge bosons. Phys. Rev. D 2007, 76, 104013. [Google Scholar] [CrossRef]
- Das, S.; Dasgupta, A. Black hole emission rates and the AdS / CFT correspondence. JHEP 1999, 9910, 25. [Google Scholar] [CrossRef]
- Gubser, S.S. Absorption of photons and fermions by black holes in four-dimensions. Phys. Rev. D 1997, 56, 7854. [Google Scholar] [CrossRef]
- al-Binni, U.A.; Siopsis, G. Particle emission from a black hole on a tense codimension-2 brane. Phys. Rev. D 2009, 79, 084041. [Google Scholar] [CrossRef]
- Sampaio, M.O.P. Charge and mass effects on the evaporation of higher-dimensional rotating black holes. JHEP 2009, 0910, 8. [Google Scholar] [CrossRef]
- Casals, M.; Dolan, S.R.; Kanti, P.; Winstanley, E. Brane Decay of a (4 + n)-Dimensional Rotating Black Hole. III. Spin-1/2 particles. JHEP 2007, 0703, 19. [Google Scholar] [CrossRef]
- Sampaio, M.O.P. Distributions of charged massive scalars and fermions from evaporating higher-dimensional black holes. JHEP 2010, 1002, 42. [Google Scholar] [CrossRef]
- Auffinger, J.; Arbey, A. Beyond the Standard Model with BlackHawk v2.0. arXiv 2022, arXiv:2207.03266. [Google Scholar]
- Chen, C.H.; Cho, H.T.; Cornell, A.S.; Harmsen, G.; Ngcobo, X. Quasinormal modes and absorption probabilities of spin-3/2 fields in D-dimensional Reissner-Nordström black hole spacetimes. Phys. Rev. D 2018, 97, 024038. [Google Scholar] [CrossRef]
- Chen, S.; Wang, B.; Su, R. Influence of Lorentz violation on Dirac quasinormal modes in the Schwarzschild black hole spacetime. Class. Quant. Grav. 2006, 23, 7581. [Google Scholar] [CrossRef]
- Cho, H.T. Dirac quasinormal modes in Schwarzschild black hole space-times. Phys. Rev. D 2003, 68, 024003. [Google Scholar] [CrossRef]
- Cho, H.T.; Lin, Y.-C. WKB analysis of the scattering of massive Dirac fields in Schwarzschild black hole spacetimes. Class. Quant. Grav. 2005, 22, 775. [Google Scholar] [CrossRef]
- Cho, H.T.; Cornell, A.S.; Doukas, J.; Naylor, W. Split fermion quasi-normal modes. Phys. Rev. D 2007, 75, 104005. [Google Scholar] [CrossRef]
- Chakrabarti, S.K. A comparative study of Dirac quasinormal modes of charged black holes in higher dimensions. Eur. Phys. J. C 2009, 61, 477. [Google Scholar] [CrossRef]
- Doran, C.; Lasenby, A.; Dolan, S.; Hinder, I. Fermion absorption cross section of a Schwarzschild black hole. Phys. Rev. D 2005, 71, 124020. [Google Scholar] [CrossRef]
- Dolan, S.; Doran, C.; Lasenby, A. Fermion scattering by a Schwarzschild black hole. Phys. Rev. D 2006, 74, 064005. [Google Scholar] [CrossRef]
- Jin, W.M. Scattering of massive Dirac fields on the Schwarzschild black hole space-time. Class. Quant. Grav. 1998, 15, 3163. [Google Scholar] [CrossRef]
- Jing, J.-l. Dirac quasinormal modes of the Reissner-Nordström de Sitter black hole. Phys. Rev. D 2004, 69, 084009. [Google Scholar] [CrossRef]
- Jing, J.-L. Late-time behaviour of massive Dirac fields in a Schwarzschild background. Phys. Rev. D 2004, 70, 065004. [Google Scholar] [CrossRef]
- Jing, J. Late-time evolution of charged massive Dirac fields in the Reissner-Nordström black-hole background. Phys. Rev. D 2005, 72, 027501. [Google Scholar] [CrossRef]
- Jung, E.; Kim, S.; Park, D.K. Low-energy absorption cross section for massive scalar and Dirac fermion by (4 + n)-dimensional Schwarzschild black hole. JHEP 2004, 0409, 5. [Google Scholar] [CrossRef]
- Lopez-Ortega, A. Hawking radiation and Dirac quasinormal modes of 3D EMD Lambda black holes. Gen. Rel. Grav. 2005, 37, 167. [Google Scholar] [CrossRef]
- Lopez-Ortega, A. Quasinormal frequencies of the Dirac field in the massless topological black hole. Rev. Mex. Fis. 2010, 56, 44. [Google Scholar]
- Lopez-Ortega, A.; Vega-Acevedo, I. Quasinormal frequencies of asymptotically flat two-dimensional black holes. Gen. Rel. Grav. 2011, 43, 2631. [Google Scholar] [CrossRef]
- Moderski, R.; Rogatko, M. Decay of Dirac Massive Hair in the Background of Spherical Black Hole. Phys. Rev. D 2008, 77, 124007. [Google Scholar] [CrossRef]
- Sini, R.; Varghese, N.; Kuriakose, V.C. Quasi normal modes of spherically symmetric black hole spacetimes with cosmic string in a Dirac field. arXiv 2008, arXiv:0802.0788. [Google Scholar]
- Shu, F.-W.; Shen, Y.-G. Quasinormal modes of charged black holes in string theory. Phys. Rev. D 2004, 70, 084046. [Google Scholar] [CrossRef]
- Wang, C.-Y.; Zhang, Y.; Gui, Y.-X.; Lu, J.-B. Quasinormal modes of Dirac field perturbation in Reissner-Nordström black hole surrounded by quintessence. arXiv 2009, arXiv:0910.5128. [Google Scholar]
- Yuan, H.; Ge, X.H. Analogue of the pole-skipping phenomenon in acoustic black holes. Eur. Phys. J. C 2022, 82, 167. [Google Scholar] [CrossRef]
- Vieira, H.S.; Destounis, K.; Kokkotas, K.D. Slowly-rotating curved acoustic black holes: Quasinormal modes, Hawking-Unruh radiation, and quasibound states. Phys. Rev. D 2022, 105, 045015. [Google Scholar] [CrossRef]
- Dolan, S.R.; Oliveira, L.A.; Crispino, L.C.B. Quasinormal modes and Regge poles of the canonical acoustic hole. Phys. Rev. D 2010, 82, 084037. [Google Scholar] [CrossRef]
- Gross, E.P. Structure of a quantized vortex in bosonsystems. Nuovo C. (1955–1965) 1961, 20, 454. [Google Scholar]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Vieira, H.S.; Destounis, K.; Kokkotas, K.D. Analog Schwarzschild black holes of Bose-Einstein condensates in a cavity: Quasinormal modes and quasibound states. arXiv 2023, arXiv:2301.11480. [Google Scholar]
- Syu, W.C.; Lee, D.S. Analogous Hawking radiation in binary Bose-Einstein condensates: Exact results for gapped excitations. arXiv 2022, arXiv:2212.06063. [Google Scholar]
- Dave, S.S.; Ganguly, O.; Srivastava, S.P.S.A.M. Hawking radiation from acoustic black holes in hydrodynamic flow of electrons. EPL 2022, 139, 60003. [Google Scholar] [CrossRef]
- Steinhauer, J. Observation of self-amplifying Hawking radiation in an analog black hole laser. Nat. Phys. 2014, 10, 864. [Google Scholar] [CrossRef]
- de Nova, J.R.M.n.; Golubkov, K.; Kolobov, V.I.; Steinhauer, J. Observation of thermal Hawking radiation and its temperature in an analogue black hole. Nature 2019, 569, 688–691. [Google Scholar] [CrossRef]
- Kolobov, V.I.; Golubkov, K.; de Nova, J.R.M.n.; Steinhauer, J. Observation of stationary spontaneous Hawking radiation and the time evolution of an analogue black hole. Nat. Phys. 2021, 17, 362–367. [Google Scholar] [CrossRef]
- Steinhauer, J.; Abuzarli, M.; Aladjidi, T.; Bienaimé, T.; Piekarski, C.; Liu, W.; Giacobino, E.; Bramati, A.; Glorieux, Q. Analogue cosmological particle creation in an ultracold quantum fluid of light. Nat. Commun. 2022, 13, 2890. [Google Scholar] [CrossRef]
- Tian, Z.; Jing, J. Towards experimentally studying some puzzles of Hawking radiation. Gen. Rel. Grav. 2014, 46, 1779. [Google Scholar] [CrossRef]
- Basak, C.S.; Das, S. Hawking radiation of anyons. Phys. Rev. D 2021, 104, 104011. [Google Scholar]
- Wald, R.M. General Relativity; The University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. II. Phys. Rev. E 2005, 72, 036108. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1983. [Google Scholar]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: New York, NY, USA, 1984. [Google Scholar]
- Perez, A.; Ribisi, S.; Viollet, S. Modelling quantum particles falling into a black hole: The deep interior limit. arXiv 2023, arXiv:2301.03951. [Google Scholar]
- Brandt, F.T.; Sánchez-Monroy, J.A. Dirac equation on a curved surface. Phys. Lett. A 2016, 380, 3036–3043. [Google Scholar] [CrossRef]
- Rarita, W.; Schwinger, J. On a Theory of Particles with Half-Integral Spin. Phys. Rev. 1941, 60, 61. [Google Scholar] [CrossRef]
- Simulik, V.M.; Vyikon, I.I. On the “old” and “new” relativistic wave equations for the particle having spin s = 3/2. arXiv 2022, arXiv:2204.05167. [Google Scholar]
- Simulik, V.M.; Vyikon, I.I. On the Choice of Relativistic Wave Equation for the Particle Having Spin s = 3/2. J. Phys. Commun. 2022, 6, 075008. [Google Scholar] [CrossRef]
- Halzen, F.; Martin, A.D. Quarks and Leptons: An Introductory Course in Modern Particle Physics; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Sakalli, I.; Övgün, A. Quantum Tunneling of Massive Spin-1 Particles From Non-stationary Metrics. Gen. Rel. Grav. 2016, 48, 1. [Google Scholar] [CrossRef]
- Jackiw, R.; Rebbi, C. Spinor Analysis of Yang-Mills Theory. Phys. Rev. D 1977, 16, 1052. [Google Scholar] [CrossRef]
- Chen, C.H.; Cho, H.T.; Cornell, A.S.; Harmsen, G. Spin- 3/2 fields in D-dimensional Schwarzschild black hole spacetimes. Phys. Rev. D 2016, 94, 044052. [Google Scholar] [CrossRef]
- Ama-Tul-Mughani, Q.; Waseem, A.; Salam, W.u.; Jawad, A. Greybody factor and thermal fluctuations of rotating regular black hole bounded by PFDM. Chin. J. Phys. 2022, 77, 2213–2227. [Google Scholar] [CrossRef]
- Ama-Tul-Mughani, Q.; Mumtaz, S.; Salam, W.u.; Ikram, A. Greybody factor and thermal fluctuations of rotating black hole with perfect fluid dark matter. Int. J. Mod. Phys. D 2022, 31, 2250046. [Google Scholar] [CrossRef]
- Okyay, M.; Övgün, A. Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors. JCAP 2022, 1, 9. [Google Scholar] [CrossRef]
- Boonserm, P.; Visser, M. Transmission probabilities and the Miller-Good transformation. J. Phys. A 2009, 42, 045301. [Google Scholar] [CrossRef]
- Devi, S.; Roy, R.; Chakrabarti, S. Quasinormal modes and greybody factors of the novel four dimensional Gauss–Bonnet black holes in asymptotically de Sitter space time: Scalar, electromagnetic and Dirac perturbations. Eur. Phys. J. C 2020, 80, 760. [Google Scholar] [CrossRef]
- Giddings, S.B. Black holes in the quantum universe. Phil. Trans. Roy. Soc. Lond. A 2019, 377, 20190029. [Google Scholar] [CrossRef]
- Lin, H.; Saifullah, K.; Yau, S.T. Accelerating black holes, spin-32 fields and C-metric. Mod. Phys. Lett. A 2015, 30, 1550044. [Google Scholar] [CrossRef]
- Harmsen, G.E.; Chen, C.H.; Cho, H.T.; Cornell, A.S. Absorption probabilities associated with spin-3/2 particles near N-dimensional Schwarzschild black holes. J. Phys. Conf. Ser. 2017, 802, 012002. [Google Scholar] [CrossRef]
- Chen, C.H.; Cho, H.T.; Cornell, A.S.; Harmsen, G.E. Master equations and quasinormal modes of spin- 3/2 fields in Schwarzschild (A)dS black hole spacetimes. Phys. Rev. D 2019, 100, 104018. [Google Scholar] [CrossRef]
- Batelaan, H.; Gay, T.J.; Schwendiman, J.J. Stern-Gerlach effect for electron beams. Phys. Rev. Lett. 1997, 79, 4517–4521. [Google Scholar] [CrossRef]
- Steinhauer, J. Measuring the entanglement of analogue Hawking radiation by the density-density correlation function. Phys. Rev. D 2015, 92, 024043. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanzi, S.; Sakallı, İ. Fermionic Greybody Factors in Schwarzschild Acoustic Black Holes. Universe 2023, 9, 108. https://doi.org/10.3390/universe9020108
Kanzi S, Sakallı İ. Fermionic Greybody Factors in Schwarzschild Acoustic Black Holes. Universe. 2023; 9(2):108. https://doi.org/10.3390/universe9020108
Chicago/Turabian StyleKanzi, Sara, and İzzet Sakallı. 2023. "Fermionic Greybody Factors in Schwarzschild Acoustic Black Holes" Universe 9, no. 2: 108. https://doi.org/10.3390/universe9020108
APA StyleKanzi, S., & Sakallı, İ. (2023). Fermionic Greybody Factors in Schwarzschild Acoustic Black Holes. Universe, 9(2), 108. https://doi.org/10.3390/universe9020108







