Abstract
We numerically study the evolution of the extrinsic energy density in the context of an inflationary regime at the background level in a five-dimensional model using a Bayesian analysis from a dynamic nested sampler (DYNESTY) code. By means of the Nash–Greene embedding theorem, we show that the corresponding model provides an effective potential driven by the influence of extrinsic geometry. We obtain a quintessential inflation that defines a model with a potential , where and are dimensionless parameters. Using some known phenomenological parameterizations, such as Chevallier–Polarski–Linder (CPL) and Barboza–Alcaniz (BA) parameterizations, we show that the model reflects a slow-varying inflation preferring a thawing behavior, suggesting an optimistic scenario for further research on the unification of inflation with late cosmic acceleration.
1. Introduction
Cosmic inflation is one of the most fantastic mechanisms for understanding the evolution of the early universe, which underwent a rapid and exponential increase in the cosmic scale factor shortly after the Big Bang. It proposes a simple solution to the horizon problem by suggesting that far-reaching regions of the universe were in close proximity before inflation occurred. Then, it explains why the universe appears homogeneous and isotropic on large scales. Moreover, the so-called flatness problem that states, Why does the universe seem to have a nearly flat geometry? is solved in the context of inflation since it naturally leads to a flat universe [1]. It also provides an explanation of the formation of a large-scale structure in the universe, including galaxies and galaxy clusters, by quantum fluctuations in a peculiar scalar field dubbed as inflaton field during that cosmic inflationary period [2,3,4,5,6,7,8,9].
The nature of the inflaton field motivated the elaboration of a plethora of competing cosmological models [10,11,12,13,14,15,16,17,18,19] due to the fact that the form of the inflation field is not determined and the standard phenomenological model cold dark matter (CDM) with the fluid parameter rapidly decays at the end of the inflationary period [20]. Thus, the inflaton field cannot be directly regarded as a cosmological constant for the late acceleration of the universe. An immediate issue arises whether the inflaton field should be some form of a dark energy (DE) fluid: how does the equation of the state parameter w significantly deviate from during the inflationary era? In this paper, we make the first steps to answer this question in the context of a modification of gravity by extra dimensions. Apart from traditional models, such as the Arkani-Hamed–Dvali–Dimopoulos (ADD) model [21], the Randall–Sundrum model [22,23], and/or the Dvali–Gabadadze–Porrati model (DPG) [24], we explore the dynamical embedding of space-times as the main mathematical structure [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. In Encyclopaedia Inflationaris [41], the reader can find various types and classifications of inflationary models, such as supergravity brane inflation, supersymmetry (SUSY), and brane inflation models.
The paper is organized into sections. The Section 2 and Section 3 summarize the essentials of previously published results on the construction of the four-dimensional embedded model and cosmological applications [26,27,28,31,39,40]. The Section 4 presents the fluid analogy necessary to make a comparison with phenomenological models. Moreover, we construct a model wherein the extrinsic curvature is thought as an inflaton field as shown in the Section 5. By means of numerical analysis generating synthetic random points using the DYNESTY [42,43] Python code, we constrain the parameters of our toy model. To analyze how the related equation of state (EoS) evolves, we use Chevallier–Polarski–Linder (CPL) [44,45] and Barboza–Alcaniz (BA) [46] parameterizations to distinguish the present model as a thawing [47,48,49] or freezing [50,51,52,53] pattern. Thawing models are conceived to be those that the fluid parameter as a function of the redshift in EoS is moving away from , which means that DE density decreases over time, gradually allowing the universe to accelerate more rapidly. On the other hand, in freezing models, DE density remains approximately constant as the universe expands, with approaching the value . Finally, the conclusion and prospects are presented in the Section 6.
2. Essentials on Embeddings
We define a model endowed with a gravitational action S in the presence of confined matter fields wherein a four-dimensional embedded space-time is embedded in five dimensions as
where is a fundamental energy scale on the embedded space, and the curly denotes the five-dimensional Ricci scalar of the bulk given by the summation of the four-dimensional Ricci scalar R and the deformation scalar Q and has the simple form . Moreover, denotes the bulk source Lagrangian in five dimensions. Since gravity should only propagate in the bulk, is localized in the four-dimensional embedded space and obeys the confinement condition
from the components of of the energy–momentum tensor of the bulk. The terms of , , and denote the energy–momentum of the tangent (tensor), vector, and scalar components of . Concerning notation, capital Latin indices are fixed to 5 to reinforce the notation of a five-dimensional space. Small-case Latin indices refer to the only one extra dimension fixed to 1. All Greek indices refer to the embedded space-time running from 1 to 4. Ordinary matter and gauge fields are represented by , and G is the gravitational Newtonian constant. From the set of equations in Equation (2), reduces to the confined four-dimensional Lagrangian related to as
where is the metric and is the absolute value of . Detailed demonstrations of the fundamental field equations, from a bulk of five or in arbitrary dimensions, can be found in Refs. [26,27,28,31,40]. In this work, in search of constructing a viable physical model, we consider the extrinsic curvature as a main character of cosmic dynamics. Mathematically speaking, besides the metric , such new curvature is a pivotal element in the embedding of geometries. As traditionally defined in [54], the nonperturbed extrinsic curvature reads,
The definition in Equation (4) essentially means a measure of bending of the embedded geometry; i.e., it reflects how a normal unitary vector in the embedded space deviates from the tangent plane. Let the coordinate define a regular map . Such a local map states that a Riemannian manifold is isometrically embedded in a larger five-dimensional Riemannian bulk space . The term is the bulk metric
Another pivotal relation is Nash’s deformation formula given by
where y is an arbitrary spatial coordinate. Nash’s deformation formula is the pivot result of Nash’s embedding theorem of 1954 applied to non-Euclidean metrics [55]. In 1956, Nash generalized his former results to Riemannian metrics [56]. Decades later, Nash’s theorem was expanded to non-Riemannian metrics by Greene [57]. From a physical point of view, Equation (6) localizes gravity closer to the four-dimensional embedded space, imposing a strong bending (warping) geometrical constraint.
Nash’s results in Equation (6) is the capital element to obtain a solution to well-known Gauss and Codazzi equations given by
where denotes the five-dimensional Riemann tensor, and is the four-dimensional Riemann tensor. The coordinate is a perturbed coordinate in the sense that . The semicolon sign in Equation (8) represents the ordinary covariant derivative with respect to the metric and . The importance of Equations (7) and (8) is that they reflect the integrability conditions for the embedding explicitly relating the bulk and embedded space, and they are the starting point to obtain the induced field equations [26,27,28,31,40].
3. Friedmann–Lemaître–Robertson–Walker (FLRW) Embedded Cosmology
From integration of Equations (7) and (8), one obtains the induced four-dimensional nonperturbed field equations as
where is the energy–momentum tensor of the confined sources, G is the gravitational Newtonian constant, and is the four-dimensional Einstein tensor. The deformation tensor is given by
where the mean curvature is given by and . The quantity is the Gaussian curvature. By direct derivation, Equation (11) is conserved in the sense that
Once the field equations of Equations (9) and (10) are set, we obtain the background cosmic evolution from the usual four-dimensional line element of the FLRW metric given by
where is the scale factor and t is the physical time. As shown in previous works [27,31], the solutions of Equations (9) and (10) are summarized as
where Q is the deformation scalar given by the contraction , and is the Hubble parameter. Defined as an “extrinsic” copy of the Hubble parameter H, we have the cosmic bending parameter . The obtainment of these results is shown in detail in Refs. [27,31]. The warping or bending function is given by
where the parameter denotes the current value of and is the current value of the scale factor.
4. The Fluid Analogy
We obtain the hydrodynamical equations for a perfect fluid in comoving coordinates as the same way as in the usual general relativity (GR) framework. Thus, the stress energy tensor has the standard form
and the conservation equation
from . Hence, one obtains the resulting Friedmann equation as
where is the nonperturbed matter density. Using Equations (20) and (23), we have
where is the current value of matter energy density. With respect to the cosmological parameters , identifies the density species, and considering only matter and extrinsic species, we write the Hubble evolution simply as
where is the Hubble parameter in terms of the redshift . The matter density parameter is denoted by . The term stands for the density parameter associated with the extrinsic curvature. The cosmological parameters and denote the present value of the matter and extrinsic contributions, respectively. The current warp (bending) of the universe denoted by has the same dimension as that is the current value of a Hubble constant in units of km·s Mpc. If vanishes with , one obtains GR limit as a background with the recovery of Einstein equations. For a flat universe, we have .
To obtain an effective cosmological model in order to make tests with real data, an effective “extrinsic fluid parameter” must be set. We define a “fluid analogy” by means of an effective equation of state (EoS) as
in which the equality happens if , where the dimensionless fluid parameter w defines an EoS related to pressure p and energy density as . Thus, one defines the dimensionless Hubble parameter that reads
which resembles an XCDM fluid [58].
5. Extrinsic Curvature as an Effective Inflaton Field
Besides Equations (26) and (27), we can explore the effective fluid approach rewriting Equation (9) in the form
where . The quantity denotes the extrinsic contribution. Mimicking Equation (21), we write as
where is the comoving four velocities. It is worth noting that the deformation tensor is independently conserved as shown in Equation (12), so is . We stress that the dynamical embedding naturally warrants the influence of the bulk over the embedded space, such as quantities with a mixture of intrinsic and extrinsic terms, as shown in Equation (11). As a consequence, is conserved unless an exotic matter-energy source is added. This result differs from a DE fluid in standard rigid brane-world models [22,23,24], where is not conserved due to the necessity of the bulk–brane energy exchange.
From the conservation of Equation (29), we obtain
In a perfect fluid analogy with Equation (22), denotes the nonperturbed “extrinsic” energy density given by
where the current “extrinsic” energy density is . Therefore, the “extrinsic” pressure is straightforwardly calculated by Equation (30) to obtain
When , the extrinsic curvature ceases, and , , and vanish, and the GR limit is reached. Alternatively, one writes the related Friedman equation in the form
5.1. The Extrinsic Inflaton Field
Since plays a role in driving the late accelerated expansion as explored in [27,31], the same energy density should have the dynamics of a scalar field potential energy density during early inflationary periods generated by the “extrinsic scalar” field . Hence, the related Lagrangian is defined as
The form written in Equation (34) shows that the field is spatially homogeneous; then it only depends on the cosmic time t. In addition, the related energy momentum of such a field is written as
From the conservation of Equation (35), i.e., , one obtains the correspondence relations
where the dot symbol denotes an ordinary derivative with respect to the cosmic time t. The forms of Equations (36) and (37) couple with the inflation dynamics given by to the background evolution. Then, the quantities and can be written as a function of the extrinsic scalar field .
In terms of fluid analogy given by Equation (26) and the direct sum of Equations (36) and (37), and using Equations (31) and (32), one obtains
Using the relation and the inflation condition , we integrate Equation (38) to obtain the potential as
where we denote the Planck mass as . We consider the initial conditions and . Putting the solution of Equation (39) in Equation (36), one obtains a potential in the form
For the sake of notation, we denote the quantity in Equation (40) as . The models of such exponential form produce a power law inflation (PLI), first introduced in Refs. [59,60,61]. For the time being, this type of potential has strong constraints imposed by Planck data [62] and is ruled out at more than 2- confidence regions. Moreover, PLI inflation requires a graceful exit in the slow-roll approximation. In such a model, the first slow-roll Hubble parameter is constant that leads to an eternal inflation [41]. Such potential was also studied in the context of M-theory [63] and RSII scenarios [64]. Due to the strong constraints on PLI, based on Equation (40), our numerical study will take an effective quintessential dimensionless potential to generalize Equation (40), such as
where denotes our PLI potential given by Equation (40). The quantity denotes a phenomenological potential that defines the so-called logamediate inflation (LMI) [65,66] in the form
in which are free dimensionless parameters. For our purposes, we need to impose on Equation (40) , , and . A similar adaptation is applied to Equation (42) with , , , , , and . Hence, the resulting potential is given by
We point out that are dimensionless parameters. Assuming that the field should roll in a direction wherein , starting at , one obtains the condition . For our purposes, the positivity of warrants a logistic equation set in the domain of real numbers. Therefore, the model turns again as being a one-parameter model from an extrinsic origin. This guarantees a reheating phase without relying on any approximation in a future work. It is worth noting that when an extrinsic curvature vanishes , then , and inflation ceases.
To study the evolution of the effective fluid parameter w and the characteristics of the potential , we adopt a dynamical system approach as in the works of Clemson and Liddle [67] and Pantazis, Nesseris, and Perivolaropoulos [68]. In the latter, they use a quintessence potential of the form
where and are free dimensionless parameters with . For comparison purposes, such potential will be also taken into account as a reference in contrast with Equation (43).
5.2. Numerical Parameter Estimation
In order to obtain the parameter estimation of our toy model by the potential in Equation (43), we define a “true” model that produces a close curve pattern with the adopted priors to the reference model in Equation (44).
As shown in Figure 1, we have a comparison between the potentials from Equation (44) (blue line) and our model defined by Equation (43) (black line). They present a similar pattern with the same peak height, and the latter model presents a narrower basis of its curve (black line). Both cases positively respond to a remote future passing through an accelerated phase.
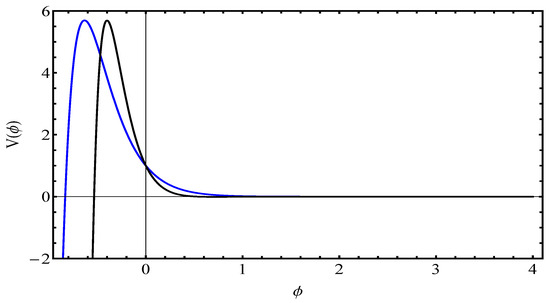
Figure 1.
Comparison between the potentials from Equation (44) (blue line) and Equation (43) (black line) that indicates a close overall pattern of such potentials. The blue line was produced by adopted parameters , as shown in Ref. [68]. The black line was produced by the adopted priors that define our “true” model with the values .
In order to use the DYNESTY [42,43] Python code for estimating Bayesian posteriors and evidences, we adopt priors for the “true model” set as , where the quantity f is defined as a mechanism to control the variance in the resulting Gaussian distributions. To estimate the values of the parameters and on how they can approximate to the “true” values, we define a prior transform as
We start generating n = 30000 synthetic random points and 8000 live points for better efficiency. On the other hand, under the circumstances we have defined, during the runs, we noted that generating larger random points does not change the results. To estimate both evidence and posteriors, DYNESTY dynamically allocates points in the runs. Each point also carries information of their covariances. It allows for creating a variable number of live points at each iteration i to realize a change in a prior volume . From Numpy 5000 random seeds and the celerite [69] library for a scalable Gaussian process, we obtained a total of 144,659 interactions in the final of the runs. We have that the prior volume and evidence are controlled when the variation , as shown in Figure 2.
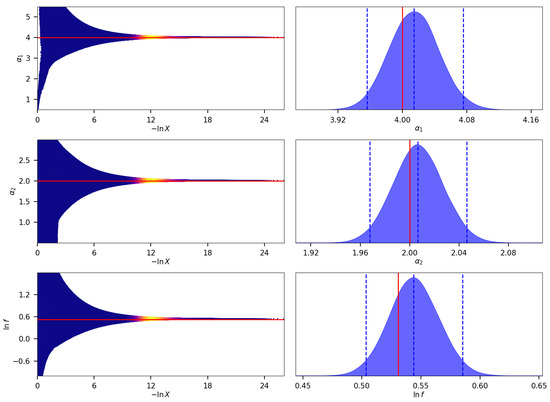
Figure 2.
In the left panels, we have the control of the prior volume of random points that shrinks exponentially over time to determine the evidence. The right panels show the posteriors (Gaussian distribution of the parameters). In both sets of panels, the red lines denote the priors (“true” values) adopted in the code.
In Figure 3, we show the posteriors in the contour plots with the values of the parameters . In the lower panels, we have confidence regions for marginalized posteriors. In the upper panels, the estimated values of the parameters and their Gaussian distributions are shown. In both panels, the vertical lines indicate the values of the “true” model, defined by the priors, and horizontal lines indicate the estimated values for the model parameters.
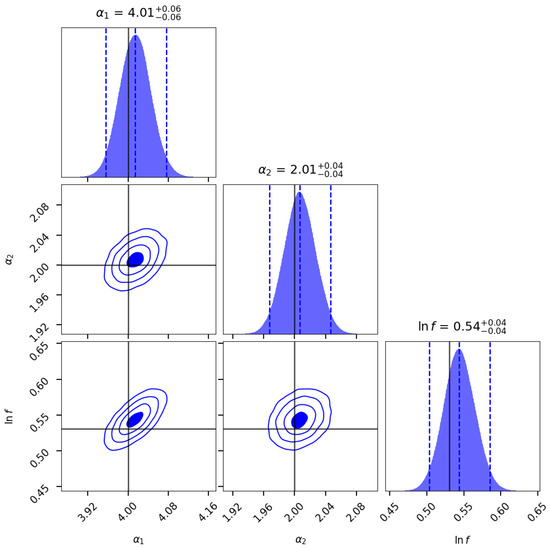
Figure 3.
Contour plot for the marginalized posteriors for parameters at , , , and confidence levels. Vertical dashed lines mark the region, while horizontal lines indicate the mean values of the marginalized parameters.
Using the logarithmic Jeffrey’s scale [70] to input a qualitative classification of the evidence, our results indicate barely worth-mentioning evidence against the model as compared with the “true” model with roughly for the Bayes factor that is well accommodated in the range . As traditionally known, Jeffrey’s scale classifies it as weak evidence against the model with the interval . The range indicates strong evidence disfavoring the competing model. Finally, very strong evidence against the competing model is achieved at .
5.3. Dynamical System and Comparison with the Potentials
Following Refs. [67,68], one constructs a dynamical system with the coordinates
where the prime sign indicates an ordinary derivative with respect to the scalar field . The variables can be written in the form of an autonomous system as
The quantity N is the number of e-foldings of inflation that is commonly defined as the logarithm of the scale factor such as . The term denotes the number of the e-folds set by the current time. The quantity is defined in terms of the related potential as
in which the double prime symbol denotes an ordinary second derivative with respect to the scalar field . From Equation (36), and using Equations (48) and (49), one obtains
for a locally universe flat space curvature. Defining a corresponding effective equation of the state , one writes
By direct calculations of Equations (48)–(50), with the initial value of , we obtain the logistic equation
In Figure 4, we show the resulting curves from the models of Equation (44) (black lines) and our model defined by Equation (43) (red lines), showing the evolution for the dynamical variable running from 0.1 to 1, denoted by the outer and inner curves, respectively. The curves were obtained, setting the values of and the thawing initial conditions to both models as . As a result, the evolution of the curves of our model begins earlier than the reference model in Equation (44) shown by the red lines. In both cases, the semicircles reach the x-axis at ∼0.82. The curves close to this value are compatible with the models of late cosmic acceleration of the universe. The origin represents an initial point in an early matter domination universe.
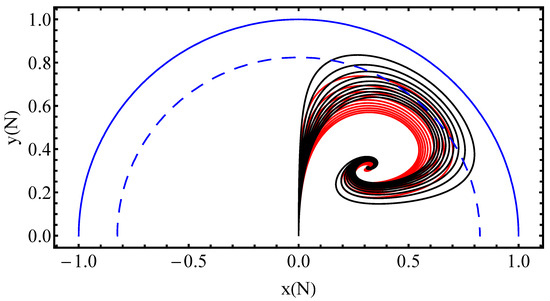
Figure 4.
Comparison between the potentials from Equation (44) (black lines) and Equation (43) (red lines) that shows the evolution of the related autonomous systems. The outer continuous blue line and the dashed blue line semicircles represent the x-axis with and , respectively.
Henceforth, we use the estimated values of the parameters of out model to evaluate how a resulting EoS of an effective evolves. For this matter, we adapt the publicly code provided in [68]. The set of equations of Equations (48)–(50) has the initial conditions for thawing models. For freezing models, one defines . We use CPL parameterization as a function of the redshift written as
where are parameters used to evaluate how tends to depart away or converge to CDM values. In conjunction with CPL, we use BA parameterization, which is given by
We adopt the maximum value for the redshift as and the maximum number of iterations i as .
In Figure 5, we have comparisons between CPL and BA parameterizations of the effective model in Equation (43) (with the values of Figure 5). Thus, we have a test adopting generic thawing and freezing models by means of Equations (48)–(50), and we obtain similar results as in Ref. [68]. The model prefers a thawing behavior from CPL (blue line) and BA (red line) parameterizations that are closer to numerical points (dotted line). When plotting the freezing pattern for the model, we obtained curves out of range with a large difference from the numerical curve, and they were omitted.
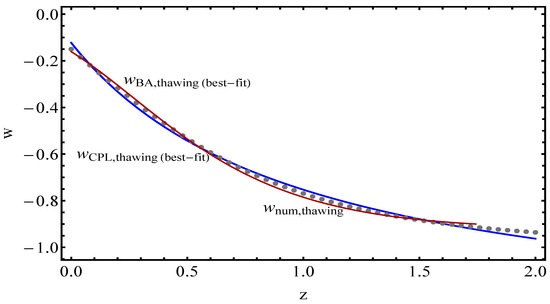
Figure 5.
Behavior of numerical curves (dotted line) produced from the related autonomous system of the model preferring a thawing pattern of CPL (blue line) and BA (red line) parameterizations.
6. Remarks
We investigate the extrinsic curvature as an inflaton scalar field. The starting point lies in the correlation of the model parameter that is constrained for both accelerated regimes. For instance, the dark energy accelerated regime relies on ; then we expect for inflationary regimes in accordance with Figure 5. We also present a fluid approach in order to provide a better understanding of the related dynamics with a relation between the model parameter and the fluid parameter w, as shown in Equation (26). Our intent is to construct the basis of a geometrical model that fully relies on gravitational interactions. In this paper, we focus our attention on the inflationary period obtaining a logarithm inflaton field that generates an exponential potential in Equation (40). This form of potential creates a PLI mechanism that has strong constraints imposed by Planck data [62]. Then, we have proposed an effective form for a new potential defined in Equation (43) to generalize Equation (40). We have numerically restrained our model parameters by means of a Bayesian analysis obtained from random points using the DYNESTY code. Establishing a quintessential potential from a reference model of Equation (44) used in Ref. [68], we have obtained the related autonomous system of equations for forecasting models compatible with the universe evolution. Moreover, we have shown a comparison with CPL and BA parameterizations of our model that prefers a thawing cosmic scenario.
In this paper, we have considered all the cosmic components to be immutable. The numerical analysis gave us an optimistic scenario for further studies on the unification of inflation with late cosmic acceleration. The stability of the present model in this numerical evaluation allows us to use more realistic contexts to produce red spectra with a scalar spectral tilt and a small tensor-to-scalar ratio. As a subject of a future work, we will consider the full perturbation equations of the model in a scenario with a matter-sourced anisotropic stress and a series of latest astronomical data from cosmic microwave background radiation (CMB) experiments, such as Planck collaboration.
Author Contributions
Conceptualization, A.J.S.C.; formal analysis, L.A.C.; methodology, A.J.S.C. and L.A.C.; software, A.J.S.C.; supervision, L.A.C.; writing—original draft, A.J.S.C.; writing—review and editing, A.J.S.C. and L.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
A.J.S.C. acknowledges Conselho Nacional de Desenvolvimento Científico e Tecnologico (CNPq, National Council for Scientific and Technological Development) for the partial financial support for this work (Grant No. 305881/2022-1) and Fundação da Universidade Federal do Paraná (FUNPAR, Paraná Federal University Foundation) through public notice 04/2023-Pesquisa/PRPPG/UFPR for the partial financial support (Process No. 23075.019406/2023-92).
Data Availability Statement
All data/codes used in this work are publicly available, and correctly cited in the references.
Acknowledgments
The authors thank the referees for their useful comments and criticisms, which substantially improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Spectrum of relict gravitational radiation and the early state of the universe. JETP Lett. 1979, 30, 682–685. [Google Scholar]
- Mukhanov, V.F.; Chibisov, G.V. Quantum Fluctuations and a Nonsingular Universe. JETP Lett. 1981, 33, 532–535. [Google Scholar]
- Linde, A.D. Chaotic Inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Hawking, S.W. The Development of Irregularities in a Single Bubble Inflationary Universe. Phys. Lett. B 1982, 115, 295. [Google Scholar] [CrossRef]
- Hawking, S.W.; Moss, I.G. Fluctuations in the Inflationary Universe. Nucl. Phys. B 1983, 224, 180. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of Phase Transition in the New Inflationary Universe Scenario and Generation of Perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Guth, A.H.; Pi, S.Y. Fluctuations in the New Inflationary Universe. Phys. Rev. Lett. 1982, 49, 1110–1113. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Steinhardt, P.J.; Turner, M.S. Spontaneous Creation of Almost Scale - Free Density Perturbations in an Inflationary Universe. Phys. Rev. D 1983, 28, 679. [Google Scholar] [CrossRef]
- Giovannini, M. Spikes in the relic graviton background from quintessential inflation. Class. Quant. Grav. 1999, 16, 2905–2913. [Google Scholar] [CrossRef]
- Giovannini, M. Production and detection of relic gravitons in quintessential inflationary models. Phys. Rev. D 1999, 60, 123511. [Google Scholar] [CrossRef]
- Giovannini, M. Low scale quintessential inflation. Phys. Rev. D 2003, 67, 123512. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Sebastiani, L.; Vagnozzi, S. Inflation in f(R,ϕ) -theories and mimetic gravity scenario. Eur. Phys. J. C 2015, 75, 444. [Google Scholar] [CrossRef]
- Salvio, A. Inflationary Perturbations in No-Scale Theories. Eur. Phys. J. C 2017, 77, 267. [Google Scholar] [CrossRef]
- Salvio, A. Quasi-Conformal Models and the Early Universe. Eur. Phys. J. C 2019, 79, 750. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Viability of the intermediate inflation scenario with F(T) gravity. Phys. Rev. D 2017, 95, 084023. [Google Scholar] [CrossRef]
- Agarwal, A.; Myrzakulov, R.; Sami, M.; Singh, N.K. Quintessential inflation in a thawing realization. Phys. Lett. B 2017, 770, 200–208. [Google Scholar] [CrossRef]
- Keskin, A.I. Viable super inflation scenario from F(T) modified teleparallel gravity. Eur. Phys. J. C 2018, 78, 705. [Google Scholar] [CrossRef]
- Castello, S.; Ilić, S.; Kunz, M. Updated dark energy view of inflation. Phys. Rev. D 2021, 104, 023522. [Google Scholar] [CrossRef]
- Arkani–Hamed, N.; Dimopoulos, S.; Dvali, G. The hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An Alternative to Compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Dvali, G.; Gabadadze, G.; Porrati, M. 4D gravity on a brane in 5D Minkowski space. Phys. Lett. B 2000, 485, 208–214. [Google Scholar] [CrossRef]
- Battye, R.A.; Carter, B. Generic junction conditions in brane-world scenarios. Phys. Lett. B 2001, 509, 331–336. [Google Scholar] [CrossRef]
- Maia, M.; Monte, E.M. Geometry of brane-worlds. Phys. Lett. A 2002, 297, 9–19. [Google Scholar] [CrossRef]
- Maia, M.D.; Monte, E.M.; Maia, J.M.F.; Alcaniz, J.S. On the geometry of dark energy. Class. Quant. Grav. 2005, 22, 1623. [Google Scholar] [CrossRef]
- Maia, M.D.; Silva, N.; Fernandes, M.C.B. Brane-world quantum gravity. J. High Energy Phys. 2007, 2007, 47. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Sepangi, H. Anisotropic brane gravity with a confining potential. Phys. Lett. B 2007, 649, 1–11. [Google Scholar] [CrossRef]
- Jalalzadeh, S.; Mehrnia, M.; Sepangi, H.R. Classical tests in brane gravity. Class. Quant. Grav. 2009, 26, 155007. [Google Scholar] [CrossRef][Green Version]
- Maia, M.D.; Capistrano, A.J.S.; Alcaniz, J.S.; Monte, E.M. The Deformable Universe. Gen. Rel. Grav. 2011, 43, 2685–2700. [Google Scholar] [CrossRef][Green Version]
- Ranjbar, A.; Sepangi, H.R.; Shahidi, S. Asymptotically Lifshitz Brane-World Black Holes. Ann. Phys. 2012, 327, 3170. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Cabral, L.A. Geometrical aspects on the dark matter problem. Ann. Phys. 2014, 348, 64–83. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Cabral, L.A. Implications on the cosmic coincidence by a dynamical extrinsic curvature. Class. Quant. Grav. 2016, 33, 245006. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S. Constraints on cosmokinetics of smooth deformations. Mon. Not. Roy. Astron. Soc. 2015, 448, 1232–1239. [Google Scholar] [CrossRef][Green Version]
- Capistrano, A.J.S.; Gutiérrez-Piñeres, A.C.; Ulhoa, S.C.; Amorim, R.G. On classical thermal stability of black holes with a dynamical extrinsic curvature. Ann. Phys. 2017, 380, 106–120. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Evolution of Density Parameters on a Smooth Embedded Universe. Annalen der Physik. 2018, 530, 1700232. [Google Scholar] [CrossRef]
- Capistrano, A.J.S. Lukewarm black holes in the Nash-Greene framework. Phys. Rev. D 2019, 100, 064049. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Seidel, P.T.Z.; Duarte, H.R. Subhorizon linear Nash–Greene perturbations with constraints on H(z) and the deceleration parameter q(z). Phys. Dark Univ. 2021, 31, 100760. [Google Scholar] [CrossRef]
- Capistrano, A.J.S.; Cabral, L.A.; Marão, J.A.P.F.; Coimbra-Araújo, C.H. Linear Nash-Greene fluctuations on the evolution of S8 and H0 tensions. Eur. Phys. J. 2022, 82, 1434–6052. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5-6, 75–235. [Google Scholar] [CrossRef]
- Higson, E.; Handley, W.; Hobson, M.; Lasenby, A. Dynamic nested sampling: An improved algorithm for parameter estimation and evidence calculation. Stat. Comput. 2019, 29, 891–913. [Google Scholar] [CrossRef]
- Speagle, J.S. dynesty: A dynamic nested sampling package for estimating Bayesian posteriors and evidences. Mon. Not. Roy. Astron. Soc. 2020, 493, 3132–3158. [Google Scholar] [CrossRef]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 2001, 10, 213–224. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Barboza, E.M., Jr.; Alcaniz, J. Probing the time dependence of dark energy. J. Cosmol. Astropart. Phys. 2012, 2012, 42. [Google Scholar] [CrossRef]
- Gupta, G.; Rangarajan, R.; Sen, A.A. Thawing quintessence from the inflationary epoch to today. Phys. Rev. D 2015, 92, 123003. [Google Scholar] [CrossRef]
- Chiba, T. Slow-roll thawing quintessence. Phys. Rev. D 2009, 79, 083517. [Google Scholar] [CrossRef]
- Scherrer, R.J.; Sen, A.A. Thawing quintessence with a nearly flat potential. Phys. Rev. D 2008, 77, 083515. [Google Scholar] [CrossRef]
- Sahlen, M.; Liddle, A.R.; Parkinson, D. Quintessence reconstructed: New constraints and tracker viability. Phys. Rev. D 2007, 75, 023502. [Google Scholar] [CrossRef]
- Schimd, C.; Tereno, I.; Uzan, J.P.; Mellier, Y.; van Waerbeke, L.; Semboloni, E.; Hoekstra, H.; Fu, L.; Riazuelo, A. Tracking quintessence by cosmic shear - constraints from virmos-descart and cfhtls and future prospects. Astron. Astrophys. 2007, 463, 405–421. [Google Scholar] [CrossRef]
- Chiba, T. w and w′ of scalar field models of dark energy. Phys. Rev. D 2006, 73, 063501. [Google Scholar] [CrossRef]
- Scherrer, R.J. Dark energy models in the w-w’ plane. Phys. Rev. D 2006, 73, 043502. [Google Scholar] [CrossRef]
- Eisenhart, L.P. On Riemannian Geometry; Dover Publications: New York, 2005. [Google Scholar]
- Nash, J. C1 Isometric Imbeddings. Ann. Math. 1954, 60, 383–396. [Google Scholar] [CrossRef]
- Nash, J. The Imbedding Problem for Riemannian Manifolds. Ann. Math. 1956, 63, 20–63. [Google Scholar] [CrossRef]
- Greene, R.E. Isometric embeddings of Riemannian and pseudo-Riemannian manifolds. Memoirs of the American Mathematical Society; American Mathematical Society: Providence, RI, USA, 1970; Volume 63. [Google Scholar] [CrossRef]
- Turner, M.S.; White, M.J. CDM models with a smooth component. Phys. Rev. D 1997, 56, R4439. [Google Scholar] [CrossRef]
- Abbott, L.F.; Wise, M.B. Constraints on Generalized Inflationary Cosmologies. Nucl. Phys. B 1984, 244, 541–548. [Google Scholar] [CrossRef]
- Lucchin, F.; Matarrese, S. Power Law Inflation. Phys. Rev. D 1985, 32, 1316. [Google Scholar] [CrossRef]
- Davies, P.C.W.; Sahni, V. Quantum gravitational effects near cosmic strings. Class. Quant. Grav. 1988, 5, 1. [Google Scholar] [CrossRef]
- Tristram, M.; Banday, A.J.; Górski, K.M.; Keskitalo, R.; Lawrence, C.R.; Andersen, K.J.; Barreiro, R.B.; Borrill, J.; Eriksen, H.K.; Fernandez-Cobos, R.; et al. Planck constraints on the tensor-to-scalar ratio. Astron. Astrophys. 2021, 647, A128. [Google Scholar] [CrossRef]
- Becker, K.; Becker, M.; Krause, A. M-theory inflation from multi M5-brane dynamics. Nucl. Phys. B 2005, 715, 349–371. [Google Scholar] [CrossRef]
- Bennai, M.; Chakir, H.; Sakhi, Z. On Inflation Potentials in Randall-Sundrum Braneworld Model. Eur. J. Phys. 2006, 9, 84–93. [Google Scholar]
- Parsons, P.; Barrow, J.D. Generalized scalar field potentials and inflation. Phys. Rev. D 1995, 51, 6757–6763. [Google Scholar] [CrossRef] [PubMed]
- Barrow, J.D.; Nunes, N.J. Dynamics of Logamediate Inflation. Phys. Rev. D 2007, 76, 043501. [Google Scholar] [CrossRef]
- Clemson, T.G.; Liddle, A.R. Observational constraints on thawing quintessence models. Mon. Not. Roy. Astron. Soc. 2009, 395, 1585–1590. [Google Scholar] [CrossRef]
- Pantazis, G.; Nesseris, S.; Perivolaropoulos, L. Comparison of thawing and freezing dark energy parametrizations. Phys. Rev. D 2016, 93, 103503. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Agol, E.; Ambikasaran, S.; Angus, R. Fast and Scalable Gaussian Process Modeling with Applications to Astronomical Time Series. Astron. J. 2017, 154, 220. [Google Scholar] [CrossRef]
- Jeffreys, H. Theory of Probability, 3rd ed.; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).