1. Introduction
The theory of general relativity has already been confirmed by the large number of observational tests such as gravitational waves by LIGO-Virgo [
1], the
black hole shadow by Event Horizon Telescope (EHT) [
2,
3,
4,
5,
6], and the emitted electromagnetic spectrum from an accretion disk [
7]. In the strong gravitational region, the dynamics of the accretion disk close to the black hole uncover the properties of the black hole and electromagnetic spectrum. It is certain that this region is influenced by the space–time curvature, which depends on the black hole spin
a and the GB-coupling constant
in General Relativity (GR) and 4-D Einstein–Gauss–Bonnet (EGB) gravity [
8].
The wind accretion onto the black hole produces energetic outflows, which can be used to define the black hole’s spin, mass, and shadow. The magnetically driven outflow onto the black hole is called the Bondi–Hoyle–Lyttleton (BHL) accretion, which is purely hydrodynamical [
9,
10]. The out-flowing gas causes the formation of a shock cone due to the strong gravity in the vicinity of the black hole. For decades, the BHL accretion was studied using Newtonian and general relativistic hydrodynamics. Newtonian hydrodynamics were used to define the structure of the disk due to the axisymmetric accretion flow for adiabatic gas [
11]. The 2-D and 3-D numerical simulations of the accretion disk had accomplished revealing the dynamical structure of the disk, radiation mechanism, and the properties of the compact objects [
12,
13,
14,
15]. Non-magnetized or magnetized relativistic BHL accretions around the non-rotating and rotating black holes were simulated using either axial or spherical symmetries [
16,
17,
18,
19,
20,
21,
22].
The modified theory of gravity received lots of attention when considering the solution of accretion disks. Accretion disk properties and their dynamical evolutions were studied in different modified gravity models, such as the innermost circular orbits of spinning and massive particles [
23,
24],
gravity [
25,
26], the Einstein–Maxwell dilation theory [
27,
28], scalar–tensor–vector gravity [
29], Einstein-scalar–Gauss–Bonnet gravity [
30], 4-D
gravity for a non-rotating black hole [
31], the effect of
coupling constant on the collapsing phenomena and its end state [
32], the observational constraint of the
coupling constant
[
33,
34], and the rotating black hole [
35]. Ref. Heydari-Fard et al. [
35] studied the thin accretion disk around a rapidly rotating black hole. It is believed that the black hole would rotate with a high-rotation velocity due to the accretion effect.
Studying the dynamical evolution of the accretion disk around non-rotating and rotating black holes using different gravities would allow us to extract detailed information about the emission spectrum and temperature distribution of the accretion disk, as well as central objects, such as the black hole’s shadow and physical properties. Many tests of general relativity in the strong gravitational field regime have been performed using pulsars [
36]. The analytic solutions of the thin accretion disk around the 4-D EGB gravity were studied in Liu et al. [
31], Heydari-Fard et al. [
35], Gyulchev et al. [
37], Guo et al. [
38], Malafarina et al. [
39] and referenced therein. They defined the electromagnetic properties of the disk and investigated the effects of the GB-coupling constant
and black hole rotation parameter
a on the properties of the accretion disk, the energy flux, and the electromagnetic spectrum. They also compared their results with the Kerr black hole solution. According to their results, the disk around the 4-D EGB black hole, for the positive value of
, is more luminous and hotter than the one in General Relativity GR [
35]. The motion of the charged test particle and charged scalar field in a 4-D EGB black hole are studied in Yang et al. [
40]. The effect of the GB-coupling constant
on the validity of the weak censorship conjecture was investigated. The general relativity and well-motivated alternative relativity theories were used to perform the shadow of SgrA* [
41]. The numerical investigation of a BHL accretion in the 4-D EGB was extensively studied in the vicinities of non-rotating [
42] and rotating black holes [
43]. They discussed the effect of the GB-coupling constant
on the shock-cone structure created during the formation of the accretion disk.
The numerical investigation of the Bondi–Hoyle accretion onto a black hole was studied in general relativity by Dönmez et al. [
16]. They explored the shock-cone structure and the flip-flop instability in the strong gravitational regime. The physical properties of the shock cone around the rotating black hole in EGB gravity was extensively studied by Donmez [
43]. They modeled the Bondi–Hoyle accretion onto the black hole to explore the shock-cone dynamics for various values of the Gauss–Bonnet coupling constant. Apart from the above references, the aim of this work is, for the first time, to model accretion disk dynamics in the presence of the 4-D EGB and Kerr strong gravities around a fast-rotating black hole and to compare the shock-cone properties from these two gravities for various values of asymptotic velocity
. We will not only extract the effect of asymptotic velocity on to the shock cone in both gravities but also on the Gauss–Bonnet coupling constant in EGB gravity. The matter will be accreted with a mechanism called a BHL accretion. A black hole traveling through a uniform medium causes the BHL accretion. The accreted matter, which moves towards the black hole from upstream side of computational domain, forms a steady-state disk around the black hole. Since we are interested in the dynamics within the accretion disk, the shock cone, and the accretion efficiency by using the different gravities, we explicitly study the effect of the GB-coupling constant
and the black hole rotation parameter
a on these dynamics.
In this paper, we model the non-magnetized BHL accretion onto the spinning black holes in 4-D EGB and Kerr strong gravity regions to have a direct comparison between the two gravities. In
Section 2, brief descriptions of 4-D EGB and Kerr rotating black hole space–time metrics are presented along with the general relativistic hydrodynamical equations. The initial and boundary conditions used in the numerical simulations are given in
Section 3 in order to inject the gas from the outer boundary of the computational domain. In
Section 4, we present the results of our numerical simulations and discuss the consequences of two different gravities on the disk and shock-cone dynamics. In
Section 5, the astrophysical motivation of the numerical results is briefly discussed. The discussion and summary are presented in
Section 6. The geometrized unit is used throughout the paper,
.
2. Rotating Black Hole Metric and General Relativistic Equations
The Bondi–Hoyle accretion of the perfect fluid in the case of rotating-Kerr and EGB black holes is studied by solving General Relativistic Hydrodynamical (GRH) equations in the curved background. The perfect fluid-stress–energy–momentum tensor is
where
h,
p,
,
, and
are the specific enthalpy, the fluid pressure, the rest-mass density, the 4-velocity of the fluid, and the metric of the curved space–time, respectively. The indexes
a,
b, and
c go from 0 to 3. Two different coordinates are used to compare the dynamical evolution of the accretion disk around the rotating black hole. First, the Kerr black hole in the Boyer–Lindquist coordinate is [
16]
where
,
, and
.
M is the mass of the black hole. The lapse function and shift vector of the Kerr metric are
and
.
Second, the rotating black hole metric in 4-D EGB gravity is [
43]
where
.
a and
are the spin parameter and Gauss–Bonnet coupling constant, respectively. The horizons of the black holes were obtained by solving
and
. The lapse function
and the shift vectors of the EGB metric are
and
, respectively.
In order to solve GRH equation numerically, we should write them in a conserved form [
44]:
where
U,
,
, and
S are the vectors of the conserved variables, of the fluxes along the
r and
directions and sources, respectively. The vectors of the conserved variables are written in terms of the primitive variables,
where
,
,
, and
are the Lorentz factor, enthalpy, internal energy, and three-velocity of the fluid, respectively. The ideal gas equation of state is adopted to define the pressure of the fluid, and the three-metric
and its determinant
are computed using the four-metric of the rotating black holes. Latin indices
i and
j go from 1 to 3. The flux and the source can be computed for any metric using the following equations
and
where
is the Christoffel symbol. The GRH equations, along with all the variables used, are explained explicitly in Dönmez [
44].
3. Initial and Boundary Conditions
To study the Bondi–Hoyle accretion onto the rotating Gauss–Bonnet black hole and compare it with the Kerr black hole, GRH equations are solved on the equatorial plane using the code explained in Dönmez [
18,
44], Donmez [
45]. The pressure of the accreted matter is handled using the standard
law equation of state for a perfect fluid,
with
. We adjusted the initial density and pressure profiles to ensure that the speed of sound equals to
in the upstream region of the computational domain. After setting the density to be constant (i.e.,
), the pressure is computed from the perfect-fluid equation of state, we then performed a numerical simulation of the equatorial plane using different values of asymptotic velocities. The initial velocities of the falling matter are given in terms of an asymptotic velocity
at the upstream region, and they are defined by the following equations [
16,
18,
42]
Using various values of
allows us to investigate different regimes around the black hole and therefore consider subsonic and supersonic accretion. The matter injected in the upstream region falls into an empty region with
,
, and
in the beginning of the simulation, (i.e.,
). The descriptions of the initial models around the rotating black holes, Kerr and Gauss–Bonnet, with a spin
are reported in
Table 1.
The uniformly spaced zones are used in radial and angular directions with and . The inner and outer boundaries of the computational domain in the radial direction are located at and , respectively, and and in the angular direction. It is confirmed that the qualitative results of the numerical solutions (i.e., the appearance of Quasi-Periodic Oscillations (QPOs) and instabilities, the shock location, and the behavior of the accretion rates) are not sensitive to the grid resolution.
The corrected treatment of the boundary is important to avoid unphysical solutions in the numerical simulations. At the inner radial boundary, we implement an outflow boundary condition to let the gas fall into a black hole by a simple zeroth-order extrapolation. On the other hand, we have to distinguish the downstream
and the upstream regions
. While we adopt the outflow boundary condition in the downstream region, the gas is injected continuously with the initial velocities given in Equation (
8) in the upstream region. The periodic boundary condition is used along the
-direction.
4. The Numerical Simulation of the Accretion onto 4-D EGB Rotating and Kerr Black Holes
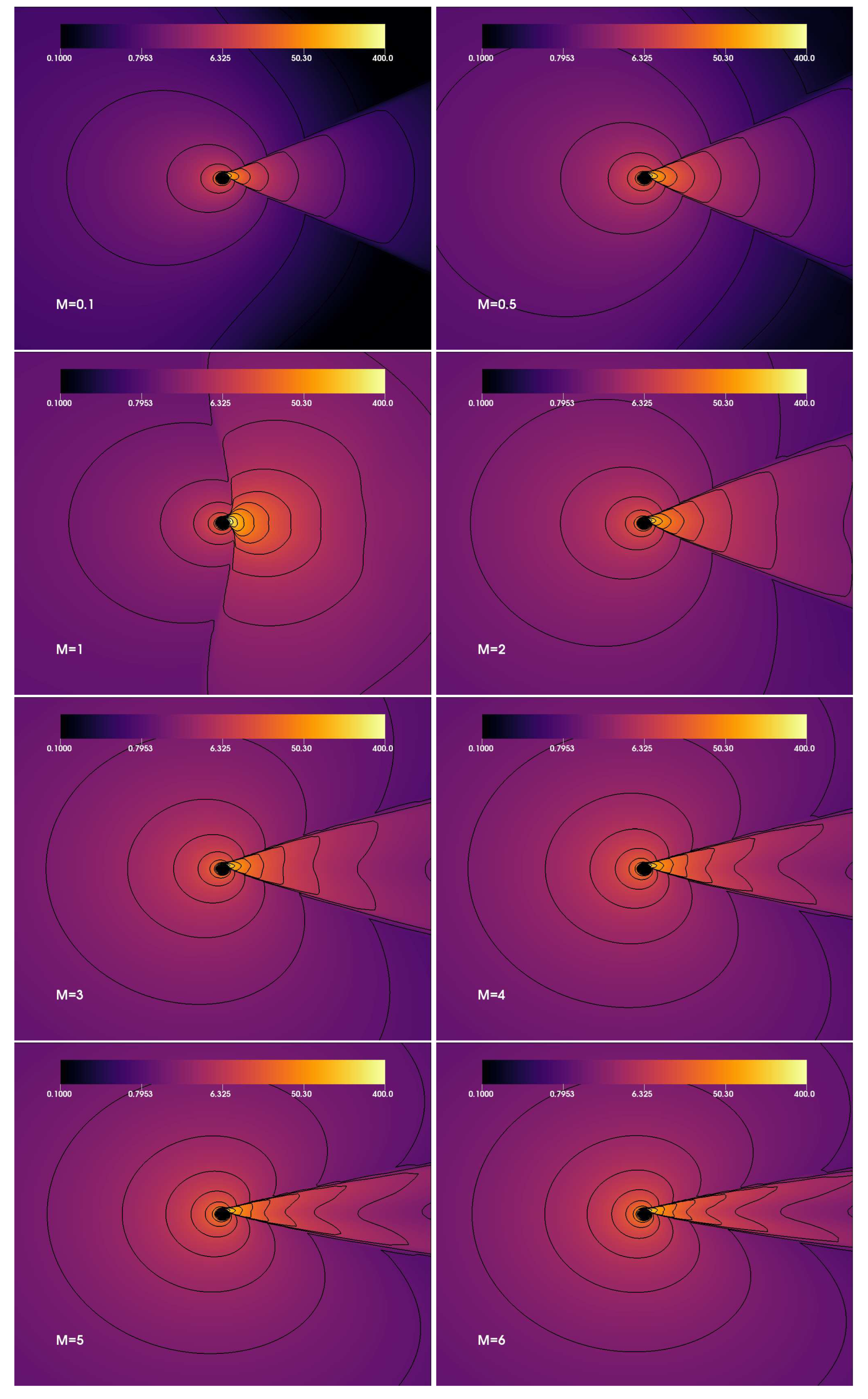
To explain the effect of the asymptotic Mach number
on the dynamics of BHL accretion, we describe the morphology of the disk using the initial model with
for the GB-coupling constant in
Table 1. For an adjusted value of the speed of sound
, there is a critical value of the asymptotic Mach number which equals to unity, above and below which shock cones form on the downstream side of the computational domain when the matter is accreted on the upstream side as seen in
Figure 1. We plot the logarithm of the rest-mass density and linearly spaced isocontours on the equatorial plane. The disk is initially filled with matter falling from the upstream side of the region. It is indicated in
Figure 1 that, for
, the shock opening angle is becoming wider, and the shock cone is forced to convert into a bow shock due to ram pressure, gas pressure and strong gravity. This model indicates that the asymptotic Mach number plays a critical role in the creation of a shock cone and its opening angle, and it prevents the shock cone from being created in the upstream region of the computational domain. Due to the strong gravity, the shock cone becomes attached to the black hole, which produces an accretion rate that is higher in the strong gravitational region [
46,
47]. As shown in
Figure 1, the higher the asymptotic Mach number, the smaller the shock opening angle. The cone with a standing shock converts kinetic energy into thermal energy by falling material toward the rapidly rotating black hole in 4-D EGB gravity. In addition, the shape of a shock cone very close to the black hole strongly depends on the black hole’s spin. As seen in
Figure 1, due to the rapidly rotating black hole with
, the induced frame dragging produces a warping in space–time as well as the shock cone connected to the black hole horizon.
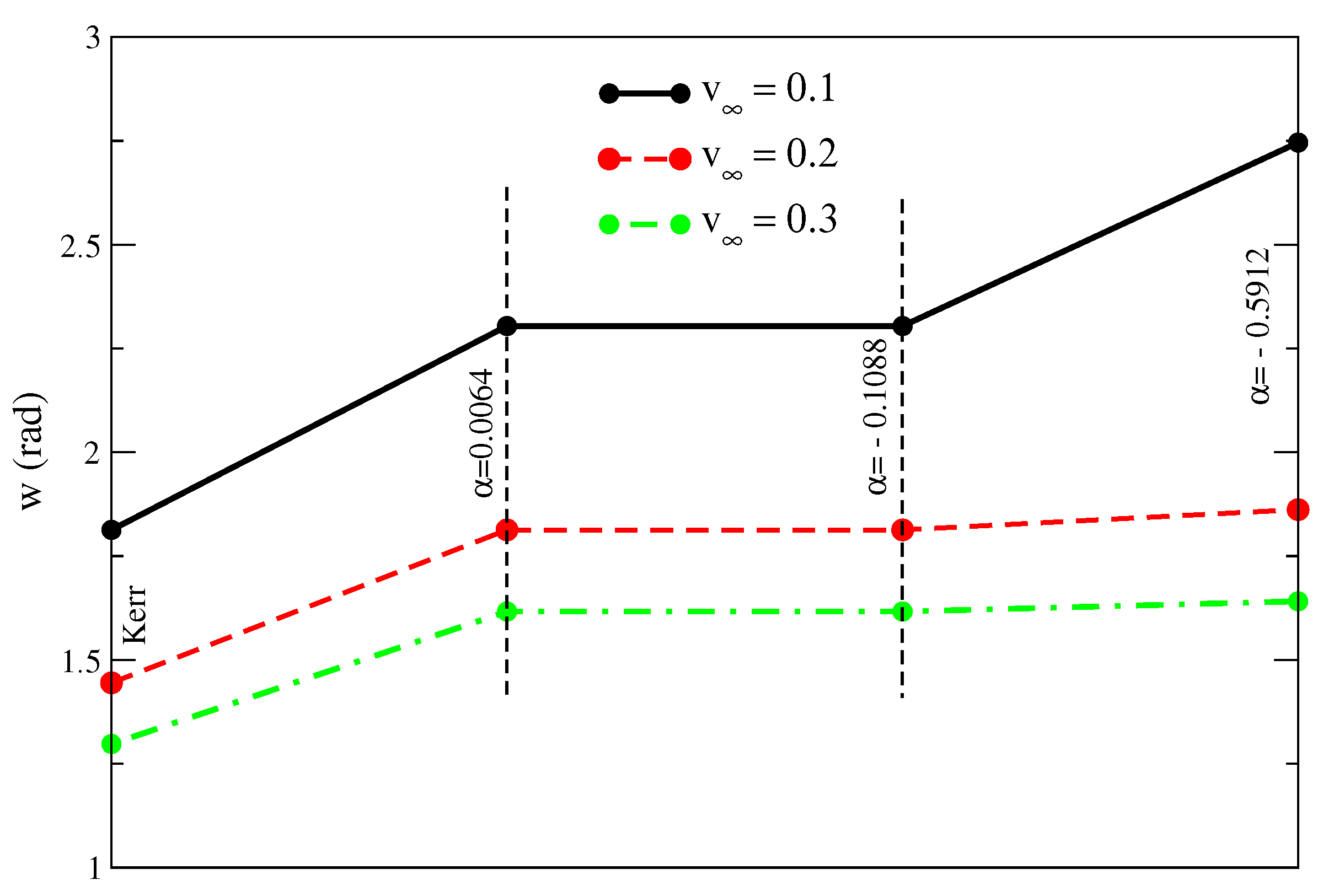
In
Figure 2, the behavior of the shock-cone width with Kerr and 4-D EGB gravities for different values of asymptotic velocities
and the comparison of the results from these two gravities are given around the rapidly rotating black hole with
. The 4-D EGB gravity has a big influence on the physical properties of the matter around a black hole (also confirmed by Liu et al. [
31]). The effect of the asymptotic velocity on the cone width is seen for the BHL accretion around the 4-D EGB gravity as well as the Kerr gravity. Although the comparison of the shock opening angle for different values of
shows the same trend in all models, the shock opening angle is smaller around the Kerr black hole. For the 4-D EGB gravity, the shock opening angle for any value of the GB-coupling constant
(positive or negative) is greater than the case in the Kerr black hole, and, as the magnitude of
in negative direction increases, the deviation from the Kerr geometry also increases. As observed in
Figure 1, the shock-cone opening angle decreases with the increasing asymptotic velocity or Mach number, as seen in
Figure 2.
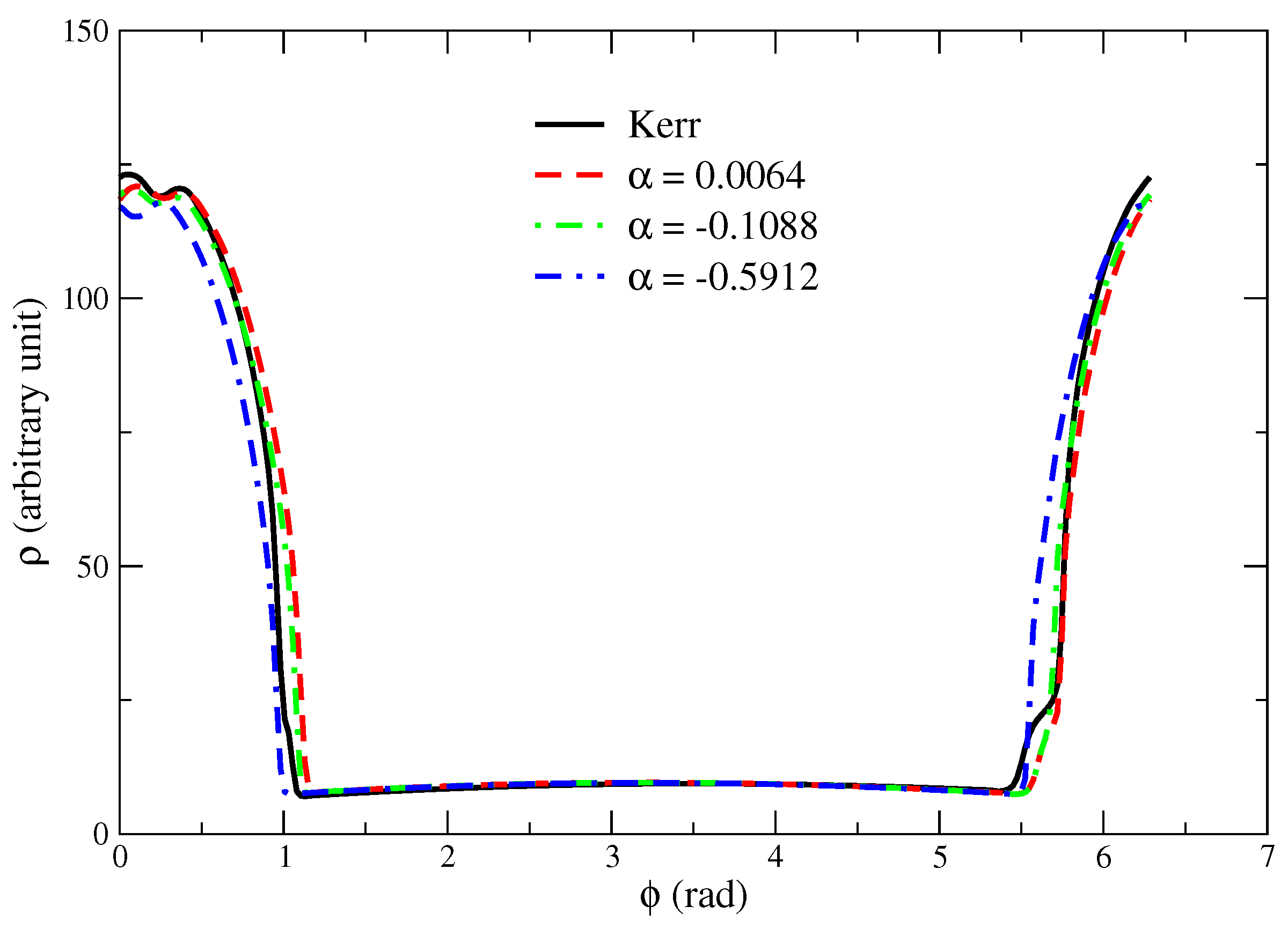
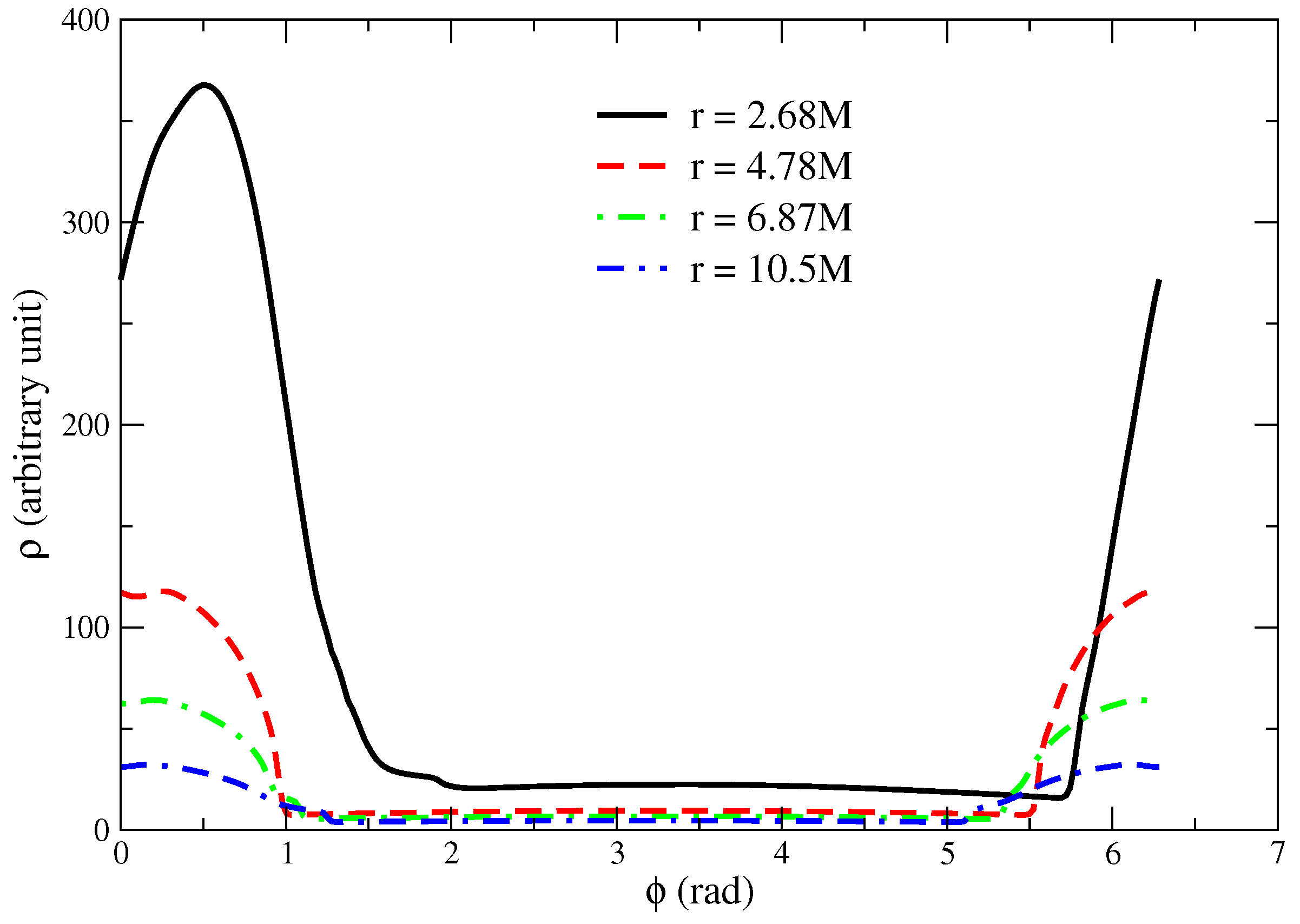
To reveal the dynamical properties of the disk structure and the shock-cone location, in
Figure 3, we show the rest-mass density plot at a fixed radial distance
M for asymptotic velocity
at the final time of the evolution
M. As seen in
Figure 4, the shock cone under these conditions formed and reached the steady-state around
M. As mentioned earlier, the critical value of the asymptotic velocity (Mach number) is
. The critical value of the Mach number causes the creation of a strongly oscillating accretion disk in our models. The effect of the GB-coupling constant
on the shock-cone density at the final time varies slightly, as seen in
Figure 3. The Kerr black hole case is also plotted on the same figure to compare with the corresponding results and find that the rest-mass density is slightly higher in the Kerr case. On the other hand, the angular position of the shock location is shifted for different values of
. The inspection of different curves displayed in
Figure 3 shows slight differences in the flow morphology.
To complete the overall picture of the shock-cone structure and the morphology of the accretion disk,
Figure 5 shows the one-dimensional profile of the rest-mass density at the final time of simulation at different locations along the radial shells for asymptotic velocity
and the GB-coupling constant
. The strong shock waves are created at the border of the shock cone. The angular location of the shock cone changes slightly and shifts with the radial distance
r. As expected, the rest-mass density gradually decreases with an increasing
r. The created shock cone would contribute to the radiation properties of the disk–black hole system. The shock cone is a very important physical mechanism that converts gravitational energy into the radiation energy and tapes and excites the oscillation modes. The shock cone could also be used to explain the erratic spin behavior variety found in different X-ray observations [
48,
49].
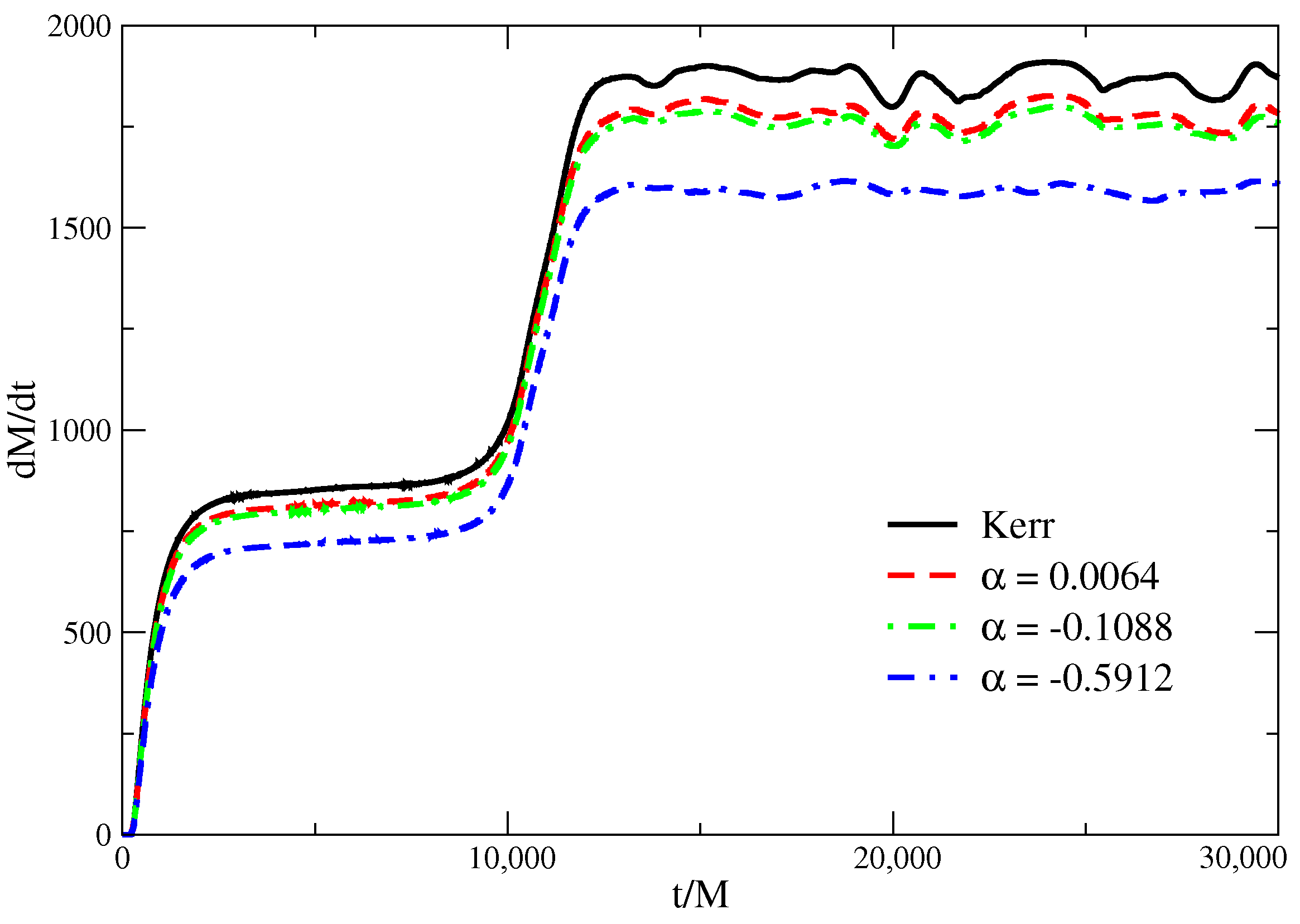
As seen in the above discussion, the shock cone is just the one of the consequences of the BHL accretion around the black hole in different gravities. The steady-state shock cone forms due to the effect of gravitation and pressure forces on the equatorial plane. Computing the mass-accretion rate gives us a more complete picture about the dynamics and instability of the shock cone around the rotating black hole. In
Figure 4, the time evolution of the mass-accretion rate for all the models for asymptotic velocity
is shown. The different colors and line styles are used to separate the different models. The accretion rate is calculated using the following expression
Although accretion would lead to an increase in the mass of the black hole during the evolution, it is assumed that the black hole mass is constant during the whole simulation. As seen in
Figure 4, the shock cone reaches steady-state around
M in all models, and the accretion rate is higher in Kerr gravity than EGB gravity for any value of the GB-coupling constant. After the cone reaches steady-state, it oscillates around a certain value. The oscillation amplitude is slightly diminished in the case of
for a fixed value of the black hole rotation parameter
. A greater oscillation amplitude inside the shock cone would lead to a varying X-ray in observed astrophysical phenomena.
In order to extract more information about the possibility of the oscillation of the shock cone depending on the asymptotic velocity and GB-coupling constant, we plot
Figure 6. Once the shock cone reaches the steady-state, we do not observe any oscillation for all values of
, except
. It is also noted that the quantitative value of accretion rate has the highest value in Kerr gravity. The accretion rate is getting smaller with an increasing magnitude of the negative GB-coupling constant. Another trend, seen in
Figure 6, is that the steady-state is fully developed around
M for any value of
except
. The same stability is first developed around
M for
, and, later, the shock cone goes into another unstable region around
M. Finally, the steady-state is attained around
M. In the steady-state, the shock cone formed in the vicinity of the black hole on the equatorial plane is supposed to be in thermodynamic equilibrium. On the other hand, it is found that the accretion efficiency depends on the GB-coupling constant
. The black hole with a negative
can provide a less efficient accretion mechanism, which causes the transformation of the gravitational energy into electromagnetic energy [
31].
Prediction of the accretion rates from the numerical simulation around the rotating black holes could be used to define the properties of the black hole as well as the X-ray mechanism. In
Figure 7, we plot the behavior of the accretion rate with an asymptotic velocity at different locations along the radial distance on the disk. As seen in
Figure 7, the accretion rates exponentially decrease around the sonic point, which occurs at
, due to the gravitational and pressure forces. The forces, which cannot balance each other, cause a sudden change in the flow morphology when the velocity goes in the direction of the subsonic or supersonic region. The gravitational force is dominant in the subsonic region, while the gas pressure is dominant in the supersonic region, especially far away from the strong gravitational region.
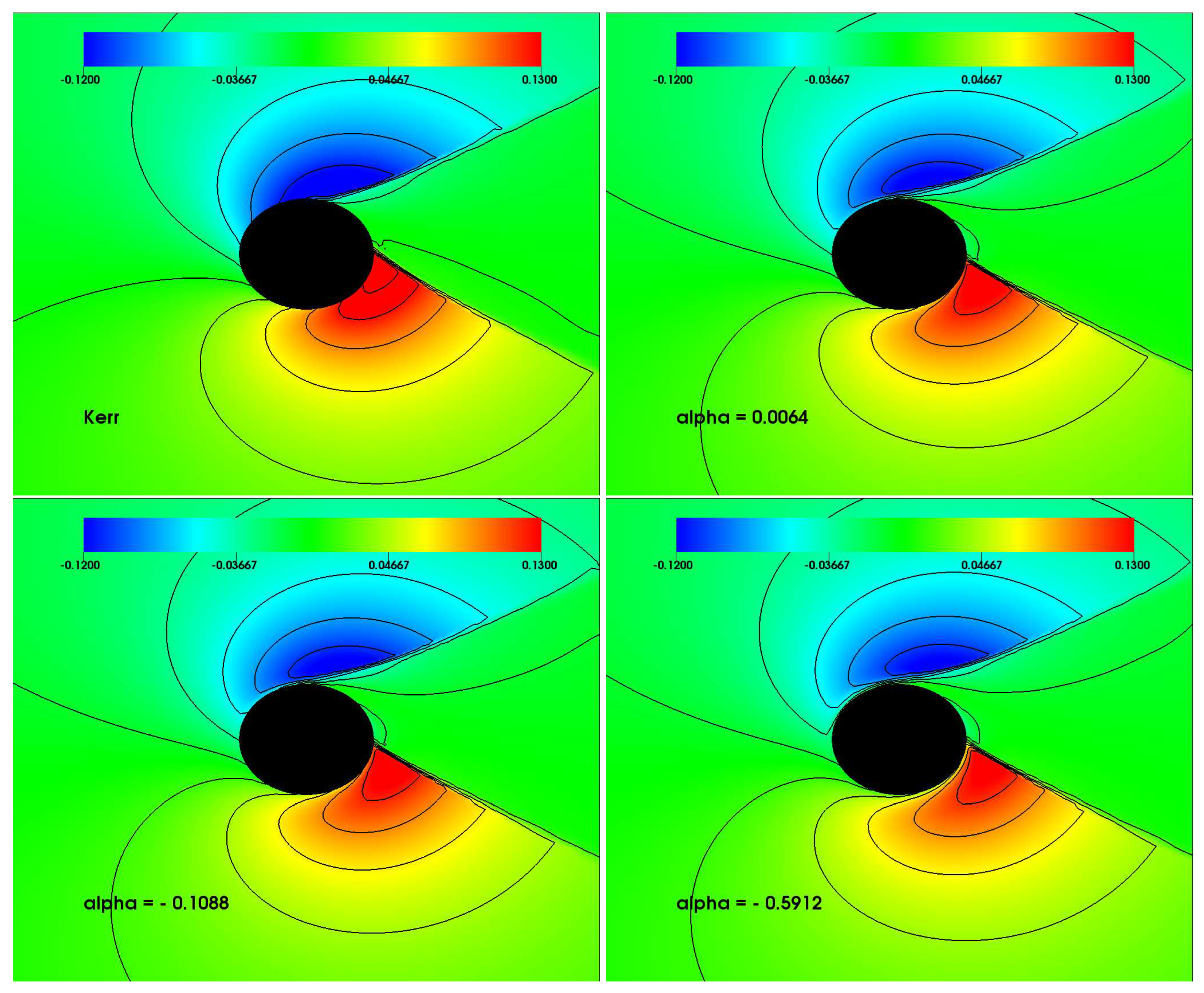
The radial velocity profile is an important indicator to extract the violent features of the accretion mechanism and shock cone created around the black hole in different gravities. The kinetic energy of the violent motion depicts the thermal efficiency of the system. The color and counter plots of the radial velocity profile of the shock cone in strong gravitational region are shown in
Figure 8 for Kerr and EGB gravities. The shock-cone structure and radial velocity can be seen in the figure. While matter is falling toward the black hole in one side of the shock-cone location (positive velocity), it moves away from the other location (negative velocity). However, the matter inside the shock cone oscillates in steady-state. The dynamically stable flow seen in
Figure 8 produces a continuum mechanism for the creation of X-rays around the rapidly rotating black holes. It is also shown that the behavior of the counter lines inside the shock cone around the Kerr black hole is slightly different from the ones in EGB gravity. In addition, there is no noticeable effect observed for the different values of the GB-coupling constant
in the strong gravitational region.
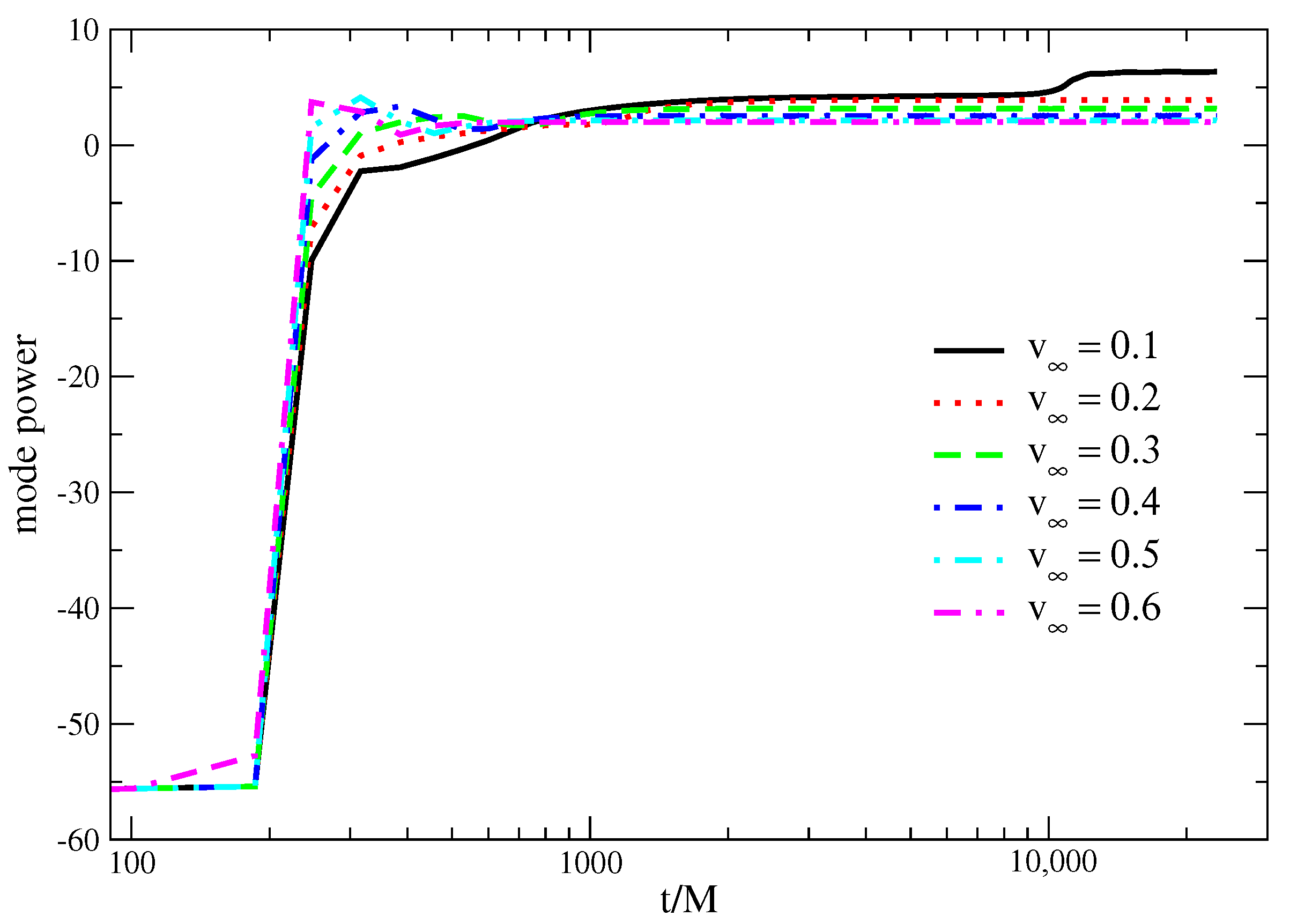
The shock-cone instabilities can be calculated by performing a power-mode analysis on the steady-state shock cone around the black hole in the Kerr and EGB gravities. This can be completed by defining the azimuthal wavenumber and finding the saturation points in the oscillating system [
50]. The growth of the instability modes for the azimuthal wavenumber
in the case of the BHL accretion in the Kerr and EGB gravities is given in
Figure 9 and
Figure 10. As expected, the mode rapidly increases due to the BHL accretion onto the black hole. The mode and saturation point are developed for all the values of asymptotic velocity about
M except
, as seen in
Figure 9. The power mode for asymptotic velocity
keeps growing until
M, and it reaches saturation. The shock cone and the disk do not show any remarkable oscillation after the system reaches saturation in all simulations. As seen in
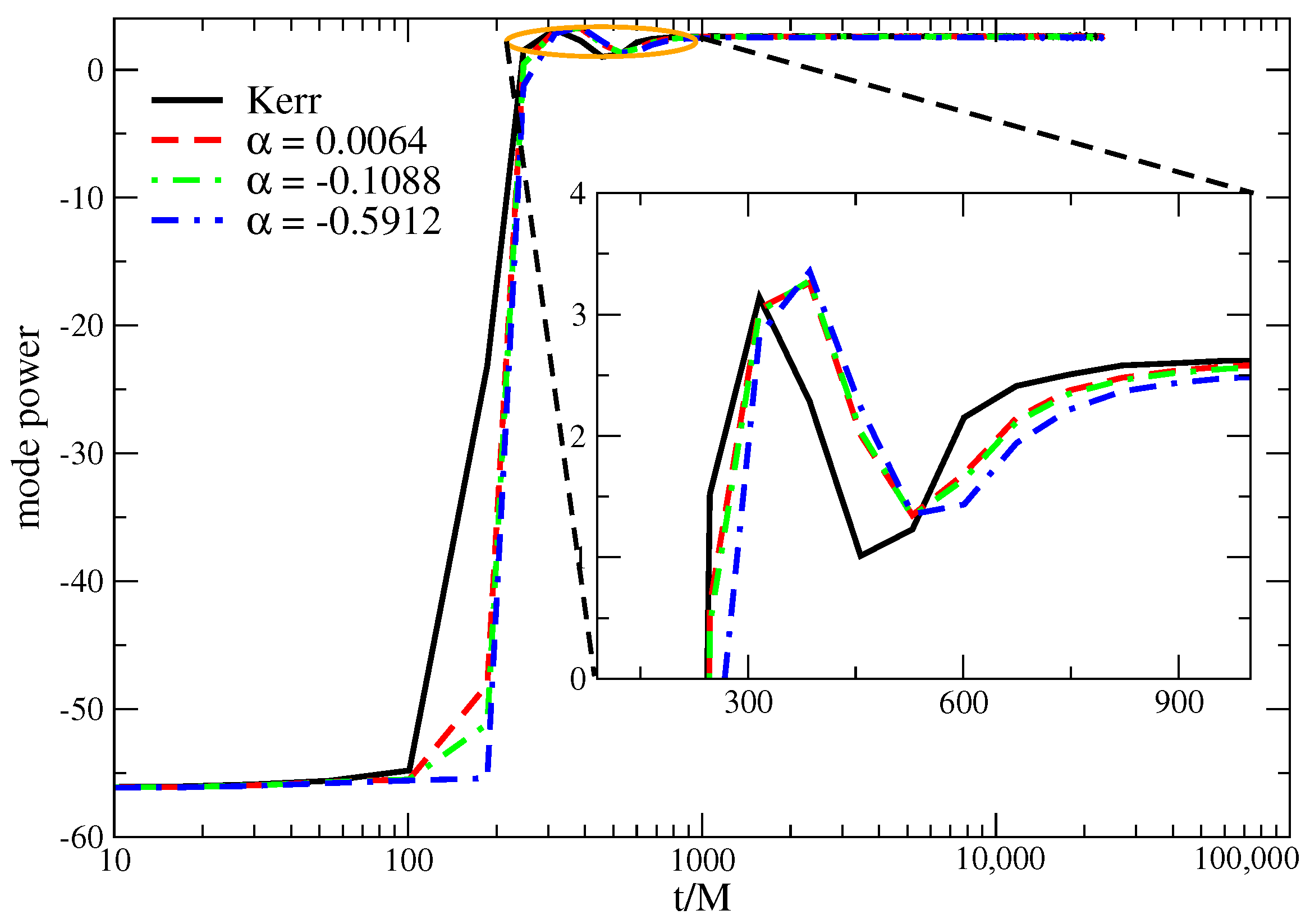
Figure 10, the power-mode analysis of the shock cone in EGB gravity shows slightly different behavior than the Kerr gravity. The instability is developed at a later time in the EGB gravity, and it saturates slightly later than the Kerr gravity (cf. the inset of
Figure 10). In addition, we did not observe any substantial difference in the behavior of the power-mode analysis for different
values.
Figure 10 also shows that the instability is developed at a slightly later time than the other ones for
.
6. Discussion and Conclusions
In this paper, we investigate and compare BHL accretion onto the Kerr and EGB rotation black holes with the rotation parameter in a strong gravitational region using the non-axisymmetric hydrodynamical simulation. We use the perfect fluid equation of state with the adiabatic index . We study the effect of different values of GB-coupling constants on subsonic, sonic, and supersonic flow regions to reveal the accretion-disk dynamics and shock-cone structure around rapidly rotating black holes.
To reveal the shock-cone structure and the physical and radiation properties we studied the mass-accretion rate, the behavior of the rest-mass density, the shock opening angle, radial velocity of the flow, and the power mode for different values of GB-coupling constants and asymptotic velocities with a fixed value of the rotation parameter. The effect of the GB-coupling constant on the shock-cone properties is discussed and compared with the Kerr black hole in general relativity. It is found that the shock opening angle is greater in EGB gravity for any value of than the Kerr gravity. In addition, the shock opening angle decreases with the increasing asymptotic velocity of the Mach number in both Kerr and EGB gravities. On the other hand, the accretion rates are nearly constant in all models after the steady-state is reached, and the rate is decreasing for increasing values of in the negative direction. The accretion rate is higher around the Kerr black hole than the EGB black hole for any value of the GB-coupling constant. After the shock cone reaches the steady-state, it oscillates around a certain value. The oscillation amplitude is slightly diminished for . The high oscillation amplitude in the shock cone could be a good candidate to observe a time-varying X-rays in astrophysical phenomena.
The shock location of the cone, which is attached to the black hole horizon, is a natural physical system which transports the angular momentum of the accreting gas emerging close to the black hole. Therefore, the transportation is responsible for the mass accretion onto the black hole. We find the efficiency of the accretion rate to be a strong function of the asymptotic velocity (Mach number). Even though the accretion rate exponentially decreases in the subsonic and supersonic regions, it reaches a maximum value at the sonic location, which occurs at . The gravitational force has a big influence in the subsonic region, while the gas pressure is dominant in the supersonic region, especially far away from the strong gravitational region.
Finally, it is shown in our numerical simulations that the axisymmetric accretion disk with the shock cone around the rotating black hole in Kerr and EGB gravities generates more violent phenomena, and it gets hotter at values of smaller than . The more violent model could be a good candidate to explore the physical features of the electromagnetic radiation of NGC 1313 X-1 and X-2. The black hole spin parameter used in our numerical simulation for Kerr and 4-D EGB black holes is , which falls within the observed values of NGC 1313 X-1 and X-2 and MAXI J1803-298.