Single- and Double-Charge Exchange Reactions and Nuclear Matrix Element for Double-Beta Decay
Abstract
1. Introduction
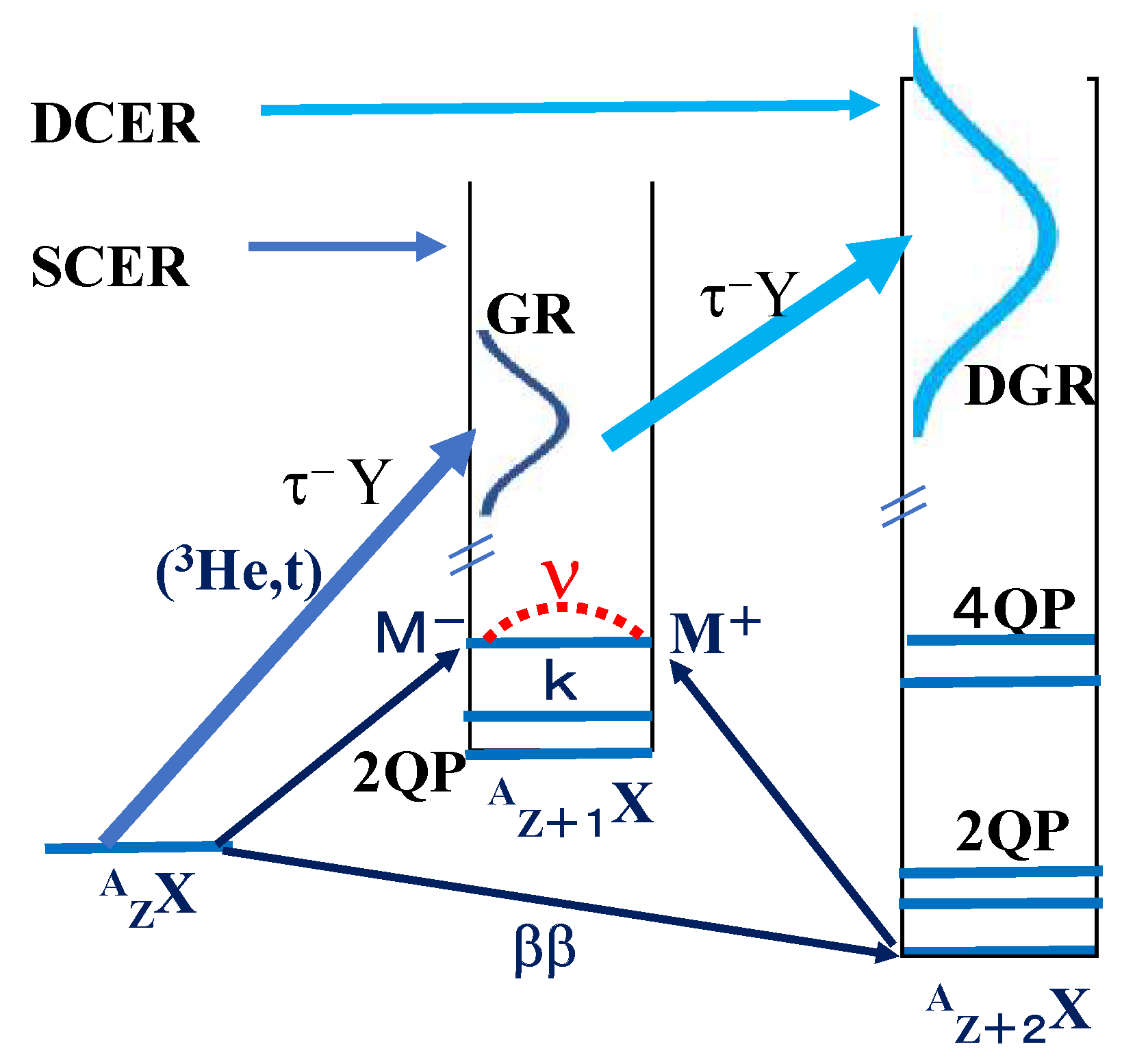
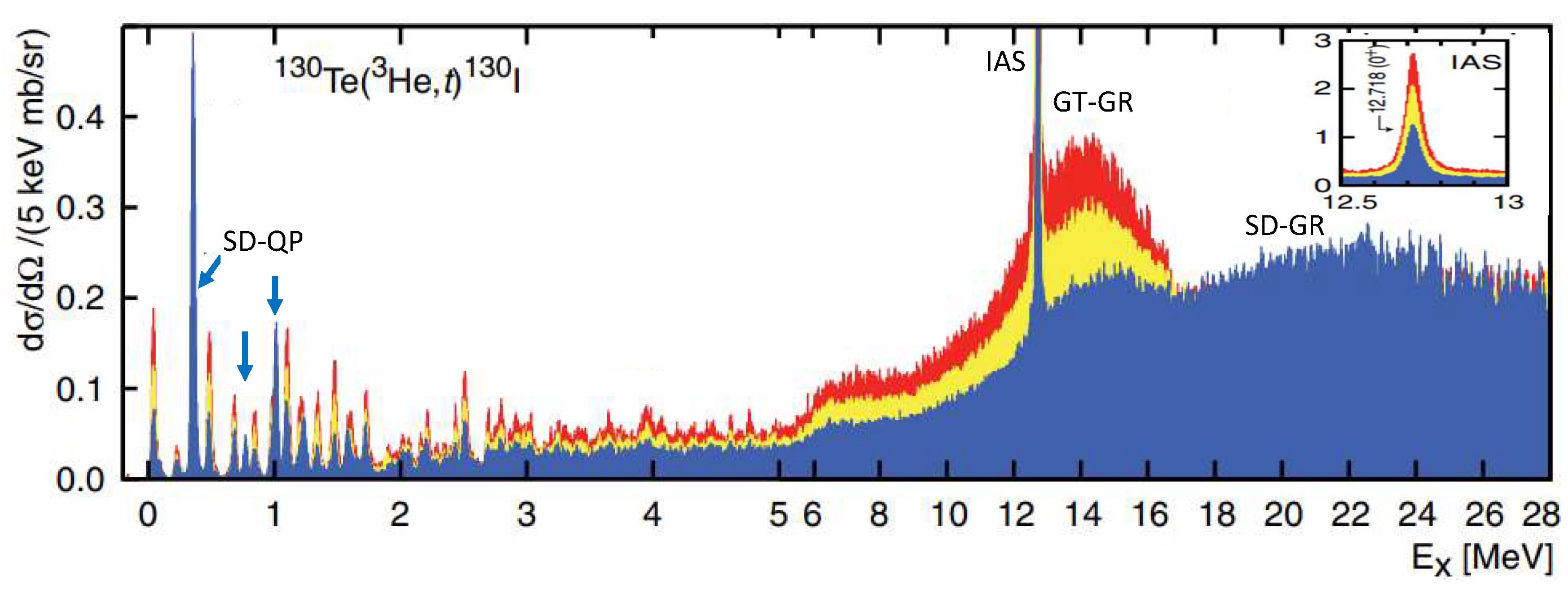
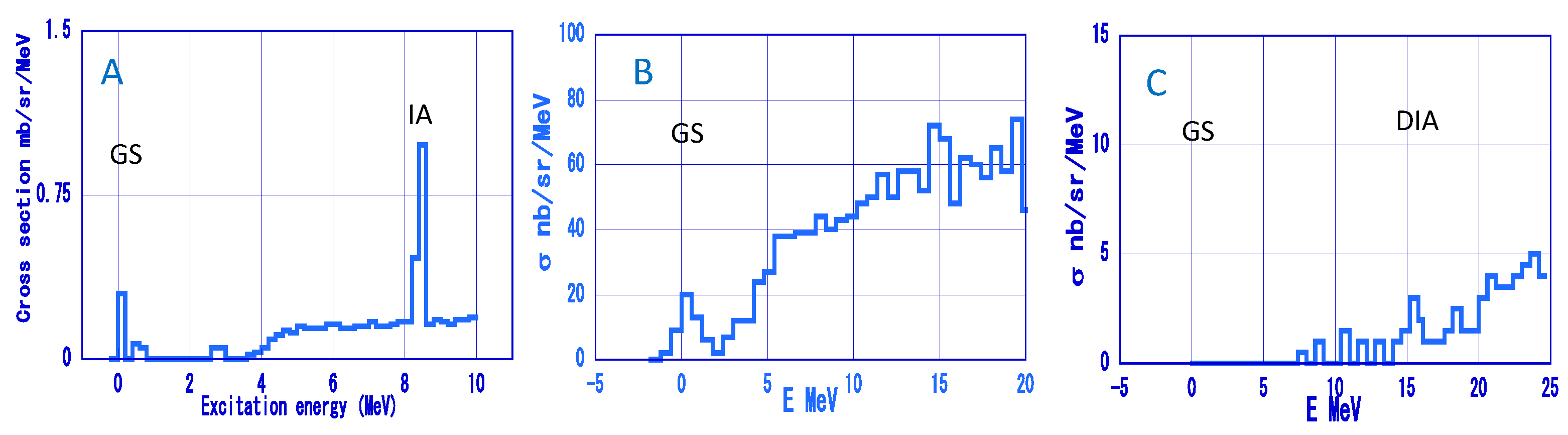
2. Single Charge-Exchange Reaction
3. Double Charge-Exchange Reaction
4. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ejiri, H. Double beta decays and neutrino masses. J. Phys. Soc. Jpn. 2005, 74, 2101–2127. [Google Scholar] [CrossRef]
- Avignone, F.; Elliott, S.; Engel, J. Double beta decay, Majorana neutrino, and neutrino mass. Rev. Mod. Phys. 2008, 80, 481–516. [Google Scholar] [CrossRef]
- Vergados, J.; Ejiri, H.; Šimkovic, F. Theory of neutrinoless double-β-decay. Rep. Prog. Phys. 2012, 75, 106301. [Google Scholar] [CrossRef] [PubMed]
- Ejiri, H. Nuclear spin isospin responses for low-energy neutrinos. Phys. Rep. 2000, 338, 265–351. [Google Scholar] [CrossRef]
- Suhonen, J.; Civitarese, O. Double-beta decay nuclear matrix elements in the pnQRPA framework. J. Phys. G Nucl. Part. Phys. 2012, 39, 035105. [Google Scholar] [CrossRef]
- Barea, J.; Korita, J.; Iachello, F. Nuclear matrix elements for double-β decay. Phys. Rev. C 2013, 87, 014315. [Google Scholar] [CrossRef]
- Engel, J.; Menéndez, J. Status and future of nuclear matrix elements for neutrinoless double β-decay: A review. Rep. Prog. Phys. 2017, 60, 046301. [Google Scholar] [CrossRef]
- Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino nuclear responses for astro-neutrinos, single β-decays, and double β-decays. Phys. Rep. 2019, 797, 1–102. [Google Scholar] [CrossRef]
- Detwiler, J. Future neutrino-less double-beta decay experiments. Proc. Neutrino 2020. [Google Scholar] [CrossRef]
- Ejiri, H. Neutrino-mass sensitivity and nuclear matrix element for neutrinoless double beta decay. Universe 2020, 6, 225. [Google Scholar] [CrossRef]
- Ejiri, H.; Frekers, D. Spin-dipole nuclear matrix elements for double beta decay nuclei by charge-exchange reactions. J. Phys. G Part. Phys. 2016, 43, 11LT01. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Ejiri, H.; Frekers, D.; Suhonen, J. Neutrinoless ββ nuclear matrix elements using isovector spin-dipole Jπ = 2− data. Phys. Rev. 2018, 98, 024608. [Google Scholar] [CrossRef]
- Ejiri, H.; Soukouti, N.; Suhonen, J. Spin-dipole nuclear matrix elements for double beta decays and astro-neutrinos. Phys. Lett. 2014, 729, 27–32. [Google Scholar] [CrossRef][Green Version]
- Ejiri, H.; Jokiniemi, L.; Suhonen, J. Nuclear matrix elements for neutrinoless ββ decays and spin dipole giant resonances. Phys. Rev. C Lett. 2022, 105, L022501. [Google Scholar] [CrossRef]
- Puppe, P.; Lennarz, A.; Adachi, T.; Akimune, H.; Ejiri, H.; Frekers, D.; Fujita, H.; Fujita, Y.; Fujiwara, M.; Ganioğlu, E.; et al. High resolution (3He,t) experiment on the double-β decaying nuclei 128Te and 130Te. Phys. Rev. 2012, 86, 044603. [Google Scholar] [CrossRef]
- Brown, G.E.; Speth, J.; Wambach, J. Energy Dependence of the Coupling Potentials in (p,n) Rections. Phys. Rev. Lett. 1981, 46, 1057. [Google Scholar] [CrossRef]
- Lov, W.G.; Petrovich, F.; Goodmann, C.D.; Austin, S.M.; Bloom, S.D.; Rapaport, J.; Satchler, G.R. (Eds.) The (p,n) Reaction and Nucleon Nucleon Force, Prenum; Springer: New York, NY, USA, 1980; p. 23. [Google Scholar]
- Thies, J.H.; Frekers, D.; Adachi, T.; Dozono, M.; Ejiri, H.; Fujita, H.; Fujita, Y.; Fujiwara, M.; Grewe, E.W.; Hatanaka, K.; et al. The (3He,t) reaction on 76Ge, and double-β decay matrix element. Phys. Rev. 2012, 86, 014304. [Google Scholar] [CrossRef]
- Frekers, D.; Alanssari, M.; Adachi, T.; Clevel, B.T.; Dozono, M.; Ejiri, H.; Elliott, S.R.; Fujita, H.; Fujita, Y.; Fujiwara, M.; et al. High energy-resolution measuements of the 82Se(3He,t) reaction for double β decay and solar neutrinos. Phys. Rev. C 2016, 94, 014614. [Google Scholar] [CrossRef]
- Thies, J.H.; Puppe, P.; Adachi, T.; Dozono, M.; Ejiri, H.; Frekers, D.; Fujita, H.; Fujita, Y.; Fujiwara, M.; Grewe, E.-W.; et al. High-resolution 96Zr(3He,t) experiment and the matrix element for double-β decay. Phys. Rev. C 2012, 86, 054323. [Google Scholar] [CrossRef]
- Thies, J.H.; Adachi, T.; Dozono, M.; Ejiri, H.; Frekers, D.; Fujita, H.; Fujita, Y.; Fujiwara, M.; Grewe, E.-W.; Hatanaka, K.; et al. High-resolution 100Mo (3He,t) charge-exchange experiment and the impact on double-β decays and neutrino charged-current reactions. Phys. Rev. 2012, 86, 44309. [Google Scholar] [CrossRef]
- Puppe, P.; Frekers, D.; Adachi, T.; Akimune, H.; Aoi, N.; Bilgier, B.; Ejiri, H.; Fujita, H.; Fujita, Y.; Fujiwara, M.; et al. High resolution (3He,t) reaction on the double-β decaying nucleus 136Xe. Phys. Rev. C 2011, 84, 051305R. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Cavallaro, M.; Agodi, C.; Bondì, M.; Carbone, D.; Consolo, A.; Foti, A. Heavy ion double charge-exchange reactions: A tool toward 0νββ nuclear matrix elements. Eur. Phys. J. 2015, 51, 145. [Google Scholar] [CrossRef]
- Takahisa, K.; Ejiri, H.; Akimune, H.; Fujita, H.; Matumiya, R.; Ohta, T.; Shima, T.; Tanaka, M.; Yosoi, M. Double charge exchange (11B,11Li) reaction for double beta decay responses. arXiv 2017, arXiv:1703.08264. [Google Scholar]
- Lenske, H.; Cappuzzello, F.; Cavallaro, M.; Colonna, M. Heavy ion charge exchange reactions as probes for nuclear beta decay. Prog. Part. Nucl. Phys. 2019, 109, 103716. [Google Scholar] [CrossRef]
- Lenske, H.; Bellone, J.; Colonna, M.; Gambacurta, D. Nuclear matrix elements for heavy ion sequential double charge exchange reactions. Universe 2021, 7, 98. [Google Scholar] [CrossRef]
- Cappuzzello, F.; Agodi, C.; Cavallaro, M.; Carbone, D.; Tudisco, S.; Lo Presti, D.; Oliveira, J.R.B.; Finocchiaro, P.; Colonna, M.; Rifuggiato, D.; et al. The NUMEN project: MUclear Matrix Elements for Neutrinoless double beta decays. Eur. Phys. J. A 2018, 54, 72. [Google Scholar] [CrossRef]
- Shimizu, N.; Menendez, J.; Yako, K. Double Gamow-Teller Transitions and its relation to neutrinoless ββ decay. Phys. Rev. Lett. 2018, 120, 142502. [Google Scholar] [CrossRef] [PubMed]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 05501. [Google Scholar] [CrossRef]
- Gysbers, P.; Hagen, G.; Holt, J.D.; Jansen, G.R.; Morris, T.D.; Navrátil, P.; Papenbrock, T.; Quaglioni, S.; Schwenk, A.; Stroberg, S.R.; et al. Discrepancy between experimental and theoretical β decay rates resolved from first principles. Nat. Phys. 2018, 15, 428. [Google Scholar] [CrossRef]
- Ejiri, H. Axial-vector weak coupling at medium momentum for astro neutrinos and double beta decays. J. Phys. G Nucl. Part Phys. 2019, 46, 125202. [Google Scholar] [CrossRef]
- Ejiri, H. Nuclear matrix elements for β and ββ decays and quenching of the weak coupling gA in QRPA. Front. Phys. 2019, 7, 30. [Google Scholar] [CrossRef]
- Coraggio, L.; De Angelis, L.; Fukui, T.; Gargano, A.; Itaco, N.; Nowacki, F. Renormalization of the Gamow-Teller operator within the realistic shell model. Phys. Rev. 2019, 100, 014316. [Google Scholar] [CrossRef]
- Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A = 100–136 nuclei. Phys. Rev. 2015, 91, 054309. [Google Scholar] [CrossRef]
- Ejiri, H. Fermi surface quasi particle model nuclear matrix elements for two neutrino double beta decays. J. Phys. Nucl. Part. Phys. 2017, 44, 15201. [Google Scholar] [CrossRef][Green Version]
- Ejiri, H. Neutrino studies in nuclei and intense neutrino sources. Nucl. Instr. Methods Phys. Res. 2003, 503, 276–278. [Google Scholar] [CrossRef]
- Hashim, I.; Ejiri, H.; Shima, T.; Takahisa, K.; Sato, A.; Kuno, Y.; Ninomiya, K.; Kawamura, N.; Miyake, Y. Muon capture reaction on 100Mo to study neutrino nuclear responses for double-β decays and neutrinos of astro-physics origins. Phys. Rev. C 2018, 97, 014617. [Google Scholar] [CrossRef]
- Jokiniemi, L.; Suhonen, J. Muon-capture strength functions in intermediate nuclei of 0νββ decays. Phys. Rev. 2019, 100, 014619. [Google Scholar] [CrossRef]
- Simkovic, F.; Dvornieky, R.; Vogel, P. Muon capture rates: Evaluation within the quasiparticle random phase approximation. Phys. Rev. 2020, 102, 034301. [Google Scholar] [CrossRef]

| Nuclide | B(SD, QP) | B(F, IA) | (SD) | (SD) |
|---|---|---|---|---|
| Ge | 0.080 ± 0.016 | 12 | 0.30 | 0.26 |
| Se | 0.091 | 14 | 0.29 | - |
| Zr | 0.024 | 16 | 0.27 | 0.31 |
| Mo | 0.053 | 16 | 0.35 | 0.33 |
| Te | 0.452 | 24 | 0.32 | 0.29 |
| Te | 0.456 | 26 | 0.31 | 0.29 |
| Xe | 0.457 | 28 | 0.34 | 0.26 |
| Nuclide | ) | ) | (GTSD) | - |
| Fe | 0.61 ± 0.12 | 8 | 0.092 ± 0.014 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ejiri, H. Single- and Double-Charge Exchange Reactions and Nuclear Matrix Element for Double-Beta Decay. Universe 2022, 8, 457. https://doi.org/10.3390/universe8090457
Ejiri H. Single- and Double-Charge Exchange Reactions and Nuclear Matrix Element for Double-Beta Decay. Universe. 2022; 8(9):457. https://doi.org/10.3390/universe8090457
Chicago/Turabian StyleEjiri, Hiroyasu. 2022. "Single- and Double-Charge Exchange Reactions and Nuclear Matrix Element for Double-Beta Decay" Universe 8, no. 9: 457. https://doi.org/10.3390/universe8090457
APA StyleEjiri, H. (2022). Single- and Double-Charge Exchange Reactions and Nuclear Matrix Element for Double-Beta Decay. Universe, 8(9), 457. https://doi.org/10.3390/universe8090457






