Abstract
We considered a vacuum polarization inside a galaxy in the eikonal approximation and found that two possible types of polarization exist. The first type is described by the equation of state , similar to radiation. Using the conformally unimodular metric allows us to construct a non-singular solution for this vacuum “substance” if a compact astrophysical object exists in the galaxy’s center. As a result, a “dark” galactical halo appears that increases the rotation velocity of a test particle as a function of the distance from a galactic center. The second type of vacuum polarization has a more complicated equation of state. As a static physical effect, it produces the renormalization of the gravitational constant, thus, causing no static halo. However, a non-stationary polarization of the second type, resulting from an exponential increase (or decrease) of the galactic nuclei mass with time in some hypothetical time-dependent process, produces a gravitational potential, appearing similar to a dark matter halo.
1. Introduction
Among the various issues of combining general relativity (GR) and quantum mechanics, one encounters the problems of vacuum energy and black holes.
The first problem is to explain why enormous zero-point vacuum energy density (here is the UV energy scale of quantum field theory associated with a hard 3-momentum cutoff of the order of the Planck mass ) does not influence a universe expansion (e.g., see [1,2,3] and references herein). The second problem is associated with the loss of unitarity and information inside of the black hole horizon (e.g., see [4,5] and references therein), that prevents the definition of a pure quantum state.
On the other hand, the basis of GR is a notion of manifold [6], i.e., a metric space, which could be covered by coordinate maps. When a concrete space–time possessing some symmetry is considered, one aims to introduce a system of coordinates allowing maximal covering of this particular manifold. For instance, the Schwarzschild solution only describes the region outside the horizon, and one has to introduce the Kruskal coordinates to cover the complete domain [7]. Nevertheless, one could admit an opposite view: restricting the manifold by sewing all the black hole horizons by some coordinate transformation. This approach is similar to a case when a man finds a hole in their trousers at the knee. In such a case, he steps back a little from the hole border and then subtends it into a node with the help of sewing.
It is allowed using the conformally unimodular (CUM) metric [8], where an ultra-compact black hole-like astrophysical object appears as a non-singular ball named “eicheons” [9]. Besides, the vacuum energy problem could be partially solved in the CUM metric if one builds a gravity theory admitting an arbitrary choice of the energy density level [8]. That is possible because the equations for evolution of the Hamiltonian and the momentum constraints admit not only the trivial solution , , but also , . The constant compensates for the main part of the vacuum energy density proportional to the Planck mass in the fourth degree [8,10]. Residual energy density, remaining after omitting the main part of the vacuum energy density, is some kind of dark energy and results in a cosmological picture containing a period of linear evolution in cosmic time [10,11] followed by late accelerated expansion.
Both dark energy and dark matter (DM) are unknown “substances” appearing in modern cosmology and astrophysics [12,13,14]. DM appears not only on cosmological scales but also on galaxy scales. The lowest scale at which there is evidence for DM is of ≈kpc [15,16]. Dark energy is associated with vacuum energy, whereas DM is expected to be some kind of a non-baryonic matter weakly interacting with the known particles of the standard model [17,18,19]. Nevertheless, there are attempts to explain the DM by a DM-like behavior of vacuum energy [20], or a vacuum polarization induced by the gravitational field. Heuristic models of vacuum polarization such as [21,22,23,24,25], which would demand dipolar fluid [26], anti-gravitation [27] or hydrodynamical phenomena in a vacuum treated as hypothetical (super-)fluid [28,29,30], are of interest.
The conventional renormalization procedure of the quantum field theory applied to vacuum energy near a massive object [31,32,33,34,35,36] leads to the modification of the gravitational potential only at small distances of the order of gravitational radius that are unobservable with current technologies. That is, the renormalization excludes the manifestation of micro-scale phenomena on the macro-scales (nevertheless, see [20]). This conclusion assumes the general covariance of the mean vacuum value of stress–energy tensor on a curved background. However, regarding the vacuum state , the invariant relatively general transformation of coordinates does not exist [37]. That raises a question: is it reasonable to demand the covariance of in the absence of invariant ? If invariance violation, which implies the existence of “æther”, takes place, then, similar to condensed-matter physics, DM still could be treated as an emergent phenomenon produced by vacuum polarization.
The outline of this paper is as follows: In Section 2, we argue the necessity of considering a vacuum polarization from a cosmological point of view and explain that the CUM metric is needed to omit the main part of vacuum energy. Section 3 contains a perturbation formalism in the CUM metric, which is required to introduce a vacuum polarization as some media, i.e., “æther”. The eikonal approximation is used in Section 4 to obtain the vacuum energy density and pressure of a quantum scalar field by summating the contributions from the distorted virtual plane waves. The expression for a vacuum equation of state is obtained. In Section 5, the F-type vacuum polarization, possessing a radiation equation of state, is used in the Tolman–Volkov–Oppenheimer (TOV) equations for two substances. This type of vacuum polarization results in a dark halo if eicheon is situated in the galactic center. In Section 6, the -type of vacuum polarization is considered. This type of polarization leads to the renormalization of the gravitational constant in the stationary case. However, it can contribute to the DM halo for the non-stationary processes. In the Conclusion, we summarize the consequences of two types of vacuum polarization for galaxies. In the Appendix A, we consider the static and empty universe to demonstrate an example of an exact solution for the system of perturbations, taking into account the F-type vacuum polarization.
2. A Spatially Uniform Universe in the CUM Metric
2.1. CUM Metric in the Five Vectors Theory of Gravity
We based our analysis on using the CUM metric, which is the foundation of the so-called five vectors theory (FVT) [8]. In the course of this analysis, we will use the particular cases of the CUM metric appropriate to the physics considered.
A general class of CUM metrics is defined as [8]
where , is a spatial metric, is a locally defined scale factor, and , is a conformal time connected with a cosmic time t through . The spatial part of the interval (1) looks as
where is a matrix with the unit determinant. The interval (1) is similar formally to the ADM one [38], but the lapse function is taken in the form of , where is a three-dimensional vector, and is a conventional partial derivative. In the gravity theory admitting arbitrary choice of the energy density level [8], there are the Lagrange multipliers , the shift function , and three triads to parameterize the spatial metric . Such model was named the FVT of gravity [8]. In contrast to GR, where the lapse and shift functions are arbitrary, the restrictions and arise in FVT. The Hamiltonian and momentum constraints in the particular gauge , obey the constraint evolution Equations [8]:
which admits adding some constant to . In the FVT frame, it is not necessary that , but is also allowed. The particular cases of the CUM metric corresponding to the Bianchi I model and the spherically symmetric space–time were analyzed in [39,40].
2.2. Uniform, Isotropic and Flat Universe
Let us consider a particular case of (1)
corresponding to a spatially uniform, isotropic and flat universe, where the Friedmann equations take the form [11,41,42]:
Here , the prime denotes the derivative with respect to the conformal time. We use the system of units and the reduced Planck mass (in physical units ). According to FVT [8], the first Friedmann Equation (6) is satisfied up to some constant, and the main parts of the vacuum energy density and pressure
do not contribute to the universe expansion because the constant in (6) compensates the vacuum energy density, whereas there is no vacuum contribution in Equation (7) by virtue of the equation of state (9).
Bosons and fermions contribute with opposite signs into a vacuum energy density (8) [43,44]. Here, we do not consider the supersymmetry hypotheses due to the absence of evidence for supersymmetric partners to date [45].
For the contributions of massive particles and condensates, we imply the Pauli sum rules [44,46]. These rules are not fulfilled at this moment due to the incompleteness of the standard model of particle physics. Nevertheless, one may hope that they will be satisfied after possible discoveries beyond the standard model.
Other contributors to the vacuum energy density are the terms depending on the derivatives of the universe expansion rate [10,41,42,46]. They have the correct order of magnitude , where H is the Hubble constant, and explain the accelerated expansion of the universe driven by the residual energy density and pressure [10,41,42,46]:
where Equation (10) includes the number of minimally coupled scalar fields plus two degrees of freedom of the gravitational waves [41]. The massless fermions and photons do not contribute to (10) [41].
According to (10), the accelerated expansion of universe allows finding a value of the momentum UV cut-off
from the measured value of the universe deceleration parameter and other cosmological observations [10,41]. It should be noted that the UV cut-off of the 3-momentums in (8) and hereafter also reflects the diffeomorphism symmetry violation1 (e.g., see [47,48,49,50,51,52] and references herein).
3. Perturbations of a Uniform Background in the CUM Metric
Here the perturbations of the locally defined scale factor are expressed through a gravitational potential :
A stress–energy tensor can be written in the hydrodynamic approximation
The perturbations of the energy density and pressure are considered around spatially uniform values.
Let us introduce new variables
for reasons which will be explained below. The perturbations of (15), (16) around the uniform values can be written now as , . The 4-velocity u is represented in the form of
where is a scalar function. Expanding all perturbations into the Fourier series etc. results in the equations for the perturbations:
where the index i denoting the kind of substance has been introduced. It is remarkable that, as a result of the choice of the variables (15)–(17), the unperturbed values and p do not appear in the system (18)–(21). This allows us to avoid the influence of the large uniform energy density and pressure (8) and (9) on the evolution of perturbation. Equations (18) and (19) are consequences of the Hamiltonian and momentum constraints, while Equations (20) and (21) are equations of motion. For consistency of the constraints with the equations of motion, every kind of fluid has to satisfy the continuity and Euler equations:
Equations (18)–(23) have the same form as in GR, but for the consistency of Hamiltonian and momentum constraints (18) and (19) with the equations of motions (20)–(23), it is sufficient for the first Friedmann Equation (6) to be valid up to some constant. Namely, for such consistency, it is necessary that the differentiation of constraints with the subsequent substitution of the second-time derivatives from the equations of motion (7), (20)–(23) leadcyans to identical equalities. This consistency is a feature of using the CUM metric, in particular, and the FVT theory, in general. In any other metrics different from CUM (that is, in a frame of GR), the first Friedmann Equation (6) with the in the right hand side is needed for consistency of the constraints and the equations of motion.
4. Vacuum as a Medium: The Eikonal Approximation for Quantum Fields
Generally, a vacuum could also be considered as some fluid (e.g., see [28,29,30]), i.e., “æther” [54], but with some stochastic properties along with its elastic ones [42,46,55]. Here we are interested in its elastic properties only. In Refs. [42,46], the speed of sound for the scalar waves of vacuum polarization was introduced, where and are given by (10). That is the only heuristic conjecture.
Here, the actual calculations of the vacuum density and pressure on the curved background are performed in the eikonal approximation. The last one has a very transparent background. In the Minkowski’s space–time, the virtual plane waves penetrate space–time and, to obtain a vacuum energy density, we must summarize the contributions of every wave. In the curved space–time, it is necessary to summarize the contributions of the distorted waves to obtain the spatially non-uniform energy density and pressure. It should be mentioned that the eikonal approximation was successfully used in high energy physics [56] and even in gravity [57], where the small-angle scattering amplitude of two massive particles were calculated in all orders on gravitational constant G.
A massless scalar field in the external gravitational field obeys the equation
This leads to
after the change of variables . Further, in the terms of the metric perturbations and F, we come to
where a “potential” operator has the form
A quantization of the scalar field in terms of creation and annihilation operators implies [37]
where the function satisfies Equation (27), and the orthogonality condition is [37]
A solution of Equations (27) and (29) for the functions can be written in the eikonal approximation
which leads to the equation for the eikonal function
and, according to Equations (12) and (13), is written in the terms of the metric perturbations , :
where
A solution of (34) can be obtained in the form
where the lower integration limit depends on the cosmological model. In particular, it could be 0 or . The mean value of the stress–energy tensor of a massless scalar field
can be averaged over the vacuum state and compared with the hydrodynamic expression (14). This gives
where only spatially non-uniform parts of the vacuum averages are implied in the second equalities on the right-hand side of (38)–(40). The last depends on the metric perturbations and contained in Equations (12) and (13). The final equalities in (38)–(40) result from calculations in the eikonal approximation (32).
Considering the quantity and using Equations (34) and (35), result in
where summation has been changed by integration and it is taken into account that . The number of the scalar fields minimally coupled with gravity has been introduced as in (10).
In consequence of Equation (41), two types of spatially non-uniform vacuum polarization exist. Namely, the F-polarization has a radiation-type equation of state3
whereas the -polarization has an equation of state
Both types of spatially non-uniform vacuum polarizations correspond to the uniform component of (8), (9), whereas the uniform polarization given by (10) has no non-uniform counterpart with an accuracy of our consideration, i.e., in the second order on derivatives. It must be emphasized that it is easy to obtain the equation of state (9) for a spatially uniform main part of the vacuum energy density, but it is not so trivial to do that for a spatially non-uniform vacuum energy density.
5. Galactic DM as a -Vacuum Polarization
As it was shown in Section 4, the F-component of vacuum polarization has the equation of state analogous to radiation (see Equation (9)). In this sense, it is similar to the uniform part of vacuum energy density in Equation (8).
At the same time, it is difficult to determine the concrete value of the non-uniform vacuum energy density because, according to (38), it contains an eikonal function , which is determined by the integral (36). For instance, one has and from (35), (36) finds
Calculation of the integral (44) requires one to know the full evolution history of . It is simpler to use only the fact that the F-contribution to the vacuum polarization has the equation of state
The distributions of matter–energy density and potential are not determined for the static case in the first order on perturbations (see Appendix A). However, it is possible to consider a nonlinear heuristic model treating the F-vacuum as an abstract substance with the above equation of state. The model consists of a core of some incompressible substance, modeling a baryonic-like matter placed on the radiation background, i.e., the F-polarized vacuum or “dark radiation”, which interacts with this core only gravitationally. Below, we find a spherically symmetric solution for an incompressible substance with the constant energy density on the background of radiation density .
5.1. Equations in the CUM Metric
The CUM metric in the case of spherical symmetry acquires the form [9]
where , , and are functions of . The matrix with the unit determinant is expressed through . The interval (46) could be also rewritten in the spherical coordinates:
to give
Restricting ourselves to static solutions, the equations for the functions and are written as [9]
where Equation (49) is the Hamiltonian constraint, which could be rewritten in a form containing no second derivatives using Equations (50) and (51):
Each kind of substance has to satisfy
A vacuum solution of Equations (49)–(51) corresponding to the point massive particle was considered in [9] where an absence of evidence for a horizon was demonstrated. Let us consider another solution, corresponding to the substance of a radiation-type filling all the space. This particular solution is written as
and, under (45), it follows from (53):
if we use (54) and (49) with in the right hand side of Equation (49). Here, is measured in the terms of , and r is measured in the units of , which is not a gravitational radius, but some arbitrary spatial scale. It should be noted that, for (45), Equations (50) and (51) look similar to those for an empty space, whereas Equation (49) could also be considered as that for an empty space, but with . Thus, in the CUM metric of the FVT where the Hamiltonian constraint is satisfied up to some constant, one could alternatively consider the F-vacuum polarization solution similar to that for an empty space, but with some non-zero value of in Equations (49) and (52).
Since the solution (55) is singular, it could be treated as unphysical. To obtain a realistic model, one has to consider at least two substances: a compact object in the center consisting of a substance with a constant energy density and a substance with the radiation equation of state (42). We must emphasize the importance of such a dense kernel for obtaining non-singular vacuum polarization of F-type.
5.2. Equations in the Schwarzschild-Type Metric
It is more convenient to begin a consideration from the Schwarzschild-type metric [58]
where Equations (54) and (55) correspond to the well-known solution [58]
obeying the TOV Equation [59,60] for a radiation fluid
in all the spatial region , where is defined by
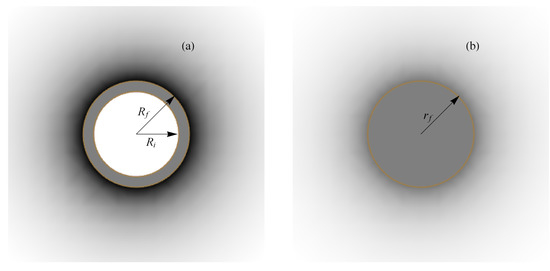
Again, is measured in the terms of , and R is measured in the units of . The solutions (57) and (55) are singular at and, thereby, non-physical. The situation changes cardinally in the presence of a core consisting of incompressible matter. More exactly, in the presence of incompressible matter of low density , the corresponding solution remains singular. However, if , a solid ball in the metric (48) looks similar to a shell over in the metric (56) [9] that is shown in Figure 1a. Here, we again imply the gravitational radius as a measure of the distances, but calculate it taking into account only an incompressible matter. Such a matter occupies a region between and , where
in the units of . Here the energy density is constant and measured in the terms of , where the gravitational radius is defined as and . A compact object of such a type arising in FVT is known as “eicheon” [9] and replaces a black hole of GR. The appearance of eicheon in the center makes the solution (58) to be non-singular because it allows for setting the finite boundary conditions for radiation.
To explain this, let us consider two fluids in the metric (56) obeying the TOV equations:
where the function satisfies
For , the above equations hold for the internal range , where , and the border of a region, occupied by , is defined through (60).
The pressure of incompressible fluid must turn to zero at the edge of the range filled by matter , and it is a boundary condition for . Then, one could set an amount of radiation at and solve the system of equations in a region of assuming . A solution allows determining , and, using this value as an initial condition, one should solve the equation for the radiation fluid (58) in an outer region of . The metric obtained by solving the equations is [58]
Comparing the metrics (46) and (56) leads to relation for the radial coordinates R and r [9]
where the dependencies and are implied. Equation (66) has to be integrated with the initial condition , which means that in the metric (56) corresponds to in the metric (46). Knowing allows plotting shown in Figure 2a as the r– dependent function (Figure 2b).
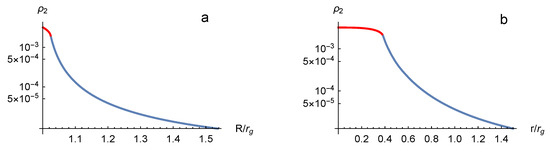
Figure 2.
(a) –nergy density of the vacuum polarization in a form of “dark radiation” in the coordinates calculated for the eicheon parameters , , , . Red part of the curve corresponds to , i.e., lies inside an eicheon. (b) calculated in the coordinates r of the metric (48). Red part of the curve corresponds to .
Let us consider the motion of a test particle on a circular orbit in the metric (56). The angular velocity on a circular orbit is calculated as [58]:
A spatial interval followed by a particle along the circular orbit is given by . To obtain the rotation velocity observed by an observer situated at rest near the moving particle, one has to divide the spatial interval over the proper time of such an observer [61]:
A qualitative example of the general form of the numerical solution for the rotation velocity is shown in Figure 3. Although the shape of the curve resembles observational data, the asymptotic of the rotation curve corresponds to . This very large velocity (in units of speed of light) corresponds to asymptotic value in (57), whereas, in the reality, the rotation velocities of galaxies are km/s . To obtain smaller velocities, one has to diminish the density of radiation in the center of eicheon, i.e., at in the metric (48) or in the metric (56). For central radiation density of g/, one has the rotation curve shown in Figure 4. That is a pure “dark radiation” contribution without the galaxy bulge or disk. It increases linearly with the distance and corresponds to the rising part of the general curve shown in Figure 3. In the logarithmic scale, one could see (Figure 5) together the contribution of the eicheon of the mass of in the center of the Milky Way (the left side of the curve) and the impact of the dark radiation (the right side of the curve), whereas the effects of the galactic bulge and disk responsible for the intermediate region are not taken into account. However, it is expected that bulge and disk attraction will influence the F-type vacuum polarization in such a way that the curve in Figure 4 will be not pure linear but slightly bent. We do not gain insight into such details because our goal is to show that the F-type vacuum polarization could arise only around a “sewed” black hole, i.e., around eicheon.
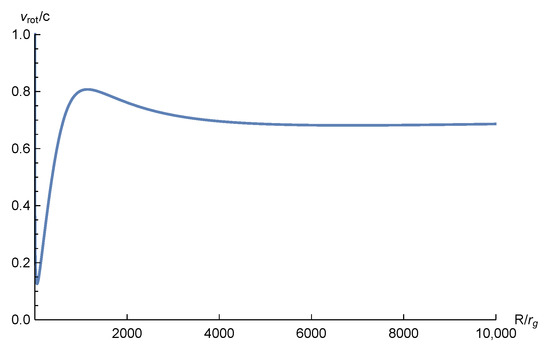
Figure 3.
The general form of a model rotational curve for the eicheon parameters specified in the caption to Figure 2.
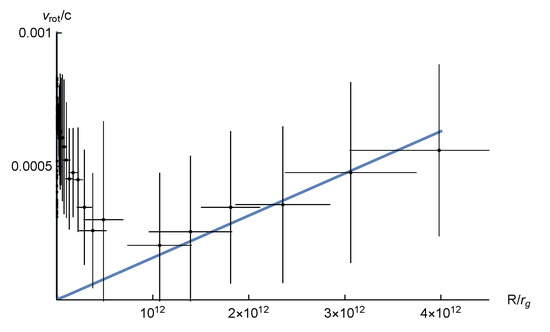
Figure 4.
The rotational curve for the eicheon parameters , and , where is defined by an eicheon mass. In the physical units, g/cm. The points and error bars correspond to the Milky Way rotational curve from [62].
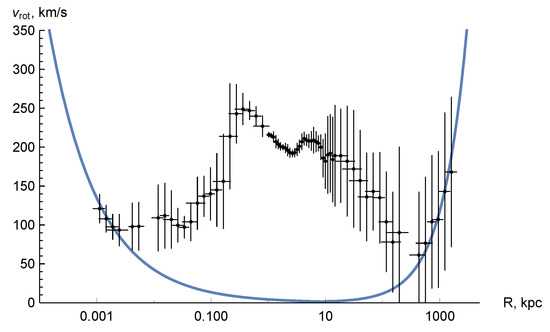
Figure 5.
The rotational curve of eicheon with the mass of Sgr A with taking into account the vacuum polarization of F-type. The logarithmic scale is used and the points correspond to the Milky Way rotational curve from [62]. The eicheon parameters are given in the caption to Figure 4.
We emphasize that the presented consideration is heuristic because, although the linear system for the perturbation and the eikonal approximation for vacuum polarization seems reasonable, we use its results in the nonlinear TOV model. Another thing is that we set the density of radiation (the F-type vacuum polarization) in the center of eicheon, i.e., at , of empirically but not calculate it from the first principles, i.e., we use only the equation of state obtained from the calculations in the eikonal approximation.
6. Vacuum Polarization of -Type
In Section 3 and Section 4, the linear system of Equations (20)–(23) and (41) was deduced, which describes the evolution of perturbation by taking into account vacuum polarization (see Equation (41) and Appendix A for an example of an exact solution). Galaxy formation is a complex nonlinear process that develops over cosmological time scales. Generally, the linear system is insufficient to describe the galaxy evolution. However, one could create a heuristic picture, setting an approximate profile of matter near the galaxy center, and obtain a gravitational potential produced by vacuum polarization obeying the linear equations. Below we will discuss that the observed galaxy halo could originate from a very fast (compared to the cosmological times) change of the galactic nucleus mass. We will neglect a cosmological evolution assuming . This reduces the above system of the equations to
where the last equation holds for the vacuum polarization of –type and is denoted by . Substituting from Equation (69), and from Equation (71) into Equation (70) gives the equation
where an effective “density” of all the substances except vacuum is denoted as
Equation (72) allows for developing a simple model: setting profile and time dependencies of the quantity empirically determines the metric perturbation and using (69).
Let us, for simplicity, take in the form of
where m is a “mass” of the object at , is a form-factor and T is some typical time of the “mass” growth. The model implies some rapid processes such as accretion occurring around the massive object, i.e., around the galaxy nucleus. Substitution of the expression (74) into Equation (72) allows finding , where
and Equation (69) give :
At , the corresponding static limit is
which implies that the vacuum polarization leads to the renormalization (increasing) of the Planck mass, i.e., decreasing the gravitational constant. In particular, using the value (11) obtained from the cosmological observations [10] gives
It seems that the vacuum polarization, in some sense, acts similar to antigravitation, and the gravitational constant appearing in Newton’s law has to differ from the gravitational constant G in the Friedmann equations for a uniform universe. Although the gravitational constant’s renormalization does not influence the cosmological balance of the different kinds of matter expressed in the units of the critical density , it should be taken into account for comparison with the directly measured (for instance, utilizing luminosity) density. Numerically, gives .
Invariant Potentials and Rotational Curves
Astrophysicists express the results of observations in terms of gauge-invariant quantities, which are not dependent on a system of coordinates. The potentials and are not invariant relatively to the infinitesimal transformations of coordinates and time of the following type
where and are some small functions. Usually, the potentials and are introduced [63,64,65] which are invariant relatively transformations (79). The potentials correspond to the metric
and are expressed through and F as
where the final equalities at the right-hand side of (81), (82) hold for our case of , and . Using (75), (76) gives
and . Thus, we obtained the Fourier transformation of the time-dependent gravitational potential , allowing us to define
To obtain a concrete empirical formula, one has to set the form factor , for instance, using the Gaussian profile . The spatial dependence of the potential (84) at the present time, i.e., , allows us to find the rotational velocity dependence on the spatial coordinate
Here, the potential (84) is time-dependent, and actually, there are no pure rotational curves because the radial velocities are present. Here, for an estimation, we discuss only tangential velocity. The parameters m, D and are adopted to produce a typical rotational curve without an DM (blue curve in Figure 6), then vacuum polarization produces a halo corresponding to black curve in Figure 6.
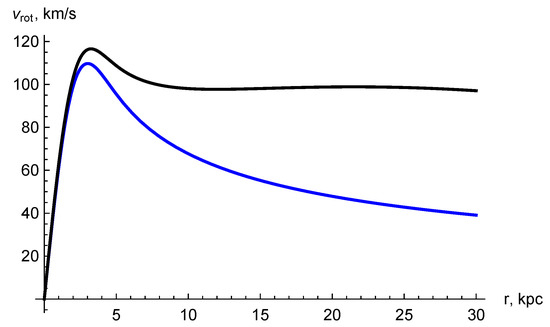
Figure 6.
The lower blue curve corresponds to the contribution of a galactic nucleus of baryonic matter, including specifically nucleus, bulge and disk. The upper black curve takes the vacuum -polarization into account. The form factor of a galaxy nuclei is taken as , , the accretion rate is of , i.e., 10 kPc, which corresponds to 32,000 years. The number of the minimally coupled scalar fields is of , and is assumed.
The rotational curve has some similarities with the conventional picture at , but in the conventional picture, the contribution of the galactic nucleus, bulge and disk are taken into account. We include all these components into the Gaussian form factor of galactic baryonic skeleton and call it “nucleus” in our oversimplified picture. Then, we permit it to increase (or decrease) with time and obtain vacuum polarization caused by this process.
7. Conclusions
We have considered two types of vacuum polarization corresponding to the F- and -types of metric perturbations in the CUM frame.
The F-type of spatially non-uniform vacuum polarization has the radiation-type equation of state. In the first order on perturbations, it is impossible to determine a form of the static gravitational potential around an astrophysical object. In the frameworks of a nonlinear heuristic model using the TOV equations for matter and radiation, it was found that the solution, which is non-singular at , only arises if an eicheon is present in the galaxy’s center. Eicheon is an analog of the black hole in GR and looks similar to an empty “nut” in the Schwarzschild-type metric. From this point of view, we assume that DM, as a vacuum polarization, arises only in the galaxies having an eicheon (i.e., a “black hole-like” object) in the center. Namely, the eicheon conjecture allows us to convert a singular solution for pure radiation into a non-singular physical one. Galaxies without an eicheon in the center (e.g., diffuse galaxies) do not have a DM halo4.
Under the oversimplified assumption of an isolated galaxy, the dark halo, in terms of a test particle’s rotation velocity, always increases with the distance from the galaxy’s center. Decreasing the halo could occur only due to a violation of the galaxy’s isolation, i.e., at the distance of ∼2 Mpc. It should be noted that the Andromeda galaxy is only 0.7 Mpc away. Generally, the galaxies tend to form clusters. These evident facts urge the development of a model of interacting galaxies with vacuum polarization.
For the -type of vacuum polarization, the renormalization of the gravitational constant (or Planck mass) has been found. This means that the gravitational constant found in the Earth, the Solar System, and galaxy observations is not equal (approximately four times less) to the gravitational constant used in cosmology to describe a spatially uniform universe. This fact does not influence the balance of the different kinds of matter in cosmology if one measures them in . Nevertheless, it increases the directly counted matter contribution fourfold, i.e., the luminous baryonic matter has to contribute -times stronger into the cosmological Friedmann equations.
The second effect of the -type polarization is the creation of the dark halo in the non-stationary process. It is found that the time-dependent evolving mass of the galaxy nuclei produces the gravitational potential of the dark halo-type. This point urges a more careful observational investigation of the possible non-stationary origin of the dark halo. However, the required time for the galaxy nuclei mass growth seems very short: ∼32,000 years. In such a situation, clarifying the physical status of the possible accretion of vacuum energy and vacuum condensates discussed in [68,69,70] is very desirable. In particular, it was shown in [68,69] that accretion of substance with the equation of state of (e.g., Higgs or QCD condensates) decreases a black hole mass, while accretion of the ordinary substance with radiation equation of state increases a black hole mass.
Investigations of these processes in the CUM metric with the applications to an eicheon are waiting. However, one may suggest some scenarios of a galaxy center evolution. Accretion by an eicheon could be more complicated than a traditional black hole. At some stage, eicheon could accrete more “dark radiation”, increasing its mass, but at some stage, it could accrete more condensates, decreasing its mass. One could associate this with the fast processes with a typical time of ∼32,000 years. Both growth of the galaxy’s center mass and its lowering produce a halo. Thus, a galaxy center is reminiscent of “Alice from Wonderland” [71], which takes a bit of a mushroom from one side and rises, then takes a bit from another side and shrinks. These processes can interlace in a galaxy center.
To summarize, it is possible to obtain an equation of the state of vacuum polarization, which is some kind of “æther”. It is challenging to find the “amount” of æther because it depends on the object’s entire history due to the nonlocality of the vacuum state on the curved background. Here, we have adjusted this “amount” to astrophysical observations. Thus, the obtained final results have, in some sense, a heuristic nature.
Author Contributions
Concepts and methodology are developed by S.L.C. and V.L.K.; software, S.L.C.; validation, writing and editing, S.L.C. and V.L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We emphasize that the presented consideration is heuristic because, although the linear system for the perturbation and the eikonal approximation for vacuum polarization seem trustable, we use its results in the nonlinear TOV model. Another point is that we empirically set the density of radiation (the vacuum polarization of F-type) in the center of an eicheon, i.e., at , of . That is, we do not calculate it from the first principles, i.e., we use only the equation of state from the eikonal calculations.
Let us consider the system of Equations (18)–(23) for an empty space–time with the vacuum polarization of F-type in the form of radiation fluid. For , the constant in Equation (6) can be chosen in such a way that there is no evolution of the scale factor, i.e., (a static universe).
Let us also place into this universe some amount of a dust matter obeying and without a uniform component, i.e., , . The complete solution of the system (18)–(23) takes the form
Then, in accordance with (38), the energy density for a F-vacuum polarization is expressed approximately as
which gives
If we consider this equation as an additional equation to the system (18)–(23), we can find that the constants have to be zero and only term is permitted because
Thus, the static gravitational potential
of arbitrary form (because could be function of q) is permitted in the framework of a linear system of the equations considered.
Notes
| 1 | The CUM metric implies a preferred time foliation of space–time. Using the CUM metric per se does not predict some visible effects in the Solar System and all satellite experiments if their results are expressed in a gauge invariant way. At the same time, the use of the UV-cutoff at implies the Lorentz invariance violation. In the local particle physics experiments, it leads to effects of the order of , where is the typical energy of a particle, but certainly does not produce some restrictions for Earth and satellite experiments. However, as it will be shown below, the consideration of vacuum physics using CUM and could produce observable effects in a galaxy scale. |
| 2 | We consider only scalar perturbations because the vector and tensor perturbations do not perturb the matter. |
| 3 | For instance, see a DM vacuum model with the equation of state “running” from radiation-type to dark energy-type [20]. |
| 4 | The diffuse galaxy NGC1052-DF2 [66] seems to contain no DM, whereas another diffuse galaxy Dragonfly 44 is supposed to contain a lot of DM [67]. However, for the last, we do not know for definite whether or not there is an eicheon in its center. |
References
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Klimchitskaya, G.L. Whether an Enormously Large Energy Density of the Quantum Vacuum Is Catastrophic. Symmetry 2019, 11, 314. [Google Scholar] [CrossRef]
- Unruh, W.; Wald, R. Information loss. Rep. Progr. Phys. 2017, 80, 092002. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Lochan, K. Black Holes: Eliminating Information or Illuminating New Physics? Universe 2017, 3, 55. [Google Scholar] [CrossRef]
- Mizner, C.W.; Thorne, K.; Wheeler, J.A. Gravitation; Freeman: San Francisco, CA, USA, 1973; Volume 1. [Google Scholar]
- Landau, L.D.; Lifshitz, E. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 1975; Volume 2. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. An approach to the theory of gravity with an arbitrary reference level of energy density. Proc. Natl. Acad. Sci. Belarus Ser. Phys. Math. 2019, 55, 83. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Eicheons instead of Black holes. Phys. Scr. 2020, 95, 085009. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Cherkas, S.L.; Kalashnikov, V.L. A reference level of the Universe vacuum energy density and the astrophysical data. Fortschr. Phys. 2020, 68, 2000047. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Universe driven by the vacuum of scalar field: VFD model. In Proceedings of the International Conference “Problems of Practical Cosmology”, Saint Petersburg, Russia, 23–27 June 2008; pp. 135–140. [Google Scholar] [CrossRef]
- Iorio, L. Solar system planetary orbital motions and dark matter. J. Cosmol. Astropart. Phys. 2006, 2006, 002. [Google Scholar] [CrossRef]
- Freese, K. Review of Observational Evidence for Dark Matter in the Universe and in upcoming searches for Dark Stars. EAS Publ. Ser. 2009, 36, 113–126. [Google Scholar] [CrossRef]
- Oks, E. Brief review of recent advances in understanding dark matter and dark energy. New Astron. Rev. 2021, 93, 101632. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Bullock, J.S.; Governato, F.; Kuzio de Naray, R.; Peter, A.H. Cold dark matter: Controversies on small scales. Proc. Natl. Acad. Sci. USA 2015, 112, 12249–12255. [Google Scholar] [CrossRef]
- de Martino, I.; Chakrabarty, S.S.; Cesare, V.; Gallo, A.; Ostorero, L.; Diaferio, A. Dark matters on the scale of galaxies. Universe 2020, 6, 107. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Buchmueller, O.; Doglioni, C.; Wang, L.T. Search for dark matter at colliders. Nat. Phys. 2017, 13, 217–223. [Google Scholar] [CrossRef]
- Aprile, E.; Abe, K.; Agostini, F.; Maouloud, S.A.; Althueser, L.; Andrieu, B.; Angelino, E.; Angevaare, J.R.; Antochi, V.C.; Martin, D.A.; et al. Search for New Physics in Electronic Recoil Data from XENONnT. arXiv 2022, arXiv:2207.11330. [Google Scholar]
- Albareti, F.; Cembranos, J.; Maroto, A. Vacuum energy as dark matter. Phys. Rev. D 2014, 90, 123509. [Google Scholar] [CrossRef]
- Hajdukovic, D.S. Quantum vacuum and dark matter. Astrophys. Space Sci. 2012, 337, 9–14. [Google Scholar] [CrossRef]
- Penner, A.R. Gravitational anti-screening as an alternative to dark matter. Astrophys. Space Sci. 2016, 361, 124. [Google Scholar] [CrossRef][Green Version]
- Hajdukovic, D. On the gravitational field of a point-like body immersed in a quantum vacuum. Mon. Not. R. Astron. Soc. 2019, 491, 4816–4828. [Google Scholar] [CrossRef]
- Fiscaletti, D. About dark matter as an emerging entity from elementary energy density fluctuations of a three-dimensional quantum vacuum. J. Theor. Appl. Phys. 2020, 14, 203–222. [Google Scholar] [CrossRef]
- Penner, A.R. A relativistic mass dipole gravitational theory and its connections with AQUAL. Class. Quant. Grav. 2022, 39, 075001. [Google Scholar] [CrossRef]
- Blanchet, L.; Le Tiec, A. Model of dark matter and dark energy based on gravitational polarization. Phys. Rev. D 2008, 78, 024031. [Google Scholar] [CrossRef]
- Chardin, G.; Dubois, Y.; Manfredi, G.; Miller, B.; Stahl, C. MOND-like behavior in the Dirac–Milne universe. Astron. Astrophys. 2021, 652, A91. [Google Scholar] [CrossRef]
- Huang, K. A Superfluid Universe; World Scientific: Singapore, 2016. [Google Scholar]
- Sbitnev, V.I. Hydrodynamics of the physical vacuum: Dark matter is an illusion. Mod. Phys. Lett. A 2015, 30, 1550184. [Google Scholar] [CrossRef]
- Zloshchastiev, K.G. An alternative to dark matter and dark energy: Scale-dependent gravity in superfluid vacuum theory. Universe 2020, 6, 180. [Google Scholar] [CrossRef]
- Hamber, H.; Liu, S. On the quantum corrections to the Newtonian potential. Phys. Lett. B 1995, 357, 51–56. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Renormalization group improved black hole spacetimes. Phys. Rev. D 2000, 62, 043008. [Google Scholar] [CrossRef]
- Ward, B. Quantum corrections to Newton’s law. Mod. Phys. Lett. A 2002, 17, 2371–2381. [Google Scholar] [CrossRef]
- Kirilin, G.G.; Khriplovich, I.B. Quantum power correction to the Newton law. J. Exp. Theor. Phys. 2002, 95, 981–986. [Google Scholar] [CrossRef]
- Satz, A.; Mazzitelli, F.D.; Alvarez, E. Vacuum polarization around stars: Nonlocal approximation. Phys. Rev. D 2005, 71, 064001. [Google Scholar] [CrossRef]
- Morley, T.; Winstanley, E.; Taylor, P. Vacuum polarization on topological black holes with Robin boundary conditions. Phys. Rev. D 2021, 103, 045007. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davis, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Arnowitt, R.; Deser, S.; Misner, C.W. Republication of: The dynamics of general relativity. Gen. Rel. Grav. 2008, 40, 1997. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Quantization of the inhomogeneous Bianchi I model: Quasi-Heisenberg picture. Nonlin. Phenom. Complex Syst. 2015, 18, 1–14. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Structure of the compact astrophysical objects in the conformally-unimodular metric. J. Belarusian State Univ. Phys. 2020, 3, 97–111. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Determination of the UV cut-off from the observed value of the Universe acceleration. J. Cosmol. Astropart. Phys. 2007, 01, 028. [Google Scholar] [CrossRef][Green Version]
- Cherkas, S.L.; Kalashnikov, V.L. The equation of vacuum state and the structure formation in universe. Vestn. Brest Univ. Ser. Fiz.-Mat. 2021, 1, 41–59. [Google Scholar] [CrossRef]
- Visser, M. Lorentz Invariance and the Zero-Point Stress-Energy Tensor. Particles 2018, 1, 138–154. [Google Scholar] [CrossRef]
- Visser, M. The Pauli sum rules imply BSM physics. Phys. Lett. B 2019, 791, 43–47. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Cherkas, S.; Kalashnikov, V. Dark-Energy-Matter from Vacuum owing to the General Covariance Violation. Nonlin. Phenom. Complex Syst. 2020, 23, 332–337. [Google Scholar] [CrossRef]
- Mattingly, D. Modern tests of Lorentz invariance. Liv. Rev. Relat. 2005, 8, 5. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Quantum-spacetime phenomenology. Liv. Rev. Relat. 2013, 16, 5. [Google Scholar] [CrossRef]
- Bluhm, R.; Yang, Y. Gravity with Explicit Diffeomorphism Breaking. Symmetry 2021, 13, 660. [Google Scholar] [CrossRef]
- Anber, M.M.; Aydemir, U.; Donoghue, J.F. Breaking diffeomorphism invariance and tests for the emergence of gravity. Phys. Rev. D 2010, 81, 084059. [Google Scholar] [CrossRef]
- Mavromatos, N.E. On CPT symmetry: Cosmological, quantum-gravitational and other possible violations and their phenomenology. In Beyond the Desert 2003; Springer: Berlin/Heidelberg, Germany, 2004; pp. 43–72. [Google Scholar]
- Nilsson, N.A. Aspects of Lorentz and CPT Violation in Cosmology. Ph.D. Thesis, National Centre for Nuclear Research, Otwock-Świerk, Poland, 2020. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. Plasma perturbations and cosmic microwave background anisotropy in the linearly expanding Milne-like universe. In Fractional Dynamics, Anomalous Transport and Plasma Science; Skiadas, C.H., Ed.; Springer: Cham, Switzerland, 2018; Chapter 9. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Is there an Aether? Nature 1951, 168, 906–907. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Wave optics of quantum gravity for massive particles. Phys. Scr. 2021, 96, 115001. [Google Scholar] [CrossRef]
- Czyz, W.; Maximon, L. High energy, small angle elastic scattering of strongly interacting composite particles. Ann. Phys. (NY) 1969, 52, 59–121. [Google Scholar] [CrossRef]
- Kabat, D.; Ortiz, M. Eikonal quantum gravity and planckian scattering. Nucl. Phys. B 1992, 388, 570–592. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Rahaman, F.; Nandi, K.; Bhadra, A.; Kalam, M.; Chakraborty, K. Perfect fluid dark matter. Phys. Lett. B 2010, 694, 10–15. [Google Scholar] [CrossRef]
- Sofue, Y. Rotation Curve and Mass Distribution in the Galactic Center—From Black Hole to Entire Galaxy. Publ. Astron. Soc. Jpn. 2013, 65, 118. [Google Scholar] [CrossRef]
- Riotto, A. Inflation and the Theory of Cosmological Perturbations. In Proceedings of the Summer School on Astroparticles Physics and Cosmology, Trieste, Italy, 17 June–5 July 2002; pp. 317–417. [Google Scholar]
- Hu, W. Covariant Linear Perturbation Formalism. In Proceedings of the Summer School on Astroparticles Physics and Cosmology, Trieste, Italy, 17 June–5 July 2002; pp. 147–185. [Google Scholar]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- van Dokkum, P.; Danieli, S.; Cohen, Y.; Merritt, A.; Romanowsky, A.J.; Abraham, R.; Brodie, J.; Conroy, C.; Lokhorst, D.; Mowla, L.; et al. A galaxy lacking dark matter. Nature 2018, 555, 629–632. [Google Scholar] [CrossRef]
- van Dokkum, P.; Abraham, R.; Brodie, J.; Conroy, C.; Danieli, S.; Merritt, A.; Mowla, L.; Romanowsky, A.; Zhang, J. A high stellar velocity dispersion and 100 globular clusters for the ultra-diffuse galaxy Dragonfly 44. Astr. J. Lett. 2016, 828, L6. [Google Scholar] [CrossRef]
- Babichev, E.; Dokuchaev, V.; Eroshenko, Y. Black Hole Mass Decreasing due to Phantom Energy Accretion. Phys. Rev. Lett. 2004, 93, 021102. [Google Scholar] [CrossRef]
- Babichev, E.O. The Accretion of Dark Energy onto a Black Hole. J. Exp. Theor. Phys. 2005, 100, 528. [Google Scholar] [CrossRef]
- Sun, C.-Y. Dark Energy Accretion onto a Black Hole in an Expanding Universe. Comm. Theor. Phys. 2009, 52, 441–444. [Google Scholar] [CrossRef]
- Carroll, L. Alice’s Adventures in Wonderland; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).