Monte Carlo Models of Comet Dust Tails Observed from the Ground
Abstract
1. Introduction
2. Description of the Monte Carlo Code
2.1. Assumption of Particle Sphericity
2.2. Particle Physical Properties
2.3. Particle Ejection Velocities
2.4. Computation of Particle Orbits
2.5. Computation of Particle Flux
3. Application of the Monte Carlo Code to Different Targets
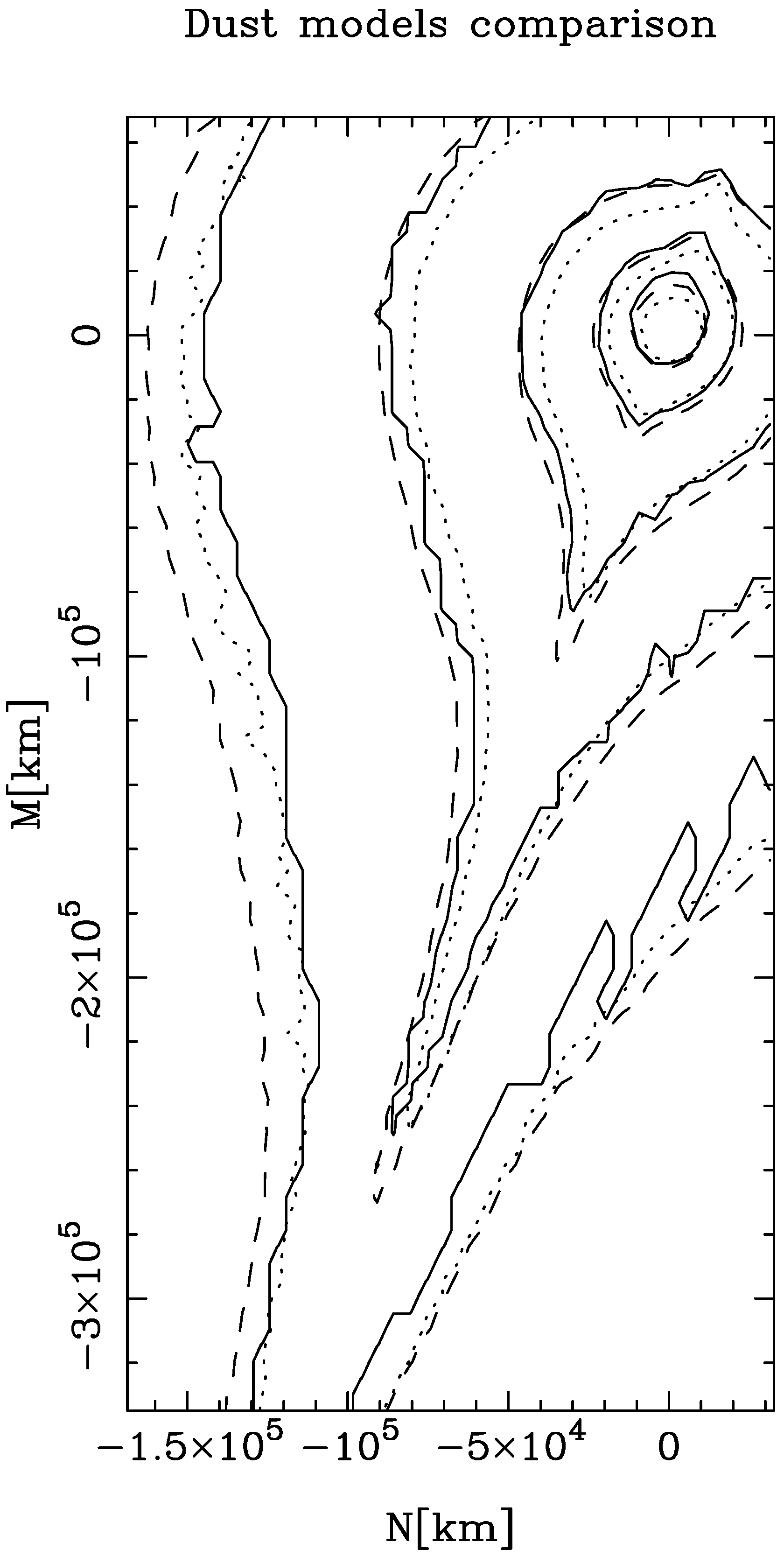
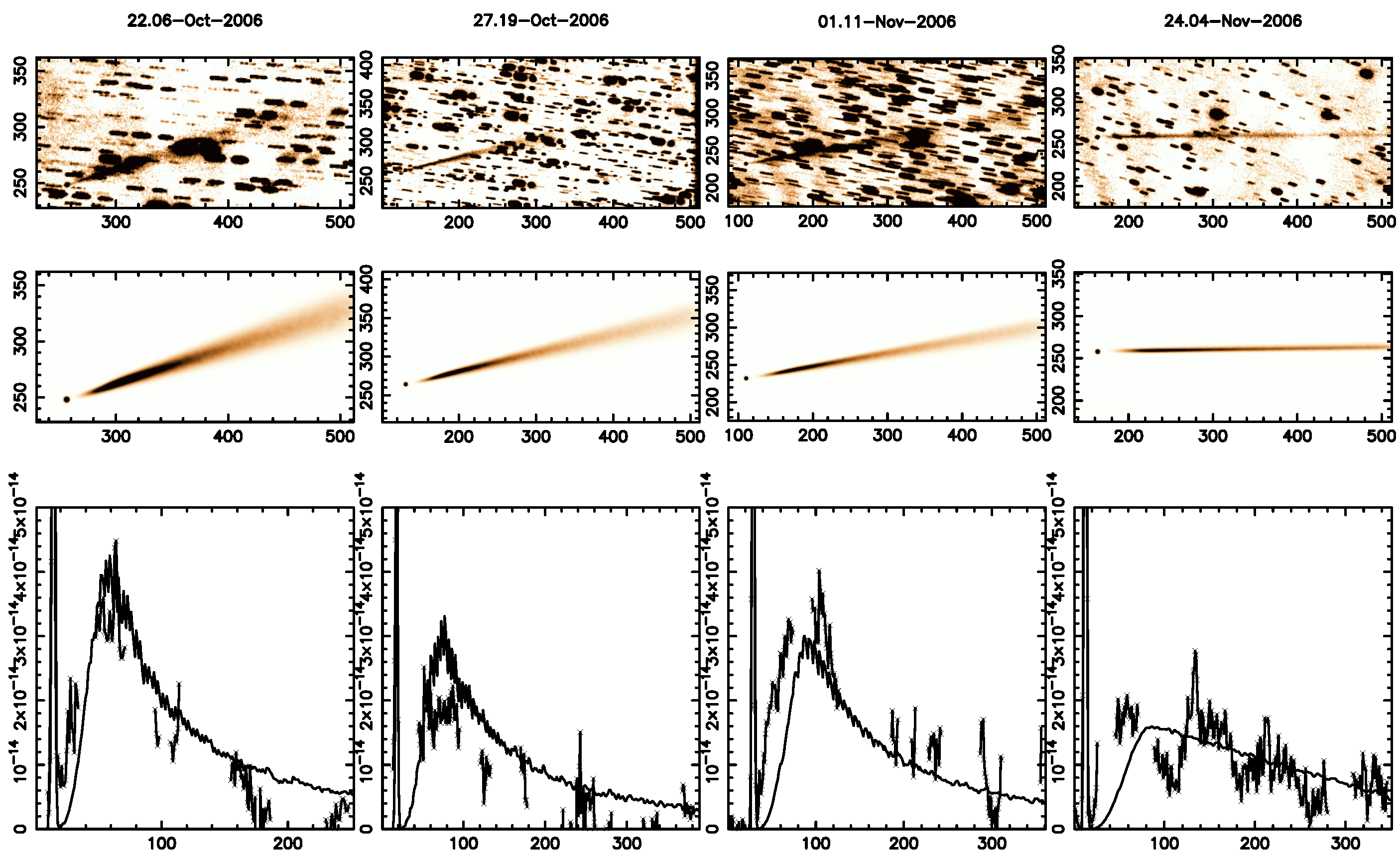
3.1. A Conspicuous Short-Period Comet: 67P/Churyumov-Gerasimenko
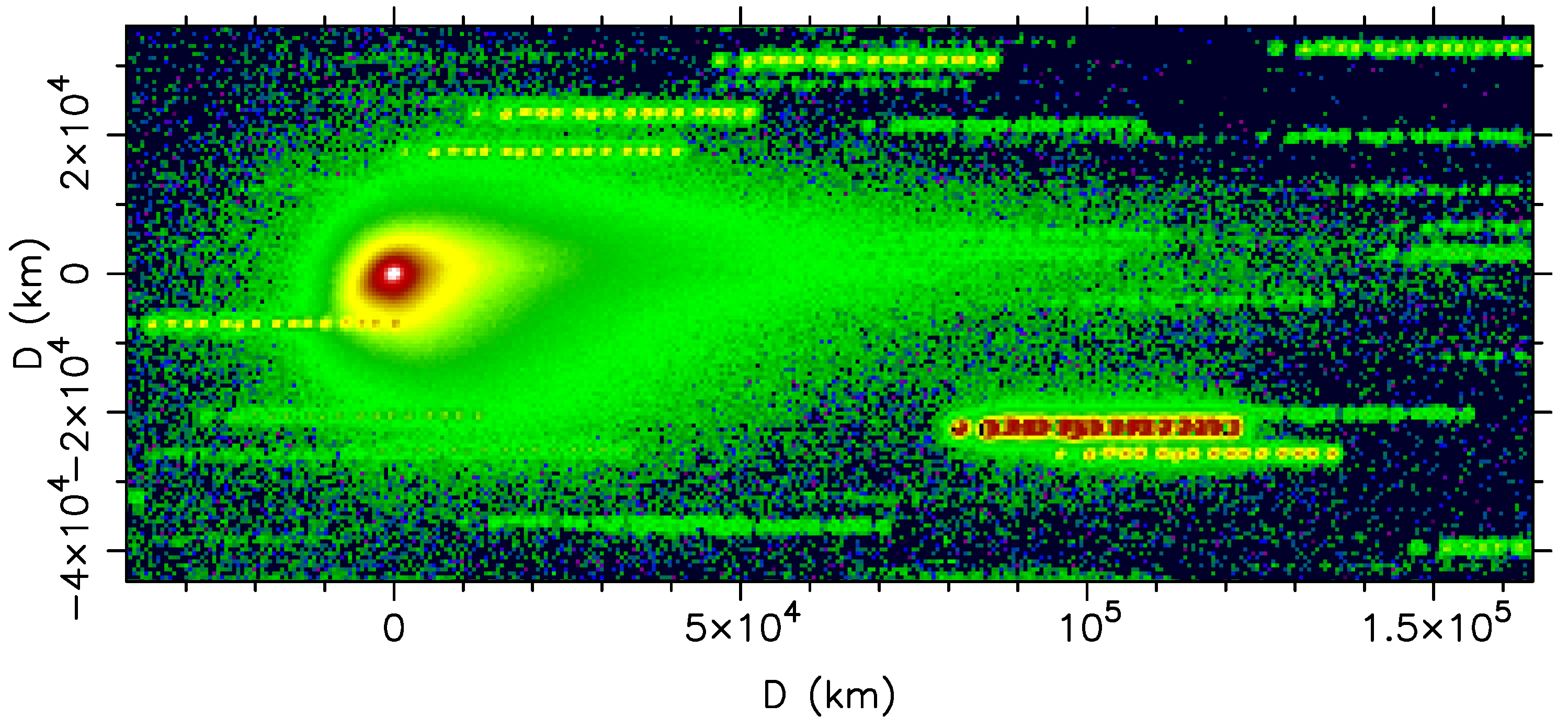
3.2. Another Peculiar Short-Period Comet: 249P/LINEAR
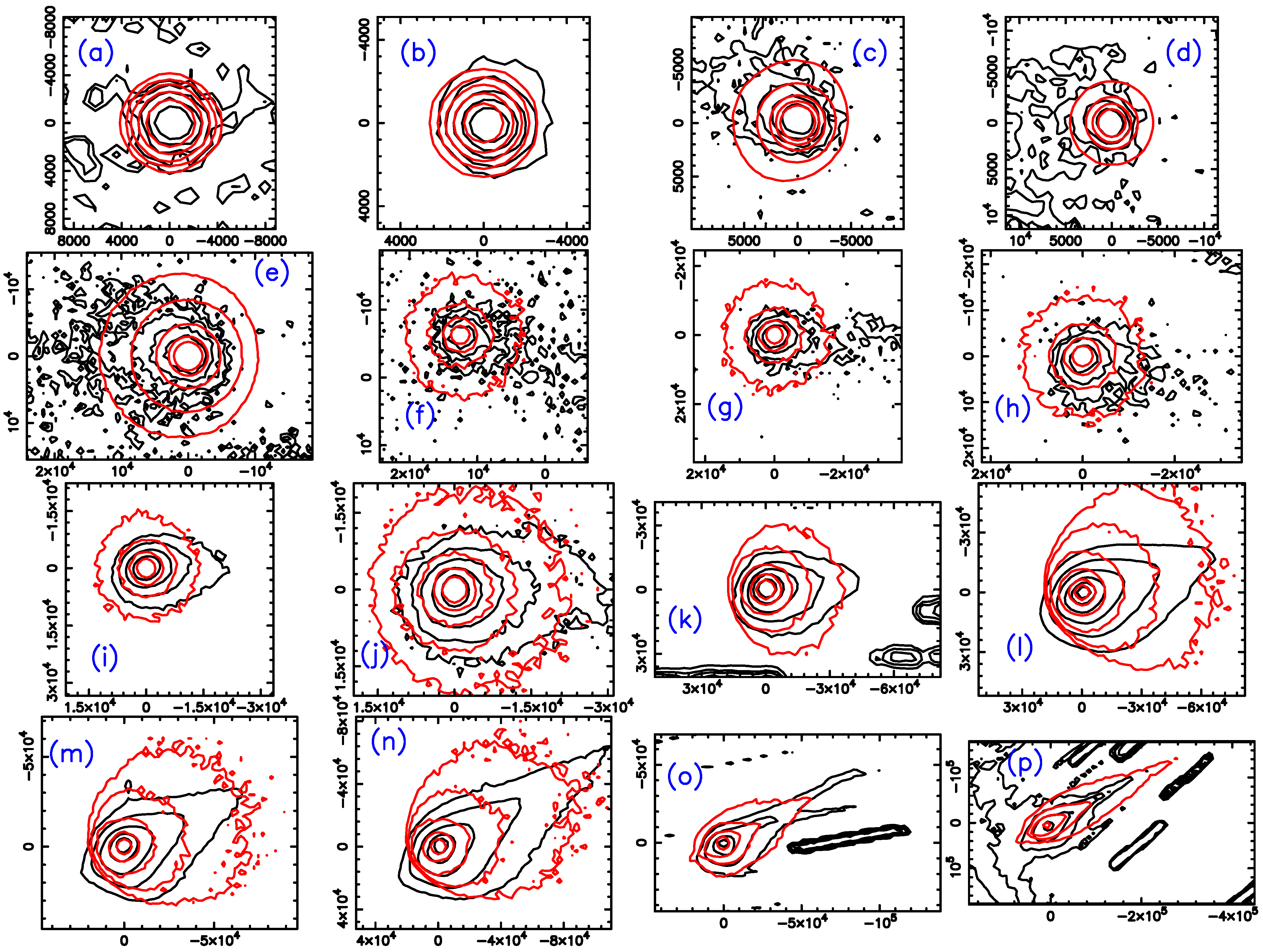
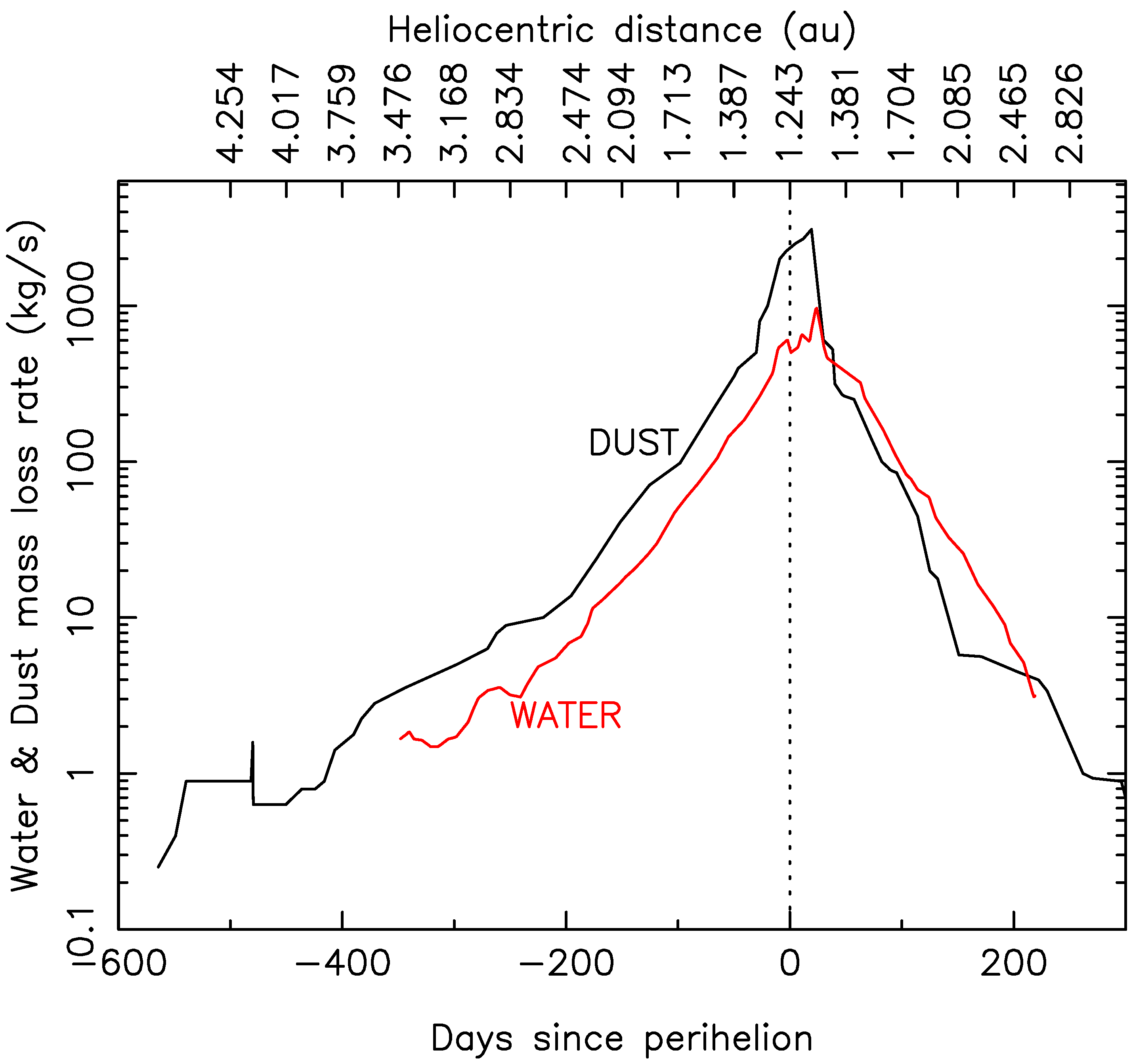
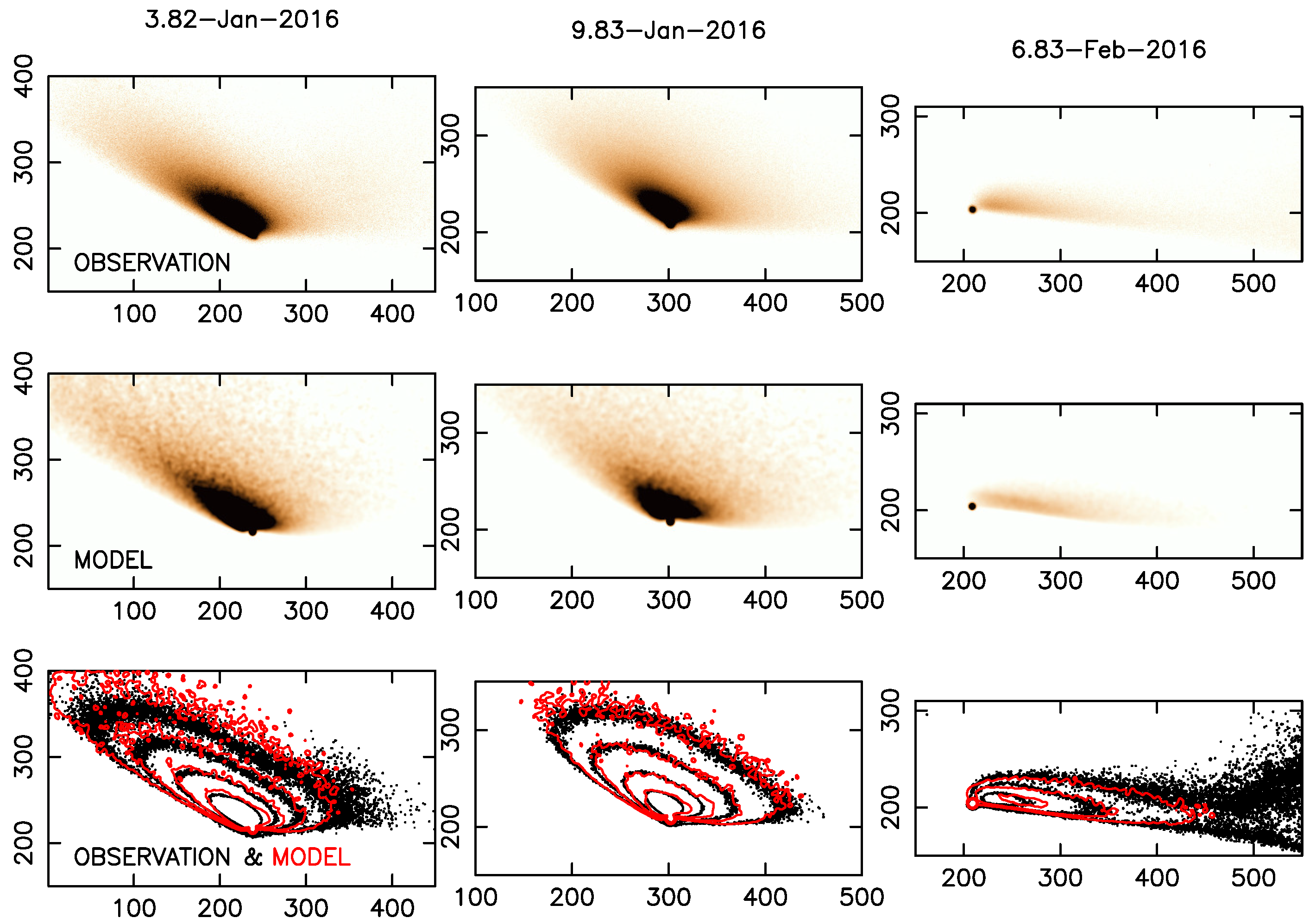
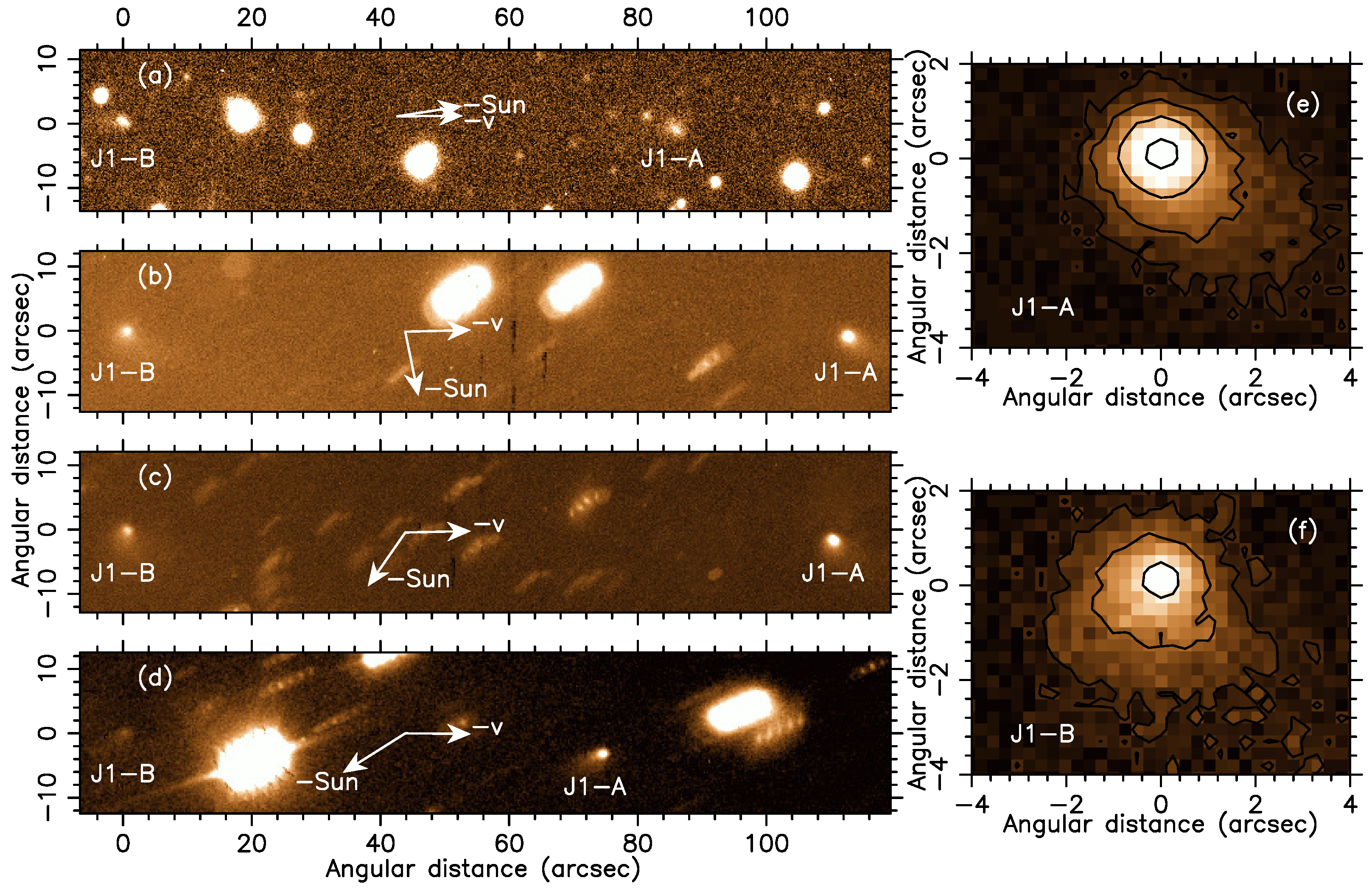
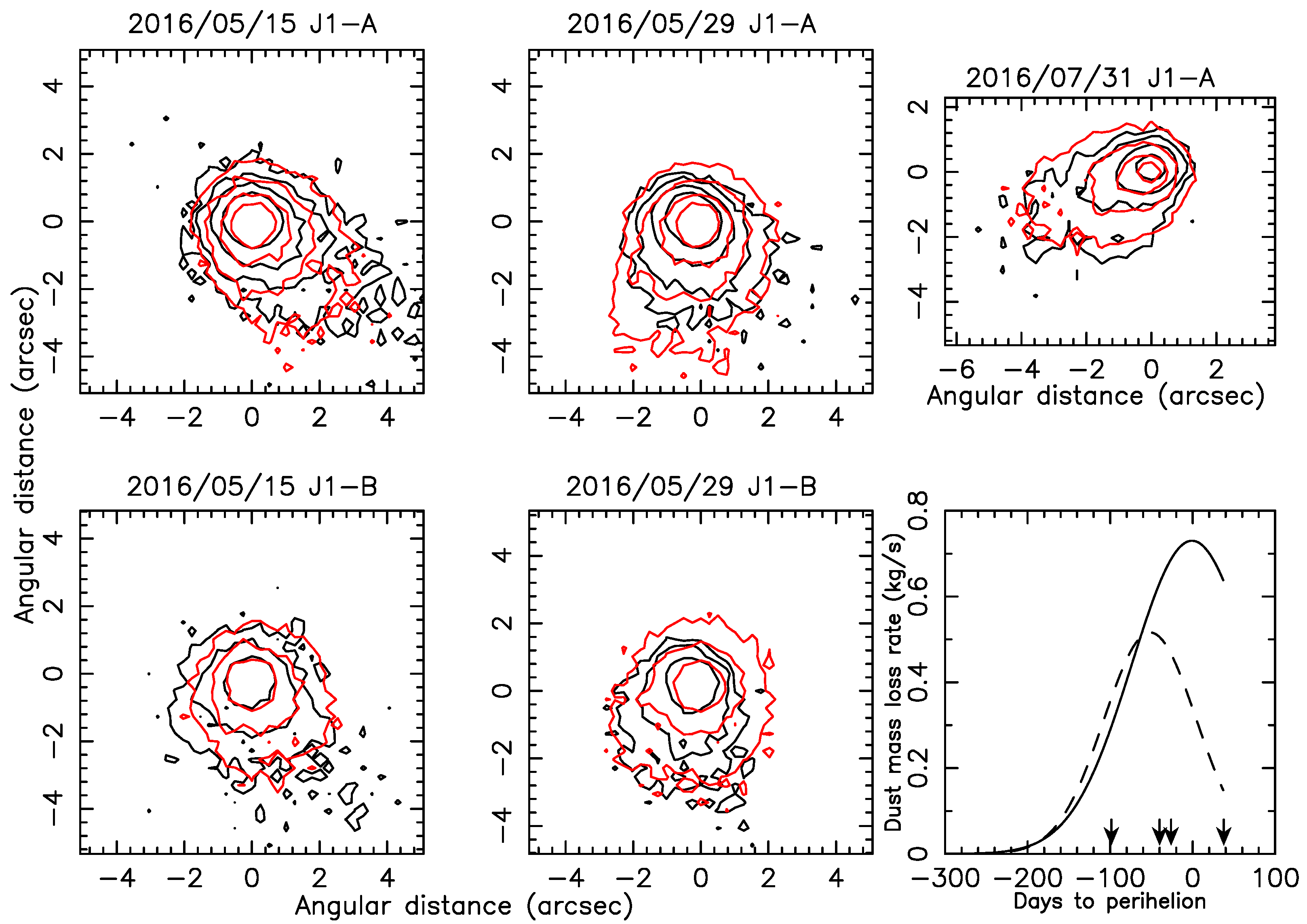
3.3. A Double-Component, Ice-Driven Activity Active Asteroid: P/2016 J1 (PANSTARRS)
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brownlee, D.; Joswiak, D.; Matrajt, G. Overview of the rocky component of Wild 2 comet samples: Insight into the early solar system, relationship with meteoritic materials and the differences between comets and asteroids. Meteor. Planet. Sci. 2012, 47, 453–470. [Google Scholar] [CrossRef]
- Blum, J.; Gundlach, B.; Krause, M.; Fulle, M.; Johansen, A.; Agarwal, J.; von Borstel, I.; Shi, X.; Hu, X.; Bentley, M.S.; et al. Evidence for the formation of comet 67P/Churyumov-Gerasimenko through gravitational collapse of a bound clump of pebbles. Mon. Not. R. Astron. Soc. 2017, 469, S755–S773. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Green, S.F.; Gundlach, B.; Herique, A.; Moreno, F.; Mottola, S.; Rotundi, A.; Snodgrass, C. The refractory-to-ice mass ratio in comets. Mon. Not. R. Astron. Soc. 2019, 482, 3326–3340. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Rotundi, A.; Gundlach, B.; Güttler, C.; Zakharov, V. How comets work: Nucleus erosion versus dehydration. Mon. Not. R. Astron. Soc. 2020, 493, 4039–4044. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Rotundi, A. How Comets Work. Astrophys. J. 2019, 879, L8. [Google Scholar] [CrossRef]
- Burns, J.A.; Lamy, P.L.; Soter, S. Radiation forces on small particles in the solar system. Icar 1979, 40, 1–48. [Google Scholar] [CrossRef]
- Meech, K.J.; Hainaut, O.R.; Marsden, B.G. Comet nucleus size distributions from HST and Keck telescopes. Icar 2004, 170, 463–491. [Google Scholar] [CrossRef]
- Fulle, M. Evaluation of cometary dust parameters from numerical simulations: Comparison with an analytical approach and the role of anisotropic emissions. Astron. Astrophys. 1989, 217, 283–297. [Google Scholar]
- Fulle, M. Motion of cometary dust. In Comets II; Festou, M., Keller, H.U., Weaver, H.A., Eds.; University of Arizona Press: Tucson, AZ, USA, 2004; pp. 565–575. [Google Scholar]
- Muñoz, O.; Frattin, E.; Jardiel, T.; Gómez-Martín, J.C.; Moreno, F.; Ramos, J.L.; Guirado, D.; Peiteado, M.; Caballero, A.C.; Milli, J.; et al. Retrieving Dust Grain Sizes from Photopolarimetry: An Experimental Approach. Astrophys. J. Suppl. Ser. 2021, 256, 17. [Google Scholar] [CrossRef]
- Kolokolova, L.; Das, H.S.; Dubovik, O.; Lapyonok, T.; Yang, P. Polarization of cosmic dust simulated with the rough spheroid model. Planet. Space Sci. 2015, 116, 30–38. [Google Scholar] [CrossRef]
- Rosenbush, V.K.; Ivanova, O.V.; Kiselev, N.N.; Kolokolova, L.O.; Afanasiev, V.L. Spatial variations of brightness, colour and polarization of dust in comet 67P/Churyumov-Gerasimenko. Mon. Not. R. Astron. Soc. 2017, 469, S475–S491. [Google Scholar] [CrossRef]
- Zubko, E.; Videen, G.; Hines, D.C.; Shkuratov, Y. The positive-polarization of cometary comae. Planet. Space Sci. 2016, 123, 63–76. [Google Scholar] [CrossRef]
- Güttler, C.; Mannel, T.; Rotundi, A.; Merouane, S.; Fulle, M.; Bockelée-Morvan, D.; Lasue, J.; Levasseur-Regourd, A.C.; Blum, J.; Naletto, G.; et al. Synthesis of the morphological description of cometary dust at comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2019, 630, A24. [Google Scholar] [CrossRef]
- Levasseur-Regourd, A.-C.; Agarwal, J.; Cottin, H.; Engrand, C.; Flynn, G.; Fulle, M.; Gombosi, T.; Langevin, Y.; Lasue, J.; Mannel, T.; et al. Cometary Dust. Space Sci. Rev. 2018, 214, 64. [Google Scholar] [CrossRef]
- Colangeli, L.; Lopez-Moreno, J.J.; Palumbo, P.; Rodriguez, J.; Cosi, M.; Corte, V.D.; Esposito, F.; Fulle, M.; Herranz, M.; Jeronimo, J.M.; et al. The Grain Impact Analyser and Dust Accumulator (GIADA) Experiment for the Rosetta Mission: Design, Performances and First Results. Space Sci. Rev. 2007, 128, 803–821. [Google Scholar] [CrossRef]
- Della Corte, V.; Rotundi, A.; Fulle, M.; Gruen, E.; Weissman, P.; Sordini, R.; Ferrari, M.; Ivanovski, S.; Lucarelli, F.; Accolla, M.; et al. GIADA: Shining a light on the monitoring of the comet dust production from the nucleus of 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2015, 583, A13. [Google Scholar] [CrossRef]
- Della Corte, V.; Rotundi, A.; Fulle, M.; Ivanovski, S.; Green, S.F.; Rietmeijer, F.J.M.; Colangeli, L.; Palumbo, P.; Sordini, R.; Ferrari, M.; et al. 67P/C-G inner coma dust properties from 2.2 au inbound to 2.0 au outbound to the Sun. Mon. Not. R. Astron. Soc. 2016, 462, S210–S219. [Google Scholar] [CrossRef]
- Fulle, M.; Marzari, F.; Corte, V.D.; Fornasier, S.; Sierks, H.; Rotundi, A.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Koschny, D.; et al. Evolution of the Dust Size Distribution of Comet 67P/Churyumov-Gerasimenko from 2.2 au to Perihelion. Astrophys. J. 2016, 821, 19. [Google Scholar] [CrossRef]
- Riedler, W.; Torkar, K.; Jeszenszky, H.; Romstedt, J.; Alleyne, H.S.C.; Arends, H.; Barth, W.; Biezen, J.V.D.; Butler, B.; Ehrenfreund, P.; et al. MIDAS The Micro-Imaging Dust Analysis System for the Rosetta Mission. Space Sci. Rev. 2007, 128, 869–904. [Google Scholar] [CrossRef]
- Bentley, M.S.; Schmied, R.; Mannel, T.; Torkar, K.; Jeszenszky, H.; Romstedt, J.; Levasseur-Regourd, A.; Weber, I.; Jessberger, E.K.; Ehrenfreund, P.; et al. Aggregate dust particles at comet 67P/Churyumov-Gerasimenko. Nature 2016, 537, 73–75. [Google Scholar] [CrossRef]
- Mannel, T.; Bentley, M.S.; Schmied, R.; Jeszenszky, H.; Levasseur-Regourd, A.C.; Romstedt, J.; Torkar, K. Fractal cometary dust—A window into the early Solar system. Mon. Not. R. Astron. Soc. 2016, 462, S304–S311. [Google Scholar] [CrossRef]
- Kissel, J.; Altwegg, K.; Clark, B.C.; Colangeli, L.; Cottin, H.; Czempiel, S.; Eibl, J.; Engrand, C.; Fehringer, H.M.; Feuerbacher, B.; et al. COSIMA—High Resolution Time-of-Flight Secondary Ion Mass Spectrometer for the Analysis of Cometary Dust Particles onboard Rosetta. Space Sci. Rev. 2007, 128, 823–867. [Google Scholar] [CrossRef]
- Paquette, J.A.; Engrand, C.; Stenzel, O.; Hilchenbach, M.; Kissel, J. Searching for calcium-aluminum-rich inclusions in cometary particles with Rosetta/COSIMA. Meteor. Planet. Sci. 2016, 51, 1340–1352. [Google Scholar] [CrossRef]
- Cremonese, G.; Fulle, M.; Cambianica, P.; Munaretto, G.; Capria, M.T.; Forgia, F.L.; Lazzarin, M.; Migliorini, A.; Boschin, W.; Milani, G.; et al. Dust Environment Model of the Interstellar Comet 2I/Borisov. Astrophys. J. 2020, 893, L12. [Google Scholar] [CrossRef]
- Fulle, M.; Della Corte, V.; Rotundi, A.; Green, S.F.; Accolla, M.; Colangeli, L.; Ferrari, M.; Ivanovski, S.; Sordini, R.; Zakharov, V. The dust-to-ices ratio in comets and Kuiper belt objects. Mon. Not. R. Astron. Soc. 2017, 469, S45–S49. [Google Scholar] [CrossRef]
- Markkanen, J.; Agarwal, J.; Väisänen, T.; Penttilä, A.; Muinonen, K. Interpretation of the Phase Functions Measured by the OSIRIS Instrument for Comet 67P/Churyumov-Gerasimenko. Astrophys. J. 2018, 868, L16. [Google Scholar] [CrossRef]
- Kimura, H.; Okamoto, H.; Mukai, T. Radiation Pressure and the Poynting-Robertson Effect for Fluffy Dust Particles. Icar 2002, 157, 349–361. [Google Scholar] [CrossRef]
- Moreno, F.; Guirado, D.; Muñoz, O.; Zakharov, V.; Ivanovski, S.; Fulle, M.; Rotundi, A.; Frattin, E.; Bertini, I. Dynamics of irregularly shaped cometary particles subjected to outflowing gas and solar radiative forces and torques. Mon. Not. R. Astron. Soc. 2022, 510, 5142–5153. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for periodic targets: Theory and tests. J. Opt. Soc. Am. A 2008, 25, 2693. [Google Scholar] [CrossRef]
- Fornasier, S.; Hasselmann, P.H.; Barucci, M.A.; Feller, C.; Besse, S.; Leyrat, C.; Lara, L.; Gutierrez, P.J.; Oklay, N.; Tubiana, C.; et al. Spectrophotometric properties of the nucleus of comet 67P/Churyumov-Gerasimenko from the OSIRIS instrument onboard the ROSETTA spacecraft. Astron. Astrophys. 2015, 583, A30. [Google Scholar] [CrossRef]
- Shevchenko, V.G. Analysis of Asteroid Brightness-Phase Relations. Sol. Syst. Res. 1997, 31, 219. [Google Scholar]
- Meech, K.J.; Jewitt, D.C. Observations of Comet P/Halley at minimum phase angle. Astron. Astrophys. 1987, 187, 585–593. [Google Scholar]
- Bertini, I.; Forgia, F.L.; Tubiana, C.; Güttler, C.; Fulle, M.; Moreno, F.; Frattin, E.; Kovacs, G.; Pajola, M.; Sierks, H.; et al. The scattering phase function of comet 67P/Churyumov-Gerasimenko coma as seen from the Rosetta/OSIRIS instrument. Mon. Not. R. Astron. Soc. 2017, 469, S404–S415. [Google Scholar] [CrossRef]
- Moreno, F.; Guirado, D.; Muñoz, O.; Bertini, I.; Tubiana, C.; Güttler, C.; Fulle, M.; Rotundi, A.; Corte, V.D.; Ivanovski, S.L.; et al. Models of Rosetta/OSIRIS 67P Dust Coma Phase Function. Astron. J. 2018, 156, 237. [Google Scholar] [CrossRef]
- Hörz, F.; Bastien, R.; Borg, J.; Bradley, J.P.; Bridges, J.C.; Brownlee, D.E.; Burchell, M.J.; Chi, M.; Cintala, M.J.; Dai, Z.R.; et al. Impact Features on Stardust: Implications for Comet 81P/Wild 2 Dust. Science 2006, 314, 1716. [Google Scholar] [CrossRef]
- McDonnell, J.A.M.; Lamy, P.L.; Pankiewicz, G.S. Comets in the Post-Halley Era; Newburn, R.L., Neugebauer, M., Rahe, J., Eds.; Kluwer: Dordretch, The Netherlands, 1991; p. 1043. [Google Scholar]
- McDonnell, J.A.M.; McBride, N.; Beard, R.; Bussoletti, E.; Colangeli, L.; Eberhardt, P.; Firth, J.G.; Grard, R.; Green, S.F.; Greenberg, J.M. Dust particle impacts during the Giotto encounter with comet Grigg-Skjellerup. Nature 1993, 362, 732–734. [Google Scholar] [CrossRef]
- Keller, H.U.; Barbieri, C.; Lamy, P.; Rickman, H.; Rodrigo, R.; Wenzel, K.-P.; Sierks, H.; A’Hearn, M.F.; Angrilli, F.; Angulo, M.; et al. OSIRIS—The Scientific Camera System Onboard Rosetta. Space Sci. Rev. 2007, 128, 433–506. [Google Scholar] [CrossRef]
- Della Corte, V.; Rotundi, A.; Zakharov, V.; Ivanovski, S.; Palumbo, P.; Fulle, M.; Longobardo, A.; Dionnet, Z.; Liuzzi, V.; Salatti, M. GIADA microbalance measurements on board Rosetta: Submicrometer- to micrometer-sized dust particle flux in the coma of comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2019, 630, A25. [Google Scholar] [CrossRef]
- Bockelée-Morvan, D.; Rinaldi, G.; Erard, S.; Leyrat, C.; Capaccioni, F.; Drossart, P.; Filacchione, G.; Migliorini, A.; Quirico, E.; Mottola, S.; et al. Comet 67P outbursts and quiescent coma at 1.3 au from the Sun: Dust properties from Rosetta/VIRTIS-H observations. Mon. Not. R. Astron. Soc. 2017, 469, S443–S458, Erratum in Mon. Not. R. Astron. Soc. 2017, 469, S842–S843. [Google Scholar] [CrossRef]
- Moreno, F.; Snodgrass, C.; Hainaut, O.; Tubiana, C.; Sierks, H.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Koschny, D.; Rickman, H.; et al. The dust environment of comet 67P/Churyumov-Gerasimenko from Rosetta OSIRIS and VLT observations in the 4.5 to 2.9 AU heliocentric distance range inbound. Astron. Astrophys. 2016, 587, A155. [Google Scholar] [CrossRef]
- Hadamcik, E.; Levasseur-Regourd, A.C. Dust evolution of comet C/1995 O1 (Hale-Bopp) by imaging polarimetric observations. Astron. Astrophys. 2003, 403, 757–768. [Google Scholar] [CrossRef]
- Bagnulo, S.; Cellino, A.; Kolokolova, L.; Nežič, R.; Santana-Ros, T.; Borisov, G.; Christou, A.A.; Bendjoya, P.; Devogèle, M. Unusual polarimetric properties for interstellar comet 2I/Borisov. Nat. Commun. 2021, 12, 1797. [Google Scholar] [CrossRef]
- Price, O.; Jones, G.H.; Morrill, J.; Owens, M.; Battams, K.; Morgan, H.; Drückmuller, M.; Deiries, S. Fine-scale structure in cometary dust tails I: Analysis of striae in Comet C/2006 P1 (McNaught) through temporal mapping. Icar 2019, 319, 540–557. [Google Scholar] [CrossRef]
- Sekanina, Z.; Farrell, J.A. The striated dust tail of Comet West 1976 VI as a particle fragmentation phenomenon. Astron. J. 1980, 85, 1538–1554. [Google Scholar] [CrossRef]
- Grün, E.; Gustafson, B.; Mann, I.; Baguhl, M.; Morfill, G.E.; Staubach, P.; Taylor, A.; Zook, H.A. Interstellar dust in the heliosphere. Astron. Astrophys. 1994, 286, 915–924. [Google Scholar]
- Mukai, T. On the charge distribution of interplanetary grains. Astron. Astrophys. 1981, 99, 1–6. [Google Scholar]
- Moreno, F.; Pozuelos, F.; Aceituno, F.; Casanova, V.; Sota, A.; Castellano, J.; Reina, E. Comet 22P/Kopff: Dust Environment and Grain Ejection Anisotropy from Visible and Infrared Observations. Astrophys. J. 2012, 752, 136. [Google Scholar] [CrossRef]
- Landgraf, M. Modeling the motion and distribution of interstellar dust inside the heliosphere. J. Phys. Conf. Ser. 2000, 105, 10303–10316. [Google Scholar] [CrossRef]
- Crifo, J.-F.; Loukianov, G.A.; Rodionov, A.V.; Zakharov, V.V. Direct Monte Carlo and multifluid modeling of the circumnuclear dust coma. Spherical grain dynamics revisited. Icar 2005, 176, 192–219. [Google Scholar] [CrossRef]
- Marschall, R.; Su, C.C.; Liao, Y.; Thomas, N.; Altwegg, K.; Sierks, H.; Ip, W.-H.; Keller, H.U.; Knollenberg, J.; Kührt, E.; et al. Modelling observations of the inner gas and dust coma of comet 67P/Churyumov-Gerasimenko using ROSINA/COPS and OSIRIS data: First results. Astron. Astrophys. 2016, 589, A90. [Google Scholar] [CrossRef]
- Tenishev, V.; Combi, M.R.; Rubin, M. Numerical Simulation of Dust in a Cometary Coma: Application to Comet 67P/Churyumov-Gerasimenko. Astrophys. J. 2011, 732, 104. [Google Scholar] [CrossRef]
- Zakharov, V.V.; Rodionov, A.V.; Fulle, M.; Ivanovski, S.L.; Bykov, N.Y.; Della Corte, V.; Rotundi, A. Practical relations for assessments of the gas coma parameters. Icar 2021, 354, 114091. [Google Scholar] [CrossRef]
- Rotundi, A.; Sierks, H.; Corte, V.D.; Fulle, M.; Gutierrez, P.J.; Lara, L.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Koschny, D.; et al. Dust measurements in the coma of comet 67P/Churyumov-Gerasimenko inbound to the Sun. Science 2015, 347, aaa3905. [Google Scholar] [CrossRef]
- Wallis, M.K. Comets; Wilkening, L.L., Ed.; Tucson University Press: Tucson, AZ, USA, 1982; pp. 357–369. [Google Scholar]
- Moreno, F.; Muñoz, O.; Gutiérrez, P.J.; Lara, L.M.; Snodgrass, C.; Lin, Z.Y.; Della Corte, V.; Rotundi, A.; Yagi, M. The dust environment of comet 67P/Churyumov-Gerasimenko: Results from Monte Carlo dust tail modelling applied to a large ground-based observation data set. Mon. Not. R. Astron. Soc. 2017, 469, S186–S194. [Google Scholar] [CrossRef]
- Whipple, F.L. A Comet Model. II. Physical Relations for Comets and Meteors. Astrophys. J. 1951, 113, 464. [Google Scholar] [CrossRef]
- Finson, M.J.; Probstein, R.F. A theory of dust comets. I. Model and equations. Astrophys. J. 1968, 154, 327–352. [Google Scholar] [CrossRef]
- Langland-Shula, L.E.; Smith, G.H. Comet classification with new methods for gas and dust spectroscopy. Icar 2011, 213, 280–322. [Google Scholar] [CrossRef]
- Hanner, M.S.; Gehrz, R.D.; Harker, D.E.; Hayward, T.L.; Lynch, D.K.; Mason, C.C.; Russell, R.W.; Williams, D.M.; Wooden, D.H.; Woodward, C.E. Thermal Emission from the Dust Coma of Comet Hale-Bopp and the Composition of the Silicate Grains. Earth Moon Planets 1997, 79, 247–264. [Google Scholar] [CrossRef]
- Reach, W.T.; Vaubaillon, J.; Lisse, C.M.; Holloway, M.; Rho, J. Explosion of Comet 17P/Holmes as revealed by the Spitzer Space Telescope. Icar 2010, 208, 276–292. [Google Scholar] [CrossRef]
- Ishiguro, M. Cometary dust trail associated with Rosetta mission target: 67P/Churyumov Gerasimenko. Icar 2008, 193, 96–104. [Google Scholar] [CrossRef][Green Version]
- Sykes, M.V.; Walker, R.G. Cometary dust trails I. Survey. Icar 1992, 95, 180–210. [Google Scholar] [CrossRef]
- Kimura, H.; Liu, C.-P. On the structure of cometary dust tails. AcASn 1975, 16, 138–166. [Google Scholar]
- Tubiana, C.; Barrera, L.; Drahus, M.; Boehnhardt, H. Comet 67P/Churyumov-Gerasimenko at a large heliocentric distance. Astron. Astrophys. 2008, 490, 377–386. [Google Scholar] [CrossRef]
- Kelley, M.S.; Reach, W.T.; Lien, D.J. The dust trail of Comet 67P/Churyumov Gerasimenko. Icar 2008, 193, 572–587. [Google Scholar] [CrossRef]
- Agarwal, J.; Müller, M.; Reach, W.T.; Sykes, M.V.; Boehnhardt, H.; Grün, E. The dust trail of Comet 67P/Churyumov-Gerasimenko between 2004 and 2006. Icar 2010, 207, 992–1012. [Google Scholar] [CrossRef]
- Fulle, M.; Barbieri, C.; Cremonese, G.; Rauer, H.; Weiler, M.; Milani, G.; Ligustri, R. The dust environment of comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2004, 422, 357–368. [Google Scholar] [CrossRef]
- Moreno, F.; Lara, L.M.; Muñoz, O.; López-Moreno, J.J.; Molina, A. Dust in Comet 67P/Churyumov-Gerasimenko. Astrophys. J. 2004, 613, 1263–1269. [Google Scholar] [CrossRef][Green Version]
- Fulle, M.; Colangeli, L.; Agarwal, J.; Aronica, A.; Corte, V.D.; Esposito, F.; Grün, E.; Ishiguro, M.; Ligustri, R.; López-Moreno, J.J.; et al. Comet 67P/Churyumov-Gerasimenko: The GIADA dust environment model of the Rosetta mission target. Astron. Astrophys. 2010, 522, A63. [Google Scholar] [CrossRef]
- Agarwal, J.; A’Hearn, M.F.; Vincent, J.-B.; Güttler, C.; Höfner, S.; Sierks, H.; Tubiana, C.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; et al. Acceleration of individual, decimetre-sized aggregates in the lower coma of comet 67P/Churyumov-Gerasimenko. Mon. Not. R. Astron. Soc. 2016, 462, S78–S88. [Google Scholar] [CrossRef]
- Hansen, K.C.; Altwegg, K.; Berthelier, J.-J.; Bieler, A.; Biver, N.; Bockelée-Morvan, D.; Calmonte, U.; Capaccioni, F.; Combi, M.R.; Keyser, J.D.; et al. Evolution of water production of 67P/Churyumov-Gerasimenko: An empirical model and a multi-instrument study. Mon. Not. R. Astron. Soc. 2016, 462, S491–S506. [Google Scholar] [CrossRef]
- Tubiana, C.; Snodgrass, C.; Bertini, I.; Mottola, S.; Vincent, J.-B.; Lara, L.; Fornasier, S.; Knollenberg, J.; Thomas, N.; Fulle, M.; et al. 67P/Churyumov-Gerasimenko: Activity between March and June 2014 as observed from Rosetta/OSIRIS. Astron. Astrophys. 2015, 573, A62. [Google Scholar] [CrossRef]
- Fernández, J.A.; Licandro, J.; Moreno, F.; Sosa, A.; Cabrera-Lavers, A.; de León, J.; Birtwhistle, P. Physical and dynamical properties of the anomalous comet 249P/LINEAR. Icar 2017, 295, 34–45. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Jewitt, D. The Active Asteroids. Astron. J. 2012, 143, 66. [Google Scholar] [CrossRef]
- Snodgrass, C.; Jones, G.H.; Boehnhardt, H.; Gibbings, A.; Homeister, M.; Andre, N.; Beck, P.; Bentley, M.S.; Bertini, I.; Bowles, N.; et al. The Castalia mission to Main Belt Comet 133P/Elst-Pizarro. AdSpR 2018, 62, 1947–1976. [Google Scholar] [CrossRef]
- Moreno, F.; Pozuelos, F.J.; Novaković, B.; Licandro, J.; Cabrera-Lavers, A.; Bolin, B.; Jedicke, R.; Gladman, B.J.; Bannister, M.T.; Gwyn, S.D.J.; et al. The Splitting of Double-component Active Asteroid P/2016 J1 (PANSTARRS). Astrophys. J. 2017, 837, L3. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno, F. Monte Carlo Models of Comet Dust Tails Observed from the Ground. Universe 2022, 8, 366. https://doi.org/10.3390/universe8070366
Moreno F. Monte Carlo Models of Comet Dust Tails Observed from the Ground. Universe. 2022; 8(7):366. https://doi.org/10.3390/universe8070366
Chicago/Turabian StyleMoreno, Fernando. 2022. "Monte Carlo Models of Comet Dust Tails Observed from the Ground" Universe 8, no. 7: 366. https://doi.org/10.3390/universe8070366
APA StyleMoreno, F. (2022). Monte Carlo Models of Comet Dust Tails Observed from the Ground. Universe, 8(7), 366. https://doi.org/10.3390/universe8070366





