Formation of Comets
Abstract
1. Introduction
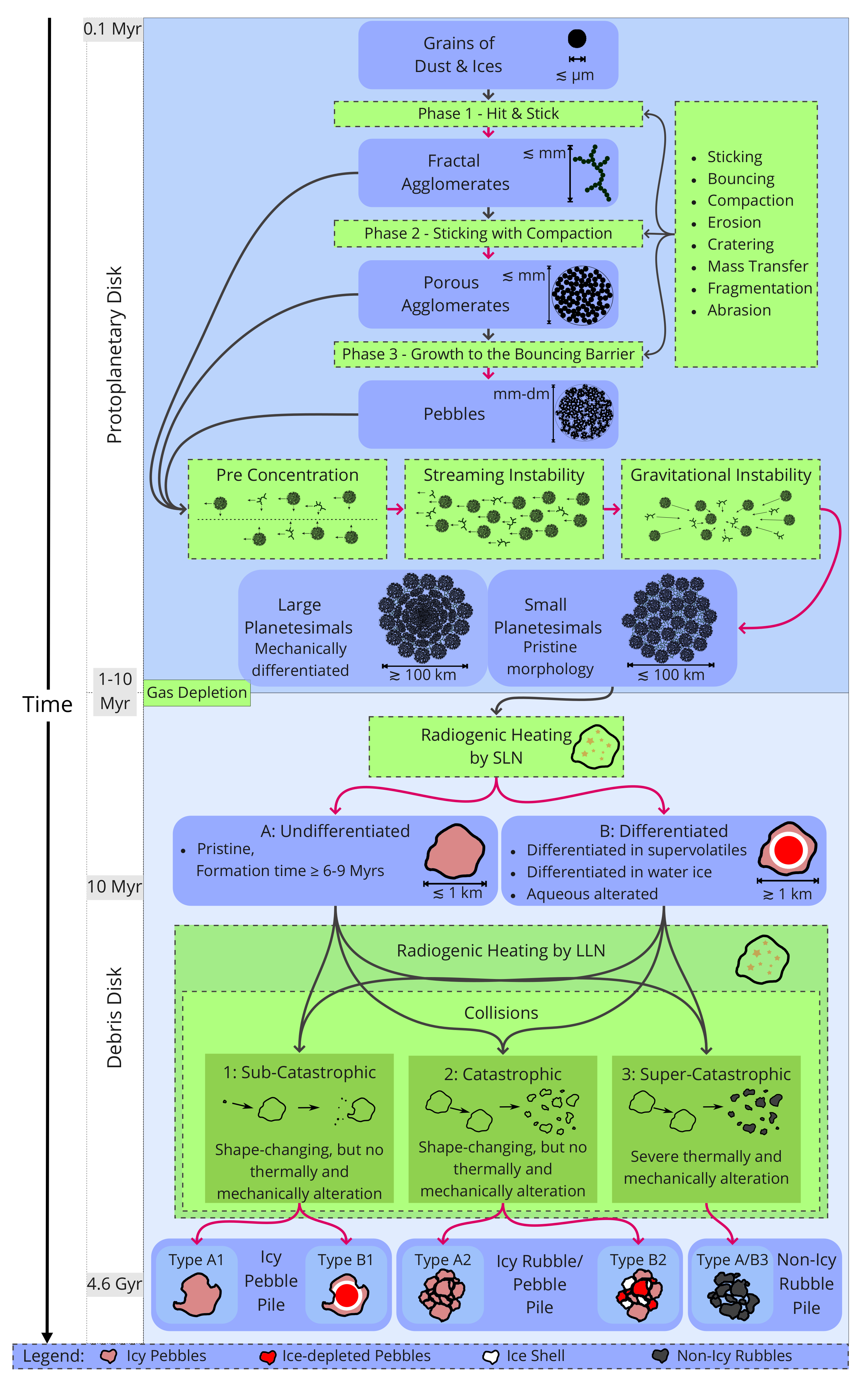
2. From Dust to Pebbles
2.1. Protoplanetary Discs
2.2. A Growth Scenario from Grains to Pebbles
3. Collapse of Pebble Clouds into Planetesimals
3.1. Pre-Concentration of Pebbles
3.2. Further Concentration of Pebbles by the Streaming Instability
3.3. Gravitational Collapse
4. Evolution of Planetesimals towards Comets
4.1. Radiogenic Heating
4.1.1. Short-Lived Radionuclides
4.1.2. Long-Lived Radionuclides
4.2. Collisional Evolution
- First, a collision can be sub-catastrophic if the largest fragment possesses at least half of the initial mass of the larger bodies. We assume that in this case, the mechanical bulk properties of the planetesimals are essentially conserved.
- Second, if the fragments are smaller, the collision is considered catastrophic. However, if the energy input into the colliding bodies was not sufficient to destroy the pebble structure, the fragments are still composed of pebbles, but the original bulk properties might have changed.
- Third, the collisions can be super-catastrophic, in which case the pebble structure and the pebbles themselves are destroyed by the collision event.
4.2.1. Sub-Catastrophic Collisions
4.2.2. Catastrophic Collisions
4.2.3. Super-Catastrophic Collisions
5. Discussion—Which Planetesimal Can Become a Comet?
- Icy Pebble Piles—Type A1 and Type B1
- Icy Rubble/Pebble Piles—Type A2 and Type B2
- Non-Icy Rubble Piles—Type A/B3
5.1. Intrinsic Physical Properties
5.1.1. Internal Morphology and Pebble Properties
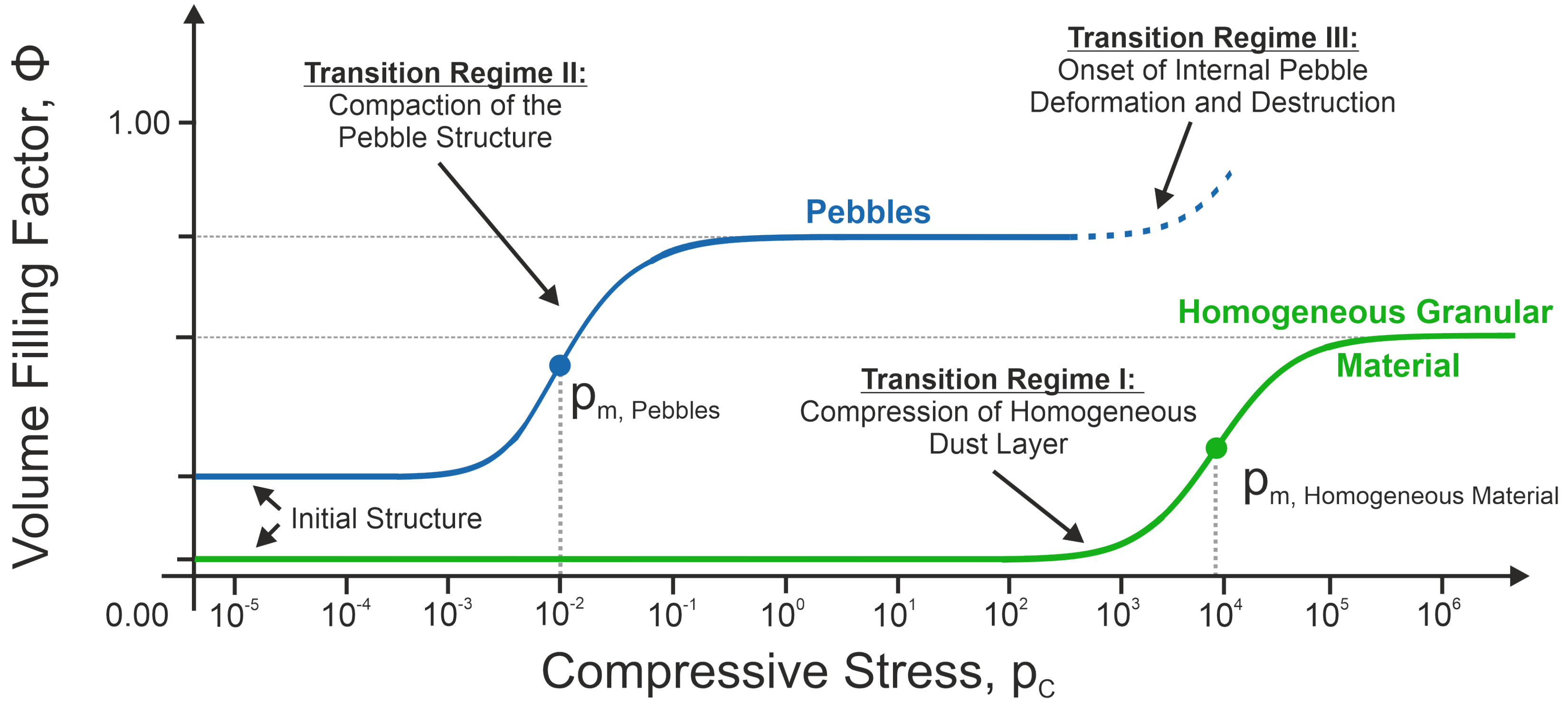
5.1.2. Bulk Porosity
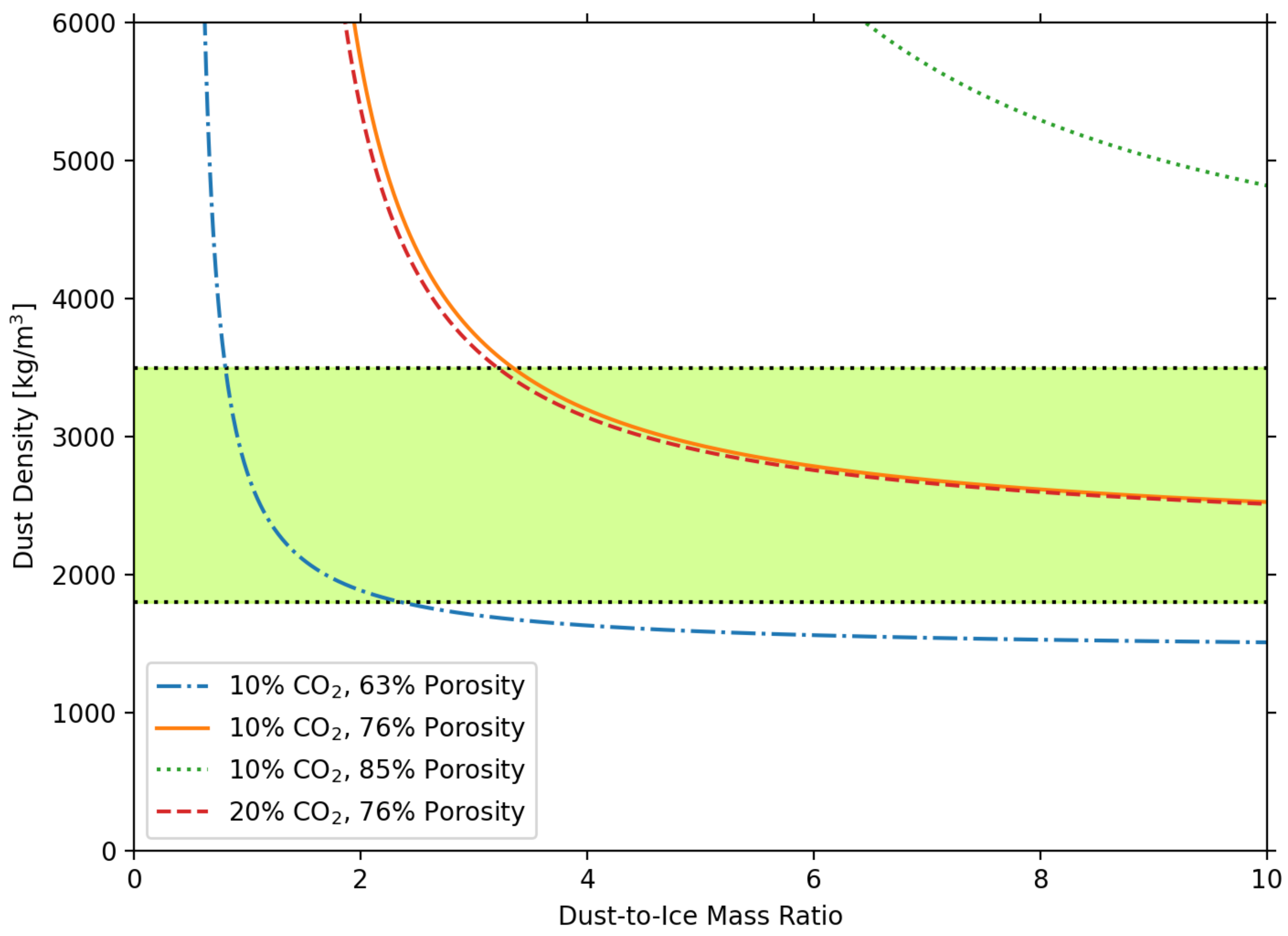
5.1.3. Dust-to-Ice Mass Ratio
5.1.4. Binarity, Flattening and Rotational Orientation
5.2. Derived Physical Properties
5.2.1. Cometary Activity
5.2.2. Thermal Conductivity
5.2.3. Tensile Strength
5.2.4. Compressive Strength
5.2.5. Gas Permeability
5.2.6. Permittivity
6. Conclusions and Open Questions
- i
- Strong positive correlation between the surface temperature at sunrise and the insolation at local noon for a subsurface made of pebbles, in contrast to no such dependency for a makeup without large void spaces [149], measurable by thermal IR mapping. Such measurements would deliver, from remote observations only, invaluable information about the presence and size of pebbles in a shallow subsurface layer.
- ii
- Proof of the absence or presence of internal volatile differentiation of comets, as predicted by [150] for comets consisting of pebbles, measurable by long-wavelength radar. Such measurements would deliver information about the formation time and/or abundance of radiogenic nuclei and about the thermal conductivity in the deep interior of the comet nucleus, and thus would confirm or disprove the gravitational-collapse theory.
- iii
- Search for traces of the collisional evolution of cometary nuclei, measurable by radar through the amplitude and length scale of internal inhomogeneities. Due to the obvious distinction of the internal makeup of bodies of type A1, B1, A2, B2 and A/B3 (see Figure 1), deep-penetrating radar measurements covering the entire body would provide information about the internal distribution of water ice, the refractory component and the void spaces inside the body.
- iv
- Determination of the physical properties and orbital parameters of extinct comets. Due to memory effect (see [134]) or differentiation (see [150]), the depth to which dust activity is possible strongly depends on the original size of the comet-precursor body, so larger comets should be going extinct on a different timescale than smaller ones (see [229]).
- v
- Determine whether positive relief features [106] are local remnants of impacts, measurable by high-frequency radar through local permittivity enhancement. If moderate-velocity impacts on the surface of a planetesimal lead to local compaction of the material and thus to loss of the pebble structure, further dust activity is impossible due to considerable enhancement of the tensile strength. Such measurements would deliver information about the collision history of the planetesimals and the abundance of small-scale (metre- to decimetre-sized) objects in the region in which the planetesimals resided throughout most of their lifetime before becoming comets.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- Kührt, E.; Keller, H.U. The Formation of Cometary Surface Crusts. Icarus 1994, 109, 121–132. [Google Scholar] [CrossRef]
- Güttler, C.; Mannel, T.; Rotundi, A.; Merouane, S.; Fulle, M.; Bockelée-Morvan, D.; Lasue, J.; Levasseur-Regourd, A.C.; Blum, J.; Naletto, G.; et al. Synthesis of the morphological description of cometary dust at comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2019, 630, A24. [Google Scholar] [CrossRef]
- Blum, J.; Gundlach, B.; Krause, M.; Fulle, M.; Johansen, A.; Agarwal, J.; von Borstel, I.; Shi, X.; Hu, X.; Bentley, M.S.; et al. Evidence for the formation of comet 67P/Churyumov-Gerasimenko through gravitational collapse of a bound clump of pebbles. Mon. Not. R. Astron. Soc. 2017, 469, S755–S773. [Google Scholar] [CrossRef]
- Weissman, P.; Morbidelli, A.; Davidsson, B.; Blum, J. Origin and Evolution of Cometary Nuclei. Space Sci. Rev. 2020, 216, 1–40. [Google Scholar] [CrossRef]
- Yorke, H.W.; Bodenheimer, P.; Laughlin, G. The formation of protostellar disks. I-1 M(solar). Astrophys. J. 1993, 411, 274. [Google Scholar] [CrossRef]
- Hueso, R.; Guillot, T. Evolution of protoplanetary disks: Constraints from DM Tauri and GM Aurigae. Astron. Astrophys. 2005, 442, 703–725. [Google Scholar] [CrossRef]
- Williams, J.P.; Cieza, L.A. Protoplanetary Disks and Their Evolution. Annu. Rev. Astron. Astrophys. 2011, 49, 67–117. [Google Scholar] [CrossRef]
- Andrews, S.M.; Huang, J.; Pérez, L.M.; Isella, A.; Dullemond, C.P.; Kurtovic, N.T.; Guzmán, V.V.; Carpenter, J.M.; Wilner, D.J.; Zhang, S.; et al. The Disk Substructures at High Angular Resolution Project (DSHARP). I. Motivation, Sample, Calibration, and Overview. Astrophys. J. Lett. 2018, 869, L41. [Google Scholar] [CrossRef]
- Huang, J.; Andrews, S.M.; Cleeves, L.I.; Öberg, K.I.; Wilner, D.J.; Bai, X.; Birnstiel, T.; Carpenter, J.; Hughes, A.M.; Isella, A.; et al. CO and Dust Properties in the TW Hya Disk from High-resolution ALMA Observations. Astrophys. J. 2018, 852, 122. [Google Scholar] [CrossRef]
- Long, F.; Pinilla, P.; Herczeg, G.J.; Harsono, D.; Dipierro, G.; Pascucci, I.; Hendler, N.; Tazzari, M.; Ragusa, E.; Salyk, C.; et al. Gaps and Rings in an ALMA Survey of Disks in the Taurus Star-forming Region. Astrophys. J. 2018, 869, 17. [Google Scholar] [CrossRef]
- Liu, B.; Ji, J. A tale of planet formation: From dust to planets. Res. Astron. Astrophys. 2020, 20, 164. [Google Scholar] [CrossRef]
- Barenfeld, S.A.; Carpenter, J.M.; Ricci, L.; Isella, A. ALMA observations of circumstellar disks in the upper scorpius OB association. Astrophys. J. 2016, 827, 142. [Google Scholar] [CrossRef]
- Ansdell, M.; Williams, J.P.; van der Marel, N.; Carpenter, J.M.; Guidi, G.; Hogerheijde, M.; Mathews, G.S.; Manara, C.F.; Miotello, A.; Natta, A.; et al. ALMA survey of lupus protoplanetary disks. I. Dust and gas masses. Astrophys. J. 2016, 828, 46. [Google Scholar] [CrossRef]
- Pascucci, I.; Testi, L.; Herczeg, G.J.; Long, F.; Manara, C.F.; Hendler, N.; Mulders, G.D.; Krijt, S.; Ciesla, F.; Henning, T.; et al. A steeper than linear disk mass–stellar mass scaling relation. Astrophys. J. 2016, 831, 125. [Google Scholar] [CrossRef]
- Ansdell, M.; Williams, J.P.; Manara, C.F.; Miotello, A.; Facchini, S.; van der Marel, N.; Testi, L.; van Dishoeck, E.F. An ALMA Survey of Protoplanetary Disks in the σ Orionis Cluster. Astron. J. 2017, 153, 240. [Google Scholar] [CrossRef]
- Cieza, L.A.; Ruíz-Rodríguez, D.; Hales, A.; Casassus, S.; Pérez, S.; Gonzalez-Ruilova, C.; Cánovas, H.; Williams, J.P.; Zurlo, A.; Ansdell, M.; et al. The Ophiuchus DIsc Survey Employing ALMA (ODISEA)–I: Project description and continuum images at 28 au resolution. Mon. Not. R. Astron. Soc. 2019, 482, 698–714. [Google Scholar] [CrossRef]
- Mulders, G.D.; Pascucci, I.; Ciesla, F.J.; Fernandes, R.B. The Mass Budgets and Spatial Scales of Exoplanet Systems and Protoplanetary Disks. Astrophys. J. 2021, 920, 66. [Google Scholar] [CrossRef]
- Terry, J.P.; Hall, C.; Longarini, C.; Lodato, G.; Toci, C.; Veronesi, B.; Paneque-Carreño, T.; Pinte, C. Constraining protoplanetary disc mass using the GI wiggle. Mon. Not. R. Astron. Soc. 2021, 510, 1671–1679. [Google Scholar] [CrossRef]
- Tripathi, A.; Andrews, S.M.; Birnstiel, T.; Wilner, D.J. A millimeter Continuum Size–Luminosity Relationship for Protoplanetary Disks. Astrophys. J. 2017, 845, 44. [Google Scholar] [CrossRef]
- Hendler, N.; Pascucci, I.; Pinilla, P.; Tazzari, M.; Carpenter, J.; Malhotra, R.; Testi, L. The Evolution of Dust Disk Sizes from a Homogeneous Analysis of 1–10 Myr old Stars. Astrophys. J. 2020, 895, 126. [Google Scholar] [CrossRef]
- Li, M.; Huang, S.; Petaev, M.I.; Zhu, Z.; Steffen, J.H. Dust condensation in evolving discs and the composition of planetary building blocks. Mon. Not. R. Astron. Soc. 2020, 495, 2543–2553. [Google Scholar] [CrossRef]
- Pignatale, F.C.; Liffman, K.; Maddison, S.T.; Brooks, G. 2D condensation model for the inner Solar Nebula: An enstatite-rich environment. Mon. Not. R. Astron. Soc. 2016, 457, 1359–1370. [Google Scholar] [CrossRef]
- Gail, H.P. Radial mixing in protoplanetary accretion disks. Astron. Astrophys. 2004, 413, 571–591. [Google Scholar] [CrossRef]
- Podolak, M.; ZUCKER, S. A note on the snow line in protostellar accretion disks. Meteorit. Planet. Sci. 2004, 39, 1859–1868. [Google Scholar] [CrossRef]
- Hayashi, C. Structure of the Solar Nebula, Growth and Decay of Magnetic Fields and Effects of Magnetic and Turbulent Viscosities on the Nebula. Prog. Theor. Phys. Suppl. 1981, 70, 35–53. [Google Scholar] [CrossRef]
- Martin, R.G.; Livio, M. On the evolution of the snow line in protoplanetary discs. Mon. Not. R. Astron. Soc. Lett. 2012, 425, L6–L9. [Google Scholar] [CrossRef]
- Panić, O.; Min, M. Effects of disc midplane evolution on CO snowline location. Mon. Not. R. Astron. Soc. 2017, 467, 1175–1185. [Google Scholar] [CrossRef]
- Xiao, L.; Niu, R.; Zhang, H. Time evolution of the water snowline in viscous discs. Mon. Not. R. Astron. Soc. 2017, 467, 2869–2878. [Google Scholar] [CrossRef]
- Ros, K.; Johansen, A. Ice condensation as a planet formation mechanism. Astron. Astrophys. 2013, 552, A137. [Google Scholar] [CrossRef]
- Weidenschilling, S.J. Dust to planetesimals: Settling and coagulation in the solar nebula. Icarus 1980, 44, 172–189. [Google Scholar] [CrossRef]
- Weidenschilling, S.J. Aerodynamics of solid bodies in the solar nebula. Mon. Not. R. Astron. Soc. 1977, 180, 57–70. [Google Scholar] [CrossRef]
- Dominik, C.; Tielens, A.G.G.M. The Physics of Dust Coagulation and the Structure of Dust Aggregates in Space. Astrophys. J. 1997, 480, 647–673. [Google Scholar] [CrossRef]
- Blum, J. Experiments on Sticking, Restructuring, and Fragmentation of Preplanetary Dust Aggregates. Icarus 2000, 143, 138–146. [Google Scholar] [CrossRef]
- Blum, J.; Wurm, G. The Growth Mechanisms of Macroscopic Bodies in Protoplanetary Disks. Annu. Rev. Astron. Astrophys. 2008, 46, 21–56. [Google Scholar] [CrossRef]
- Wada, K.; Tanaka, H.; Suyama, T.; Kimura, H.; Yamamoto, T. Numerical Simulation of Dust Aggregate Collisions. II. Compression and Disruption of Three–Dimensional Aggregates in Head–on Collisions. Astrophys. J. 2008, 677, 1296–1308. [Google Scholar] [CrossRef]
- Wada, K.; Tanaka, H.; Suyama, T.; Kimura, H.; Yamamoto, T. Collisional growth conditions for dust aggregates. Astrophys. J. 2009, 702, 1490. [Google Scholar] [CrossRef]
- Güttler, C.; Blum, J.; Zsom, A.; Ormel, C.W.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? I. Mapping the zoo of laboratory collision experiments. Astron. Astrophys. 2010, 513, A56. [Google Scholar] [CrossRef]
- Schräpler, R.; Blum, J.; Krijt, S.; Raabe, J.H. The physics of protoplanetesimal dust agglomerates. X. High-velocity collisions between small and large dust agglomerates as growth barrier. Astrophys. J. 2018, 853, 74. [Google Scholar] [CrossRef]
- Jankowski, T.; Wurm, G.; Kelling, T.; Teiser, J.; Sabolo, W.; Gutiérrez, P.J.; Bertini, I. Crossing barriers in planetesimal formation: The growth of mm-dust aggregates with large constituent grains. Astron. Astrophys. 2012, 542, A80. [Google Scholar] [CrossRef]
- Gundlach, B.; Blum, J. The stickiness of micrometer-sized water-ice particles. Astrophys. J. 2015, 798, 34. [Google Scholar] [CrossRef]
- Kempf, S. N-Particle-Simulations of Dust Growth I. Growth Driven by Brownian Motion. Icarus 1999, 141, 388–398. [Google Scholar] [CrossRef]
- Blum, J.; Wurm, G.; Kempf, S.; Poppe, T.; Klahr, H.; Kozasa, T.; Rott, M.; Henning, T.; Dorschner, J.; Schräpler, R.; et al. Growth and form of planetary seedlings: Results from a microgravity aggregation experiment. Phys. Rev. Lett. 2000, 85, 2426–2429. [Google Scholar] [CrossRef]
- Krause, M.; Blum, J. Growth and form of planetary seedlings: Results from a sounding rocket microgravity aggregation experiment. Phys. Rev. Lett. 2004, 93, 021103. [Google Scholar] [CrossRef]
- Blum, J.; Schrapler, R.; Davidsson, B.J.R.; Trigo-Rodriguez, J.M. The Physics of Protoplanetesimal Dust Agglomerates. I. Mechanical Properties and Relations to Primitive Bodies in the Solar System. Astrophys. J. 2006, 652, 1768–1781. [Google Scholar] [CrossRef]
- Paszun, D.; Dominik, C. Collisional evolution of dust aggregates. From compaction to catastrophic destruction. Astron. Astrophys. 2009, 507, 1023–1040. [Google Scholar] [CrossRef]
- Blum, J.; Münch, M. Experimental Investigations on Aggregate-Aggregate Collisions in the Early Solar Nebula. Icarus 1993, 106, 151–167. [Google Scholar] [CrossRef]
- Beitz, E.; Güttler, C.; Blum, J.; Meisner, T.; Teiser, J.; Wurm, G. Low-velocity collisions of centimeter-sized dust aggregates. Astrophys. J. 2011, 736, 34. [Google Scholar] [CrossRef]
- Schräpler, R.; Blum, J. The physics of protoplanetesimal dust agglomerates. VI. Erosion of large aggregates as a source of micrometer-sized particles. Astrophys. J. 2011, 734, 108. [Google Scholar] [CrossRef]
- Deckers, J.; Teiser, J. COLLIDING DECIMETER DUST. Astrophys. J. 2013, 769, 151. [Google Scholar] [CrossRef]
- Bukhari Syed, M.; Blum, J.; Jansson, K.W.; Johansen, A. The role of pebble fragmentation in planetesimal formation. I. Experimental study. Astrophys. J. 2017, 834, 145. [Google Scholar] [CrossRef]
- Heißelmann, D.; Fraser, H.J.; Blum, J. Experimental Studies on the Aggregation Properties of Ice and Dust in Planet-Forming Regions. In Proceedings of the 58th International Astronautical Congress, Hyderabad, India, 24–28 September 2007. [Google Scholar]
- Weidling, R.; Güttler, C.; Blum, J. Free Collisions in a Microgravity Many-Particle Experiment. I. Dust Aggregate Sticking at Low Velocities. Icarus 2012, 218, 688–700. [Google Scholar] [CrossRef]
- Kothe, S.; Blum, J.; Weidling, R.; Güttler, C. Free Collisions in a Microgravity Many-Particle Experiment III: The Collision Behavior of sub-Millimeter-Sized Dust Aggregates. Icarus 2013, 225, 75–85. [Google Scholar] [CrossRef]
- Brisset, J.; Heißelmann, D.; Kothe, S.; Weidling, R.; Blum, J. Submillimetre-sized dust aggregate collision and growth properties. Astron. Astrophys. 2016, 593, A3. [Google Scholar] [CrossRef]
- Brisset, J.; Heißelmann, D.; Kothe, S.; Weidling, R.; Blum, J. Low-velocity collision behaviour of clusters composed of sub-millimetre sized dust aggregates. Astron. Astrophys. 2017, 603, A66. [Google Scholar] [CrossRef]
- Weidling, R.; Güttler, C.; Blum, J.; Brauer, F. The physics of protoplanetesimal dust agglomerates. III. Compaction in multiple collisions. Astrophys. J. 2009, 696, 2036–2043. [Google Scholar] [CrossRef]
- Wurm, G.; Paraskov, G.; Krauss, O. Growth of planetesimals by impacts at ∼25 m/s. Icarus 2005, 178, 253–263. [Google Scholar] [CrossRef]
- Teiser, J.; Wurm, G. Decimetre dust aggregates in protoplanetary discs. Astron. Astrophys. 2009, 505, 351–359. [Google Scholar] [CrossRef]
- Teiser, J.; Wurm, G. High-velocity dust collisions: Forming planetesimals in a fragmentation cascade with final accretion. Mon. Not. R. Astron. Soc. 2009, 393, 1584–1594. [Google Scholar] [CrossRef]
- Teiser, J.; Küpper, M.; Wurm, G. Impact angle influence in high velocity dust collisions during planetesimal formation. Icarus 2011, 215, 596–598. [Google Scholar] [CrossRef]
- Meisner, T.; Wurm, G.; Teiser, J.; Schywek, M. Preplanetary scavengers: Growing tall in dust collisions. Astron. Astrophys. 2013, 559, A123. [Google Scholar] [CrossRef]
- Deckers, J.; Teiser, J. Macroscopic dust in protoplanetary disks—From growth to destruction. Astrophys. J. 2014, 796, 99. [Google Scholar] [CrossRef]
- Wurm, G.; Paraskov, G.; Krauss, O. Ejection of dust by elastic waves in collisions between millimeter- and centimeter-sized dust aggregates at 16.5 to 37.5 m/s impact velocities. Phys. Rev. E 2005, 71, 021304. [Google Scholar] [CrossRef]
- Paraskov, G.B.; Wurm, G.; Krauss, O. Impacts into weak dust targets under microgravity and the formation of planetesimals. Icarus 2007, 191, 779–789. [Google Scholar] [CrossRef]
- Seizinger, A.; Speith, R.; Kley, W. Tensile and shear strength of porous dust agglomerates. Astron. Astrophys. 2013, 559, A19. [Google Scholar] [CrossRef][Green Version]
- Krijt, S.; Ormel, C.W.; Dominik, C.; Tielens, A.G.G.M. Erosion and the limits to planetesimal growth. Astron. Astrophys. 2015, 574, A83. [Google Scholar] [CrossRef]
- Bischoff, D.; Kreuzig, C.; Haack, D.; Gundlach, B.; Blum, J. Sticky or not sticky? Measurements of the tensile strength of microgranular organic materials. Mon. Not. R. Astron. Soc. 2020, 497, 2517–2528. [Google Scholar] [CrossRef]
- Kouchi, A.; Kudo, T.; Nakano, H.; Arakawa, M.; Watanabe, N.; Sirono, S.i.; Higa, M.; Maeno, N. Rapid Growth of Asteroids Owing to Very Sticky Interstellar Organic Grains. Astrophys. J. 2002, 566, L121–L124. [Google Scholar] [CrossRef]
- Kudo, T.; Kouchi, A.; Arakawa, M.; Nakano, H. The role of sticky interstellar organic material in the formation of asteroids. Meteorit. Planet. Sci. 2002, 37, 1975–1983. [Google Scholar] [CrossRef]
- Musiolik, G.; Teiser, J.; Jankowski, T.; Wurm, G. Collisions of CO2 ice grains in planet formation. Astrophys. J. 2016, 818, 16. [Google Scholar] [CrossRef]
- Arakawa, S.; Krijt, S. On the Stickiness of CO2 and H2O Ice Particles. Astrophys. J. 2021, 910, 130. [Google Scholar] [CrossRef]
- Zsom, A.; Ormel, C.W.; Güttler, C.; Blum, J.; Dullemond, C.P. The outcome of protoplanetary dust growth: Pebbles, boulders, or planetesimals? II. Introducing the bouncing barrier Astron. Astrophys. 2010, 513, A57. [Google Scholar] [CrossRef]
- Lorek, S.; Lacerda, P.; Blum, J. Local growth of dust- and ice-mixed aggregates as cometary building blocks in the solar nebula. Astron. Astrophys. 2018, 611, A18. [Google Scholar] [CrossRef]
- Van Boekel, R.; Min, M.; Leinert, C.; Waters, L.B.F.M.; Richichi, A.; Chesneau, O.; Dominik, C.; Jaffe, W.; Dutrey, A.; Graser, U.; et al. The building blocks of planets within the ’terrestrial’ region of protoplanetary disks. Nature 2004, 432, 479–482. [Google Scholar] [CrossRef] [PubMed]
- D’Alessio, P.; Calvet, N.; Hartmann, L.; Franco-Hernandez, R.; Servin, H. Effects of Dust Growth and Settling in T Tauri Disks. Astrophys. J. 2006, 638, 314–335. [Google Scholar] [CrossRef]
- Birnstiel, T.; Ricci, L.; Trotta, F.; Dullemond, C.P.; Natta, A.; Testi, L.; Dominik, C.; Henning, T.; Ormel, C.W.; Zsom, A. Testing the theory of grain growth and fragmentation by millimeter observations of protoplanetary disks. Astron. Astrophys. 2010, 516, L14. [Google Scholar] [CrossRef]
- Ricci, L.; Testi, L.; Natta, A.; Brooks, K.J. Dust grain growth in ρ-Ophiuchi protoplanetary disks. Astron. Astrophys. 2010, 521, A66. [Google Scholar] [CrossRef]
- Pérez, L.M.; Carpenter, J.M.; Chandler, C.J.; Isella, A.; Andrews, S.M.; Ricci, L.; Calvet, N.; Corder, S.A.; Deller, A.T.; Dullemond, C.P.; et al. Constraints on the radial variation of grain growth in the AS 209 circumstellar disk. Astrophys. J. Lett. 2012, 760, L17. [Google Scholar] [CrossRef]
- Trotta, F.; Testi, L.; Natta, A.; Isella, A.; Ricci, L. Constraints on the radial distribution of the dust properties in the CQ Tauri protoplanetary disk. Astron. Astrophys. 2013, 558, A64. [Google Scholar] [CrossRef][Green Version]
- Testi, L.; Birnstiel, T.; Ricci, L.; Andrews, S.; Blum, J.; Carpenter, J.; Dominik, C.; Isella, A.; Natta, A.; Williams, J.; et al. Dust Evolution in Protoplanetary Disks. Protostars Planets VI 2014, 914, 339–361. [Google Scholar] [CrossRef]
- Pérez, L.M.; Chandler, C.J.; Isella, A.; Carpenter, J.M.; Andrews, S.M.; Calvet, N.; Corder, S.A.; Deller, A.T.; Dullemond, C.P.; Greaves, J.S.; et al. Grain growth in the circumstellar disks of the young stars CY Tau and DoAr 25. Astrophys. J. 2015, 813, 41. [Google Scholar] [CrossRef]
- Tazzari, M.; Testi, L.; Ercolano, B.; Natta, A.; Isella, A.; Chandler, C.J.; Pérez, L.M.; Andrews, S.; Wilner, D.J.; Ricci, L.; et al. Multiwavelength analysis for interferometric (sub-)mm observations of protoplanetary disks. Astron. Astrophys. 2016, 588, A53. [Google Scholar] [CrossRef]
- Liu, Y.; Henning, T.; Carrasco-González, C.; Chandler, C.J.; Linz, H.; Birnstiel, T.; van Boekel, R.; Pérez, L.M.; Flock, M.; Testi, L.; et al. The properties of the inner disk around HL Tau: Multi-wavelength modeling of the dust emission. Astron. Astrophys. 2017, 607, A74. [Google Scholar] [CrossRef]
- Okuzumi, S. Electric charging of dust aggregates and its effect on dust coagulation in protoplanetary disks. Astrophys. J. 2009, 698, 1122–1135. [Google Scholar] [CrossRef]
- Okuzumi, S.; Tanaka, H.; Takeuchi, T.; Sakagami, M.A. Electrostatic barrier against dust growth in protoplanetary disks. I. Classifying the evolution of size distribution. Astrophys. J. 2011, 731, 95. [Google Scholar] [CrossRef]
- Okuzumi, S.; Tanaka, H.; Takeuchi, T.; Sakagami, M.A. Electrostatic barrier against dust growth in protoplanetary disks. II. Measuring the size of the “frozen” zone. Astrophys. J. 2011, 731, 96. [Google Scholar] [CrossRef]
- Akimkin, V.V. A possible mechanism for overcoming the electrostatic barrier against dust growth in protoplanetary disks. Astron. Rep. 2015, 59, 747–761. [Google Scholar] [CrossRef][Green Version]
- Akimkin, V.V.; Ivlev, A.V.; Caselli, P. Inhibited Coagulation of Micron-size Dust Due to the Electrostatic Barrier. Astrophys. J. 2020, 889, 64. [Google Scholar] [CrossRef]
- Xiang, C.; Matthews, L.S.; Carballido, A.; Hyde, T.W. Detailed Model of the Growth of Fluffy Dust Aggregates in a Protoplanetary Disk: Effects of Nebular Conditions. Astrophys. J. 2020, 897, 182. [Google Scholar] [CrossRef]
- Steinpilz, T.; Joeris, K.; Jungmann, F.; Wolf, D.; Brendel, L.; Teiser, J.; Shinbrot, T.; Wurm, G. Electrical charging overcomes the bouncing barrier in planet formation. Nat. Phys. 2020, 16, 225–229. [Google Scholar] [CrossRef]
- Johansen, A.; Blum, J.; Tanaka, H.; Ormel, C.; Bizzarro, M.; Rickman, H. The multifaceted planetesimal formation process. Protostars and Planets VI 2014. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I - Linear analysis. II - Nonlinear evolution. Astrophys. J. 1991, 376, 214. [Google Scholar] [CrossRef]
- Klahr, H.H.; Bodenheimer, P. Turbulence in Accretion Disks: Vorticity Generation and Angular Momentum Transport via the Global Baroclinic Instability. Astrophys. J. 2003, 582, 869–892. [Google Scholar] [CrossRef]
- Lyra, W.; Klahr, H. The baroclinic instability in the context of layered accretion. Astron. Astrophys. 2011, 527, A138. [Google Scholar] [CrossRef]
- Lyra, W.; Johansen, A.; Klahr, H.; Piskunov, N. Standing on the shoulders of giants. Astron. Astrophys. 2009, 493, 1125–1139. [Google Scholar] [CrossRef]
- Lyra, W.; Johansen, A.; Klahr, H.; Piskunov, N. Embryos grown in the dead zone. Astron. Astrophys. 2008, 491, L41–L44. [Google Scholar] [CrossRef]
- Dzyurkevich, N.; Flock, M.; Turner, N.J.; Klahr, H.; Henning, T. Trapping solids at the inner edge of the dead zone: 3-D global MHD simulations. Astron. Astrophys. 2010, 515, A70. [Google Scholar] [CrossRef]
- Van der Marel, N.; van Dishoeck, E.F.; Bruderer, S.; Birnstiel, T.; Pinilla, P.; Dullemond, C.P.; van Kempen, T.A.; Schmalzl, M.; Brown, J.M.; Herczeg, G.J.; et al. A major asymmetric dust trap in a transition disk. Science 2013, 340, 1199–1202. [Google Scholar] [CrossRef]
- Youdin, A.N.; Goodman, J. Streaming Instabilities in Protoplanetary Disks. Astrophys. J. 2005, 620, 459–469. [Google Scholar] [CrossRef]
- Carrera, D.; Johansen, A.; Davies, M.B. How to form planetesimals from mm-sized chondrules and chondrule aggregates. Astron. Astrophys. 2015, 579, A43. [Google Scholar] [CrossRef]
- Yang, C.C.; Johansen, A. On the feeding zone of planetesimal formation by the streaming instability. Astrophys. J. 2014, 792, 86. [Google Scholar] [CrossRef]
- Bai, X.N.; Stone, J.M. Particle-gas dynamics with athena: Method and convergence. Astrophys. J. Suppl. Ser. 2010, 190, 297–310. [Google Scholar] [CrossRef]
- Johansen, A.; Youdin, A.N.; Lithwick, Y. Adding particle collisions to the formation of asteroids and Kuiper belt objects via streaming instabilities. Astron. Astrophys. 2012, 537, A125. [Google Scholar] [CrossRef]
- Carrera, D.; Gorti, U.; Johansen, A.; Davies, M.B. Planetesimal Formation by the Streaming Instability in a Photoevaporating Disk. Astrophys. J. 2017, 839, 16. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Davidsson, B.J.R.; Sierks, H.; Güttler, C.; Marzari, F.; Pajola, M.; Rickman, H.; A’Hearn, M.F.; Auger, A.T.; El-Maarry, M.R.; Fornasier, S.; et al. The primordial nucleus of comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2016, 592, A63. [Google Scholar] [CrossRef]
- Li, R.; Youdin, A. Thresholds for Particle Clumping by the Streaming Instability. Astrophys. J. 2021, 919, 107. [Google Scholar] [CrossRef]
- Carrera, D.; Thomas, A.J.; Simon, J.B.; Small, M.A.; Kretke, K.A.; Klahr, H. Resilience of Planetesimal Formation in Weakly Reinforced Pressure Bumps. Astrophys. J. 2022, 927, 52. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; McNally, C.P.; Lovascio, F. Polydisperse streaming instability—I. Tightly coupled particles and the terminal velocity approximation. Mon. Not. R. Astron. Soc. 2020, 499, 4223–4238. [Google Scholar] [CrossRef]
- Paardekooper, S.J.; McNally, C.P.; Lovascio, F. Polydisperse streaming instability—II. Methods for solving the linear stability problem. Mon. Not. R. Astron. Soc. 2021, 502, 1579–1595. [Google Scholar] [CrossRef]
- McNally, C.P.; Lovascio, F.; Paardekooper, S.J. Polydisperse streaming instability—III. Dust evolution encourages fast instability. Mon. Not. R. Astron. Soc. 2021, 502, 1469–1486. [Google Scholar] [CrossRef]
- Zhu, Z.; Yang, C.C. Streaming Instability with Multiple Dust Species: I. Favourable Conditions for the Linear Growth. Mon. Not. R. Astron. Soc. 2021, 501, 467–482. [Google Scholar] [CrossRef]
- Schaffer, N.; Johansen, A.; Lambrechts, M. Streaming instability of multiple particle species: II. Numerical convergence with increasing particle number. Astron. Astrophys. 2021, 653, A14. [Google Scholar] [CrossRef]
- Umurhan, O.M.; Estrada, P.R.; Cuzzi, J.N. Streaming Instability in Turbulent Protoplanetary Disks. Astrophys. J. 2020, 895, 4. [Google Scholar] [CrossRef]
- Wahlberg Jansson, K.; Johansen, A.; Syed, M.B.; Blum, J. The role of pebble fragmentation in planetesimal formation. II. Numerical simulations. Astrophys. J. 2017, 835, 109. [Google Scholar] [CrossRef]
- Blum, J. Dust evolution in protoplanetary discs and the formation of planetesimals. What have we learned from laboratory experiments? Space Sci. Rev. 2018, 214, 992. [Google Scholar] [CrossRef]
- Wahlberg Jansson, K.; Johansen, A. Radially resolved simulations of collapsing pebble clouds in protoplanetary discs. Mon. Not. R. Astron. Soc. 2017, 469, S149–S157. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J. Fractal dust constrains the collisional history of comets. Mon. Not. R. Astron. Soc. 2017, 469, S39–S44. [Google Scholar] [CrossRef]
- Johansen, A.; Oishi, J.S.; Mac Low, M.M.; Klahr, H.; Henning, T.; Youdin, A. Rapid planetesimal formation in turbulent circumstellar disks. Nature 2007, 448, 1022–1025. [Google Scholar] [CrossRef]
- Johansen, A.; Youdin, A.; Mac Low, M.M. Particle clumping and planetesimal formation depend strongly on metallicity. Astrophys. J. 2009, 704, L75–L79. [Google Scholar] [CrossRef]
- Johansen, A.; Klahr, H.; Henning, T. High-resolution simulations of planetesimal formation in turbulent protoplanetary discs. Astron. Astrophys. 2011, 529, A62. [Google Scholar] [CrossRef][Green Version]
- Kato, M.T.; Fujimoto, M.; Ida, S. Planetesimal formation at the boundary between steady super/sub-keplerian flow created by inhomogeneous growth of magnetorotational instability. Astrophys. J. 2012, 747, 11. [Google Scholar] [CrossRef]
- Gerbig, K.; Murray-Clay, R.A.; Klahr, H.; Baehr, H. Requirements for Gravitational Collapse in Planetesimal Formation—The Impact of Scales Set by Kelvin–Helmholtz and Nonlinear Streaming Instability. Astrophys. J. 2020, 895, 91. [Google Scholar] [CrossRef]
- Gole, D.A.; Simon, J.B.; Li, R.; Youdin, A.N.; Armitage, P.J. Turbulence Regulates the Rate of Planetesimal Formation via Gravitational Collapse. Astrophys. J. 2020, 904, 132. [Google Scholar] [CrossRef]
- Klahr, H.; Schreiber, A. Turbulence Sets the Length Scale for Planetesimal Formation: Local 2D Simulations of Streaming Instability and Planetesimal Formation. Astrophys. J. 2020, 901, 54. [Google Scholar] [CrossRef]
- Simon, J.B.; Armitage, P.J.; Li, R.; Youdin, A.N. The mass and size distribution of planetesimals formed by streaming instability. I. The role of self-gravity. Astrophys. J. 2016, 822, 55. [Google Scholar] [CrossRef]
- Simon, J.B.; Armitage, P.J.; Youdin, A.N.; Li, R. Evidence for Universality in the Initial Planetesimal Mass Function. Astrophys. J. 2017, 847, L12. [Google Scholar] [CrossRef]
- Schäfer, U.; Yang, C.C.; Johansen, A. Initial mass function of planetesimals formed by the streaming instability. Astron. Astrophys. 2017, 597, A69. [Google Scholar] [CrossRef]
- Abod, C.P.; Simon, J.B.; Li, R.; Armitage, P.J.; Youdin, A.N.; Kretke, K.A. The Mass and Size Distribution of Planetesimals Formed by the Streaming Instability. II. The Effect of the Radial Gas Pressure Gradient. Astrophys. J. 2019, 883, 192. [Google Scholar] [CrossRef]
- Rucska, J.J.; Wadsley, J.W. Streaming instability on different scales—I. Planetesimal mass distribution variability. Mon. Not. R. Astron. Soc. 2020, 500, 520–530. [Google Scholar] [CrossRef]
- Nesvorný, D.; Youdin, A.N.; Richardson, D.C. Formation of kuiper belt binaries by gravitational collapse. Astron. J. 2010, 140, 785–793. [Google Scholar] [CrossRef]
- Nesvorny, D.; Li, R.; Youdin, A.N.; Simon, J.B.; Grundy, W.M. Trans-Neptunian Binaries as Evidence for Planetesimal Formation by the Streaming Instability. Nat. Astron. 2019, 3, 808–812. [Google Scholar] [CrossRef]
- Lichtenberg, T.; Dra Żkowska, J.; Schönbächler, M.; Golabek, G.J.; Hands, T.O. Bifurcation of planetary building blocks during Solar System formation. Science 2021, 371, 365–370. [Google Scholar] [CrossRef] [PubMed]
- Blum, J.; Gundlach, B.; Mühle, S.; Trigo-Rodriguez, J.M. Comets formed in solar-nebula instabilities!—An experimental and modeling attempt to relate the activity of comets to their formation process. Icarus 2014, 235, 156–169. [Google Scholar] [CrossRef]
- Grundy, W.M. Pluto and Charon as templates for other large Trans-Neptunian objects. In The Trans-Neptunian Solar System; Prialnik, D., Barucci, M.A., Young, L.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 291–305. [Google Scholar] [CrossRef]
- Gkotsinas, A.; Guilbert-Lepoutre, A.; Raymond, S.N.; Nesvorny, D. Thermal Processing of Jupiter-family Comets during Their Chaotic Orbital Evolution. Astrophys. J. 2022, 928, 43. [Google Scholar] [CrossRef]
- Gregory, T.; Luu, T.H.; Coath, C.D.; Russell, S.S.; Elliott, T. Primordial formation of major silicates in a protoplanetary disc with homogeneous 26Al/27Al. Sci. Adv. 2020, 6, eaay9626. [Google Scholar] [CrossRef] [PubMed]
- Prialnik, D.; Podolak, M. Radioactive Heating of Porous Comet Nuclei. Icarus 1995, 117, 420–430. [Google Scholar] [CrossRef]
- Choi, Y. Long-Term Evolution of Objects in the Kuiper Belt Zone—Effects of Insolation and Radiogenic Heating. Icarus 2002, 160, 300–312. [Google Scholar] [CrossRef]
- Merk, R.; Breuer, D.; Spohn, T. Numerical Modeling of 26Al-Induced Radioactive Melting of Asteroids Considering Accretion. Icarus 2002, 159, 183–191. [Google Scholar] [CrossRef]
- Merk, R.; Prialnik, D. Early Thermal and Structural Evolution of Small Bodies in the Trans-Neptunian Zone. Earth, Moon, Planets 2003, 92, 359–374. [Google Scholar] [CrossRef]
- Merk, R.; Prialnik, D. Combined modeling of thermal evolution and accretion of trans-neptunian objects—Occurrence of high temperatures and liquid water. Icarus 2006, 183, 283–295. [Google Scholar] [CrossRef]
- De Sanctis, M.C.; Capria, M.T.; Coradini, A. Thermal evolution models of Kuiper Belt Objects. Mem. Della Soc. Astron. Ital. Suppl. 2007, 11, 135. [Google Scholar]
- Mousis, O.; Guilbert-Lepoutre, A.; Lunine, J.I.; Cochran, A.L.; Waite, J.H.; Petit, J.M.; Rousselot, P. The dual origin of the nitrogen deficiency in comets: Selective volatile trapping in the nebula and postaccretion radiogenic heating. Astrophys. J. 2012, 757, 146. [Google Scholar] [CrossRef]
- Holm, N.G.; Oze, C.; Mousis, O.; Waite, J.H.; Guilbert-Lepoutre, A. Serpentinization and the Formation of H2 and CH4 on Celestial Bodies (Planets, Moons, Comets). Astrobiology 2015, 15, 587–600. [Google Scholar] [CrossRef]
- Mousis, O.; Drouard, A.; Vernazza, P.; Lunine, J.I.; Monnereau, M.; Maggiolo, R.; Altwegg, K.; Balsiger, H.; Berthelier, J.J.; Cessateur, G.; et al. Impact of Radiogenic Heating on the Formation Conditions of Comet 67P/Churyumov–Gerasimenko. Astrophys. J. Lett. 2017, 839, L4. [Google Scholar] [CrossRef]
- Golabek, G.J.; Jutzi, M. Modification of icy planetesimals by early thermal evolution and collisions: Constraints for formation time and initial size of comets and small KBOs. Icarus 2021, 363, 114437. [Google Scholar] [CrossRef]
- Gundlach, B.; Blum, J. Outgassing of icy bodies in the Solar System—II. Heat transport in dry, porous surface dust layers. Icarus 2012, 219, 618–629. [Google Scholar] [CrossRef]
- Bischoff, D.; Gundlach, B.; Blum, J. A method to distinguish between micro- and macro-granular surfaces of small Solar System bodies. Mon. Not. R. Astron. Soc. 2021, 508, 4705–4721. [Google Scholar] [CrossRef]
- Malamud, U.; Landeck, W.A.; Bischoff, D.; Kreuzig, C.; Perets, H.B.; Gundlach, B.; Blum, J. Are there any pristine comets? Constraints from pebble structure. Mon. Not. R. Astron. Soc. 2022, 514, 3366–3394. [Google Scholar] [CrossRef]
- Whipple, F.L.; Stefanik, R.P. On the Physics and Splitting of Cometary Nuclei. SAO Spec. Rep. 1965, 182, 1–25. [Google Scholar]
- Prialnik, D.; Bar-Nun, A.; Podolak, M. Radiogenic heating of comets by 26Al and implications for their time of formation. Astrophys. J. 1987, 319, 993–1002. [Google Scholar] [CrossRef]
- Abedin, A.Y.; Kavelaars, J.J.; Greenstreet, S.; Petit, J.M.; Gladman, B.; Lawler, S.; Bannister, M.; Alexandersen, M.; Chen, Y.T.; Gwyn, S.; et al. Collision Probabilities in the Edgeworth–Kuiper Belt. Astron. J. 2021, 161, 195. [Google Scholar] [CrossRef]
- Davison, T.M.; Ciesla, F.J.; Collins, G.S.; Elbeshausen, D. The effect of impact obliquity on shock heating in planetesimal collisions. Meteorit. Planet. Sci. 2014, 49, 2252–2265. [Google Scholar] [CrossRef]
- Davison, T.M.; Collins, G.S.; Ciesla, F.J. Numerical modelling of heating in porous planetesimal collisions. Icarus 2010, 208, 468–481. [Google Scholar] [CrossRef]
- Charnoz, S.; Morbidelli, A. Coupling dynamical and collisional evolution of small bodies. Icarus 2007, 188, 468–480. [Google Scholar] [CrossRef]
- Jutzi, M.; Asphaug, E. The shape and structure of cometary nuclei as a result of low-velocity accretion. Science 2015, 348, 1355–1358. [Google Scholar] [CrossRef]
- Jutzi, M.; Benz, W. Formation of bi-lobed shapes by sub-catastrophic collisions. Astron. Astrophys. 2017, 597, A62. [Google Scholar] [CrossRef]
- Schwartz, S.R.; Michel, P.; Jutzi, M.; Marchi, S.; Zhang, Y.; Richardson, D.C. Catastrophic disruptions as the origin of bilobate comets. Nat. Astron. 2018, 2, 379–382. [Google Scholar] [CrossRef]
- Jutzi, M.; Michel, P. Collisional heating and compaction of small bodies: Constraints for their origin and evolution. Icarus 2020, 350, 113867. [Google Scholar] [CrossRef]
- Krivov, A.V.; Ide, A.; Löhne, T.; Johansen, A.; Blum, J. Debris Disc Constraints on Planetesimal Formation. Mon. Not. R. Astron. Soc. 2018, 474, 2564–2575. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Rotundi, A.; Gundlach, B.; Güttler, C.; Zakharov, V. How comets work: Nucleus erosion versus dehydration. Mon. Not. R. Astron. Soc. 2020, 493, 4039–4044. [Google Scholar] [CrossRef]
- Ciarniello, M.; Fulle, M.; Tosi, F.; Capaccioni, F.; Filacchione, G.; Raponi, A.; Rinaldi, G.; Rotundi, A.; Mottola, S.; De Sanctis, M.C.; et al. Modeling the Seasonal Evolution of 67P/Churyumov-Gerasimenko Water Loss Rate. In Proceedings of the 52nd Lunar and Planetary Science Conference, Virtual, 15–19 March 2021; p. 2031. [Google Scholar]
- Ciarniello, M.; Fulle, M.; Raponi, A.; Filacchione, G.; Capaccioni, F.; Rotundi, A.; Rinaldi, G.; Formisano, M.; Magni, G.; Tosi, F.; et al. Macro and micro structures of pebble-made cometary nuclei reconciled by seasonal evolution. Nat. Astron. 2022, 6, 546–553. [Google Scholar] [CrossRef]
- Kofman, W.; Herique, A.; Goutail, J.P.; Hagfors, T.; Williams, I.P.; Nielsen, E.; Barriot, J.P.; Barbin, Y.; Elachi, C.; Edenhofer, P.; et al. The Comet Nucleus Sounding Experiment by Radiowave Transmission (CONSERT): A Short Description of the Instrument and of the Commissioning Stages. Space Sci. Rev. 2007, 128, 413–432. [Google Scholar] [CrossRef]
- Pätzold, M.; Häusler, B.; Aksnes, K.; Anderson, J.D.; Asmar, S.W.; Barriot, J.P.; Bird, M.K.; Boehnhardt, H.; Eidel, W.; Grün, E.; et al. Rosetta Radio Science Investigations (RSI). Space Sci. Rev. 2007, 128, 599–627. [Google Scholar] [CrossRef]
- Kofman, W.; Herique, A.; Barbin, Y.; Barriot, J.P.; Ciarletti, V.; Clifford, S.; Edenhofer, P.; Elachi, C.; Eyraud, C.; Goutail, J.P.; et al. Properties of the 67P/Churyumov-Gerasimenko interior revealed by CONSERT radar. Science 2015, 349, aab0639. [Google Scholar] [CrossRef]
- Kofman, W.; Zine, S.; Herique, A.; Rogez, Y.; Jorda, L.; Levasseur-Regourd, A.C. The interior of Comet 67P/C–G; revisiting CONSERT results with the exact position of the Philae lander. Mon. Not. R. Astron. Soc. 2020, 497, 2616–2622. [Google Scholar] [CrossRef]
- Jorda, L.; Gaskell, R.; Capanna, C.; Hviid, S.; Lamy, P.; Ďurech, J.; Faury, G.; Groussin, O.; Gutiérrez, P.; Jackman, C.; et al. The global shape, density and rotation of Comet 67P/Churyumov-Gerasimenko from preperihelion Rosetta/OSIRIS observations. Icarus 2016, 277, 257–278. [Google Scholar] [CrossRef]
- Poulet, F.; Lucchetti, A.; Bibring, J.P.; Carter, J.; Gondet, B.; Jorda, L.; Langevin, Y.; Pilorget, C.; Capanna, C.; Cremonese, G. Origin of the local structures at the Philae landing site and possible implications on the formation and evolution of 67P/Churyumov-Gerasimenko. Mon. Not. R. Astron. Soc. 2016, 462, S23–S32. [Google Scholar] [CrossRef]
- Lisse, C.M.; A’Hearn, M.F.; Hauser, M.G.; Kelsall, T.; Lien, D.J.; Moseley, S.H.; Reach, W.T.; Silverberg, R.F. Infrared Observations of Comets by COBE. Astrophys. J. 1998, 496, 971–991. [Google Scholar] [CrossRef][Green Version]
- Trigo-Rodríguez, J.M.; Blum, J. Learning about comets from the study of mass distributions and fluxes of meteoroid streams. Mon. Not. R. Astron. Soc. 2021, 512, 2277–2289. [Google Scholar] [CrossRef]
- Skorov, Y.; Blum, J. Dust release and tensile strength of the non-volatile layer of cometary nuclei. Icarus 2012, 221, 1–11. [Google Scholar] [CrossRef]
- Herique, A.; Kofman, W.; Zine, S.; Blum, J.; Vincent, J.B.; Ciarletti, V. Homogeneity of 67P/Churyumov-Gerasimenko as seen by CONSERT: Implication on composition and formation. Astron. Astrophys. 2019, 630, A6. [Google Scholar] [CrossRef]
- Brouet, Y.; Levasseur-Regourd, A.C.; Sabouroux, P.; Neves, L.; Encrenaz, P.; Poch, O.; Pommerol, A.; Thomas, N.; Kofman, W.; Le Gall, A.; et al. A porosity gradient in 67P/C-G nucleus suggested from CONSERT and SESAME-PP results: An interpretation based on new laboratory permittivity measurements of porous icy analogues. Mon. Not. R. Astron. Soc. 2016, 462, S89–S98. [Google Scholar] [CrossRef]
- Pätzold, M.; Andert, T.; Hahn, M.; Asmar, S.W.; Barriot, J.P.; Bird, M.K.; Häusler, B.; Peter, K.; Tellmann, S.; Grün, E.; et al. A homogeneous nucleus for comet 67P/Churyumov-Gerasimenko from its gravity field. Nature 2016, 530, 63–65. [Google Scholar] [CrossRef]
- Colangeli, L.; Lopez-Moreno, J.J.; Palumbo, P.; Rodriguez, J.; Cosi, M.; Della Corte, V.; Esposito, F.; Fulle, M.; Herranz, M.; Jeronimo, J.M.; et al. The Grain Impact Analyser and Dust Accumulator (GIADA) Experiment for the Rosetta Mission: Design, Performances and First Results. Space Sci. Rev. 2007, 128, 803–821. [Google Scholar] [CrossRef]
- Fulle, M.; Della Corte, V.; Rotundi, A.; Rietmeijer, F.J.M.; Green, S.F.; Weissman, P.; Accolla, M.; Colangeli, L.; Ferrari, M.; Ivanovski, S.; et al. Comet 67P/Churyumov–Gerasimenko preserved the pebbles that formed planetesimals. Mon. Not. R. Astron. Soc. 2016, 462, S132–S137. [Google Scholar] [CrossRef]
- Lorek, S.; Gundlach, B.; Lacerda, P.; Blum, J. Comet formation in collapsing pebble clouds. Astron. Astrophys. 2016, 587, A128. [Google Scholar] [CrossRef][Green Version]
- Pätzold, M.; Andert, T.P.; Hahn, M.; Barriot, J.P.; Asmar, S.W.; Häusler, B.; Bird, M.K.; Tellmann, S.; Oschlisniok, J.; Peter, K. The Nucleus of comet 67P/Churyumov–Gerasimenko—Part I: The global view–nucleus mass, mass-loss, porosity, and implications. Mon. Not. R. Astron. Soc. 2019, 483, 2337–2346. [Google Scholar] [CrossRef]
- Bardyn, A.; Baklouti, D.; Cottin, H.; Fray, N.; Briois, C.; Paquette, J.; Stenzel, O.; Engrand, C.; Fischer, H.; Hornung, K.; et al. Carbon-rich dust in comet 67P/Churyumov-Gerasimenko measured by COSIMA/Rosetta. Mon. Not. R. Astron. Soc. 2017, 469, S712–S722. [Google Scholar] [CrossRef]
- Fulle, M.; Della Corte, V.; Rotundi, A.; Green, S.F.; Accolla, M.; Colangeli, L.; Ferrari, M.; Ivanovski, S.; Sordini, R.; Zakharov, V. The dust-to-ices ratio in comets and Kuiper belt objects. Mon. Not. R. Astron. Soc. 2017, 469, S45–S49. [Google Scholar] [CrossRef]
- Choukroun, M.; Altwegg, K.; Kührt, E.; Biver, N.; Bockelée-Morvan, D.; Drążkowska, J.; Hérique, A.; Hilchenbach, M.; Marschall, R.; Pätzold, M.; et al. Dust-to-Gas and Refractory-to-Ice Mass Ratios of Comet 67P/Churyumov-Gerasimenko from Rosetta Observations. Space Sci. Rev. 2020, 216, 44. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Green, S.F.; Gundlach, B.; Herique, A.; Moreno, F.; Mottola, S.; Rotundi, A.; Snodgrass, C. The refractory-to-ice mass ratio in comets. Mon. Not. R. Astron. Soc. 2019, 482, 3326–3340. [Google Scholar] [CrossRef]
- Fraser, W.C.; Bannister, M.T.; Pike, R.E.; Marsset, M.; Schwamb, M.E.; Kavelaars, J.J.; Lacerda, P.; Nesvorný, D.; Volk, K.; Delsanti, A.; et al. All planetesimals born near the Kuiper belt formed as binaries. Nat. Astron. 2017, 1, 1–6. [Google Scholar] [CrossRef]
- McKinnon, W.B.; Richardson, D.C.; Marohnic, J.C.; Keane, J.T.; Grundy, W.M.; Hamilton, D.P.; Nesvorný, D.; Umurhan, O.M.; Lauer, T.R.; Singer, K.N.; et al. The solar nebula origin of (486958) Arrokoth, a primordial contact binary in the Kuiper Belt. Science 2020, 367, eaay6620. [Google Scholar] [CrossRef]
- Nesvorný, D.; Vokrouhlický, D. Binary survival in the outer solar system. Icarus 2019, 331, 49–61. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Y.; Gong, S. Analysis of the potential field and equilibrium points of irregular-shaped minor celestial bodies. Astrophys. Space Sci. 2014, 353, 105–121. [Google Scholar] [CrossRef]
- Jiang, Y.; Schmidt, J.; Baoyin, H.; Li, H.; Li, J. Hamiltonian Formulation and Perturbations for Dust Motion Around Cometary Nuclei. Earth Moon Planets 2017, 120, 147–168. [Google Scholar] [CrossRef]
- Massironi, M.; Simioni, E.; Marzari, F.; Cremonese, G.; Giacomini, L.; Pajola, M.; Jorda, L.; Naletto, G.; Lowry, S.; El-Maarry, M.R.; et al. Two independent and primitive envelopes of the bilobate nucleus of comet 67P. Nature 2015, 526, 402–405. [Google Scholar] [CrossRef] [PubMed]
- Penasa, L.; Massironi, M.; Naletto, G.; Simioni, E.; Ferrari, S.; Pajola, M.; Lucchetti, A.; Preusker, F.; Scholten, F.; Jorda, L.; et al. A three-dimensional modelling of the layered structure of comet 67P/Churyumov-Gerasimenko. Mon. Not. R. Astron. Soc. 2017, 469, S741–S754. [Google Scholar] [CrossRef]
- Ruzicka, B.K.; Penasa, L.; Boehnhardt, H.; Pack, A.; Dolives, B.; Souvannavong, F.; Remetean, E. Analysis of layering-related linear features on comet 67P/Churyumov–Gerasimenko. Mon. Not. R. Astron. Soc. 2019, 482, 5007–5011. [Google Scholar] [CrossRef]
- Keller, H.U.; Delamere, W.A.; Reitsema, H.J.; Huebner, W.F.; Schmidt, H.U. Comet P/Halley’s nucleus and its activity. Astron. Astrophys. 1987, 187, 807–823. [Google Scholar]
- Soderblom, L.; Boice, D.; Britt, D.; Brown, R.; Buratti, B.; Kirk, R.; Lee, M.; Nelson, R.; Oberst, J.; Sandel, B.; et al. Imaging Borrelly. Icarus 2004, 167, 4–15. [Google Scholar] [CrossRef]
- Tsou, P.; Brownlee, D.E.; Anderson, J.D.; Bhaskaran, S.; Cheuvront, A.R.; Clark, B.C.; Duxbury, T.; Economou, T.; Green, S.F.; Hanner, M.S.; et al. Stardust encounters comet 81P/Wild 2. J. Geophys. Res. Planets 2004, 109, E12S01. [Google Scholar] [CrossRef]
- Berger, E.L.; Zega, T.J.; Keller, L.P.; Lauretta, D.S. Evidence for aqueous activity on comet 81P/Wild 2 from sulfide mineral assemblages in Stardust samples and CI chondrites. Geochim. Cosmochim. Acta 2011, 75, 3501–3513. [Google Scholar] [CrossRef]
- A’Hearn, M.F.; Belton, M.J.S.; Delamere, W.A.; Kissel, J.; Klaasen, K.P.; McFadden, L.A.; Meech, K.J.; Melosh, H.J.; Schultz, P.H.; Sunshine, J.M.; et al. Deep Impact: Excavating comet Tempel 1. Science 2005, 310, 258–264. [Google Scholar] [CrossRef]
- A’Hearn, M.F.; Belton, M.J.S.; Delamere, W.A.; Feaga, L.M.; Hampton, D.; Kissel, J.; Klaasen, K.P.; McFadden, L.A.; Meech, K.J.; Melosh, H.J.; et al. EPOXI at comet Hartley 2. Science 2011, 332, 1396–1400. [Google Scholar] [CrossRef]
- Shi, X.; Hu, X.; Sierks, H.; Güttler, C.; A’Hearn, M.; Blum, J.; El-Maarry, M.R.; Kührt, E.; Mottola, S.; Pajola, M.; et al. Sunset jets observed on comet 67P/Churyumov-Gerasimenko sustained by subsurface thermal lag. Astron. Astrophys. 2016, 586, A7. [Google Scholar] [CrossRef]
- Läuter, M.; Kramer, T.; Rubin, M.; Altwegg, K. Surface localization of gas sources on comet 67P/Churyumov-Gerasimenko based on DFMS/COPS data. Mon. Not. R. Astron. Soc. 2019, 483, 852–861. [Google Scholar] [CrossRef]
- Ott, T.; Drolshagen, E.; Koschny, D.; Güttler, C.; Tubiana, C.; Frattin, E.; Agarwal, J.; Sierks, H.; Bertini, I.; Barbieri, C.; et al. Dust mass distribution around comet 67P/Churyumov–Gerasimenko determined via parallax measurements using Rosetta’s OSIRIS cameras. Mon. Not. R. Astron. Soc. 2017, 469, S276–S284. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Rotundi, A. CO-driven activity constrains the origin of comets. Astron. Astrophys. 2020, 636, L3. [Google Scholar] [CrossRef]
- Coradini, A.; Capaccioni, F.; Drossart, P.; Arnold, G.; Ammannito, E.; Angrilli, F.; Barucci, A.; Bellucci, G.; Benkhoff, J.; Bianchini, G.; et al. Virtis: An Imaging Spectrometer for the Rosetta Mission. Space Sci. Rev. 2007, 128, 529–559. [Google Scholar] [CrossRef]
- Tosi, F.; Capaccioni, F.; Capria, M.T.; Mottola, S.; Zinzi, A.; Ciarniello, M.; Filacchione, G.; Hofstadter, M.; Fonti, S.; Formisano, M.; et al. The changing temperature of the nucleus of comet 67P induced by morphological and seasonal effects. Nat. Astron. 2019, 3, 649–658. [Google Scholar] [CrossRef]
- Gulkis, S.; Frerking, M.; Crovisier, J.; Beaudin, G.; Hartogh, P.; Encrenaz, P.; Koch, T.; Kahn, C.; Salinas, Y.; Nowicki, R.; et al. MIRO: Microwave Instrument for Rosetta Orbiter. Space Sci. Rev. 2007, 128, 561–597. [Google Scholar] [CrossRef]
- Gulkis, S.; Allen, M.; von Allmen, P.; Beaudin, G.; Biver, N.; Bockelée-Morvan, D.; Choukroun, M.; Crovisier, J.; Davidsson, B.J.R.; Encrenaz, P.; et al. Subsurface properties and early activity of comet 67P/Churyumov-Gerasimenko. Science 2015, 347, aaa0709. [Google Scholar] [CrossRef]
- Schloerb, F.P.; Keihm, S.; von Allmen, P.; Choukroun, M.; Lellouch, E.; Leyrat, C.; Beaudin, G.; Biver, N.; Bockelée-Morvan, D.; Crovisier, J.; et al. MIRO observations of subsurface temperatures of the nucleus of 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2015, 583, A29. [Google Scholar] [CrossRef]
- Marshall, D.; Groussin, O.; Vincent, J.B.; Brouet, Y.; Kappel, D.; Arnold, G.; Capria, M.T.; Filacchione, G.; Hartogh, P.; Hofstadter, M.; et al. Thermal inertia and roughness of the nucleus of comet 67P/Churyumov–Gerasimenko from MIRO and VIRTIS observations. Astron. Astrophys. 2018, 616, A122. [Google Scholar] [CrossRef]
- Spohn, T.; Seiferlin, K.; Hagermann, A.; Knollenberg, J.; Ball, A.J.; Banaszkiewicz, M.; Benkhoff, J.; Gadomski, S.; Gregorczyk, W.; Grygorczuk, J.; et al. Mupus—A Thermal and Mechanical Properties Probe for the Rosetta Lander Philae. Space Sci. Rev. 2007, 128, 339–362. [Google Scholar] [CrossRef]
- Spohn, T.; Knollenberg, J.; Ball, A.J.; Banaszkiewicz, M.; Benkhoff, J.; Grott, M.; Grygorczuk, J.; Hüttig, C.; Hagermann, A.; Kargl, G.; et al. Thermal and mechanical properties of the near-surface layers of comet 67P/Churyumov-Gerasimenko. Science 2015, 349, aab0464. [Google Scholar] [CrossRef] [PubMed]
- Snodgrass, C.; Jones, G.H. The European Space Agency’s Comet Interceptor lies in wait. Nat. Commun. 2019, 10, 5418. [Google Scholar] [CrossRef] [PubMed]
- Gundlach, B.; Schmidt, K.P.; Kreuzig, C.; Bischoff, D.; Rezaei, F.; Kothe, S.; Blum, J.; Grzesik, B.; Stoll, E. The tensile strength of ice and dust aggregates and its dependence on particle properties. Mon. Not. R. Astron. Soc. 2018, 479, 1273–1277. [Google Scholar] [CrossRef]
- San Sebastián, I.L.; Dolff, A.; Blum, J.; Parisi, M.G.; Kothe, S. The tensile strength of compressed dust samples and the catastrophic disruption threshold of pre-planetary matter. Mon. Not. R. Astron. Soc. 2020, 497, 2418–2424. [Google Scholar] [CrossRef]
- Kimura, H.; Wada, K.; Yoshida, F.; Hong, P.K.; Senshu, H.; Arai, T.; Hirai, T.; Kobayashi, M.; Ishibashi, K.; Yamada, M. The tensile strength of dust aggregates consisting of small elastic grains: Constraints on the size of condensates in protoplanetary discs. Mon. Not. R. Astron. Soc. 2020, 496, 1667–1682. [Google Scholar] [CrossRef]
- Attree, N.; Groussin, O.; Jorda, L.; Nébouy, D.; Thomas, N.; Brouet, Y.; Kührt, E.; Preusker, F.; Scholten, F.; Knollenberg, J.; et al. Tensile strength of 67P/Churyumov–Gerasimenko nucleus material from overhangs. Astron. Astrophys. 2018, 611, A33. [Google Scholar] [CrossRef]
- Schräpler, R.; Blum, J.; von Borstel, I.; Güttler, C. The stratification of regolith on celestial objects. Icarus 2015, 257, 33–46. [Google Scholar] [CrossRef]
- O’Rourke, L.; Heinisch, P.; Blum, J.; Fornasier, S.; Filacchione, G.; van Hoang, H.; Ciarniello, M.; Raponi, A.; Gundlach, B.; Blasco, R.A.; et al. The Philae lander reveals low-strength primitive ice inside cometary boulders. Nature 2020, 586, 697–701. [Google Scholar] [CrossRef]
- Heinisch, P.; Auster, H.U.; Gundlach, B.; Blum, J.; Güttler, C.; Tubiana, C.; Sierks, H.; Hilchenbach, M.; Biele, J.; Richter, I.; et al. Compressive strength of comet 67P/Churyumov-Gerasimenko derived from Philae surface contacts. Astron. Astrophys. 2019, 630, A2. [Google Scholar] [CrossRef]
- Gundlach, B.; Fulle, M.; Blum, J. On the activity of comets: Understanding the gas and dust emission from comet 67/Churyumov–Gerasimenko’s south-pole region during perihelion. Mon. Not. R. Astron. Soc. 2020, 493, 3690–3715. [Google Scholar] [CrossRef]
- Skorov, Y.; Reshetnyk, V.; Bentley, M.; Rezac, L.; Agarwal, J.; Blum, J. The effect of varying porosity and inhomogeneities of the surface dust layer on the modelling of comet gas production. Mon. Not. R. Astron. Soc. 2021, 501, 2635–2646. [Google Scholar] [CrossRef]
- Skorov, Y.; Reshetnyk, V.; Bentley, M.S.; Rezac, L.; Hartogh, P.; Blum, J. The effect of hierarchical structure of the surface dust layer on the modelling of comet gas production. Mon. Not. R. Astron. Soc. 2022, 510, 5520–5534. [Google Scholar] [CrossRef]
- Reshetnyk, V.; Skorov, Y.; Vasyuta, M.; Bentley, M.; Rezac, L.; Agarwal, J.; Blum, J. Transport Characteristics of the Near-Surface Layer of the Nucleus of Comet 67P/Churyumov–Gerasimenko. Sol. Syst. Res. 2021, 55, 106–123. [Google Scholar] [CrossRef]
- Brouet, Y.; Levasseur-Regourd, A.C.; Encrenaz, P.; Gulkis, S. Permittivity of porous granular matter, in relation with Rosetta cometary mission. Planet. Space Sci. 2014, 103, 143–152. [Google Scholar] [CrossRef]
- Artemov, V.G. A unified mechanism for ice and water electrical conductivity from direct current to terahertz. Phys. Chem. Chem. Phys. 2019, 21, 8067–8072. [Google Scholar] [CrossRef]
- Herique, A.; Kofman, W.; Beck, P.; Bonal, L.; Buttarazzi, I.; Heggy, E.; Lasue, J.; Levasseur-Regourd, A.C.; Quirico, E.; Zine, S. Cosmochemical implications of CONSERT permittivity characterization of 67P/CG. Mon. Not. R. Astron. Soc. 2016, 462, S516–S532. [Google Scholar] [CrossRef]
- Seidensticker, K.J.; Möhlmann, D.; Apathy, I.; Schmidt, W.; Thiel, K.; Arnold, W.; Fischer, H.H.; Kretschmer, M.; Madlener, D.; Péter, A.; et al. Sesame—An Experiment of the Rosetta Lander Philae: Objectives and General Design. Space Sci. Rev. 2007, 128, 301–337. [Google Scholar] [CrossRef]
- Lethuillier, A.; Le Gall, A.; Hamelin, M.; Schmidt, W.; Seidensticker, K.J.; Grard, R.; Ciarletti, V.; Caujolle-Bert, S.; Fischer, H.H.; Trautner, R. Electrical properties and porosity of the first meter of the nucleus of 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2016, 591, A32. [Google Scholar] [CrossRef][Green Version]
- Bürger, J.; Glißmann, T.; Lethuillier, A.; Bischoff, D.; Gundlach, B.; Mutschke, H.; Höfer, S.; Wolf, S.; Blum, J. Sub-mm/mm optical properties of real protoplanetary matter derived from Rosetta/MIRO observations of comet 67P. Mon. Not. R. Astron. Soc. 2020. submitted. [Google Scholar]
- Gundlach, B.; Blum, J. Why are Jupiter-family comets active and asteroids in cometary-like orbits inactive? Astron. Astrophys. 2016, 589, A111. [Google Scholar] [CrossRef]
| Type A1 | Type B1 | Type A2 | Type B2 | Type A/B3 | |
|---|---|---|---|---|---|
 |  |  |  |  | |
| Intrinsic Physical Properties | Icy Pebble Piles | Icy Rubble/Pebble Piles | Non-Icy Rubble Piles | ||
| Internal morphology and pebble properties (Section 5.1.1) | Pristine, pebbles, void size equals pebble size, voids filled with fractals | Pristine, pebbles, void size equals pebble size, voids filled with fractals | Pebbles, void size equals pebble size, fractals locally depleted | Pebbles, void size equals pebble size, fractals locally depleted | Pebbles are destroyed and highly compacted, rubble remains, large void spaces within rubble |
| Total porosity (Section 5.1.2) | High pristine porosity | Enhanced porosity in the interior, reduced porosity at ice shell locations, bulk porosity preserved | High pristine porosity | Heterogeneous, macro-scale mixture of material with enhanced and reduced porosity, pristine porosity may not be preserved | No intra-rubble porosity, macro-scale voids within rubble, bulk porosity smaller compared to pristine porosity |
| Dust-to-ice mass ratio (Section 5.1.3) | Pristine dust-to-ice ratio, homogeneous distribution | Interior depleted of ices, enriched ice shells—pristine ratio preserved | Pristine ratio preserved, homogeneous distribution | Heterogeneous mixture of material from depleted and enriched areas | No ices |
| Binarity, flattening and rotational orientation (Section 5.1.4) | Many binaries, flattened shape and aligned along the principal axis, more prograde rotating objects | Many binaries, flattened shape and aligned along the principal axis, more prograde rotating objects | Pristine binarity is destroyed, creation of new binaries after collision is possible, random alignment and distribution of inclinations | Pristine binarity is destroyed, creation of new binaries after collision is possible, random alignment and distribution of inclinations | Pristine binarity is destroyed, creation of new binaries after collision is possible, random alignment and distribution of inclinations |
| Type A1 | Type B1 | Type A2 | Type B2 | Type A/B3 | |
|---|---|---|---|---|---|
 |  |  |  |  | |
| Derived Physical Properties | Icy Pebble Piles | Icy Rubble/Pebble Piles | Non-Icy Rubble Piles | ||
| Cometary activity (Section 5.2.1) Instruments: Camera, dust collector, gas detector | Possible everywhere at the surface, activity will not change when eroded | Possible everywhere at the surface, but activity changes when eroded | Possible everywhere at the surface, but activity changes when eroded | Possible at specific locations, erosion can change activity patterns | Not possible |
| Thermal conductivity (Section 5.2.2) Instruments: Thermal IR, microwave, in situ temperature sensors | Low network and radiative conductivity at night, radiative part strongly increases at day due to strong temperature dependence | High radiative thermal conductivity in the interior, the shells have a moderately increased network conductivity, and the mantle material behaves like Type A1 | Low network and radiative conductivity at night, radiative part strongly increases at day due to strong temperature dependence | Different locations are either dominated by the low network or the varying radiative thermal conductivity | Relatively high network conductivity inside the rubble, the large voids in between are dominated by radiation |
| Tensile strength (Section 5.2.3) Instruments: e.g., camera (cliff collapse) | Ultra-low intra-pebble tensile strength and low inter-pebble tensile strength | Ultra-low intra-pebble tensile strength and low inter-pebble tensile strength, both enhanced in ice-enriched areas and decreased in ice-depleted areas | Ultra-low intra-pebble tensile strength and low inter-pebble tensile strength | Ultra-low intra-pebble tensile strength and low inter-pebble tensile strength, both enhanced in ice-enriched areas and decreased in ice-depleted areas | High intra-rubble tensile strength, but almost no tensile strength within the rubble |
| Compressive strength (Section 5.2.4) Instruments: Measurement of impact deceleration | Low pressures required to compress the pebble material | Low pressures required to compress the material in the mantle, the pressure required for compression is increased in the ice shells and decreased in the depleted interior | Low pressures required to compress the pebble material | Varying compression response of the material depending on the ice fraction | Rubble requires more compression pressure to be compacted to the same volume-filling factor as the pebbles |
| Gas permeability (Section 5.2.5) Instruments: Gas detector | High permeability inside the large voids between the pebbles and low permeability inside the pebbles | Gas permeability is decreased in layers of enhanced ice content (ice shells), gas permeability is decreased where ice is less abundant | High permeability inside the large voids between the pebbles and low permeability inside the pebbles | Varying gas permeability at different locations at the surface and in the interior | Very low gas permeability |
| Permittivity (Section 5.2.6) Instruments: Deep penetrating radar, DC geo-electric | Homogeneous electrical permittivity on the surface and in the interior | Varying electrical permittivity for different parts of the nucleus (mantle, shells, interior) | Homogeneous electrical permittivity on the surface and in the interior | Inhomogeneous electrical permeability on the rubble scale, but homogeneous inside the rubble | Homogeneous electrical permittivity inside the rubble, but variations because of the large voids |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blum, J.; Bischoff, D.; Gundlach, B. Formation of Comets. Universe 2022, 8, 381. https://doi.org/10.3390/universe8070381
Blum J, Bischoff D, Gundlach B. Formation of Comets. Universe. 2022; 8(7):381. https://doi.org/10.3390/universe8070381
Chicago/Turabian StyleBlum, Jürgen, Dorothea Bischoff, and Bastian Gundlach. 2022. "Formation of Comets" Universe 8, no. 7: 381. https://doi.org/10.3390/universe8070381
APA StyleBlum, J., Bischoff, D., & Gundlach, B. (2022). Formation of Comets. Universe, 8(7), 381. https://doi.org/10.3390/universe8070381






