Slow Neutron-Capture Process: Low-Mass Asymptotic Giant Branch Stars and Presolar Silicon Carbide Grains

Abstract

Presolar grains are microscopic dust grains that formed in the stellar winds or explosions of ancient stars that died before the formation of the solar system. The majority (~90% in number) of presolar silicon carbide (SiC) grains, including types mainstream (MS), Y, and Z, came from low-mass C-rich asymptotic giant branch (AGB) stars, which is supported by the ubiquitous presence of SiC dust observed in the circumstellar envelope of AGB stars and the signatures of slow neutron-capture process preserved in these grains. Here, we review the status of isotope studies of presolar AGB SiC grains with an emphasis on heavy element isotopes and highlight the importance of presolar grain studies for nuclear astrophysics. We discuss the sensitives of different types of nuclei to varying AGB stellar parameters and how their abundances in presolar AGB SiC grains can be used to provide independent, detailed constraints on stellar parameters, including ¹³C formation, stellar temperature, and nuclear reaction rates.

1. Introduction

In 1957, B²FH and Cameron [1,2] proposed that elements heavier than Fe are made in stars by three nucleosynthesis processes, including the slow neutron-capture process (s-process), the rapid neutron-capture process (r-process), and the proton-capture process (p-process). Since then, an important research theme in the field of nuclear astrophysics is to identify the stellar sites of the s-, r-, and p-processes. While the stellar sites of the r- and p-processes are still hotly debated [3,4,5], the detection of Tc absorption lines in Mira-type variable stars by astronomer Paul Merrill [6] pointed out that ⁹⁹Tc, with a half-lifetime of 0.21 Ma, is freshly made in the stellar interior by the s-process operating along the valley of beta stability, thus linking the s-process nucleosynthesis1 to low-mass asymptotic giant branch (AGB) stars. Sophisticated stellar models have been developed by different groups [8,9,10] to describe the evolution of AGB stars and associated stellar nucleosynthesis, with special attention given to the s-process. According to AGB stellar models, it is recognized that the s-process operates in the He-intershell of low-mass (~1.5 M_⊙ ≤ M ≤ ~3.5 M_⊙) AGB stars [11]. During the interpulse phase, the s-process is powered by a main neutron source, the ¹³C(α,n)¹⁶O reaction, at a neutron density of ~10⁷–10⁸ cm⁻³ on the timescale of 5–20 ka. As shell H-burning proceeds, the He-intershell is heated and compressed so that a thermal pulse (TP) is triggered when the temperature and density are high enough. During a TP, s-process products are further modified by neutron capture as the ²²Ne(α,n)²⁵Mg reaction—a minor neutron source for the s-process—becomes partially activated in the He-intershell, providing neutrons at a density of 10⁹–10¹⁰ cm⁻³ on the timescale of a few years. The high-density neutron exposure produced by the minor neutron source controls the production of nuclei affected by s-process branch points, at which the neutron-capture rates are comparable to the beta-decay rates [12,13].

Despite the abovementioned general consensus among AGB models, parameters in AGB stellar models such as mass-loss rate and uncertain nuclear reaction rates such as the ¹³C(α,n)¹⁶O reaction rate [14], contribute to uncertainties in model predictions for the s-process [13,15]. In particular, the formation of the major neutron source ¹³C in the He-intershell is a key fundamental problem that is directly related to the s-process nucleosynthesis. The formation of ¹³C in the He-intershell requires the occurrence of the ¹²C(p,γ)¹³N(β⁺)¹³C reaction chain and, in turn, a partial mixing of H from the convective envelope border into the underlying He-intershell, which is initially H free but contains abundant ¹²C produced by He-burning. Note that the so-called ¹³C pocket refers to the top thin He-intershell region that contains the major neutron source ¹³C. Over the last several decades, multiple physical mechanisms have been proposed to account for the partial mixing of H into the underlying He-intershell, including overshooting [9,16,17,18,19], gravity waves [20], rotation-induced instabilities [21,22], and magnetic buoyancy [23,24]. It is still a hot debate in the community regarding which mechanism is primarily responsible for the partial mixing of H. Below, we will highlight the unique role of the heavy element isotope data of presolar SiC grains from AGB stars in constraining AGB stellar parameters and the recent progress in this research area.

2. Presolar Grains and In Situ Isotope Analyses

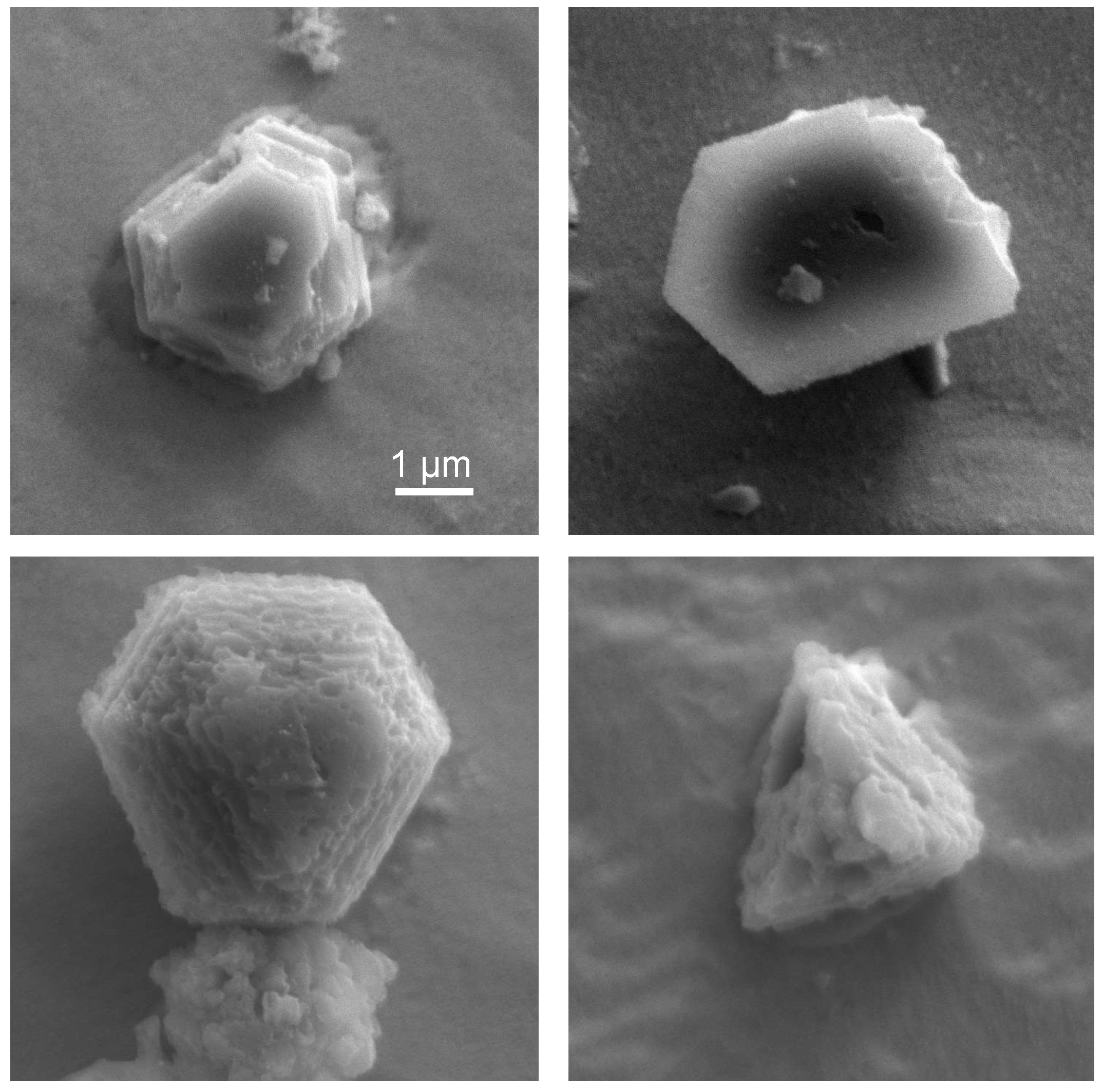
2.1. Presolar SiC Grains from Low-Mass C-Rich AGB Stars

AGB stars experience strong stellar winds and, thus, significant mass losses from the surface (10⁻⁸–10⁻⁵ M_⊙/year) (see [25] for a review). As hot gas is lost from the stellar surface and cools down, various dust components start to condense out of the gas, when the temperature drops below ~2500 K and the SiC dust starts to condense at a temperature below 2000 K [26]. AGB stellar models predict that stars with initial masses between ~1.5 to ~3.5 M_⊙ can eventually become C-rich in the envelope during the AGB phase, as during third dredge-up (TDU) events the bottom of the convective envelope penetrates into the underlying He-intershell and brings newly synthesized materials, including the He-burning product ¹²C and s-process products, to the surface. SiC dust has been observed to be present in the circumstellar envelopes of C-rich AGB stars, according to a solid-state emission band at ~11.3 μm [27,28]. AGB dust grains and their gas are lost from the surface, enter the interstellar medium (ISM), and become ISM components. Due to compression, a molecular cloud forms in a dense ISM region, and, later, stars such as the Sun form as parts of the molecular cloud collapse. Thus, the solar system incorporated stardust grains formed in the stellar winds of ancient stars that died before the formation of the solar system.

In extraterrestrial materials from small solar system bodies such as primitive asteroids (i.e., asteroids that have never experienced any significant heating since their formation), dust grains from stars that died before the solar system formation (see Figure 1 for examples) are preserved and identified by their exotic isotopic compositions, reflecting the compositions of their parent stars (see [29,30] for reviews). As these stardust grains formed before the solar system formation, they are known as presolar grains. Various presolar phases from multiple stellar sources have been identified in primitive extraterrestrial materials, reflecting diverse physicochemical condensation environments among stars. Regarding SiC, ancient AGB stars are inferred to be the dominant stellar source with small contributions from core-collapse Type II supernovae [31,32], J-type carbon stars [33], and maybe born-again AGB stars [33,34] and novae [35,36,37].

Presolar SiC grains from AGB stars include mainstream (MS, ~85–90%), Y (~1–3%), and Z (~1–3%) grains, which are classified based on C and Si isotope ratios (Figure 2). MS grains are estimated to have come from AGB stars with initial masses of ~1.5 to ~3.5 M_⊙, mainly because stellar models predict that such stars can become C-rich in the envelope during the AGB phase so that SiC can form in their stellar winds [8,9,10]. The initial metallicities of the parent stars of MS grains are more ambiguous. Given that MS grains mostly have higher-than-solar ²⁹Si/²⁸Si and ³⁰Si/²⁸Si ratios (Figure 2) and that both isotope ratios are expected to increase with increasing metallicity during Galactic chemical evolution (GCE) [39], it implies that MS grains came dominantly from higher-than-solar metallicity AGB stars. Chemical heterogeneities in the Galaxy, i.e., heterogenous GCE, however, could have blurred a simple, positive correlation between the Si isotope ratios and metallicity expected from homogenous GCE [40,41], in which case the Si isotope ratios of MS grains cannot be used to directly infer the initial metallicities of their parent stars. The current consensus in the community is that MS grains came from low-mass (~1.5 to ~3.5 M_⊙), close-to-solar metallicity (>0.5–2.0 Z_⊙) AGB stars [41,42,43,44]. For a long time, types Y and Z grains were thought to have come from lower-metallicity (e.g., 0.3–0.5 Z_⊙) AGB stars than MS grains based on light element isotope ratios, i.e., C, Si, and Ti isotope ratios [45,46]. Recent studies of heavy element isotopic compositions of Y and Z grains result in a conundrum regarding the stellar origins of Y and Z grains: while the higher ⁸⁸Sr/⁸⁷Sr and ¹³⁸Ba/¹³⁶Ba ratios observed in Y and Z grains (compared to MS grains) support the lower-metallicity stellar origins of the two rare types [47], Y and Z grains exhibit Mo isotopic compositions indistinguishable from MS grains, in contrast to varying Mo isotopic patterns predicted by stellar nucleosynthesis models for AGB stars with varying stellar metallicities [48]. Moreover, recent statistical investigations based on natural-clustering-analysis techniques suggest that the classifications of MS, Y, and Z grains are quite arbitrary and are not statistically significant [49,50]. Thus, the stellar origins of Y and Z grains remain ambiguous. Finally, the wide range of ¹⁴N/¹⁵N ratios observed in types MS, Y, and Z grains result mainly from contamination with terrestrial and asteroidal materials [51]. The intrinsic N isotopic compositions of AGB dust grains are characterized by large ¹⁴N excesses compared to the solar composition [51]. It remains a question whether “uncontaminated” MS, Y, and Z grains have different ¹⁴N/¹⁵N ratios [52].

2.2. In Situ Isotope Analysis of Presolar SiC Grains

2.2.1. NanoSIMS and Isotope Analyses of Light Elements

Nanoscale secondary ion mass spectrometry (NanoSIMS) is one of the primary tools for the in situ analysis of presolar grains, especially for light element isotope analyses [54]. Current Cameca NanoSIMS 50/50L instruments are equipped with two ion sources, Cs⁺ and O⁻, thus allowing the analysis of both electronegative, e.g., C⁻, and electropositive, e.g., Ti⁺, elements. The recent invention of a Hyperion radio-frequency ion source allows producing an O⁻ beam of reduced size, thus enabling isotope imaging of both electronegative and electropositive elements at comparable spatial resolutions (on the order of ~100 nm at a few pA). Recent studies [51,55,56,57] have shown that such high-resolution imaging is critical for excluding contamination from grain rims and adjacent grains, thus enabling a better determination of the intrinsic isotopic signatures of their ancient parent stars. Depending on the instrument model, a Cameca NanoSIMS instrument is equipped with either five (NanoSIMS 50) or seven (NanoSIMS 50L) detectors, allowing simultaneous detection of five or seven ion species, respectively. In SIMS, ions of different masses are separated using a combination of an electrostatic analyzer and a magnetic analyzer. For presolar SiC, isotopes of elements such as C, N, Si, S, Mg-Al, Ca-Ti, and Ti-V are routinely measured using NanoSIMS.

2.2.2. RIMS and Isotope Analyses of Heavy Elements

Isotope analyses of heavy elements face two main challenges, low concentration and isobaric interference. For instance, the solar abundance of Ba is ~200,000 times lower than that of Mg [58], and the analysis of Ba isotopes may suffer from isobaric interferences at masses 134 u (¹³⁴Ba with ¹³⁴Xe), 136 u (¹³⁶Ba with ¹³⁶Xe), and 138 u (¹³⁸Ba with ¹³⁸La). Assuming that the Ba concentration in presolar SiC is 10 ppm [59], it translates to ~10⁵ Ba atoms within a 1 μm grain, distributed over seven isotopes. Thus, heavy element isotope analysis of microscopic presolar grains requires the use of a mass spectrometric technique with both high efficiency and selectivity, which points to resonance ionization mass spectrometry (RIMS) thanks to its resonant ionization capability. In contrast to SIMS, RIMS is a type of time-of-flight (ToF) mass spectrometry and targets neutral atoms instead of secondary ions released from a sample. To ionize isotopes of an element of interest in the cloud of released neutrals, RIMS shines post-ionization lasers onto the cloud with their wavelengths tuned to match the atomic structure of the element of interest. As resonant ionization is more efficient by orders of magnitude than nonresonant ionization, atoms of the element of interest are efficiently ionized while potential isobaric interferences are greatly suppressed. So far, RIMS instruments have mainly utilized ultraviolet laser beams to desorb atoms from presolar SiC, and the desorption laser beams are 1 to a few μm in size. RIMS analysis is conducted in spot mode, and imaging analysis is not yet available. For presolar SiC, isotopes of Ti, Fe, Ni, Sr, Zr, Mo, Ru, Ba, and Nd [34,60,61,62,63,64,65,66,67,68] have been measured using several RIMS instruments, including CHARISMA, CHILI, and LION [60,69,70]. In principle, the combination of the NanoSIMS and RIMS instruments allows analyzing isotopes of most elements (except for noble gases) in the periodic table in μm-sized presolar grains.

3. Isotope versus Element Abundances

We first briefly describe the details of the s-process as laid out in the seminal papers of [1,2]. For the s-process nucleosynthesis, we have

$$\frac{d{N}^i}{dt}=-n_n{<{\sigma }^{i}v>}^i{N}^i+n_n{<{\sigma }^{i-1}v>}^{i-1}{N}^{i-1}$$

(1)

in which Nⁱ denotes the s-process abundance of a nuclide with mass i, n_n the neutron density, σⁱ the (n,γ) cross section of the nuclide i, and $v$ the relative neutron velocity.

Then we define two terms, neutron exposure $\tau$ [71]—an evolutionary parameter for the s-process—and Maxwellian-averaged neutron-capture cross-section ${\sigma }_{MACS}^i$ as follows,

$$\tau ={{\displaystyle \int }}^{ }{n}_n{v}_{th}dt$$

(2)

$${\sigma }_{MACS}^i=\frac{<{\sigma }^{i}v>}{v_{th}} ,$$

(3)

in which $v_{th}$ is the thermal velocity.

By substituting dt and ${\sigma }_{MACS}^i$ in Equation (1) with their expressions in Equations (2) and (3), respectively, we obtain

$$\frac{d{N}^i}{d\tau }=-{\sigma }_{MACS}^i{N}^i+{\sigma }_{MACS}^{i-1}{N}^{i-1}$$

(4)

Thus, if the s-process achieves a steady state, $\frac{d{N}^i}{d\tau }$ becomes zero so that we obtain

$${\sigma }_{MACS}^i{N}^i={\sigma }_{MACS}^{i-1}{N}^{i-1}$$

(5)

Equation (5) explains the observation that in regions between nuclei with magic numbers of neutrons, the ${\sigma }_{MACS}^i{N}^i$ product for the solar system s-process isotopes remains approximately constant (see Figure 2 of [13]). The s-process can approximately reach a steady state in this case because it occurs on a long timescale due to slow neutron-capture rates at low neutron densities (10⁷–10⁸ cm⁻³). However, for magic nuclei, since the s-process cannot achieve a steady state due to their small neutron-capture cross sections, $\frac{d{N}^i}{d\tau } \ne 0$. Thus, according to Equation (1), the s-process production of magic nuclei depends on neutron density and, thus, on the distribution of the major neutron source ¹³C (i.e., varying ¹³C density with stellar radius) in the He-intershell (see examples in Section 4.2). The study of [72] showed that the classical approach based on an exponential distribution of neutron exposures, which was first introduced by [71,73], overproduces the solar abundance of ¹⁴²Nd (a magic nuclide), which, however, is well reproduced by AGB stellar models by adopting the same set of nuclear reaction rates. Thus, the s-process productions of magic nuclei have complex dependences on neutron density and need to be investigated in detail by AGB stellar nucleosynthesis models, which couple stellar models with a full nuclear reaction network to calculate s-process yields as a function of time (e.g., [9]) and, thus, differ from the classical approach that adopts a steady s-process flow [71,73].

Such bottleneck effects at magic nuclei along the s-process path, resulting from their stable nuclear structures, explain the fact that the solar system pattern is characterized by three s-process peaks at ⁸⁸Sr (N_n = 50, in which N_n is the number of neutrons), ¹³⁸Ba (N_n = 82), and ²⁰⁸Pb (N_n = 126, doubly magic with the number of protons equal to 82). The three magic nuclei ⁸⁸Sr, ¹³⁸Ba, and ²⁰⁸Pb act as the most important bottlenecks along the s-process path, resulting in accumulation of neutrons at these mass regions to boost their own s-process productions. [hs/ls] is defined as the ratio of heavy s-elements (e.g., Ba) at the second s-process peak to light s-elements (e.g., Sr) at the first s-process peak observed in a star, which is normalized to the respective solar ratio and in logarithmic scale, and [Pb/Fe] is similar to [hs/ls] but for the ratio of Pb to Fe elemental abundance. Because of the accumulation of neutrons and nonequilibrium effects at the three bottlenecks, [hs/ls] and [Pb/Fe] are often used for comparing stellar observations with AGB model calculations to constrain the s-process neutron flux [74]. Physical models for partially mixing H into the He-intershell based on different mechanisms all contain free parameters, which can be tuned to result in varying degrees of partial mixing of H and, thus varying neutron fluxes. In turn, AGB models by considering most of the proposed mechanisms2 have been shown to be capable of reproducing existing stellar observations [9,10,24,44,75,76], which, thus, cannot distinguish between the various mechanisms. Since the s-process nucleosynthesis operates at the level of isotopes instead of elements, [hs/ls] and [Pb/Fe] are, thus, degenerate information for investigating the s-process. It is desirable to obtain the ratios of ⁸⁸Sr/⁸⁶Sr and ¹³⁸Ba/¹³⁶Ba, in which the denominator isotopes are both pure s-process isotopes and follow Equation (5), to investigate the problem of ¹³C formation. The ratio of ²⁰⁸Pb/²⁰⁴Pb in presolar grains may be complicated by the radiogenic decay of ²³²Th to ²⁰⁸Pb with a half-lifetime of 14 Ga. Based on postprocessing Torino AGB stellar models, the study of [62] showed that the s-process production of ⁸⁸Sr/⁸⁶Sr and ¹³⁸Ba/¹³⁶Ba ratios depends strongly on the detailed distribution of ¹³C in the He-intershell and that the Sr and Ba isotope ratios of MS grains could only be explained by AGB models that adopted large ¹³C pockets with low ¹³C densities (see Figure 9 of [62]).

Isotope ratios of certain heavy elements have been determined for a few metal-poor stars, thanks to large line-broadening effects caused by the hyperfine substructures of their odd isotopes (see [77] for a review). In Figure 3, we compare the high-resolution spectrographic measurement [78] of Ba isotopes for a metal-poor star with the Ba isotopic composition of a randomly selected grain among MS grains analyzed [34,62,64,79,80], which highlights the superb precision of presolar grain measurements. Panels (a–c) of Figure 3 illustrate that compared to ¹³⁷Ba/¹³⁶Ba, the ratios of ¹³⁴Ba/¹³⁶Ba and ¹³⁸Ba/¹³⁶Ba are more variable among SiC grains because the s-process productions of ¹³⁴Ba and ¹³⁸Ba are affected by a branch point at ¹³⁴Cs (t_1/2 = 2.1 years) and the distribution of the major neutron source ¹³C in the He-intershell, respectively [34]. In turn, it means that we can provide constraints on different modeling inputs using these Ba isotope ratios. In detail, ¹³⁴Ba/¹³⁶Ba is sensitive to the maximum stellar temperature in the He-intershell in AGB stars, mainly because the stellar β⁻ decay rate of ¹³⁴Cs has a strong temperature dependence [81]; the AGB model predictions for the ¹³⁷Ba/¹³⁶Ba and ¹³⁵Ba/¹³⁶Ba data in panel (b) of Figure 3 are controlled by the adopted σ¹³⁵_MACS and σ¹³⁷_MACS values in AGB models (see Equation (5)), and ¹³⁸Ba/¹³⁶Ba can be used to probe the distribution of ¹³C in the He-intershell [34,42,62]. In summary, presolar grain measurements provide a unique opportunity to determine isotope abundances in stars, at a precision that far exceeds the current capability of spectrographic measurements using state-of-the-art telescopes (see Figure 3d). In turn, presolar grain isotope data can be used to provide the most precise and detailed constraints on modeling inputs.

4. Constraints on AGB Stellar Models from Presolar Grain Data

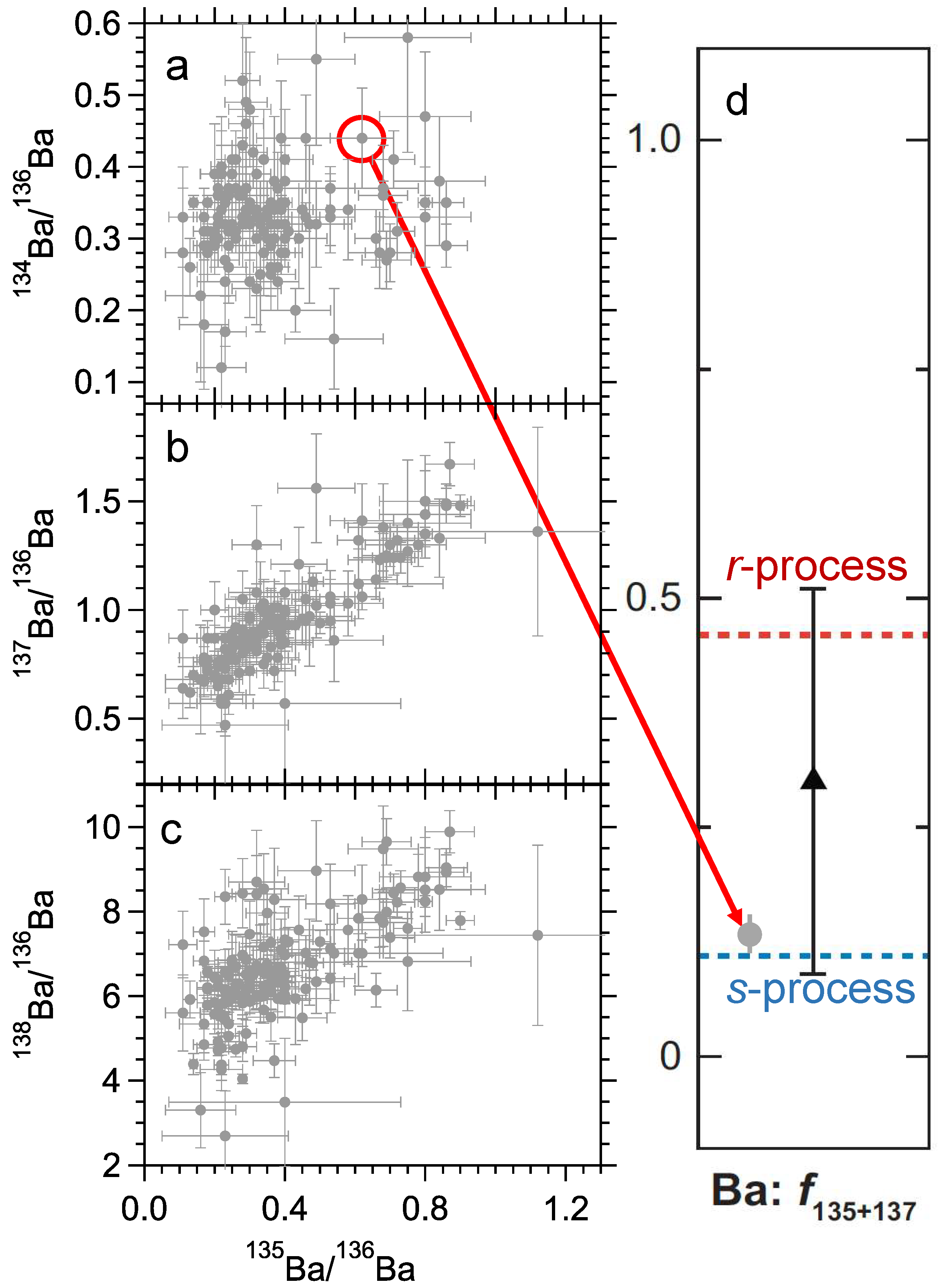
4.1. Minor Neutron Source ²²Ne and Branch Points

Based on solar system s-process isotope abundances and AGB stellar models, the study of [12] tested the sensitives of various s-process branch points to the two neutron sources and concluded that the short, high-density neutron exposure produced by the ²²Ne(α,n)²⁵Mg reaction has major effects on controlling branch points along the s-process path. The reaction rate of the minor neutron source ²²Ne(α,n)²⁵Mg depends strongly on temperature and increases by 18 orders of magnitude from 1 × 10⁸ K, typical He-intershell temperature during the interpulse phase in low-mass AGB stars, to 3 × 10⁸ K, the typical temperature in the He-intershell during TPs [82]. As the ²²Ne(α,n)²⁵Mg reaction rate becomes increasingly higher than the rate of ²²Ne(α,γ)²⁶Mg at T ⪆ 3 × 10⁸ K, the minor neutron source ²²Ne(α,n)²⁵Mg becomes partially activated during TPs, providing neutrons of high density to affect branch points along the s-process [11,12,83]. While s-process branch points are all affected by the short, high-density neutron exposure to varying degrees, certain branch points show more complex dependences on stellar temperature and/or electron density (see [12] for details). Below, we showcase one interesting branch point at ¹³⁴Cs, which has a strong dependence on stellar temperature.

Cesium-134 (t_1/2 = 2 years) acts as a branch point along the s-process, and its β⁻ decay rate increases by a factor of ~65, as the temperature increases from 1 × 10⁸ to 3 × 10⁸ K [81]. Uncertainties in AGB model predictions for δ¹³⁴Ba are mainly controlled by uncertainties in the β⁻ decay rate of ¹³⁴Cs [34]. Figure 4 reveals a poor match between MS and unclassified (MS grain data hereafter) grain data and the default magnetic FRUITY (Full-network Repository of Updated Isotopic Tables & Yields) AGB models3 (filled symbols), which are barely varied compared to the corresponding nonmagnetic FRUITY models (see Figure 6 of [34]). The similar δ¹³⁴Ba values predicted by the magnetic and nonmagnetic FRUITY AGB models, which adopted different ¹³C pockets (see Section 4.2 for details), demonstrate that AGB model predictions for δ¹³⁴Ba are unaffected by the adopted ¹³C pocket and instead controlled by the activation strength of the ¹³⁴Cs branch point.

As discussed in [34], model predictions for δ¹³⁴Ba can be lowered if (i) the efficiency of the minor neutron source ²²Ne(α,n)²⁵Mg is increased, e.g., enhanced ²²Ne(α,n)²⁵Mg reaction rate and/or (ii) ¹³⁴Cs β⁻ decay rate is reduced. Recent experimental and theoretical studies are in favor of possibility (ii), because significantly lowered ²²Ne(α,n)²⁵Mg rate, which was adopted in the magnetic FRUITY models in Figure 4, is inferred at relevant low-mass AGB temperatures [87,92] and ¹³⁴Cs β⁻ decay rate is estimated to be significantly lower [89,93,94] than that recommended by [81]. The study of [93] showed that adopting their newly calculated ¹³⁴Cs β⁻ decay rate reduces Monash AGB model predictions for δ¹³⁴Ba by ~300‰. The reduced ¹³⁴Cs β⁻ decay rate of [93] also allows Monash AGB model predictions for δ¹³⁴Ba to reach as low as –200‰, thus explaining several MS grains with negative δ¹³⁴Ba values. These negative δ¹³⁴Ba values were shown to be a problem for AGB models with the old ¹³⁴Cs β⁻ decay rate, based on which the grains were speculated to have come from born-again AGB stars that experienced an intermediate neutron-capture process [34]. The new ¹³⁴Cs β⁻ decay rate thus provides a better explanation to the δ¹³⁴Ba values of MS grains. However, when we adopted the new ¹³⁴Cs and ¹³⁵Cs β⁻ decay rates from [89] (Set 1 rates in Figure 4), our 2 M_⊙, Z_⊙ magnetic FRUITY-model prediction for δ¹³⁴Ba dropped by only ~100‰, likely because the maximum stellar temperatures during TPs are lower in FRUITY stellar models than in Monash stellar models. It is possible to reach the center of the grain distribution if the FRUITY model also adopts the upper limits for both the ¹³⁴Cs(n,γ)¹³⁵Cs and ¹³⁴Ba(n,γ)¹³⁵Ba reaction rates from [90] and [91], respectively (Set 2 rates in Figure 4). It remains a question whether MS grains with large negative δ¹³⁴Ba values came from low-mass AGB stars or born-again AGB stars.

Other important branch points that affect the isotope abundances of heavy elements that have been measured in MS SiC grains, include ⁸⁵Kr (isomeric state, t_1/2 = 4.5 h; ground state, t_1/2 = 11 years), ⁹⁴Nb (t_1/2 = 2.0 × 10⁴ years), ⁹⁵Zr (t_1/2 = 64 days), ¹³⁵Cs (t_1/2 = 2.3 × 10⁶ years), and ¹³⁷Cs (t_1/2 = 30 years). Future RIMS measurements of rare-earth-element isotope ratios in MS grains [63] will likely provide better constraints on the maximum stellar temperature in the He-intershell during TPs, as there are many strong branch points along the s-process in this mass region, e.g., ¹⁴⁷Pm (t_1/2 = 2.6 years), ¹⁵¹Sm (t_1/2 = 90 years), and ¹⁵²Eu (t_1/2 = 13.5 years).

4.2. Formation of Major Neutron Source ¹³C

Because of bottleneck effects, MS grain data for ⁸⁸Sr/⁸⁶Sr and ¹³⁸Ba/¹³⁶Ba can be used to probe the distribution of ¹³C formed in the He-intershell (see discussion in Section 3). In Figure 5, we compare MS grain data with two sets of FRUITY models for 2 M_⊙ AGB stars with 0.36–1.20 Z_⊙, which consider different mechanisms for the ¹³C formation.

Convective overshooting can lead to a partial mixing of H into the He-intershell, as convective eddies in the envelope cross the bottom of the envelope and move downward into the He-intershell. For the nonmagnetic FRUITY models in Figure 5a, convective overshooting is considered to be primarily responsible for driving the partial mixing of H into the He-intershell [9,18], and the mixing velocity is estimated as $v\left(r\right)=v_{cb}{e}^{-\frac{\delta r}{\beta H_P}}$, where $v\left(r\right)$ is the velocity of envelope material injected into the He-intershell at distance r from the border, $v_{cb}$ the velocity at the convective border, δr the distance from the border, H_P the pressure scale height at the border, and β a free parameter. The β value is set to 0.1 for the nonmagnetic models in Figure 5a to maximize the efficiency of ¹³C formation [9].

For the magnetic FRUITY models in Figure 5b, magnetic buoyancy is the mechanism that drives partial mixing of H downward because of mass conservation, since uprising magnetic flux tubes carry mass flows to move upward [23,24,76,94,95]. The mixing velocity in this case is estimated as $v\left(r\right)=u_p{\left(\frac{r_p}{r}\right)}^{k+2}$, where u_p is proportionally related to the initial velocity of magnetic flux tubes and, thus, the magnetic field strength B_φ, r_p is the distance from the stellar center, and k describes the dependence of density ρ on the stellar radius, ρ ∝ r_p^k.

It was shown in [76] that the two abovementioned mechanisms lead to different ¹³C distributions in the He-intershell: while in the overshooting scenario the amount of ¹³C drops quickly to zero in the He-intershell because the overshooting velocity follows an exponential decaying profile, magnetic buoyancy can lead to the formation of ¹³C in deeper He-intershell with a more flattened ¹³C distribution, given the power-law dependence of the mixing velocity (see Figure 3 of [76] for comparison). The study of [76] further showed that while varying the β value could not reach a good match between MS grain data and low-mass FRUITY AGB models, it provides a satisfying match to the MS grain data by adopting B_φ = 5 ×10⁴ G and u_p = 5 ×10⁻⁵ cm/s in 2 M_⊙ magnetic FRUITY AGB models (Figure 5b).

In addition to the ¹³C distribution in the He-intershell, AGB model predictions for δ⁸⁸Sr are also affected by the branch point at ⁸⁵Kr along the s-process. However, we noticed negligible changes in the model predictions for δ⁸⁸Sr when we increased the ²²Ne(α,n)²⁵Mg reaction rate by a factor of 2–3 in the magnetic FRUITY models, thus pointing to a negligible effect of the ⁸⁵Kr branch point (and, thus, the minor neutron source) on FRUITY AGB model predictions for δ⁸⁸Sr. The differences in the predicted δ⁸⁸Sr and δ¹³⁸Ba values between the magnetic and nonmagnetic FRUITY models (which adopted slightly different ²²Ne(α,n)²⁵Mg and ²²Ne(α,γ)²⁶Mg reaction rates) in Figure 5, therefore, result primarily from the different ¹³C pockets formed in the two sets of models.

Although it is tempting to conclude based on the data-model comparisons in Figure 5 that magnetic buoyancy is the mechanism primarily responsible for the ¹³C formation, more efforts are needed in different subfields to corroborate the results of Figure 5.

(1)

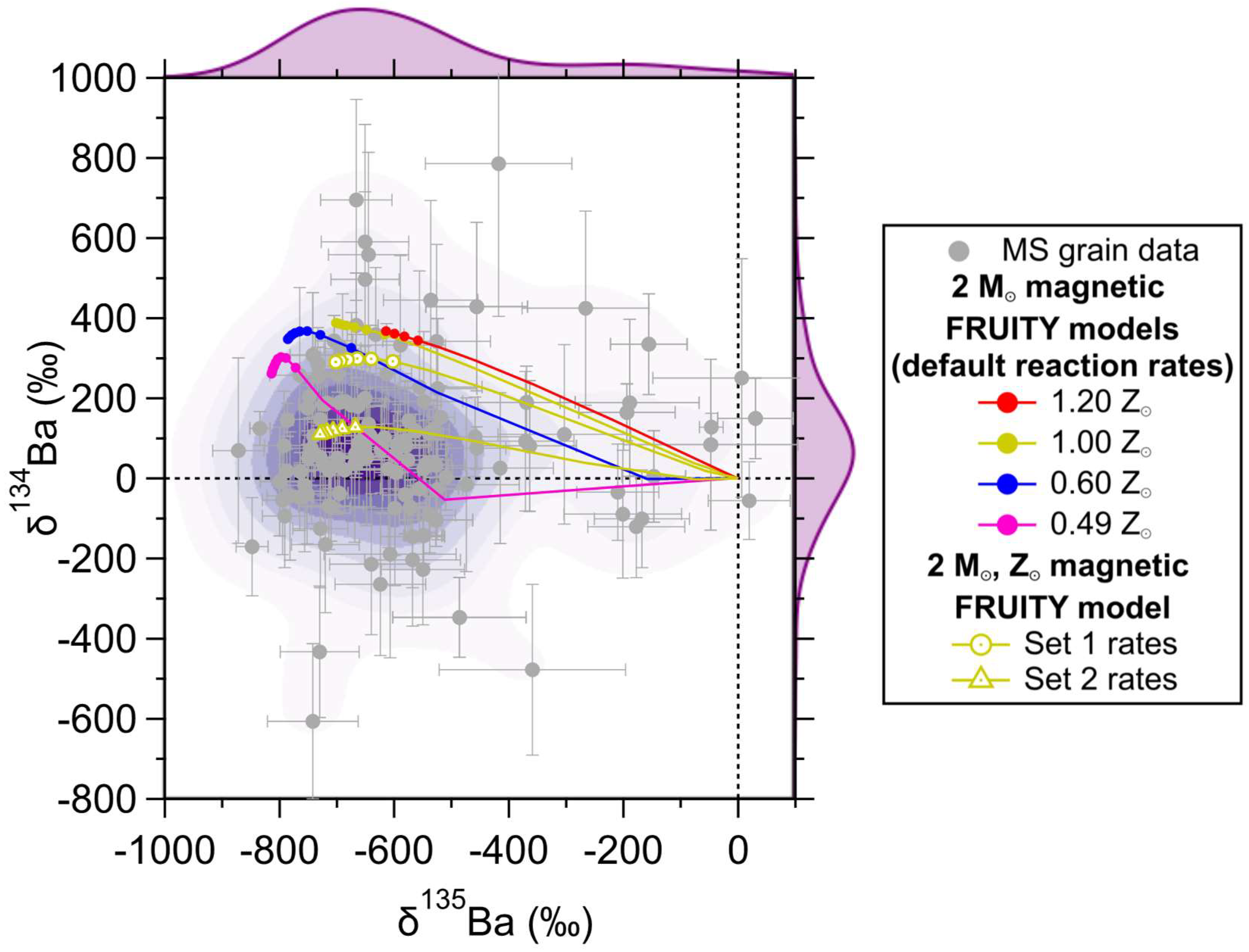
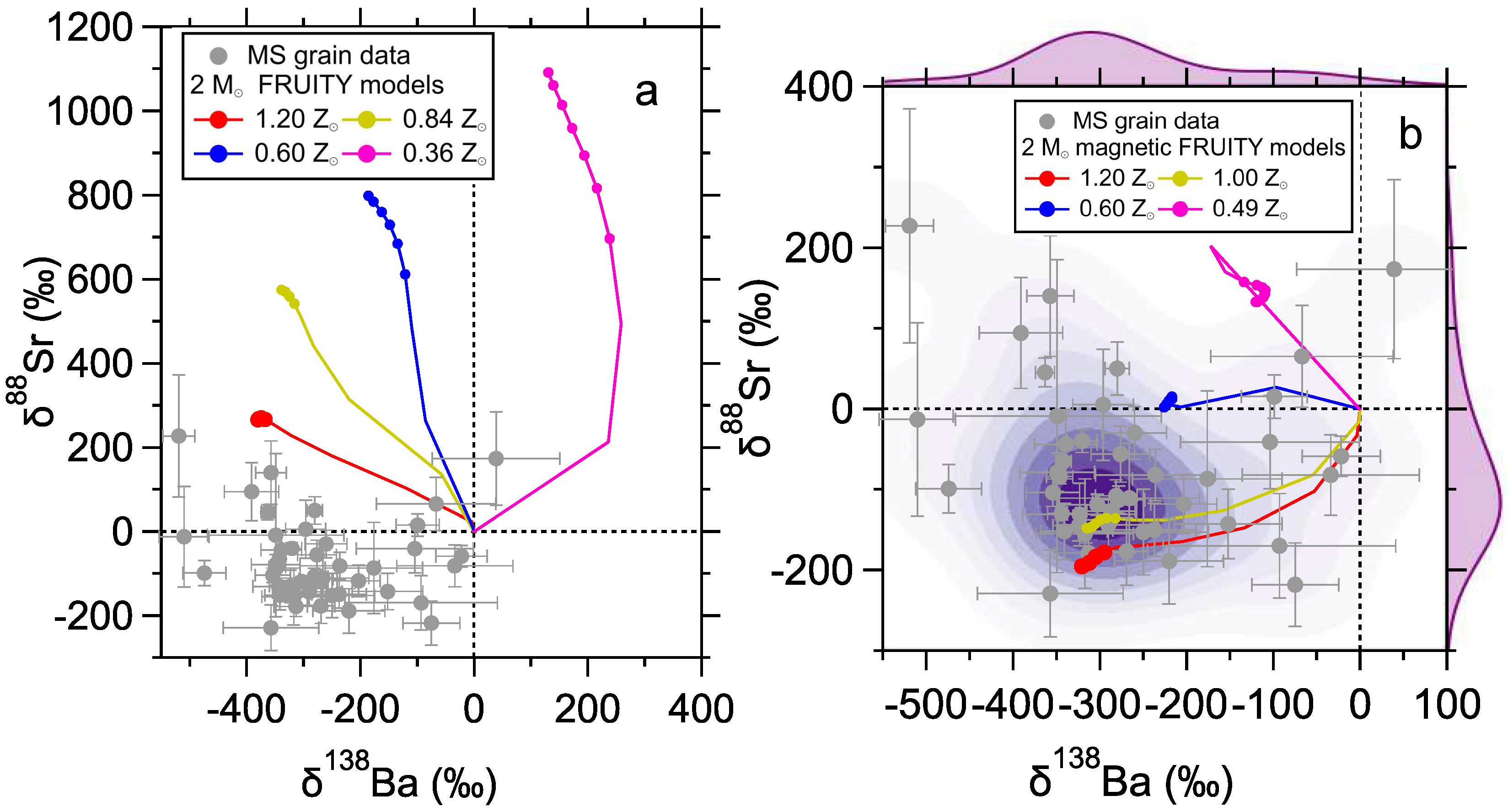
Presolar Grains: Correlated Sr and Ba isotope analyses of more MS grains using the new generation of RIMS instruments [60,69] are needed to better quantify the MS grain distribution. The study of [42] showed that compared to the exponential distribution by overshooting, the deeper, more flattened ¹³C distribution resulting from magnetic buoyancy reduces the sensitives of δ⁸⁸Sr and δ¹³⁸Ba to the H mixing depth. Thus, we need more MS grain data for δ⁸⁸Sr and δ¹³⁸Ba to determine the data variability, which will help to assess the primary mechanism responsible for the ¹³C formation. A better understanding of the MS grain data distribution will also allow for a quantitative assessment of the quality of data-model comparisons, which, so far, have been conducted mainly in a qualitative way.

(2)

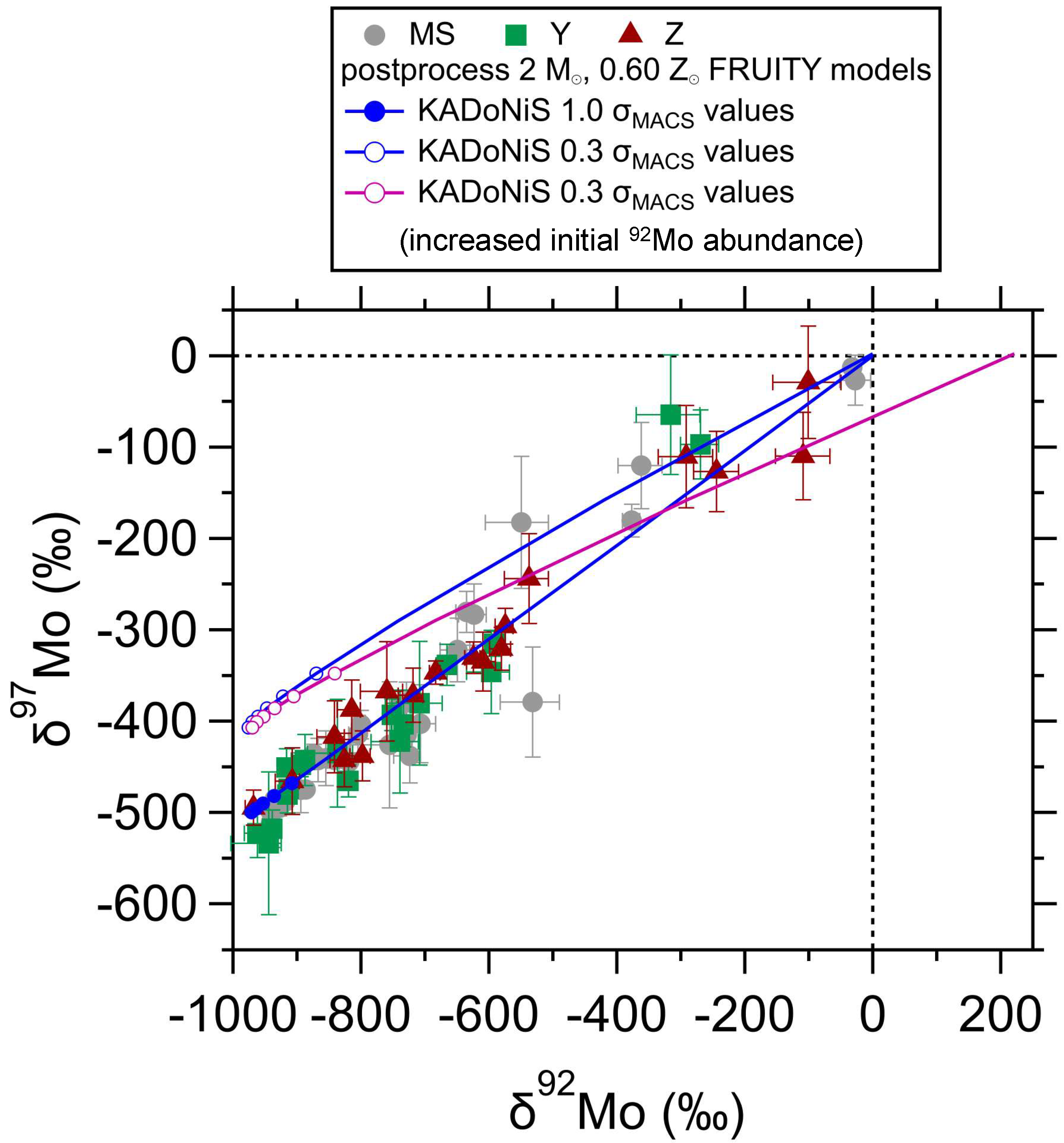
Nuclear Experiments: AGB model predictions for δ⁸⁸Sr and δ¹³⁸Ba rely directly on the σ_MACS values of ⁸⁶Sr, ⁸⁸Sr, ¹³⁶Ba, and ¹³⁸Ba. Given the small ⁸⁸Sr and ¹³⁸Ba σ_MACS values, current AGB model uncertainties in δ⁸⁸Sr and δ¹³⁸Ba are controlled by uncertainties in the ⁸⁶Sr (±10%) and ¹³⁶Ba (±3%) σ_MACS values [96], respectively, which correspond to ~200‰ and ~50‰ uncertainties in low-mass AGB model predictions for δ⁸⁸Sr and δ¹³⁸Ba, respectively [34,62]. As the full range of δ⁸⁸Sr values observed among MS grains is only ~400‰ (Figure 5), new measurements of ⁸⁶Sr σ_MACS values are urgently needed to reduce the model uncertainty for δ⁸⁸Sr.

(3)

Stellar Modeling: Implementation of magnetic buoyancy effects in other stellar codes such as NuGrid [10] is needed to test whether the effect of magnetic buoyancy on the s-process production is stellar code dependent. It was shown in [43,44] that 2 Z_⊙ Monash models that adopt an exponentially decayed mixing profile also provide a good match to the heavy element isotope data of MS grains. It remains to see whether adoption of the formula for magnetic buoyancy can further improve the data-model agreements for 2 Z_⊙ and other lower-metallicity Monash models, given uncertainties in the initial metallicities of the grains’ parent stars. Finally, we note that the good grain-model agreement in Figure 5b mainly points out that the MS grain data are in favor of a deep, flattened ¹³C distribution in the He-intershell. More modeling efforts are needed to investigate whether magnetic buoyancy is the sole mechanism that could lead to such a distribution.

4.3. Constraints on Neutron-Capture Cross Sections

Besides isotopes that are affected by branching effects and magic nuclei, the relative s-process productions of other nuclei in the heavy mass region are dominantly controlled by the adopted neutron-capture cross sections according to Equation (5). Thus, the abundances of such nuclei can be measured in AGB dust grains, for comparison with AGB models to examine the adopted σ_MACS values. Such an example is shown in Figure 6, for illustration. Among Mo isotopes, ⁹²Mo and ⁹⁴Mo are p-process isotopes with a small s-process contribution to ⁹⁴Mo [76]. The p-process is an umbrella term for multiple nucleosynthesis processes that can produce proton-rich nuclei in the heavy mass region. So far, it has been proposed that the p-process includes gamma process in Type II core-collapse supernovae and Type Ia supernovae and neutrino-p process in Type II core-collapse supernovae (see [97] and references therein).

It was shown that AGB model predictions for Mo isotopes are unaffected by the two neutron sources and are controlled by the adopted Mo σ_MACS values [98]. According to Equation (5), the ratio of ⁹⁷Mo/⁹⁶Mo (i.e., N⁹⁷/N⁹⁶) is approximately related to σ⁹⁶_MACS/σ⁹⁷_MACS. The p-process isotope ⁹²Mo is off the s-process path and is, therefore, destroyed by neutron capture during the s-process in AGB stars. As a result, the final ⁹²Mo abundance in the AGB envelope is dominantly controlled by the initially adopted ⁹²Mo abundance, which is poorly known due to uncertainties in modeling the GCE of p-process nuclei [97]. AGB models in Figure 6 predict extremely low ⁹²Mo/⁹⁶Mo ratios for the final envelope composition because the pure s-process isotope ⁹⁶Mo is significantly overproduced, by a factor of ~40 in the envelope, compared to its initial abundance. A comparison of the two KADoNiS4 0.3 AGB models with different initial ⁹²Mo abundances in Figure 6 reveals that a 200‰ increase in the initial ⁹²Mo abundance leads to an ~80‰ increase in ⁹²Mo/⁹⁶Mo for the final envelope composition but only a 6‰ increase in δ⁹²Mo due to the nonlinearity of the delta notation when approaching −1000‰ (i.e., a negligible difference in the final envelope composition between the two KADoNiS 0.3 models). Thus, variation in the initial stellar composition cannot resolve the data-model discrepancy by adopting KADoNiS 0.3 σ_MACS values. Instead, the grain data are well reproduced by adopting the Mo isotope σ_MACS recommended by KADoNiS 1.0 [96]. Better agreements with KADoNiS 1.0 Mo σ_MACS values were also observed for the ⁹⁵Mo/⁹⁶Mo and ⁹⁸Mo/⁹⁶Mo ratios. The AGB grain data, thus, provide strong support to the new Mo σ_MACS values recommended by KADoNiS 1.0 (see [48] for more details). Other examples include ¹³⁷Ba/¹³⁶Ba versus ¹³⁵Ba/¹³⁶Ba (Figure 3b) and ^99,101,102Ru/¹⁰⁰Ru versus ¹⁰⁴Ru/¹⁰⁰Ru, which can be used to constrain the respective σ_MACS values [68].

Finally, we note that except for pure p- and r-process isotopes, other heavy element isotopes that receive major s-process contributions can be significantly overproduced by the s-process nucleosynthesis in AGB stars; as a result, their final abundances in the envelope are dominantly controlled by the s-process nucleosynthesis. Taking ⁹⁵Mo, ⁹⁶Mo, ⁹⁷Mo, and ⁹⁸Mo for example, the AGB models in Figure 6 predict that their final abundances in the envelope are increased by factors of ~20, ~40, ~25, and ~35, respectively, which means that the contributions of the initial abundances are small (<5%) in these cases. Besides, the heavy element isotopic compositions of the AGB SiC grain data all seem to suggest that their parent AGB stars had close-to-solar initial heavy element isotopic compositions (see [67] for details), although the data could alternatively imply significant asteroidal/terrestrial contamination.

5. Conclusions

Presolar grains are bona fide stellar materials. The discovery of presolar grains in primitive extraterrestrial materials allows for isotope analysis in the laboratory using modern mass spectrometric techniques at a precision that far exceeds what can be achieved by spectrographic measurements using state-of-the-art telescopes. In this short review, we summarized the sensitives of different types of heavy element isotopes and how their abundances in MS grains can be used to constrain AGB stellar parameters.

Branch points exist along the s-process path, where neutron capture competes with beta decay. For isotopes that are affected by branch points, their isotope ratios in MS grains can be used to constrain the He-intershell temperature during TPs because (i) the efficiency of the ²²Ne(α,n)²⁵Mg reaction depends strongly on the maximum temperature in the He-intershell during TPs, and (ii) the β⁻ decay rates of certain branch points are sensitive to temperature. One good example is the ratio of ¹³⁴Ba/¹³⁶Ba, though a stringent constraint on the maximum temperature is hampered by the uncertain β⁻ decay rate of ¹³⁴Cs. The reduced ¹³⁴Cs β⁻ decay rates reported by two recent independent theoretical studies, enable a better match of AGB model calculations with MS grain data. AGB model predictions for ¹³⁴Ba/¹³⁶Ba, however, still suffer from uncertainties in stellar parameters such as the maximum temperature during TPs. Thus, it remains a question whether a few MS grains with quite low ¹³⁴Ba/¹³⁶Ba ratios came from low-mass AGB stars or born-again AGB stars.

Isotopes with magic numbers of neutrons have stable nuclear structures and thus extremely small neutron-capture cross sections, resulting in accumulation of neutrons at these bottlenecks along the s-process path. We showed that the combination of ⁸⁸Sr/⁸⁶Sr and ¹³⁸Ba/¹³⁶Ba ratios of MS grains can be used to probe the ¹³C distribution in the He-intershell. Although several studies have shown that magnetic-buoyancy-induced ¹³C formation leads to better data-model agreements, it requires more grain data, more precise nuclear inputs, and more modeling efforts to corroborate this observation.

For pure s-isotopes and mixed s,r-isotopes that are unaffected by branching and bottleneck effects, their relative s-process productions are barely affected by the two neutron sources and are dominantly controlled by the respective σ_MACS values adopted in AGB models. Thus, measuring their isotope abundances in MS grains allows for examination of the currently recommended σ_MACS values. We showcased the Mo isotopic compositions of MS, Y, and Z grains, which are in favor of the σ_MACS values recommended by KADoNiS v1.0 as compared to KADoNiS v0.3. Thus, analyses of these isotope abundances in MS grains provide a novel way to scrutinize currently recommended neutron-capture cross sections at relevant AGB temperatures.

Given the multielement-isotope-analysis capabilities of both NanoSIMS and the new generation of RIMS instruments [60,69], it is promising to obtain heavy element isotope data for a larger number of MS grains (and also more Y and Z grains) and for other elements, e.g., rare-earth-elements [63], and also with better precisions in the coming years. Accompanied by the synergic efforts in the communities of nuclear physics and stellar modeling, we will likely gain more insights into the evolution and stellar nucleosynthesis of low-mass C-rich AGB stars in the near future.